Volume 2020, Issue 1 2904861

Research Article

Open Access

Efficient Boolean Keywords Search over Encrypted Cloud Data in Public Key Setting

Yu Zhang,

Yu Zhang

School of Computer and Information Technology, Xinyang Normal University, Xinyang 464000, China xynu.edu.cn

Search for more papers by this author

Wei He,

Wei He

School of Computer and Information Technology, Xinyang Normal University, Xinyang 464000, China xynu.edu.cn

Search for more papers by this author

Yin Li,

Corresponding Author

Yin Li

[email protected]

orcid.org/0000-0002-9529-8481

School of Computer and Information Technology, Xinyang Normal University, Xinyang 464000, China xynu.edu.cn

Search for more papers by this author

Yu Zhang,

Yu Zhang

School of Computer and Information Technology, Xinyang Normal University, Xinyang 464000, China xynu.edu.cn

Search for more papers by this author

Wei He,

Wei He

School of Computer and Information Technology, Xinyang Normal University, Xinyang 464000, China xynu.edu.cn

Search for more papers by this author

Yin Li,

Corresponding Author

Yin Li

[email protected]

orcid.org/0000-0002-9529-8481

School of Computer and Information Technology, Xinyang Normal University, Xinyang 464000, China xynu.edu.cn

Search for more papers by this author

First published: 26 August 2020

https://doi.org/10.1155/2020/2904861

Citations: 1

Academic Editor: Laurence T. Yang

Share a link

Email
Wechat
Bluesky

Abstract

Searchable public key encryption- (SPE-) supporting keyword search plays an important role in cloud computing for data confidentiality. The current SPE scheme mainly supports conjunctive or disjunctive keywords search which belongs to very basic query operations. In this paper, we propose an efficient and secure SPE scheme that supports Boolean keywords search, which is more advanced than the conjunctive and disjunctive keywords search. We first develop a keyword conversion method, which can change the index and Boolean keywords query into a group of vectors. Then, through applying a technique so-called dual pairing vector space to encrypt the obtained vectors, we propose a concrete scheme proven to be secure under chosen keyword attack. Finally, we put forward a detailed theoretical and experimental analysis to demonstrate the efficiency of our scheme.

1. Introduction

Currently, thousands of information retrieval systems, such as e-mail systems, database management systems, and document management systems, are operating successfully in both the government and private sectors. As the data stored in these systems increase rapidly, more and more people want to migrate these data to cloud. To keep data privacy, users often encrypt these data before uploading them to the cloud. Since the encrypted data are difficult to retrieve, how to execute keyword search over encrypted data has attracted tremendous research attention over the past few years. Among these research studies, the searchable encryption (SE) is one of the most important techniques to address the issue of searching over encrypted data [1, 2].

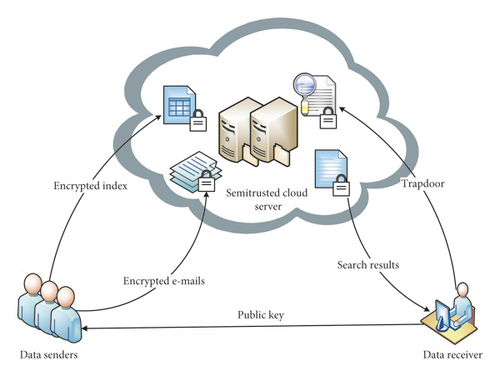
The SE enables data users to retrieve the encrypted data of interest from a cloud server without decrypting the data. Commonly, SE is divided into two categories: one is searchable symmetric key encryption (SSE); the other is searchable public key encryption (SPE). During recent years, many SSE schemes have been proposed to support keyword search over encrypted data [3–6]. The key of SSE for encrypting data is the same as the key for generating search trapdoor. By contrast, the key of SPE for encrypting data is open to public, while the key for generating search trapdoor is only given to the authorized data receivers. Compared with SSE, SPE is more suitable for the situation in which there are many data senders and only a few data receivers, e.g., e-mail system [7], personal health record [8], and wireless sensor network [9]. As illustrated in Figure 1, in the scenario of e-mail system, the security requirements can be summarized as follows: (1) any data senders can generate encrypted e-mail data; (2) only data receiver can query and decrypt the encrypted e-mail data; (3) except the data receiver, none of the other entities, including the cloud server, can know the content of the encrypted e-mail data. Since security characteristics of SPE satisfy all these requirements in the above scenario, it is argued that SPE is very suitable for this application. Therefore, how to construct an efficient and secure SPE scheme supporting keyword search is always a hotspot in the field of SE.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

An example of the scenario of SPE: e-mail system.

1.1. Motivation

The very first SPE scheme supporting keyword search was introduced by Boneh et al., and it is so-called public key with keyword search (PEKS) [7]. However, their work only supports a single keyword search. In order to support more expressive query, many SPE schemes [10–12, 16] were proposed to realize advanced search, for example, conjunctive and disjunctive keywords search. In practice, most of the applications need more advanced keywords search function than the conjunctive and disjunctive keywords search. More precisely, many applications require Boolean keywords search. For example, in an e-mail system, users want to make a query like (A∧B)∨(C∧D), where A, B, C, and D are keywords. A naive thought is that a Boolean query can be obtained by remoulding a PECK or PEDK scheme, i.e., by combining the query results of conjunctive or disjunctive keywords search. However, we argue this simple method has many drawbacks. To better illustrate our motivation, based on a PEDK or PECK scheme, we construct a naive scheme supporting the Boolean keywords search like q₁∨q₂∧q₃, where q₁, q₂, and q₃ are three keywords. We then briefly review the simple solution and explain why it is unsatisfactory.

The approach is that we first execute the query q₁ and the query q₂∧q₃ by making use of the PECK scheme, respectively, and obtain the union of the results of q₁ query and q₂∧q₃ query. However, this method will leak the trapdoors of q₁ and q₂∧q₃. By utilizing the trapdoors, the search results of q₁ and q₂∧q₃ are also leaked. Over time, the adversary may combine this information to derive the contents of user’s documents. In addition, we also can execute the query of q₁∨q₂ and q₃ by making use of the PEDK scheme, respectively, and then obtain the intersection of the results of the query q₁∨q₂ and the query q₃. However, this method carries the same drawback.

1.2. Contribution

In this paper, we seek to construct a secure and efficient SPE scheme supporting Boolean keyword search which is not based on the PECK and PEDK schemes. We define a Boolean keywords search Q as a combination of conjunctive normal form (CNF) and disjunctive normal form (DNF), denoted by Q = (CNF₁)∨(CNF₂)∨⋯∨(CNF_m), where CNF_i is defined as

. Here, q_ij is a keyword, i ∈ [1, m] and j ∈ [1, n_i]. This Boolean keywords search is more expressive than the conjunctive and disjunctive keywords search. The contributions of our work are summarized as follows:

(1)
Inspired by the keyword conversion method introduced in [17], we create a novel keyword conversion method which can transform the index keyword set and Boolean query into an attribute and a predicate vector, respectively. These vectors can efficiently realize Boolean keywords search by an inner product operation. Moreover, the vector dimension is much less than that generated by adopting the previous method.
(2)
Through elaborately applying the existing technique called dual pairing vector space (DPVS) to encrypt the attribute and predicate vectors, we propose a secure and efficient SPE scheme supporting Boolean keywords search (SPE-BKS), which can accomplish Boolean keywords search over encrypted data with a better search efficiency than the previous schemes.

Moreover, for security concern, we introduce a formal security definition for SPE-BKS and give a detailed proof to demonstrate that our scheme is secure against chosen keyword attack. To verify the efficiency of the proposed scheme, we conduct an experiment for comparing our scheme with some recent schemes over a real-world dataset (Enron Email Dataset).

1.3. Related Work

The first SPE scheme supporting keyword search was introduced by Boneh et al. [7]. They called it as public key encryption with keyword search (PEKS), which only supports a single keyword search. To support multikeyword search, Park et al. proposed an SPE scheme supporting conjunctive keyword search, which is called public key encryption with conjunctive keywords search (PECK) [10]. In their scheme, each keyword is associated with a keyword field. The mechanism of the keyword field is based on two assumptions: one is that the keywords in a keyword field must be arranged in a preset order; the other is that the same keyword never appears in two different keyword fields of the same document. However, in many applications, the keyword field will make the multikeyword search unpractical. For instance, in an e-mail system, the keyword fields usually contain “From,” “To,” and “Title.” Many e-mails may have the same keyword in different keyword fields, e.g., “From: LeBron James” and “To: James Harden.” Moreover, the keywords in the keyword field “Title” may be organized in an alphabet order. To address this issue, the subsequence work is to create a PECK scheme without keyword field. In [11], Boneh and Waters proposed a public key encryption scheme called hidden vector encryption, which can efficiently support conjunctive keywords search without keyword field. After this, some efficient PECK schemes with better performance were proposed in [12–15]. To support disjunctive keyword search over encrypted data without keyword field, Katz et al. introduced a novel encryption scheme called predicate encryption supporting inner product, which is also named as inner product encryption (IPE) [16]. Through changing the index and query into an attribute and a predicate vector, respectively, a public key encryption with disjunctive keywords search (PEDK) scheme can be built based on the IPE scheme. Considering that the previous SPE schemes cannot use one trapdoor to realize conjunctive and disjunctive keywords search simultaneously, Zhang et al. proposed two public key encryption with conjunctive and disjunctive keyword search (PECDK) schemes [17, 18], which can efficiently support conjunctive and disjunctive keyword search at the same time. In order to support expressive query over encrypted data, based on the Paillier cryptosystem with threshold decryption (PCTD) [19], Yang et al. proposed an SPE scheme supporting versatile search query patterns, such as the range, conjunctive, disjunctive, and Boolean keywords search [20]. Miao et al. presented a hybrid keyword-field search scheme that supports both keyword search and range search simultaneously [21]. In addition, their scheme also provides an efficient key management mechanism to reduce the storage cost of keys. For the issue of fuzzy keyword search, Yang et al. designed a method to segment keyword according to the position of wildcards and proposed an SPE scheme supporting wildcard keyword search by combining the segmentation method and PCTD [22]. To support keyword search over arbitrary languages, Yang et al. realized a general method which can convert a variety of languages into a uniform big integer. By utilizing this conversion method and PCTD, they can carry out an SPE scheme supporting multikeyword rank search in arbitrary language [23]. To add the access control mechanism to SE, Li et al. created an attribute-based encryption (ABE) scheme which supports not only keyword search but also update operations for users ciphertext and secret key [24]. Then, they presented an outsourced ABE scheme supporting keyword search, which can transfer operations of decryption and key issuing to the cloud server partially [25]. He et al. proposed an SPE scheme which can control user’s search permission according to an access control policy [26]. Miao et al. proposed an attribute-based keyword search scheme under a shared multiowner setting [27]. Zhang et al. proposed an SPE scheme achieving both Boolean keywords search and fine-grained search permission [28]. For the problem of tensor decomposition over encrypted data, by elaborately combining homomorphic encryption and block chain techniques, Feng et al. designed several schemes to implement different types of tensor decomposition, such as high-order Bi-Lanczos and Tucker decomposition [29–31]. To improve the efficiency of SPE, Hwang et al. created a more efficient SPE scheme, by replacing the operation of bilinear pairing with ElGamal encryption system [32]. Lu et al. proposed a certificate-less encryption supporting keyword search under a multirecipient setting [33]. In order to obtain a better efficiency, their scheme avoids using a costly operation called bilinear pairing. Considering the scenario in which devices have limited resources, two secure and efficient energy-saving platforms were proposed to protect user’s sensitive data [34, 35]. To resist the DoS attack, Li et al. gave an efficient remote user authentication and privacy-preserving scheme by adopting the technique called extended chaotic maps [36]. In order to improve search accuracy, Zhang et al. proposed an SPE scheme supporting semantic keywords search by adopting a method called “Word2vec” [37].

1.4. Organization

This paper is organized as follows. In Section 2, we give the framework of SPE-BKS and its security definition. Some basic tools are also provided in the section. In Section 3, the construction of SPE-BKS is given, and its security proof is also presented. The experimental and theoretical analysis is provided in Section 4. We conclude this paper in Section 5.

2. Preliminaries

In this section, we will give a formal definition of the framework and security model of SPE-BKS. In addition, we also briefly introduce some basic ingredients used in our scheme, including dual pairing vector space (DPVS), two important lemmas, and complexity assumption.

2.1. Framework of SPE-BKS

The SPE-BKS consists of three roles: data sender, data receiver, and cloud server. The responsibilities of these three roles are listed as follows:

(1)
Data receiver generates the public key (pk) and secret key (sk) and sends the pk to the public. Data receiver also generates the trapdoor for any query of his/her interest and sends the trapdoor to the cloud server.
(2)
For a message M with a keyword set W, data sender encrypts W to create the encrypted index I_W by using pk. Moreover, data sender will produce the encrypted message C for M. After this, data sender sends I_W and C to the cloud server.
(3)
When the cloud server receives the trapdoor generated by the data receiver, the server tests the trapdoor against each encrypted index and returns the matched messages to the receiver.

According to the responsibilities of these three roles, we give a formal definition of the framework of SPE-BKS.

Definition 1. SPE-BKS consists of four polynomial-time algorithms (KeyGen, IndexBuild, Trapdoor, and Test) as follows:

(1)
KeyGen (λ): this algorithm is run by the data receiver. It takes a security parameter λ as input and outputs pk and sk.
(2)
IndexBuild (pk, W): this algorithm is executed by the data sender to encrypt the keyword set W = {w₁, w₂, …, w_n}. It produces a searchable encrypted index I_W by using pk and W.
(3)
Trapdoor (pk, sk, and Q): the algorithm is executed by the receiver to construct a trapdoor of Q. It takes pk, sk, and Q as input and outputs a trapdoor T_Q.
(4)
Test (pk, I_W, and T_Q): for the query Q = (CNF₁)∨(CNF₂)∨⋯∨(CNF_m) and the index keyword set W, we define the function f(W, Q) as follows: if there exists some i ∈ [1, m] such that the keyword set in CNF_i is a subset of W, then f(W, Q) = 1. Otherwise, f(W, Q) = 0. This algorithm is run by the cloud server. It takes a trapdoor T_Q, a secure index I_W, and pk as input and outputs 1 if f(W, Q) = 1, or 0 otherwise.

2.1.1. Correctness

For a query Q and a keyword set W, for pk, sk, I_W, and T_Q correctly generated by the algorithms KeyGen (λ), IndexBuild (pk, W), and Trapdoor (pk, sk, Q), respectively, the correctness property asks that the following two situations are needed to be met:

(1)
If f(W, Q) = 1, Test (pk, I_W, T_Q) outputs 1
(2)
If f(W, Q) = 0, Test (pk, I_W, T_Q) outputs 1 with negligible probability

In practice, data senders will send a message M with a keyword set W. The above algorithms aim to construct a secure and searchable index for W. For the message M, we can apply the symmetric encryption scheme, e.g., AES and triple DES, to protect the security of M. Like the previous SPE schemes, we only concentrate on searchable encryption part.

2.2. Security Definition of the SPE-BKS

In this section, we present a formal definition for SPE-BKS, which defines a group of adversaries who can adaptively query the trapdoors of chosen keyword sets, and issue two challenge ciphertexts. The essential of the security of SPE-BKS is that the adversaries fail to distinguish these two ciphertexts based on the given trapdoors. Depending on the above description, inspired by the security definition of the previous SPE schemes, the security definition of SPE-BKS is given as follows.

Definition 2. An SPE-BKS scheme is adaptively index-hiding against chosen keyword attack if for all probabilistic polynomial-time (PPT) adversaries , the advantage of in the following game is negligible for the security parameter λ:

(1)
Setup: the challenger runs the KeyGen (λ) algorithm to generate pk and sk and gives pk to the attacker .
(2)
Phase 1: the attacker can adaptively ask the challenger for the trapdoor T_Q for any query Q of his choice.
(3)
Challenge: first selects two keyword sets W⁽⁰⁾ and W⁽¹⁾ and sends them to . Suppose that Q⁽¹⁾, Q⁽²⁾, …, Q^(t), Q⁽²⁾, …, Q^(t) are the keyword queries which are queried to construct trapdoors in Phase 1; the only restriction is that these queries cannot distinguish these two challenge keyword sets. Then, randomly chooses a bit β ∈ {0, 1} and generates I_β = IndexBuild(pk, W^(β)). Finally, {I_β, W⁽⁰⁾, W⁽¹⁾} are sent to .
(4)
Phase 2: continues to ask for trapdoor T_Q for any query Q of his/her choice under the restriction mentioned in the Challenge phase.
(5)
Response: the attacker outputs β^′ ∈ {0, 1} and wins the game if β^′ = β.

Based on the above game, the advantage of is defined as follows:

()

2.3. Prime Order Bilinear Group

Let G, G_T be two cyclic groups of prime order p. There are three properties in the bilinear pairings map

as follows:

(1)
Bilinear: , where a, b ∈ G and
(2)
Nondegenerate: if g ∈ G, then
(3)
Computable: for any a, b ∈ G, can be efficiently computable

An efficient bilinear map can be obtained by applying the Weil pairing or the Tate pairing [38].

2.4. Dual Pairing Vector Space

Suppose that and g ∈ G; we have . We can perform the scalar multiplication and vector addition in the exponent. For any a ∈ Z_p and , we have and . We can also have and . Here, the dot product is taken as modulo p.

We will employ the concept of DPVS which is introduced in [39]. The notation used to describe DPVS is introduced in [40]. Suppose that and are two random bases of , where l is a fixed dimension; if whenever i ≠ j and for all i ∈ n, where λ is a random elements in Z_p, then we call B and B^∗ dual orthonormal bases. Obviously, for a generator g ∈ G, whenever i ≠ j, where 1 can be seen as the identity element of G_T.

2.5. Two Important Lemmas

We will introduce two important lemmas used in the security proof of our scheme. The first lemma is presented in [40]. To describe the lemma formally, first of all, we give some notations and definitions which are also introduced in [40]. Let t, l be two fixed positive integers where t < l, be an invertible matrix and S_t⊆{1,2, …, l} be a subset of size t. Suppose that B and B^∗ are random dual orthonormal bases; a new pair of dual orthonormal bases B_A and was defined as follows.

Let B_t be a l × t matrix over Z_p whose columns are the vectors such that i ∈ S_t. We can easily find that B_tA is also a l × t matrix. By keeping all of the vectors for i ∉ S_t and exchanging for i ∈ S_t with the columns of B_tA, B_A is then constructed. Because is also a l × t matrix, also can be constructed by using the same method.

For a fixed dimension l and prime p, we denote randomly choosing a pair of dual orthonormal bases B and B^∗ by . can be viewed as a dual orthonormal bases set.

The first lemma is described as follows.

Lemma 1. For any fixed positive integers t < l, any fixed invertible and set S_t⊆{1,2, …, l} of size t, if , is also distributed as a random sample from . In particular, the distribution of is independent of A.

The second lemma introduced in [39] (Lemma 23) is described as follows.

Lemma 2. Let , where V is l-dimensional vector space, and and V^∗ are its dual. For all , ,

()

where

and s = #C = (p^l − 1)(p^l − p^l−1).

2.6. Complexity Assumption

In order to prove our scheme’s security, subspace complexity assumption introduced in [40] is needed. This validity of this assumption is also given in [40].

For a fixed dimension n^′ ≥ 3 and a prime p, the dual orthonormal bases B and B^∗ which are randomly chosen are denoted by . can be seen as a dual orthonormal bases set. For a positive integer k ≤ (n^′/3), the definition of this assumption is described as follows.

Definition 3 (subspace complexity). Given a group generator , we define the following distribution:

()

We assume that, for any PPT algorithm A with output in {0, 1}, the advantage of defined by is negligible in the security parameter λ.

3. The Proposed SPE-BKS Scheme

In this section, we first introduce a keyword conversion method which converts the index and query keywords into a group of vectors. Then, through taking advantage of DPVS to encrypt these vectors, the construction of SPE-BKS is given. Finally, the security proof of our scheme is presented.

3.1. Keyword Conversion Method

Before describing the method, some notations will be introduced. Suppose that any keyword w can be expressed as a string in {0, 1}^∗, we define a function . Since p is a large prime and is larger than the number of all words, H₁ can be collision-resistant. This means that if i ≠ j, then H₁(w_i) ≠ H₁(w_j), where w_i and w_j are two distinct keywords.

For the index keyword set W = {w₁, w₂, …, w_n}, we construct an equation of degree n with one unknown:

()

According to the coefficient of the f(x), the vector for W is obtained.

For the query Q = (CNF₁)∨(CNF₂)∨⋯∨(CNF_m), we first split Q into a group of keyword sets. For each

, we obtain a keyword set

, where i ∈ [1, m]. For each Q_i, we can create a vector:

()

Note that if it exists some i such that Q_i⊆W, where i ∈ [1, m], according to (4) and (5), it is not difficult to verify that .

As a result, we can test each Q_i in Q against W to make a Boolean keywords search. If f(W, Q) = 1, there is at least an i ∈ [1, m] such that . Based on this property, a concrete SPE-BKS scheme will be proposed in the next section.

3.2. Construction

According to Definition 1, we present a concrete construction of our SPE-BKS scheme:

(i)
KeyGen: choosing a bilinear group G of a prime order p and setting n′ = 3n + 3, the algorithm randomly selects a pair of dual orthonormal bases (B, B^∗) from the dual orthonormal bases set , where , and (mod p), where i ∈ [1, 3n + 3]. The algorithm outputs pk and sk as follows:

()

where i ∈ [0, n].

(i)
IndexBuild: given a keyword set W = {w₁, w₂, …, w_n}, the algorithm constructs an n-degree polynomialf(x) = (x − H₁(w₁))(x − H₁(w₂)), …, (x − H₁(w_n)) = a_nxⁿ + a_n−1xⁿ⁻¹ + ⋯+a₀x⁰ , where H₁(w₁), H₁(w₂), …, H₁(w_n) are n roots of the equation f (x) = 0. Choosing two random elements s₁, s₂ ∈ Z_p, for the vector , this algorithm creates the index I_W as follows:
()
(i)
Trapdoor: given a query Q, this algorithm first generates a group of vectors , by using the keyword conversion method introduced in Section 3.1. Then, it randomly chooses r₁, r₂, …, r_m, t₁, t₂, …, t_m ∈ Z_p and an invertible matrix α. Suppose that and in which and , where j ∈ [1, m], for each j, the trapdoor generation algorithm computes
()
(i)
The trapdoor of Q is T_Q = {K₁, K₂, …, K_m, α⁻¹}.
(ii)
Test: the test algorithm first computes for each j ∈ [1, m]. Suppose that ; it outputs
()
where and j ∈ [1, m]. Based on , the test algorithm works as follows:
(1)
Choose a counter v, and set v = 1.
(2)
If v > m, then go to step (3); otherwise, the algorithm computes. If D_j = 1, the algorithm outputs 1 and ends. Otherwise, it sets v = v + 1 and goes to step (2).
(3)
The algorithm outputs 0 and ends.

3.2.1. Correctness

Suppose that I_W and T_Q are correctly generated by the “IndexBuild” and “Trapdoor” algorithms, respectively, then we have the following equation:

()

where

and j ∈ [1, m].

Owing to

, based on the equation above, we have the following equation:

()

If there exists some j ∈ [1, m] such that , it has x_j=0, which makes , and, thus, the test algorithm outputs 1.

3.2.2. Application

According to the user’s identity, the proposed scheme works as follows:

(1)
Data Receiver. Data receiver runs the “KeyGen” function to generate pk and sk, and pk is open to the public. When data receiver wants to perform Boolean keywords search, the “Trapdoor” function is called to generate a trapdoor by using sk and a Boolean query condition. After this, the trapdoor is sent to the cloud server.
(2)
Data Sender. For a document set, the data sender builds the secure index by calling the “IndexBuild” function and sends the index to the cloud server.
(3)
Cloud Server. Upon receiving a trapdoor generated by the data receiver, the cloud server launches the “Test” function and returns documents associated with the query to the data receiver.

In the real world, any practical application that needs ciphertext retrieval can integrate our scheme to realize the function of searching on encrypted data.

3.3. Security

To prove the security of our SPE-BKS system, we adopt the dual system encryption method proposed in [41, 42]. According to this method, we give the construction of semifunctional index and trapdoor in our scheme. The semifunctional index and trapdoor will not be implemented in the real system but used in the proof:

(i)
Semifunctional Index. Let , where i ∈[0, n] and is introduced in “KeyGen” algorithm. A normal index is constructed by the “IndexBuild” algorithm. Choosing random values y₀, y₁, …, y_n ∈ Z_p, the semifunctional index is created as follows:
()
(i)
Semifunctional Trapdoor. Let , where i ∈[0, n]. A normal trapdoor is constructed by the “Trapdoor” algorithm. Choosing random values z_j0, z_j1, …, z_jn ∈ Z_p where j ∈ [1, m], the semifunctional trapdoor is created as follows:
()

When using the semifunctional trapdoor to test the semifunctional index, the additional factors will be generated, where j ∈ [1, m].

The security proof of our SPE-BKS scheme relies on subspace complexity assumption which is presented in Section 2.6. We will prove security by using a hybrid method which consists of a sequence of games. These games are described as follows:

(1)
Game_Real: this game is the real security game.
(2)
Game_k: for each k ∈ [0, q], Game_k is similar to Game_Real except that the index given to is semifunctional and the first k trapdoors are semifunctional. The remaining trapdoors are normal. In Game₀, all the trapdoors given to are normal and the index is semifunctional. In Game_q, the index and all trapdoors are semifunctional.
(3)
: suppose that a keyword set W = {w₁, w₂, …, w_n} is the challenge keyword set; we construct an n-degree polynomial f(x) = (x − H₁(w₁))(x − H₁(w₂)), …, (x − H₁(w_n)) = a_nxⁿ + a_n−1xⁿ⁻¹ + ⋯+a₀x⁰ by using the function H₁, where H₁(w₁), H₁(w₂), …, H₁(w_n) are n roots of the equation f (x) = 0. Then, we define this game. For each k ∈ [−1, n], is similar to Game_q except that index is a semifunctional encryption of a vector in which the first k + 1 elements are random and the remaining elements are {a_k+1, a_k+2, …, a_n}.
is a game such that the index is a semifunctional encryption of a real challenge keyword set, which is identical to Game_q. is a game such that the index is a semifunctional encryption of a random keyword set. We will show that these games are indistinguishable in the following lemmas.

Lemma 3. Suppose that there exists a PPT algorithm such that is nonnegligible. Then, we can build a PPT algorithm with nonnegligible advantage in breaking subspace complexity assumption, with n′ = 3n + 3, k = n + 1.

Lemma 4. Suppose that there exists a PPT algorithm such that is nonnegligible. Then, we can build a PPT algorithm with nonnegligible advantage in breaking subspace complexity assumption, with n′ = 3n + 3, k = n + 1.

Lemma 5. Suppose that there exists a PPT algorithm such that is nonnegligible. Then, we can build a PPT algorithm with nonnegligible advantage in breaking subspace complexity assumption, with n′ = 6, k = 2.

Considering the length of the article and the coherence of the article structure, the proofs of Lemmas A–C are given in Appendix.

Theorem 1. If subspace complexity assumption holds, then our SPE-BKS scheme is secure.

Proof. If subspace complexity assumption holds, the real security game is indistinguishable from based on the previous lemmas. In , the value of β is information-theoretically hidden from the attackers. Hence, we can state that the attackers can attain no advantage in breaking our SPE-BKS scheme.

4. Performance Evaluation

In this section, we present a detailed experiment to demonstrate that our scheme can efficiently perform Boolean keywords search over the encrypted data. We implement our scheme in JAVA with Java Pairing-Based Cryptography (JPBC) Library [43]. In our implementation, the bilinear map is instantiated as Type A pairing (base field size is 128 bits), which offers a level of security equivalent to 1024-bit DLOG [43]. Our experiment is run on Intel® Core™ i7 CPU at 2.90 GHz processor and 16 GB memory size and is over a real-world e-mail dataset called Enron Email Dataset [44]. In our experiment, we randomly choose 1000 e-mails from the Enron Email Dataset and denote the number of documents by d (d = 1000). To show the efficiency of our scheme, we compare our scheme to three previous SPE schemes in terms of key generation, index building, trapdoor generation, and search. For simplicity, we denote these three schemes introduced in [17, 18, 20] by PECDK-1, PECDK-2, and YY18. These three SPE schemes can perform conjunctive, disjunctive, and Boolean keywords search over encrypted data.

4.1. Key Generation

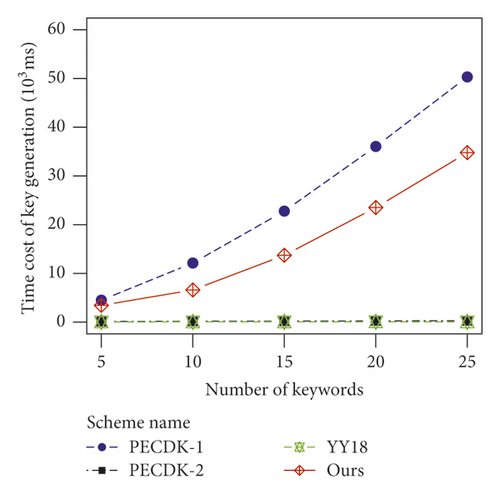
From Figure 2(a), the time costs of key generation in PECDK-1 and our scheme are both linear with, while that in PECDK-2 is linear with O (n). The reason for this phenomenon is the case that both our scheme and PECDK-1 adopt DPVS to generate group elements in G. Because the dimension of DPVS in our scheme is 3n while that in PECDK-1 is 4n, the time cost of key generation in our scheme is less than that in PECDK-1. In addition, since the key generation algorithm in YY18 is independent of n, the time cost of key generation is not related to n. Although the time cost of key generation in our scheme is higher than that in PECDK-2 and YY18, it has little impact on our practical application since this algorithm only runs when system initialization and key pair replacement are carried out.

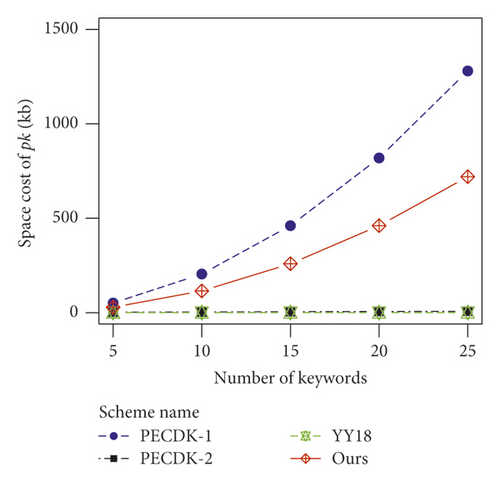
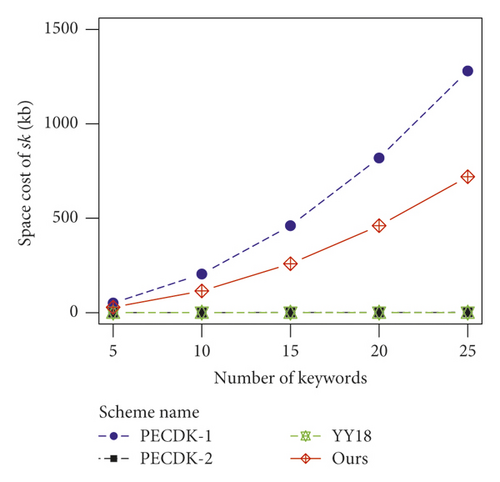
As shown in Figures 3(a) and 3(b), because both pk and sk contain group elements in G, the space cost for key pair in our scheme and PECDK-1 are both linear with the square of n. By contrast, the space cost for key pair in PECDK-2 is linear with O (n). Besides, for YY18, since both pk and sk contain constant big integers, the space cost for key pair is not related to n. Though the storage cost of keys in our scheme is more than that in the other three schemes, our scheme still does not need much space to store the keys as these keys are stored only a few copies.

4.2. Index Building

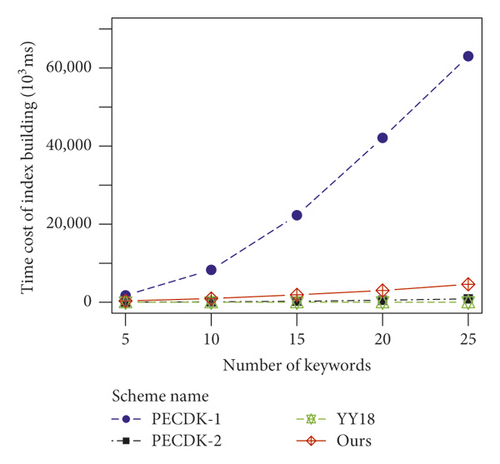
From Figure 2(b), the time costs of index building in PECDK-1, PECDK-2, and our scheme are all linear with, while that in YY18 is linear with O (n). For PECDK-2, the index building algorithm needs to convert the keywords into a matrix and then needs exponentiation computation of G to encrypt the keywords. For the proposed scheme and PECDK-1, they also require exponentiation computation of G owing to DPVS. More precisely, compared to PECDK-1, our scheme needs less time cost in index building since the dimension of DPVS in our scheme is less than that in PECDK-1. Besides, the time cost of index building in our scheme is slightly higher than that in PECDK-2 since our scheme needs exponentiation computations while PECDK-2 requires exponentiation computations. The reason for this phenomenon is that, compared to PECDK-2, our scheme needs more group elements to support more complex search function. Compared with YY18, our scheme needs more index building time since our scheme needs exponentiation computations while YY18 only runs the encryption algorithm of PCTD n times.

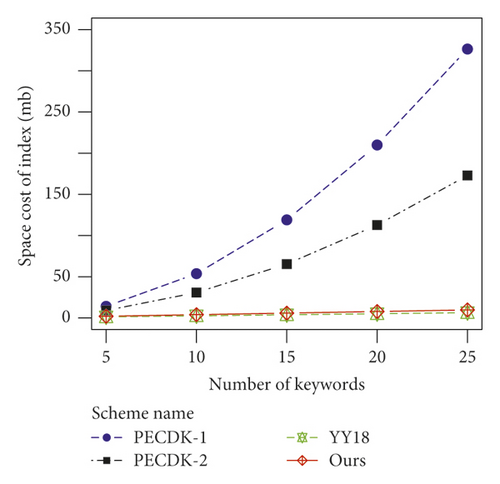
For the storage cost of indices, the group elements on G in the index for our scheme are linear with n. For YY18, since each document’s index contains n ciphertexts generated by PCTD, the space cost of index building is linear with O (n). By contrast, the group elements in the index for PECDK-1 and PECDK-2 are both linear with the square of n since the index structures for PECDK-1 and PECDK-2 are both a matrix. As shown in Figure 3(c), the storage costs of indices in our scheme and YY18 are linear with O (n) while those in PECDK-1 and PECDK-2 are both linear with.

4.3. Trapdoor Generation

As shown in Figure 2(c), the time costs of trapdoor generation in PECDK-1, PECDK-2, YY18, and the proposed scheme are linear with m, m, and respectively. More precisely, for PECDK-1, the keywords in the query are first converted to be a vector, whose dimension is n. Then, this vector will be encrypted by using DPVS. Since the encryption operation needs exponentiation computations of G, the time cost of trapdoor generation in PECDK-1 is linear with. For PECDK-2, suppose that the number of keywords in the query is m, the query is converted to be a vector whose dimension is m, and each dimension needs one exponentiation computation on G. Thus, the time cost of trapdoor generation in PECDK-2 is linear with m. For YY18, if the query contains m keywords, the trapdoor algorithm will perform encryption algorithm of PCTD n times, so the time cost of trapdoor generation is linear with O (m). For the proposed scheme, the query is converted to be m vectors in which each vector’s dimension is n. After this, each vector is encrypted by making use of DPVS, and thus, the time consumption of trapdoor generation in our scheme is linear with.

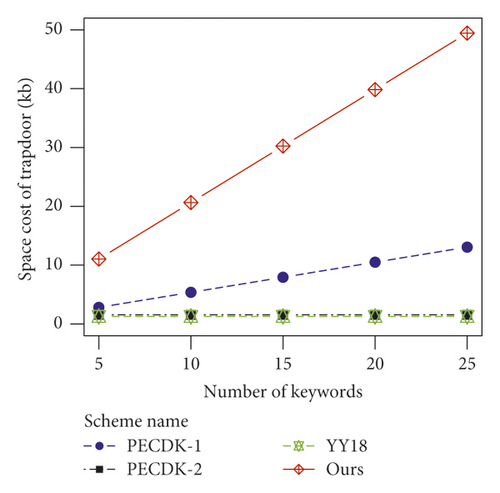
From Figure 3(d), the space costs for PECDK-1, PECDK-2, YY18, and our scheme are linear with n, n, n, and mn, respectively. The reason for this phenomenon is that the trapdoors in PECDK-1, PECDK-2, and our scheme contain n, m, and mn group elements on G, respectively, and the trapdoor in YY18 involves m ciphertexts of PCTD.

4.4. Search

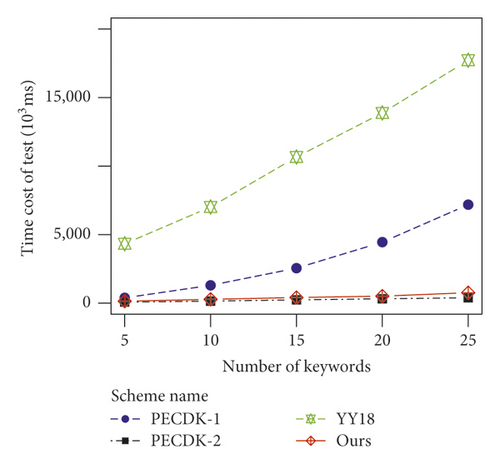
As shown in Figure 2(d), the time cost of search in PECDK-1 is linear with, while that in PECDK-2, YY18, and our scheme is linear with mn. More precisely, for PECDK-1, the index of W contains n ciphertexts, and each ciphertext needs n pairing operations. For PECDK-2, the index is a matrix, and the trapdoor is a vector whose dimension is m. The test algorithm in PECKD-2 performs mn pairing operations between the first m rows of the matrix and the vector. For YY18, since the index and trapdoor hold n and m ciphertext of PCTD, respectively, the test algorithm will run secure less or equal (SLE) protocol and secure multiplication protocol across domains (SMD) mn times. For the proposed scheme, the trapdoor has m items, and the test algorithm in our scheme performs n pairing operations between each item and the index. Thus, total pairing operations in our scheme are mn. Since PECDK-1, PECDK-2, and our scheme need nearly 2 mn and 3 mn pairing operations, respectively, the time consumption in our scheme is slightly more than that in PECDK-2 and is less than that in PECDK-1. Moreover, since the time cost of a pairing operation is less than that of SLE and SMD, our scheme is more efficient than YY18 in test phase.

4.5. More Comments

As shown in the experimental results, when n = 5, d = 1000, and m = 5, the time cost of index building in our scheme is 331 s, the generation time of a single trapdoor is 1.7 s, and the search time is 142 s. According to the statistical data given in [17, 45], the number of keywords in a document (n) is usually less than 20, e.g., only 3∼5 keywords in the scientific paper, and the number of keywords in a query (m) is often less than 10. We can argue that our scheme is suitable for the applications with fewer keywords, such as the keywords in the scientific literature, e-mail title and summaries, medical data summaries, and so on.

Although Figure 2 shows that the time complexity of our scheme is as good as that of PECDK-2, our scheme can support Boolean keywords search, which is much advanced than the conjunctive and disjunctive keywords search. Compared with YY18 that supports Boolean keywords search, our scheme needs less search time, despite the fact that it increases index building time. In practice, the index building in real-world application is usually a one-time activity, while queries are frequently performed. Thus, we reckon that it is worth sacrificing index building time to reduce retrieval time. For the space complexity, from Figure 3, our scheme needs less space for index storage, though requiring more storage space for the trapdoor and keys. Considering the fact that trapdoor and keys often require much less storage space than the index, we argue that our scheme is practicable in the real world.

5. Conclusions

In this paper, by applying DPVS and the bilinear pairing, we proposed a searchable public key encryption scheme supporting Boolean keyword search, which is proven to be secure under chosen keyword search attack. Compared to previous SPE schemes supporting conjunctive and disjunctive keywords search, the proposed scheme can support more advanced search function. Moreover, through a detailed experiment over a real-world dataset, we can argue that the efficiency of our scheme is suitable for practical applications with fewer keywords. Considering that the efficiency in our scheme still needed to be improved, we will construct a more efficient scheme in the forthcoming work.

Conflicts of Interest

The authors declare that they have no conflicts of interest regarding the publication of this paper.

Acknowledgments

The authors gratefully acknowledge the support of the National Natural Science Foundation of China under Grant nos. 61402393 and 61601396 and Nanhu Scholars Program for Young Scholars of XYNU.

Appendix

A. Proof of Lemma 3

Proof. Given , C needs to decide whether T₁, T₂, …, T_n and T_n+1 are , distributed as , or , .

By using T₁, T₂, …, T_n and T_n+1, C can simulate Game₀ or Game_Real with . To create pk, firstly, randomly selects an invertible matrix . Then, we define a dual orthonormal bases F and F^∗ by , , , , , and , , , , , .

C implicitly sets and where the matrix A is applied as a change of basis matrix to and is applied as a change of basis matrix to , as described in Section 2.5. Note that the first 2n + 2 basis vectors are unchanged. According to Lemma 2, E and E^∗ are properly distributed.

Choosing a function H₁, C computes and sends it to A. Each time A asks C to provide a key for a keyword query Q, C creates a normal trapdoor of Q. Choosing and an invertible matrix and , C computes

()

and sends T_Q = {K₁, K₂, …, K_m, α⁻¹} to A, where

, j ∈ [1, m].

At some point, A sends C two challenge keyword sets, and . By randomly choosing β ∈ [0,1] and computing an n-degree polynomial , C sets

()

where C implicitly sets τ₁ = s₁, τ₂ = s₂.

Then, C gives the index I_W to A . If T₁, T₂, …, T_n and T_n+1 are equal to , , then this is a properly distributed normal index. In this case, C has properly simulated Game_Real.If T₁, T₂, …, T_n and T_n+1 are equal to , , then there is an additional term of in the exponent part of the index. The coefficients in the basis are the vector τ₃(a₀, a₁, …, a_n). In order to acquire the coefficients in the basis , we multiply the matrix A⁻¹ by the transpose of these vectors and obtain τ₃A⁻¹(a₀, a₁, …, a_n). Since A is random, these coefficients are uniformly random. Therefore, in this case, C has properly simulated Game₀. So, if A can distinguish Game_Real from Game₀ with nonnegligible advantage, then C can use the output of A to break subspace assumption with nonnegligible advantage.

B. Proof of Lemma 4

Proof. Given , needs to decide whether T₁, T₂, …, T_n and T_n+1 are distributed as follows: , or , .

By using T₁, T₂, …, T_n and T_n+1, can simulate Game_k−1 or Game_k with . To create pk, firstly, randomly selects an invertible matrix and implicitly sets , and , where A is applied as a change of basis matrix to and is applied as a change of basis matrix to , as described in Section 2.5. Then, , , , for i ∈ [0, n]. According to Lemma 2, E and E^∗ are properly distributed.

Choosing a function H₁, computes and sends it to .

When requests the lth trapdoor query, generates the normal trapdoor or the semifunctional trapdoor as follows:

For l < k, choosing and implicitly setting , , where j ∈ [1, m] and i ∈ [0, n], can produce semifunctional trapdoor by using .

For l > k, runs the normal trapdoor generation algorithm to produce the normal trapdoor.

To create the kth requested trapdoor, firstly chooses and an invertible matrix α. Let and . Then, for each j ∈ [1, m], computes

()

The above equation implicitly sets and , where j ∈ [1, m]. If T₁, T₂, …, T_n and T_n+1 are equal to , ; then this is a properly distributed normal trapdoor. If T₁, T₂, …, T_n and T_n+1 are equal to , , then this is a properly distributed semifunctional trapdoor. For each j ∈ [1, m], K_j’s exponent vector contains the item .

At some point, sends two challenge keyword sets, and . By randomly choosing β ∈ [0, 1] and computing an n-degree polynomial , where , are n roots of the equation f (x) = 0, sets

()

where

implicitly sets μ₁ = s₁ and μ₂ = s₂.

After that, sends the semifunctional index I_W to . Obviously, I_W contains the exponent vector . The authors observe that if attempts to test whether the kth trapdoor of Q is semifunctional by creating a semifunctional index of keyword set W which satisfies f(W, Q) = 1, then can find that test algorithm can still work whether the kth key is semifunctional or not, since V_j and V will be eliminated when f(W, Q) = 1. Therefore, we can say that the kth key is a nominally semifunctional key.

In view of this, for each j ∈ [1, m], V_j and V are distributed as random vectors in the spans of and . In V_j, the coefficients in the basis are the vector , where and i ∈ [0, n], j ∈ [1, m]. In order to acquire the coefficients in the basis , we multiply the matrix A^t by the transpose of these vectors and obtain ). Since is random and if i ≠ j, we can say that E₁, E₂, …, E_m are uniformly random. In V, the coefficients in the basis are the vector μ₃(a₀, a₁, …, a_n). In order to acquire the coefficients in the basis , we multiply the matrix A⁻¹ by the transpose of these vectors and obtain E_j = μ₃A⁻¹(a₀, a₁, …, a_n). Since is random and , the coefficients E_j and mentioned above are uniformly random according to Lemma 2, where j ∈ [1, m] and , .

According to the above analysis, we conclude that if T₁, T₂, …, T_n and T_n+1are distributed as , , has properly simulated Game_k−1. If T₁, T₂, …, T_n and T_n+1 are equal to , , has properly simulated Game_k. Thus, we argue that if can distinguish Game_k−1 from Game_k with nonnegligible advantage, then can use the output of to break subspace complexity assumption with nonnegligible advantage.

C. Proof of Lemma 5

Proof. Given , T₁ and T₂, C needs to decide whether T₁ and T₂ are distributed as and or as and , respectively.

By using T₁ and T₂, for k ∈ [0, n], C can simulate or with A. To construct pk, C implicitly sets and , where i ∈ [0, k]. Apparently, E and E^∗ are properly distributed dual orthonormal bases.

Because C can obtain , pk can be easily created. Each time A asks C to provide a key for a keyword query Q, C creates a semifunctional trapdoor of Q. Choosing r₁, r₂, …, r_m, t₁, t₂, …, t_m, z_ji ∈ Z_p and an invertible matrix and , C computes

()

and sends T_Q = {K₁, K₂, …, K_m, α⁻¹} to A, where j ∈ [1, m].

At some point, A sends C two challenge keyword sets, and . By randomly choosing β ∈ [0,1], s₁, s₂ ∈ Z_p, two random vectors , , and computing an n-degree polynomial by using the function H₁, where are n roots of the equation f (x) = 0, then C sets

()

Then, C gives the indexI_w to A. If T₁ and T₂ are equal to and , then this is a properly distributed semifunctional index of the vector {x₀, x₁, …, x_k−1, a_k, a_k+1, …, a_n}. In this case, C has properly simulated . If T₁ and T₂ are equal to and , respectively, then this is a properly distributed semifunctional index of the vector {x₀, x₁, …, x_k−1, b_k, a_k+1, …, a_n}, where b_k = a_k + τ₃. In this case, C has properly simulated . So, if A can distinguish from with nonnegligible advantage, then C can use the output of A to break subspace assumption with nonnegligible advantage.

Open Research

Data Availability

The data used to support the findings of this study are available from the website http://www.cs.cmu.edu/∼./enron/.

References

1 Zerr S., Olmedilla D., Nejdl W., and Siberski W., Zerber + r: top-k retrieval from a confidential index, Proceedings of the 12th International Conference on Extending Database Technology: Advances in Database Technology, March 2009, Saint Petersburg, Russia, 439–449.
Google Scholar
2 Xia Z., Wang X., Sun X., and Wang Q., A secure and dynamic multi-keyword ranked search scheme over encrypted cloud data, IEEE Transactions on Parallel and Distributed Systems. (2016) 27, no. 2, 340–352, https://doi.org/10.1109/tpds.2015.2401003, 2-s2.0-84962448916.
10.1109/TPDS.2015.2401003
Web of Science® Google Scholar
3 Fu Z., Ren K., Shu J., Sun X., and Huang F., Enabling personalized search over encrypted outsourced data with efficiency improvement, IEEE Transactions on Parallel and Distributed Systems. (2016) 27, no. 9, 2546–2559, https://doi.org/10.1109/tpds.2015.2506573, 2-s2.0-84982135416.
10.1109/TPDS.2015.2506573
Web of Science® Google Scholar
4 Fu Z., Wu X., Guan C., Sun X., and Ren K., Toward efficient multi-keyword fuzzy search over encrypted outsourced data with accuracy improvement, IEEE Transactions on Information Forensics and Security. (2016) 11, no. 12, 2706–2716, https://doi.org/10.1109/tifs.2016.2596138, 2-s2.0-84991088919.
10.1109/TIFS.2016.2596138
Web of Science® Google Scholar
5 Guo C., Zhuang R., Chang C.-C., and Yuan Q., Dynamic multi-keyword ranked search based on bloom filter over encrypted cloud data, IEEE Access. (2019) 7, 35826–35837, https://doi.org/10.1109/access.2019.2904763, 2-s2.0-85063964226.
10.1109/ACCESS.2019.2904763
Web of Science® Google Scholar
6 Jiang Q., Qi Y., Qi S., Zhao W., and Lu Y., Pbsx: a practical private boolean search using Intel SGX, Information Sciences. (2020) 521, 174–194, https://doi.org/10.1016/j.ins.2020.02.031.
10.1016/j.ins.2020.02.031
Web of Science® Google Scholar
7 Boneh D., Di Crescenzo G., Ostrovsky R., and Persiano G., Public key encryption with keyword search, Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, May 2004, Berlin, Germany, ., 506–522.
Google Scholar
8 Zhu Y., Ma D., and Wang S., Secure data retrieval of outsourced data with complex query support, Proceedings of the 2012 32nd International Conference on Distributed Computing Systems Workshops, June 2012, 481–490.
Google Scholar
9 Xu P., He S., Wang W., Susilo W., and Jin H., Lightweight searchable public-key encryption for cloud-assisted wireless sensor networks, IEEE Transactions on Industrial Informatics. (2017) 14, no. 8, 3712–3723.
10.1109/TII.2017.2784395
Web of Science® Google Scholar
10 Park D. J., Kim K., and Lee P. J., Public key encryption with conjunctive field keyword search, Proceedings of the International Workshop on Information Security Applications, August 2004, Berlin, Germany, 73–86.
Google Scholar
11 Boneh D. and Waters B., Conjunctive, subset, and range queries on encrypted data, Proceedings of the Theory of Cryptography Conference, February 2007, Berlin, Germany, 535–554.
Google Scholar
12 Zhang B. and Zhang F., An efficient public key encryption with conjunctive-subset keywords search, Journal of Network and Computer Applications. (2011) 34, no. 1, 262–267, https://doi.org/10.1016/j.jnca.2010.07.007, 2-s2.0-78649325305.
10.1016/j.jnca.2010.07.007
Web of Science® Google Scholar
13 Lee C. C., Hsu S. T., and Hwang M. S., A study of conjunctive keyword searchable schemes, International Journal of Network Security. (2013) 15, no. 5, 321–330.
Google Scholar
14 Hwang M. S., Hsu S. T., and Lee C. C., A new public key encryption with conjunctive field keyword search scheme, Information Technology and Control. (2014) 43, no. 3, 277–288, https://doi.org/10.5755/j01.itc.43.3.6429, 2-s2.0-84907538800.
10.5755/j01.itc.43.3.6429
Web of Science® Google Scholar
15 Zhang Y., Li Y., and Wang Y., Efficient conjunctive keywords search over encrypted e-mail data in public key setting, Applied Sciences. (2019) 9, no. 18, https://doi.org/10.3390/app9183655, 2-s2.0-85072408295.
10.3390/app9183655
Google Scholar
16 Katz J., Sahai A., and Waters B., Predicate encryption supporting disjunctions, polynomial equations, and inner products, Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, April 2008, Berlin, Germany, 146–162.
Google Scholar
17 Zhang Y., Li Y., and Wang Y., Conjunctive and disjunctive keyword search over encrypted mobile cloud data in public key system, Mobile Information Systems. (2018) 2018, 11, 3839254, https://doi.org/10.1155/2018/3839254, 2-s2.0-85048178961.
10.1155/2018/3839254
Web of Science® Google Scholar
18 Zhang Y., Li Y., and Wang Y., Secure and efficient searchable public key encryption for resource constrained environment based on pairings under prime order group, Security and Communication Networks. (2019) 2019, 14, 5280806, https://doi.org/10.1155/2019/5280806, 2-s2.0-85066406664.
10.1155/2019/5280806
Google Scholar
19 Liu X., Deng R. H., Choo K. K. R. et al., An efficient privacy-preserving outsourced calculation toolkits with multiple keys, IEEE Transactions on Information Forensics and Security. (2016) 11, no. 11, 2401–2414, https://doi.org/10.1109/tifs.2016.2573770, 2-s2.0-84984984895.
10.1109/TIFS.2016.2573770
Web of Science® Google Scholar
20 Yang Y., Liu X., and Deng R., Expressive query over outsourced encrypted data, Information Sciences. (2018) 442-443, 33–53, https://doi.org/10.1016/j.ins.2018.02.017, 2-s2.0-85042349273.
10.1016/j.ins.2018.02.017
Web of Science® Google Scholar
21 Miao Y., Liu X., Deng R. H. et al., Hybrid keyword-field search with efficient key management for industrial Internet of Things, IEEE Transactions on Industrial Informatics. (2019) 15, no. 6, 3206–3217, https://doi.org/10.1109/tii.2018.2877146, 2-s2.0-85055211841.
10.1109/TII.2018.2877146
Web of Science® Google Scholar
22 Yang Y., Liu X., Deng R. H., and Weng J., Flexible wildcard searchable encryption system, IEEE Transactions on Services Computing. (2020) 13, no. 3, 464–477, https://doi.org/10.1109/tsc.2017.2714669, 2-s2.0-85021815465.
10.1109/TSC.2017.2714669
Web of Science® Google Scholar
23 Yang Y., Liu X., and Deng R. H., Multi-user multi-keyword rank search over encrypted data in arbitrary language, IEEE Transactions on Dependable and Secure Computing. (2020) 17, no. 2, 320–334, https://doi.org/10.1109/tdsc.2017.2787588, 2-s2.0-85040048708.
10.1109/TDSC.2017.2787588
Web of Science® Google Scholar
24 Li J., Shi Y., and Zhang Y., Searchable ciphertext policy attribute based encryption with revocation in cloud storage, International Journal of Communication Systems. (2017) 30, no. 1, e2942, https://doi.org/10.1002/dac.2942, 2-s2.0-85006097002.
10.1002/dac.2942
Web of Science® Google Scholar
25 Li J., Lin X., Zhang Y., and Han J., KSF-OABE: outsourced attribute based encryption with keyword search function for cloud storage, IEEE Transactions on Services Computing. (2017) 10, no. 5, 715–725, https://doi.org/10.1109/tsc.2016.2542813, 2-s2.0-85032285888.
10.1109/TSC.2016.2542813
Web of Science® Google Scholar
26 He K., Guo J., Weng J., Weng J., Liu J. K., and Yi X., Attribute-based hybrid Boolean keyword search over outsourced encrypted data, IEEE Transactions on Dependable and Secure Computing. (2018) https://doi.org/10.1109/tdsc.2018.2864186, 2-s2.0-85051375507.
10.1109/tdsc.2018.2864186
Web of Science® Google Scholar
27 Miao Y., Liu X., Choo K. K. R. et al., Privacy-preserving attribute-based keyword search in shared multi-owner setting, IEEE Transactions on Dependable and Secure Computing. (2019) https://doi.org/10.1109/tdsc.2019.2897675, 2-s2.0-85061258211.
10.1109/tdsc.2019.2897675
Web of Science® Google Scholar
28 Zhang K., Wen M., Lu R., and Chen K., Multi-client sub-linear boolean keyword searching for encrypted cloud storage with owner-enforced authorization, IEEE Transactions on Dependable and Secure Computing. (2020) https://doi.org/10.1109/tdsc.2020.2968425.
10.1109/tdsc.2020.2968425
Web of Science® Google Scholar
29 Feng J., Yang L. T., Zhu Q., and Choo K. K. R., Privacy-preserving tensor decomposition over encrypted data in a federated cloud environment, IEEE Transactions on Dependable and Secure Computing. (2020) 17, no. 4, 857–868, https://doi.org/10.1109/tdsc.2018.2881452, 2-s2.0-85056602689.
10.1109/TDSC.2018.2881452
Web of Science® Google Scholar
30 Feng J., Yang L. T., and Zhang R., Practical privacy-preserving high-order Bi-lanczos in integrated edge-fog-cloud architecture for cyber-physical-social systems, ACM Transactions on Internet Technology. (2019) 19, no. 2, 1–18, https://doi.org/10.1145/3230641, 2-s2.0-85063965845.
10.1145/3230641
Web of Science® Google Scholar
31 Feng J., Yang L. T., Zhang R., and Gavuna B. S., Privacy preserving tucker train decomposition over Blockchain-based encrypted industrial IoT data, IEEE Transactions on Industrial Informatics. (2020) https://doi.org/10.1109/tii.2020.2968923.
10.1109/tii.2020.2968923
Google Scholar
32 Hwang M.-S., Lee C.-C., and Hsu S.-T., An ElGamal-like secure channel free public key encryption with keyword search scheme, International Journal of Foundations of Computer Science. (2019) 30, no. 2, 255–273, https://doi.org/10.1142/s0129054119500047, 2-s2.0-85062840218.
10.1142/S0129054119500047
Web of Science® Google Scholar
33 Lu Y., Li J., and Zhang Y., Privacy-preserving and pairing-free multi-recipient certificateless encryption with keyword search for cloud-assisted IIoT, IEEE Internet of Things Journal. (2020) 7, no. 4, 2553–2562, https://doi.org/10.1109/jiot.2019.2943379.
10.1109/JIOT.2019.2943379
Web of Science® Google Scholar
34 Singh S., Sharma P. K., Moon S. Y., and Park J. H., EH-GC: an efficient and secure architecture of energy harvesting Green cloud infrastructure, Sustainability. (2017) 9, no. 4, https://doi.org/10.3390/su9040513, 2-s2.0-85017346465.
10.3390/su9040673
PubMed Web of Science® Google Scholar
35 Lim K.-S., Park J., and Park J., An energy-efficient virtualization-based secure platform for protecting sensitive user data, Sustainability. (2017) 9, no. 7, https://doi.org/10.3390/su9071250, 2-s2.0-85025128991.
10.3390/su9071250
PubMed Web of Science® Google Scholar
36 Li C.-T., Lee C.-C., and Weng C.-Y., An extended chaotic maps based user authentication and privacy preserving scheme against DoS attacks in pervasive and ubiquitous computing environments, Nonlinear Dynamics. (2013) 74, no. 4, 1133–1143, https://doi.org/10.1007/s11071-013-1029-y, 2-s2.0-84888642495.
10.1007/s11071-013-1029-y
Web of Science® Google Scholar
37 Zhang Y., Wang Y., and Li Y., Searchable public key encryption supporting semantic multi-keywords search, IEEE Access. (2019) 7, 122078–122090, https://doi.org/10.1109/access.2019.2937846.
10.1109/ACCESS.2019.2937846
Web of Science® Google Scholar
38 Joux A., The Weil and Tate pairings as building blocks for public key cryptosystems, Proceedings of the International Algorithmic Number Theory Symposium, July 2002, Berlin, Germany, 20–3.
Google Scholar
39 Lewko A., Okamoto T., Sahai A., Takashima K., and Waters B., Fully secure functional encryption: attribute-based encryption and (hierarchical) inner product encryption, Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, May 2009, Berlin, Germany, 62–91.
Google Scholar
40 Lewko A., Tools for simulating features of composite order bilinear groups in the prime order setting, Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, April 2012, Berlin, Germany, 318–335.
Google Scholar
41 Lewko A. and Waters B., New techniques for dual system encryption and fully secure HIBE with short ciphertexts, Proceedings of the Theory of Cryptography Conference, February 2010, Berlin, Germany, 455–479.
Google Scholar
42 Waters B., Dual system encryption: realizing fully secure IBE and HIBE under simple assumptions, Proceedings of the Annual International Cryptology Conference, August 2009, Berlin, Germany, 619–636.
Google Scholar
43 Caro A. D., The java pairing based cryptography library (JPBC), 2013, http://gas.dia.unisa.it/projects/jpbc/laatstnagekekenop.
Google Scholar
44 Cohen W. W., Enron e-mail dataset, http://www.cs.cmu.edu/∼./enron/.
Google Scholar
45 Cui H., Wan Z., Deng R. H., Wang G., and Li Y., Efficient and expressive keyword search over encrypted data in cloud, IEEE Transactions on Dependable and Secure Computing. (2018) 15, no. 3, 409–422, https://doi.org/10.1109/tdsc.2016.2599883, 2-s2.0-85047227096.
10.1109/TDSC.2016.2599883
Web of Science® Google Scholar

Citing Literature

All articles