To investigate the thermal unstable vibration caused by journal whirls with large amplitude in journal bearing, an analysis model of lubricant film thickness is established. The journal surface temperature distribution is solved, and the reason for journal surface temperature difference appearance and its influence on rotor vibration are analyzed. Taking a turbogenerator as an example, the journal surface temperature difference and the induced rotor thermal bending under synchronous whirl in the bearing are calculated. Meanwhile, an engineering vibration fault with its treatment is presented. Results show that, the journal surface circumferential temperature difference is caused by viscous shearing within lubricant film under journal whirls with large amplitude in journal bearing. The direction of temperature difference is related to the direction of unbalanced force acting on journal. The temperature difference causes rotor thermal bending, which can be converted to a thermal unbalance on the rotor. The rotor vibration is caused by both thermal and initial unbalance. When the rotor is running below or at the critical speed, the vibration is on the increase until it leads to instability of the rotor eventually. When the rotor is running above the critical speed, the rotor vibration fluctuates periodically. Reducing the initial (mechanical) unbalances decreases the rotor vibration and the journal surface circumferential temperature difference.

1. Introduction

Rotor vibration problem of rotating machinery can be extremely frustrating and may lead to greatly reduced reliability. The factors causing rotor vibration are various, including but not limited to: poor stability of bearing system [1, 2], mass unbalance of rotor [3, 4], asymmetric loading and asymmetric aerodynamic forces [5, 6]. In recent years, the unstable vibration in rotor systems caused by rotor thermal deformation has gradually increased. The rub between dynamic and static components is one of the most common causes for unstable vibration faults. The asymmetric temperature difference appears on shaft surface when rub occurs. It results in rotor thermal bending, which leads to unstable vibration [7–9]. The previous studies mainly concentrate on rub between seals and shaft. However, there is another kind of unstable vibration fault which is similar to rub [10–12]. Unfortunately, no rub point can be found when cylinders are opened. The causes of the faults are still under exploring.

Morton effect is a synchronous vibration phenomenon that results from journal surface temperature difference caused by viscous shearing within lubricant film. The journal surface temperature difference results in temporary rotor thermal bending, which leads to an increase in rotor vibration. The journal surface temperature distribution in journal bearing is uniform in traditional views [13]. However, de Jongh, Morton [14] and Tong et al. [15] indicated that journal surface temperature is unevenly distributed by theoretical and experimental studies. The temperature difference is caused by viscous shearing within lubricant film. Panara et al. [16] found the phenomenon that synchronous vibration instability of overhung rotor due to viscous shearing within lubricant film in engineering. Suh et al. [17, 18] suggested that there is a large journal surface temperature difference when the journal whirls in journal bearing. It causes temporary rotor thermal bending and leads to vibration instability of the rotor. Kirk et al. [19] proposed an analysis model for overhung rotor to study the synchronous thermal instability caused by viscous shearing within the lubricant. They pointed out that the instability of a rotor is determined by both thermal and mechanical unbalance. Most of the previous studies focused on the thermal unstable vibration of overhung rotors. It is considered that overhung rotors are sensitive to the temperature difference caused by journal whirls, and are easy to suffer from such faults. The journal whirls with large amplitude due to large unbalanced force acting on journal. The average lubricant film thickness of each point on journal surface is unevenly distributed, which can also cause thermal bending. However, little attention has been devoted to the issue at present.

In this study, considering the problem of journal whirls with large amplitude, an analysis model of lubricant film thickness is established. This study has solved the journal surface temperature distribution, and analyzed the journal surface circumferential temperature difference caused by journal whirl and its influence on rotor vibration. Meanwhile, an engineering vibration fault with its treatment is presented.

2. Journal Surface Temperature Distribution Modeling

2.1. Lubricant Film Thickness under Journal Synchronous Whirl

Figure 1 depicts the synchronous whirl elliptic orbit. The journal whirls in an elliptic orbit around its static equilibrium position O_js in the journal bearing, under the action of unbalanced force. Points O_b and O_j are bearing center and journal center, respectively, as shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Schematic diagram of synchronous whirl elliptic orbit.

At time t = 0, the journal center and the thinnest lubricant film thickness point on journal surface are located at O_j0 and S, respectively. The angle between point S and horizontal position is β. At this moment, points O_b, O_js and O_j0 are collinear:

(1)

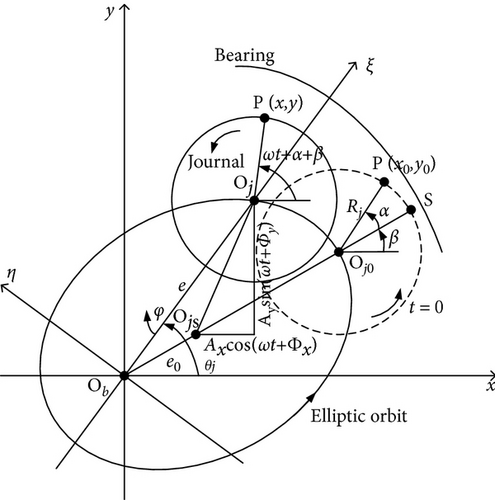
where A_x, A_y, Φ_x and Φ_y are amplitude parameters and phase parameters for elliptic orbit at x- and y-direction, respectively.

With point S as the initial position in the circumferential direction, the angle between a general point, P, on journal surface and point S is α. At time t, the position of the general point (P(x, y)) is constituted of three parts: static equilibrium position, journal whirl and journal rotation around its own axis.

(2)

where e₀ is static eccentricity, ω is whirl/journal angular speed, and R_j is journal radius.

With the line connecting bearing center O_b and journal center O_j as ξ-axis, ξ-η coordinate system is established (see Figure 1). At time t, the time-varying eccentricity ratio of the journal can be expressed as

(3)

where e is time-varying eccentricity and C_b is bearing radius clearance. θ_j is the angle to journal center O_j:

(4)

The lubricant film thickness (h) at point P can be mathematically described as:

(5)

where,

(6)

The average lubricant film thickness in a whirl cycle is:

(7)

where N is the number of grid time point in a whirl cycle, i = 1, 2, …, N.

2.2. Journal Surface Temperature Distribution

When the lubricant film in journal bearing is on stead-state condition, the lubricant film temperature distribution equation is [20]:

(8)

where T is lubricant film temperature. T_b and T_j are bearing temperature and journal surface circumferential temperature, respectively. The lubricant in journal bearings has a density of ρ, a specific heat capacity of c and a viscosity of μ. The convection heat transfer coefficient (H) between lubricant film and journal or bearing can be expressed by the following formula as (Ettles, 1992) [21]:

(9)

Assuming that the heat transfer time is negligible, the journal surface temperature distribution can be approximately considered to be equal to the lubricant film temperature distribution. Meanwhile, assuming that the bearing temperature (T_b) is constant and equals to the ambient temperature (T_a), the one-dimensional thermal equilibrium equation for solving the lubricant film temperature distribution can be given:

(10)

where , means the temperature difference between lubricant film temperature and ambient temperature.

The lubricant film temperature rise is

(11)

where T₀ is lubricant supply temperature.

The lubricant film temperature distribution can be obtained by solving Equation (10). It is equivalent to acquiring the journal surface temperature distribution. The average temperature of a point on journal surface in a whirl cycle can be taken as the journal surface temperature at the point:

(12)

3. Results and Discussion

3.1. Calculation and Analysis on Journal Surface Temperature Difference

Taking a turbogenerator as an example, the journal surface temperature distribution under journal synchronous whirls in the front bearing of the generator is calculated. Table 1 lists the parameters for journal and lubricant for calculation.

Table 1. Parameters for journal and lubricant.

Parameters	Value
Journal properties
Journal radius R_j (mm)	250
Bearing radius clearance C_b (mm)	0.5
Lubricant properties
Label (turbine oil)	#46
Supply temperature T₀ (°C)	40
Density ρ (kg/m³)	860
Specific heat capacity c (J/(kg•K))	1943
Viscosity μ (Pa•s)	0.0396
Ambient temperature T_a (°C)	20
Calculation parameters
Working speed n (rpm)	3000
Static eccentricity ratio ε₀	0.5
x-Direction amplitude A_x/C_b	0.15
y-Direction amplitude A_y/C_b	0.10
x-Direction phase Φ_x	π/6
y-Direction phase Φ_y	π/6

Figure 2 depicts the average lubricant film thickness distribution and the journal surface temperature distribution under different journal whirl conditions. Figure 2 indicates that: (1) the journal surface temperature distribution is uniform under no journal whirl condition. While it is nonuniform under journal whirl conditions. Taking the whirl amplitude in Table 1 as an example, the maximum journal surface temperature difference reaches 5.02℃. (2) Repositioning the direction of unbalanced force acting on the journal by 180° (can cause a change of initial phases for journal whirl of 180°) results in a change of the direction of journal surface temperature difference of about the same angle.

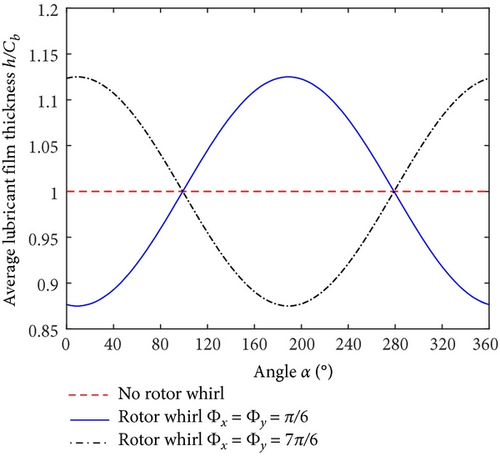
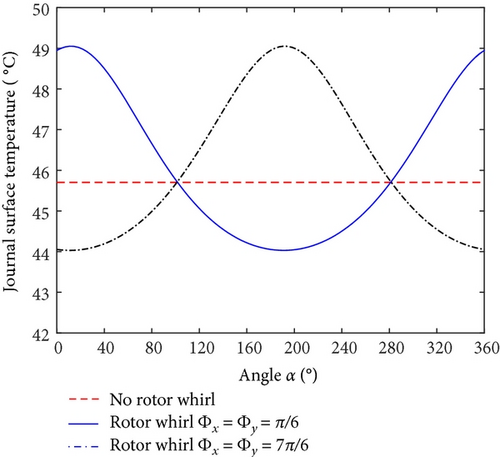
Figure 3 depicts the maximum lubricant film thickness difference and the maximum journal surface temperature difference under different whirl amplitudes (A_x = 1.5A_y). It can be observed from Figure 3 that the maximum lubricant film thickness difference and the maximum journal surface temperature difference increase with growing whirl amplitude. When the vibration reaches an excellent level (A_x < 40 μm), the maximum journal surface temperature difference is lower than 2.5℃. It is higher than 10.6℃ when the vibration exceeds the value for tripping (A_x > 125 μm).

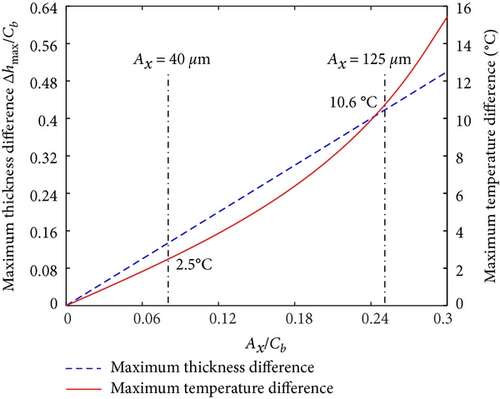
It can also be observed from Figure 3 that the maximum lubricant film thickness difference increases linearly. However, the maximum journal surface temperature difference increases nonlinearly. Its growth rate is higher under large whirl amplitude. As shown in Equation (10), the journal surface temperature is noninear with lubricant film thickness. Therefore, the journal surface temperature cannot be directly calculated by average lubricant film thickness.

3.2. Experimental Study and Comparative Analysis

An experiment was carried out to investigate the journal temperature distribution in journal bearing in Ref. [22]. The test rotor was supported by two tilting-pad journal bearings. In the nondriving end (NDE) journal, four calibrated temperature sensors were installed at 1.0 mm below the journal surface and spaced 90° apart. The testing speed was 12500 rpm.

Figure 4 depicts the measurement results of journal surface temperature distribution under balanced state, and an unbalance weight applied on the shaft at a defined location at 0° and 180°, respectively. Under the balanced state, the vibration amplitude was only around 2 μm peak-to-peak at the testing speed. The journal surface temperature distribution was basically uniform, as shown in Figure 4(a). When the unbalance weight was applied at 0° or 180°, the journal whirled in the NDE bearing. The journal surface temperature differences were 6.6℃ and 6.8℃, respectively. However, the direction of temperature difference vector rotated over around 180° (see Figures 4(b) and 4(c)).

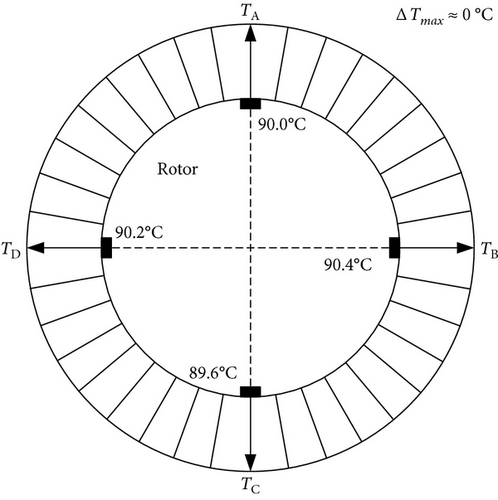
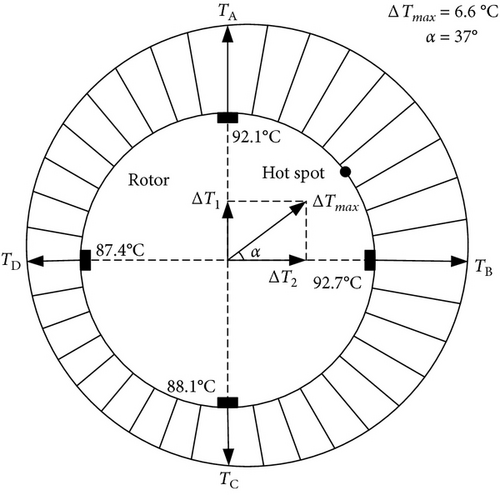
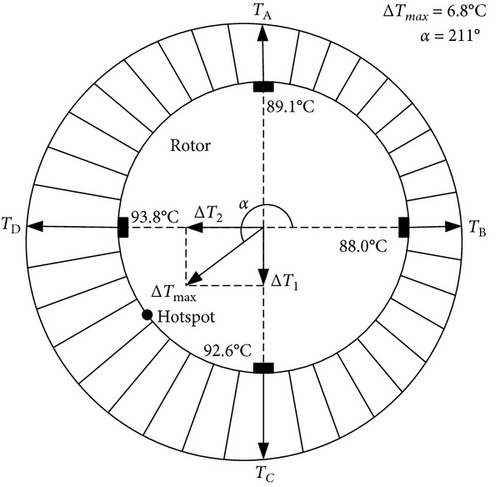
When the journal whirls with large amplitude in journal bearing, the lubricant film thickness distribution is nonuniform. Because of the different lubricant film thickness, the extrusion strength acting on lubricant film is different. It results in different heat generated by viscous shearing. When the heat transfers into the journal, the journal surface circumferential temperature difference occurs.

The phenomena shown by calculation are in accordance with experimental studies. The results show that the lubricant film thickness distribution on journal surface is nonuniform when the journal synchronously whirls in journal bearing. It causes a journal surface circumferential temperature difference. The value of journal surface temperature difference is related to the whirl orbit. The direction is associated with the direction of unbalanced force acting on journal surface.

3.3. Rotor Vibration Influenced by Temperature Difference

The journal surface circumferential temperature difference causes rotor thermal bending. Figure 5 depicts the simplified model of a generator rotor. Table 2 lists the sizes of generator rotor segments, and Table 3 lists the properties of rotor material. Both ends of the rotor are supported by journal bearings. The first-order critical speed (900 rpm) of the generator rotor is low, and the second-order critical speed (2600 rpm) is close to its working speed (3000 rpm). The vibration at working speed is mainly second-order mode shape. Thus, the vibrations at both ends of the rotor are antisymmetric (equal in amplitude but opposite in phase). A temperature difference of 5.02°C is imposed on the journal surfaces at both ends, with a difference of 180° in the direction. The rotor thermal deformation due to journal surface temperature differences is calculated. As shown in Figure 6, the rotor thermal bending at both ends reach 20.10 μm. The thermal bending shape is similar to the second-order mode shape. The working speed of the rotor is close to its second-order critical speed. Hence, the rotor is sensitive to unbalances. A small bending deformation has a great impact on rotor vibration.

Table 2. The sizes of generator rotor segments.

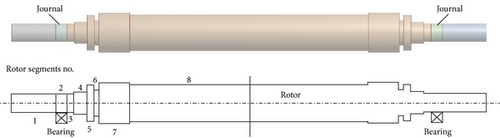
No.	1	2	3	4	5	6	7	8
Diameter (mm)	500	500	500	600	980	700	1100	1000
Length (mm)	1218	311	200	350	200	120	850	3275

Table 3. Properties of rotor material.

Properties	Value
Density (kg/m³)	7850
Young’s modulus (GPa)	210
Poisson’s ratio	0.269
Isotropic thermal conductivity (W/(m•K))	50.2
Coefficient of thermal expansion (/°C)	11.59 × 10⁻⁶

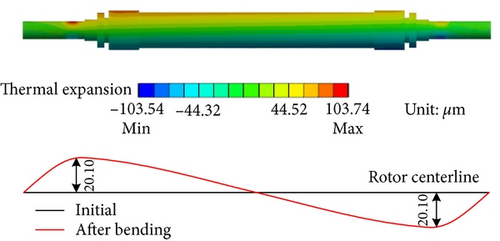
The rotor thermal bending can be converted to a thermal unbalance U_t, which is determined by the vibration due to the initial unbalance U. The thermal and initial unbalance can be added vectorially to produce the resultant unbalance, which can change the rotor vibration. Figure 7 depicts the relationship between thermal unbalance, initial unbalance and resultant unbalance. Assuming that the initial unbalance is U₀, the thermal unbalance caused by U₀ at time t₀ is U_t0, and the resultant unbalance is U₁.

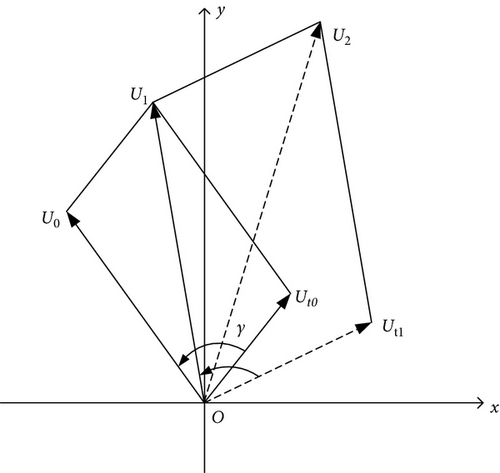
When the rotor is running below the critical speed, the lagging angle of the rotor vibration γ is less than 90°. As shown in Figure 7(a), the resultant unbalance U₁ > U₀. In the same way, the thermal unbalance U_t1 at time t₁ can be obtained, then the resultant unbalance U₂ > U₁. In this process, the resultant unbalance, the rotor thermal bending and the vibration are on the increase, which will lead to instability of the rotor eventually. When the rotor is running at the critical speed, the phenomenon is similar to the above.

When the rotor is running above the critical speed, the lagging angle γ exceeds 90°. As shown in Figure 7(b), the resultant unbalance U₂ < U₁ < U₀. In this process, the resultant unbalance and the vibration become smaller. The rotor thermal bending is gradually restored. After an interval, the vibration gradually increases again due to the initial unbalance, which will result in that the rotor vibration fluctuates periodically at a constant speed.

4. Case Study

A turbogenerator unit suffered from abnormal vibration fault of its generator. Its first- and second-order critical speed was 1052 rpm and 2736 rpm, respectively. The working speed was 3000 rpm.

4.1. Vibration Phenomenon

On-site vibration test was carried out firstly after the abnormal vibration fault had occurred. Figures 8 and 9 depict the trend analysis diagram and frequency spectrum of shaft vibrations at the front bearing (denoted as bearing A) and rear bearing (denoted as bearing B) of the generator, respectively. Figure 10 depicts the changes of vibration vectors.

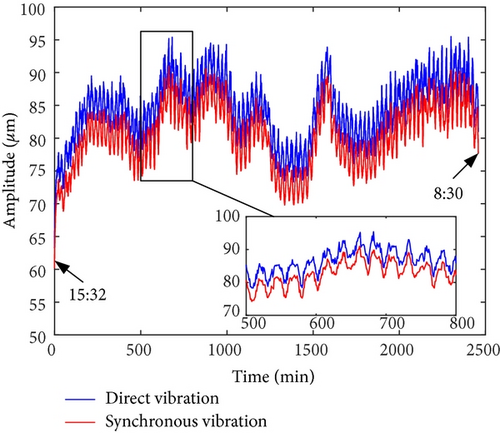
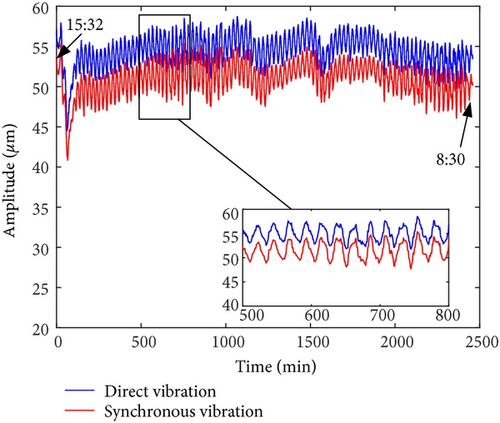
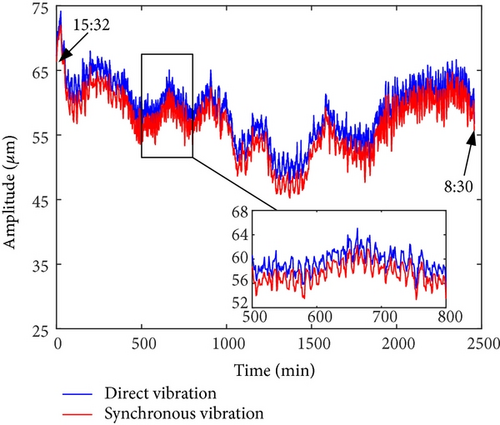
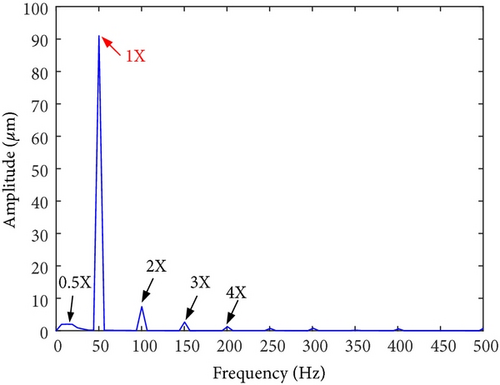
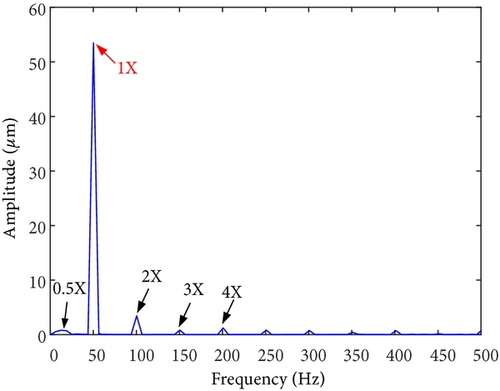
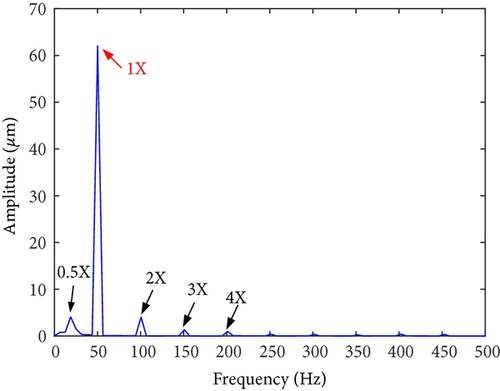
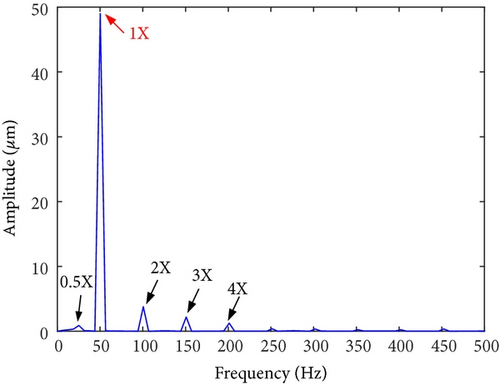
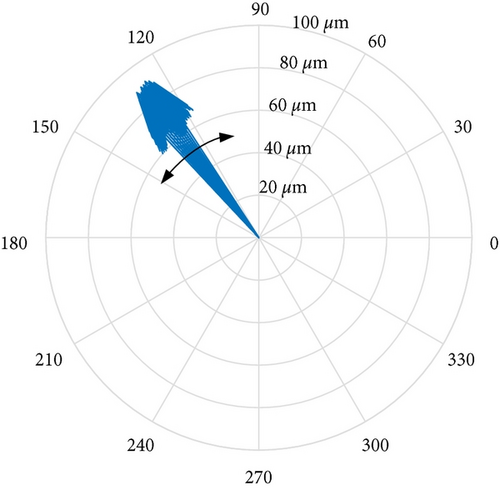
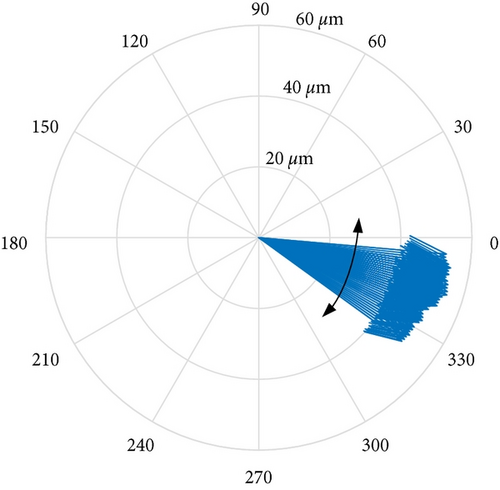
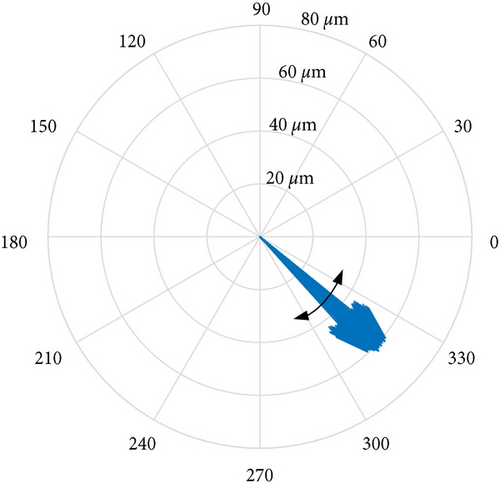
The test results showed that the shaft vibrations fluctuated periodically in constant speed operation. The synchronous component (1X, equaled to rotation frequency of the rotor) was extremely dominant in frequency spectrum. The fluctuation cycle was about 24 minutes. The direct vibration amplitude (peak-to-peak, A_pp) of x-direction shaft vibration at bearing A fluctuated between 63.3 μm and 95.5 μm, with a fluctuation range of 32.2 μm. The 1X component accounted for 95.3%. Similarly, the periodic fluctuations also occurred on y-direction shaft vibration at bearing A, x- and y-direction shaft vibrations at bearing B. Meanwhile, the phases of vibration vectors also fluctuate periodically.

4.2. Analysis on Vibration Cause

The gaps between lubricant baffles and journals exceeded the vibration amplitudes. Thus, the lubricant baffles would not rub against the journals.

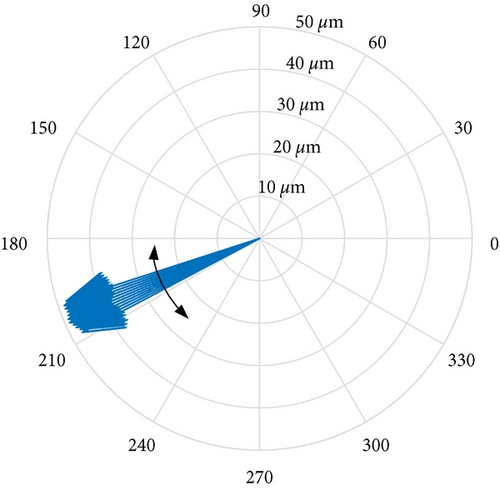
In order to find out the abnormal vibration cause, shaft vibrations and journal surface temperature at bearing A were measured on site. Table 4 lists the 1X component amplitudes (peak-to-peak, A_pp) of shaft vibrations at bearings A and B. Figure 11 depicts the journal surface temperature distribution (before dynamic balance) at bearing A. The starting point 0° was the location of the cursor. Figure 12 depicts the journal orbit (before dynamic balance) at bearing A under synchronous vibration. The orbit center was the static equilibrium position of the journal.

Table 4. 1X component amplitudes of shaft vibrations at bearings A and B, maximum journal surface temperature difference at bearing A.

Test conditions	1X component amplitudes (μm∠°)				Maximum temperature differences (°C)
	Bearing A		Bearing B
	x-Direction	y-Direction	x-Direction	y-Direction
Before dynamic balance	91∠126	53∠355	62∠316	49∠203	4.6
Trial counterweights	Bearing A side: 420 g∠60°, bearing B side: 420 g∠240°
After adding trial counterweights	45∠306	44∠95	45∠121	38∠300	3.5
Balancing counterweights	Remove trial counterweights firstly; then bearing A side: 270 g∠70°, bearing B side: 270 g∠250°
After dynamic balance	20∠42	23∠68	11∠172	18∠259	1.6

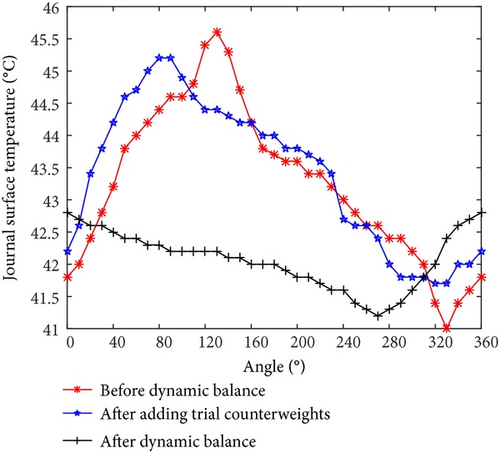
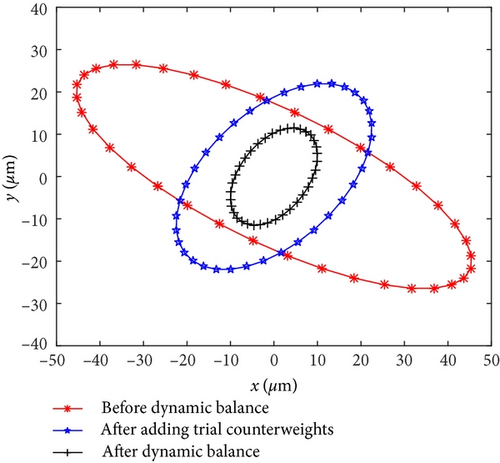
The on-site test results showed that the journal surface temperature distribution was nonuniform at bearing A. It can be confirmed that the journal surface temperature difference was caused by journal whirl with large amplitude. In other words, the periodic fluctuations of shaft vibrations were closely related to the journal whirl with large amplitude. The 1X components were extremely dominant in vibration frequency spectrums (see Figure 9). The characteristics are consistent with those of unbalance faults. The root cause for the vibration fault was a mass unbalance on the rotor.

4.3. Treatment for Vibration Fault

The reason for journal whirls with large amplitude was a large mass unbalance on the rotor. On-site dynamic balance technology was determined to treat the abnormal vibration fault. Table 4 lists the on-site dynamic balance data. Two on-site dynamic balance experiments were carried out. The counterweights were added in the balance grooves at both sides of the generator. Based on the vibration characteristics, a couple was determined to be applied to the generator rotor. In order to obtain the influence coefficients for measuring points, the trial counterweights were added. The trial counterweight scheme was as follows: adding a counterweight of 420 g∠60° at bearing A side, and a counterweight of 420 g∠240° at bearing B side. The method used to calculate the influence coefficients can be expressed as:

(13)

where P is the counterweight added to the rotor. [A₀] and [A₁] are the shaft vibrations before and after adding counterweights, respectively. Table 5 lists the influence coefficients for measuring points. Then the trial counterweights were removed. A system of overdetermined equations is given by the influence coefficients as follows:

(14)

Table 5. Influence coefficients for measuring points.

Measuring points	Bearing A		Bearing B
Measuring points	x-Direction	y-Direction	x-Direction	y-Direction
Influence coefficients (μm∠°/g∠°)	0.324∠246	0.177∠79	0.253∠70	0.156∠288

By solving the system of Equations (14) with least-square method, the balancing counterweight Q can be obtained:

(15)

Meanwhile, considering the vector optimization method, the balancing counterweight scheme was obtained as follows: removing the trial counterweights firstly, then adding a counterweight of 270 g∠70° at bearing A side, and a counterweight of 270 g∠250° at bearing B side.

The unit vibrations had reached a good level after on-site dynamic balance. The unit vibrations were stable with little fluctuation.

It can be observed from Figure 11 and Table 4 that the rotor vibration amplitudes decreased after adding trial counterweights and dynamic balance, indicating that the rotor unbalance reduced. Based on the regularity in Figure 3, the journal surface temperature difference would decrease. Meanwhile, the rotor vibration phases changed, indicating that the position of rotor unbalance changed. According to the calculation and experimental results shown in Sections 3.1 and 3.2, the direction of journal surface temperature difference would change. The maximum journal surface temperature difference reached 4.6°C before dynamic balance. While it was only 1.6°C after on-site dynamic balance. The whirl amplitude was larger under large vibration amplitude, and the journal surface temperature difference was also higher. Results show that reducing the initial (mechanical) unbalances not only reduces the shaft vibrations, but also decreases the journal surface circumferential temperature difference.

5. Conclusion

In this study, an analysis model is established to investigate the influence of the synchronous whirls caused by rotor unbalance on the journal surface temperature distribution from the point of lubricant film thickness. Taking a turbogenerator as an example, the influence of unbalanced force on the journal surface temperature distribution is studied. Based on the calculation results above, the rotor thermal bending is calculated. The relationship between rotor vibration and journal surface temperature difference is analyzed. The found phenomenon explains an engineering vibration fault commendably. The main conclusions involved are as follows:

(1)
The journal surface circumferential temperature difference is caused by viscous shearing within lubricant film under journal whirls with large amplitude in journal bearing. The whirl amplitude is larger under large vibration amplitude, and the journal surface temperature difference is also higher. The direction of temperature difference is related to the direction of unbalanced force acting on journal.
(2)
The journal surface temperature difference can cause rotor thermal bending, which can be converted to a thermal unbalance on rotor.
(3)
The rotor vibration is caused by both thermal and initial unbalance. When the rotor is running below or at the critical speed, the vibration is on the increase until it leads to instability of the rotor eventually. When the rotor is running above the critical speed, the rotor vibration fluctuates periodically.
(4)
Reducing the initial (mechanical) unbalances not only reduces the shaft vibrations, but also decreases the journal surface circumferential temperature difference.

Nomenclature

Dimensions:: M = mass, L = length, t = time, T = temperature
A_x, A_y:: Amplitude parameters for elliptic orbit (L)
A₀, A₁:: Vibrations before and after adding counterweights
c:: Lubricant specific heat capacity (L² t⁻² T⁻¹)
C_b:: Bearing radius clearance (L)
e:: Time-varying eccentricity (L)
e₀:: Static eccentricity (L)
h:: Lubricant film thickness (L)
:: Average lubricant film thickness in a whirl cycle (L)
H:: Convection heat transfer coefficient (M t⁻³ T⁻¹)
n:: Working speed (t⁻¹)
N:: Number of grid time point in a whirl cycle
O_b:: Bearing center
O_j:: Journal center
O_j0:: Journal center at t = 0
O_js:: Journal center at static equilibrium position
P:: A general point on journal surface
P, Q:: Counterweights added in dynamic balance
R_j:: Journal radius (L)
S:: Thinnest lubricant film thickness point on journal surface at t = 0
t:: Time (t)
T:: Lubricant film temperature (T)
:: Average journal surface circumferential temperature in a whirl cycle (T)
:: Temperature difference between lubricant film temperature and ambient temperature (T)
T₀:: Lubricant supply temperature (T)
T_a:: Ambient temperature (T)
T_b:: Bearing temperature (T)
T_j:: Journal surface circumferential temperature (T)
ΔT:: Lubricant film temperature rise (T)
U₀:: Initial unbalance (M L)
U₁, U₂:: Resultant unbalance (M L)
U_t0, U_t1:: Thermal unbalance (M L)
α:: Angle between points P and S
α:: Influence coefficient
β:: Angle between point S and horizontal position at t = 0
γ:: Lagging angle of rotor vibration
ε:: Time-varying eccentricity ratio
ε₀:: Static eccentricity ratio
θ_j:: Angle to journal center
μ:: Lubricant viscosity (M L⁻¹ t⁻¹)
φ:: Circumferential angle
ω:: Whirl/journal angular speed (t⁻¹)
Φ_x, Φ_y:: Phase parameters for elliptical orbit
ξ, η:: Local coordinates
ρ:: Lubricant density (M L⁻³).

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

The authors would like to extend their sincere thanks to staffs at National Engineering Research Center of Turbogenerator Vibration, Southeast University, China, for the support and experimental tests.

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Wang C. C., Lee R. M., Yau H. T., and Lee T. E., Nonlinear analysis and simulation of active hybrid aerodynamic and aerostatic bearing system, Journal of Low Frequency Noise, Vibration and Active Control. (2019) 38, no. 3-4, 1404–1421.
10.1177/1461348418792737
Web of Science® Google Scholar
2 Wang C. C. and Lee T. E., Nonlinear dynamic analysis of bi-directional porous aero-thrust bearing systems, Advances in Mechanical Engineering. (2017) 9, no. 12, 1–11, https://doi.org/10.1177/1687814017738153, 2-s2.0-85039909723.
10.1177/1687814017738153
Web of Science® Google Scholar
3 Tresser S., Dolev A., and Bucher I., Dynamic balancing of super-critical rotating structures using slow-speed data via parametric excitation, Journal of Sound and Vibration. (2018) 415, 59–77, https://doi.org/10.1016/j.jsv.2017.11.029, 2-s2.0-85038092805.
10.1016/j.jsv.2017.11.029
Web of Science® Google Scholar
4 Cao H., He D., Xi S., and Chen X., Vibration signal correction of unbalanced rotor due to angular speed fluctuation, Mechanical Systems and Signal Processing. (2018) 107, 202–220, https://doi.org/10.1016/j.ymssp.2018.01.030, 2-s2.0-85042085126.
10.1016/j.ymssp.2018.01.030
Web of Science® Google Scholar
5 Xu C. and Amano R. S., The performance influences of a centrifugal compressor due to volute local deformation, Journal of Energy Resources Technology. (2019) 141, no. 9, 091202, https://doi.org/10.1115/1.4043134, 2-s2.0-85064163397.
10.1115/1.4043134
Web of Science® Google Scholar
6 Xu C. and Amano R. S., Effects of asymmetric radial clearance on performance of a centrifugal compressor, Journal of Energy Resources Technology. (2018) 140, no. 5, 052003, https://doi.org/10.1115/1.4038387, 2-s2.0-85051368532.
10.1115/1.4038387
Web of Science® Google Scholar
7 Xu H., Wang N., Jiang D., Han T., and Li D., Dynamic characteristics and experimental research of dual-rotor system with rub-impact fault, Shock and Vibration. (2016) 2016, 6239281.
10.1155/2016/6239281
Web of Science® Google Scholar
8 Cha S. and Na S., Physical analysis of rotor-to-stator rub in a large-capacity low-pressure steam turbogenerator, Journal of Engineering for Gas Turbines and Power. (2016) 138, no. 7, 072605, https://doi.org/10.1115/1.4032415, 2-s2.0-84958793686.
10.1115/1.4032415
Web of Science® Google Scholar
9 Mokhtar M. A., Darpe A. K., and Gupta K., Analysis of stator vibration response for the diagnosis of rub in a coupled rotor-stator system, International Journal of Mechanical Sciences. (2018) 144, 392–406, https://doi.org/10.1016/j.ijmecsci.2018.05.019, 2-s2.0-85048524705.
10.1016/j.ijmecsci.2018.05.019
Web of Science® Google Scholar
10 Marscher W. D. and Illis B., Journal bearing ‘morton effect’ cause of cyclic vibration in compressors, Tribology Transactions. (2007) 50, no. 1, 104–113, https://doi.org/10.1080/10402000601147781, 2-s2.0-34548625915.
10.1080/10402000601147781
CAS Web of Science® Google Scholar
11 He W., Tian Y., and Yang J., Influence of journal temperature difference on vibration of the sliding bearing, Journal of Chinese Society of Power Engineering. (2015) 35, no. 6, 451–456.
Google Scholar
12 Gu L., A review of morton effect: from theory to industrial practice, Tribology Transactions. (2017) 61, no. 2, 381–391, https://doi.org/10.1080/10402004.2017.1333663, 2-s2.0-85023184174.
10.1080/10402004.2017.1333663
Web of Science® Google Scholar
13 Liu D. and Miao T., One-dimensional steady state thermal effects of journal bearings, Proceedings of the CSEE. (2010) 132, no. 5, 91–95.
Google Scholar
14 de Jongh F. M. and Morton P. G., The synchronous instability of a compressor rotor due to bearing journal differential heating, Journal of Engineering for Gas Turbines & Power. (1996) 118, no. 4, 816–824, https://doi.org/10.1115/1.2816998, 2-s2.0-0030482704.
10.1115/1.2816998
Web of Science® Google Scholar
15 Tong X. and Palazzolo A., Measurement and prediction of the journal circumferential temperature distribution for the rotordynamic morton effect, Journal of Tribology. (2018) 140, no. 3, 031702, https://doi.org/10.1115/1.4038104, 2-s2.0-85032268566.
10.1115/1.4038104
Web of Science® Google Scholar
16 Panara D., Baldassare L., Griffini D., Mattana A., Panconi S., and Meli E., Numerical prediction and experimental validation of rotor thermal instability, Proceedings of 44th Turbomachinery & 31th Pump Symposia, 2015, Houston, TX, USA.
Google Scholar
17 Suh J. and Palazzolo A., Three-dimensional thermohydrodynamic morton effect simulation—Part I: theoretical model, Journal of Tribology. (2014) 136, no. 3, 031706, https://doi.org/10.1115/1.4027309, 2-s2.0-84899477160.
10.1115/1.4027309
Web of Science® Google Scholar
18 Suh J. and Palazzolo A., Three-dimensional thermohydrodynamic morton effect analysis—Part II: parametric studies, Journal of Tribology. (2014) 136, no. 3, 031707, https://doi.org/10.1115/1.4027310, 2-s2.0-84899484706.
10.1115/1.4027310
Web of Science® Google Scholar
19 Kirk R. G., Guo Z., and Balbahadur A. C., Synchronous thermal instability prediction for overhung rotors, Proceeding of the Thirty-Second Turbomachinery Symposium, 2003, ASME, TX, USA.
Google Scholar
20 Balbahadur A. C. and Kirk R. G., Part I—Theoretical model for a synchronous thermal instability operating in overhung rotors, International Journal of Rotating Machinery. (2004) 10, no. 6, 477–487.
10.1155/S1023621X04000478
Google Scholar
21 Ettles C. M., The analysis of pivoted pad journal bearing assemblies considering thermoelastic deformation and heat transfer effects, Tribology Transactions. (1992) 35, no. 1, 156–162, https://doi.org/10.1080/10402009208982103, 2-s2.0-0026715383.
10.1080/10402009208982103
Web of Science® Google Scholar
22 de Jongh F. M., The synchronous rotor instability phenomenon—Morton effect, Proceedings of 2018 Turbomachinery & Pump Symposium, 2018, Houston, TX, USA.
Google Scholar

All articles

Study on Thermal Unstable Vibration of Rotor under Journal Whirl with Large Amplitude in Journal Bearing

Abstract