Volume 2019, Issue 1 7431239

Research Article

Open Access

Nonlinear Torsional Vibration Analysis and Control of Semidirect Electromechanical Coupling Transmission System in Shearer

Song Jiang,

Song Jiang

orcid.org/0000-0002-4801-9005

School of Mechatronic Engineering, China University of Mining and Technology, Xuzhou 221116, China cumt.edu.cn

Search for more papers by this author

Wei Li,

Corresponding Author

Wei Li

[email protected]

orcid.org/0000-0002-7586-4829

School of Mechatronic Engineering, China University of Mining and Technology, Xuzhou 221116, China cumt.edu.cn

Search for more papers by this author

Lianchao Sheng,

Lianchao Sheng

School of Mechatronic Engineering, China University of Mining and Technology, Xuzhou 221116, China cumt.edu.cn

Search for more papers by this author

Jiajun Chen,

Jiajun Chen

School of Mechatronic Engineering, China University of Mining and Technology, Xuzhou 221116, China cumt.edu.cn

Search for more papers by this author

Min Li,

Min Li

School of Mechatronic Engineering, China University of Mining and Technology, Xuzhou 221116, China cumt.edu.cn

Search for more papers by this author

Song Jiang,

Song Jiang

orcid.org/0000-0002-4801-9005

School of Mechatronic Engineering, China University of Mining and Technology, Xuzhou 221116, China cumt.edu.cn

Search for more papers by this author

Wei Li,

Corresponding Author

Wei Li

[email protected]

orcid.org/0000-0002-7586-4829

School of Mechatronic Engineering, China University of Mining and Technology, Xuzhou 221116, China cumt.edu.cn

Search for more papers by this author

Lianchao Sheng,

Lianchao Sheng

School of Mechatronic Engineering, China University of Mining and Technology, Xuzhou 221116, China cumt.edu.cn

Search for more papers by this author

Jiajun Chen,

Jiajun Chen

School of Mechatronic Engineering, China University of Mining and Technology, Xuzhou 221116, China cumt.edu.cn

Search for more papers by this author

Min Li,

Min Li

School of Mechatronic Engineering, China University of Mining and Technology, Xuzhou 221116, China cumt.edu.cn

Search for more papers by this author

First published: 2019

https://doi.org/10.1155/2019/7431239

Citations: 7

Academic Editor: Jean-Jacques Sinou

Share a link

Email
Wechat
Bluesky

Abstract

The nonlinear torsional vibration and instability oscillation caused by nonlinear damping in the shearer electromechanical coupling cutting transmission system in shearer driven by the permanent magnet synchronous motor (PMSM) is investigated in this paper. The electromechanical coupling transmission system in the shearer is equivalent to a concentrated mass model for the purpose of establishing the system dynamic model by the Lagrange–Maxwell equation. Then, the Routh–Hurwitz criterion is used to determine the torsional vibration critical point and stability region for the Hopf bifurcation for the cutting transmission system. According to the Routh–Hurwitz stability criterion, the Hopf bifurcation type and the effect of the supercritical Hopf bifurcation in the torsional vibration of the cutting transmission system are analyzed. Furthermore, based on the washout filter, the Hopf bifurcation controller is designed for suppressing the transmission system’s large vibration amplitude and unstable oscillation. In addition, the influences of the linear gain and nonlinear gain on the bifurcation point and the limit cycle amplitude are discussed. Finally, the numerical simulation results indicate the effectiveness of the designed controller. The research achievements can provide a theoretical basis for design or optimize the cutting transmission system of high-reliability shearer driven by PMSM.

1. Introduction

In recent years, with the continuous development of coal mining mechanization, it requires higher requirements for the fully mechanized mining equipment in high efficiency and high reliability [1, 2]. As an integral part of fully mechanized mining equipment, the shearers may easily break down due to the terrible working environment. Currently, the traditional main transmission mode of the cutting transmission system is “three-phase asynchronous motor + three-stage straight tooth retarder + planetary gear reducer + cutting drum,” which has a long transmission chain and many transmission components. The long-chain transmission mode is prone to failure [3–5]. Therefore, a semidirect driving system [6, 7] is proposed in this paper, which consists of PMSM, three-stage straight tooth retarder, and cutting drum, and is shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Schematic diagram semidirect cutting transmission system.

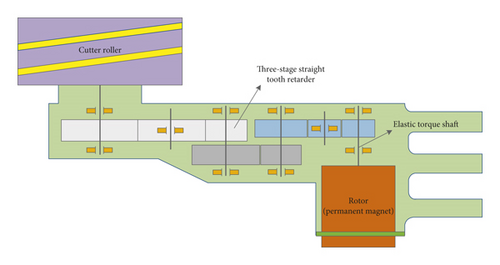
Comparing to the original system, the electromagnetic torque and load torque will greatly increase due to the system reduction ratio that is reduced by removing the planetary gear [8, 9], which is prone to torsional vibration of the cutting transmission system. Therefore, it has a great significance to research the torsional vibration of the cutting transmission system. Fortunately, this multimass elastic torsional system like the shearer cutting section has been researched by many domestic and foreign scholars who mainly study from the perspectives of natural frequency and disturbance. It is found that the nonlinear factors are the main cause of torsional vibration, and furthermore, bifurcation and chaos may occur in the system due to some nonlinear factors [10–12]. On the coupled bending and torsional vibration model of rubbing rotor, with rotational speed as the bifurcation parameter, the bifurcation and chaotic behavior of the rotor system are studied by Al-Bedoor [13]. Liu et al. [14] studied the static bifurcation characteristics and rotor system stability with time-delay nonlinear parameters, and then the vibration was controlled with the delay feedback. In [15], the self-excited oscillations caused by nonlinear factors in the power system are analyzed. And the system Hopf bifurcation motion was researched with nonlinear mode and Floquet theory with different resistance parameters. The mechanical rotor system Hopf bifurcation was researched by Yuan [16], which was frequently encountered in the mechanical structure, and may cause the shafting instability and damage. Saigo et al. [17] studied the suppression of forced vibration of the concentrated mass torsion system by a wave absorption. The results demonstrate that smaller mass and larger spring stiffness of an imaginary system absorb vibration energy better.

However, the cutting transmission system in shearer not only includes the motor but also mechanical parts, which belongs to the electromechanical coupling system. Due to the effect of electromechanical coupling, the cutting transmission system will exhibit complex dynamic behavior [18–20]. Therefore, the torsional vibrations of the system cannot be interpreted rationally, neither from electrical nor from mechanical aspect. It is important to establish an accurate model of the electromechanical coupling system to further analyze the torsional vibration dynamic characteristics in the semidirect transmission system of the shearer and control the torsional vibration from the aspect of motor [21]. Gustavsson and Aidanpää [22] established the model of electromagnetic excitation produced by the uniform magnetic field, and the influence of nonlinear magnetic pull on rotor vibration of the hydrogenerator unit was discussed. Szolc et al. [23] researched the dynamic electromechanical coupling effects in machine drive systems driven by asynchronous motors, and the electromagnetic stiffness and damping coefficients of the interaction between motor and mechanical system were determined by means of the analytical method. Ju et al. [24] constructed the global electromechanical-coupling dynamic models for the main transmission system of the scraper conveyor, and the Hopf bifurcation characteristic is analyzed, which was caused by sliding friction. In view of the above mentioned, Hopf bifurcation is a significant factor affecting the stability of the electromechanical coupling transmission system. However, the dynamic analysis of the electromechanical coupling system mainly focus on the induction motor, and the PMSM are rarely considered. It is a remarkable fact that the damping of the semidirect transmission shafting would change with the shafting vibration, the shaft fatigue, the wear, and lubrication of the bearing [25, 26]. Torsional vibrations of the cutting transmission system caused by shaft damping variations would further lead to the shafting destabilization [27, 28].

Different from the above references, this paper analyses the effect of Hopf bifurcation produced by variable damping in shearer semidirect transmission system driven by the PMSM. Furthermore, based on the washout filter, the Hopf bifurcation controller is designed for suppressing the transmission system’s unstable oscillation. Finally, this paper is organized as follows. The electromechanical-coupling dynamics modelling for the main transmission system of the shearer driven by the high-torque and low-speed PMSM is provided in Section 2. The Hopf bifurcation characteristics analysis for the system torsional vibration and numerical simulation verification is given in Section 3. The washout filter controller for the system torsional vibration is designed, and numerical simulation verification is given in Section 4. Finally, the conclusions are drawn in Section 5.

2. Electromechanical Coupling Torsional Vibration Modelling

The semidirect cutting transmission system of the shearer driven by PMSM mainly consists of PMSM, three-stage gear, shafting, cutting drum, and so on. There are both resilient elements with small quality and inertia with large mass. Therefore, it is a multimass spring damping system with electromechanical coupling. To analyze the coupling dynamic characteristic of the electrical parameters and mechanical parameters, the PMSM and the cutting drum are regarded as the power source and load system, respectively, and ignore the effect of the reducer gear clearance. As a protective shaft for PMSM, the elastic torque shaft is more vulnerable to damage due to the relief groove and the low torsional strength. However, all other components have the feature of large mass and the small elasticity. Hence, the effect of the elastic torque shaft is only considered, and the other shaft and gear are equivalent to the PMSM and cutting drum. Then, the transmission system is equivalent to the two-mass spring torsional vibration system with resilient elements (PMSM and cutting drum) and inertia element (elastic torque shaft), as shown in Figure 2. To simplify the analysis, take the following assumptions: (1) neglecting the iron core saturation effect in the PMSM; (2) no consideration of eddy current and hysteresis loss in the PMSM; and (3) the motor stator winding current is a three-phase symmetric sine current.

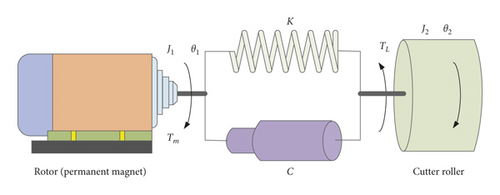
In Figure 2, J₁ is the PMSM inertia; J₂ is the sum of the moment of the cutting drum and the transformation of the gear and other elements inertia; i_a, i_b, and i_c are the three-phase stator current of the PMSM, respectively; K and C are the torsional stiffness and damping coefficient of the elastic torque shaft; T_m and T_L are the electromagnetic torque of the PMSM and load torque of cutting drum; and θ₁ and θ₂ are the mechanical angle of the PMSM shaft and cutting drum shaft.

Two mass systems are modelled by the Lagrange equation [29]. The kinetic energy of the shearer cutting transmission shafting mainly includes the PMSM rotational kinetic energy and the cutting drum rotational kinetic energy, which can be expressed as follows:

\begin{matrix} E = E_{1} + E_{2} = \frac{1}{2} J_{1} θ_{1}^{2} + \frac{1}{2} J_{2} θ_{2}^{2} . \end{matrix}

(1)

The system potential energy can be represented as

\begin{matrix} V = \frac{1}{2} K {(θ_{1} - θ_{2})}^{2} . \end{matrix}

(2)

As a result of the downhole environment, water is sprayed to reduce the dust concentration, so the cutting environment is wet. In the process of cutting coal, system will produce nonlinear sliding friction forces due to relative displacement of cutting drum and coal seam. In view of the linear damping and nonlinear stick, slip frictional force is studied [26], which can be shown as follows:

\begin{matrix} \{\begin{cases} F_{1}^{c} = - C ({\dot{θ}}_{1} - {\dot{θ}}_{2}) - C^{'} {({\dot{θ}}_{1} - {\dot{θ}}_{2})}^{3}, \\ F_{2}^{c} = - C ({\dot{θ}}_{2} - {\dot{θ}}_{1}) - C^{'} {({\dot{θ}}_{2} - {\dot{θ}}_{1})}^{3} . \end{cases} \end{matrix}

(3)

The nonconservative generalized force of the electromagnetic system is electromagnetic torque and damping force. And the nonconservative generalized force of the mechanical part is the external load and damping force, and it are expressed as

\begin{matrix} Q_{i} = \sum_{j = 1}^{2} F_{j}^{j} \frac{\partial θ_{j}}{\partial q_{i}}, (i = 1,2), \end{matrix}

(4)

where ∂q_i(i = 1,2) is the generalized coordinate. Substituting equation (3) into equation (4) yields the generalized torque:

\begin{matrix} \{\begin{cases} Q_{1} = T_{m} - C ({\dot{θ}}_{1} - {\dot{θ}}_{2}) - C^{'} {({\dot{θ}}_{1} - {\dot{θ}}_{2})}^{3}, \\ Q_{2} = - T_{L} - C ({\dot{θ}}_{2} - {\dot{θ}}_{1}) - C^{'} {({\dot{θ}}_{2} - {\dot{θ}}_{1})}^{3} . \end{cases} \end{matrix}

(5)

The system Lagrange–Maxwell equation is

\begin{matrix} \frac{d}{d t} (\frac{\partial L}{\partial {\dot{q}}_{i}}) - \frac{\partial L}{\partial {\dot{q}}_{i}} + \frac{\partial F}{\partial {\dot{q}}_{i}} = Q_{i} . \end{matrix}

(6)

For the mechanical system, the dynamic equation of the PMSM can be obtained by taking the rotation angle θ₁ of the PMSM as the generalized coordinates (q₁) and substituting equations (1)∼(5) into equation (6):

\begin{matrix} J_{1} {\ddot{θ}}_{1} + K (θ_{1} - θ_{2}) + C ({\dot{θ}}_{1} - {\dot{θ}}_{2}) + C^{'} {({\dot{θ}}_{1} - {\dot{θ}}_{2})}^{3} = T_{e} . \end{matrix}

(7)

Similarly, the dynamic equation of the cutting drum is

\begin{matrix} J_{2} {\ddot{θ}}_{2} - K (θ_{1} - θ_{2}) - C ({\dot{θ}}_{1} - {\dot{θ}}_{2}) - C^{'} {({\dot{θ}}_{1} - {\dot{θ}}_{2})}^{3} = - T_{L} . \end{matrix}

(8)

The mathematical model of PMSM in abc three-phase stationary coordinate system can be obtained [30] as follows:

\begin{matrix} \{\begin{cases} u_{a} = R_{s} i_{a} + \frac{d}{d t} (L_{s} i_{a} + ψ_{f a}), \\ u_{b} = R_{s} i_{b} + \frac{d}{d t} (L_{s} i_{b} + ψ_{f b}), \\ u_{c} = R_{s} i_{c} + \frac{d}{d t} (L_{s} i_{c} + ψ_{f c}) . \end{cases} \end{matrix}

(9)

Based on the electromagnetic field theory, electromagnetic torque T_e is equal to the deflection of magnetic energy storage on the mechanical angular displacement θ₁. ψ_a, ψ_b, and ψ_c are the magnetic chain of three-phase winding. ψ_fa, ψ_fb, and ψ_fc are the magnetic chain produced by a permanent magnet on the three-phase winding, and p is the number of pole pairs:

\begin{matrix} T_{e} = \frac{1}{2} p \frac{\partial}{\partial θ_{1}} (i_{a} ψ_{a} + i_{b} ψ_{b} + i_{c} ψ_{c}) \\ = \frac{1}{2} p \frac{\partial}{\partial θ_{1}} (L_{s} i_{a} + ψ_{f a} + L_{s} i_{b} + ψ_{f b} + L_{s} i_{c} + ψ_{f c}) . \end{matrix}

(10)

By introducing the Clark transform and Park transform, the stator current of the PMSM can be transformed from the three-phase stationary coordinate system (abc) to two-phase rotating coordinate system (dq). Equation (9) can be converted to

\begin{matrix} [\begin{matrix} u_{d} \\ u_{q} \end{matrix}] = \frac{2}{3} [\begin{matrix} sin θ_{e} & \sin (θ_{e} - \frac{2 π}{3}) & \sin (θ_{e} + \frac{2 π}{3}) \\ cos θ_{e} & \cos (θ_{e} - \frac{2 π}{3}) & \cos (θ_{e} + \frac{2 π}{3}) \end{matrix}] [\begin{matrix} u_{a} \\ u_{b} \\ u_{c} \end{matrix}] \\ = [\begin{matrix} R_{d} i_{d} + L_{d} \frac{d i_{d}}{d t} - p ω_{1} L_{q} i_{q} \\ R_{q} i_{q} + L_{q} \frac{d i_{q}}{d t} + ω_{1} L_{d} i_{d} + ω_{1} ψ_{f} \end{matrix}], \end{matrix}

(11)

where p is the number of pole pairs, R_d = R_q = R, i_d and i_q are the direct and quadrature axis current in the dq coordinate system, L_d and L_q are the direct and quadrature axis inductor in the dq coordinate system and L_d = L_q in stick-type PMSM, ψ_f is the magnetic chain of the permanent magnets, and θ_e is the electric mechanical angular displacement.

Based on the electromagnetic field theory, in the two-phase rotating coordinate system (dq), the electromagnetic torque T_e is

\begin{matrix} T_{e} = \frac{3}{2} p i_{q} [i_{d} (L_{d} - L_{q}) + ψ_{f}] \\ = \frac{3}{2} p ψ_{f} i_{q} . \end{matrix}

(12)

When the load torque and the electromagnetic torque are balanced, the mechanical angular velocity of the rotor is constant; therefore, θ₁ = ∫Ωdt + φ₁, θ₂ = ∫Ωdt + φ₂, θ₁ − θ₂ = φ₁ − φ₂, and J₁φ₁ + J₂φ₂ = 0 [31], so

\begin{matrix} \{\begin{cases} θ_{1} - θ_{2} = φ_{1} - φ_{2} = \frac{J_{1} + J_{2}}{J_{2}} φ_{1}, \\ ω_{1} = {\dot{θ}}_{1} = Ω + {\dot{φ}}_{1} = Ω + \frac{J_{2}}{J_{1} + J_{2}} ({\dot{θ}}_{1} - {\dot{θ}}_{2}) . \end{cases} \end{matrix}

(13)

Finally, substituting equation (13) into equation (11) and combing with equations (7), (8), and (12), the electromechanical coupling torsional vibration model of the cutting transmission shafting is

\begin{matrix} \{\begin{cases} {\dot{I}}_{d} = - \frac{R}{L_{d}} I_{d} + \frac{L_{q}}{L_{d}} I_{q} [Ω + \frac{J_{2}}{J_{1} + J_{2}} ({\dot{θ}}_{1} - {\dot{θ}}_{2})] p + \frac{u_{d}}{L_{d}}, \\ {\dot{I}}_{q} = - \frac{R}{L_{q}} I_{q} - \frac{L_{d}}{L_{q}} I_{d} [Ω + \frac{J_{2}}{J_{1} + J_{2}} ({\dot{θ}}_{1} - {\dot{θ}}_{2})] p - \frac{ψ_{f}}{L_{q}} [Ω + \frac{J_{2}}{J_{1} + J_{2}} ({\dot{θ}}_{1} - {\dot{θ}}_{2})] + \frac{u_{q}}{L_{q}} p, \\ {\ddot{θ}}_{1} + \frac{K}{J_{1}} (θ_{1} - θ_{2}) + \frac{C}{J_{1}} ({\dot{θ}}_{1} - {\dot{θ}}_{2}) + \frac{C^{'}}{J_{1}} {({\dot{θ}}_{1} - {\dot{θ}}_{2})}^{3} = - \frac{3 p}{2 J_{1}} ψ_{f} I_{q}, \\ {\ddot{θ}}_{2} - \frac{K}{J_{2}} (θ_{1} - θ_{2}) - \frac{C}{J_{2}} ({\dot{θ}}_{1} - {\dot{θ}}_{2}) - \frac{C^{'}}{J_{2}} {({\dot{θ}}_{1} - {\dot{θ}}_{2})}^{3} = - \frac{T_{L}}{J_{2}} . \end{cases} \end{matrix}

(14)

In equation (13), I_d, I_q, θ₁, and θ₂ are variable items which will change with time. This system will exhibit complex dynamical behavior due to the variation of the damping C.

3. Cutting Transmission System Bifurcation Analysis

For the convenience of the calculation, the difference value of two angles (θ₁, θ₂) is used to describe the strength of the vibration. Therefore, let the third type minus the fourth type in equation (14) merge nonvariable items in the system, defined as follows:

\begin{matrix} x_{1} = I_{d}, \\ x_{2} = I_{q}, \\ x_{3} = θ_{1} - θ_{2}, \\ {\dot{x}}_{3} = x_{4} = {\dot{θ}}_{1} - {\dot{θ}}_{2}, \\ {\dot{x}}_{4} = {\ddot{θ}}_{1} - {\ddot{θ}}_{2}, \\ a = - \frac{R}{L_{d}}, \\ b = \frac{Ω p L_{q}}{L_{d}}, \\ c = \frac{p L_{q}}{L_{d}} \frac{J_{2}}{J_{1} + J_{2}}, \\ d = - \frac{Ω p L_{d}}{L_{q}}, \\ e = - \frac{R}{L_{q}}, \\ f = - \frac{p L_{d}}{L_{q}} \frac{J_{2}}{J_{1} + J_{2}}, \\ g = - \frac{p ψ_{f}}{L_{q}} \frac{J_{2}}{J_{1} + J_{2}}, \\ h = - \frac{3 p ψ_{f}}{2 J_{1}}, \\ m = - (\frac{K}{J_{1}} + \frac{K}{J_{2}}), \\ k = - (\frac{C^{'}}{J_{1}} + \frac{C^{'}}{J_{2}}), \\ s = \frac{u_{q}}{L_{q}} - \frac{Ω p ψ_{f}}{L_{q}}, \\ n = - (\frac{C}{J_{1}} + \frac{C}{J_{2}}), \\ l = \frac{u_{d}}{L_{d}}, \\ z = T_{L}, \end{matrix}

(15)

where x₁ is the quadrature axis current in the dq coordinate system, x₂ is the direct axis current in the dq coordinate system, x₃ is the difference between the mechanical angle of the PMSM and the angle of the cylinder, and x₄ is x₃’s derivative of time.

Therefore, equation (14) is simplified to

\begin{matrix} \dot{x} = g (x, C), \\ \{\begin{cases} {\dot{x}}_{1} = a x_{1} + b x_{2} + c x_{2} x_{4} + l, \\ {\dot{x}}_{2} = d x_{1} + e x_{2} + f x_{1} x_{4} + g x_{4} + s, \\ {\dot{x}}_{3} = x_{4}, \\ {\dot{x}}_{4} = h x_{2} + m x_{3} + n x_{4} + k x_{4}^{3} + z . \end{cases} \end{matrix}

(16)

After the cutting transmission system of the shearer is changed to semidirect drive, the damping will change in the following cases: (1) the intensity of the vibration in the shaft system and (2) the wearing and the lubrication condition of the shaft. In addition, there may be oscillation vibration and Hopf bifurcation with the damping changes in the shafting, so the damping C is selected as the bifurcation parameter.

The equilibrium point of equation (16) can be transferred to the coordinate origin through simple linear transformation. Therefore, the dynamic characteristics of the system balance at the origin are of universal significance without loss of generality. Hence, let l = 0, s = 0, and z = 0, and then equilibrium point can be transferred to the coordinate origin x₀ = (0,0,0,0) for equation (16). The Jacobian matrix and nonlinear terms of the system at x₀, respectively, are as follows:

\begin{matrix} A (x_{0}, C) = [\begin{matrix} a & b & 0 & 0 \\ d & e & 0 & g \\ 0 & 0 & 0 & 1 \\ 0 & h & m & n \end{matrix}], \\ f (x_{0}, C) = [\begin{matrix} c x_{2} x_{4} \\ f x_{1} x_{4} \\ 0 \\ k x_{4}^{3} \end{matrix}] . \end{matrix}

(17)

According to the Hopf bifurcation theory, the necessary and sufficient conditions for Hopf bifurcation are expressed as follows: there are only one pair of conjugate imaginary roots in the characteristic root of A(x₀, C) and the other n − 2 characteristic roots have negative real parts. The system is unstable at the origin when positive real part exists. While the eigenvalues have all negative real parts, the system is asymptotically stable. In order to simplify the calculation, the Hurwitz criterion is used to determine the existence of the Hopf bifurcation in this paper.

The characteristic polynomial of A(x₀, C) can be expressed as

\begin{matrix} λ^{4} + p_{1} λ^{3} + p_{2} λ^{2} + p_{3} λ^{1} + p_{4} = 0, \end{matrix}

(18)

where p₁ = −n − e − a, p₂ = ae − m − b d + an − gh + en, and p₃ = am + em + agh − aen + b dn , p₄ = b dm − aem.

Hurwitz criterion can be shown as

\begin{matrix} \{\begin{cases} p_{i} (C^{*}) > 0, & (i = 1,2,3,4), \\ Δ_{i} (C^{*}) > 0, & (i = 1,2,3), \\ Δ_{3} (C^{*}) = 0, \\ {\frac{d (Δ_{3} (C))}{d (C)}|}_{C = C^{*}} \neq 0. \end{cases} \end{matrix}

(19)

In equation (19), Δ_i is the order principal minor determinant of equation (18):

\begin{matrix} Δ_{i} = [\begin{matrix} p_{1} & p_{3} & p_{5} & \dots & p_{21 i -} \\ 1 & p_{2} & p_{4} & \dots & p_{22 i -} \\ 0 & p_{1} & p_{3} & \dots & p_{23 i -} \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ 0 & 0 & 1 & \dots & p_{i} \end{matrix}], \end{matrix}

(20)

where the possible threshold is derived from Δ₃(C^∗) = 0. And if the resulting point C^∗ satisfies the other requirements of equation (19) at the same time, the Hopf bifurcation occurs at this point. The parameters in the model are selected according to the data in the actual system shearer. Therefore, the main parameters of semidirect cutting transmission system in the form are as follows:

\begin{matrix} J_{1} = 1.96 kg \cdot m^{2}, \\ J_{2} = 1.425 kg \cdot m^{2}, \\ R_{d} = R_{q} = R = 0.136 Ω, \\ L_{d} = L_{q} = 0.0284 H, \\ ψ_{f} = 1.235 v \cdot s, \\ Ω = 5 rad / s, \\ K = 4100 N \cdot m / rad, \end{matrix}

(21)

where Ω is the rated speed of PMSM, J₁ is the moment of inertia for PMSM, J₂ is the sum of the moment of the cutting drum and the transformation of the gear and other elements inertia, and K is the stiffness coefficient of the elastic torque shaft. R, L_d, L_q, and ψ_f can be obtained, respectively, by off-line identification of PMSM.

By calculation, the couple transmission system of the shearer semidirect drive met equation (19) at C^∗ = 41.4675. In this case, the characteristic root of A(x₀, C) has one pair of conjugate imaginary roots. The pure virtual root is ω₀i, and vector U and W are right and left feature vectors corresponding to the characteristic root A(x₀, C^∗), respectively. Their relationship can be expressed as

\begin{matrix} \{\begin{cases} U A = ω_{0} i U, \\ A W = ω_{0} i W, \\ U W = 1. \end{cases} \end{matrix}

(22)

Through equation (22), the stability index b of the Hopf bifurcation is defined as

\begin{matrix} b = Re (- U f_{x x x} W W W^{*} + 2 U f_{x x} W A^{- 1} (0) f_{x x} W W^{*} + U f_{x x} W^{*} \times {[A (0) - 2 i ω_{0} I]}^{- 1} f_{x x} W W) . \end{matrix}

(23)

In equation (23), W^∗ is the conjugate plural of W, and

A (0) = {A (x_{0}, C)|}_{C = C^{*}}

\begin{matrix} f_{x x x} W W W^{*} = {(\frac{\partial}{\partial x} (\frac{\partial}{\partial x} (\frac{\partial f (x, C)}{\partial x} \times W) W) W)|}_{C = C^{*}, x = x_{0}} . \end{matrix}

(24)

According to the value of $b_{C^{*}}$ , the stability of periodic solutions of Hopf bifurcation in the original system can be determined. If $b_{C^{*}} < 0$ , the bifurcation type of the system is subcritical Hopf bifurcation, and the periodic solution is unstable. On the contrary, $b_{C^{*}} > 0$ , the bifurcation type of the system is supercritical Hopf bifurcation, and the bifurcated periodic solution is stable. The stability index of Hopf bifurcation is $b_{C^{*}} = 0.001740 >$ through calculation, and therefore, the type of Hopf bifurcation is supercritical Hopf bifurcation.

The Runge–Kutta method is used to verify the dynamic characteristics generated by the system Hopf bifurcation point C^∗, and the parameters are brought into equation (16). In Figure 3 of torsional vibration amplitude figure variation with the damping C, the system exhibits different dynamics on both sides of the bifurcation point because of supercritical Hopf bifurcation. When C is greater than the bifurcation point C^∗, the running state of the main transmission system is stable and no limit cycle appears, as shown in Figure 4.

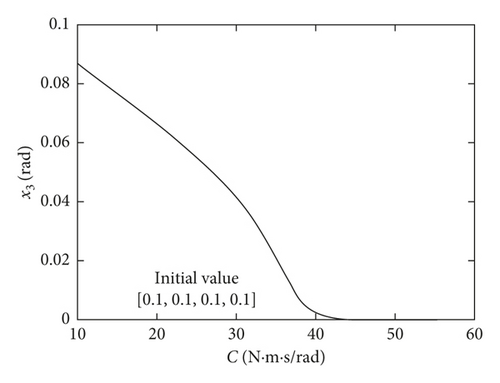
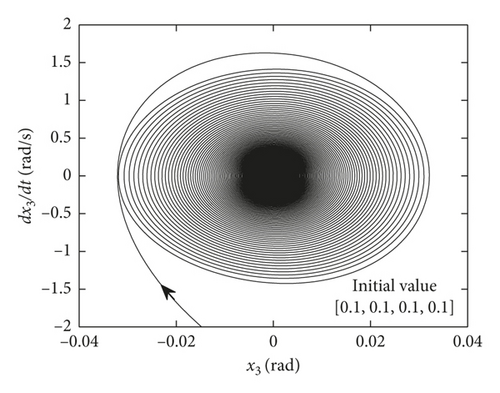
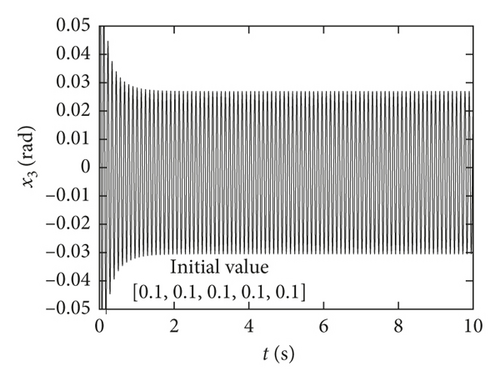
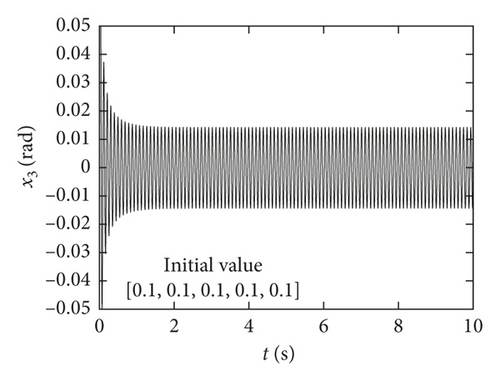
When C is smaller than the bifurcation point C^∗, the system exhibits a stable limit cycle motion. Figure 3 shows that when the C is less than the critical value C^∗, the smaller the value of the damping C, the bigger the limit cycle. At the same time, when the damping is greater than the critical damping, the amplitude of the vibration is close to 0. It can be available from the comparison of time-history response of identical initial value in Figure 5, and the amplitude of the limit cycles is obviously larger in the case of smaller damping. Furthermore, when C is fixed, the amplitude of the limit cycle has nothing to do with the initial value, as shown in Figure 6, which shows that the amplitudes are basically the same under two different initial values. From the above analysis, the conclusion of the simulation results is consistent with the theoretical analysis.

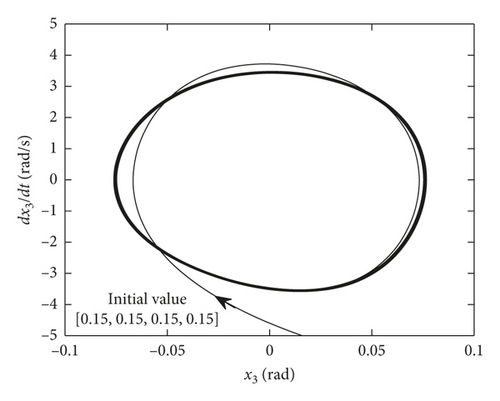
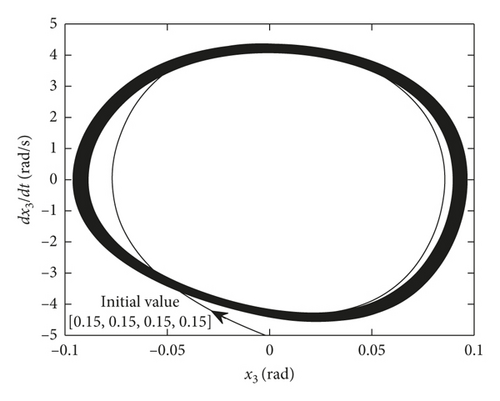
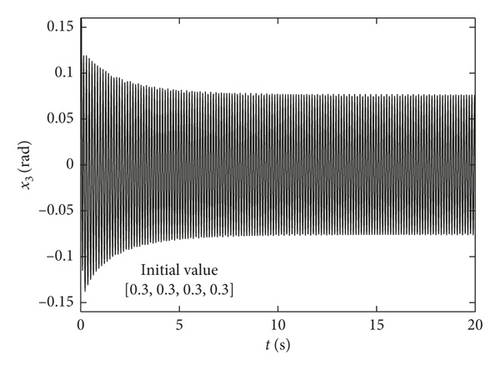
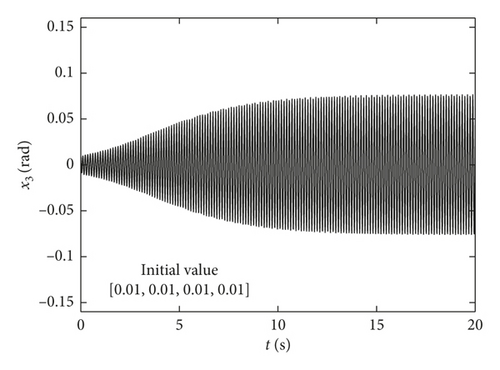
4. Cutting Transmission System Vibration Control

The numerical simulation results in Figures 3 and 5 show that, the system oscillates and the limit cycle appears when the damping C is smaller than C^∗. When the system responds to a smaller limit cycle, it has little harm to the elastic torque shaft. However, when the external conditions cause damping C to be smaller, the amplitude of the limit cycle will increase. At this time, the cutting transmission shaft system of the shearer will have strong vibration, which will cause great harm to the fatigue damage of the elastic torque shaft. In order to control the unstable oscillation of shafting, the washout filter controller is introduced, which is a kind of the extended linear or nonlinear state feedback method.

The state equation of the washout filter can be represented as

\begin{matrix} \dot{ω} = α - ε ω, \end{matrix}

(25)

where ω is the state variables of the washout filter, α is the input variables, ε is the time constant, and α − εω is the output variable. In this paper, from the perspective of implementation, x₂ is used as the input variable, and x₅ is used as the state variables. In nonlinear systems with Hopf bifurcation, the squared term and the cubic term can affect the stability of Hopf bifurcation. So, nonlinear feedback controller can be shown as

w = k_{m} (x_{2} - ε x_{5}) + k_{n} {(x_{2} - ε x_{5})}^{3}

; k_m and k_n are the linear gains and nonlinear control gain, respectively. w is added to the second term in equation (16) as the output feedback.

So, the controlled system can be shown as

\begin{matrix} \{\begin{cases} {\dot{x}}_{1} = a x_{1} + b x_{2} + c x_{2} x_{4}, \\ {\dot{x}}_{2} = d x_{1} + e x_{2} + f x_{1} x_{4} + g x_{4} + w, \\ {\dot{x}}_{3} = x_{4}, \\ {\dot{x}}_{4} = h x_{2} + m x_{3} + n x_{4} + k x_{4}^{3}, \\ {\dot{x}}_{5} = x_{2} - ε x_{5} . \end{cases} \end{matrix}

(26)

The Jacobian matrix and nonlinear terms of the control system can be represented as

\begin{matrix} B (x_{0}, C) = [\begin{matrix} a & b & 0 & 0 & 0 \\ d & e + k_{m} & 0 & 0 & - ε k_{m} \\ 0 & 0 & 0 & 1 & 0 \\ 0 & h & m & n & 0 \\ 0 & 1 & 0 & 0 & - ε \end{matrix}], \\ h (x_{0}, C) = [\begin{matrix} c x_{2} x_{4} \\ f x_{1} x_{4} + k_{n} {(x_{2} - ε x_{5})}^{3} \\ 0 \\ k x_{4}^{3} \\ 0 \end{matrix}] . \end{matrix}

(27)

If ε = 0.1, k_m ≠ 0, k_n = 0, and C = 41.4675, the washout filter will not change the position of the equilibrium point. And the characteristic equation of B(x₀, C) in equation (26) is

\begin{matrix} λ^{5} + p_{1} λ^{4} + p_{2} λ^{3} + p_{3} λ^{2} + p_{4} λ + p_{5} = 0, \end{matrix}

(28)

where p₁ = 59.93 − k_m, p₂ = −55.05k_m + 5972, p₃ = −5210k_m + 124400, p₄ = −23800k_m + 8077000, and p₅ = 806400.

If all eigenvalues of matrix B(x₀, C) have the negative real part, the controlled system will not occur Hopf bifurcation at C^∗, which means Δ_i > 0(i = 1,2,3,4), k_m < −0.006597. When ε = 0.1, k_m = −1, and k_n = 0, the roots of B(x₀, C) have negative real parts at this time, and the system is asymptotically stable, as shown in Figure 7(b). At this moment, the bifurcation characteristics are controlled at the Hopf bifurcation point C^∗, but the other dynamics of the system have not been determined.

According to the Hopf bifurcation theory, when Hopf bifurcation occurs at the equilibrium point, system (26) must satisfy the condition of equation (29). The relationship between the linear control gain k_m and the bifurcation critical point C^∗ can be drawn, which is shown in Figure 8. When k_m = 0, the controlled system has Hopf bifurcation same as the original system at C = 41.4675. And if k_m = −1, the controlled system has the Hopf bifurcation point at C = 18.09. Comparing to the original system, the system stability domain increases greatly. Therefore, when the linear gain part of the controller selects the appropriate value, the bifurcation characteristics of the nonlinear system can be effectively controlled and the bifurcation point is transferred to the safe working area:

\begin{matrix} \{\begin{cases} p_{i} (C^{*}) > 0, & (i = 1,2,3,4,5), \\ Δ_{i} (C^{*}) > 0, & (i = 1,2,3,4), \\ Δ_{4} (C^{*}) = 0, \\ {\frac{d (Δ_{4} (C))}{d (C)}|}_{C = C^{*}} \neq 0. \end{cases} \end{matrix}

(29)

Take ε = 0.1, k_m = −1, and k_n ≠ 0, and the Hopf bifurcation of the controlled system occurs at C = 18.09 through calculation. The Jacobian matrix B(x₀, C) has a pair of pure imaginary roots λ_1,2 = ±50.5163i, whose corresponding eigenvectors can be expressed as

\begin{matrix} φ = \bar{φ} = [\begin{matrix} 0 \\ - 5.29892.6000 - i \\ 0.03620.0178 + i \\ 0.66150.0432 + i \\ 0.00080.0003 + i \end{matrix}] . \end{matrix}

(30)

Since it is more complicated to calculate the three-order normal form of the controlled system through the central manifold theorem, the direct calculation method of normal form in [32] can be used. This method only needs to calculate the pure virtual root of the controlled system and its corresponding eigenvector, and then the normal form of the controlled system can be obtained through the nonlinear transformation. The linear transformation is introduced here:

\begin{matrix} X = φ u + \bar{φ} \bar{u} + \sum_{j + k \geq 2} H_{j k} u^{j} {\bar{u}}^{k} . \end{matrix}

(31)

The Hopf bifurcation specification of the controlled system can be shown as

\begin{matrix} \dot{u} = 50.5163 i u + E u^{2} \bar{u} . \end{matrix}

(32)

The nonlinear transformation is introduced to the nonlinear terms, and then the polynomial form of u and

\bar{u}

as follows:

\begin{matrix} f (X) = \sum_{j + k \geq 2} F_{j k} u^{j} {\bar{u}}^{k}, \end{matrix}

(33)

where F₂₁ is coefficient vector corresponding to

u^{2} \bar{u}

\begin{matrix} F_{21} = [\begin{matrix} F_{21,1} & F_{21,2} & 0 & F_{21,4} & 0 \end{matrix}], \\ F_{21,1} = c (φ_{2} H_{11,4} + {\bar{φ}}_{2} H_{20,4} + φ_{4} H_{11,2} + {\bar{φ}}_{4} H_{20,2}) = 0.00220.0015 + i, \\ F_{21,2} = f (φ_{1} H_{11,4} + {\bar{φ}}_{1} H_{20,4} + φ_{4} H_{11,1} + {\bar{φ}}_{4} H_{20,1}) + k_{n} {(φ_{2} - 0.1 φ_{5})}^{2} ({\bar{φ}}_{2} - 0.1 {\bar{φ}}_{5}) \\ = k_{n} (0.47510.0009404 + i) + 0.0019230.002212 - i, \\ F_{21,4} = k φ_{4}^{2} {\bar{φ}}_{4} = 1.17352.5612 \times 10^{- 4} + \times 10^{- 4} i . \end{matrix}

(34)

In the above equation,

\begin{matrix} \{\begin{cases} H_{11} = - A^{- 1} F_{11}, H_{20} = {[250.5163 \times i I - A]}^{- 1} F_{20}, \\ F_{11} = {[0000 φ_{2} {\bar{φ}}_{4} + {\bar{φ}}_{2} ϖ_{4}]}^{T}, \\ F_{20} = {[0000 φ_{2} {\bar{φ}}_{4}]}^{T} . \end{cases} \end{matrix}

(35)

Finally, the parameters E is

\begin{matrix} E = 0.0042650.4751 + k_{n} + (0.00094040.0004616 k_{n} -) i . \end{matrix}

(36)

So normal form of the controlled system can be expressed as

\begin{matrix} \dot{u} = 50.5163 i u + [0.0042650.4751 + k_{n} + (0.00094040.0004616 k_{n} -) i] u^{2} \bar{u} . \end{matrix}

(37)

According to the Hopf bifurcation theory, the controlled system will have a supercritical bifurcation at C = 18.09 when Re(E) < 0 and k_n < −0.009. The bifurcation type of the system stays the same by calculating. At the same time, subcritical Hopf bifurcation will occur at k_n > −0.009, as shown in Figure 9. It can be seen from Figure 9(b) that the time-history response is stable when the initial values are close to the equilibrium point. When initial values are far from the equilibrium point, the time-history response increases with time in Figure 9(a). It is necessary to avoid the generation of subcritical bifurcation in the actual situation.

The amplitude of the limit cycle can be effectively controlled through the selection of the value of k_m and k_n reasonably. Figure 10 shows that the amplitude of the controlled system is obviously lower than that of the original system without subcritical Hopf bifurcation (Figure 10(b) is the time-history diagram of the controlled system at k_m = −1 and k_n = −1), and the significant effect is achieved after addition of the control system. In contrast to the two controlled systems in Figure 11 (k_m = −1 and k_n = −0.1 in Figure 11(a); k_m = −1 and k_n = −10 in Figure 11(b)), if the case of k_m is fixed, the smaller the k_n is, the smaller the amplitude of the limit cycle is.

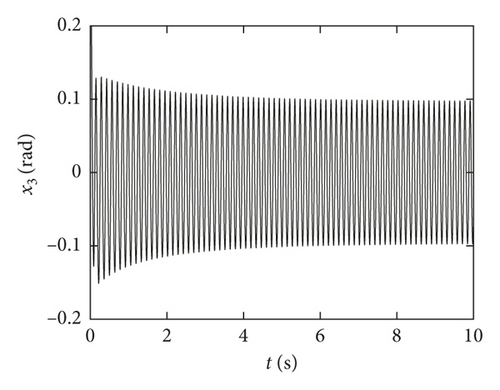
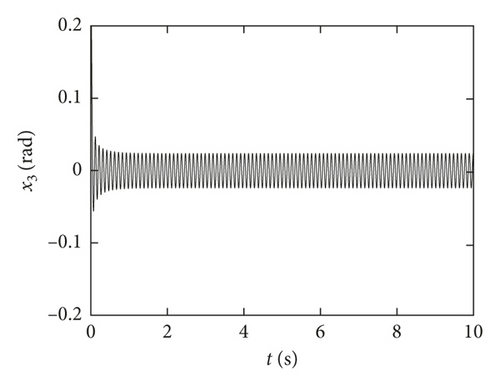
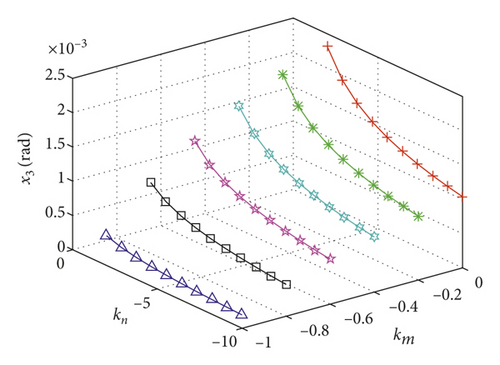
The bifurcation point will vary with k_m, and the bifurcation type will change with k_n. At the same time, it is necessary to calculate the eigenvalue and eigenvector of the system to determine the type of bifurcation, but the eigenvalue and eigenvector are difficult to calculate due to the change of k_m. So it is hard to calculate the type of bifurcation for the system through the theoretical method when k_m and k_n change simultaneously. However according to the simulation, the subcritical Hopf bifurcation only occurs when k_n is near 0. Figure 12 shows the amplitude variation of k_m and k_n change at the same time when k_n is far less than 0. It can be seen from Figure 12 that the vibration amplitude decreases with the reduction of linear gain k_m and nonlinear gain k_n.

5. Conclusion

In this paper, the Hopf bifurcation caused by the change of the system damping was studied concerning the shearer transmission shafting semidirect driven by the PMSM. The electromechanical coupling dynamic model was established by the Lagrange–Maxwell equation. The dynamic bifurcation behavior of the system transmission shafting was analyzed through theoretical analysis and numerical simulation. Based on the washout filter, the torsional vibration bifurcation of the shafting was effectively controlled. The research work of this article mainly includes the following:

(1)
Due to the harsh environment of coal cutting, there is the supercritical and subcritical Hopf bifurcation with the diversification of the damping in the cutting transmission system. When the C is less than the critical value C^∗, the smaller the value of the damping C, the bigger the limit cycle in supercritical Hopf bifurcation. Simultaneously, the amplitude of the limit cycle has nothing to do with the initial value.
(2)
Based on the normative theory, the Hopf bifurcation controller of the shearer cutting transmission shaft was designed by the washout filter. The results show that the system stability domain increases with the linear gain of the controller and the generation of the subcritical Hopf bifurcation can be inhibited by the cube nonlinear parts.
(3)
For supercritical Hopf bifurcation, selecting the linear and nonlinear gain reasonably can effectively control the torsional vibration and the shafting torsional vibration. And the limit cycle amplitude decreases with the nonlinear gain of the controller when the linear gain is zero. At the same time, when k_n and k_m are varied simultaneously, the limit cycle amplitude decreases with the reduction of linear gain k_m and nonlinear gain k_n in supercritical Hopf bifurcation.

All these results are of important theoretical significance to reduce the torsional vibration caused by nonlinear factors in the shearer cutting transmission system and provide a guarantee for the safe and reliable application of the low-speed and large-torque PMSM on the shearer.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant no. 51775543), the Key Research and Development Project of Xuzhou (Grant no. KC17014), and the project funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD).

Open Research

Data Availability

All data included in this study are available upon request by contact with the corresponding author.

References

1 Wang G., Jiao S., and Cheng G., Fully mechanized coal mining technology for thin coal seam under complicated geological conditions, Energy Exploration & Exploitation. (2011) 29, no. 2, 169–177, https://doi.org/10.1260/0144-5987.29.2.169, 2-s2.0-79956075043.
10.1260/0144-5987.29.2.169
Web of Science® Google Scholar
2 Paithankar A. and Chatterjee S., Forecasting time-to-failure of machine using hybrid Neuro-genetic algorithm—a case study in mining machinery, International Journal of Mining, Reclamation and Environment. (2016) 32, no. 3, 182–195, https://doi.org/10.1080/17480930.2016.1262499, 2-s2.0-85000838190.
10.1080/17480930.2016.1262499
Web of Science® Google Scholar
3 Si L., Wang Z., Liu X., Tan C., and Zhang L., Cutting state diagnosis for shearer through the vibration of rocker transmission part with an improved probabilistic neural network, Sensors. (2016) 16, no. 4, https://doi.org/10.3390/s16040479, 2-s2.0-84962877329.
10.3390/s16040479
Web of Science® Google Scholar
4 Reid A. W., McAree P. R., Meehan P. A., and Gurgenci H., Longwall shearer cutting force estimation, Journal of Dynamic Systems, Measurement, and Control. (2014) 136, no. 3, 833–846, https://doi.org/10.1115/1.4026326, 2-s2.0-84894499140.
10.1115/1.4026326
Web of Science® Google Scholar
5 Qin X., Pang R., Zhao X., and Li F., Fracture failure analysis of internal teeth of ring gear used in reducer of coal mining machine, Engineering Failure Analysis. (2017) 84, 70–76, https://doi.org/10.1016/j.engfailanal.2017.08.022, 2-s2.0-85033392770.
10.1016/j.engfailanal.2017.08.022
Web of Science® Google Scholar
6 Sheng L., Li W., Wang Y., Fan M., and Yang X., Sensorless control of a shearer short-range cutting interior permanent magnet synchronous motor based on a new sliding mode observer, IEEE Access. (2017) 5, no. 99, 18439–18450, https://doi.org/10.1109/access.2017.2734699, 2-s2.0-85028711483.
10.1109/ACCESS.2017.2734699
Web of Science® Google Scholar
7 Hu T., Tang R., and Li Y., Thermal and fluid flow field calculation and analysis of preparation of semi-direct drive PMWG, Proceedings of International Conference on Electrical Machines and Systems (ICEMS), October 2013, Busan, South Korea, 1153–1156.
Google Scholar
8 Teng W., Jiang R., Ding X., Liu Y., and Ma Z., Detection and quantization of bearing fault in direct drive wind turbine via comparative analysis, Shock and Vibration. (2016) 2016, 12, 2378435, https://doi.org/10.1155/2016/2378435, 2-s2.0-84975089346.
10.1155/2016/2378435
Web of Science® Google Scholar
9 Lu E., Li W., Yang X., and Xu S., Composite sliding mode control of a permanent magnet direct-driven system for a mining scraper conveyor, IEEE Access. (2017) 5, 22399–22408, https://doi.org/10.1109/access.2017.2761846, 2-s2.0-85038365732.
10.1109/ACCESS.2017.2761846
Web of Science® Google Scholar
10 Wang X. and Wang M., A hyperchaos generated from Lorenz system, Physica A: Statistical Mechanics and Its Applications. (2008) 387, no. 14, 3751–3758, https://doi.org/10.1016/j.physa.2008.02.020, 2-s2.0-41649108176.
10.1016/j.physa.2008.02.020
Web of Science® Google Scholar
11 Ma C. and Wang X., Hopf bifurcation and topological horseshoe of a novel finance chaotic system, Communications in Nonlinear Science and Numerical Simulation. (2012) 17, no. 2, 721–730, https://doi.org/10.1016/j.cnsns.2011.05.029, 2-s2.0-80052361678.
10.1016/j.cnsns.2011.05.029
Web of Science® Google Scholar
12 Wenzhi G. and Zhiyong H., Active control and simulation test study on torsional vibration of large turbo-generator rotor shaft, Mechanism and Machine Theory. (2010) 45, no. 9, 1326–1336, https://doi.org/10.1016/j.mechmachtheory.2010.04.005, 2-s2.0-77953694389.
10.1016/j.mechmachtheory.2010.04.005
Web of Science® Google Scholar
13 Al-Bedoor B. O., Transient torsional and lateral vibrations of unbalanced rotors with rotor-to-stator rubbing, Journal of Sound and Vibration. (2000) 229, no. 3, 627–645, https://doi.org/10.1006/jsvi.1999.2513, 2-s2.0-0033734265.
10.1006/jsvi.1999.2513
Web of Science® Google Scholar
14 Liu S., Zhao S., Niu B., Li J., and Li H., Stability analysis of a nonlinear electromechanical coupling transmission system with time delay feedback, Nonlinear Dynamics. (2016) 86, no. 3, 1863–1874, https://doi.org/10.1007/s11071-016-3000-1, 2-s2.0-84983782671.
10.1007/s11071-016-3000-1
Web of Science® Google Scholar
15 Niu X. and Qiu J., Investigation on torsional instability, bifurcation, and chaos of a generator set, IEEE Power Engineering Review. (2007) 22, no. 3, https://doi.org/10.1109/mper.2002.4312049.
10.1109/mper.2002.4312049
Google Scholar
16 Yuan H., Study on the stability and bifurcation behavior of the vibration system with nonlinear hysteresis properties, Journal of Vibration and Shock. (2001) 20, no. 3.
Google Scholar
17 Saigo M., Tanaka N., and Nam D. H., Torsional vibration suppression by wave-absorption control with imaginary system, Journal of Sound and Vibration. (2004) 270, no. 4-5, 657–672, https://doi.org/10.1016/s0022-460x(03)00185-8, 2-s2.0-1542316081.
10.1016/S0022-460X(03)00185-8
Web of Science® Google Scholar
18 Xu X., Han Q., and Chu F., Nonlinear vibration of a generator rotor with unbalanced magnetic pull considering both dynamic and static eccentricities, Archive of Applied Mechanics. (2016) 86, no. 8, 1521–1536, https://doi.org/10.1007/s00419-016-1133-9, 2-s2.0-84962016532.
10.1007/s00419-016-1133-9
Web of Science® Google Scholar
19 Yu Q., A study of destabilizing oscillation in the mechanics and electricity coupling system by dynamical bifurcation method, Acta Mechanica Sinica. (2004) 36, no. 2.
Google Scholar
20 Li Z., Zheng L., Gao W., and Zhan Z., Electromechanical coupling mechanism and control strategy for in-wheel motor driven electric vehicles, IEEE Transactions on Industrial Electronics. (2018) 66, no. 6, 4524–4533, https://doi.org/10.1109/tie.2018.2863204.
10.1109/TIE.2018.2863204
Web of Science® Google Scholar
21 Vromen T., van de Wouw N., Doris A., Astrid P., and Nijmeijer H., Nonlinear output-feedback control of torsional vibrations in drilling systems, International Journal of Robust and Nonlinear Control. (2017) 27, no. 17.
10.1002/rnc.3759
Web of Science® Google Scholar
22 Gustavsson R. K. and Aidanpää J.-O., The influence of nonlinear magnetic pull on hydropower generator rotors, Journal of Sound and Vibration. (2006) 297, no. 3-5, 551–562, https://doi.org/10.1016/j.jsv.2006.04.016, 2-s2.0-33747666120.
10.1016/j.jsv.2006.04.016
Web of Science® Google Scholar
23 Szolc T., Konowrocki R., Michajłow M., and Pręgowska A., An investigation of the dynamic electromechanical coupling effects in machine drive systems driven by asynchronous motors, Mechanical Systems and Signal Processing. (2014) 49, no. 1-2, 118–134, https://doi.org/10.1016/j.ymssp.2014.04.004, 2-s2.0-84902543522.
10.1016/j.ymssp.2014.04.004
Web of Science® Google Scholar
24 Ju J., Li W., Wang Y., Fan M., and Yang X., Dynamics and nonlinear feedback control for torsional vibration bifurcation in main transmission system of scraper conveyor direct-driven by high-power PMSM, Nonlinear Dynamics. (2018) 93, no. 2, 307–321, https://doi.org/10.1007/s11071-018-4193-2, 2-s2.0-85044020023.
10.1007/s11071-018-4193-2
Web of Science® Google Scholar
25 Jacobs W., Boonen R., and Sas P., The influence of the lubricant film on the stiffness and damping characteristics of a deep groove ball bearing, Mechanical Systems and Signal Processing. (2014) 42, no. 1-2, 335–350, https://doi.org/10.1016/j.ymssp.2013.07.018, 2-s2.0-84887035858.
10.1016/j.ymssp.2013.07.018
Web of Science® Google Scholar
26 Thomsen J. J. and Fidlin A., Analytical approximations for stick–slip vibration amplitudes, International Journal of Non-Linear Mechanics. (2003) 38, no. 3, 389–403.
10.1016/S0020-7462(01)00073-7
Web of Science® Google Scholar
27 Zi B. and Zhou B., A modified hybrid uncertain analysis method for dynamic response field of the LSOAAC with random and interval parameters, Journal of Sound and Vibration. (2016) 374, 111–137, https://doi.org/10.1016/j.jsv.2016.03.032, 2-s2.0-84964380429.
10.1016/j.jsv.2016.03.032
Web of Science® Google Scholar
28 Zhou L., Zheng S. F., and Lian X. M., Modeling and research on torsional vibration of transmission system under speeding-up condition, Journal of Vibration Engineering. (2010) 23, no. 6, 601–605.
Google Scholar
29 Neimark J. I., Mathematical Models in Natural Science and Engineering, 2012, Springer Science & Business Media, Berlin, Germany.
Google Scholar
30 Hintenaus P., Energy Conversion-Motor Control, 2015, Springer International Publishing, Berlin, Germany.
10.1007/978-3-319-10680-9_8
Google Scholar
31 Chen X., Hu J., Peng Z., and Yuan C., Bifurcation and chaos analysis of torsional vibration in a PMSM-based driven system considering electromechanically coupled effect, Nonlinear Dynamics. (2017) 88, no. 1, 277–292, https://doi.org/10.1007/s11071-017-3419-z, 2-s2.0-85013669505.
10.1007/s11071-017-3419-z
Web of Science® Google Scholar
32 Wu Z. Q., Normal form model and direct method of the nonlinear system, 1996, University of Tianjin, Tianjin, China, Ph.D. dissertation.
Google Scholar

Citing Literature

All articles

Nonlinear Torsional Vibration Analysis and Control of Semidirect Electromechanical Coupling Transmission System in Shearer

Abstract

1. Introduction

2. Electromechanical Coupling Torsional Vibration Modelling

3. Cutting Transmission System Bifurcation Analysis

4. Cutting Transmission System Vibration Control

5. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Nonlinear Torsional Vibration Analysis and Control of Semidirect Electromechanical Coupling Transmission System in Shearer

Abstract

1. Introduction

2. Electromechanical Coupling Torsional Vibration Modelling

3. Cutting Transmission System Bifurcation Analysis

4. Cutting Transmission System Vibration Control

5. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information