Robust H_∞ consensus control problems of linear swarm systems with parameter uncertainties and time-varying delays are investigated. In this literature, a linear consensus protocol for high-order discrete-time swarm systems is proposed. Firstly, the robust H_∞ consensus control problem of discrete-time swarm systems is transformed into a robust H_∞ control problem of a set of independent uncertain systems. Secondly, sufficient linear matrix inequality conditions for robust H_∞ consensus analysis of discrete-time swarm systems are given by the stability theory, and a H_∞ performance level γ is determined meanwhile. Thirdly, the convergence result is derived as a final consensus value of swarm systems. Finally, numerical examples are presented to demonstrate theoretical results.

1. Introduction

As a hot topic of swarm systems, distributed cooperative control for swarm systems has gained an increasing attention from many communities because of its wide applications in various areas including rendezvous [1–3], filtering [4–6], formation control [7–9], synchronization of power-driven machine [10–12], and other areas [13–16]. It should be also pointed out that some relevant novel nearest results in aerospace have been reported in [17–19]. Furthermore, as an essential research aspect of distributed cooperative control for swarm systems, the consensus problem, which is referred to an agreement on some common values by all agents, has received extensive research in recent years [20–22].

According to the difference of the system dynamics, the research objective of the consensus problem for swarm systems can be classified into three types: first-order swarm systems, second-order swarm systems, and high-order swarm systems. For first-order swarm systems, the consensus problem with input and communication delays was studied by the frequency analysis in [23]. The consensus of second-order agents with multiple time-varying delays was investigated based on the graph theory in [24]. In combination with realistic applications, high-order swarm systems are more valuable and general than low-order swarm systems due to the practicality and complexity of the former. Some significant theoretical achievements about the consensus of continuous-time high-order swarm systems have been discovered in [25]. However, digital signals are processed rather than analog signals under engineering background, so discrete-time swarm systems should be paid more attention. The distributed output feedback consensus problem of general linear model discrete-time swarm systems with fixed topology was presented in [26, 27]. Based upon the leader-following model, the consensus problem of discrete-time swarm systems with directed graphs and external disturbances was investigated in [28]. Furthermore, the consensus problem of discrete-time swarm systems with switching topologies based on the matrix inequality theory was presented in [29–31].

As the industrial technology continues to develop, the research on the control theory becomes more mature. Due to operating state changes, external disturbances and model errors of swarm systems in the real world, robust H_∞ consensus control problems of swarm systems were wildly explored by researchers, as shown in [32–34]. Robust H_∞ consensus control problems of first-order swarm systems with external disturbances and model uncertainties were presented in [32]. The second-order robust H_∞ consensus control problem of swarm systems with measurement noises and asymmetric delays was studied in [33]. Distributed H₂ and H_∞ consensus control problems of high-order linear swarm systems with (x, y, z)-dependent noise were investigated in [34]. However, due to the general existence of parameter uncertainties and time delays of swarm systems in practical application, it is more meaningful and important to take these constraints into consideration in the theoretical analysis of robust H_∞ consensus control problems of high-order linear discrete-time swarm systems, which can been deemed as inadequately available in current literature.

As is well known, precise dynamics models of swarm systems can be hardly established in practice, and many kinds of faults in systems can also contribute to uncertainties of the dynamics model. Besides, components of systems will be out of order or aged with the increase of working hours. Therefore, researches on the robust H_∞ consensus problem of high-order linear discrete-time swarm systems with parameter uncertainties are very valuable and significant. Moreover, time delays cannot be avoided in nature and they take place so commonly in biological, physical, and electrical systems. The acquisition of parameters becomes more difficult when time delays exist in systems. If time delays are ignored when the consensus problem of swarm systems with parameter uncertainties is discussed, the stability of the system is hard to be guaranteed. Motivated by the above analysis, for high-order linear discrete-time swarm systems with parameter uncertainties to achieve consensus by the robust H_∞ control method, time delays are necessary to be considered and the problem remains the most open as we know.

This paper studies robust H_∞ control consensus problems of high-order linear discrete-time swarm systems with parameter uncertainties and time-varying delays, and the innovations of this paper are threefold: (i) a sufficient linear matrix inequality (LMI) condition such that swarm systems can achieve the robust H_∞ consensus subject to parameter uncertainties and time-varying delays is derived; (ii) a H_∞ performance index γ of swarm systems is obtained; and (iii) the final consensus value of swarm systems is developed. Compared with the previous work on the robust H_∞ consensus of high-order swarm systems, the novelties of this literature are also threefold. Firstly, only the robust H_∞ consensus of high-order linear swarm systems was investigated in [35–39], where the H_∞ performance index was not obtained. However, in order to show the performance of the robust consensus of high-order linear discrete-time swarm systems, the H_∞ performance index, which is necessary and important, was involved in this paper. Secondly, the final consensus value was obtained by LMI theory in this paper, which could better show the advantages of the proposed consensus protocol, but most existing works for the robust H_∞ consensus of high-order linear swarm systems subject to parameter uncertainties and time delays, including [35–38], did not consider this useful point. Thirdly, to better correspond with the practical application, influences of time delays on the robust consensus of swarm systems were sufficiently considered in this paper, which did not appear in [37–39].

The remainder of the paper is organized as follows. Section 2 states several important conclusions of the graph theory and the problem description in which the robust H_∞ consensus protocol is proposed. Section 4 shows a sufficient LMI condition that can guarantee the robust H_∞consensus of swarm systems and a final consensus value of swarm systems. The effectiveness of theoretical results is illustrated via simulation examples in Section 5. Finally, Section 5 draws the conclusion.

Notations. A matrix can be defined to be positive if each entry of the matrix is positive. A square matrix can be known as Schur stable if each eigenvalue of the matrix lies in the open unit disk Θ = {λ ∈ ℂ : |λ| < 1}. diag{a₁₁, a₂₂, ⋯, a_nn} denotes the diagonal matrix, where a₁₁, a₂₂, ⋯, a_nn are diagonal entries. refers to the expectation. The symbol ⊗ represents the Kronecker product. The transpose of a matrix M is denoted as M^T. I stands for the identity matrix with appropriate dimension. Let 1_N = [1,⋯,1]^T be the vector of N ones with all components 1.

2. Preliminaries and Problem Description

2.1. Graph Theory

In general, exchanges of information among N agents in swarm systems can be shown as a directed graph

, where

denotes the node set,

represents the edge set, and

refers to the weighted adjacency matrix with the element a_ij > 0 if (v_j, v_i) ∈ ℰ while a_ij = 0 if (v_j, v_i) ∉ ℰ. Define the node index of graph G as a finite index set ℐ = {1, 2, ⋯, N}. Let

stand for the set of all neighbours of node v_i, where the information flows from node v_j to node v_i. Let subset

of the nodes in graph G be a cluster. Suppose that

represents the neighbour set of a cluster N_J. It can be defined that the in-degree matrix of node v_i is

, and the out-degree matrix of node v_i is

. Note that a diagonal matrix Δ = [Δ_ij] can be provided to describe the degree matrix of digraph G, which is defined as follows:

(1)

The definition of the Laplacian matrix in connection with digraph G can be shown in matrix form as .

2.2. Problem Description

Consider a linear swarm system composed of N homogeneous agents marked as 1, 2, ⋯, N, in which the ith agent’s dynamics can be expressed as a state update equation

(2)

where

indicates the state vector;

and

, respectively, represent the input matrix and the external disturbance;

, and

are the given constant matrices;

is the control output; ΔA and ΔB stand for uncertainties in the system matrix and input channel, respectively, such that

(3)

where D denotes a positive constant matrix and F refers to an unknown matrix function which meets constraints as follows:

(4)

The parameter uncertainties ΔA and ΔB are considered permissible when equations (3) and (4) hold meanwhile.

Remark 1. When there is the external disturbance in system (2), external disturbance belongs to l₂ signal shown in [33, 40], which satisfies , that is, the energy of the external disturbance in system (2) is bounded on any finite interval. In this case, the robust H_∞ control problem can be analysed in an appropriate and meaningful way.

To achieve consensus for linear swarm system (2), the following control protocols are adopted:

(5)

where 0 ≤ τ(k) ≤ τ_max, K is a constant gain matrix with appropriate dimensions, and τ(k) ∈ ℤ^∗ denotes time-varying delays of swarm systems. Then, to show the consensus analysis and design for swarm system (2), the definition is presented as follows:

Definition 1. For the given gain matrix K and any given bounded initial states, swarm system (2) with consensus protocol (5) are assured to arrive consensus if there exists a vector-valued c(k) depending on the initial states such that lim_k→∞(x(k) − 1_N ⊗ c(k)) = 0, where c(k) denotes the final consensus value.

Let , , and , and we can write swarm system (2) with equation (5) into a compact form as follows:

(6)

where B_ΔBK = (B + ΔB)K and ϕ(k) is an initial value at k.

The suboptimal robust H_∞ consensus control problem of system (6) is stated to find a distributed protocol (5) such that

(i)
with ω_x(k) = 0, system (6) is asymptotically stable for all acceptable uncertain matrices F
(ii)
with ω_x(k) interpreted as deterministic l₂ signal, the transfer function from ω_x(k) to z(k) of system (6), which is denoted by T_ωz, satisfies for all acceptable uncertain matrices F and a given allowable scalar γ > 0, where , is the H_∞ norm of T_ωz, defined by

In order to make an in-depth analysis for the robust H_∞ consensus control problem of system (6), we presume henceforth that the communication graph G is connected and give the following lemma about the graph theory.

Lemma 1 (see [41].)For the Laplacian matrix L associated with an undirected graph G, the following description holds: (i) 0 is an eigenvalue of L, and its corresponding eigenvector is 1_N, and (ii) 0 is a simple eigenvalue of L, and all the other eigenvalues are positive and real if G is connected.

Assume that λ_i(i = 1, 2, ⋯, N) denotes eigenvalues of matrix

of an undirected graph G. Moreover, λ₁ = 0, which satisfies λ₁ ≤ λ₂≤⋯≤λ_N, is related to its corresponding eigenvector

. Thus, an orthogonal matrix can be found in the form

(7)

such that U^TLU = diag{λ₁, λ₂, ⋯, λ_N}.

Theorem 1. For a given γ > 0, system (6) is asymptotically stable and , if and only if the following N systems are simultaneously and asymptotically stable and all of the H_∞ norms of their transfer function matrices are less than γ:

(8)

where

and

Proof. Let λ_i(i = 1, 2, ⋯, N) be the eigenvalues of matrix for an undirected topology G, where λ₁ = 0 with the corresponding eigenvector , and λ₁ ≤ λ₂≤⋯≤λ_N. An orthogonal matrix can be found in the form

(9)

such that U^TLU = diag{λ₁, λ₂, ⋯, λ_N} = Λ. Assume that

(10)

Then, system (6) can be rewritten in terms of as

(11)

Furthermore, reformulate the disturbance variable ω_x(k) and the performance variable z(k) via

(12)

(13)

Subsequently, substituting (12) and (13) into (11) gives

(14)

In fact, system (14) consists of N individual systems in (6). Denote by and the transfer function matrices of system (14) and (6), respectively. Afterwards, we can deduce from equations (6), (12), (13), and (14) that

(15)

which implies that

(16)

Therefore, the proof of Theorem 1 is completed.

In addition, it is worth mentioning that, let

(17)

By Lemma 1, we can convert system (14) into N subsystems as follows:

(18)

(19)

Obviously, swarm system (6) can achieve consensus if subsystem (19) is asymptotically stable. Note that subsystem (18) determines the final consensus value of swarm system (6), and the details of it will be discussed below.

Remark 2. By Theorem 1, the distributed H_∞ consensus control problem of swarm system (6) is transformed into the robust H_∞ control problems of N subsystems (8), so that a set of independent systems which have the same dimensions as a single agent in (2) is obtained. Therefore, the computational complexity is decreased evidently and the stability theory of swarm systems can be used. The essential tools producing this result by right of the state space decomposition approach.

3. Main Results

In this section, the robust stability and existence conditions of the H_∞ consensus control problem for swarm system (2) with protocol (5) is provided by using a basis-dependent Lyapunov function and the LMI approach. Above all, we should introduce the following two lemmas.

Lemma 2 (Jensen inequality [42]). For any constant matrix M ≥ 0, , and , positive integers α₁ and α₂ satisfying α₂ ≥ α₁ ≥ 1, an inequality holds as follows:

(20)

Lemma 3. Suppose that equal positive integer time-varying delays τ(k) exist in whole communication network of swarm system (2). Meanwhile, the undirected graph G is fixed and connected. Then, by use of control protocol (5), the robust consensus of swarm system (2) with H_∞-norm consensus performance bound γ can be achieved globally asymptotically if we can prove that, there are a feedback matrix K with suitable dimensions and four positive-definite matrices P, R, Q₁, and Q₂ with d × d dimensions satisfying

(21)

where

(22)

Proof. For purpose of consensus analysis, we construct a Lyapunov function as follows:

(23)

where

(24)

for

Then, we can define the derivative of V(k) as

(25)

From the solution of (8), ΔV₁(k) can be rewritten as follows:

(26)

ΔV₂(k) can be reformulated as

(27)

ΔV₃(k) can be rewritten as

(28)

ΔV₄(k) can be reformulated as

(29)

ΔV₅(k) can be rewritten as

(30)

Furthermore, the term can be shown that

(31)

At the same time, according to Lemma 2, the following inequality holds:

(32)

Let . Then, it follows from (8) and (25)–(32) that

(33)

if system (8) is asymptotically stable. This implies that the robust consensus of swarm system (2) with H_∞-norm consensus performance bound γ can be achieved globally asymptotically by the use of control protocol (5) if matrix inequality (21) holds.

Therefore, the conclusion of Lemma 3 is drawn.

Remark 3. In Lemma 3, for making sure that system (8) can achieve robust consensus with a H_∞ performance index γ, a sufficient condition is obtained. Nevertheless, it is not difficult to find that (21) is a nonlinear matrix inequality (NMI) and therein lies parameter uncertainties.

To cope with the uncertain matrices F and the nonlinear terms of (21), the following two lemmas are given.

Lemma 4 (see [43].)For given matrices Y, D, and E of appropriate dimensions where Y is symmetric, a matrix inequality holds as follows:

(34)

for all F subject to F^TF ≤ I, if and only if there exists a scalar ε > 0 such that

(35)

Lemma 5 (Schur complement [44]). The linear matrix inequality

(36)

where Q(x) = Q(x)^T, R(x) = R(x)^T, and S(x) are dependent on x, is the identical meaning as anyone of the following two descriptions:

(1)
Q(x) > 0, R(x) − S(x)^TQ(x)⁻¹S(x) > 0
(2)
R(x) > 0, Q(x) − S(x)R(x)⁻¹S(x)^T > 0

Theorem 2. Consider swarm system (2) with a fixed, undirected, and connected communication topologyG. The robust consensus of swarm system (2) with H_∞-norm consensus performance bound γ can be achieved globally asymptotically by use of control protocol (5) if we can find two scaling factors ε₁ > 0 and ε₂ > 0, a feedback matrix K with suitable dimensions and six positive-definite matrices P, S, R, M, Q₁, and Q₂ with d × d dimensions which are a settlement of the minimization problem as follows:

(37)

subject to

(38)

(39)

(40)

where A_iBK = A − Δ_iiBK and

. It can also be said if the minimization problem (37)–(40) has an available settlement P, S, R, M, Q₁, Q₂, and K, the robust consensus of swarm system (2) with H_∞-norm consensus performance bound γ can be achieved globally asymptotically by the use of control protocol (5).

Proof. Inequality (21) can be expressed as

(41)

According to Lemma 5, one can obtain that inequality (41) can be rewritten as follows:

(42)

By replacing ΔA = DFE₁ and ΔB = DFE₂, inequality (42) is equivalently written as follows:

(43)

In virtue of Lemma 4 and Lemma 5, inequality (43) comes into existence for all acceptable uncertain matrices F if and only if we can prove that there are two scaling factors ε₁ > 0 and ε₂ > 0 satisfying

(44)

By the Cone Complementarity Linearization (CCL) algorithm in [45], we set S = P⁻¹ and M = R⁻¹. Then, the optimization problem (37)–(40) can be reasonably settled by transforming the nonlinear matrix inequality (NMI) (21).

Thus, the proof of Theorem 2 is completed.

Remark 4. According to Theorem 2, notice that the optimization problem (40)–(45) transformed from the NMI (21) can be reasonably solved based upon Algorithm 1. Hereafter, the linear swarm system (2) with the control protocol (5) achieves robust H_∞consensus.

Algorithm 1: A possible way to the optimization problem (37)–(40).

Step 1: Seek out a set of available values of P₀, S₀, R₀, and M₀ for LMI (38)–(40), if there does not exist, then exit. Set k = 0.
Step 2: Set P_k = P₀, S_k = S₀, R_k = R₀, and M_k = M₀ and seek out P_k, S_k, R_k, and M_k which are a settlement for the LMI problem min tr(P_kS + S_kP + R_kM + M_kR) subject to LMI (38)–(40).
Step 3: If tr(P_kS + S_kP + R_kM + M_kR) < 4d + ε, then exit. Otherwise, set k = k + 1 and switch to Step 2.

It should be pointed out that the final outcome of first “exit” in Step 1 is that available initial values of P₀, S₀, R₀, and M₀ cannot be obtained. In this case, we set k = 0 and repeat Step 1. As long as the available values are obtained, we switch to Step 2. Then, second “exit” in Step 3 means that suitable values of P_k, S_k, R_k, and M_k are obtained.

Theorem 3. With ω_x(k) interpreted as deterministic l₂ signal, when swarm system (6) achieves robust H_∞ consensus with parameter uncertainties and time-varying delays, the final consensus value c(k) satisfies

(45)

where x_C(k) can be the following form:

(46)

for

Proof. In the following, we consider two cases for the proof.

Case 1. (k ≤ τ(k)).

In this case, system (18) can be equivalently written as follows:

(47)

Assume that and , then from (10), we can uniquely decompose x(k) into . Considering the mentioned above, we can also conclude that if the robust H_∞ consensus of system (6) is achieved, the subsystem (19) should be Schur stable, which implies that the response of system (19) due to complies with . Therefore, the final consensus value c(k) depends totally on x_C(k). Since , we have , and because , then we can obtain , that is to say

(48)

Likewise, let and , then by (12), x(k) can be uniquely decomposed as . If system (6) achieves the robust H_∞ consensus, the response of system (19) due to also should comply with . Since , we have , and because , then we can obtain , that is

(49)

Hence, we have

(50)

Case 2. (k > τ(k)).

In this case, we also define and . Similarly, we can have and . By (18), we can obtain

(51)

Thus, the final consensus value c(k) complies with .

The conclusion of Theorem 3 is obtained.

Remark 5. With ω_x(k) interpreted as deterministic l₂ signal, the final consensus value c(k) of system (6) is presented by Theorem 3. In the k ≤ τ(k) case, the final consensus value c(k) has two divisions, one is , which is associated with the system matrix A + ΔA, the neighbouring feedback matrix K, and the initial state x(0); and the other is , which is related to the external disturbance ω_x(k). This implies that the external disturbance ω_x(k) has an effect on the final consensus value, which is also related to the system matrix A + ΔA, the neighbouring feedback matrix K, and the initial state x(0). The result is different from that of the swarm system without external disturbances and parameter uncertainties, which is discussed in [29]. In the k > τ(k) case, we get a linear recursion formula (51) for x_C(k), which is the limit of the final consensus value c(k) as k → ∞. This implies that the final consensus value c(k) is associated with the states x_C(k), x_C(k − τ(k)), and the external disturbance ω_x(k) when k > τ(k).

4. Results and Discussion

In this section, we firstly use a simulation example to validate the effectiveness of the theoretical results, and then apply the control protocol (5) to achieve state consensus for a swarm system which consists of 8 agents. The dynamics of these agents are represented by (2), and relevant system matrices is given as follows:

(52)

where r₁, r₂, and r₃ are uncertain parameters satisfying −1 ≤ r₁ ≤ 1, −1 ≤ r₂ ≤ 1, and −1 ≤ r₃ ≤ 1, respectively. Then, swarm system (2) can be reformulated as

(53)

We analyze the robust H_∞ consensus among the above 8 agents with an undirected topology G as shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Communication topology G.

Assume that the initial state of each agent is randomly given as x₁(0) = [1, 5,−2]^T, x₂(0) = [2, 4, 3]^T, x₃(0) = [1, 1, 2]^T, x₄(0) = [3, 2, 1]^T, x₅(0) = [5, 6,−2]^T, x₆(0) = [−3, 3, 4]^T, x₇(0) = [−2,−4,−3]^T, and x₈(0) = [−5,−2,−1]^T and set r₁ = 0.15, r₂ = 0.25, r₃ = 0.15, and τ_max = 2. The dynamics of each agent is combined with protocol (5). Let γ = 2 and suppose that the exogenous disturbance inputs are selected as ω_i,x(k) = 0.1ie^−0.5ksin(k). By Theorem 2, we can get that

(54)

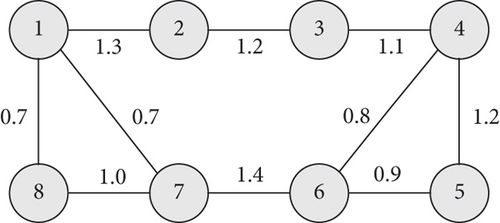
The simulation results are produced from Figures 2, 3–4. The state trajectories of swarm system (2) are shown. In addition, the final consensus value c(k) deduced from Theorem 3 is marked with the red asterisk.

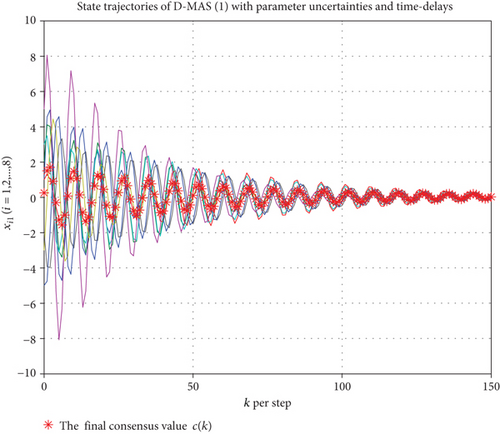
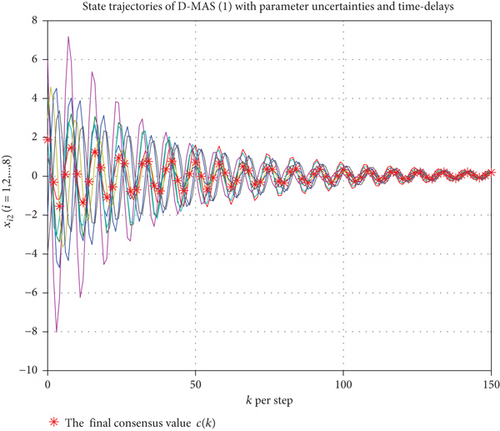
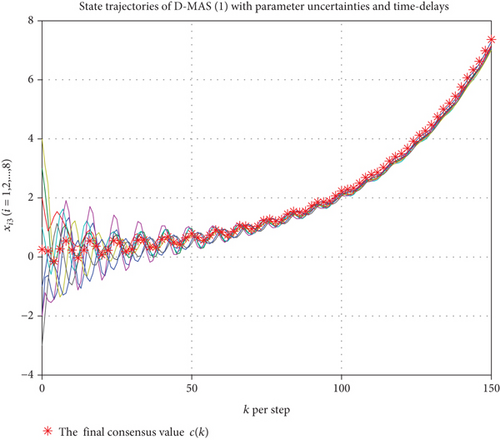
In view of Figures 2–4, we can see easily that the state trajectories of swarm system (2) can be asymptotically convergent to the common value c(k), associated with r_j(j = 1, 2, 3). From Definition 1, we can also find clearly that the robust H_∞ consensus of swarm system (2) with control protocol (5) is achieved. Therefore, the effectiveness of the theoretical results is demonstrated.

5. Conclusions

Robust H_∞ consensus control problems of linear high-order discrete-time swarm systems with parameter uncertainties and time-varying delays were investigated. A robust H_∞ consensus control protocol was proposed while the impact of time-varying delays is involved. LMI conditions for robust H_∞ consensus analysis were given, and a final consensus value was obtained from the derivation process. If swarm systems satisfy the sufficient LMI conditions, then we can ensure that swarm systems with parameter uncertainties and time-varying delays could achieve robust H_∞ consensus, and the convergence result could be determined as a final consensus value. Finally, the effectiveness of the theoretical results was verified by relevant simulation examples. Further studies will focus on the impact of switching topologies and directed graphs on the consensus problem of linear discrete-time swarm systems.

Conflicts of Interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

Acknowledgments

This work is supported by National Natural Science Foundation under grant #61763040 and grant #61867005. The authors would like to express my faithful gratitude to all those who helped me during the writing of this paper. We gratefully acknowledge the help of our supervisors, Mister Xiaogang Yang and Mister Jianxiang Xi, who have offered us patient instruction in the academic studies.

Open Research

Data Availability

The data used to support the findings of this study are included within the article.

References

1 Li H., Peng J., Zhang X., and Huang Z., Flocking of mobile agents using a new interaction model: a cyber-physical perspective, IEEE Access. (2017) 5, 2665–2675, https://doi.org/10.1109/ACCESS.2017.2669438, 2-s2.0-85017662168.
10.1109/ACCESS.2017.2669438
Web of Science® Google Scholar
2 Cai N., He M., Wu Q., and Khan M. J., On almost controllability of dynamical complex networks with noises, Journal of Systems Science and Complexity. In presshttps://doi.org/10.1007/s11424-017-6273-7.
10.1007/s11424-017-6273-7
Web of Science® Google Scholar
3 Gao J., Xu X., Ding N., and Li E., Flocking motion of multi-agent system by dynamic pinning control, IET Control Theory & Applications. (2017) 11, no. 5, 714–722, https://doi.org/10.1049/iet-cta.2016.1150, 2-s2.0-85014640384.
10.1049/iet-cta.2016.1150
Web of Science® Google Scholar
4 Açıkmeşe B., Mandić M., and Speyer J. L., Decentralized observers with consensus filters for distributed discrete-time linear systems, Automatica. (2014) 50, no. 4, 1037–1052, https://doi.org/10.1016/j.automatica.2014.02.008, 2-s2.0-84898913141.
10.1016/j.automatica.2014.02.008
Web of Science® Google Scholar
5 Cui G., Ma Q., Zhang B., Lewis F. L., and Xu S., Distributed consensus tracking for non-linear multi-agent systems with input saturation: a command filtered backstepping approach, IET Control Theory & Applications. (2016) 10, no. 5, 509–516, https://doi.org/10.1049/iet-cta.2015.0627, 2-s2.0-84961572690.
10.1049/iet-cta.2015.0627
Web of Science® Google Scholar
6 Liu C. L., Shan L., Chen Y. Y., and Zhang Y., Average-consensus filter of first-order multi-agent systems with disturbances, IEEE Transactions on Circuits and Systems II: Express Briefs. (2018) 65, no. 11, 1763–1767, https://doi.org/10.1109/tcsii.2017.2762723, 2-s2.0-85055833762.
10.1109/tcsii.2017.2762723
Web of Science® Google Scholar
7 Liu H., Ma T., Lewis F. L., and Wan Y., Robust formation control for multiple quadrotors with nonlinearities and disturbances, IEEE Transactions on Cybernetics. (2018) 1–10, https://doi.org/10.1109/TCYB.2018.2875559, 2-s2.0-85055693022.
10.1109/TCYB.2018.2875559
Web of Science® Google Scholar
8 Dong X., Zhou Y., Ren Z., and Zhong Y., Time-varying formation tracking for second-order multi-agent systems subjected to switching topologies with application to quadrotor formation flying, IEEE Transactions on Industrial Electronics. (2017) 64, no. 6, 5014–5024, https://doi.org/10.1109/TIE.2016.2593656, 2-s2.0-85027483171.
10.1109/TIE.2016.2593656
Web of Science® Google Scholar
9 Qi Y., Zhou S., Kang Y., and Yan S., Formation control for unmanned aerial vehicles with directed and switching topologies, International Journal of Aerospace Engineering. (2016) 2016, 8, 7657452, https://doi.org/10.1155/2016/7657452, 2-s2.0-84988849679.
10.1155/2016/7657452
Web of Science® Google Scholar
10 Monshizadeh N., Trentelman H. L., and Camlibel M. K., Uniform synchronization in multi-agent systems with switching topologies, International Journal of Robust and Nonlinear Control. (2016) 26, no. 9, 1888–1901, https://doi.org/10.1002/rnc.3387, 2-s2.0-84936797208.
10.1002/rnc.3387
Web of Science® Google Scholar
11 Cruz-Ancona C. D., Martínez-Guerra R., and Pérez-Pinacho C. A., Generalized multi-synchronization: a leader-following consensus problem of multi-agent systems, Neurocomputing. (2017) 233, 52–60, https://doi.org/10.1016/j.neucom.2016.07.063, 2-s2.0-85008199367.
10.1016/j.neucom.2016.07.063
Web of Science® Google Scholar
12 Xi J., Wang C., Liu H., and Wang Z., Dynamic output feedback guaranteed-cost synchronization for multiagent networks with given cost budgets, IEEE Access. (2018) 6, 28923–28935, https://doi.org/10.1109/ACCESS.2018.2819989, 2-s2.0-85048607620.
10.1109/ACCESS.2018.2819989
Web of Science® Google Scholar
13 Tan Z. Y., Cai N., Zhou J., and Zhang S. G., On performance of peer review for academic journals: analysis based on distributed parallel system, IEEE Access. (2019) 7, no. 99, 19024–19032, https://doi.org/10.1109/ACCESS.2019.2896978, 2-s2.0-85062245091.
10.1109/ACCESS.2019.2896978
Web of Science® Google Scholar
14 Liu X. and Ji Z., Controllability of multiagent systems based on path and cycle graphs, International Journal of Robust and Nonlinear Control. (2018) 28, no. 1, 296–309, https://doi.org/10.1002/rnc.3870, 2-s2.0-85021697375.
10.1002/rnc.3870
Web of Science® Google Scholar
15 Ji Z. and Yu H., A new perspective to graphical characterization of multi-agent controllability, IEEE Transactions on Cybernetics. (2017) 47, no. 6, 1471–1483, https://doi.org/10.1109/TCYB.2016.2549034, 2-s2.0-84981719235.
10.1109/TCYB.2016.2549034
PubMed Web of Science® Google Scholar
16 Ma H., Jia X., Cai N., and Xi J., Adaptive guaranteed-performance consensus control for multiagent systems with an adjustable convergence speed, Discrete Dynamics in Nature and Society. (2019) 2019, 9, 5190301, https://doi.org/10.1155/2019/5190301.
10.1155/2019/5190301
Web of Science® Google Scholar
17 Sabatini M., Palmerini G. B., and Gasbarri P., Control laws for defective swarming systems, Advances in Astronautical Sciences. (2015) 153, 749–768.
Google Scholar
18 Chen K., Zhao S., and Lv N., Network monitoring information collection in the SDN-enabled airborne tactical network, International Journal of Aerospace Engineering. (2018) 2018, 20, 1940842, https://doi.org/10.1155/2018/1940842, 2-s2.0-85059077293.
10.1155/2018/1940842
Web of Science® Google Scholar
19 Carpentiero M., Gugliermetti L., Sabatini M., and Palmerini G. B., A swarm of wheeled and aerial robots for environmental monitoring, 2017 IEEE 14th International Conference on Networking, Sensing and Control (ICNSC), May 2017, Calabria, Italy, 90–95, https://doi.org/10.1109/ICNSC.2017.8000073, 2-s2.0-85028508516.
10.1109/ICNSC.2017.8000073
Google Scholar
20 Wang S. and Huang J., Adaptive leader-following consensus for multiple Euler–Lagrange systems with an uncertain leader system, IEEE Transactions on Neural Networks and Learning Systems. (2019) 30, no. 7, 2188–2196, https://doi.org/10.1109/tnnls.2018.2878463, 2-s2.0-85057394610, 30489275.
10.1109/TNNLS.2018.2878463
PubMed Web of Science® Google Scholar
21 Deng X., Sun X., Liu R., and Liu S., Consensus control of time-varying delayed multiagent systems with high-order iterative learning control, International Journal of Aerospace Engineering. (2018) 2018, 12, 4865745, https://doi.org/10.1155/2018/4865745, 2-s2.0-85056547098.
10.1155/2018/4865745
Web of Science® Google Scholar
22 Xi J., Fan Z., Liu H., and Zheng T., Guaranteed-cost consensus for multiagent networks with Lipschitz nonlinear dynamics and switching topologies, International Journal of Robust and Nonlinear Control. (2018) 28, no. 7, 2841–2852, https://doi.org/10.1002/rnc.4051, 2-s2.0-85043701128.
10.1002/rnc.4051
Web of Science® Google Scholar
23 Tian Y. P. and Liu C. L., Consensus of multi-agent systems with diverse input and communication delays, IEEE Transactions on Automatic Control. (2008) 53, no. 9, 2122–2128, https://doi.org/10.1109/TAC.2008.930184, 2-s2.0-54349087390.
10.1109/TAC.2008.930184
Web of Science® Google Scholar
24 Zhu W. and Cheng D., Leader-following consensus of second-order agents with multiple time-varying delays, Automatica. (2010) 46, no. 12, 1994–1999, https://doi.org/10.1016/j.automatica.2010.08.003, 2-s2.0-78249246617.
10.1016/j.automatica.2010.08.003
Web of Science® Google Scholar
25 Xi J., He M., Liu H., and Zheng J., Admissible output consensualization control for singular multi-agent systems with time delays, Journal of the Franklin Institute. (2016) 353, no. 16, 4074–4090, https://doi.org/10.1016/j.jfranklin.2016.07.021, 2-s2.0-84995518928.
10.1016/j.jfranklin.2016.07.021
Web of Science® Google Scholar
26 Zhao H., Park J. H., Zhang Y., and Shen H., Distributed output feedback consensus of discrete-time multi-agent systems, Neurocomputing. (2014) 138, no. 9, 86–91, https://doi.org/10.1016/j.neucom.2014.02.043, 2-s2.0-84899729295.
10.1016/j.neucom.2014.02.043
Web of Science® Google Scholar
27 Liu X., Du C., Lu P., and Yang D., Distributed event-triggered feedback consensus control with state-dependent threshold for general linear multi-agent systems, International Journal of Robust and Nonlinear Control. (2017) 27, no. 15, 2589–2609, https://doi.org/10.1002/rnc.3700, 2-s2.0-85002700617.
10.1002/rnc.3700
Web of Science® Google Scholar
28 Lv Y., Li Z., Duan Z., and Feng G., Novel distributed robust adaptive consensus protocols for linear multi-agent systems with directed graphs and external disturbances, International Journal of Control. (2017) 90, no. 2, 137–147, https://doi.org/10.1080/00207179.2016.1172259, 2-s2.0-84969835583.
10.1080/00207179.2016.1172259
Web of Science® Google Scholar
29 Cheng L., Wang H., Hou Z. G., and Tan M., Reaching a consensus in networks of high-order integral agents under switching directed topologies, International Journal of Systems Science. (2016) 47, no. 8, 1966–1981, https://doi.org/10.1080/00207721.2014.966281, 2-s2.0-84954396383.
10.1080/00207721.2014.966281
Web of Science® Google Scholar
30 Zhang G., Xu J., Zeng J., Xi J., and Tang W., Consensus of high-order discrete-time linear networked multi-agent systems with switching topology and time delays, Transactions of the Institute of Measurement and Control. (2017) 39, no. 8, 1182–1194, https://doi.org/10.1177/0142331216629197, 2-s2.0-85025831305.
10.1177/0142331216629197
Web of Science® Google Scholar
31 Xi J., Wang C., Liu H., and Wang L., Completely distributed guaranteed-performance consensualization for high-order multiagent systems with switching topologies, IEEE Transactions on Systems, Man, and Cybernetics: Systems. (2019) 49, no. 7, 1338–1348, https://doi.org/10.1109/TSMC.2018.2852277, 2-s2.0-85050625185.
10.1109/TSMC.2018.2852277
Web of Science® Google Scholar
32 Lin P., Jia Y., and Li L., Distributed robust consensus control in directed networks of agents with time-delay, Systems & Control Letters. (2008) 57, no. 8, 643–653, https://doi.org/10.1016/j.sysconle.2008.01.002, 2-s2.0-44349172249.
10.1016/j.sysconle.2008.01.002
Web of Science® Google Scholar
33 Huang W., Zheng W., and Mo L., Distributed robust H_∞ composite-rotating consensus of second-order multi-agent systems, International Journal of Distributed Sensor Networks. (2017) 13, no. 7, https://doi.org/10.1177/1550147717722513, 2-s2.0-85026742577.
10.1177/1550147717722513
PubMed Web of Science® Google Scholar
34 Sheng L., Wang Z., and Zou L., Output-feedback H₂/H_∞ consensus control for stochastic time-varying multi-agent systems with (x,u,v)-dependent noises, Systems & Control Letters. (2017) 107, 58–67, https://doi.org/10.1016/j.sysconle.2017.07.004, 2-s2.0-85027843738.
10.1016/j.sysconle.2017.07.004
Web of Science® Google Scholar
35 Liu Y. and Jia Y., Robust H_∞ consensus control of uncertain multi-agent systems with time delays, International Journal of Control, Automation and Systems. (2011) 9, no. 6, 1086–1094, https://doi.org/10.1007/s12555-011-0609-1, 2-s2.0-84862920524.
10.1007/s12555-011-0609-1
Web of Science® Google Scholar
36 Li Z. X. and Ji H. B., Robust delay-dependent H_∞ consensus control for multi-agent systems with input delays, Acta Automatica Sinica. (2014) 40, no. 11, 2556–2562, https://doi.org/10.1016/S1874-1029(14)60401-8.
10.1016/S1874-1029(14)60401-8
Google Scholar
37 Wang X. and Yang G. H., Distributed reliable H_∞ consensus control for a class of multi-agent systems under switching networks: a topology-based average dwell time approach, International Journal of Robust and Nonlinear Control. (2016) 26, no. 13, 2767–2787, https://doi.org/10.1002/rnc.3474, 2-s2.0-84949035516.
10.1002/rnc.3474
Web of Science® Google Scholar
38 Rezaee H. and Abdollahi F., Decentralized H_∞ consensus protocol for a class of high-order multiagent systems, International Journal of Robust and Nonlinear Control. (2016) 26, no. 15, 3330–3343, https://doi.org/10.1002/rnc.3509, 2-s2.0-84985955328.
10.1002/rnc.3509
Web of Science® Google Scholar
39 Zhang D., Xu Z., Wang Q. G., and Zhao Y. B., Leader-follower H_∞ consensus of linear multi-agent systems with aperiodic sampling and switching connected topologies, ISA Transactions. (2017) 68, 150–159, https://doi.org/10.1016/j.isatra.2017.01.001, 2-s2.0-85012009152, 28202181.
10.1016/j.isatra.2017.01.001
PubMed Web of Science® Google Scholar
40 Dullerud G. E. and Paganini F., A Course in Robust Control Theory: A Convex Approach, 2013, 36, Springer, Berlin, https://doi.org/10.1007/978-1-4757-3290-0.
Google Scholar
41 Fax J. A. and Murray R. M., Information flow and cooperative control of vehicle formations, IEEE Transactions on Automatic Control. (2004) 49, no. 9, 1465–1476, https://doi.org/10.1109/TAC.2004.834433, 2-s2.0-4644317383.
10.1109/TAC.2004.834433
Web of Science® Google Scholar
42 Wu M., He Y., She J. H., and Liu G. P., Delay-dependent criteria for robust stability of time-varying delay systems, Automatica. (2004) 40, no. 8, 1435–1439, https://doi.org/10.1016/j.automatica.2004.03.004, 2-s2.0-2942604608.
10.1016/j.automatica.2004.03.004
Web of Science® Google Scholar
43 XIE L., Output feedback H_∞ control of systems with parameter uncertainty, International Journal of Control. (1996) 63, no. 4, 741–750, https://doi.org/10.1080/00207179608921866, 2-s2.0-0030108725.
10.1080/00207179608921866
Web of Science® Google Scholar
44 Yaz E. E., Linear matrix inequalities in system and control theory, Proceedings of the IEEE. (1998) 86, no. 12, 2473–2474, https://doi.org/10.1109/jproc.1998.735454.
10.1109/JPROC.1998.735454
Google Scholar
45 El Ghaoui L., Oustry F., and AitRami M., A cone complementarity linearization algorithm for static output-feedback and related problems, IEEE Transactions on Automatic Control. (1997) 42, no. 8, 1171–1176, https://doi.org/10.1109/9.618250, 2-s2.0-0031197472.
10.1109/9.618250
Web of Science® Google Scholar

Citing Literature

All articles

Robust H_∞ Consensus Control for Linear Discrete-Time Swarm Systems with Parameter Uncertainties and Time-Varying Delays

Abstract

1. Introduction

2. Preliminaries and Problem Description

2.1. Graph Theory

2.2. Problem Description

3. Main Results

4. Results and Discussion

5. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Robust H∞ Consensus Control for Linear Discrete-Time Swarm Systems with Parameter Uncertainties and Time-Varying Delays

Abstract

1. Introduction

2. Preliminaries and Problem Description

2.1. Graph Theory

2.2. Problem Description

3. Main Results

4. Results and Discussion

5. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information

Robust H_∞ Consensus Control for Linear Discrete-Time Swarm Systems with Parameter Uncertainties and Time-Varying Delays