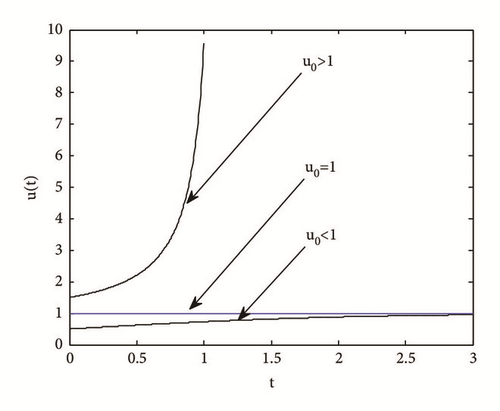
Modified-Logistic-Diffusion Equation u_t = Du_xx + u | 1 − u| with Neumann boundary condition has a global solution, if the given initial condition ψ satisfies ψ(x) ≤ 1, for all x ∈ [0,1]. Other initial conditions can lead to another type of solutions; i.e., an initial condition that satifies will cause the solution to blow up in a finite time. Another initial condition will result in another kind of solution, which depends on the diffusion coefficient D. In this paper, we obtained the lower bound of D, so that the solution of Modified-Logistic-Diffusion Equation with a given initial condition will have a global solution.

1. Introduction

Logistic-Difussion Equation was first introduced by Fisher at 1937. It describes the growth of mutant gene on long habitat R [1]. The equation is given by

(1)

with u(x, t) being the number of mutant genes at time t > 0, at location x ∈ R with initial condition ψ ∈ C²(R). Lots of researches had been done on this type of partial differential equation (PDE), including how to approximate the solution with various methods [2–5]. This PDE has been applied on different disciplines of knowledge, such as in chemical reaction and economic growth [6–9]. This research will focus on the behavior of solution if the nonlinear factor in (1) is modified with absolute function; i.e., the rate of growth is always positive,

(2)

PDE (2) explains that the rate of growth is slowing down around u = 1 and is always positive. The state u = 1 for all x is the steady state of (1) and (2). In (1), u = 1 is a stable equilibrium, while in (2) it is a semi-stable equilibrium. This research is conducted on a bounded domain

with Neumann boundary condition.

Consider the modified logistic ordinary differential equation

(3)

Equation (3) has a global solution if 0 ≤ u₀ ≤ 1. Completely, the solution of (3) for initial condition u₀ > 0 is given by

(4)

The behavior of the solution for the three types of initial conditions can be seen in Figure 1. Equation (4) shows that the interval of the solution of (3) for u₀ > 1 is [0, t^∗) with

(5)

On the contrary, (3) has a global solution for u₀ < 1. According to the solution (4), we can see that, for given initial condition ψ with 0 ≤ ψ(x) < 1 or 1 < ψ(x) for all x ∈ R, the diffusion factor does not play many roles in the behavior of solution.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The solution of the equation u_t = u | 1 − u| for the initial conditions u₀ < 1, u₀ = 1, and u₀ > 1.

Now, we will discuss the behavior of solution of (2) for other initial conditions ψ, that is,

(6)

The effect of the diffusion coefficient D will be observed to guarantee the existence of global solution.

Definition 1. Let ψ be the initial condition for (2). ψ is called D-initial condition if ψ satisfies (6).

2. Diffusion Time

Let f(u) = u | 1 − u|. This function is Lipchitz continuous, and so, by the following theorem, (2) has a solution.

Theorem 2 (see [10].)If f is Lipchitz continuous, there is δ > 0 dependent on u₀ such that

(7)

has a solution at time interval [t₀, t₀ + δ].

The function f(u) = u | 1 − u | ≥ 0 for all u ≥ 0. Thus, in the absence of diffusion, u_t ≥ 0 for all u ≥ 0. This means that the value of u(x, t) will grow for every x ∈ [0,1]. If there exist x ∈ [0,1] such that ψ(x) > 1, then the solutions interval of (2) is [0, t^∗] with

(8)

On the value of initial condition ψ with

, the diffusion coefficient is not affected much. It is because the diffusion coefficient is just distributing the concentration from high to low without addition or substraction of the total of concentration on interval [0,1]. As a result, there is any x ∈ [0,1] such that u(x, t) > 1 for all t > 0. Furthermore the solution of (2) will blow up at finite time.

For further discussion, assume there is x ∈ [0,1] such that ψ(x) > 1 and . If the diffusion coefficient D is quite large, then (2) has global solution.

Definition 3. Let u(x, t) be the solution of (2) with initial condition ψ. Diffusion time for (2) with respect to ψ, denoted by T_D(ψ), is defined by minimum time t such that u(., t) ≤ 1.

Notice the following usual diffusion equation:

(9)

If u₁ and u₂ are the solutions of (2) and (9), respectively, with the same initial condition ψ, then u₁(x, t) ≥ u₂(x, t) for every (x, t)∈[0,1]×[0, ∞). Hence, the diffusion time of (9) with respect to ψ is last or equal to diffusion time of (2) with respect to ψ. Let T_D be the diffusion time of (9) with respect to ψ; then T_D is a lower bound for diffusion time of (2) with respect to ψ. In [11], the solution of (9) for initial condition ψ is

(10)

with

. For certain initial condition, the T_D value can be obtained easily, while for other initial conditions, we could only determine the lower bound of T_D.

In this section, we will discuss the diffusion time for two elementary function such as linear and trigonometric functions. A particular linear function family of initial condition, ψ(x) = ax + b, a, b ≥ 0, is a D-initial condition if a + b > 1 and a + b/2 < 1. For this specific family, we found a lower bound of diffusion time with respect to (2).

Theorem 4. Let ψ(x) = a + bx be initial condition for (2). If b > 0 and (2π²(1 − a)/(8 + π²)) < b, then

(11)

Moreover if b < 0, and b < (2π²(1 − a)/(π² − 8)), then

(12)

Proof. The linear function ψ(x) = a + bx, a, b > 0, is a monotone function and reaches the maximum at x = 1. The volume of ψ is a + b/2, so that, for a + b/2 ≥ 1, diffusion time T_D(ψ) = ∞, and for a + b ≤ 1, diffusion time T_D(ψ) = 0. The initial condition ψ will satisfy the condition (6); a and b satisfy

(13)

The solution of

(14)

for initial condition ψ(x) = a + bx on x = 1 is

(15)

Define

(16)

It is clear that

(17)

and if

, then T < T_D(ψ). The time T with

(18)

In this case T > 0 for

(19)

For ψ(x) = a − bx with a > 1, the condition and ψ > 1 for some x ∈ [0,1], satisfied by 2a − 2 < b < a < 2. Assume x = 1 − y, and substituting to (14), we get

(20)

It means that the diffusion time for ψ(x) = a − bx is equal to diffusion time for φ(y) = a − b + by. Diffusion time for φ (by (18)) is

(21)

and T > 0 is satisfied for

(22)

Next, the sinusoidal function class of initial condition , will be considered. The function ψ will satisfy D-initial condition if a < 1 and a+|b | > 1. The diffusion time for this class of function is given by this theorem.

Theorem 5. Let the initial condition , given for (2). If 0 < a < 1 and a+|b | > 1, then

(23)

Proof. For ψ(x) = a + bcos⁡(nπx), where , the local maximum or local minimum points of ψ(x) have the same character; that is, they have the same concavity. The volume of ψ is a. So, T_D(ψ) = ∞ for a > 1 and T_D(ψ) = 0 for a + |b| < 1. We will check the time diffusion for ψ = a + bcos⁡(nπx) with a < 1 and a + |b| > 1.

First, we check for n = 1. The solution of (14) for initial condition ψ(x) = a + bcos⁡(πx) is given by

(24)

For b > 0, the solution u(x, t) is decreasing with respect to x for t > 0, so u(x, t) reach maximum at x = 0. Furthermore, if u(0, T) = 1, then u(x, T) ≤ 1 for all x. This time T is

(25)

On the other side, for ψ(x) = a − bcos⁡(πx) with b > 0, u(x, t) is increasing with respect to x for t > 0. The maximum value of u(x, t) was reached at x = 1. By substituting y = 1 − x, we have the problem (14) with initial condition ψ(x) = a + bcos⁡(πx). The time given by (25) is positive for b > 1 − a. Therefore, the diffusion time for ψ(x) = a ± bcos⁡(πx) is

(26)

For n ≥ 2, we can see the problem on interval I_i = [(i − 1)/n, i/n], i = 1, …, n. It is clear that ψ(x) = a + bcos⁡(nπx) is monotone on each interval I_i for all i = 1, …, n, and u(x, t) _x(i/n) = 0 for t > 0. Therefore, we can see the problem (14) with Neumann Boundary condition on interval I_i = [(i − 1)/n, i/n], and we write it as

(27)

By translation and dilatation

(28)

so, the problem (27) became

(29)

The diffusion time for ψ(x) = a − bcos⁡(nπx) in (14) is equal to the diffusion time for ψ(x) = a − bcos⁡(πx) in (29). Therefore, the diffusion time for ψ(x) = a − bcos⁡(nπx) in (14) is

(30)

3. Reaction Time

The function f(u) = u | 1 − u | ≥ 0 for all u ≥ 0. It means the reaction factor is causing the increase of concentration for all time. If f could contribute to the increasing of the concentration such that u(x, t) > 1 for time t < ∞, the solution will blow up.

Let Ω₁ = {x∣ψ(x) ≤ 1} and Ω₂ = {x∣ψ(x) > 1}. Then the reaction time for initial condition ψ is defined as follows.

Definition 6. Assuming f is D-initial condition, let u(x, t) be the solution of (2) for D-initial condition ψ. The minimum time T that meets is defined as the reaction time for ψ and is notated as T_R(ψ).

For initial condition that has minimum value at [0,1], the reaction time is given by Theorem 7 below.

Theorem 7. Let ψ be the D-initial condition of (2) and have minimum value on [0,1] with m = min_x⁡ψ(x); then

(31)

is an upper bound for T_R(ψ).

Proof. Let T_R(ψ) = T and . So,

(32)

Let min_x⁡ψ(x) = m; then

(33)

Furthermore, let

(34)

If P(T) = δ, then T is an upper bound of T_R(ψ). The time T that satisfies this condition is

(35)

Since ψ(x) > 1 for every x ∈ Ω₂, then

(36)

This shows that T > 0 for some D-initial condition ψ.

The upper bound of reaction time for initial condition of linear and sinusoidal function class is obtained as follows.

Theorem 8. Let the D-initial condition be given by ψ(x) = a + bx, a > 0 with a + b/2 < 1, a ≠ b and a ≠ 1.

(1) If b > 0, then T_R(ψ) < log(1 + 2b(1 − a − b/2)/a(1 + a + b)²).

(2) If b < 0, then T_R(ψ) < log(1 + 2b(1 − a + b/2)/(a − b)(1 − a)²).

Proof. For D-initial condition ψ(x) = a + bx, b > 0, that is, 0 < a < 1 and 1 − a < b < 2 − 2a, we obtain

(37)

Therefore, by Theorem 7 for D-initial condition ψ(x) = a + bx, b > 0 we obtain the upper bound of reaction time T_R(ψ) as

(38)

In the same way, we obtain the upper bound of reaction time for D-initial condition ψ(x) = a − bx as

(39)

From the first result in Theorem 8 we obtain the upper bound of the reaction time for some family of linear functions with positive gradient, while the second result is for the negative gradient.

Theorem 9. Let the D-initial condition be given by ψ(x) = a + bcos⁡(nπx) with n ≠ 0. The reaction time for ψ will satisfy

(40)

Proof. Let ψ(x) = a − bcos⁡(πx) satisfying condition (6); that is,

(41)

We have

(42)

By Theorem 7, we get an upper bound of reaction time for ψ(x) = a − bcos⁡(πx), as

(43)

Since the behavior of solution for initial condition ψ(x) = a − bcos⁡(πx) is the same as the behavior of solution for initial condition φ(x) = a + bcos⁡(πx), T_R(ψ) = T_R(φ).

For ψ(x) = a + bcos⁡(nπx) with , we can see the behavior solution on interval [0, 1/n]. The behavior solution on each interval I_i = [(i − 1)/n, i/n] is the same for all i = 1, …, n. To increase volume as mount of δ on the interval [0,1] is equal to increasing volume as mount of δ/n on each interval I_i. The upper bound of time T to increase the volume as mount of δ/n on interval [0, 1/n] is

(44)

This result will be used to show the relationship between diffusion coefficient D and the behavior of the solution of (2) for a given D-initial condition ψ.

4. The Lower Bound of D for Global Solution

The solution of (2) with D-initial condition ψ will blow up for t^∗ < ∞ if T_R(ψ) < T_D(ψ). This is because the reaction term is growing much faster to supply the volume than the suppressing of diffusion term. From Theorems 4, 5, 8, and 9, we obtained the lower bound for diffusion coefficient D such that the global solution for linear and sinusoidal function family of initial condition exists.

Theorem 10. Let the Modified-Logistic-Diffusion be

(45)

with

and a + b > 1. For b > 0 and 2π²(1 − a)/(8 + π²) < b, the solution u(x, t) will blow up if

(46)

and for b < 0, 0 < 2π²(a − 1)/(π² − 8) + b and 0 < b + a, the solution u(x, t) will blow up if

(47)

Theorem 10 gives the lower bound of D such that (2) on [0,1] with the D-initial conditions of the increasing linear function and the decreasing linear function has a global solution. In this case

(48)

is lower bound of D so the system with D-initial condition of the increasing linear function ψ(x) = a + bx, b > 0 has a global solution. As for the decreasing linear function ψ(x) = a + bx, b < 0, the lower bound of D is

(49)

The next theorem discusses some family of trigonometric function of initial condition.

Theorem 11. Let the Modified-Logistic-Difussion be

(50)

with n ≠ 0, 1/2 < a < 1, and 1 − a < b < a. The solution u(x, t) will blow up if

(51)

5. Discussion

The diffusion-reaction equation with modified logistic function of reaction term and Neumann’s boundary condition at [0,1] can have a global or blow-up solution. If the initial conditions given are D-initial conditions, then the diffusion term plays an important role in determining whether the system will have a global solution or a blow-up solution. In this study, we obtain the lower bound of the diffusion coefficient D such that the system has a global solution. The objective for further investigation is determining the limiting value of the diffusion coefficient D such that, for D-initial condition, the solution has a global soluton or a blow-up solution.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Open Research

Data Availability

No data were used to support this study.

References

1 Golan A., Information and entropy econometrics - volume overview and synthesis, Journal of Econometrics. (2007) 138, no. 2, 379–387, 2-s2.0-34247547839, https://doi.org/10.1016/j.jeconom.2006.05.001, Zbl06578057.
10.1016/j.jeconom.2006.05.001
Web of Science® Google Scholar
2 Ruiz M. D. C., Guillamón A., and Gabaldón A., A new approach to measure volatility in energy markets, Entropy. (2012) 14, no. 1, 74–91, 2-s2.0-84861128979, https://doi.org/10.3390/e14010074.
10.3390/e14010074
Web of Science® Google Scholar
3 Lebiedz D., Entropy-related extremum principles for model reduction of dissipative dynamical systems, Entropy. (2010) 12, no. 4, 706–719, 2-s2.0-77953534048, https://doi.org/10.3390/e12040706, Zbl1229.37019.
10.3390/e12040706
CAS Web of Science® Google Scholar
4 Baierlein R., Thermal Physics, 1999, Cambridge University Press, Cambridge, UK, https://doi.org/10.1017/CBO9780511840227.
10.1017/CBO9780511840227
Google Scholar
5 Glansdorff P. and Prigogine I., Thermodynamic Theory of Structure, Stability, and Fluctuations, WileyInterscience, 1971, John Wiley & Sons, London.
Google Scholar
6 Bennett C. H., Notes on Landauer′s principle, reversible computation, and Maxwell′s demon, Studies in History and Philosophy of Modern Physics. (2003) 34, no. 3, 501–510, https://doi.org/10.1016/S1355-2198(03)00039-X, MR2011729, Zbl1222.81039.
10.1016/S1355-2198(03)00039-X
Web of Science® Google Scholar
7 Incropera F. P. and DeWitt D. P., Introduction to heat transfer, 1996, 3rd edition, Wiley, New York, USA, Introduction to heat transfer.
Google Scholar
8 Lucia U., Thermodynamic paths and stochastic order in open systems, Physica A: Statistical Mechanics and its Applications. (2013) 392, no. 18, 3912–3919, 2-s2.0-84879688465, https://doi.org/10.1016/j.physa.2013.04.053, Zbl1395.82203.
10.1016/j.physa.2013.04.053
Web of Science® Google Scholar
9 Chen B., Wong S., and Li C., On the calculation of system entropy in nonlinear stochastic biological networks, Entropy. (2015) 17, no. 10, 6801–6833, https://doi.org/10.3390/e17106801.
10.3390/e17106801
Web of Science® Google Scholar
10 Chen B.-S. and Li C.-W., On the interplay between entropy and robustness of gene regulatory networks, Entropy. (2010) 12, no. 5, 1071–1101, https://doi.org/10.3390/e12051071, MR2653294, Zbl1229.92037, 2-s2.0-77953528177.
10.3390/e12051071
CAS Web of Science® Google Scholar
11 Chen B.-S. and Lin Y.-P., On the information transmission ability of nonlinear stochastic dynamic networks, Entropy. (2012) 14, no. 9, 1652–1670, 2-s2.0-84867478074, https://doi.org/10.3390/e14091652, Zbl1305.94121.
10.3390/e14091652
Web of Science® Google Scholar

All articles

Blow-Up Solution of Modified-Logistic-Diffusion Equation

Abstract

1. Introduction

2. Diffusion Time

3. Reaction Time

4. The Lower Bound of D for Global Solution

5. Discussion

Conflicts of Interest

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Blow-Up Solution of Modified-Logistic-Diffusion Equation

Abstract

1. Introduction

2. Diffusion Time

3. Reaction Time

4. The Lower Bound of D for Global Solution

5. Discussion

Conflicts of Interest

Open Research

Data Availability

References

Figures

References

Related

Information