Volume 2019, Issue 1 5715694

Research Article

Open Access

Analysis of Complex Modal Characteristics of Fractional Derivative Viscoelastic Rotating Beams

Tianle Lu,

Tianle Lu

School of Civil Engineering and Architecture, Xi’an University of Technology, 710048 Xi’an, China xaut.edu.cn

Search for more papers by this author

Zhongmin Wang,

Corresponding Author

Zhongmin Wang

[email protected]

orcid.org/0000-0001-8657-8628

School of Civil Engineering and Architecture, Xi’an University of Technology, 710048 Xi’an, China xaut.edu.cn

Search for more papers by this author

Dongdong Liu,

Dongdong Liu

School of Civil Engineering and Architecture, Xi’an University of Technology, 710048 Xi’an, China xaut.edu.cn

Search for more papers by this author

Tianle Lu,

Tianle Lu

School of Civil Engineering and Architecture, Xi’an University of Technology, 710048 Xi’an, China xaut.edu.cn

Search for more papers by this author

Zhongmin Wang,

Corresponding Author

Zhongmin Wang

[email protected]

orcid.org/0000-0001-8657-8628

School of Civil Engineering and Architecture, Xi’an University of Technology, 710048 Xi’an, China xaut.edu.cn

Search for more papers by this author

Dongdong Liu,

Dongdong Liu

School of Civil Engineering and Architecture, Xi’an University of Technology, 710048 Xi’an, China xaut.edu.cn

Search for more papers by this author

First published: 2019

https://doi.org/10.1155/2019/5715694

Citations: 3

Guest Editor: Franco Concli

Share a link

Email
Wechat
Bluesky

Abstract

For the transverse vibration problem of a fractional derivative viscoelastic rotating beam, the differential equation of the system is obtained based on the Euler–Bernoulli beam theory and Hamilton principle. Then, introducing dimensionless quantities to differential equations and boundary conditions, the generalized complex eigenvalue equations of the system are obtained by the differential quadrature method. The effects of the slenderness ratio, the viscoelastic ratio, the hub radius-beam length ratio, and dimensionless hub speed and fractional order on the vibration characteristics of fractional derivative viscoelastic rotating beams are discussed by numerical examples. Numerical calculations show that when the dimensionless hub speed is constant, the real part of complex frequency increases with the increase of the fractional order, and the higher-order growth trend is more obvious. Through the study of displacement response at different points on the beam, it can be seen that the closer to the free end, the larger the response amplitude. And, the amplitude of response has been attenuated, which is also consistent with the vibration law of free vibration considering damping.

1. Introduction

With the rapid development of manufacturing industry and mechanical structure engineering, rotating structure is more and more widely used in mechanical engineering, such as internal combustion engines, satellites, turbines, and CNC machine tools.

Many scholars have made a lot of research on the dynamics of rotating beams. Bannerjee and Su [1] analyzed the free vibration characteristics of Timoshenko beams by the dynamic stiffness method and compared the results with Euler–Bernoulli theory. In consideration of Coriolis force and centrifugal force, Tian et al. [2] investigated the influence of hub radius, slenderness ratio, and angular velocity on the vibration characteristics of rotating beam. Aksencer and Aydogdu [3] studied the vibration problem of rotating composite beams by using the Ritz method, and the effects of several geometric factors on the vibration characteristics of composite beams under different boundary conditions were analyzed. Considering geometric nonlinearity, Zhang et al. [4] studied the nonlinear vibration of a variable cross-section viscoelastic rotating beam, which is based on Kelvin–Voigt viscoelastic constitutive relation, and the amplitude-frequency response of the rotating beam is obtained by the multiscale method. Li et al. [5] studied the vibration characteristics of a rotating FGM circular section flexible beam. Srivatsa and Ranjan [6] solved the vibration problem of a rotating Rayleigh beam with variable cross-section and obtained the frequency and mode shapes of the beam by the finite element method. Tang et al. [7] investigated the free vibration of the rotating cone cantilever beam based on the Hamiltonian principle, and then analyzed the effects of angular velocity and the moment of inertia on the free vibration of the system. Sofiyev and Hui [8] used FOSDT and Donnell shell theory to study the vibration and stability of cylindrical shells with functionally graded materials under mixed boundary conditions and analyzed the influence of factors such as FG distribution on the critical parameters of FGMCSS containing MBCS. Based on FOSDT and isotropic constitutive relation, Yao et al. [9] studied the nonlinear dynamic response of a rotating cylindrical shell with pretorsion angle by using Hamilton principle, and the effects of excitation parameters, damping coefficient, rotational speed, prerotation angle, and pretorsion angle on the nonlinear dynamic response of the system were analyzed. Based on the dynamic stiffness method, Banerjee and Jackson [10] investigated the free vibration characteristics of the rotating cone-shaped Rayleigh beam and analyzed the effects of the viscosity-elasticity rate on the free vibration characteristics of the rotating conical Rayleigh beam. Based on Euler–Bernoulli, Timoshenko, Reid, and Levison’s four different beam theories, Chakraverty and Behera [11] used the DQM to investigate the buckling of nanobeams and analyzed the effects of nonlocal parameters, aspect ratio, boundary conditions, and nonuniform parameters on the critical buckling load parameters.

The fractional derivative viscoelastic model is considered to be a model that can accurately describe the constitutive relation of viscoelastic materials, and it can describe the mechanical behavior of materials in a wide frequency range and determine the experimental parameters required for the model. Based on fractional derivative theory, Gao et al. [12] investigated the viscoelastic mechanical parameters of three standard linear solid material properties. Tarasov [13] investigated the characteristics of fractional derivatives of noninteger order and proposed the nonlocality principle of fractional derivatives. Achouri et al. [14] investigated the initial-boundary value problem of Euler–Bernoulli beam equation with fractional derivative boundary conditions and analyzed the existence and attenuation of its initial-boundary value solution. Based on Euler–Bernoulli beam theory, Ansari et al. [15] studied the geometric nonlinearity vibration of fractional order viscoelastic nanobeams. Bahraini et al. [16] studied the free vibration of viscoelastic cantilever beams with different boundary conditions under concentrated loads and analyzed the influence of fractional derivatives on the large deflection of viscoelastic cantilever beams.

At present, the theory and application of the differential quadrature method (DQM) are quite mature, and it is mainly used to solve some problems such as high-order differential equations with variable coefficients. Li and Ying [17] solved the transverse vibration of elastic Euler–Bernoulli beams under interharmonic loads by the differential quadrature method and analyzed its vibration characteristics. Based on the Euler–Bernoulli beam model, Zhang et al. [18] studied the large deformation mechanical behavior of members by the differential quadrature method. Cao [19] investigated the static response of reinforced concrete (RC) beams using the generalized differential quadrature method by virtual work principle. Through the differential quadrature method, Matbuly et al. [20] solved the free vibration problem of functionally graded elastic beams and studied the influence of geometric parameters on the natural frequency of the beam. Li et al. [21] studied the dynamic properties of viscoelastic Timoshenko beams by the differential quadrature method and the nonlinear numerical method. Considering the geometric parameters, moment of inertia, and quadratic coupling deformations of variable cross-section beams, Wang and Li [22] studied the transverse vibration characteristics of a rotating cone cantilever beam by using Hamiltonian variational principle, and the DQM was used to solve the differential equation of motion. Based on the thin plate theory, Zhou and Wang [23] solved the vibration problem of variable thickness viscoelastic plates by the differential quadrature method and studied the influence of length to diameter ratio and thickness to diameter ratio on the vibration of linear thickness viscoelastic plates.

In this paper, based on Euler–Bernoulli beam theory and Hamilton principle, the vibration model and motion differential equation of the fractional derivative viscoelastic rotating beam are established. The dimensionless quantity is introduced, and the differential equations and boundary conditions are processed in a dimensionless manner. Then, the differential quadrature method is used to discretize the differential equation and boundary conditions, and the generalized complex eigenequation of the system is obtained. The effects of slenderness ratio, the hub radius-beam length ratio, the viscoelastic ratio, dimensionless hub speed, and fractional order on the complex frequency characteristics of the system are analyzed.

2. One-Dimensional Fractional Kelvin–Voigt Model Theory

The classical Kelvin–Voigt model is composed of a spring and a Newton viscous pot in parallel, and the stress-strain relationship of the fractional Kelvin model is as follows:

\begin{matrix} σ_{x} (t) = E ε_{x} (t) + η D^{α} [ε_{x} (t)], \end{matrix}

(1)

where E and η are the Young’s modulus of elasticity and damping modulus of the material, ε_x(t) is the Lagrange strain of finite deformation; D^α is the Riemann-Liouville fractional differential operator, and α is a fractional order.

Set 0 ≤ α ≤ 1, the α order Riemann–Liouville fractional derivative of the function f(t) defined on [0, t] is expressed as follows [12]:

\begin{matrix} D^{α} [f (t)] = \frac{f (0)}{Γ (1 - α)} t^{- α} + \frac{1}{Γ (1 - α)} \int_{0}^{t} \frac{f^{'} (τ)}{{(t - τ)}^{α}} d τ . \end{matrix}

(2)

3. Differential Equation of Motion

3.1. Deformation Field Description

Figure 1(a) shows that the schematic diagram of the fractional derivative viscoelastic rotating hollow beam, which has length L of the beam, radius a, and rotating angular velocity ω of the hub. The oxy and OXY are the floating coordinate system and the inertial coordinate system, respectively. The θ represents rotation angle of the viscoelastic beam in a wide range of motion, that is, the rotation angle of the oxy is relative to the OXY. The ox-axis coincides with the axis of the viscoelastic hollow circular section beam before deformed.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Dynamic model of fractional derivative viscoelastic rotating hollow beam. (a) Fractional derivative viscoelastic rotating hollow beam. (b) Viscoelastic rotating hollow beam profile.

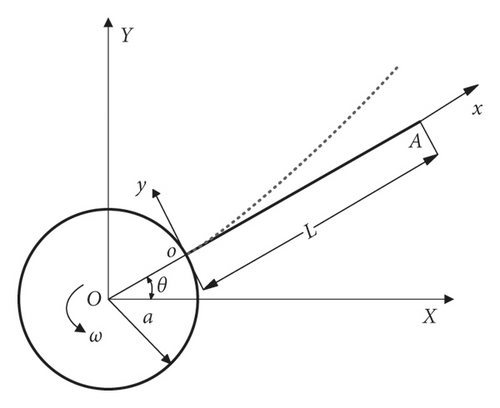
In Figure 1(b), the cross-section of the beam is a hollow section with wall thickness h and R_n is the radius of the wall thickness for any cross-section at the middle line. In the n − s coordinate system, n is the normal direction and s is the tangential direction.

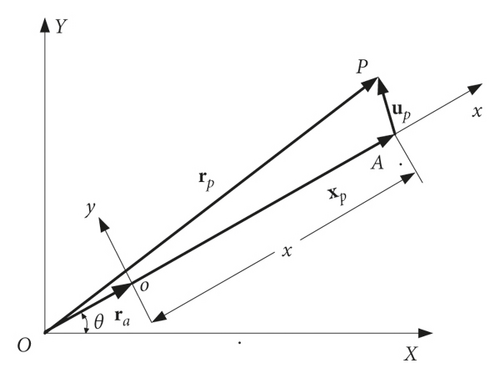
In Figure 2, r_a is a radius vector of the hub, x_p is the vector diameter of any point P on the axis of a fractional derivative viscoelastic beam relative to the point o in the floating coordinate system when it is not deformed, and u_p is a displacement vector of the point P.

The position vector of point P relative to the point O can be written as follows:

\begin{matrix} r_{p} = r_{a} + A_{θ} (x_{p} + u_{p}), \end{matrix}

(3)

where

\begin{matrix} r_{a} = {[\begin{matrix} a \cos θ & a \sin θ \end{matrix}]}^{T}, \\ x_{p} = {[\begin{matrix} x & 0 \end{matrix}]}^{T}, \\ A_{θ} = [\begin{matrix} \cos θ & - \sin θ \\ \sin θ & \cos θ \end{matrix}], \\ u_{p} = [\begin{matrix} u_{p x} \\ u_{p y} \end{matrix}] = [\begin{matrix} u + u_{c} + u_{b} \\ w \end{matrix}] \\ = [\begin{matrix} u - \frac{1}{2} \int_{0}^{x} {(w_{, x})}^{2} d x - y w_{, x} \\ w \end{matrix}], \end{matrix}

(4)

where A_θ, u, and w are the transformation matrices of the oxy relative to the OXY, the axial displacement, and the lateral bending deformation displacement on the beam axis, respectively; u_b = −yw_,x is the axial displacement caused by the rotation of the beam cross-section,

u_{c} = - 12 / \int_{0}^{x} {(w_{, x})}^{2} d x

is the secondary deformation coupling of the beam, that is, the axial expansion amount caused by the lateral bending deformation of the fractional derivative viscoelastic rotating hollow beam, and “, x” represents the first derivative of x.

Taking the first derivative of time for equation (3), we get the velocity vector of point P as follows:

\begin{matrix} {\dot{r}}_{p} = {\dot{r}}_{a} + \dot{θ} \times Α_{θ} (x_{p} + u_{p}) + Α_{θ} {\dot{u}}_{p} \\ = [\begin{matrix} - (a + x + u_{c} + u_{b}) \dot{θ} \sin θ - w \dot{θ} \cos θ + ({\dot{u}}_{c} + {\dot{u}}_{b}) \cos θ - \dot{w} \sin θ \\ (a + x + u_{c} + u_{b}) \dot{θ} \cos θ - w \dot{θ} \sin θ + ({\dot{u}}_{c} + {\dot{u}}_{b}) \sin θ + \dot{w} \cos θ \end{matrix}], \end{matrix}

(5)

where

\dot{θ} = [\begin{matrix} 0 & - \dot{θ} \\ \dot{θ} & 0 \end{matrix}]

is the antisymmetric matrix of angular velocity

\dot{θ}

and “⋅” represents the first derivative of t.

3.2. Differential Equations of Motion

The total kinetic energy of the system can be seen as the sum of the kinetic energy of the hub and the kinetic energy of the fractional derivative viscoelastic rotating beam, namely

\begin{matrix} T_{s} = T_{H} + T \\ = \frac{1}{2} J_{H} {\dot{θ}}^{2} + \frac{1}{2} ρ \int_{V} {\dot{r}}_{p}^{T} {\dot{r}}_{p} d V \\ = \frac{1}{2} J_{H} {\dot{θ}}^{2} + \frac{1}{3} ρ I {\dot{θ}}^{2} \int_{0}^{L} {(w_{, x})}^{2} d x + \frac{1}{3} ρ I \int_{0}^{L} {({\dot{w}}_{, x})}^{2} d x \\ + \frac{1}{2} \int_{0}^{L} ρ A [{\dot{w}}^{2} + {\dot{u}}_{c}^{2} + {\dot{θ}}^{2} [w^{2} + {(a + x + u_{c})}^{2}]] d x \\ + \int_{0}^{L} ρ A \dot{θ} [- {\dot{u}}_{c} w + \dot{w} (a + x + u_{c})] d x, \end{matrix}

(6)

where J_H is the inertia moment of the hub with respect to the central axis.

The strain energy of the system can be divided into two parts, one part is potential energy and the other part is dissipative energy.

The potential energy can be expressed as follows:

\begin{matrix} V_{0} = \int_{V} \frac{1}{2} σ_{x} ε_{x} d V = \int_{V} \frac{1}{2} E ε_{x}^{2} d V, \end{matrix}

(7)

where σ_x, ε_x, and V are the normal stress, normal strains of the beam, and the volume of the viscoelastic beam, respectively.

In equation (4), not considering the axial displacement and ignoring nonlinear term, the normal strain can be obtained by the relationship between strain and displacement, namely,

\begin{matrix} ε_{x} = u_{p x, x} = {[- \frac{1}{2} \int_{0}^{x} {(w_{, x})}^{2} d x - y w_{, x}]}_{, x} \\ = - [y (s) - n z_{, s}] w_{, x x} - \frac{1}{2} {(w_{, x})}^{2} . \end{matrix}

(8)

According to Figure 1(b), the geometric relations can be obtained:

\begin{matrix} \frac{d z}{d s} = - \sin ϕ = - \sin (\frac{s}{R_{n}}), \\ \frac{d y}{d s} = \cos ϕ = \cos (\frac{s}{R_{n}}) . \end{matrix}

(9)

Then, the potential energy can be expressed as follows:

\begin{matrix} V_{o} = \int_{0}^{L} \int_{A} \frac{1}{2} E ε_{x}^{2} (t) d A d x \\ = \int_{0}^{L} \int_{- h / 2}^{h / 2} \int_{0}^{π R_{n}} \frac{1}{2} E {[(R_{n} + n) \sin \frac{s}{R_{n}} w_{, x x} + \frac{1}{2} {(w_{, x})}^{2}]}^{2} \frac{R_{n} + n}{R_{n}} d s d n d x \\ = \frac{1}{2} E I \int_{0}^{L} {(w_{, x x})}^{2} d x + \frac{1}{8} E A \int_{0}^{L} {(w_{, x})}^{4} d x, \end{matrix}

(10)

where I and A are the inertia moment and the cross-sectional area of the beam, respectively,

\begin{matrix} I = \frac{1}{64} π [{(2 R_{n} + h)}^{4} - {(2 R_{n} - h)}^{4}] = \frac{1}{4} π (4 R_{n}^{3} h + R_{n} h^{3}), \\ A = π [{(R_{n} + \frac{h}{2})}^{2} - {(R_{n} - \frac{h}{2})}^{2}] = 2 π R_{n} h . \end{matrix}

(11)

The expression of the system’s dissipative energy is

\begin{matrix} W_{c} = \int_{V} \int_{0}^{ε_{x} (t)} η D^{α} [ε_{x} (t)] d ε_{x} (t) d V . \end{matrix}

(12)

From equation (2), the following equation can be obtained

\begin{matrix} D^{α} [ε_{x} (t)] = \frac{ε_{x} (0)}{Γ (1 - α)} t^{- α} + \frac{1}{Γ (1 - α)} \int_{0}^{t} \frac{{\dot{ε}}_{x} (τ)}{{(t - τ)}^{α}} d τ . \end{matrix}

(13)

Substituting equation (12) into equation (13), the following equation can be obtained:

\begin{matrix} W_{c} = \int_{V} η D^{α} [ε_{x} (t)] ε_{x} (t) d V \\ = \int_{V} \int_{0}^{ε_{x} (t)} η \frac{ε_{x} (0)}{Γ (1 - α)} t^{- α} d ε_{x} (t) d V \\ + \int_{V} \int_{0}^{ε_{x} (t)} η \frac{1}{Γ (1 - α)} \int_{0}^{t} \frac{{\dot{ε}}_{x} (τ)}{{(t - τ)}^{α}} d τ d ε_{x x} d V \\ = η I \int_{0}^{L} w_{, x x} D^{α} (w_{, x x}) d x + \frac{1}{4} η A \int_{0}^{L} {(w_{, x})}^{2} D^{α} [{(w_{, x})}^{2}] d x . \end{matrix}

(14)

In this paper, based on Hamiltonian variational principle, the differential equation of fractional derivative viscoelastic rotating beam is derived. Hamilton’s variational principle takes the form of

\begin{matrix} δ \int_{t_{1}}^{t_{2}} L d t = δ \int_{t_{1}}^{t_{2}} (T_{s} - V_{0} - W_{c}) d t = 0. \end{matrix}

(15)

Substituting equations (6), (10), and (14) into equation (15) and ignoring the nonlinear term in the equation, the vibration differential equation of the uniformly rotating (

\dot{θ} = ω_{0}, \ddot{θ} = 0

) fractional derivative viscoelastic beam can be obtained:

\begin{matrix} - E I w_{, x x x x} + ρ A (- \ddot{w} + ω_{0}^{2} w) - \frac{2}{3} ρ I ω_{0}^{2} w_{, x x} \\ + \frac{2}{3} ρ I {\ddot{w}}_{, x x} + ρ A ω_{0}^{2} a (L - x) w_{, x x} - η I D^{α} (w_{, x x x x}) \\ + \frac{1}{2} ρ A ω_{0}^{2} (L^{2} - x^{2}) w_{, x x} - ρ A ω_{0}^{2} (a + x) w_{, x} = 0. \end{matrix}

(16)

The boundary conditions of the fractional derivative viscoelastic beam are as follows:

x = 0:

\begin{matrix} w = 0, \end{matrix}

(17a)

\begin{matrix} w_{, x} = 0. \end{matrix}

(17b)

x = L:

\begin{matrix} E I w_{, x x} + η I D^{α} w_{, x x} = 0, \end{matrix}

(17c)

\begin{matrix} E I \frac{\partial}{\partial x} (\frac{\partial^{2} w}{\partial x^{2}}) - \frac{2}{3} ρ I \frac{\partial^{3} w}{\partial x \partial t^{2}} \\ + \frac{2}{3} ρ I ω_{0}^{2} \frac{\partial w}{\partial x} + η I \frac{\partial}{\partial x} (D^{α} w_{, x x}) = 0. \end{matrix}

(17d)

3.3. Dimensional Normalization of the Equation

To facilitate subsequent calculations, the following dimensionless quantities have been introduced:

\begin{matrix} ξ = \frac{x}{L}, \\ W = \frac{w}{L}, \\ r_{0} = \frac{a}{L}, \\ r = \frac{R}{L}, \\ \tilde{t} = \frac{t}{L^{2} \sqrt{(ρ A / E I)}}, \\ ω_{1} = ω {}_{0}L^{2} \sqrt{\frac{ρ A}{E I}}, \\ g = \frac{η}{E L^{2} \sqrt{(ρ A / E I)}}, \end{matrix}

(18)

where r₀ is the hub radius-beam length ratio, r is slenderness ratio, ω₁ is dimensionless hub speed, and g is viscoelastic ratio.

Substituting the above dimensionless quantity into equation (16)

\begin{matrix} \frac{\partial^{4} W}{\partial ξ^{4}} + \frac{\partial^{2} W}{\partial {\tilde{t}}^{2}} - ω_{1}^{2} r_{0} (1 - ξ) \frac{\partial^{2} W}{\partial ξ^{2}} + \frac{1}{6} ω_{1}^{2} r^{2} \frac{\partial^{2} W}{\partial ξ^{2}} \\ - \frac{1}{2} ω_{1}^{2} (1 - ξ^{2}) \frac{\partial^{2} W}{\partial ξ^{2}} - ω_{1}^{2} W + g \frac{\partial^{α}}{\partial {\tilde{t}}^{α}} (\frac{\partial^{4} W}{\partial ξ^{4}}) \\ - \frac{1}{6} r^{2} \frac{\partial^{4} W}{\partial ξ^{2} \partial {\tilde{t}}^{2}} + ω_{1}^{2} (r_{0} + ξ) \frac{\partial W}{\partial ξ} = 0. \end{matrix}

(19)

The solution of equation (19) can be set as

W (ξ, \tilde{t}) = W (ξ) \exp (ω_{f} \tilde{t})

, and the differential equation of mode shape can be written as follows:

\begin{matrix} W_{, ξ ξ ξ ξ} (ξ) + ω_{f}^{2} W (ξ) - ω_{1}^{2} W (ξ) + \frac{1}{6} ω_{1}^{2} r^{2} W_{, ξ ξ} (ξ) \\ - ω_{1}^{2} [r_{0} (1 - ξ) + \frac{1}{2} (1 - ξ^{2})] W_{, ξ ξ} (ξ) + g ω_{f}^{α} W_{, ξ ξ ξ ξ} (ξ) \\ + ω_{1}^{2} (r_{0} + ξ) W_{, ξ} (ξ) - \frac{1}{6} ω_{f}^{2} r^{2} W_{, ξ ξ} (ξ) = 0, \end{matrix}

(20)

where ω_f is a dimensionless complex frequency.

Substituting the dimensionless quantity into equations (17a) and –(17d), respectively, the dimensionless boundary conditions of the fractional derivative viscoelastic beam can be expressed as follows:

\begin{matrix} W (0) = 0, \end{matrix}

(21a)

\begin{matrix} W_{, ξ} (0) = 0, \end{matrix}

(21b)

\begin{matrix} W_{, ξ ξ} (1) + g ω_{f}^{α} W_{, ξ ξ} (1) = 0, \end{matrix}

(21c)

\begin{matrix} W_{, ξ ξ ξ} (1) - \frac{1}{6} r^{2} ω_{f}^{2} W_{, ξ} (1) \\ + \frac{1}{6} r^{2} ω_{1}^{2} W_{, ξ} (1) + g ω_{f}^{α} W_{, ξ ξ ξ} (1) = 0. \end{matrix}

(21d)

3.4. Differential Quadrature Method

When the differential quadrature method is used to solve the equation, most of the calculation accuracy will be determined by the selection of the weight function. Therefore, when using this method for calculation, the node distribution must be selected reasonably. For the equations of the specific problem to be solved, the properties of the solution region are different, often using nonuniform node partitioning, and more mesh points can be selected for regions close to the boundary where the physical properties change more prominently. And for the boundary region, the small variable δ is used for the adjacency processing.

The values of the nodes by nonuniform sampling method are as follows:

\begin{matrix} ξ_{1} = 0, \\ ξ_{2} = δ, \\ ξ_{i} = \frac{1}{2} (1 - \cos \frac{i - 2}{N - 3} π), i = 3,42, \dots, N -, \\ ξ_{N - 1} = 1 - δ, \\ ξ_{N} = 1, \end{matrix}

(22)

where set δ = 1 × 10⁻⁶ and N = 13 in subsequent calculation.

Then the discretization of equation (20) can be written as follows:

\begin{matrix} \sum_{j = 1}^{N} A_{i j}^{(4)} W_{j} + \frac{1}{6} ω_{1}^{2} r^{2} \sum_{j = 1}^{N} A_{i j}^{(2)} W_{j} + g ω_{f}^{α} \sum_{j = 1}^{N} A_{i j}^{(4)} W_{j} \\ - ω_{1}^{2} [r_{0} (1 - ξ_{i}) + \frac{1}{2} (1 - ξ_{i}^{2})] \sum_{j = 1}^{N} A_{i j}^{(2)} W_{j} - ω_{1}^{2} W_{i} + ω_{f}^{2} W_{i} \\ + ω_{1}^{2} (r_{0} + ξ_{i}) \sum_{j = 1}^{N} A_{i j}^{(1)} W_{j} - \frac{1}{6} ω_{f}^{2} r^{2} \sum_{j = 1}^{N} A_{i j}^{(2)} W_{j} = 0, \end{matrix}

(23)

where

A_{i j}^{(1)}

A_{i j}^{(2)}

A_{i j}^{(3)}

, and

A_{i j}^{(4)}

are first-order, second-order, third-order, and fourth-order weight coefficients, respectively,

\begin{matrix} A_{i j}^{(1)} = \{\begin{cases} \frac{\prod_{\begin{cases} k = 1 \\ k \neq i, j \end{cases}}^{N} (x_{i} - x_{k})}{\prod_{\begin{cases} k = 1 \\ k \neq j \end{cases}}^{N} (x_{j} - x_{k})}, i, j = 1,2, \dots, N; i \neq j, \\ \sum_{\begin{cases} k = 1 \\ k \neq i \end{cases}}^{N} \frac{1}{x_{i} - x_{k}}, i, j = 1,2, \dots, N; i = j, \end{cases} \\ A_{i j}^{(2)} = \sum_{k = 1}^{N} A_{i k}^{(1)} A_{k j}^{(1)}, \\ A_{i j}^{(3)} = \sum_{k = 1}^{N} A_{i k}^{(1)} A_{k j}^{(2)}, i, j = 1,2, \dots, N, \\ A_{i j}^{(4)} = \sum_{k = 1}^{N} A_{i k}^{(2)} A_{k j}^{(2)} . \end{matrix}

(24)

The discretization of the boundary conditions is

\begin{matrix} W_{1} = 0, \end{matrix}

(25a)

\begin{matrix} \sum_{j = 1}^{N} A_{2 j}^{(1)} W_{j} = 0, \end{matrix}

(25b)

\begin{matrix} (1 + g ω_{f}^{α}) \sum_{j = 1}^{N} A_{N - 1, j}^{(2)} W_{j} = 0, \end{matrix}

(25c)

\begin{matrix} \sum_{j = 1}^{N} A_{N j}^{(3)} W_{j} - \frac{1}{6} r^{2} ω_{f}^{2} \sum_{j = 1}^{N} A_{N j}^{(1)} W_{j} \\ + \frac{1}{6} r^{2} ω_{1}^{2} \sum_{j = 1}^{N} A_{N j}^{(1)} W_{j} + g ω_{f}^{α} \sum_{j = 1}^{N} A_{N j}^{(3)} W_{j} = 0. \end{matrix}

(25d)

Equations (23), (25a) and –(25d) can be written in matrix form:

\begin{matrix} (ω_{f}^{2} M + ω_{f}^{α} C + K) W = 0, \end{matrix}

(26)

where M, C, and K are all (N − 1) square matrix and

W = {[\begin{matrix} W_{2} & W_{3} & \dots & W_{N - 1} & W_{N} \end{matrix}]}^{T}

is column matrix.

Thus, the generalized characteristic equation corresponding to equation (26) can be obtained as follows:

\begin{matrix} |ω_{f}^{2} M + ω_{f}^{α} C + K| = 0, \end{matrix}

(27)

where M, C and K contain the hub radius-beam length ratio, the slenderness ratio, the viscoelastic ratio, the dimensionless hub speed, fractional order, and dimensionless complex frequency of the system.

4. Numerical Results and Analyses

4.1. Comparison and Verification

The correctness and feasibility of the differential quadrature method used in this paper are analyzed by comparing the numerical results with reference [7]. In the case when g = 0, α = 0, r = 0, and r₀ = 0.125, set the dimensionless hub speed at 0, 5, and 10, the result of the compared first three-order natural frequency with reference [7] is shown in Table 1:

Table 1. Comparison of the first three dimensionless natural frequencies of elastic cantilever rotating beams at g = 0, α = 0, r = 0, and r₀ = 0.125.

ω₁	0		5		10
ω₁	Present	Reference [7]	Present	Reference [7]	Present	Reference [7]
1st	3.515	3.507	6.302	6.425	10.953	11.159
2nd	22.029	21.647	24.951	24.973	32.122	32.965
3rd	60.673	59.207	65.011	63.539	73.672	71.497

It can be seen from the Table 1 that when the dimensionless hub rotational speed ω₁ is 0, 5, and 10 respectively, the dimensionless natural frequency of the system is basically the same as that of reference [7], and all errors are below 2%.

4.2. Numerical Calculation and Analysis

Considering the influence of moment of inertia, the effects of slenderness ratio r, the hub radius-beam length ratio r₀, viscoelastic ratio g, dimensionless hub speed ω₁, and fractional order α on the first three-order dimensionless Im(ω_f) (imaginary part of complex frequency) and Re(ω_f) (real part of complex frequency) of the fractional derivative rotating viscoelastic beam are analyzed.

Figure 3 plots the curves of complex frequency of the system with the hub radius-beam length ratio at r = 1/30, g = 0.025, ω₁ = 10, and α = 1/2. And we can see that the complex frequency of the system vary linearly with r₀, and r₀ is positively correlated with the Im(ω_f), but negatively correlated with the Re(ω_f). With the increase of the order, the effect of r₀ on the Re(ω_f) is more obvious.

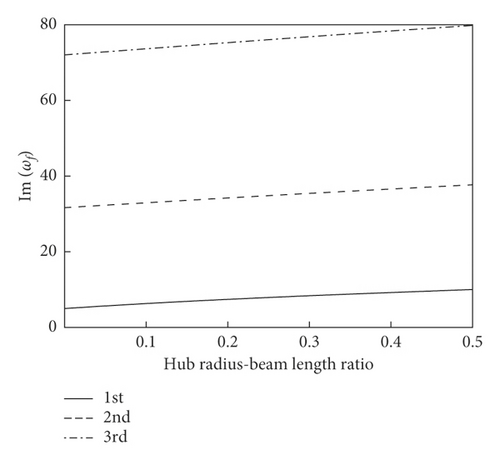
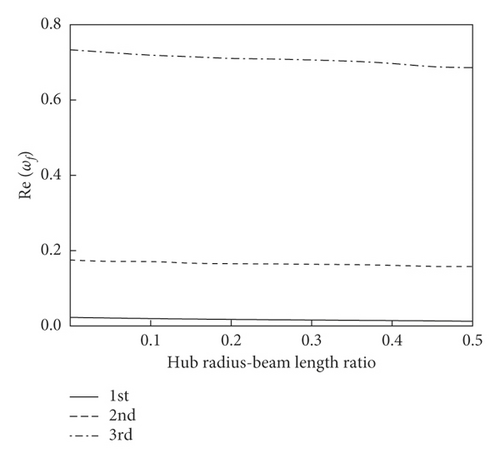
Figure 4 plots the curves of complex frequency of the system with slenderness ratio at r₀ = 0.25, g = 0.025, ω₁ = 10, and α = 1/2.

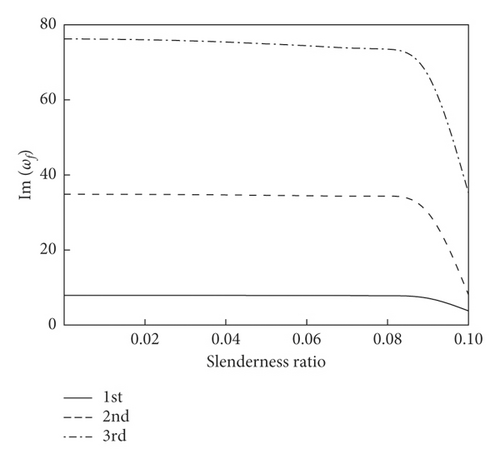
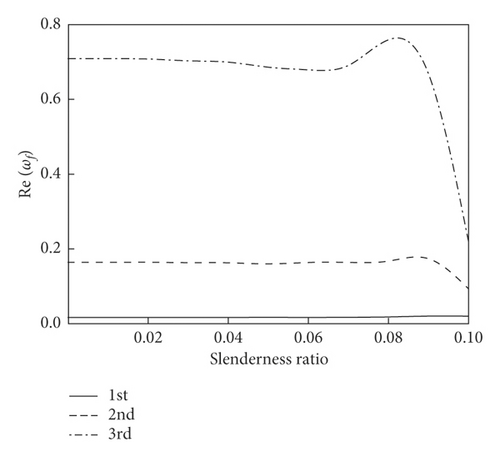
And we can see that when the slenderness ratio is between 0 and 0.08, slenderness ratio has less influence on the complex frequency of the system, and when slenderness ratio is between 0.08 and 0.10, the Im(ω_f) of the system is negatively correlated with slenderness ratio, and the Re(ω_f) increases first and then decreases. With the increase of the order of the system, the peak value of the Re(ω_f) moves forward.

Figure 5 plots the curves of complex frequency of the system with viscoelastic ratio at r₀ = 0.25, r = 1/30, ω₁ = 10, and α = 1/2.

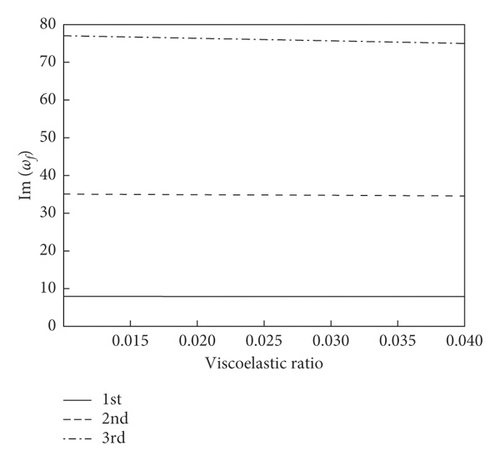
And we can see that the viscoelastic ratio has slight effect on the Im(ω_f) of the system, and with the increase of the viscoelastic ratio, the Im(ω_f) hardly changes. Meanwhile, the viscoelastic ratio has a great influence on the Re(ω_f), and there is a positive correlation between them, and with the increase of order, the Re(ω_f) increases more obviously. Therefore, the viscoelastic ratio can be used to describe the damping characteristics of materials.

Figure 6 plots the curve of complex frequency of the system with dimensionless hub speed at different fractional order α = 1/10, α = 1/5, and α = 1/2 at r₀ = 0.25, r = 1/30, and g = 0.025. And we can see that the dimensionless hub speed has a significant influence on the complex frequency of the system, and as the speed of the dimensionless hub increases, the Im(ω_f) increases, the Re(ω_f) decreases, and the attenuation of higher-order Re(ω_f) becomes more obvious.

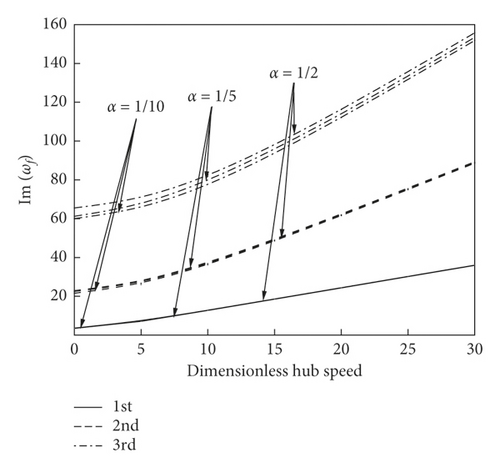
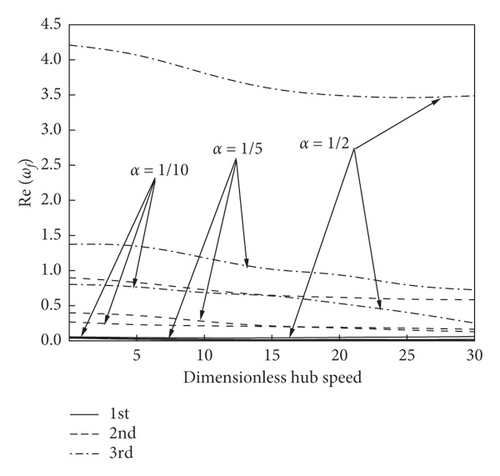
Meanwhile, fractional order has little effect on the Im(ω_f) of the system, but the influence on the Re(ω_f) is great, and the influence of fractional order on the high-order Re(ω_f) is obvious. When α = 1/2, the attenuation rate of the Re(ω_f) is faster than α = 1/5. Thus, viscoelastic materials with larger fractional order will be more conducive to the stability of the system.

4.3. Response of Viscoelastic Rotating Beams with Kelvin–Voigt Fractional Derivatives

For the system, set the number of mesh points N = 13, small variables δ = 1 × 10⁻⁶, and nonuniform meshing of Kelvin–Voigt viscoelastic material beam with fractional derivative, when ξ₃ = 0.02447, ξ₇ = 0.5, ξ₁₁ = 0.97553, and ξ₁₃ = 1, and the response curve of different points on the viscoelastic beam is as follows Figure 7:

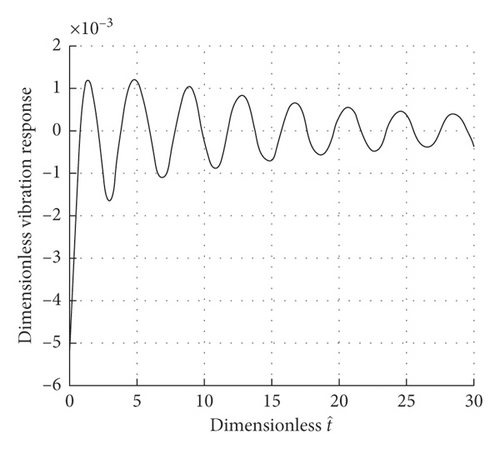
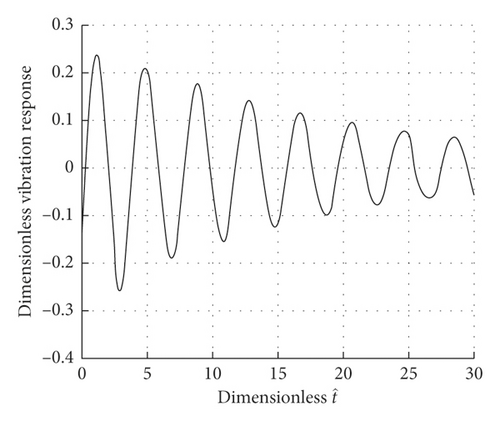
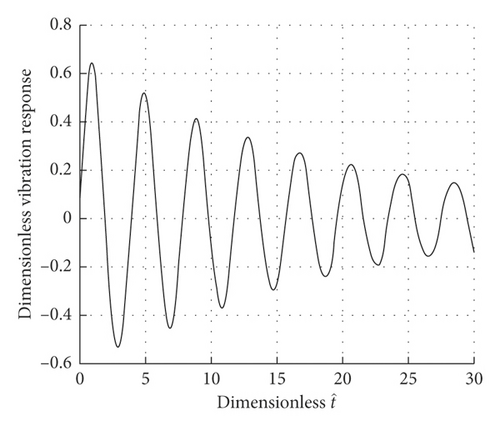
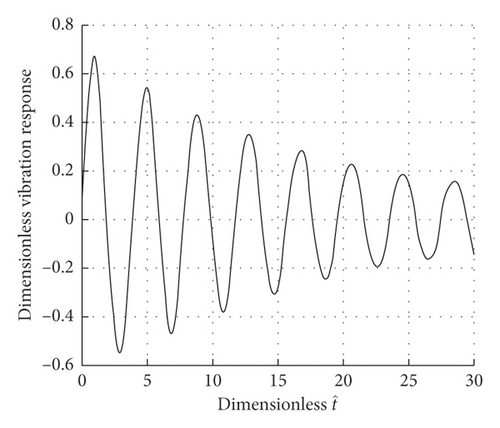
Figure 7 plots the curves of response of the Kelvin–Voigt viscoelastic beam with fractional derivative when r₀ = 0.25, r = 1/20, g = 0.025, ω₁ = 10, and α = 1/2. And we can see that the response at different points of the Kelvin–Voigt viscoelastic material beam.

As ξ_i increases, the corresponding response amplitude also increases, which indicates that the closer to the free end, the greater the response amplitude. Moreover, the amplitude of the system’s response decreases with time, which is due to the damping effect in the material.

5. Conclusion

Based on Hamilton principle and Euler–Bernoulli beam theory, the influence of slenderness ratio, the hub radius-beam length ratio, dimensionless hub speed, viscoelastic ratio, and fractional order on the vibration characteristics of viscoelastic rotating beams with fractional derivatives is investigated by the differential quadrature method. The calculation results in this paper have little error with the existing literature, which shows the feasibility and correctness of the differential quadrature method. Compared with other methods, the solving process of the differential quadrature method is more intuitive and easier to program.

When the dimensionless hub speed is constant, the dimensionless Im(ω_f) and Re(ω_f) of the system both increases slightly with the hub radius-beam length ratio increase. For a fractional derivative viscoelastic rotating hollow beam at a constant velocity, when slenderness ratio is about 0.08, the Im(ω_f) and Re(ω_f) have a sudden change; the former has been attenuating, while the latter has increased first and then decreased rapidly. The viscoelastic ratio has little effect on the Im(ω_f) of the system, but it has a great influence on the Re(ω_f), and at high order, the Re(ω_f) increases rapidly.

With the increase of dimensionless hub speed, the Im(ω_f) of the system decreases, while the Re(ω_f) increases, and the attenuation of higher-order Re(ω_f) is more significant. Fractional order has little effect on the Im(ω_f) of the system, but it has great influence on the Re(ω_f), and the effect on the higher-order Re(ω_f) is more obvious.

Through the study of response at different points on a fractional derivative Kelvin–Voigt viscoelastic beam, we can see that the response at different points on a viscoelastic beam varies with time in a wave function, and the closer to the fixed end, the smaller the amplitude of response. When near the free end, the amplitude of response is larger but the amplitude of the system′s response decreases with time.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Acknowledgments

Thanks are due to the support of the National Natural Science Foundation of China (Grant no. 11972286).

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Banerjee J. R. and Su H., Dynamic stiffness formulation and free vibration analysis of a spinning composite beam, Computers & Structures. (2006) 84, no. 19-20, 1208–1214, https://doi.org/10.1016/j.compstruc.2006.01.023, 2-s2.0-33744508290.
10.1016/j.compstruc.2006.01.023
Web of Science® Google Scholar
2 Tian J., Su J., Zhou K., and Hua H., A modified variational method for nonlinear vibration analysis of rotating beams including Coriolis effects, Journal of Sound and Vibration. (2018) 426, no. 15, 258–277, https://doi.org/10.1016/j.jsv.2018.04.027, 2-s2.0-85046094849.
10.1016/j.jsv.2018.04.027
Web of Science® Google Scholar
3 Aksencer T. and Aydogdu M., Flapwise vibration of rotating composite beams, Composite Structures. (2015) 134, no. 16, 672–679, https://doi.org/10.1016/j.compstruct.2015.08.130, 2-s2.0-84941897678.
10.1016/j.compstruct.2015.08.130
Web of Science® Google Scholar
4 Zhang Y. F., Yang E. C., and Li Y. H., Studies on nonlinear parametric vibration a rotating viscoelastic beam with variable cross-sections, Journal of Dynamics and Control. (2018) 16, no. 5, 418–423.
CAS Google Scholar
5 Li R. R., Wang Z. M., and Yao X. S., Vibration characteristics of rotating flexible ring beam made of functionally graded material, Chinese Journal of Applied Mechanics. (2017) 34, no. 3, 418–422.
Google Scholar
6 Srivatsa B. K. and Ranjan G., Non-rotating beams isospectral to rotating Rayleigh beams, International Journal of Mechanical Sciences. (2018) 142-143, no. 7, 440–455, https://doi.org/10.1016/j.ijmecsci.2018.04.049, 2-s2.0-85047074368.
10.1016/j.ijmecsci.2018.04.049
Web of Science® Google Scholar
7 Tang A.-Y., Li X.-F., Wu J.-X., and Lee K. Y., Flapwise bending vibration of rotating tapered Rayleigh cantilever beams, Journal of Constructional Steel Research. (2015) 112, no. 9, 1–9, https://doi.org/10.1016/j.jcsr.2015.04.010, 2-s2.0-84929178671.
10.1016/j.jcsr.2015.04.010
CAS Web of Science® Google Scholar
8 Sofiyev A. H. and Hui D., On the vibration and stability of FGM cylindrical shells under external pressures with mixed boundary conditions by using FOSDT, Thin-Walled Structures. (2019) 134, no. 1, 419–427, https://doi.org/10.1016/j.tws.2018.10.018, 2-s2.0-85055901100.
10.1016/j.tws.2018.10.018
Web of Science® Google Scholar
9 Yao M., Niu Y., and Hao Y., Nonlinear dynamic responses of rotating pretwisted cylindrical shells, Nonlinear Dynamics. (2019) 95, no. 1, 151–174, https://doi.org/10.1007/s11071-018-4557-7, 2-s2.0-85053823948.
10.1007/s11071-018-4557-7
Web of Science® Google Scholar
10 Banerjee J. R. and Jackson D. R., Free vibration of a rotating tapered Rayleigh beam: a dynamic stiffness method of solution, Computers & Structures. (2013) 124, no. 10, 11–20, https://doi.org/10.1016/j.compstruc.2012.11.010, 2-s2.0-84885180242.
10.1016/j.compstruc.2012.11.010
Web of Science® Google Scholar
11 Chakraverty S. and Behera L., Buckling analysis of nanobeams with exponentially varying stiffness by differential quadrature method, Chinese Physics B. (2017) 26, no. 7, 074602, https://doi.org/10.1088/1674-1056/26/7/074602, 2-s2.0-85022078986.
10.1088/1674-1056/26/7/074602
Web of Science® Google Scholar
12 Gao H. B., Fu L., and Niu J. N., Mechanical properties research on fractional derivative standard linear solid viscoelastic material, Journal of Henan University (Natural Science). (2018) 48, no. 1, 86–91.
Google Scholar
13 Tarasov V. E., No nonlocality: no fractional derivative, Communications in Nonlinear Science and Numerical Simulation. (2018) 62, no. 9, 157–163, https://doi.org/10.1016/j.cnsns.2018.02.019, 2-s2.0-85042644425.
10.1016/j.cnsns.2018.02.019
Web of Science® Google Scholar
14 Achouri Z., Amroun N. E., and Benaissa A., The Euler-Bernoulli beam equation with boundary dissipation of fractional derivative type, Mathematical Methods in the Applied Sciences. (2016) 40, no. 11, 3837–3854, https://doi.org/10.1002/mma.4267, 2-s2.0-85007199238.
10.1002/mma.4267
Web of Science® Google Scholar
15 Ansari R., Faraji Oskouie M., and Gholami R., Size-dependent geometrically nonlinear free vibration analysis of fractional viscoelastic nanobeams based on the nonlocal elasticity theory, Physica E: Low-Dimensional Systems and Nanostructures. (2016) 75, no. 1, 266–271, https://doi.org/10.1016/j.physe.2015.09.022, 2-s2.0-84943546186.
10.1016/j.physe.2015.09.022
Web of Science® Google Scholar
16 Bahraini S. M. S., Eghtesad M., Farid M., and Ghavanloo E., Large deflection of viscoelastic beams using fractional derivative model, Journal of Mechanical Science and Technology. (2013) 27, no. 4, 1063–1070, https://doi.org/10.1007/s12206-013-0302-9, 2-s2.0-84876090774.
10.1007/s12206-013-0302-9
Web of Science® Google Scholar
17 Li P. and Ying W., Differential quadrature method for vibration analysis of beams on viscoelastic foundations, Journal of Shanghai Normal University. (2015) 44, no. 2, 143–149.
Google Scholar
18 Zhang Q., Du Y. F., and Zhu Q. K., Study on large deformation mechanical behavior of Euler-Bernoulli beam using DQM, Engineering Mechanics. (2014) 31, no. S1, 1–4.
Google Scholar
19 Cao Z. G., Static analysis of reinforced concrete beam using the differential quadrature method, Chinese Quarterly of Mechanics. (2015) 4, 749–756.
Google Scholar
20 Matbuly M. S., Ragb O., and Nassar M., Natural frequencies of a functionally graded cracked beam using the differential quadrature method, Applied Mathematics and Computation. (2009) 215, no. 6, 2307–2316, https://doi.org/10.1016/j.amc.2009.08.026, 2-s2.0-70349992908.
10.1016/j.amc.2009.08.026
Web of Science® Google Scholar
21 Li J. J., Hu Y. J., and Cheng C. J., Differential quadrature method for nonlinear dynamical behavior of a viscoelastic Timoshenko beam, Journal of Vibration and Shock. (2010) 29, no. 4, 143–146.
Google Scholar
22 Wang Z. and Li R., Transverse vibration of rotating tapered cantilever beam with hollow circular cross-section, Shock and Vibration. (2018) 2018, 14, 1056397, https://doi.org/10.1155/2018/1056397, 2-s2.0-85045449521.
10.1155/2018/1056397
Web of Science® Google Scholar
23 Zhou Y. F. and Wang Z. M., Application of the differential quadrature method to free vibration of viscoelastic thin plate with linear thickness variation, Meccanica. (2014) 49, no. 12, 2817–2828, https://doi.org/10.1007/s11012-014-0043-6, 2-s2.0-84912021597.
10.1007/s11012-014-0043-6
Web of Science® Google Scholar

Citing Literature

All articles

Analysis of Complex Modal Characteristics of Fractional Derivative Viscoelastic Rotating Beams

Abstract

1. Introduction

2. One-Dimensional Fractional Kelvin–Voigt Model Theory

3. Differential Equation of Motion

3.1. Deformation Field Description

3.2. Differential Equations of Motion

3.3. Dimensional Normalization of the Equation

3.4. Differential Quadrature Method

4. Numerical Results and Analyses

4.1. Comparison and Verification

4.2. Numerical Calculation and Analysis

4.3. Response of Viscoelastic Rotating Beams with Kelvin–Voigt Fractional Derivatives

5. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Analysis of Complex Modal Characteristics of Fractional Derivative Viscoelastic Rotating Beams

Abstract

1. Introduction

2. One-Dimensional Fractional Kelvin–Voigt Model Theory

3. Differential Equation of Motion

3.1. Deformation Field Description

3.2. Differential Equations of Motion

3.3. Dimensional Normalization of the Equation

3.4. Differential Quadrature Method

4. Numerical Results and Analyses

4.1. Comparison and Verification

4.2. Numerical Calculation and Analysis

4.3. Response of Viscoelastic Rotating Beams with Kelvin–Voigt Fractional Derivatives

5. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information