Volume 2019, Issue 1 5635047

Research Article

Open Access

Structural Parameter Optimization of a Tubular Permanent-Magnet Linear Machine for Regenerative Suspension

Dongsheng Lu,

Dongsheng Lu

Jiangsu Province Power Company, 215# Shanghai Street, Gulou District, Nanjing, China sgcc.com.cn

Search for more papers by this author

Hailong Zhang,

Corresponding Author

Hailong Zhang

[email protected]

orcid.org/0000-0003-2213-1573

Vibration Control Lab, School of Electrical and Automation Engineering, Nanjing Normal University, Nanjing 210042, China njnu.edu.cn

Search for more papers by this author

Jian Liu,

Jian Liu

Vibration Control Lab, School of Electrical and Automation Engineering, Nanjing Normal University, Nanjing 210042, China njnu.edu.cn

Search for more papers by this author

Enrong Wang,

Enrong Wang

Vibration Control Lab, School of Electrical and Automation Engineering, Nanjing Normal University, Nanjing 210042, China njnu.edu.cn

Search for more papers by this author

Dongsheng Lu,

Dongsheng Lu

Jiangsu Province Power Company, 215# Shanghai Street, Gulou District, Nanjing, China sgcc.com.cn

Search for more papers by this author

Hailong Zhang,

Corresponding Author

Hailong Zhang

[email protected]

orcid.org/0000-0003-2213-1573

Vibration Control Lab, School of Electrical and Automation Engineering, Nanjing Normal University, Nanjing 210042, China njnu.edu.cn

Search for more papers by this author

Jian Liu,

Jian Liu

Vibration Control Lab, School of Electrical and Automation Engineering, Nanjing Normal University, Nanjing 210042, China njnu.edu.cn

Search for more papers by this author

Enrong Wang,

Enrong Wang

Vibration Control Lab, School of Electrical and Automation Engineering, Nanjing Normal University, Nanjing 210042, China njnu.edu.cn

Search for more papers by this author

First published: 2019

https://doi.org/10.1155/2019/5635047

Citations: 1

Academic Editor: Luca Landi

Share a link

Email
Wechat
Bluesky

Abstract

The regenerative suspension can effectively recover the vibration potential energy of the vehicle suspension, thus has broad prospects in application. In this paper, a tubular permanent-magnet linear motor (TPMLM) with the Halbach array magnetic pole is analyzed. The magnetic field analysis method of the excitation source separation is proposed, and then, the transient analytical model of output electromagnetic force and the external circuit characteristic under displacement excitation is established. A modified particle swarm optimization algorithm is further adopted to optimize the structural parameters of TPMLM. By comparing with the finite element analysis, the correctness of the proposed analytical model and the optimization are verified. This work lays the theoretical foundation for extensive application of the regenerative suspension.

1. Introduction

Vehicle body vibrates while running on the uneven road surface. This potential energy is mostly dissipated by the suspension system of 10–600 Watts [1, 2], accounting for about 30% of the power output energy. The recycling of this power will benefit the traditional fuel vehicles to reduce fuel consumption and improve the battery life cycle of electric vehicles. Due to the same travel direction as the suspension vibration and a higher power level and power density, the tubular permanent-magnet linear machine (TPMLM) is able to directly convert to electric power, which is convenient for storage and utilization. Therefore, compared to common ones like piezoelectric and electrostatic, the TPMLM has more application prospects in developing regenerated suspension, and it is also widely used in wave energy, road/bridge vibration energy regeneration, and so on. [3].

The TPMLM-based regenerative suspension system requires not only to maintain the suspension performance but also to ensure high energy-feeding efficiency. It is necessary to optimize the structural parameters of the TPMLM. Scholars have carried out a lot of research studies and achieved some results. Zuo et al. [4] designed a four-phase linear generator. The finite element analysis (FEA) was used to analyze the magnetic field and assist in the design optimization. A simplified model was derived to qualitatively characterize the waveforms and regenerate power of the harvester at various vibration amplitude, frequencies, equilibrium positions, and structure parameters. The regenerative shock absorber will be able to harvest 16–64 W power. Asadi et al. [5, 6] proposed a hybrid damper combining TPMLM with hydraulic structure. The theoretical model and FEA were utilized to optimize the structural parameters. Damping and regenerative characteristics were tested by the prototype experiment, and the influence of the change of some structural parameters on the performance of the damper was revealed. Jiang et al. [7] made improvements in the structure of TPMLM. The simplified model was then established to optimize the thickness of the permanent magnet and the ratio of the pole pitch with the maximum air-gap magnetic flux. Characteristics of speed versus power under constant velocity excitation are simulated. Tang et al. [8] focused on the structural characteristics of TPMLM, such as the radial thickness of the coil. The FEA was used to optimize the regenerated power density and damping force. And, the novel TPMLM with double-layer permanent-magnet array was proposed, of which the power density was improved 5.6 times than the predesigned prototype. Liu et al. [9] established a new energy-regenerative active suspension system, employing an actuator composed of a shock absorber and a DC motor. The results verified the suspension performance and energy-regenerative efficiency. Wang et al. [10] proposed a supercapacitor mode-switching control strategy for the regenerative and semiactive suspension system.

Among the above research studies, the magnetic circuit analysis or FEA is mainly used to optimize the TPMLM structure with the targets of damping and regenerated ability, by scanning the single or multiple parameters. Nevertheless, as a solution for the parameter optimization, sweeping under the complex external excitation using FEA consumes a long calculation time. It is therefore difficult to achieve global optimization of structural parameters because of the inability to solve multiple-parameter optimization at the same time. Optimization with analytical model can reduce calculating time to solve the abovementioned problem. But, due to the discontinuous inner magnetic field distribution of the TPMLM, it is difficult to establish analytical model which has similar precision to the FEA model, especially in dynamic characteristic. Representative research is the analytical model introducing the Carter coefficient correction for a three-phase tubular modular permanent-magnet machine proposed by Wang et al. [11–13]. The model was introduced in detail on the open-circuit magnetic field distribution with a quasi-Halbach magnetized armature. In addition, the electromagnetic force and electromechanical conversion efficiency are optimized for several sets of structural parameters. The analytical model proposed by Wang mainly describes the performance of the motor under static and constant velocity excitation. However, for complex random excitation such as road surface, it is necessary to further establish the transient analytical model to obtain the dynamic and winding circuit characteristics.

This paper, therefore, proposed an analytical method based on excitation source separation for a moving-coil TPMLM. The transient model of the electromagnetic force and winding circuit under universal external excitation was derived. Furthermore, particle swarm optimization (PSO) algorithm is easy to implement, especially does not require different objective functions and constraints. Thus, the global optimal solution can be obtained with a large probability. A modified dual adaptive PSO was used to optimize the structural parameters globally, taking regenerated power as the target function. The FEA of TPMLM was then employed to verify the correctness of the transient analytical model and the effectiveness of structural optimization.

2. Analytical Model

2.1. Structure of TPMLM

The Halbach magnetized single-phase nonslot permanent-magnet linear machine (TPMLM, tubular permanent-magnet linear machine) is adopted, as shown in Figure 1. The TPMLM is divided into five regions (I–V) according to the material medium, namely, the direct-axis region, the winding region, the air-gap region, the permanent magnet region, the back iron region, to derive dynamic and electric model based on the magnetic field analysis. With the actual motor structure considered, the following assumptions are made to facilitate the analysis of the electromagnetic field:

(1)
The axial length is sufficiently large relative to its radial length, and the axial direction can be made infinitely long when resolving magnetic field
(2)
Linearization of the B-H curve of the motor magnetic medium

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Halbach magnetized nonslot moving-coil cylindrical permanent-magnet linear machine structure. Region I, direct-axis region; region II, winding region; region III, air-gap region; region IV, permanent magnet region; region V, back iron region.

2.2. Magnetic Vector Potential

The electromagnetic force-displacement dynamics of the TPMLM and the transient model of the winding voltage-displacement circuit based on magnetic field analysis are established. The key here lies in solving the magnetic field equation in the TPMLM, especially in winding region II. Based on Maxwell equations and substituting the magnetic medium constitutive equation, the vector potential differential equation is derived:

\begin{matrix} \nabla \times \frac{1}{μ_{0} μ_{r}} \nabla \times A = J + \nabla \times H_{c}, \end{matrix}

(1)

where A represents the magnetic vector potential. B is the magnetic induction, which can be expressed by the magnetic vector potential B = ∇×A under the Coulomb specification constraint. J represents the conduction current vector. H_c represents the magnetic medium coercive force vector. In the cylindrical coordinates, the magnetic vector potential A (r, θ, z) can be regarded only as the direction component of A_θ (r, z) [8] since the internal magnetic field of TPMLM is axisymmetric. Then, equation (1) is transformed into the following:

\begin{matrix} - \frac{1}{μ_{0} μ_{r}} (\frac{\partial^{2}}{\partial z^{2}} A_{θ} + \frac{\partial}{\partial r} (\frac{1}{r} \frac{\partial}{\partial r} (r A_{θ}))) \vec{θ} = {(J + \nabla \times H_{c})}_{θ} . \end{matrix}

(2)

Considering the magnetic medium characteristics of each region and expanding the winding conduction current density vector and the permanent magnet coercive force vector in the form of Fourier series, the magnetic vector potential equations in each region are derived;

\begin{matrix} \{\begin{cases} \frac{\partial^{2}}{\partial z^{2}} A_{θ i} + \frac{\partial}{\partial r} (\frac{1}{r} \frac{\partial}{\partial r} (r A_{θ i})) = 0, Region i = \{I, III, V\}, \\ \frac{\partial^{2}}{\partial z^{2}} A_{θ II} + \frac{\partial}{\partial r} (\frac{1}{r} \frac{\partial}{\partial r} (r A_{θ I I})) = J_{s} \sum_{n = 1}^{\infty} Q_{n} \sin [m_{n} (z - x)], Region II, \\ \frac{\partial^{2}}{\partial z^{2}} A_{θ IV} + \frac{\partial}{\partial r} (\frac{1}{r} \frac{\partial}{\partial r} (r A_{θ I V})) = \sum_{n = 1}^{\infty} P_{n} \cos [k_{n} (z + \frac{τ_{p}}{4})], Region IV, \end{cases} \end{matrix}

(3)

where J_s represents θ direction component of the winding current density. Q_n and P_n represent the series coefficient of Fourier series expansion of the winding current density and the permanent magnet coercive force (refer to the appendix). m_n = k_n = (2n − 1)π/τ_p, where τ_p represents the pole pitch of the permanent magnet and x represents the displacement along the positive direction of the z-axis of the motor mover portion.

The vector potential equations have a uniform homogeneous form with different nonhomogeneous terms in different regions. For the homogeneous part of the vector potential equation, the separation variable method is used to transform the original Laplace equation to the first-order modified Bessel equation and the second-order differential equation. The homogeneous solution is their universal solution product. Moreover, since magnetic field of TPMLM is produced by both the conduction current J and the coercive force H_cIV of the permanent magnet, the homogeneous solution of the magnetic flux solution is as follows:

\begin{matrix} A_{θ i} (r, z) = A_{θ i}^{1} (r, z) + A_{θ i}^{2} (r, z) \\ = \sum_{n} [a_{i n}^{1} I_{1} (k_{i n} r) + b_{i n}^{1} K_{1} (k_{i n} r)] \cdot c_{i n}^{1} \cos [k_{i n} (z + d_{i n}^{1})] + \sum_{n} [a_{i n}^{2} I_{1} (m_{i n} r) + b_{i n}^{2} K_{1} (m_{i n} r)] \cdot c_{i n}^{2} \cos [m_{i n} (z + d_{i n}^{2})], Region i = \{I, II, III, IV, V\}, \end{matrix}

(4)

where

A_{θ i}^{1}

represents the homogeneous solution of the magnetic field equation generated by the conduction current and

A_{θ i}^{2}

represents the homogeneous solution of the magnetic field equation generated by the coercive force of the permanent magnet. I₁ is the solution of the first-order modified Bessel equation of the first kind. K₁ is the solution of the first-order modified Bessel equation of the second kind.

Firstly, the radial vector potential equation is simplified by the Fourier series. The variation of constants formula is further introduced to solve the radial equation in form of homogeneous Bessel equation. And then, special solutions of the nonhomogeneous vector potential equation for regions II and IV are derived:

\begin{matrix} A_{θ II}^{*} (r, z, x) = J_{s} \sum_{n = 1}^{\infty} [G_{1} (m_{n} r) I_{1} (m_{n} r) + G_{2} (m_{n} r) K_{1} (m_{n} r)] \cdot \sin [m_{n} (z - x)], \\ A_{θ IV}^{*} (r, z) = \sum_{n = 1}^{\infty} [E_{1} (k_{n} r) I_{1} (k_{n} r) + E_{2} (k_{n} r) K_{1} (k_{n} r)] \cdot \cos [k_{n} (z + \frac{τ_{p}}{4})] . \end{matrix}

(5)

Amongst, E₁, E₂, G₁, and G₂ are the coefficients of the nonhomogeneous Bessel function (refer to the appendix).

Based on the general solution of the vector potential equation, the magnetic field boundary condition at the interface of the magnetic medium is further substituted, including the continuous condition of the normal condition of the magnetic induction intensity and the tangential condition of the magnetic field strength.

\begin{matrix} \vec{n} \cdot (B_{1} - B_{2}) = 0, \\ \vec{n} \times (H_{1} - H_{2}) = 0, \end{matrix}

(6)

where

\vec{n}

denotes the normal vector of the interface of the magnetic medium. B₁/B₂ and H₁/H₂ denote the magnetic induction intensity and magnetic field strength in the magnetic medium on both sides of the interface, respectively. For the motor to solve the region, the outer boundary has a vector potential at the outer boundary of zero, namely,

{A_{θ}|}_{r = R_{0}, r = R_{b}} = 0

. By substituting in the above boundary conditions, the vector potential solutions of each region are obtained:

\begin{matrix} A_{θ i} (r, z, x) = \sum_{n = 1}^{\infty} [a_{i n}^{1} I_{1} (k_{n} r) + b_{i n}^{1} K_{1} (k_{n} r)] \cdot \cos [k_{n} (z + \frac{τ_{p}}{4})] + \sum_{n = 1}^{\infty} [a_{i n}^{2} I_{1} (m_{n} r) + b_{i n}^{2} K_{1} (m_{n} r)] \cdot \sin [m_{n} (z - x)], Region i = \{I, III, V\}, \\ A_{θ II} (r, z, x) = \sum_{n = 1}^{\infty} [a_{II n}^{1} I_{1} (k_{n} r) + b_{II n}^{1} K_{1} (k_{n} r)] \cdot \cos [k_{n} (z + \frac{τ_{p}}{4})] + \sum_{n = 1}^{\infty} [J_{s} G_{1} (m_{n} r) I_{1} (m_{n} r) + J_{s} G_{2} (m_{n} r) K_{1} (m_{n} r) + a_{II n}^{2} I_{1} (m_{n} r) + b_{II n}^{2} K_{1} (m_{n} r)] \cdot \sin [m_{n} (z - x)], \\ A_{θ IV} (r, z, x) = \sum_{n = 1}^{\infty} [E_{1} (m_{n} r) I_{1} (m_{n} r) + E_{2} (m_{n} r) K_{1} (m_{n} r) + a_{IV n}^{1} I_{1} (k_{n} r) + b_{IV n}^{1} K_{1} (k_{n} r)] \cdot \cos [k_{n} (z + \frac{τ_{p}}{4})] + \sum_{n = 1}^{\infty} [a_{IV n}^{2} I_{1} (m_{n} r) + b_{IV n}^{2} K_{1} (m_{n} r)] \cdot \sin [m_{n} (z - x)] . \end{matrix}

(7)

The solution coefficients of Bessel function are as follows, and for the definition of

A_{n}^{1}

A_{n}^{2}

B_{n}^{1}

, and

B_{n}^{2}

, refer to the appendix:

\begin{matrix} \{\begin{cases} A_{n}^{1} {[\begin{matrix} a_{I n}^{1} & b_{I n}^{1} & a_{II n}^{1} & b_{II n}^{1} & a_{III n}^{1} & b_{III n}^{1} & a_{IV n}^{1} & b_{IV n}^{1} & a_{V n}^{1} & b_{V n}^{1} \end{matrix}]}^{T} = B_{n}^{1}, \\ A_{n}^{2} {[\begin{matrix} a_{I n}^{2} & b_{I n}^{2} & a_{II n}^{2} & b_{II n}^{2} & a_{III n}^{2} & b_{III n}^{2} & a_{IV n}^{2} & b_{IV n}^{2} & a_{V n}^{2} & b_{V n}^{2} \end{matrix}]}^{T} = J_{s} B_{n}^{2} . \end{cases} \end{matrix}

(8)

2.3. Thrust Force and Winding Circuit

Based on the above analytical solution of the internal magnetic field, the thrust force and winding equation can be derived directly. Since the electromagnetic force of the nonslot linear motor is mainly generated by the armature reaction and the edge force generated by the asymmetry of the magnetic field is negligible compared to the ampere force, the thrust force of the TPMLM mover is derived as follows:

\begin{matrix} F_{z} = {(\int_{RegionII} J \times B d v)}_{z} = - \int_{RegionII} J_{s} B_{r II} d v, \end{matrix}

(9)

where B_rII represents the radial component of magnetic induction in region II; B_rII = −dA_θII/dz. Considering only the pure resistive load R_L connected to the winding end, the winding circuit is expressed as follows:

\begin{matrix} \frac{d}{d t} Ψ_{s} (x (t)) + \frac{d}{d t} Ψ_{js} (x (t)) + (R_{DC} + R_{L}) \cdot i_{s} (x (t)) = 0, \end{matrix}

(10)

where R_DC represents the winding DC resistance;

R_{DC} = 4 m_{N} ρ_{c} (R_{s0} + R_{s}) N_{w}^{2} / [K_{c} (R_{s} - R_{s0}) τ_{p}]

. ρ_c represents the winding wire conductivity. K_c represents full slot ratio. m_N represents the winding slot amount. N_w represents the turns in the winding. i_s represents the winding current. i_L is load current, i_L (x) = −i_s (x). Ψ_s represents the winding flux linkage. Ψ_js represents the winding current flux linkage.

The volume integral of the winding magnetic induction can convert to surface integral in r-z plane by Stokes–Cartan theorem. Besides, due to the trigonometric characteristics of the axial integration of the vector potential, the expressions of the electromagnetic force and the flux linkage integral are simplified as follows:

\begin{matrix} Ψ_{s} (x (t)) = \sum_{n = 1}^{\infty} H_{1 n} \cos [k_{n} (x (t) + \frac{3 τ_{p}}{4})], \\ Ψ_{js} (x (t)) = i_{s} (x (t)) \sum_{n = 1}^{\infty} H_{2 n}, \\ F_{z} (x (t)) = i_{s} (x (t)) \sum_{n = 1}^{\infty} H_{3 n} \sin [k_{n} (x (t) + \frac{3 τ_{p}}{4})] . \end{matrix}

(11)

The simplified series coefficients are as follows:

\begin{matrix} H_{1 n} = m_{N} \frac{N_{w}}{S_{w}} \frac{2 \cdot {(- 1)}^{n + 1}}{k_{n}} \int_{R_{s0}}^{R_{s}} 2 π r [a_{II n}^{1} I_{1} (k_{n} r) + b_{II n}^{1} K_{1} (k_{n} r)] d r, \\ H_{2 n} = m_{N} {(\frac{N_{w}}{S_{w}})}^{2} \frac{2}{m_{n}} \int_{R_{s0}}^{R_{s}} 2 π r [G_{1} (m_{n} r) I_{1} (m_{n} r) + G_{2} (m_{n} r) K_{1} (m_{n} r) + a_{II n}^{2} I_{1} (m_{n} r) + b_{II n}^{2} K_{1} (m_{n} r)] d r, \\ H_{3 n} = - k_{n} H_{1 n}, \end{matrix}

(12)

where S_w represents the cross-sectional area of the winding slot.

2.4. Model Verification

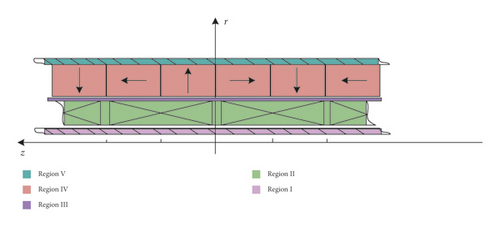
A set of TPMLM structural parameters is selected, namely, motor dimensions R₀ = 4 mm, R_s0 = 8 mm, R_s = 16 mm, R_m = 17 mm, R_mb = 36 mm, and R_b = 40 mm. Relative permeability of each region are μ_rI = 800, μ_rII = 1, μ_rIII = 1, μ_rIV = 1.02, and μ_rV = 800. Pole pitch and residual magnetism of the permanent magnet are τ_p = 33 mm and B_rem = 1.41 T, respectively. At the same time, the TPMLM FEM is established in the FEA software, to verify the proposed analytical model. According to Figure 1, the model is composed of iron core in direct-axis, winding coil, air-gap, permanent magnet, and back iron. The parameters of winding are m_N = 6, N_w = 100, and K_c = 0.9. The boundary condition of solved region is balloon boundary. For the exterior area of iron core and back iron, the boundary condition is vectorpotential boundary. The motionsetup is moving along the direction of z-axis. The solver time is set as 0 to 5 s with the step of 0.001 s. Figure 2 shows the comparison between the FEA and the analytical analysis of the magnetic field in the winding region (r = 12 mm) along the z-axis, when the current density is zero.

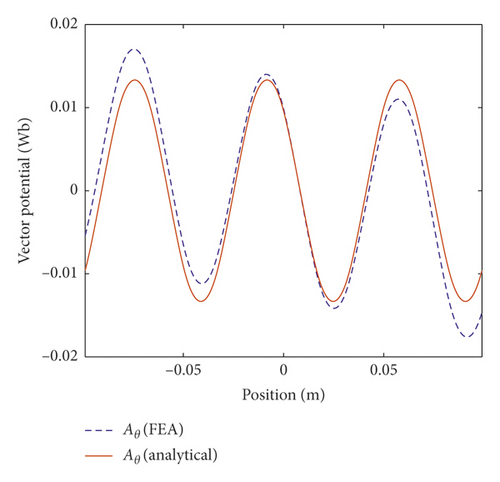
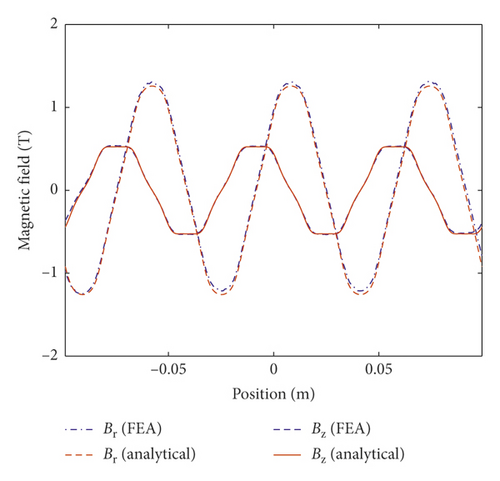
The results indicate that the curve of analytical magnetic induction is nearly consistent with that of FEA. Note, the vector potential has a not-too-large offset at the edge, which is because the number of permanent magnet arrays is limited. The comparison verifies the correctness and accuracy of the proposed internal vector potential analysis method.

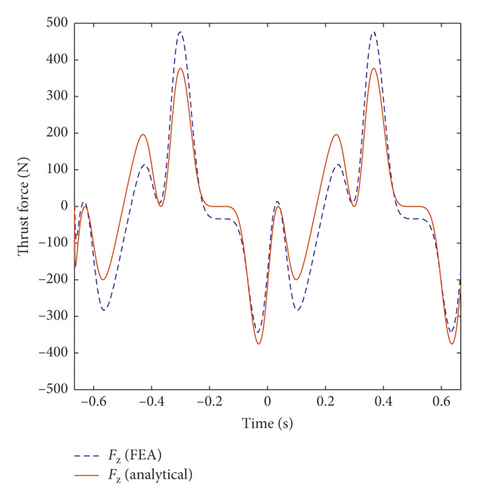
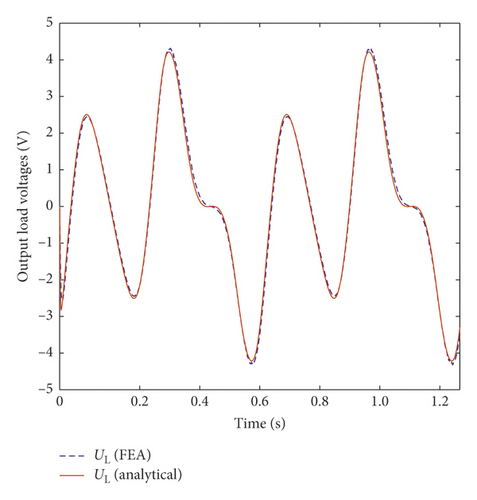
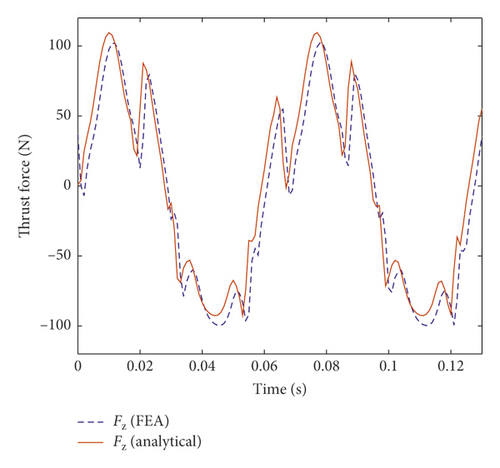
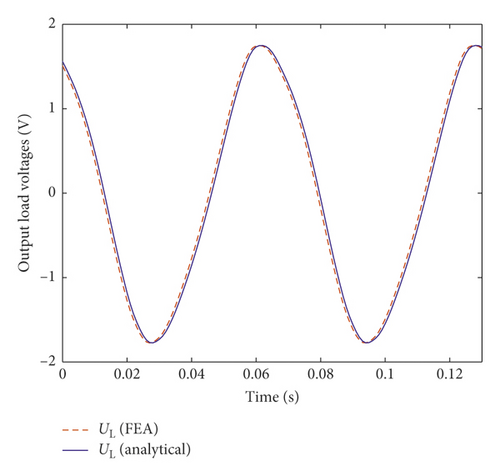
The axial damping force and the load voltage of the TPMLM when R_L = R_DC are further carried out, under harmonic excitation x(t) = A_m sin(2πft), where A_m = 25 mm and f = 1.5 Hz, 15 Hz(the first and second resonant frequency of vehicle suspension is around 1.5 Hz and 15 Hz [14]). The two outputs of TPMLM, namely, axial damping force and load voltage, are selected as comparison data. They also represent mechanical and electrical properties, respectively. Figure 3 shows the comparison of FEA and the analytical result. Due to the finite length of the axial length of the iron and iron core and a limited number of permanent magnet arrays, the analytical damping force is somewhat different from the FEA, but the overall trend and the numerical values are basically consistent. Most of all, the analytical calculation process takes far less time than FEA.

3. Structural Parameter Optimization

The size of the TPMLM is limited by the processing technique, installing environmental conditions and other limitations. It is necessary to optimize parameters of the TPMLM, with target of the maximum power point. The winding equation is deformed as follows, considering characteristic of general load R_X {R, L}:

\begin{matrix} \frac{d}{d t} Ψ_{s} (x (t)) + L_{s} \cdot \frac{d}{d t} i_{s} (x (t)) + R_{DC} \cdot i_{s} (x (t)) + R_{X} (i_{s}, i_{s}^{'}) = 0. \end{matrix}

(13)

The winding inductance L_s of the nonslot TPMLM is extremely small, and the electromotive force by armature reaction is much smaller than the voltage of the internal resistance of the winding. Hence, it can be considered that the maximum output power P_max is obtained when R_X = R_DC. The motor structure dimensions such as air gap thickness, iron/core thickness, permanent magnet thickness, and maximum outer diameter are constrained, and the optimization model of the structural size {R_X} = {R₀, R_s0, R_s, R_m, R_mb, R_b} is proposed as follows, whose objective function is output power:

\begin{matrix} \begin{matrix} \min & f (R_{X}) = - P_{\max} (R_{X}), \\ s.t. & \{\begin{cases} g_{j} (R_{X}) \geq 0, j = \{1, \dots, m\}, \\ L_{b} \leq \{R_{X}\} \leq U_{b}, \end{cases} \end{matrix} \end{matrix}

(14)

where P_max (R_X) represents the maximum average power under the structure size of {R_X} and

P_{\max} = \int_{t_{0}}^{t_{0} + T} R_{L} \cdot i_{L}^{2} d t / T

indicates m groups of inequality linear and nonlinear constraints. L_b and U_b represent the lower and upper boundaries of the structural size, respectively. The feasible solution region composed of the constraint condition is defined as f.

Generally, the optimal size of the motor will appear around the boundary. Therefore, the proposed dual fitness function PSO algorithm is used to solve the optimization problem of the TPMLM, to regenerate maximum output power under constraint. The two fitness functions of each particle are

\begin{matrix} \{\begin{cases} fitness (i) = f (R_{X}), i = 1,2, \dots, n, \\ voilation (i) = \sum_{j = 1}^{m} |\min \{g_{j} (R_{X}), 0\}|, \end{cases} \end{matrix}

(16)

where i denotes the i-th particle, n denotes the population size of the particle group, fitness(i) denotes the particle fitness of the objective function, and voilation(i) denotes the particle fitness of the conditional constraint. The comparison criterions between each particle are as follows:

(1)
Both particles a and b are in the feasible region, and the particle with smaller fitness(i) is better.
(2)
Both particles a and b are not in the feasible region, and the particle with smaller voilation(i) is better.
(3)
The particle a is in the feasible region, while the particle b is not. If the voilation(b) < ε, the particle with smaller fitness(i) is better, otherwise the particle a is better.

The comparison of two fitness functions allows the particles to quickly approach the feasible domain boundary and obtain a feasible solution that satisfies the constraints. At the same time, a certain infeasible solution ratio can be ensured by controlling the tolerant boundary, thus making the optimization be more quick and stable.

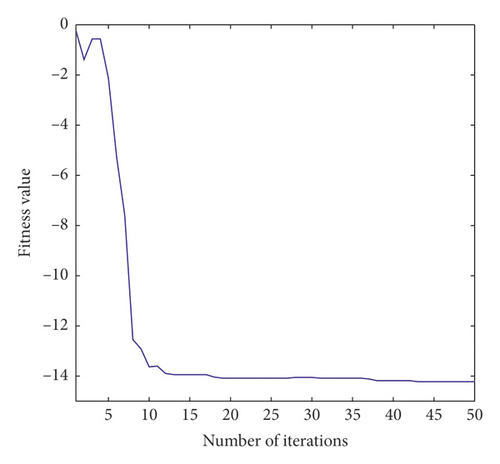
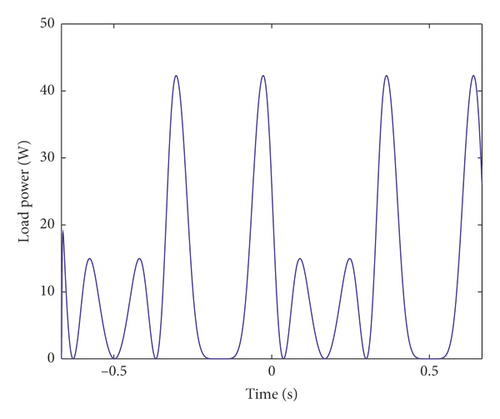
Figure 4(a) shows the PSO calculation process. The population size n is set to 80, the tolerance boundary ε = 0.02 mm, the infeasible solution ratio p is 0.15, and the excitation is a harmonic with a amplitude of 25 mm and a frequency of 1.5 Hz. Waves, the particle swarm converges to the optimal solution after 30 iterations. Figure 4(b) shows the optimal instantaneous output power. Table 1 is comparison of performance with structural parameters before and after optimization. The results demonstrate the feasibility of the TPMLM maximum power optimization model and the applicability of the established TPMLM dynamic and electric transient models.

Table 1. Performance comparison before and after optimization.

	Structure parameters {RX} (mm)	Average power (W)		RMS of damping force (N)
	Structure parameters {RX} (mm)	1.5 Hz	15 Hz	1.5 Hz	15 Hz
Before optimization	{4, 8, 16, 17, 36, 40}	11.80	1.86	172.75	67.68
After optimization	{4, 10.9, 15.9, 16.9, 36, 40}	13.36	2.59	195.54	74.36

4. Conclusions

In this paper, a Halbach magnetized single-phase nonslot moving-coil TPMLM is designed. The magnetic analysis method which separates excitation is proposed, and then, transient analysis model of the damping force and winding circuit is established under external excitation. The transient model has the similar accuracy to FEA. Based on the analytical model, the improved dual-adaptive particle swarm optimization algorithm is utilized to obtain the optimal parameter of the TPMLM maximum power point operation with a short calculation time, which further indicates that the proposed TPMLM analytical model is applicable for optimization. The proposed analytical model can also be applied to the dynamic analysis of combined vibration damping system.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Acknowledgments

This research has received funding from the National Science Foundation of China (grant nos. 51475246 and 51075215), National Science Foundation for Young Scientists of Jiangsu Province, China (grant no. BK20171039), National Science Foundation for Postdoctoral Scientists of China (grant no. 2017M611855), Natural Science Foundation of the Higher Education Institutions of Jiangsu Province, China (grant no. 17KJB470010), and the Research Innovation Program for College Graduates of Jiangsu Province (KYCX17_1080).

Appendix

Coefficient Expression

Definition of Q_n and P_n:

\begin{matrix} Q_{n} = - \frac{4 μ_{0} μ_{r II}}{m_{n} τ_{p}}, \\ P_{n} = - \frac{4 B_{rem}}{τ_{p}} \sin (k_{n} \frac{τ_{p}}{4}) \sin (k_{n} \frac{τ_{p}}{2}), \end{matrix}

(A.1)

where B_rem represents the permanent magnet remanence.

Definition of E₁, E₂, G₁, and G₂:

\begin{matrix} [\begin{matrix} E_{1} (k_{n} r) \\ E_{2} (k_{n} r) \end{matrix}] = [\begin{matrix} P_{n} \int_{R_{m}}^{r} x \cdot K_{1} (k_{n} x) d x \\ - P_{n} \int_{R_{m}}^{r} x \cdot I_{1} (k_{n} x) d x \end{matrix}], \\ [\begin{matrix} G_{1} (k_{n} r) \\ G_{2} (k_{n} r) \end{matrix}] = [\begin{matrix} Q_{n} \int_{R_{s0}}^{r} x \cdot K_{1} (m_{n} x) d x \\ - Q_{n} \int_{R_{s0}}^{r} x \cdot I_{1} (m_{n} x) d x \end{matrix}], \end{matrix}

(A.2)

where E₁, E₂, G₁, and G₂ are the solution coefficient of inhomogeneous Bessel equation.

Definition of

A_{n}^{1}

B_{n}^{1}

A_{n}^{2}

, and

B_{n}^{2}

\begin{matrix} A_{n}^{1} = [\begin{matrix} I_{1} (k_{n} R_{0}) & K_{1} (k_{n} R_{0}) & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ I_{1} (k_{n} R_{s0}) & K_{1} (k_{n} R_{s0}) & - I_{1} (k_{n} R_{s0}) & - K_{1} (k_{n} R_{s0}) & 0 & 0 & 0 & 0 & 0 & 0 \\ \frac{μ_{r II}}{μ_{r I}} I_{0} (k_{n} R_{s0}) & - \frac{μ_{r II}}{μ_{r I}} K_{0} (k_{n} R_{s0}) & - I_{0} (k_{n} R_{s0}) & K_{0} (k_{n} R_{s0}) & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & I_{1} (k_{n} R_{s}) & K_{1} (k_{n} R_{s}) & - I_{1} (k_{n} R_{s}) & - K_{1} (k_{n} R_{s}) & 0 & 0 & 0 & 0 \\ 0 & 0 & \frac{μ_{r III}}{μ_{r II}} I_{0} (k_{n} R_{s}) & - \frac{μ_{r III}}{μ_{r II}} K_{0} (k_{n} R_{s}) & - I_{0} (k_{n} R_{s}) & K_{0} (k_{n} R_{s}) & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & I_{1} (k_{n} R_{m}) & K_{1} (k_{n} R_{m}) & - I_{1} (k_{n} R_{m}) & - K_{1} (k_{n} R_{m}) & 0 & 0 \\ 0 & 0 & 0 & 0 & \frac{μ_{r IV}}{μ_{r III}} I_{0} (k_{n} R_{m}) & - \frac{μ_{r IV}}{μ_{r III}} K_{0} (k_{n} R_{m}) & - I_{0} (k_{n} R_{m}) & K_{0} (k_{n} R_{m}) & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & - I_{1} (k_{n} R_{mb}) & - K_{1} (k_{n} R_{mb}) & I_{1} (k_{n} R_{mb}) & K_{1} (k_{n} R_{mb}) \\ 0 & 0 & 0 & 0 & 0 & 0 & - I_{0} (k_{n} R_{mb}) & K_{0} (k_{n} R_{mb}) & \frac{μ_{r IV}}{μ_{r V}} I_{0} (k_{n} R_{mb}) & - \frac{μ_{r IV}}{μ_{r V}} K_{0} (k_{n} R_{mb}) \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & I_{1} (k_{n} R_{b}) & K_{1} (k_{n} R_{b}) \end{matrix}], \end{matrix}

(A.3)

\begin{matrix} B_{n}^{1} = [\begin{matrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ - {(- 1)}^{n + 1} \frac{P_{n}}{{(k_{n})}^{2}} \\ E_{1} (k_{n} R_{mb}) I_{1} (k_{n} R_{mb}) + E_{2} (k_{n} R_{mb}) K_{1} (k_{n} R_{mb}) \\ E_{1} (k_{n} R_{mb}) I_{0} (k_{n} R_{mb}) - E_{2} (k_{n} R_{mb}) K_{0} (k_{n} R_{mb}) - {(- 1)}^{n + 1} \frac{P_{n}}{{(k_{n})}^{2}} \\ 0 \end{matrix}], \end{matrix}

(A.4)

\begin{matrix} A_{n}^{2} = [\begin{matrix} I_{1} (m_{n} R_{0}) & K_{1} (m_{n} R_{0}) & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ I_{1} (m_{n} R_{s0}) & K_{1} (m_{n} R_{s0}) & - I_{1} (m_{n} R_{s0}) & - K_{1} (m_{n} R_{s0}) & 0 & 0 & 0 & 0 & 0 & 0 \\ \frac{μ_{r II}}{μ_{r I}} I_{0} (m_{n} R_{s0}) & - \frac{μ_{r II}}{μ_{r I}} K_{0} (m_{n} R_{s0}) & - I_{0} (m_{n} R_{s0}) & K_{0} (m_{n} R_{s0}) & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & - I_{1} (m_{n} R_{s}) & - K_{1} (m_{n} R_{s}) & I_{1} (m_{n} R_{s}) & K_{1} (m_{n} R_{s}) & 0 & 0 & 0 & 0 \\ 0 & 0 & - I_{0} (m_{n} R_{s}) & K_{0} (m_{n} R_{s}) & \frac{μ_{r II}}{μ_{r III}} I_{0} (m_{n} R_{s}) & - \frac{μ_{r II}}{μ_{r III}} K_{0} (m_{n} R_{s}) & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & I_{1} (m_{n} R_{m}) & K_{1} (m_{n} R_{m}) & - I_{1} (m_{n} R_{m}) & - K_{1} (m_{n} R_{m}) & 0 & 0 \\ 0 & 0 & 0 & 0 & \frac{μ_{r IV}}{μ_{r III}} I_{0} (m_{n} R_{m}) & - \frac{μ_{r IV}}{μ_{r III}} K_{0} (m_{n} R_{m}) & - I_{0} (m_{n} R_{m}) & K_{0} (m_{n} R_{m}) & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & I_{1} (m_{n} R_{mb}) & K_{1} (m_{n} R_{mb}) & - I_{1} (m_{n} R_{mb}) & - K_{1} (m_{n} R_{mb}) \\ 0 & 0 & 0 & 0 & 0 & 0 & \frac{μ_{r V}}{μ_{r IV}} I_{0} (m_{n} R_{mb}) & - \frac{μ_{r V}}{μ_{r IV}} K_{0} (m_{n} R_{mb}) & - I_{0} (m_{n} R_{mb}) & K_{0} (m_{n} R_{mb}) \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & I_{1} (m_{n} R_{b}) & K_{1} (m_{n} R_{b}) \end{matrix}], \end{matrix}

(A.5)

\begin{matrix} B_{n}^{2} = [\begin{matrix} 0 \\ 0 \\ 0 \\ G_{1} (m_{n} R_{s}) I_{1} (m_{n} R_{s}) + G_{2} (m_{n} R_{s}) K_{1} (m_{n} R_{s}) \\ G_{1} (m_{n} R_{s}) I_{0} (m_{n} R_{s}) - G_{2} (m_{n} R_{s}) K_{0} (m_{n} R_{s}) \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{matrix}], \end{matrix}

(A.6)

where

A_{n}^{1}

and

B_{n}^{1}

are the parameter matrix of homogeneous solution coefficient of magnetic field generated by coercivity of permanent magnet,

A_{n}^{2}

and

B_{n}^{2}

are the homogeneous solution coefficient matrix of magnetic field generated by conduction current, I₀ is the solution of the zero-order modified Bessel equation of the first kind, and K₀ is the solution of the zero-order modified Bessel equation of the second kind.

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Zhang H., Guo X., Fang Z., Xu L., and Zhang J., Potential energy harvesting analysis and test on energy-regenerative suspension system, Journal of Vibration Measurement & Diagnosis. (2015) 35, no. 2, 225–230.
Google Scholar
2 Zou J. Y., Guo X. X., Xu L. et al., Design, modeling, and analysis of a novel hydraulic energy-regenerative shock absorber for vehicle suspension, Shock and Vibration. (2017) 2017, 12, 3186584, https://doi.org/10.1155/2017/3186584, 2-s2.0-85028435412.
10.1155/2017/3186584
Web of Science® Google Scholar
3 El-Sayed A. R., Tai K., Biglarbegian M., and Mahmud S., A survey on recent energy harvesting mechanisms, Proceedings of the IEEE Canadian Conference on Electrical and Computer Engineering, May 2016, Vancouver, Canada, 1–5.
Google Scholar
4 Zuo L., Scully B., Shestani J., and Zhou Y., Design and characterization of an electromagnetic energy harvester for vehicle suspensions, Smart Material Structures. (2010) 19, no. 4, 1007–1016, https://doi.org/10.1088/0964-1726/19/4/045003, 2-s2.0-77949910828.
10.1088/0964-1726/19/4/045003
Web of Science® Google Scholar
5 Asadi E., Ribeiro R., Khamesee M. B., and Khajepour A., A new adaptive hybrid electromagnetic damper: modelling, optimization, and experiment, Smart Materials & Structures. (2015) 24, no. 7, https://doi.org/10.1088/0964-1726/24/7/075003, 2-s2.0-84933074222.
10.1088/0964-1726/24/7/075003
PubMed Web of Science® Google Scholar
6 Asadi E., Ribeiro R., Khamesee M. B., and Khajepour A., Analysis, prototyping and experimental characterization of an adaptive hybrid-electromagnetic damper for automotive suspension systems, IEEE Transactions on Vehicular Technology. (2017) 66, no. 5, https://doi.org/10.1109/tvt.2016.2606607, 2-s2.0-85022052374.
10.1109/TVT.2016.2606607
Web of Science® Google Scholar
7 Jiang X., Li Y., and Li J., Design of a novel linear permanent magnet vibration energy harvester, Proceedings of the IEEE International Conference on Advanced Intelligent Mechatronics, June 2013, Wollongong, Australia, 1090–1095, https://doi.org/10.1109/AIM.2013.6584239, 2-s2.0-84883719055.
10.1109/AIM.2013.6584239
Google Scholar
8 Tang X., Lin T., and Zuo L., Design and optimization of a tubular linear electromagnetic vibration energy harvester, IEEE/ASME Transactions on Mechatronics. (2014) 19, no. 2, 615–622, https://doi.org/10.1109/tmech.2013.2249666, 2-s2.0-84895927103.
10.1109/TMECH.2013.2249666
Web of Science® Google Scholar
9 Liu J., Li X., Zhang X. et al., Modeling and simulation of energy-regenerative active suspension based on BP neural network PID control, Shock and Vibration. (2017) 2019, 8, 4609754.
Web of Science® Google Scholar
10 Wang R., Ding Y., Ye Q. et al., Research into the effect of supercapacitor terminal voltage on regenerative suspension energy-regeneration and dynamic performance, Shock and Vibration. (2017) 2017, 8, 6542015, https://doi.org/10.1155/2017/6542015, 2-s2.0-85029230087.
10.1155/2017/6542015
Web of Science® Google Scholar
11 Wang Q., Wang J., Zhao B. et al., Modeling, design optimization, and verifications of permanent magnet linear actuators for structural vibration mitigation applications, Magnetics IEEE Transactions on. (2017) 53, no. 11, 8205304.
10.1109/TMAG.2017.2699974
Web of Science® Google Scholar
12 Wang J. and Howe D., Tubular modular permanent-magnet machines equipped with Quasi-halbach magnetized magnets-part I: magnetic field distribution, EMF, and thrust force, IEEE Transactions on Magnetics. (2005) 41, no. 9, 2470–2478.
10.1109/TMAG.2005.854328
Web of Science® Google Scholar
13 Wang J. and Howe D., Tubular modular permanent-magnet machines equipped with Quasi-Halbach magnetized magnets-part II: armature reaction and design optimization, IEEE Transactions on Magnetics. (2005) 41, no. 9, 2479–2489.
10.1109/TMAG.2005.854327
Web of Science® Google Scholar
14 Zhang H., Wang E., Min F., Subash R., and Su C., Skyhook-based semi-active control of full-vehicle suspension with magneto-rheological dampers, Chinese Journal of Mechanical Engineering. (2013) 26, no. 3, 498–505, https://doi.org/10.3901/cjme.2013.03.498, 2-s2.0-84877901063.
10.3901/CJME.2013.03.498
Web of Science® Google Scholar

Citing Literature

All articles

Structural Parameter Optimization of a Tubular Permanent-Magnet Linear Machine for Regenerative Suspension

Abstract

1. Introduction