Dynamic Modeling and Development of Symbolic Calculation Software for N-DOF Flexible-Link Manipulators Incorporating Lumped Mass
Abstract
Considering the complex dynamic modeling of multi-DOF planar flexible manipulators, a general-purpose method for the rigid-flexible coupling dynamic modeling of N-DOF flexible manipulators is proposed in this paper, and symbolic calculation software is developed. The modeling method is based on the Lagrange equation and assumed mode method (AMM). First, the N-DOF flexible manipulator is divided into two parts, which are assumed to be rigid and flexible. On this basis, the rigid part and the flexible part are coupled, and the calculation process of the model is further simplified. Then, the simplest general symbolic expression of the dynamic model of the N-DOF flexible manipulator is obtained with the induction method. According to the modeling method, “symbolic expression computation software for dynamic equations of N-DOF flexible manipulators” is developed using the symbolic calculation software Mathematica. Finally, the dynamic modeling method and the symbolic calculation software are verified by a trajectory tracking experiment with a PD control applied to a 2-DOF flexible manipulator. Compared with the traditional modeling method, the calculation time can be reduced by more than 90% using the modeling method proposed in this paper, which significantly reduces the complexity of the modeling process.
1. Introduction
Robotic manipulators are widely used in environments that are hazardous to humans and in situations where there are substantial amounts of repetitive work to reduce the burden on humans and to assist in accomplishing special tasks. To ensure sufficient positioning accuracy at the end of a manipulator, the links of the manipulator can generally be stiffened by a bulky structure to prevent the links from vibrating and to avoid elastic deflection during operation [1–4]. However, heavy links limit the speed of the manipulator’s movement and consume excessive amounts of energy. In some cases, thickening the structure of the links to ensure the positioning accuracy of the end of the manipulator may not be practical. For example, the weight of a manipulator operating on the space station must be as light as possible because of launch costs [5]. In addition, to ensure that the manipulator can perform in a greater workspace, the boom of a concrete pump truck structure should be more slender [6]. Robotic manipulators are also used in nuclear maintenance [7, 8], for spraying large aircraft [9], etc. Under these circumstances, these robotic manipulators have to be designed as flexible-link manipulators (FLMs) with a slender structure.
FLMs have been found in extensive applications because of their advantages in terms of being lightweight and having high load ratios (the ratio of load mass to manipulator mass), high movement speeds, and low energy consumption [10–12]. Moreover, in human-robot interactions, a lightweight FLM is safer to humans and has smaller workload requirements on joint drivers, sensors [13, 14], etc. However, such an FLM experiences vibration and elastic deformation during movement, which will greatly affect the stability of the entire system and the positioning accuracy of the end [15, 16]. Therefore, it is important to study the effects of the dynamic characteristics of FLMs, in terms of the vibration suppression and elastic deformation compensation of the flexible links. For example, the dynamic model of a single-joint flexible manipulator has been developed to suppress the vibration of the flexible manipulator [3, 13].
Because multijoint FLMs are highly nonlinear, strongly coupled, multi-degree-of-freedom (DOF) systems, the dynamic modeling is complex. In addition, considering the payload mass at the end of the manipulator and the lumped mass (for example, the mass of the actuators) on each link, multi-DOF rigid-flexible coupling dynamic modeling is more complicated. These challenging topics have attracted a large number of excellent researchers, who have conducted a considerable amount of research on the dynamic modeling of FLMs. In Giorgio and Del Vescovo’s work [17], the lumped parameter method is used to model the dynamics of flexible links, and although this modeling method is simple, the number of elements must be as large as possible to obtain an adequate model accuracy. The modeling and control of a special class of single-link, an arbitrary number of lumped masses, flexible arms is presented in [18], in which the arm consists of massless flexible structures. Subudhi and Morris adopted the Lagrange equation and the assumed mode method (AMM) to establish the dynamic model of a manipulator with flexible links and joints [19]. A dynamic model of 3-PRR parallel manipulator with flexible links based on AMM was proposed in [20]. Wei et al. provided a global mode method for dynamic modeling of a flexible arm flexible joint manipulator with a tip mass [21]. Some other modeling methods, such as the finite element method (FEM), are also commonly used. For example, the dynamic modeling of the flexible links using FEM is presented in [22]. The FEM is used to derive the dynamic equations for finding the maximum allowable dynamic load of flexible-link mobile manipulators [23]. In addition, the Newton–Euler method is also used to dynamically model the flexible arms [24]. Nonlinear dynamics of motion are developed for flexible manipulator links consisting of rotary joints that connect pairs of flexible links [25]. Bascetta et al. developed a closed-form dynamic model of flexible manipulators based on the Newton–Euler equations [26]. However, the dynamic modeling in the above studies only considers flexible arms with a certain number of DOFs or flexible links without payload mass, and the expressions of the dynamic model are still very computationally expensive in practice.
Considering the complexity of the dynamic modeling of multi-DOF FLMs with a lumped mass on the links, a general-purpose dynamic modeling method for N-DOF FLMs based on the Lagrange equation is presented in this paper, and the symbolic expression computation software for the dynamic equations of N-DOF flexible manipulators is developed. In a more general situation, where the lumped mass is located not only on the end of the links but also at other positions of the links (for example, the flexible arms composed of functionally graded materials (FGM) in the fields of spacecraft, nuclear industries, robotics, etc., the flexibility of the arms can be increased or changed, or changing the vibration frequency of the flexible arm structure by adding concentrated mass to the intermediate position of flexible arms, see [27]) is also considered in this paper. The modeling method is as follows. First, the flexible arms are divided into imaginary rigid and flexible parts and modeled separately. Then, the rigid and flexible parts are coupled, and the dynamic model is further simplified. Finally, the simplest general expression of the dynamic model of the flexible arm with N-DOFs is obtained by the induction method, and “symbolic expression computation software for dynamic equations of N-DOF flexible manipulators” is developed using the symbolic calculation software Mathematica. The test results indicate that compared with the traditional modeling method, the proposed modeling method can reduce the computation time by more than 90% and the software can quickly calculate and generate the dynamic model of the flexible manipulator, thereby greatly reducing the difficulty of the dynamic modeling of the flexible manipulator. Finally, the position tracking control experiment of a 2-DOF flexible manipulator is taken as an example and the dynamic model is generated automatically by the program. Meanwhile, a physical model is also constructed. In an experiment on the end effector of the manipulator tracking a trajectory of a circle, the numerical simulation results of the dynamic model are compared with the experimental results. The dynamic model and the dynamic modeling method are both verified to be correct.
The remainder of this paper is organized as follows. In Section 2, the motion of N-DOF FLM systems is described. Then, in Section 3, the dynamic equations of N-DOF FLMs are derived and established. “The symbolic expression computation software for dynamic equations of N-DOF flexible manipulators” is developed in Section 4, in which the dynamic equations of two-DOF FLMs are automatically generated by the program, and the experiments are conducted. Finally, conclusions are drawn in Section 5.
2. Motion of Flexible Links
To study the general situation of dynamic modeling for serial multijoint FLMs and to simplify the derivation process, fixed-base and small-deformation flexible manipulators moving in the vertical plane are the focus of this paper. Before we derive and establish the dynamic model of the multi-DOF FLM, the appropriate float frame for each flexible link should be assigned, as shown in Figure 1.
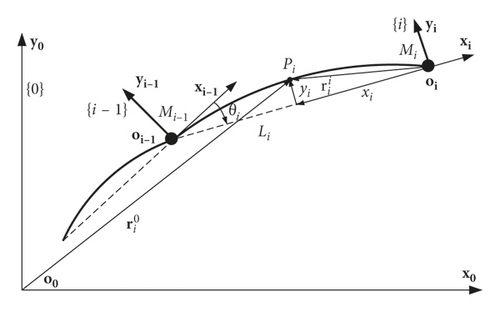
In general, the elements in matrix are a function of (θ1 θ2 ⋯ θi) and the elements in vector are a function of (fi1 fi2).
Equation (11) can be interpreted as the interaction effects of the motions of joint j and joint k on all points on virtual link i.
3. Derivation of Dynamic Equations for Flexible Links with Lumped Mass
3.1. Calculation of Kinetic Energy
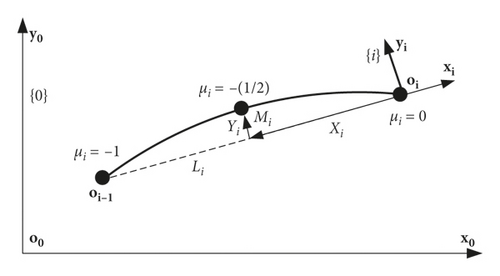
3.2. Calculation of Potential Energy
Before we apply the Lagrange–Euler formulation to the Lagrangian function of equation (22), we should note that the transformation matrix and the matrix Uij are only functions of generalized coordinates θi, i = 1,2, …, n; thus, the derivation of or Uij with respect to fiλ, i = 1,2, …, n, λ = 1,2 will be zero. The matrices Jui, Jvi, and Jwi are only functions of the generalized coordinates fiλ, λ = 1,2 and generalized velocity ; thus, the derivatives of Jui, Jvi, and Jwi with respect to θi, i = 1,2, …, n will be zero.
For i = 1,2, …, n, λ = 1,2, where Riλ is a partial derivative of with respect to the generalized coordinate fiλ and .
From equations (24) and (25), we find that there are not only rigid motion terms with but also flexible motion terms with , in addition to the coupling terms between rigid motion and rigid motion and flexible link deformation . Notably, there are no flexible deformation coupling terms, which should have been . This makes solving the dynamic equations easier, and this is an important reason for establishing such float frames to describe the FLMs. In essence, the two equations also reflect the vibration of the FLMs during movement.
3.3. Relationship between the Generalized Forces and Actual Driving Forces
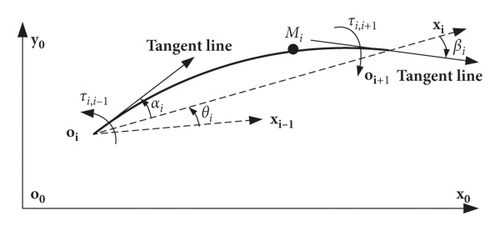
3.4. Matrix Form of Dynamic Equations for FLM
3.5. Symbolic Expression Calculation Procedure
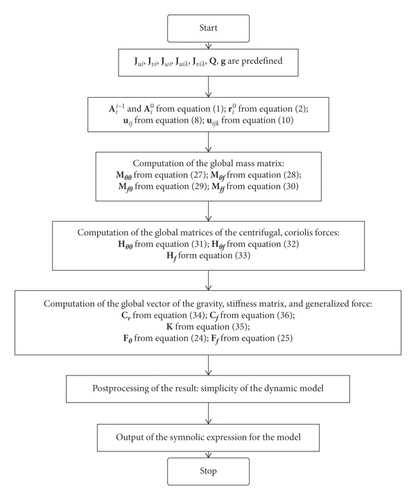
The complete symbolic expression of the rigid-flexible coupling dynamic equation of the N-DOF flexible manipulator with the lumped mass on an arbitrary location of links has been obtained. According to the whole derivation process of this paper and from equations (33) to (44), software that can automatically generate the rigid-flexible coupling dynamic equation of an N-DOF flexible manipulator is developed by using Wolfram Mathematica symbolic calculation software. The operating interface of the software is shown in Figure 4.

- (i)
Step 0. Initialization of the algorithm
-
The number of DOFs and the parameters of the FLM, such as N, mi, Mi, Li, Ei, Ii, θi, μi, are predefined
-
Computation of
-
Jui, Jvi, Jwi, Juiλ, Juiλ, Q, g are predefined
- (ii)
Step 1. Computation of the global mass matrix
-
Computation of
- (iii)
Step 2. Computation of the global matrices of the centrifugal and Coriolis forces
-
Computation of
-
Hf from (40)
- (iv)
Step 3. Computation of the global vector of the gravity, stiffness matrix, and generalized force
-
Computation of
-
K from (42)
- (v)
Step 4. Postprocessing of the result
-
Simplicity of the dynamic model: some terms can be ignored for special situations
-
Output of the symbolic expression for the model.
The flowchart of the symbolic expression computation procedures of the dynamic equation of the flexible manipulator with N-DOFs is shown in Figure 5.
3.6. Comparison with Traditional Modeling Methods
The traditional dynamic modeling methods of flexible manipulators include the Lagrange method, Newton–Euler method, and Kane method, which have their advantages and disadvantages. In this paper, the traditional modeling method is compared with the proposed method, which is also based on the Lagrange equation. The traditional modeling method is as shown in [19].
The traditional modeling method is relatively simple, but it is quite complex in terms of the actual calculation process for solving the dynamic model expression and there is no general formula for flexible manipulators with different DOFs. Therefore, it often takes substantial time to calculate the dynamic model of various types of flexible manipulators in practice.
Here, the program developed in Section 3.5 is tested. Additionally, according to the modeling method in [19], the calculation programs for flexible manipulators with different DOFs developed using Mathematica are also tested. The time required for the two modeling methods to run the computational program (on a PC with a i3-7100 3.90 GHz CPU with 8 GB of RAM) was tested when N = 1, 2, …, 5. The comparison results are shown in Table 1.
| DOF | Proposed method (s) | Traditional method (s) | Time saved (%) |
|---|---|---|---|
| N = 1 | t = 0.36 | t = 41.63 | 99.12 |
| N = 2 | t = 0.92 | t = 106.28 | 99.17 |
| N = 3 | t = 4.21 | t = 212.57 | 98.01 |
| N = 4 | t = 21.3 | t = 365.28 | 94.14 |
| N = 5 | t = 114.6 | t = 1316.45 | 91.29 |
As shown in Table 1, the modeling method proposed in this paper can reduce the modeling time by more than 90% compared with the traditional modeling method. This result is mainly because in the traditional modeling process, the Lagrange energy function of the manipulator system requires a large number of integral operations; then, in the derivation of the generalized coordinates, there are many differential operations. Moreover, there are many repeated intermediate calculations in the differential calculations. The method proposed in this paper eliminates the repetitive intermediate calculation process theoretically and directly derives the simplest expression of the dynamic model equation.
Note that to explain the modeling method proposed in this paper, the simplest planar flexible manipulator is selected as the research object. However, from the entire modeling process shown above, the flexibility characteristics of rigid-flexible coupling manipulators are related only to the matrices Jui, Jvi, and Jwi and their derivatives. Thus, for the dynamic modeling of complex spatial flexible manipulators, large-deformation flexible arms, or even irregularly shaped flexible links, we only need to modify the matrices Jui, Jvi, and Jwi and their derivatives. The structure of the symbolic expressions remains unchanged; thus, this dynamic modeling approach also has good portability. It can be predicted that to satisfy the increasingly complex working conditions, the structure of the flexible arm will be more complex, and it will be a difficult problem to establish a sufficiently accurate dynamic model. Therefore, the modeling method proposed in this paper will have substantial advantages in terms of modeling convenience and computational efficiency.
4. Experimental Study
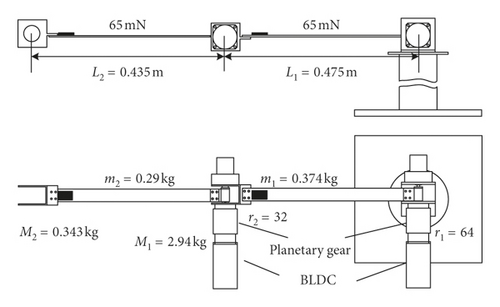
To verify the correctness of the modeling method proposed in this paper, the dynamic model of a 2-DOF flexible manipulator is automatically generated using the software. Simultaneously, a flexible manipulator experimental platform is set up, as shown in Figure 6. Figure 7 is a schematic diagram of the assembly structure of the flexible arm device.

The expressions of the dynamic equations for the 2-DOF flexible manipulator are shown in the appendix. The symbols in the formula are the same as those in the derivation process.
In this experiment, the two arms of the flexible manipulator are controlled to follow the given trajectories. The torque τref output from the controller and the angles q of the joints of the flexible manipulator measured by the encoders are recorded. Simultaneously, the angles are transmitted to the dynamics simulation model, and the estimations of the control torques τest are calculated for comparison with the actual situation. The whole experimental scheme and recorded data are shown in Figure 8. Figure 9 is a schematic diagram of the experimental signal acquisition and control.

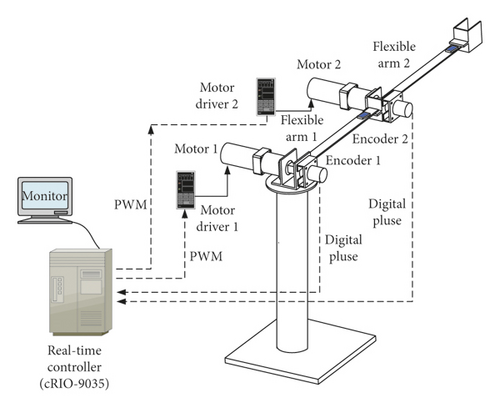
According to the scheme shown in Figure 8, the Simulink control model is established and compiled into a “.so file,” the input and output (IO) interface between the control model and the real manipulator is configured using VeriStand, and finally, all the related control model files are downloaded to the real-time cRIO-9035 controller. The output torque calculated by the controller is converted into a PWM signal by dividing the motor torque constant and the gear ratio of the reducer. A 40 MHz FPGA chip is mounted onto the back of the control slot to acquire the high-speed pulse signal produced by the encoders through the digital IO interface. The motors, gears, and drivers are manufactured by Times Brilliant in China. The type of brushless DC motor 1 with the power of 150 W and brushless DC motor 2 with the power of 100 W is 57BL95S15-230TF9B and 57BL75S10-230TF9, respectively. The type of driver 1 and driver 2 is ZM-6610M. Reduction ratios of PX series planetary gears matched with motors are 64 and 32, respectively. The other specific parameters of the components in the experimental device are listed in Table 2.
| Parameters | Values |
|---|---|
| Length of arms (L1, L2(m)) | 0.475, 0.435 |
| Mass of arms (m1, m2(kg)) | 0.374, 0.29 |
| Young’s modulus of arms (E1, E2(GPa)) | 2.06 × 1011 |
| Second moment of area of arms (I1(m4)) | 16 × 10−11 |
| Second moment of area of arms (I2(m4)) | 6.75 × 10−11 |
| Lumped mass of joints (M1, M2(Kg)) | 2.94, 0.343 |
| Torque values of motors (τ1, τ2(Nm)) | 0.5, 0.32 |
| Gear reduction ratio (r1, r2) | 64,32 |
| Coulomb friction of actuators (kc1, kc2(Nm)) | 0.0345, 0.0226 |
| Viscous friction of actuators (kv1, kv2(Nms/rad)) | 0.0037, 0.0023 |
4.1. Case 1: Free Vibration of the End
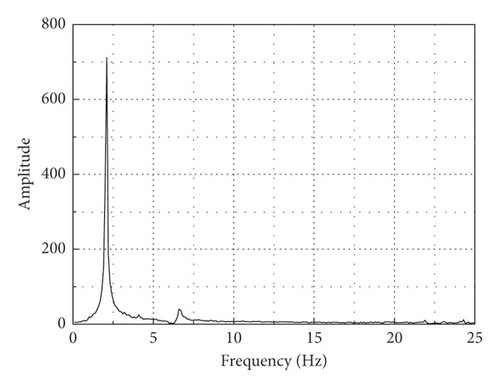
In the experiment, the initial working positions of the flexible manipulator are selected as θ1 = 45∘ and θ2 = −45∘. At the beginning, the external support makes the manipulator as free as possible from gravity and the second flexible manipulator keeps the horizontal position. Then, the flexible manipulator system is allowed to vibrate freely under the force of gravity, and the acceleration of the end of the flexible manipulator under free vibration is observed and recorded. In addition, the accelerometer type is WT901C485, the acquisition time and sampling time are 10 s and 20 ms, respectively, and the simulation interval of Simulink is 0.001 s. The measured acceleration graph is compared with the simulation graph, as shown in Figure 10(a). It is apparent that there are very good correlations between the measured values and simulated values and the amplitude of simulation is smaller, which can be due to model approximation and initial attitude error between the simulation model and the physical model. The spectrum of the end acceleration curve of the simulation model is obtained by fast Fourier transform, as shown in Figure 10(b). It can be seen that the first-order vibration frequency is ω1 = 12.246 rad/s and the second-order vibration frequency is ω2 = 40.82 rad/s. From the experiment, it is obvious that the simulation curves are basically consistent with the experimental curves, which verifies the correctness of the proposed modeling method to some extent. The similar results of vibration characteristics of flexible manipulators can be referred to [30], which can be used to compare with these experimental results.

4.2. Case 2: End Effector Tracking a Trajectory of Circle
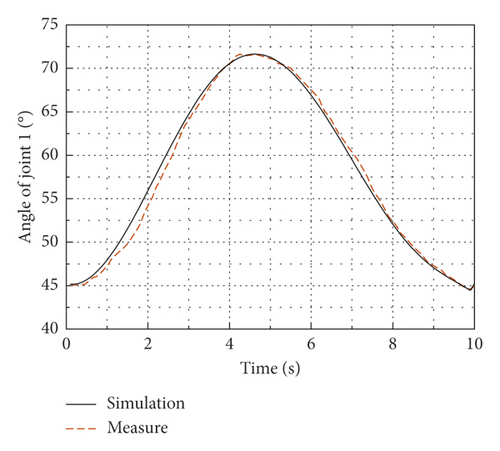
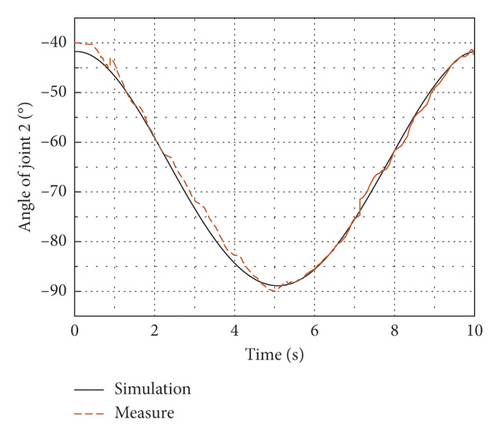
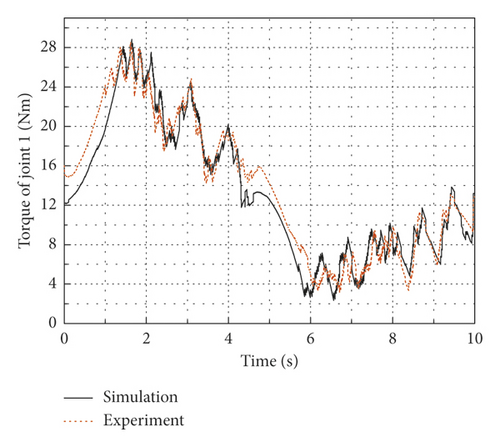
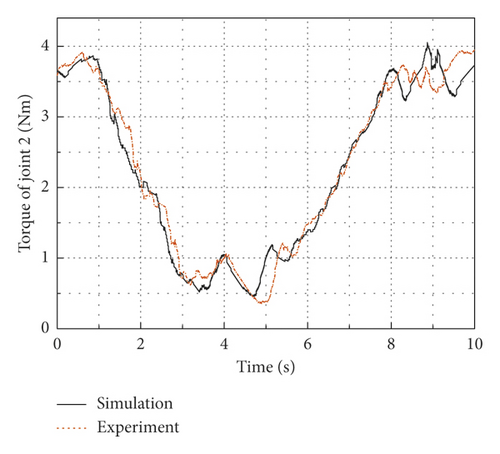
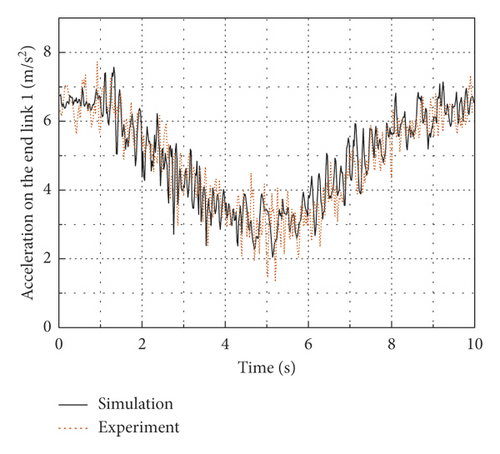
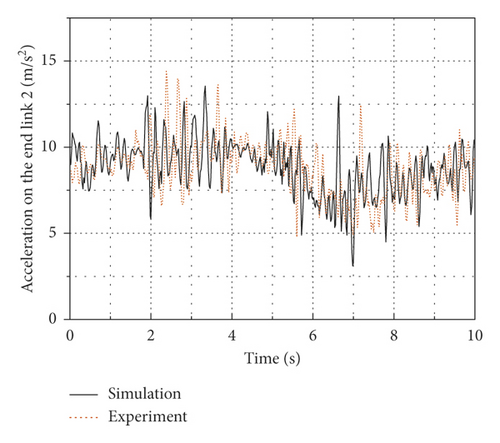
In this experiment, the initial working positions of the flexible manipulator are selected as θ1 = 45∘ and θ2 = −45∘. A circle with a radius of 0.1 m in the XOY plane is selected as the end track of the flexible arm, as shown in Figure 11. The equations of the circle are x = x0 + 0.1 cos(0.2πt), y = y0 + 0.1 sin(0.2πt), whereas the center coordinate of the circle is (x0, y0), x0 = 0.67m , y0 = 0.34m . The end of the flexible arm is substituted into the inverse equation of rigid kinematics, and the desired joint angles are obtained by real-time operation. In addition, the simple PD control is adopted in the cRIO-9035 controller to make the joints track the desired angles, in which kp and k d were debugged through repeated simulation experiments and finally determined to be kp = 125 and k d = 25, and the calculation interval is 0.001 s. Figures 12(a) and 12(b) are the angle curves of joint 1 and joint 2. It can be seen from the figures that when the flexible arm starts to move, the experimental curve and the simulation curve have some errors, and then the errors gradually decreases and the curves tracking effect is better. The input torque curves of the joint 1 and the joint 2 are as shown in Figures 13(a) and 13(b), and the vertical acceleration curves of the flexible arm 1 and the flexible arm 2 are as shown in Figures 14(a) and 14(b). It can be seen that the torque simulation curves and the experimental curves follow the same trend, and there are small tracking errors, due to the inevitable vibration of the flexible mechanical arm during the tracking process, the acceleration will cause frequent fluctuations, but the simulation curve and the experimental curve can also achieve a better tracking effect on the whole. The main cause of some vibration of the manipulator during movement is that, to simplify the control model, the distance between the output shafts of two motors is regarded as the arm length of the flexible arms, the mass of the motor reducers is treated as the lumped mass, and the unavoidable clearance of the motor reducers makes the simulation model and the actual model have certain errors, but these errors are within acceptable ranges.

5. Conclusions
A general modeling method for the dynamic equations of an N-DOF flexible manipulator based on the Lagrange equation and the small deformation assumption of an Euler beam is proposed in this paper. According to this modeling method, symbolic calculation software for the dynamic equations of N-DOF flexible manipulators is developed, greatly reducing the computational complexity. Compared with the traditional modeling method, the modeling time can be reduced by more than 90%. Finally, the correctness of the modeling method is verified by experiments.
The modeling method proposed in this paper takes the planar flexible manipulator as the research object, but according to the modeling process, it can be applied to the more complex rigid-flexible coupling dynamic modeling of flexible manipulators only through modifying the corresponding matrices of the flexible part. This is also future work that needs to be studied. Simultaneously, the modeling method proposed in this paper is also helpful for the dynamic modeling of N-DOF spatial flexible manipulators, large deformation flexible manipulators, etc.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.
Acknowledgments
This work was supported by the Development and Demonstration of Intelligent Slag Feeder Robot for Continuous Casting Crystallizer, Hubei Science and Technology Support Plan (grant no. 2015BAA023).
Appendix
Open Research
Data Availability
The data used to support the findings of this study are available from the corresponding author upon request.




