The cracking of piezoelectric ceramics is the main reason of failure of an ultrasonic motor. Since the fault information is too weak to reflect the condition of piezoelectric ceramics especially in the early degradation stage, a fault feature extraction method based on multiscale morphological spectrum and permutation entropy is proposed. Firstly, a signal retaining the morphological feature under different scales is reconstructed with multiscale morphological spectrum components. Then, the permutation entropy of the reconstructed signal is taken as the fault feature of piezoelectric ceramics. Furthermore, a sensitivity factor is defined to optimize the embedded dimension and delay time of permutation entropy according to double sample Z value analysis. Finally, a matrix composed of the probability distributions, obtained from permutation entropy calculation, is applied for the degradation state identification by means of probability distribution divergence. The analysis of actual test data demonstrates that this method is feasible and effective.

1. Introduction

Ultrasonic motor has been widely used in the areas such as aerospace, medical equipment, optical instruments, robots, and new military equipment, due to some advantages of high torque, quick response, no electromagnetic interference, and autolocking [1, 2]. Piezoelectric ceramics is the key part of the ultrasonic motor, but this material is brittle, and it is prone to crack due to high-frequency excitation for a long time operation. The propagation of cracking would result in the failure of the piezoelectric ceramics, and then the torque and speed performance would also be greatly affected. So it is necessary to pay considerable attention to the fault feature extraction and degradation state identification for piezoelectric ceramics of an ultrasonic motor.

With the development of maintenance theory and relative technologies, more and more advanced fault diagnosis methods have been used for rotating machinery. However, few literatures refer to the fault feature extraction or degradation state identification for piezoelectric ceramics of an ultrasonic motor, and the research mainly focuses on the mechanism and stress analysis [3–5].

Unlike other mechanical devices, the ultrasonic motor comes with a monitor electrode used to reflect the vibration state of a stator, and the monitor electrode voltage (MEV) generated by the positive piezoelectric effect can be used for fault information extraction. From this point of view, the fault diagnosis methods based on vibration signal analysis seem to have great reference value for this study. From the relevant research in recent years, wavelet transform and empirical mode decomposition (EMD) are the current popular methods applied for the rotating machinery fault diagnosis. In the aspect of wavelet transform, Heidari et al. proposed a method based on the wavelet support vector machine with Morlet wavelet transform to diagnose different types of fault in the gearbox [6]. Wang et al. proposed Gauss–Hermite integration-based Bayesian inference method to estimate the posterior distribution of wavelet parameters, and then an optimal wavelet filtering was conducted to extract bearing fault features [7]. In the aspect of EMD, Abdelkader et al. realized the early fault detection of rolling bearing based on the improved EMD method [8]. Yuan et al. applied the EMD method to the multifault diagnosis of bearing [9]. Unfortunately, these popular methods also have unsolved problems: one is the selection of thresholds and wavelet basis in wavelet transform, and another one is the mode fixing and end effect in the EMD method [10].

A method called morphological signal processing, which can extract fault feature from strong background noise while retaining the shape characteristics of the useful information, has received considerable attentions [11]. Yu et al. proposed an improved morphological component analysis method for the compound fault of the gear and the bearing in gearboxes [12]. In order to solve the problem that single-scale analysis may suffer from the completeness in the extracted features, Yan et al. proposed an adaptive multiscale combination morphological filter-hat transform for bearing fault diagnosis [13]. Furthermore, entropy is able to quantify the disorder or uncertainty of probability distribution, and it has been widely applied in damage monitoring [14]. Yu et al. applied the time-frequency entropy method to gear fault diagnosis with the help of Hilbert–Huang transform [15]. Among the applications of entropy, it is worthy noting that permutation entropy (PE) has been widely used in the mutation detection of electroencephalogram, heart interbeat signal, and mechanical signal in past few years [16–18]. PE not only reflects the complexity of one-dimensional time series but also has a high sensitivity to information influenced by dynamic changes in complex systems [19]. Considering the fact that the wave transmission would be subjected to a disturbance when the traveling wave passes through the crack of piezoelectric ceramics in the ultrasonic motor, PE is possible to be used to indicate the degradation trend.

With regard to the method of degradation state identification, gray relational analysis is a dynamic mapping for the relative changes in the signal [20]. However, the distinguishing coefficient limited by prior experience has a great influence on the recognition results. In past years, probability distribution divergence (PDD) analysis has made remarkable achievement in fault diagnosis of bearing, gears, motor, and hydraulic pump [21–23]. Based on this idea, the probability distributions that were obtained from PE calculation are expected to be applied for the degradation state identification of piezoelectric ceramics in the ultrasonic motor.

In this paper, the MEV signal will be used to extract the fault information. The paper is organized as follows: Section 2 briefly reviews the principles of multiscale morphological decomposition, and then the reconstructing signal method based on multiscale morphological spectrum (MMS) components is introduced. In Section 3, the MMS-PE scheme is detailed, and a sensitivity factor is proposed to optimize the selection of embedded dimension and delay time in PE calculation. In Section 4, the flowchart of degradation state identification based on PDD analysis is given. The effectiveness of the proposed method will be validated with experiment results in Section 5. Finally, the conclusions are provided in Section 6.

2. MMS Components

For the one-dimensional signal {f(n) | n = 0, 1, …, N − 1}, the expansion and corrosion can be calculated by the following formula [24]:

\begin{matrix} \{\begin{cases} (f \oplus g) (n) = \max \{f (n - m) + g (m)\}, \\ (f Θ g) (n) = \min \{f (n + m) - g (m)\}, \end{cases} \end{matrix}

(1)

where g(m) denotes the structural element, m = 0, 1, …, M − 1, N ≥ M. And N is the length of signal, and M is the length of structural element.

According to Equation (1), we can easily notice that the expansion and corrosion operations are just maximum and minimum value filtering within the structural element for f(n). The expansion operation can increase the valley value of the function, while corrosion operation can reduce the peak value of the function. Equation (1) involves only the addition, subtraction, and extreme value operation, so there is a great advantage in the speed of signal processing.

The structural element under scale λ can be calculated by the following equation:

\begin{matrix} λ g = g \oplus g \dots \oplus g . \end{matrix}

(2)

Then, the expansion and corrosion calculations of signal f(n) under scale λ can be represented as follows:

\begin{matrix} \{\begin{cases} {(f \oplus g)}_{λ} = (f \oplus λ g) (n), \\ {(f Θ g)}_{λ} = (f Θ λ g) (n) . \end{cases} \end{matrix}

(3)

The morphological opening and closing operations which are obtained by combination of expansion and corrosion operations are defined as follows:

\begin{matrix} \{\begin{cases} (f \circ g) (n) = (f Θ g \oplus g) (n), \\ (f • g) (n) = (f \oplus g Θ g) (n) . \end{cases} \end{matrix}

(4)

Multiscale morphological decomposition based on morphological opening and closing operations under scale λ can be expressed as follows:

\begin{matrix} MMD (f, λ, g) = \{\begin{cases} (f \circ λ g) (n) = (f Θ λ g \oplus λ g) (n), & 0 \leq λ \leq λ_{\max}, \\ (f • λ g) (n) = (f \oplus λ g Θ λ g) (n), & λ_{\min} \leq λ < 0. \end{cases} \end{matrix}

(5)

The opening operation can filter out the peak noise, while the closing operation can deal with the valley noise. So the above two operations have the abilities of smoothing edge burrs and filling the signal holes.

Assume that g is a convex function. MMS can be obtained based on the following equation:

\begin{matrix} MMS (f, λ, g) = \{\begin{cases} - \frac{d A (f \circ λ g)}{d λ}, & 01 \leq λ \leq λ_{\max} -, \\ - \frac{d A (f • (- λ) g)}{d λ}, & λ_{\min} + 10 \leq λ < . \end{cases} \end{matrix}

(6)

As the frequency spectrum can directly reflect the frequency components in the signal, MMS can reflect the shape change of the signal under scale λ. Since λ is the continuous integer value, the component under scale λ in the MMS can be calculated as follows:

\begin{matrix} MMS (f, λ, g) = \{\begin{cases} f \circ λ g - f \circ (λ + 1) g, & 0 \leq λ \leq λ_{\max} - 1, \\ f • (- λ) g - f • (- λ + 1) g, & λ_{\min} + 10 \leq λ \leq . \end{cases} \end{matrix}

(7)

According to Equations (6) and (7), the number of morphological spectral components is λ_max−1 under the maximum analysis scale λ_max. Let us denote the morphological spectral component of the MEV signal as f_c(n), where c = 1, 2, …, λ_max−1. MMS has the ability to present the morphological features in different scales, and the magnitude of f_c(n) can reflect the content of morphological feature matching the structural elements of responding scale in the signal [25].

3. MMS-PE

Based on the MMS components, a weight coefficient is defined as

\begin{matrix} α_{c} = \frac{P_{c}}{\sum_{c = 1}^{λ_{\max - 1}} P_{c}}, \end{matrix}

(8)

where P_c is the root mean square (RMS) value of the MMS component f_c(n). Then, the reconstructed signal r(n) can be obtained by

\begin{matrix} r (n) = \sum_{c = 1}^{λ_{\max - 1}} α_{c} f_{c} (n) . \end{matrix}

(9)

Let us construct further the following matrix [26]:

\begin{matrix} [\begin{matrix} r (1) & r (1 + τ) & \cdot \cdot \cdot & r (1 + (m - 1) τ) \\ r (2) & r (2 + τ) & \cdot \cdot \cdot & r (2 + (m - 1) τ) \\ r (i) & r (i + τ) & \cdot \cdot \cdot & r (i + (m - 1) τ) \\ \cdot \cdot \cdot & \cdot \cdot \cdot & \cdot \cdot \cdot & \cdot \cdot \cdot \\ r (K) & r (K + τ) & \cdot \cdot \cdot & r (K + (m - 1) τ) \end{matrix}], \end{matrix}

(10)

where m is the embedding dimension, τ denotes time delay, and i = 1,2, ⋅⋅⋅K and K = n − (m − 1)r. For each row vector, rank the elements in the ascending order and then record a new sequence based on the column index of each element in the matrix. Because the matrix contains m columns, there are m! combinations that may appear in the above sequence. The probability of the k permutation is recorded as P = {p_i | i = 1, 2, …, k}, and the PE can be defined as follows:

\begin{matrix} E_{P} = - \sum_{i = 1}^{k} p_{i} \ln p_{i} . \end{matrix}

(11)

The PE can be normalized by the following equation:

\begin{matrix} 0 \leq E_{P N} = \frac{E_{P}}{\ln (m!) \leq 1} . \end{matrix}

(12)

PE is an indicator which can be used to measure the complexity and randomness of one-dimensional time series, and it is suitable for detecting the changes in the monitoring signal for a dynamic system. The smaller the randomness of the signal, the lower the complexity and the PE value. As far as the ultrasonic motor is concerned, the driving voltage with high frequency is a sinusoidal signal; therefore, MEV generated by the positive piezoelectric effect is also sinusoidal. When the ceramic piece is intact, the MMS-PE of the MEV signal is small due to the regularity of the sinusoidal signal. Once a crack appears, the vibration of the stator will be affected, and the fluctuation of the speed will also lead to the nonstationary characteristics of the MEV. As the degree of degradation increases, MEV will become more and more irregular, and the MMS-PE value which characterizes the complexity of the signal will also be larger. Based on the above analysis, it is reasonable to take MMS-PE as the fault feature of piezoelectric ceramics in this paper.

Furthermore, embedding dimension m and time delay τ are the main parameters affecting the calculation result of PE. In order to optimize the selection of the two parameters, a sensitivity factor is defined to reflect the fault feature difference between adjacent degenerate states. In this paper, the degradation states are divided into four categories: normal state, slight degradation, severe degradation, and failure state. Select n groups of the sample in each degradation state according to the above order, and the four MMS-PE subsets of the degradation states are noted as X₁, X₂, X₃, and X₄ successively. Based on double sample Z value analysis, the sensitivity factor is given as follows:

\begin{matrix} α_{Z} = \frac{1}{3} \sum_{i = 1}^{3} \frac{|\bar{X_{i}} - \bar{X_{i + 1}}|}{\sqrt{(μ_{X_{i}}^{2} + μ_{X_{i + 1}}^{2}) / n}}, \end{matrix}

(13)

where

\bar{X}

represents the mean value of the MMS-PE subset and

μ_{X}^{2}

represents the standard deviation. The definition of the sensitivity factor is mainly according to the discrimination and the stability of calculation results. On the one hand,

|\bar{X_{i}} - \bar{X_{i + 1}}|

represents the difference of fault feature’s mean value between two adjacent states. The larger the difference, the better the discrimination between the two adjacent states, and the proposed sensitivity factor is proportional to the difference; on the other hand,

\sqrt{μ_{X_{i}}^{2} + μ_{X_{i + 1}}^{2} / n}

represents the pooled standard deviation of the fault feature in two adjacent states. The smaller the pooled standard deviation, the better the stability of the calculation results, and the proposed sensitivity factor is inversely proportional to the pooled standard deviation. The defined factor in Equation (13) is a comprehensive judgement for three groups of adjacent states.

Both embedding dimension m and time delay τ should be selected within a certain range because large m will cost overmuch computation and large τ will bring to overmuch loss of wave information. The two parameters are integer, so the preferred combination of m and τ can be selected by the maximum value of the sensitivity factor within limited combinations.

4. Degradation State Identification Based on PDD Analysis

Kullback–Leibler divergence is an effective way to describe the difference of two probability distributions. If the probability distributions of test data is noted as P_t = {p_ti | i = 1, 2, …, k} and the one of standard data is noted as P_s = {p_si | i = 1, 2, …, k}, the Kullback–Leibler divergence can be described as follows [27]:

\begin{matrix} KLD (P_{t} ||P_{s}) = \sum_{i = 1}^{k} p_{t} \log \frac{p_{t}}{p_{s}} . \end{matrix}

(14)

For the reason that log(x) is the convex function, it can be concluded that KLD(P_t||P_s) ≥ 0 according to Gibbs’ inequality. The smaller the divergence, the larger the similarity between these two probability distributions, and vice versa. However, it is obvious that KLD(P_t||P_s) ≠ KLD(P_s||P_t). In order to solve this problem, the PDD between standard data and test data is defined as follows:

\begin{matrix} \{\begin{cases} PDD (P_{t}, P_{s}) = \frac{1}{2} D_{KLD} (P_{t} ||\overset{\land}{P}) + \frac{1}{2} D_{KLD} (P_{s} ||\overset{\land}{P}) = \frac{1}{2} \sum_{i = 1}^{k} p_{t i} \log \frac{p_{t i}}{(p_{t i} + p_{s i}) / 2} + \frac{1}{2} \sum_{i = 1}^{k} p_{s i} \log \frac{p_{s i}}{(p_{t i} + p_{s i}) / 2}, \\ p_{t i} \log \frac{p_{t i}}{(p_{t i} + p_{s i}) / 2} = 00, if p_{t i} =, \\ p_{s i} \log \frac{p_{s i}}{(p_{t i} + p_{s i}) / 2} = 00, if p_{s i} =, \end{cases} \end{matrix}

(15)

where

\overset{\land}{P}

is the average probability distribution. From Equation (15), it can be concluded that PDD has the following properties:

(1)
PDD(P_t, P_s) = PDD(P_t, P_s)
(2)
PDD(P_t, P_s) ≥ 0
(3)
PDD(P_t, P_s) = 0 if P_t = P_s

In this way, the divergence between the test data and standard data can be used to identify the degradation state. Procedures for the degradation state identification based on PDD analysis are detailed in the following.

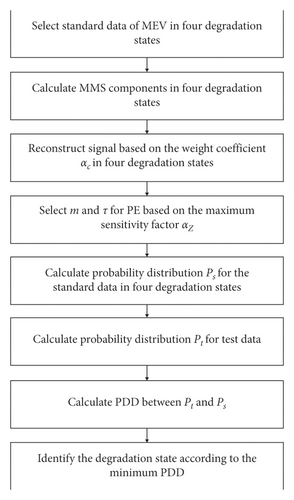
Step 1. Select standard degradation data in normal state, slight degradation, severe degradation, and failure state. Calculate the probability distributions of MMS-PE in four degradation states, which are recorded as P_{s_normal}, P_{s_slight}, P_{s_severe}, and P_{s_failure}.

Assuming that the number of the standard data group in each degradation state is N_s, the matrix composed of the probability distributions of standard data is described as follows based on Equation (11):

\begin{matrix} [\begin{matrix} p_{1}^{1} & p_{2}^{1} & \dots & p_{k}^{1} \\ p_{1}^{2} & p_{2}^{2} & \dots & p_{k}^{2} \\ \dots & \dots & \dots & \dots \\ p_{1}^{N_{s}} & p_{2}^{N_{s}} & \dots & p_{k}^{N_{s}} \end{matrix}] . \end{matrix}

(16)

The probability distributions of standard data P_s = {p_si | i = 1, 2, …, k} can be obtained by the mean of the column in the above matrix, where $p_{s i} = (1 / N_{s}) \sum_{l = 1}^{N_{s}} p_{i}^{l}$ .

Step 2. Calculate the divergence between P_t and P_s in each degradation state according to Equation (15):

\begin{matrix} [\begin{matrix} {PDD}_{normal} \\ {PDD}_{slight} \\ {PDD}_{severe} \\ {PDD}_{failure} \end{matrix}] = [\begin{matrix} PDD (P_{t}, P_{s_normal}) \\ PDD (P_{t}, P_{s_slight}) \\ PDD (P_{t}, P_{s_severe}) \\ PDD (P_{t}, P_{s_failure}) \end{matrix}] . \end{matrix}

(17)

Step 3. The state corresponding to the minimum PDD is seen as the result of degradation state identification.

The whole flowchart of identification is concluded as Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The flowchart of degradation state identification.

5. Experimental Results

5.1. Data Sampling

The data sampling was carried out on the ultrasonic motor testbed, which is shown in Figure 2.

The tested ultrasonic motor is TRUM-60-P. Its maximum torque is 0.6 N·m, and no load speed is 120 rp min⁻¹. The speed is controlled by a variable frequency driver. The signal frequency generated from the sensor part of the stator is 40.65 kHz, and it is sampled and stored by the Handyscope HS4 data acquisition card of TiePie engineering. The sampling frequency is set to be 500 kHz, and the sampling time of each group data is 2 s.

The piezoelectric ceramics of four degradation states are shown in Figure 3.

In actual observation, the copper elastomer can be distinguished from all the cracks in Figure 3. Therefore, the depth of three reality cracks is 0.5 mm (the thickness of ceramic). The classification of degradation states is primarily according to the width and defect area, which are the factors affecting operating performance of the ultrasonic motor. The surface conditions of the cracks are described as follows:

(1)
Normal state: intact.
(2)
Slight degradation: the average width of the crack is 0.2 mm, and the length is 7.6 mm.
(3)
Severe degradation: the average width of the crack is 0.7 mm, and the length is 8.7 mm.
(4)
Failure state: the average width of the central crack is 0.4 mm, and the length is 2.3 mm. In addition, there are defects (12.2 mm²) and pitting corrosion (4.1 mm²) located on both sides of the crack, respectively.

There are 80 groups of data that were collected in each degradation state, in which 10 groups of data noted as D₁ will be used as standard data for verifying the rationality and feasibility of MMS-PE, 30 groups of data noted as D₂ will be used for parameter optimization of PE, and the remaining 40 group of data noted as D₃ will be used as the test data for degradation state identification. The waveform of one group of standard data selected from D₁ is shown in Figure 4.

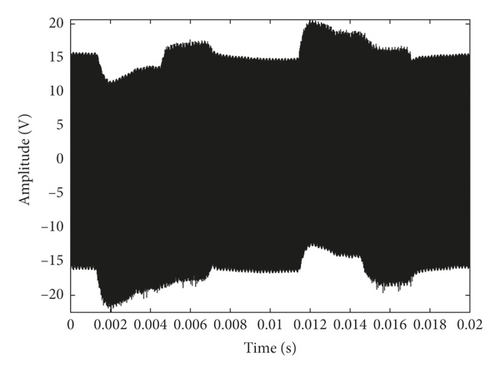
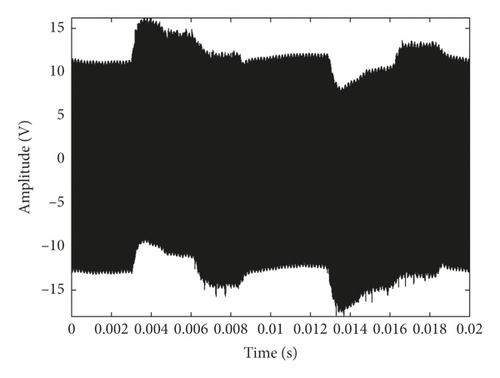
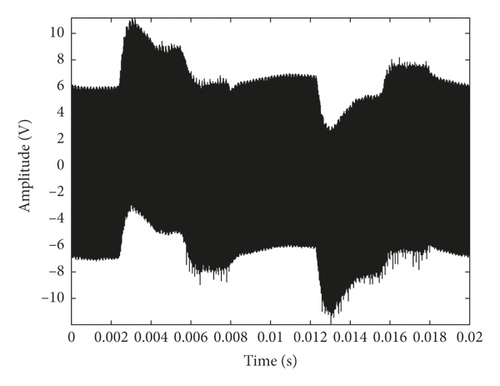
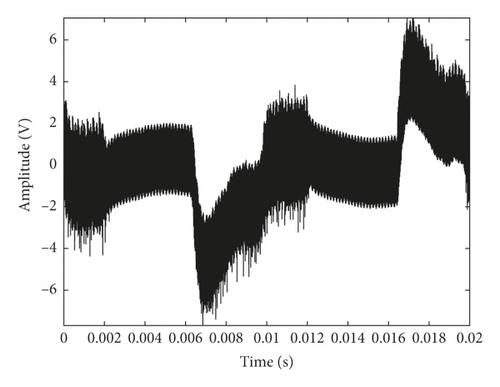
From Figure 4, we can easily notice that the amplitude of the signal is gradually decreasing with the development of degradation, and the changes of the signals also become more and more violent. However, in fact, as the motor load increases, the amplitude of MEV will also decrease correspondingly. So the complexity of the signal, in stead of the amplitude, is suitable to be adopted as the analysis object for fault feature extraction of piezoelectric ceramics in this paper.

5.2. Signal Reconstruction Based on MMS Components

The flat structure element g = [0, 0, 0] is used for multiscale morphological analysis. Take a group of standard data selected from D₁ as an example, and the MMS components in four degradation states are shown in Figure 5. The sixth and subsequent components are close to 0, so there are only five components (0.02 s) given in Figure 5 due to limitation of the paper space.

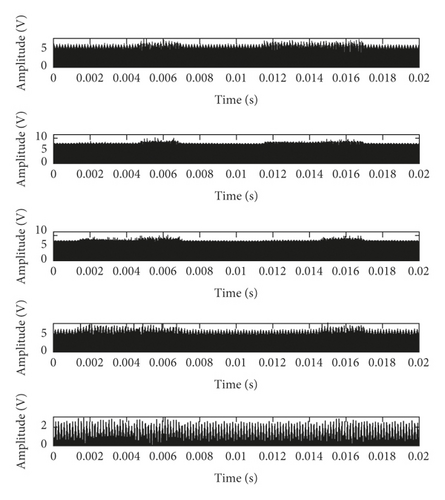
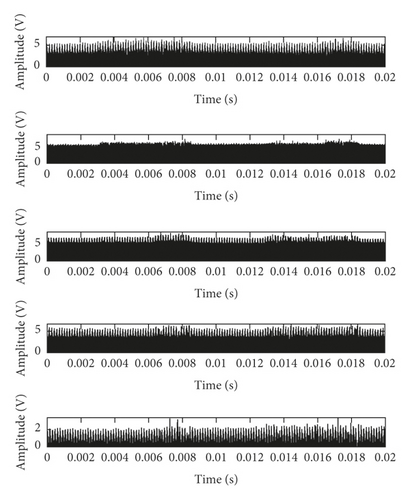
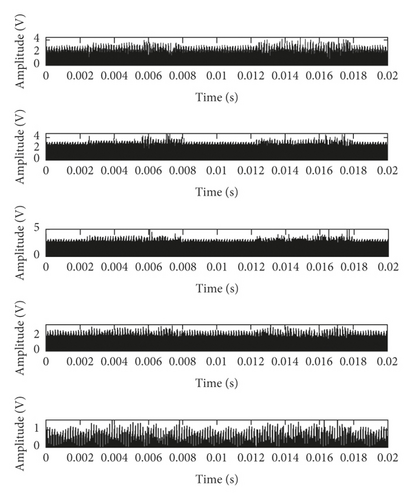
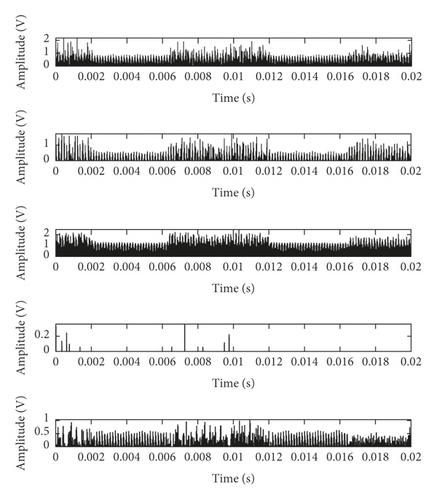
The RMS statistics of the MMS components are shown in Table 1.

Table 1. RMS statistics of MMS components.

	Layer 1	Layer 2	Layer 3	Layer 4	Layer 5
Normal state	3.27 V	5.36 V	6.29 V	5.19 V	1.52 V
Slight degradation	2.30 V	4.21 V	4.92 V	4.02 V	1.35 V
Severe degradation	1.43 V	2.05 V	2.36 V	2.02 V	0.67 V
Failure state	0.43 V	0.34 V	0.93 V	0.02 V	0.30 V

The waveform of the reconstructed signal in Equation (9) based on weight coefficient α_c is shown in Figure 6.

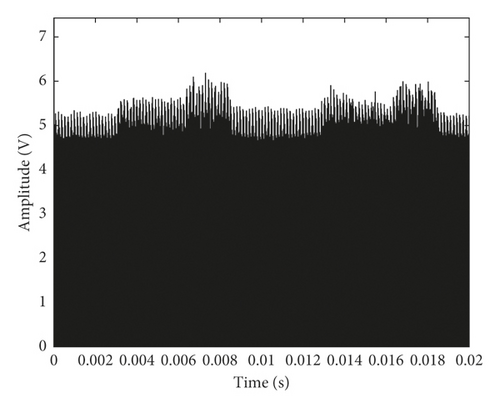
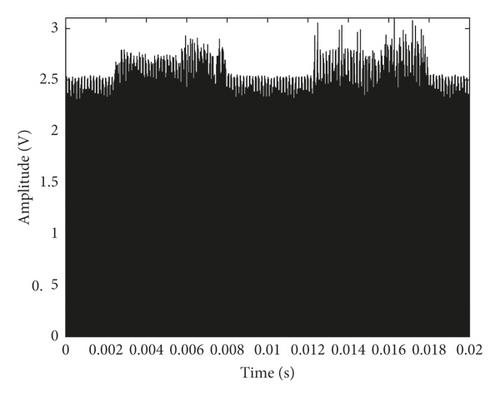
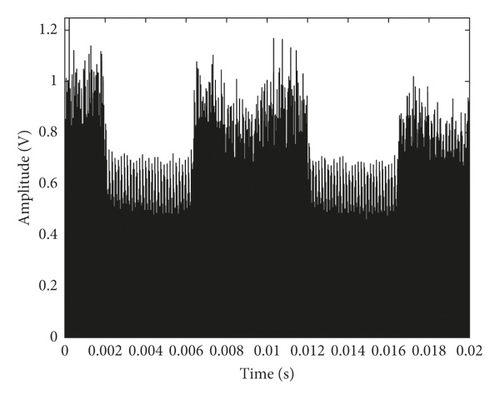
From Figure 6, it can be seen that the waveform retains the morphological features in different degradation states. However, in order to describe the fault feature quantitatively for degradation state identification, MMS-PE should be calculated based on this waveform information in the following discussion.

5.3. Fault Feature Extraction

In consideration of computation and the loss of wave information, the values of embedding dimension m and time delay τ need to be limited to a certain range in MMS-PE calculation. In this paper, the selection of above two parameters will be discussed in the integer range where m is from 3 to 6 and τ is from 2 to 6. Among the 80 groups of data in each degradation state, there are 30 groups of data noted as D₂, which will be used for parameter optimization of MMS-PE. After the reconstructed signals of D₂ were obtained via MMS components, the sensitivity factor of the normalized MMS-PE according to Equation (13) is shown in Figure 7 and Table 2.

Table 2. Statistical results of the sensitivity factor.

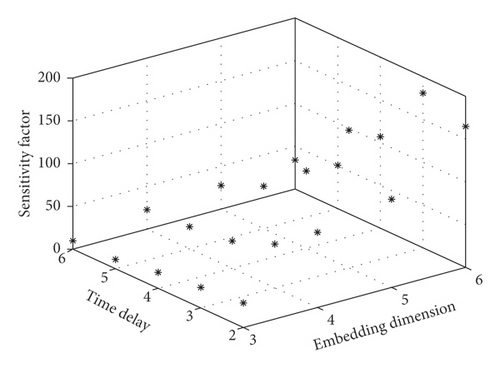
	τ = 2	τ = 3	τ = 4	τ = 5	τ = 6
m = 3	28.70	23.98	18.66	10.86	9.84
m = 4	87.85	51.20	31.91	25.71	22.67
m = 5	103.07	160.89	90.36	49.55	27.54
m = 6	164.72	180.80	107.02	50.64	33.88

According to the above statistical results, the sensitivity factor reaches the peak 180.80 as m = 6 and τ = 3.

In order to verify the sensitivity factor α_Z, the MMS-PE of the standard data D₁ is calculated by the following cases based on different combinations of m and τ:

(1)
Sensitivity factor α_Z is the minimum value in Table 2 (m = 3 and τ = 6)
(2)
Sensitivity factor α_Z is the closest to the average of maximum and minimum values in Table 2 (m = 5 and τ = 2)
(3)
Sensitivity factor α_Z is the maximum value in Table 2 (m = 6 and τ = 3)

The results of above three cases are shown in Figure 8.

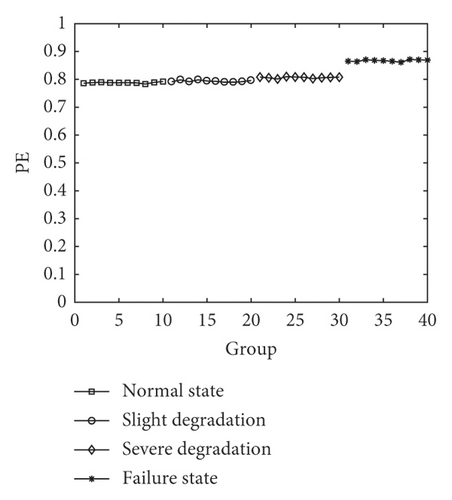
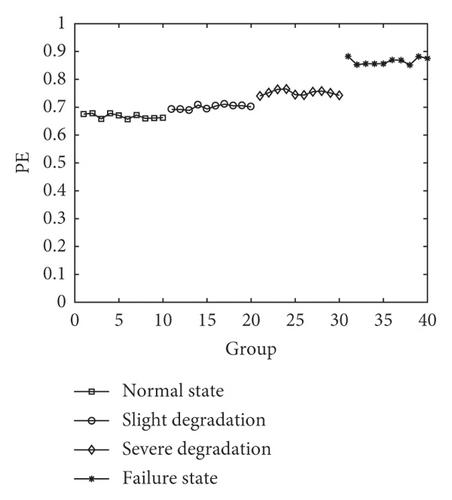
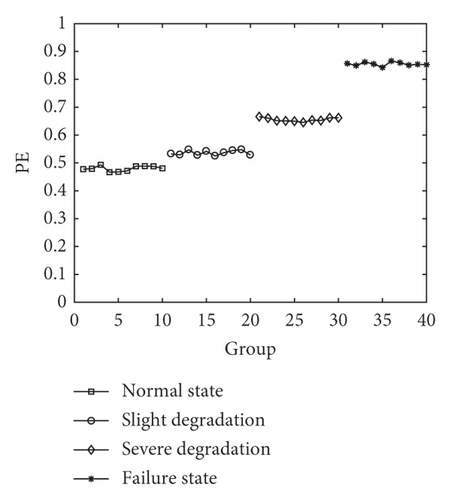
From Figure 8, we can conclude that the distinction between adjacent states is more and more obvious with the increase of factor. In Figure 8(a), dimension (m = 3) limits the numerical accuracy of PE so that the MMS-PE values in the first three states almost coincide. In Figure 8(b), it can be seen that the result reflects only a slight uptrend as the fault degradation, and it presents a strained distinction from the normal state to severe degradation. There seems to be not enough space for the subsequent degradation state identification. Figure 8(c) reflects a clear uptrend of the MMS-PE value with the degradation of piezoelectric ceramics, and it shows a better discrimination especially from the normal state to severe degradation. Therefore, m = 6 and τ = 3 is regarded as the parameter optimization result in this paper.

In order to explain the necessity of signal reconstruction based on MMS components, the normalized PE (m = 6 and τ = 3) results of the original standard data are given as Figure 9.

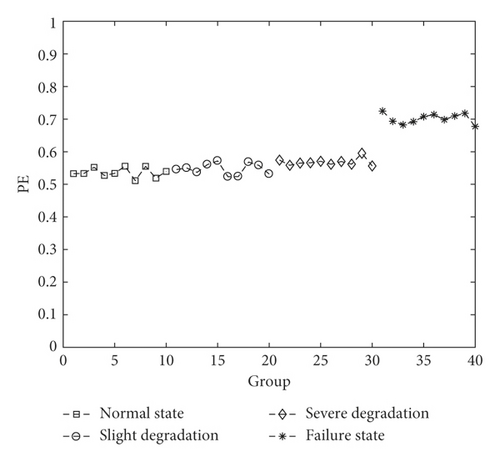
Compared with Figure 8(c), the PE result of the first three states in Figure 9 has no obvious monotonous trend, and the amplitudes of these points too close to be distinguished. The main reason is that the complexity of the original signal is similar. In fact, such a result coincides with the waveform information in Figure 4. In addition, the value of the failure state is obviously bigger than the ones of the first three states, while the waveform of the failure state is obviously more violent than the ones of the first three states in Figure 4. And it also an explanation that PE does have the ability to reflect the complexity of the signal.

5.4. Comparison with the Other Methods

Recently, the local characteristic-scale decomposition (LCD) as a new adaptive time-frequency analysis method based on intrinsic time-scale decomposition was proposed by Yang et al. [28]. LCD method has been applied for the fault feature extraction of the hydraulic pump and bearing successfully [29, 30]. In order to further validate the performance of the proposed method in this paper, the LCD method is adopted to extract the fault feature of piezoelectric ceramics in the ultrasonic motor for the following comparative analysis.

Let us take 10 groups of standard data in D₁ as the object of LCD analysis which is detailed in [30]. Based on the LCD method, the signal can be decomposed into n intrinsic-scale components (ISC) which are independent of each other. The energy of the components is noted as E = {E_i | i = 1, 2, …, n}, and then the LCD energy entropy is defined as follows:

\begin{matrix} E_{LCD} = - \sum_{i = 1}^{n} p_{i} \ln p_{i}, \end{matrix}

(18)

where

p_{i} = E_{i} / \sum_{i = 1}^{n} E_{i}

.The normalization of Equation (18) can be obtained by Equation (19):

\begin{matrix} 0 \leq E_{LCDN} = \frac{E_{LCD}}{\ln (n!) \leq 1} . \end{matrix}

(19)

The LCD energy entropy calculation results of the original signal and reconstructed signal based on MMS components are both given in Figure 10.

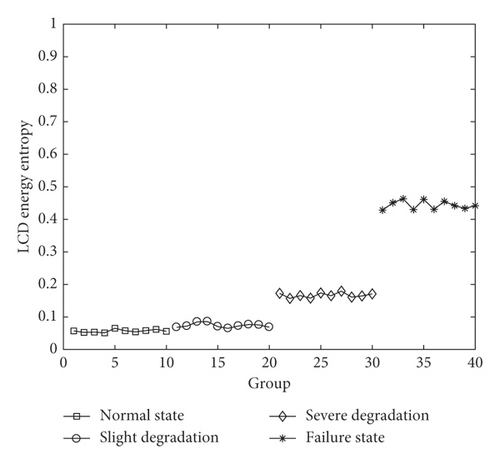
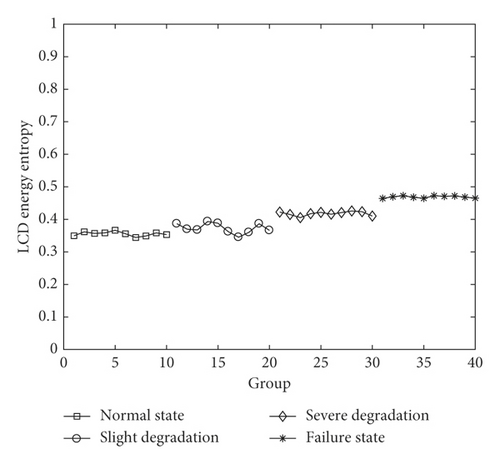
According to Equation (18), the more homogeneous the energy of ISCs, the greater the entropy. Figure 10 presents a reasonable trend that the LCD energy entropy increases with the fault degradation. The main reason is that, as the piezoelectric ceramics is intact, the MEV signal is caused by sinusoidal vibration via the sinusoidal driving signal, and the energy is mainly concentrated on a few ISCs, so the entropy is small. Once the crack appears, the complexity of the signal will increase. The energy of the signal disperses to some other ISCs, and the energy entropy will also increase. However, normal state and slight degradation cannot be distinguished in Figure 10(a), and the entropy difference between adjacent states is too small to be applied for the degradation identification in Figure 10(b). On comparing Figures 10(b) with 8(c), the effect based on LCD energy entropy seems not as outstanding as the proposed method.

5.5. Application on Degradation State Identification via PDD Analysis

There are 10 groups of standard data in each degradation state. According to the results of parameter optimization, the embedding dimension m is 6. The matrix composed of the probability distributions of standard data is described as follows:

\begin{matrix} [\begin{matrix} p_{1}^{1} & p_{2}^{1} & \dots & p_{720}^{1} \\ p_{1}^{2} & p_{2}^{2} & \dots & p_{720}^{2} \\ \dots & \dots & \dots & \dots \\ p_{1}^{10} & p_{2}^{10} & \dots & p_{720}^{10} \end{matrix}], \end{matrix}

(20)

where the number of elements in each row vectors is 6! = 720.

The average probability distributions of 10 groups of standard data can be noted as P_s = {p_si | i = 1, 2, …, 720}, where $p_{s i} = (1 / 10) \sum_{l = 1}^{10} p_{i}^{l}$ . Then, we can obtain the four standard probability distributions corresponding to four degradation states, which are recorded as P_{s_normal}, P_{s_slight}, P_{s_severe}, and P_{s_failure}. According to Equation (15), PDD between test data and standard data of four degradation states can be calculated, and the result of state identification is the degradation state whose PDD is the smallest. In this way, we can determine whether the identification results are consistent with the actual state so as to verify the validity of the method.

In total, there are 160 groups of data in D₃ which is used as the test data for degradation state identification. The test data in D₃ are numbered as follows: 0–40 groups are normal state data, 41–80 groups are slight degradation data, 81–120 groups are severe degradation data, and 121–160 groups are failure state data. Limited by the paper space, only the first 5 groups of test data’s PDD statistics in each degradation state are given in Table 3.

Table 3. The first 5 groups of test data’s PDD statistics in each degradation state.

Group number	PDD to normal state	PDD to slight degradation	PDD to severe degradation	PDD to failure state	Identification results	Judgement
1	0.0744	0.1573	0.3542	0.6758	Normal state	Right
2	0.0687	0.1128	0.4031	0.6743	Normal state	Right
3	0.0956	0.1254	0.3755	0.6392	Normal state	Right
4	0.0842	0.1363	0.3687	0.6654	Normal state	Right
5	0.0659	0.1124	0.3255	0.6171	Normal state	Right
41	0.1706	0.0990	0.2498	0.5751	Slight degradation	Right
42	0.1032	0.0776	0.2960	0.5255	Slight degradation	Right
43	0.1277	0.0619	0.2342	0.5506	Slight degradation	Right
44	0.1046	0.1155	0.2585	0.5699	Normal state	Wrong
45	0.1197	0.0463	0.2224	0.5861	Slight degradation	Right
81	0.3052	0.2650	0.1047	0.3786	Severe degradation	Right
82	0.3531	0.2497	0.0639	0.4257	Severe degradation	Right
83	0.3285	0.2651	0.0449	0.3880	Severe degradation	Right
84	0.3250	0.2661	0.0758	0.4068	Severe degradation	Right
85	0.3417	0.2873	0.0362	0.3649	Severe degradation	Right
121	0.6126	0.5602	0.3374	0.0632	Failure state	Right
122	0.5838	0.5263	0.3997	0.1069	Failure state	Right
123	0.6296	0.5654	0.3511	0.0962	Failure state	Right
124	0.5378	0.4982	0.3729	0.0512	Failure state	Right
125	0.5743	0.5148	0.3364	0.0837	Failure state	Right

The recognition results of the whole 160 groups of test data are shown in Figure 11.

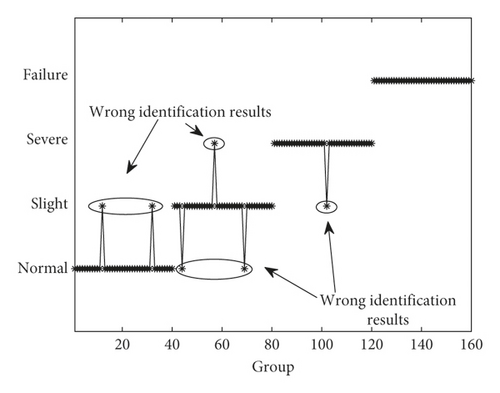
In the whole 160 groups of test data, there are only 6 wrong identification results, and that is to say, the accuracy rate is as high as 96.25%. In addition, the identification results of failure state test data (141–160) in Figure 11 are completely correct, and this result shows good agreement with Figure 8(c) where the difference value of MMS-PE between failure state and the first three states is clear and large enough. The wrong identification results are mainly focused on the states between normal and slight degradation for the reason that the MMS-PE values of normal state and slight degradation are relatively similar to each other. Overall, the PDD analysis based on MMS-PE is feasible to identify the degradation states of piezoelectric ceramics in the ultrasonic motor accurately. Furthermore, proposing a more effective method to distinguish the morphological feature between normal state and slight degradation will be the main work of our future research.

6. Conclusions

A method for fault feature extraction and degradation state identification based on MMS-PE is proposed in this paper, which is verified by the analysis of the actual test data. The conclusions can be drawn as follows:

(1)
The crack of piezoelectric ceramics in the ultrasonic motor can affect the vibration of the stator. As a result, the mathematical morphology of MEV generated from the monitor part changes. MMS components of the MEV signal can be used for fault feature extraction.
(2)
MMS-PE increases obviously with the deterioration of ceramics, and it is feasible to be taken as the fault feature of piezoelectric ceramics of the ultrasonic motor. The proposed sensitivity factor based on double sample Z value analysis can be used for parameter optimization of embedding dimension and time delay in the PE calculation to improve the discrimination of fault feature in different degradation states.
(3)
The PDD analysis based on MMS-PE is feasible to ensure the high accuracy of degradation state identification for piezoelectric ceramics of the ultrasonic motor. It is meaningful for the condition-based maintenance of the ultrasonic motor.

Conflicts of Interest

The authors declare that there are no conflicts of interests regarding the publication of this paper.

Acknowledgments

This project was supported by National Natural Science Foundation of China (Grant no. 51877070), China Postdoctoral Science Foundation (Grant no. 2017M623404), Natural Science Youth Foundation of Hebei (Grant no. E2017208086), and Science and Technology Research Youth Foundation for Hebei College (Grant no. QN2017329).

Open Research

Data Availability

The data are confidential for the reason that it comes from military research institute.

References

1 Stepanenko D. A. and Minchenya V. T., Development and study of novel non-contact ultrasonic motor based on principle of structural asymmetry, Ultrasonics. (2012) 52, no. 7, 866–872, https://doi.org/10.1016/j.ultras.2012.02.004, 2-s2.0-84863726663.
10.1016/j.ultras.2012.02.004
PubMed Web of Science® Google Scholar
2 Li X., Yao Z., Zhou S., Lv Q., and Liu Z., Dynamic modeling and characteristics analysis of a modal-independent linear ultrasonic motor, Ultrasonics. (2016) 72, 117–127, https://doi.org/10.1016/j.ultras.2016.07.018, 2-s2.0-84982803926.
10.1016/j.ultras.2016.07.018
PubMed Web of Science® Google Scholar
3 Zhou Y.-T. and Kim T.-W., A moving thermal dielectric crack in piezoelectric ceramics with a shearing force applied on its surface, Applied Mathematical Modelling. (2018) 63, no. 11, 1–17, https://doi.org/10.1016/j.apm.2018.06.016, 2-s2.0-85049484681.
10.1016/j.apm.2018.06.016
Web of Science® Google Scholar
4 Viun O., Komarov A., Lapusta Y., and Loboda V., A polling direction influence on fracture parameters of a limited permeable interface crack in a piezoelectric bi-material, Engineering Fracture Mechanics. (2018) 191, no. 15, 143–152, https://doi.org/10.1016/j.engfracmech.2018.01.024, 2-s2.0-85041552551.
10.1016/j.engfracmech.2018.01.024
Web of Science® Google Scholar
5 Zhao Y., Guo Y., Miao T., Zhao M., and Fan C., An iterative approach for analyzing cracks in two-dimensional piezoelectric media with exact boundary conditions, Engineering Analysis with Boundary Elements. (2018) 90, no. 5, 76–85, https://doi.org/10.1016/j.enganabound.2018.01.005, 2-s2.0-85042634195.
10.1016/j.enganabound.2018.01.005
Web of Science® Google Scholar
6 Heidari M. and Shateyi S., Wavelet support vector machine and multi-layer perceptron neural network with continues wavelet transform for fault diagnosis of gearboxes, Journal of Vibroengineering. (2017) 19, no. 1, 125–137, https://doi.org/10.21595/jve.2016.16813, 2-s2.0-85020380070.
10.21595/jve.2016.16813
Web of Science® Google Scholar
7 Wang D., Tsui K.-L., and Zhou Q., Novel Gauss-Hermite integration based Bayesian inference on optimal wavelet parameters for bearing fault diagnosis, Mechanical Systems and Signal Processing. (2016) 72-73, 80–91, https://doi.org/10.1016/j.ymssp.2015.11.018, 2-s2.0-84955514672.
10.1016/j.ymssp.2015.11.018
Web of Science® Google Scholar
8 Abdelkader R., Kaddour A., and Derouiche Z., Enhancement of rolling bearing fault diagnosis based on improvement of empirical mode decomposition denoising method, International Journal of Advanced Manufacturing Technology. (2018) 97, no. 5-8, 3099–3117, https://doi.org/10.1007/s00170-018-2167-7, 2-s2.0-85049242996.
10.1007/s00170-018-2167-7
Web of Science® Google Scholar
9 Yuan R., Lv Y., and Song G., Multi-fault diagnosis of rolling bearings via adaptive projection intrinsically transformed multivariate empirical mode decomposition and high order singular value decomposition, Sensors. (2018) 18, no. 4, https://doi.org/10.3390/s18041210, 2-s2.0-85045650243.
10.3390/s18041210
Web of Science® Google Scholar
10 Sun J., Li H., and Xu B., The morphological undecimated wavelet decomposition - discrete cosine transform composite spectrum fusion algorithm and its application on hydraulic pumps, Measurement. (2016) 94, no. 9, 794–805, https://doi.org/10.1016/j.measurement.2016.09.024, 2-s2.0-84991054916.
10.1016/j.measurement.2016.09.024
Web of Science® Google Scholar
11 Dong Y., Liao M., Zhang X., and Wang F., Faults diagnosis of rolling element bearings based on modified morphological method, Mechanical Systems and Signal Processing. (2011) 25, no. 4, 1276–1286, https://doi.org/10.1016/j.ymssp.2010.10.008, 2-s2.0-79952311306.
10.1016/j.ymssp.2010.10.008
Web of Science® Google Scholar
12 Yu D., Wang M., and Cheng X., A method for the compound fault diagnosis of gearboxes based on morphological component analysis, Measurement. (2016) 91, no. 9, 519–531, https://doi.org/10.1016/j.measurement.2016.05.087, 2-s2.0-84979529669.
10.1016/j.measurement.2016.05.087
Web of Science® Google Scholar
13 Yan X., Jia M., Zhang W., and Zhu L., Fault diagnosis of rolling element bearing using a new optimal scale morphology analysis method, ISA Transactions. (2018) 73, no. 2, 165–180, https://doi.org/10.1016/j.isatra.2018.01.004, 2-s2.0-85040236761.
10.1016/j.isatra.2018.01.004
PubMed Web of Science® Google Scholar
14 Chai M., Zhang Z., and Duan Q., A new qualitative acoustic emission parameter based on Shannon’s entropy for damage monitoring, Mechanical Systems and Signal Processing. (2017) 100, 617–629.
10.1016/j.ymssp.2017.08.007
Web of Science® Google Scholar
15 Yu D., Yang Y., and Cheng J., Application of time-frequency entropy method based on Hilbert-Huang transform to gear fault diagnosis, Measurement. (2007) 40, no. 9-10, 823–830, https://doi.org/10.1016/j.measurement.2007.03.004, 2-s2.0-34848863970.
10.1016/j.measurement.2007.03.004
Web of Science® Google Scholar
16 Nicolaou N. and Georgiou J., Detection of epileptic electroencephalogram based on permutation entropy and support vector machines, Expert Systems with Applications. (2012) 39, no. 1, 202–209, https://doi.org/10.1016/j.eswa.2011.07.008, 2-s2.0-81855221797.
10.1016/j.eswa.2011.07.008
Web of Science® Google Scholar
17 Frank B., Pompe B., Schneider U., and Hoyer D., Permutation entropy improves fetal behavioural state classification based on heart rate analysis from biomagnetic recordings in near term fetuses, Medical & Biological Engineering & Computing. (2006) 44, no. 3, 179–187, https://doi.org/10.1007/s11517-005-0015-z, 2-s2.0-33745473438.
10.1007/s11517-005-0015-z
CAS PubMed Web of Science® Google Scholar
18 Li Y., Zhang W., Xiong Q., Luo D., Mei G., and Zhang T., A rolling bearing fault diagnosis strategy based on improved multiscale permutation entropy and least squares SVM, Journal of Mechanical Science and Technology. (2017) 31, no. 6, 2711–2722, https://doi.org/10.1007/s12206-017-0514-5, 2-s2.0-85021199793.
10.1007/s12206-017-0514-5
Web of Science® Google Scholar
19 Liu Y., Long Q., Feng Z., and Liu W., Detection method for nonlinear and non-stationary signals, Journal of Vibration and Shock. (2007) 26, no. 12, 131–134.
Google Scholar
20 Lin Y.-H., Lee P.-C., and Chang T.-P., Practical expert diagnosis model based on the grey relational analysis technique, Expert Systems with Applications. (2009) 36, no. 2, 1523–1528, https://doi.org/10.1016/j.eswa.2007.11.046, 2-s2.0-56349108245.
10.1016/j.eswa.2007.11.046
Web of Science® Google Scholar
21 Li Y., Liang X., Yang Y., Xu M., and Huang W., Early Fault diagnosis of rotating machinery by combining differential rational spline-based LMD and K-L divergence, IEEE Transactions on Instrumentation and Measurement. (2017) 66, no. 11, 3077–3090, https://doi.org/10.1109/tim.2017.2664599, 2-s2.0-85016492788.
10.1109/TIM.2017.2664599
Web of Science® Google Scholar
22 Giantomassi A., Ferracuti F., Iarlori S., Ippoliti G., and Longhi S., Electric motor fault detection and diagnosis by kernel density estimation and kullback-Leibler divergence based on stator current measurements, IEEE Transactions on Industrial Electronics. (2015) 62, no. 3, 1770–1780, https://doi.org/10.1109/tie.2014.2370936, 2-s2.0-84923172290.
10.1109/TIE.2014.2370936
Web of Science® Google Scholar
23 Tian Z., Li H., Gu H., and Xu B., Degradation status identification of a hydraulic pump based on local characteristic-scale decomposition and JRD, Journal of Vibration and Shock. (2016) 35, no. 20, 54–59.
CAS Google Scholar
24 Li H., Wang Y., Wang B., Sun J., and Li Y., The application of a general mathematical morphological particle as a novel indicator for the performance degradation assessment of a bearing, Mechanical Systems and Signal Processing. (2017) 82, 490–502, https://doi.org/10.1016/j.ymssp.2016.05.038, 2-s2.0-84971597325.
10.1016/j.ymssp.2016.05.038
Web of Science® Google Scholar
25 Zhang K., Cheng J., and Yang Y., Fault diagnosis method of rotating machinery based on local mean decomposition and morphology spectrum, Journal of Vibration and Shock. (2013) 32, no. 9, 135–140.
Google Scholar
26 Wang Y., Li H., Wang B., and Xu B., Spatial Information Entropy and its application in the degradation state identification of hydraulic pump, Mathematical Problems in Engineering. (2015) 2015, 11, 532684, https://doi.org/10.1155/2015/532684, 2-s2.0-84945969920.
10.1155/2015/532684
Web of Science® Google Scholar
27 Liang Z., Li Y., and Xia S., Adaptive weighted learning for linear regression problems via Kullback-Leibler divergence, Pattern Recognition. (2013) 46, no. 4, 1209–1219, https://doi.org/10.1016/j.patcog.2012.10.017, 2-s2.0-84871271277.
10.1016/j.patcog.2012.10.017
Web of Science® Google Scholar
28 Yang Y., Zeng M., and Cheng J., Research on local characteristic-scale decomposition and its capacities, Journal of Vibration Engineering. (2012) 25, no. 5, 602–608.
Google Scholar
29 Sun J., Li H., and Xu B., Degradation feature extraction of the hydraulic pump based on high-frequency harmonic local characteristic-scale decomposition sub-signal separation and discrete cosine transform high-order singular entropy, Advances in Mechanical Engineering. (2013) 8, no. 7, 1–12.
Google Scholar
30 Yu H., Li H., and Xu B., Rolling bearing degradation state identification based on LCD relative spectral entropy, Journal of Failure Analysis and Prevention. (2016) 16, no. 4, 655–666, https://doi.org/10.1007/s11668-016-0133-y, 2-s2.0-84976385385.
10.1007/s11668-016-0133-y
Google Scholar

Citing Literature

All articles

Degradation State Identification of Cracked Ultrasonic Motor by Means of Fault Feature Extraction Method

Abstract

1. Introduction

2. MMS Components

3. MMS-PE

4. Degradation State Identification Based on PDD Analysis