Fault diagnosis of bearing based on variational mode decomposition (VMD)-phase space reconstruction (PSR)-singular value decomposition (SVD) and improved binary particle swarm optimization (IBPSO)-K-nearest neighbor (KNN) which is abbreviated as VPS-IBPSOKNN is presented in this study, among which VMD-PSR-SVD (VPS) is presented to obtain the features of the bearing vibration signal (BVS), and IBPSO is presented to select the parameter K of KNN. In IBPSO, the calculation of the next position of each particle is improved to fit the evolution of the particles. The traditional KNN with different parameter K and trained by the training samples with the features based on VMD-SVD (VS-KNN) can be used to compare with the proposed VPS-IBPSOKNN method. The experimental result demonstrates that fault diagnosis ability of bearing of VPS-IBPSOKNN is better than that of VS-KNN, and it can be concluded that fault diagnosis of bearing based on VPS-IBPSOKNN is effective.

1. Introduction

Defects of bearing can lead to serious damage for the entire mechanical system [1–4], so it is very important to study the reliable fault diagnosis method to prevent the bearing from malfunction [5–7]. The features of the bearing vibration signal (BVS) are key to the fault diagnosis results of bearing. Thus, in this study, variational mode decomposition (VMD)-phase space reconstruction (PSR)-singular value decomposition (SVD) which is abbreviated as VPS is presented to obtain the features of the BVS. VMD [8–10] can decompose the signal into a set of band-limited intrinsic mode functions (BLIMFs) with certain sparsity properties. In this study, the BVS can be decomposed into several BLIMFs by VMD. By PSR for BLIMFs of the BVS, the dynamic characteristics of BLIMFs of the BVS can be reflected.

K-nearest neighbor (KNN) classifier is a simple and reliable classification method [11]. KNN classifier is a multiclassification method, which can recognize the several states of bearing simultaneously. However, the selection of the parameter K of KNN has a certain influence on the classification performance of KNN. The improved binary particle swarm optimization (IBPSO) is presented to select the parameter K of KNN. In IBPSO, the calculation of the next position of each particle is improved to fit the evolution of the particles.

In this study, the hybrid method of VMD-PSR-SVD and IBPSO-KNN (VPS-IBPSOKNN) is presented for fault diagnosis of bearing. The traditional KNN with different parameter K and trained by the training samples with the features based on VMD-SVD can be used to compare with the proposed VPS-IBPSOKNN method. The experimental result demonstrates that fault diagnosis ability of bearing of VPS-IBPSOKNN is better than that of VS-KNN.

2. K-Nearest Neighbor Classifier

In the KNN classifier, for a new sample to be classified, its distance to each sample in the sampling set must be computed, and the new sample is classified to the class that contains the most samples from this set of closest K instances [12, 13].

The Euclidean distance approach is employed in the KNN model in this study, and the Euclidean distance between two samples Z₁ = (z₁₁, z₁₂, …, z_1L) and Z₂ = (z₂₁, z₂₂, …, z_2L) is described as follows:

\begin{matrix} Dist (Z_{1}, Z_{2}) = \sqrt{\sum_{l = 1}^{L} {(z_{1 l} - z_{2 l})}^{2}} . \end{matrix}

()

KNN classifier is a multiclassification method, which can recognize the several states of bearing simultaneously.

3. Variational Mode Decomposition

The signal f(t) can be decomposed into a set of band-limited intrinsic mode functions (BLIMFs) u_g(t) with certain sparsity properties by VMD [8,14–16], and VMD can be used to decompose the signal f(t) into a set of BLIMFs u_g(t) around the center frequencies ω_g according to the following constrained optimization formula:

\begin{matrix} \min_{\{u_{g}\}, \{ω_{g}\}} \{\sum_{g = 1}^{G} {‖\partial_{t} [(δ (t) + \frac{j}{π t}) * u_{g} (t)] e^{- j ω_{g} t}‖}_{2}^{2}\}, \\ subject to \sum_{g = 1}^{G} u_{g} (t) = f (t), \end{matrix}

()

where f(t) denotes the time series signal, u_g(t) denotes the decomposed BLIMF, ω_g denotes the center frequency of BLIMF, G denotes the number of BLIMFs, δ(t) denotes the Dirac distribution, and ^∗denotes the convolution operator.

The minimization problem in equation (2) is transformed into the unconstrained optimization problem:

\begin{matrix} L (\{u_{g}\}, \{ω_{g}\}, λ) = a {\sum_{g = 1}^{G} ‖\partial_{t} [(δ (t) + \frac{j}{π t}) * u_{g} (t)] e^{- j ω_{g} t}‖}_{2}^{2} + {‖f (t) - \sum_{g = 1}^{G} u_{g} (t)‖}_{2}^{2} + 〈λ (t), f (t) - \sum_{g = 1}^{G} u_{g} (t)〉, \end{matrix}

()

where a denotes the data fidelity constraint factor, and λ(t) denotes the Lagrangian multiplier.

4. Feature Extraction of BVS Based on VPS

In this study, the BVS is decomposed into four BLIMFs by VMD. Assuming the data set of the qth BLIMF is described as b_q,1, b_q,2, …, b_q,n, (q = 1,2,3,4) and defining m as embedding space dimension and τ as time delay, the PSR signal of the qth BLIMF is given as follows:

\begin{matrix} Y_{q} = [\begin{matrix} b_{q, 1} & b_{q, 2} & \dots & b_{q, n - (m - 1) \times τ} \\ b_{q, 1 + τ} & b_{q, 2 + τ} & \dots & b_{q, n - (m - 2) \times τ} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ b_{q, 1 + (m - 1) \times τ} & b_{q, 2 + (m - 1) \times τ} & \dots & b_{q, n} \end{matrix}] . \end{matrix}

()

SVD for matrix Y_q which is the PSR signal of the qth BLIMF can be performed, and define h_q,1, h_q,2, …, h_q,R(R = min{m, n − (m − 1) × τ}) as the singular values of the matrix Y_q, h_q,r ≥ 0 (q = 1,2,3,4; r = 1,2, …, R).

The singular values of the PSR signals of the four BLIMFs of the BVS constitute a vector as [h_1,1 ⋯ h_1,R h_2,1 ⋯ h_2,R h_3,1 ⋯ h_3,R h_4,1 ⋯ h_4,R]. By calculating the relative values of the elements in the vector as follows: ${\overset{\land}{h}}_{q, r} = h_{q, r} / (\sum_{q = 1}^{4} \sum_{r = 1}^{R} h_{q, r})$ , the features of the BVS based on VPS are described as $[{\overset{\land}{h}}_{1,1} \dots {\overset{\land}{h}}_{1, R} {\overset{\land}{h}}_{2,1} \dots {\overset{\land}{h}}_{2, R} {\overset{\land}{h}}_{3,1} \dots {\overset{\land}{h}}_{3, R} {\overset{\land}{h}}_{4,1} \dots {\overset{\land}{h}}_{4, R}]$ . When m is less than or equal to n − (m − 1) × τ, the features of the BVS based on VPS can be described as $[{\overset{\land}{h}}_{1,1} \dots {\overset{\land}{h}}_{1, m} {\overset{\land}{h}}_{2,1} \dots {\overset{\land}{h}}_{2, m} {\overset{\land}{h}}_{3,1} \dots {\overset{\land}{h}}_{3, m} {\overset{\land}{h}}_{4,1} \dots {\overset{\land}{h}}_{4, m}]$ .

5. Parameter Optimization of KNN Based on IBPSO

In binary particle swarm optimization (BPSO), solutions are encoded as binary vectors, the position of the ith particle is defined by the following vector:

\begin{matrix} x_{i} = (p_{i}^{1}, p_{i}^{2}, \dots, p_{i}^{D}), i = 1,2, \dots, E, \end{matrix}

()

where

p_{i}^{d} (d = 1,2, \dots, D)

denotes the position of particle i in the dth dimension and E denotes the number of the particles.

In traditional BPSO [17, 18], the next position of each particle is calculated according to the following formula:

\begin{matrix} S (v_{i}^{d} (t + 1)) = \frac{1}{1 + \exp (- v_{i}^{d} (t + 1))}, \\ p_{i}^{d} (t + 1) = \{\begin{cases} 1 & rand < S (v_{i}^{d} (t + 1)), \\ 0 & rand \geq S (v_{i}^{d} (t + 1)), \end{cases} \end{matrix}

()

where t denotes the iteration counter,

v_{i}^{d} (t + 1)

denotes the ith particle’s velocity at the (t + 1)th iteration in the dth dimension,

p_{i}^{d} (t + 1)

denotes the ith particle’s position at the (t + 1)th iteration in the dth dimension, and rand denotes the random value in the range of 0∼1.

In this study, the parameter K of the KNN model is selected by IBPSO, and $VT (v_{i}^{d} (t + 1))$ is employed as transform function to fit the evolution of the particles instead of $S (v_{i}^{d} (t + 1))$ in IBPSO.

Thus, in IBPSO, the next position of each particle is calculated as follows:

\begin{matrix} VT (v_{i}^{d} (t + 1)) = |\tanh (v_{i}^{d} (t + 1))|, \end{matrix}

()

\begin{matrix} p_{i}^{d} (t + 1) = \{\begin{cases} {\tilde{p}}_{i}^{d} (t) & rand < VT (v_{i}^{d} (t + 1)), \\ p_{i}^{d} (t) & rand \geq VT (v_{i}^{d} (t + 1)), \end{cases} \end{matrix}

()

where

{\tilde{p}}_{i}^{d} (t)

denotes the complement of

p_{i}^{d} (t)

, rand denotes the random value in the range of 0∼1, and the maximum value of

|v_{i}^{d} (t + 1)|

is set to 6 here.

Figure 1 shows the process of the selection of the parameter K of KNN by IBPSO, which can be described in detail as follows:

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The process of the selection of the parameter K of KNN by IBPSO.

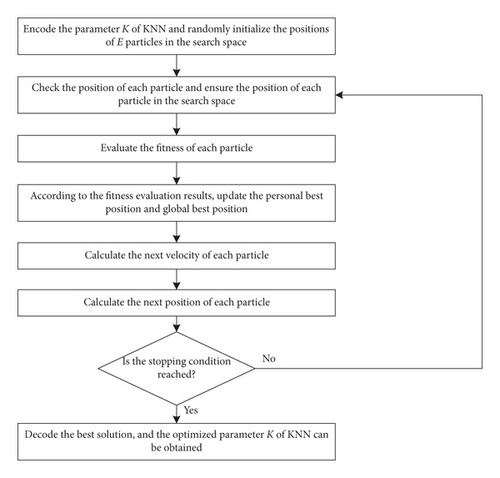
Step 1. Encode the parameter K of KNN and randomly initialize the positions of E particles in the search space.

As shown in Table 1, the binary code string represents the parameter K of KNN, and D denotes the length of binary code string representing the parameter K.

Table 1. Encoding the parameter K of KNN.

K
$p_{i}^{1}$	…	$p_{i}^{D}$

Step 2. Check the position of each particle and ensure the position of each particle in the search space.

Check the binary codes representing the parameter K of KNN and ensure that one of the binary codes representing the parameter K of each particle is “1” at least.

Step 3. Evaluate the fitness of each particle.

J-fold cross validation is employed in the process of evaluating the fitness of each particle. Divide the training samples equally into J subsets of the samples, among which J − 1 subsets of the samples are employed to train the KNN model, and the remaining subset is used to test the KNN model. Each subset can be employed as the testing subset. Then, the total diagnosis accuracy A_i of the J subsets of the samples can be obtained as A_i = N_correct/N_total, where N_total denotes the total number of the J subsets of the samples, N_correct denotes the total number of the J subsets of the samples with correct diagnosis, and J is set to 5 here.

Here, the fitness of the ith particle is defined as follows:

\begin{matrix} {fit}_{i} = 1 - A_{i} . \end{matrix}

()

Step 4. According to the fitness evaluation results, update the personal best position and global best position.

Step 5. Calculate the next velocity of each particle.

Each particle flies toward a new position by the velocity calculated as follows:

\begin{matrix} v_{i}^{d} (t + 1) = w \cdot v_{i}^{d} (t) + c_{1} \cdot rand \cdot ({Pbest}_{i}^{d} (t) - p_{i}^{d} (t)) + c_{2} \cdot rand \cdot ({Gbest}^{d} (t) - p_{i}^{d} (t)), \end{matrix}

()

where w denotes the inertia weight; rand denotes the random value in the range of 0∼1; the positive constants c₁ and c₂ denote personal learning factor and social learning factor, respectively;

{Pbest}_{i}^{d}

denotes the personal best position of particle i in the dth dimension; and Gbest^d denotes the global best position of the swarm in the dth dimension.

Step 6. Calculate the next position of each particle.

In this study, instead of the traditional calculation method of the next position of each particle, the next position of each particle is calculated according to equations (7) and (8).

Step 7. The same procedures from Step 2 to Step 6 are repeated until the stopping condition is reached.

Step 8. Decode the best solution, and the optimized parameter K of KNN can be obtained.

6. Experimental Analysis

The bearing vibration data are employed from “bearings vibration data set” of Case Western Reserve University in the experiment [19], and the fault data used here are collected under the condition of single point faults with fault diameter of 0.014 inches. Three groups of samples are derived from BVSs acquired under three different loads, among which the samples are obtained based on BVS acquired under 1 HP motor load in group 1, the samples are obtained based on BVS acquired under 2 HP motor load in group 2, and the samples are obtained based on BVS acquired under 3 HP motor load in group 3. Each group includes 300 samples, among which 75 samples represent normal state, 75 samples represent inner race (IR) fault, 75 samples represent outer race (OR) fault, and 75 samples represent ball fault.

The first 50 samples of each state in each group are employed as the training samples, and the remaining 25 samples of each state in each group are employed as the testing samples. Thus, the training samples include 600 samples, among which 150 samples represent normal state, 150 samples represent IR fault, 150 samples represent OR fault, and 150 samples represent ball fault; the testing samples include 300 samples, among which 75 samples represent normal state, 75 samples represent IR fault, 75 samples represent OR fault, and 75 samples represent ball fault.

Each BVS is decomposed into four BLIMFs by VMD. The four BLIMFs of one of the samples representing normal state in group 2 are shown in Figure 2.

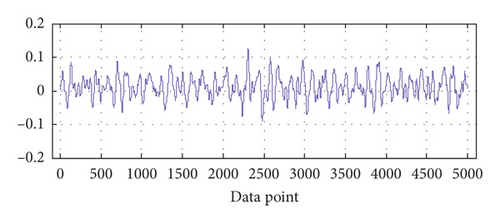
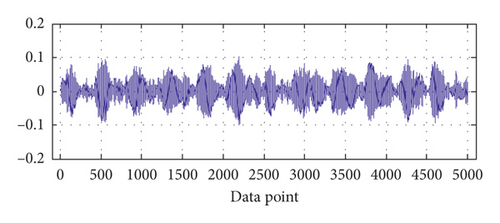
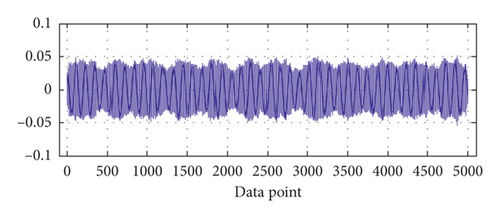
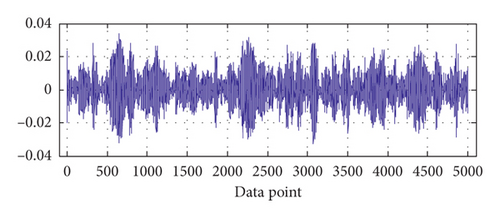
Here, m (embedding space dimension) is set to 5, and τ (time delay) is set to 3; it is obvious that m is less than n − (m − 1) × τ. Thus, the features of the BVS based on VMD-PSR-SVD can be described as $[{\overset{\land}{h}}_{1,1} \dots {\overset{\land}{h}}_{1,5} {\overset{\land}{h}}_{2,1} \dots {\overset{\land}{h}}_{2,5} {\overset{\land}{h}}_{3,1} \dots {\overset{\land}{h}}_{3,5} {\overset{\land}{h}}_{4,1} \dots {\overset{\land}{h}}_{4,5}]$ .

In this study, the parameter K of KNN is selected by IBPSO. The value range of the parameter K is [1, 2⁴ − 1], and the adjacent values’ intervals of the parameter K are 1, thus, the length of binary code string representing the parameter K is 4.

The traditional KNN with different parameter K and trained by the training samples with the features based on VMD-SVD can be used to compare with the proposed VPS-IBPSOKNN method. Here, the value range of the parameter K is [1, 2⁴ − 1], and the intervals of the adjacent values of the parameter K are 1.

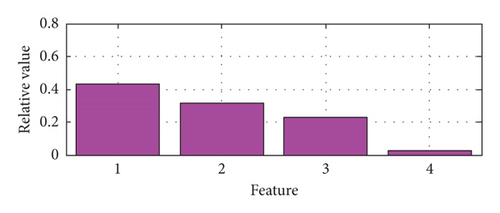
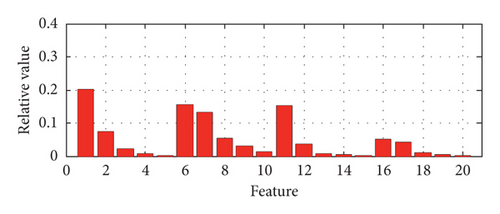
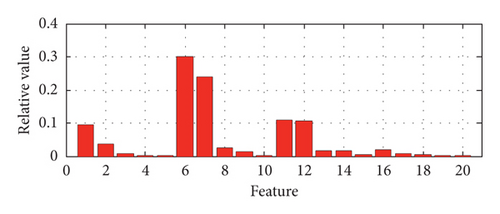
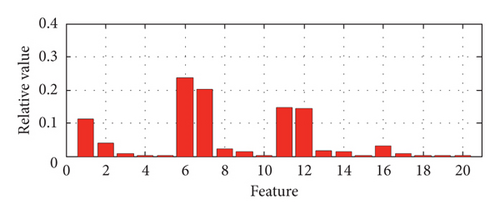
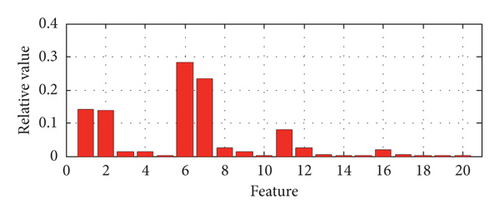
The relative singular values of the matrix composed of the four BLIMFs are obtained as the features of the BVS in the feature extraction method of the BVS based on VMD-SVD. The features of a set of samples with different states including normal state, IR fault, OR fault, and ball fault based on VMD-SVD are shown in Figure 3. For the same samples as above, their features based on VMD-PSR-SVD are shown in Figure 4.

The diagnosis accuracy (DA) which is used to evaluate the performance of the diagnosis models is expressed as follows:

\begin{matrix} DA = \frac{Ψ_{correct}}{Ψ_{total}} \times 100 %, \end{matrix}

()

where Ψ_total is the number of testing samples and Ψ_correct is the number of testing samples with correct diagnosis in the case.

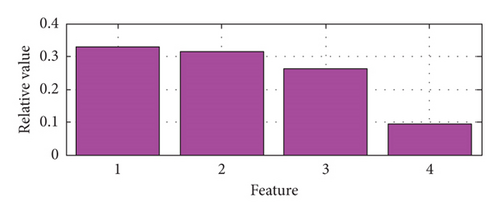
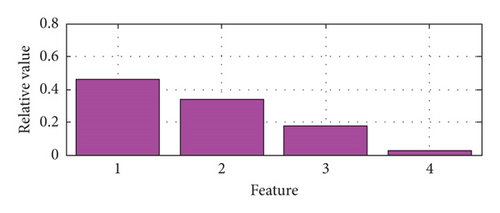
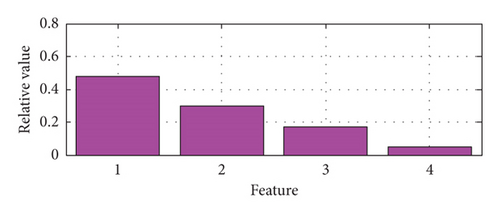
As shown in Table 2, the number of testing samples with correct diagnosis of VPS-IBPSOKNN is 295, and the diagnosis accuracy of VPS-IBPSOKNN is 98.33%; the number of testing samples with correct diagnosis among the 15 VS-KNN models (K = 1∼15) is at most 280, and the best diagnosis accuracy among the 15 VS-KNN models (K = 1∼15) is 93.33% in this case. It can be seen that fault diagnosis ability of bearing of VPS-IBPSOKNN is better than that of VS-KNN.

Table 2. The comparison of the diagnosis accuracy of bearing between VPS-IBPSOKNN and VS-KNN

The number of training samples	The number of testing samples	Diagnosis method	The number of testing samples with correct diagnosis	Diagnosis accuracy (%)
600	300	VPS-IBPSOKNN	295	98.33
		VS-KNN (K = 1)	268	89.33
		VS-KNN (K = 2)	269	89.67
		VS-KNN (K = 3)	278	92.67
		VS-KNN (K = 4)	277	92.33
		VS-KNN (K = 5)	280	93.33
		VS-KNN (K = 6)	278	92.67
		VS-KNN (K = 7)	279	93.00
		VS-KNN (K = 8)	278	92.67
		VS-KNN (K = 9)	278	92.67
		VS-KNN (K = 10)	278	92.67
		VS-KNN (K = 11)	277	92.33
		VS-KNN (K = 12)	278	92.67
		VS-KNN (K = 13)	277	92.33
		VS-KNN (K = 14)	276	92.00
		VS-KNN (K = 15)	273	91.00

7. Conclusion

The VPS-IBPSOKNN method for fault diagnosis of bearing is presented in this study. VPS is presented to obtain the features of the BVS, among which VMD is employed to decompose the BVS into several BLIMFs, and by PSR for BLIMFs of the BVS, the dynamic characteristics of BLIMFs of the BVS can be reflected. IBPSO is presented to select the parameter K of KNN, and in IBPSO, the calculation of the next position of each particle is improved to fit the evolution of the particles. The experimental result demonstrates that fault diagnosis ability of bearing of VPS-IBPSOKNN is better than that of VS-KNN, and it can be concluded that fault diagnosis of bearing based on VPS-IBPSOKNN is effective.

Conflicts of Interest

The author declares that there are no conflicts of interest.

Acknowledgments

This project is supported by the Fundamental Research Funds for the Central Universities (no. 2232017D-14).

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Glowacz A., Fault diagnosis of single-phase induction motor based on acoustic signals, Mechanical Systems and Signal Processing. (2019) 117, 65–80, https://doi.org/10.1016/j.ymssp.2018.07.044.
10.1016/j.ymssp.2018.07.044
Web of Science® Google Scholar
2 Chen Y. H., Peng G. L., Xie C. H., Zhang W., Li C. H., and Liu S. H., ACDIN: bridging the gap between artificial and real bearing damages for bearing fault diagnosis, Neurocomputing. (2018) 294, 61–71, https://doi.org/10.1016/j.neucom.2018.03.014, 2-s2.0-85044327325.
10.1016/j.neucom.2018.03.014
Web of Science® Google Scholar
3 Zhang X., Liu Z. W., Miao Q., and Wang L., Bearing fault diagnosis using a whale optimization algorithm-optimized orthogonal matching pursuit with a combined time-frequency atom dictionary, Mechanical Systems and Signal Processing. (2018) 107, 29–42, https://doi.org/10.1016/j.ymssp.2018.01.027, 2-s2.0-85042106369.
10.1016/j.ymssp.2018.01.027
Web of Science® Google Scholar
4 Cheng Y., Zhou N., Zhang W. H., and Wang Z. W., Application of an improved minimum entropy deconvolution method for railway rolling element bearing fault diagnosis, Journal of Sound and Vibration. (2018) 425, 53–69, https://doi.org/10.1016/j.jsv.2018.01.023, 2-s2.0-85045063477.
10.1016/j.jsv.2018.01.023
Web of Science® Google Scholar
5 Zhang W., Li C. H., Peng G. L., Chen Y. H., and Zhang Z. J., A deep convolutional neural network with new training methods for bearing fault diagnosis under noisy environment and different working load, Mechanical Systems and Signal Processing. (2018) 100, 439–453, https://doi.org/10.1016/j.ymssp.2017.06.022, 2-s2.0-85028727944.
10.1016/j.ymssp.2017.06.022
Web of Science® Google Scholar
6 Lu S. L., He Q. B., and Zhao J. W., Bearing fault diagnosis of a permanent magnet synchronous motor via a fast and online order analysis method in an embedded system, Mechanical Systems and Signal Processing. (2018) 113, 36–49, https://doi.org/10.1016/j.ymssp.2017.02.046, 2-s2.0-85015262003.
10.1016/j.ymssp.2017.02.046
Web of Science® Google Scholar
7 Xin G., Hamzaoui N., and Antoni J., Semi-automated diagnosis of bearing faults based on a hidden Markov model of the vibration signals, Measurement. (2018) 127, 141–166, https://doi.org/10.1016/j.measurement.2018.05.040, 2-s2.0-85048511670.
10.1016/j.measurement.2018.05.040
Web of Science® Google Scholar
8 Upadhyay A., Sharma M., and Pachori R. B., Determination of instantaneous fundamental frequency of speech signals using variational mode decomposition, Computers & Electrical Engineering. (2017) 62, 630–647, https://doi.org/10.1016/j.compeleceng.2017.04.027, 2-s2.0-85019365745.
10.1016/j.compeleceng.2017.04.027
Web of Science® Google Scholar
9 Xiao Q. Y., Li J., Sun J. D., Feng H., and Jin S. J., Natural-gas pipeline leak location using variational mode decomposition analysis and cross-time-frequency spectrum, Measurement. (2018) 124, 163–172, https://doi.org/10.1016/j.measurement.2018.04.030, 2-s2.0-85045441184.
10.1016/j.measurement.2018.04.030
Web of Science® Google Scholar
10 Jianwei E., Bao Y. L., and Ye J. M., Crude oil price analysis and forecasting based on variational mode decomposition and independent component analysis, Physica A: Statistical Mechanics and its Applications. (2017) 484, 412–427, https://doi.org/10.1016/j.physa.2017.04.160, 2-s2.0-85019939875.
10.1016/j.physa.2017.04.160
Web of Science® Google Scholar
11 Glowacz A. and Glowacz Z., Recognition of images of finger skin with application of histogram, image filtration and K-NN classifier, Biocybernetics and Biomedical Engineering. (2016) 36, no. 1, 95–101, https://doi.org/10.1016/j.bbe.2015.12.005, 2-s2.0-84957848982.
10.1016/j.bbe.2015.12.005
Web of Science® Google Scholar
12 Li F., Wang J. X., Tang B. P., and Tian D. Q., Life grade recognition method based on supervised uncorrelated orthogonal locality preserving projection and K-nearest neighbor classifier, Neurocomputing. (2014) 138, 271–282, https://doi.org/10.1016/j.neucom.2014.01.037, 2-s2.0-84899736273.
10.1016/j.neucom.2014.01.037
Web of Science® Google Scholar
13 Saini I., Singh D., and Khosla A., QRS detection using K-Nearest Neighbor algorithm (KNN) and evaluation on standard ECG databases, Journal of Advanced Research. (2013) 4, no. 4, 331–344, https://doi.org/10.1016/j.jare.2012.05.007, 2-s2.0-84884704150.
10.1016/j.jare.2012.05.007
PubMed Google Scholar
14 Sahani M. and Dash P. K., Variational mode decomposition and weighted online sequential extreme learning machine for power quality event patterns recognition, Neurocomputing. (2018) 310, 10–27, https://doi.org/10.1016/j.neucom.2018.03.056, 2-s2.0-85048577861.
10.1016/j.neucom.2018.03.056
Web of Science® Google Scholar
15 Maji U., Mitra M., and Pal S., Characterization of cardiac arrhythmias by variational mode decomposition technique, Biocybernetics and Biomedical Engineering. (2017) 37, no. 3, 578–589, https://doi.org/10.1016/j.bbe.2017.04.007, 2-s2.0-85021630559.
10.1016/j.bbe.2017.04.007
Web of Science® Google Scholar
16 Zhang M., Jiang Z. N., and Feng K., Research on variational mode decomposition in rolling bearings fault diagnosis of the multistage centrifugal pump, Mechanical Systems and Signal Processing. (2017) 93, 460–493, https://doi.org/10.1016/j.ymssp.2017.02.013, 2-s2.0-85015345572.
10.1016/j.ymssp.2017.02.013
Web of Science® Google Scholar
17 Chatterjee A., Tudu B., and Paul K. C., Towards optimized binary pattern generation for grayscale digital halftoning: a binary particle swarm optimization (BPSO) approach, Journal of Visual Communication and Image Representation. (2012) 23, no. 8, 1245–1259, https://doi.org/10.1016/j.jvcir.2012.09.001, 2-s2.0-84868124412.
10.1016/j.jvcir.2012.09.001
Web of Science® Google Scholar
18 Pookpunt S. and Ongsakul W., Optimal placement of wind turbines within wind farm using binary particle swarm optimization with time-varying acceleration coefficients, Renewable Energy. (2013) 55, 266–276, https://doi.org/10.1016/j.renene.2012.12.005, 2-s2.0-84872894121.
10.1016/j.renene.2012.12.005
Web of Science® Google Scholar
19 Loparo K. A., Bearings Vibration Data Set, 2003, Case Western Reserve University, Cleveland, OH, USA.
Google Scholar

Citing Literature

All articles

The Hybrid Method of VMD-PSR-SVD and Improved Binary PSO-KNN for Fault Diagnosis of Bearing

Abstract

1. Introduction

2. K-Nearest Neighbor Classifier

3. Variational Mode Decomposition

4. Feature Extraction of BVS Based on VPS

5. Parameter Optimization of KNN Based on IBPSO

6. Experimental Analysis

7. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

The Hybrid Method of VMD-PSR-SVD and Improved Binary PSO-KNN for Fault Diagnosis of Bearing

Abstract

1. Introduction

2. K-Nearest Neighbor Classifier

3. Variational Mode Decomposition

4. Feature Extraction of BVS Based on VPS

5. Parameter Optimization of KNN Based on IBPSO

6. Experimental Analysis

7. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information