Electronic Structure, Spectroscopic (IR, Raman, UV-Vis, NMR), Optoelectronic, and NLO Properties Investigations of Rubescin E (C31H36O7) Molecule in Gas Phase and Chloroform Solution Using Ab Initio and DFT Methods
Abstract
Quantum chemical methods were used to study the electronic structure and some physicochemical properties of Rubescin E molecule. Good agreement with experiment was found for 3JH-H coupling constant, IR, 1H NMR, and 13C NMR. The excitation energy and oscillator strength calculated by TD-DFT also complement with experiment. Large values were obtained for dipole moment, polarizability, first static hyperpolarizability, electric susceptibility, refractive index, and dielectric constant, meaning that Rubescin E has strong optical and phonon application and can be a good candidate as NLOs material. The 3D analysis of the title molecule leads us to the conclusion that electron can easily be transferred from furan to tetrahydrofuran ring. The global reactivity descriptors were evaluated. Mulliken, ESP, and NBO charges comparisons were carried out and described.
1. Introduction
Many molecules from plant research were found nowadays to have application in the field of medicine, where there are use for the treatment of many diseases among which we found malaria caused by plasmodium falciparum. The new limonoid name Rubescin E (C31H36O7), extracted from the roots of Trichilia Rubescens, collected from Cameroon, has been evaluated against erythrocytic stages of strain 3D7 plasmodium falciparum and also exhibited significant antiplasmodial in vitro activity with IC50 value of 1.13μM [1]. The FT-IR performed on Rubescin E molecule revealed the presence of α, β-unsaturated carbonyl moiety at 1720 cm−1 and 1664 cm−1. These values can be obtained theoretically by performing the vibrational frequencies calculation on the title molecule and used to explain the different motion of atoms or group of atoms in a molecular system. The 1D (1H, 13C NMR) and 2D NMR spectra were run on a Bruker AV spectrometer [1] in order to predict the structure of the title molecule and were done in this work in order to take out similarities between experiment done previously and theoretical calculation performed here.
In this work, quantum chemical calculation was performed in order to take out the electronic structure (energy gap, charge distributions, NLO properties, vibrational frequencies, NMR, and UV-vis calculation) and some physicochemical properties ( 3JH-H chemical coupling-coupling constant, the global reactivity descriptors, and some geometrical parameters such as bonds lengths and bonds angles) of Rubescin E molecule. To the best of our knowledge, no theoretical study was performed yet on the title molecule, that is what motivated us to investigate the electronic structure, the spectroscopic, and some physicochemical properties of Rubescin E molecule. Except for NMR, UV-vis, 3JH-H chemical coupling-coupling constant, and the vibrational frequencies obtained for the two α, β-unsaturated carbonyl moiety, most of our results were not compared and we are optimistic that it can be used as threshold for future experimental or theoretical research. Hartree Fock and DFT (using B3LYP and B3PW91 functionals) methods were used for these purposes. These properties were calculated by employing the triple split valence basis set along with polarization functions with and without diffuse functions as implemented in Gaussian 09, Rev. A02 in both gas phase and in a solution of chloroform. The methods and basis sets used are among the most widely used [2–5] and provide excellent results which are generally very close to experiments [6–8].
2. Computational Methods
Theoretical calculations were performed on Rubescin E using HF and DFT methods at the B3LYP and B3PW91 levels as implemented in Gaussian 09W code [9]. All these calculations were done in gas phase and in a solution of chloroform. No geometry restriction was applied during the optimization procedure. The solvent effects were treated within the conductor-like polarizable continuum model (CPCM). For the geometry optimization, the 6-311G(d,p) and 6-311++G(d,p) basis set were used in both gas and solvent. Convergence criteria in which both the maximum force and displacement are smaller than the cut-off of 0.000015 and 0.000060 and RMS force and displacement less than the cut-off values of 0.000010 and 0.000040 were used in the calculations in order to increase the accuracy of our results. The chemical 3JH-H proton-proton coupling constant function of angle between two C-H vectors was calculated from the optimization output using the original Karplus equation [10]. The optimized form of our molecule was then used to determine the global reactivity descriptors, electronic and NLOs properties. The net charges were also evaluated using MPA, ESP, and NBOs methods at the three levels mentioned above, and all this was done in both gas phase and chloroform with the 6-311++G(d,p) basis set. In order to confirm the stability of our molecule, the vibrational frequencies (IR and Raman) were evaluated at the 6-311G(d,p) and no imaginary frequencies were found leading us to the results that our molecule was stable at the levels and basis set considered. The time dependent density functional theory (TD-DFT) field was used in gas phase with the 6-311++G(d,p) basis in order to understand the electronic transition of our molecule and the obtained results were compared to experiment. The GIAO (gauge independent atomic orbital) method was used on the optimized form of our molecule in a solution of chloroform to determine the 1H and 13C NMR spectra parameters at the three levels and with the 6-311++G(d,p) basis set. In order to compare the calculated values of 1H and 13C chemical shift with experimental results, the reference and widely used molecule TMS (tetramethylsilane) for this purpose were exploited at the same level, at the same phase, and with the same basis set.
3. Results and Discussion
3.1. Optimized Structure
The optimized geometry of Rubescin E obtained using the B3LYP/6-311++G(d,p) method in chloroform is shown in Figure 1. The value of the total electronic energy of the molecule obtained at the B3LYP shows that Figure 1 is the most stable structure of the molecule. The total electronic energy calculated within the two methods in gas and in a solution of chloroform with the 6-311++G(d,p) is given in Table 1.
| Levels | RHF | B3LYP | B3PW91 | Theory a[11], b[12], c[13] | |||
|---|---|---|---|---|---|---|---|
| Basis set | Gaz | CDCl3 | Gaz | CDCl3 | Gaz | CDCl3 | |
| Bond length | |||||||
| R1 (C1-C2) | 1.5503 | 1.5490 | 1.5603 | 1.5583 | 1.5521 | 1.5500 | |
| R2 (C1-C3) | 1.5698 | 1.5672 | 1.5811 | 1.5777 | 1.5719 | 1.5684 | |
| R3 (C1-C20) | 1.5167 | 1.5157 | 1.5221 | 1.5215 | 1.5153 | 1.5147 | |
| R4 (C1-C22) | 1.5474 | 1.5481 | 1.5510 | 1.5509 | 1.5439 | 1.5438 | |
| R5 (C2=O7) | 1.1900 | 1.1948 | 1.2167 | 1.2213 | 1.2152 | 1.2197 | 2.10b |
| R6 (C2-C34) | 1.5041 | 1.4992 | 1.4966 | 1.4910 | 1.4920 | 1.4867 | |
| R7 (C3-C4) | 1.5898 | 1.5887 | 1.5973 | 1.5968 | 1.5866 | 1.5860 | |
| R8 (C3-C40) | 1.4814 | 1.4800 | 1.4972 | 1.4958 | 1.4931 | 1.4918 | 1.462b |
| R9 (C3-O59) | 1.3994 | 1.4024 | 1.4311 | 1.4335 | 1.4236 | 1.4256 | 1.428b |
| R10 (C4-C5) | 1.5515 | 1.5518 | 1.5549 | 1.5548 | 1.5473 | 1.5471 | |
| R11 (C4-C12) | 1.5707 | 1.5733 | 1.5756 | 1.5787 | 1.5676 | 1.5707 | |
| R12 (C4-C36) | 1.5501 | 1.5503 | 1.5543 | 1.5543 | 1.5471 | 1.5472 | |
| R13 (C5-C6) | 1.5428 | 1.5442 | 1.5477 | 1.5487 | 1.5401 | 1.5410 | |
| R14 (C5-C46) | 1.4556 | 1.4553 | 1.4720 | 1.4717 | 1.4686 | 1.4684 | 1.462b |
| R15 (C5-O61) | 1.4206 | 1.4235 | 1.4568 | 1.4590 | 1.4473 | 1.4492 | 1.428b |
| R16 (C6-C26) | 1.5259 | 1.5260 | 1.5306 | 1.5307 | 1.5246 | 1.5248 | |
| R17 (C6-C42) | 1.5352 | 1.5350 | 1.5373 | 1.5373 | 1.5298 | 1.5298 | |
| R18 (C6-C51) | 1.5703 | 1.5708 | 1.5810 | 1.5814 | 1.5724 | 1.5728 | |
| R19 (C8-C16) | 1.5423 | 1.5424 | 1.5477 | 1.5481 | 1.5405 | 1.5408 | |
| R20 (C8-C20) | 1.5256 | 1.5244 | 1.5348 | 1.5335 | 1.5276 | 1.5264 | 1.536c |
| R21 (C8-C29) | 1.5405 | 1.5402 | 1.5479 | 1.5468 | 1.5416 | 1.5406 | 1.536c |
| R22 (C8-C32) | 1.5036 | 1.5036 | 1.5010 | 1.5010 | 1.4958 | 1.4960 | |
| R23 (C9-O11) | 1.4120 | 1.4133 | 1.4389 | 1.4411 | 1.4304 | 1.4324 | 1.428c |
| R24 (C9-C12) | 1.5288 | 1.5302 | 1.5357 | 1.5373 | 1.5311 | 1.5329 | |
| R25 (C9-C20) | 1.4997 | 1.4993 | 1.5044 | 1.5042 | 1.4999 | 1.4998 | 1.536c |
| R26 (O11-C29) | 1.4261 | 1.4287 | 1.4530 | 1.4551 | 1.4438 | 1.4457 | 1.428c |
| R27 (C12-O60) | 1.4104 | 1.4131 | 1.4339 | 1.4369 | 1.4255 | 1.4283 | |
| R28 (C14-C51) | 1.5035 | 1.5041 | 1.5003 | 1.5010 | 1.4953 | 1.4959 | |
| R29 (C14-C53) | 1.4493 | 1.4505 | 1.4428 | 1.4438 | 1.4387 | 1.4397 | 1.430a |
| R30 (C14=C57) | 1.3411 | 1.3410 | 1.3621 | 1.3619 | 1.3614 | 1.3614 | 1.364a |
| R31 (O15-C55) | 1.3382 | 1.3412 | 1.3609 | 1.3638 | 1.3548 | 1.3574 | 1.364a |
| R32 (O15-C57) | 1.3467 | 1.3496 | 1.3659 | 1.3686 | 1.3592 | 1.3616 | 1.364a |
| R33 (C26-C40) | 1.5162 | 1.5158 | 1.5190 | 1.5181 | 1.5137 | 1.5129 | |
| R34 (C32=C34) | 1.3270 | 1.3285 | 1.3431 | 1.3445 | 1.3422 | 1.3436 | |
| R35 (C40-O59) | 1.4010 | 1.4054 | 1.4353 | 1.4395 | 1.4282 | 1.4320 | 1.428b |
| R36 (C46-C48) | 1.5086 | 1.5076 | 1.5135 | 1.5123 | 1.5088 | 1.5077 | |
| R37 (C46-O61) | 1.4005 | 1.4051 | 1.4326 | 1.4376 | 1.4254 | 1.4297 | 1.428b |
| R38 (C48-C51) | 1.5407 | 1.5405 | 1.5478 | 1.5475 | 1.5408 | 1.5405 | |
| R39 (C53=C55) | 1.3381 | 1.3381 | 1.3567 | 1.3567 | 1.3559 | 1.3559 | 1.364a |
| R40 (O60-C62) | 1.3485 | 1.3397 | 1.3805 | 1.3700 | 1.3743 | 1.3650 | |
| R41 (C62-C63) | 1.5033 | 1.5030 | 1.4998 | 1.5000 | 1.4956 | 1.4952 | |
| R42 (C62=O65) | 1.1810 | 1.1873 | 1.2059 | 1.2113 | 1.2046 | 1.2098 | |
| R43 (C63=C64) | 1.3222 | 1.3230 | 1.3402 | 1.3403 | 1.3394 | 1.3398 | |
| R44 (C63-C71) | 1.5153 | 1.5159 | 1.5127 | 1.5135 | 1.5071 | 1.5083 | |
| R45 (C64-C67) | 1.5001 | 1.5002 | 1.4954 | 1.4959 | 1.4898 | 1.4901 | |
| Bond angles | |||||||
| A1 (C2-C1-C3) | 115.3869 | 115.1538 | 115.3519 | 115.0591 | 115.3042 | 114.9661 | |
| A2 (C2-C1-C20) | 104.9116 | 105.2360 | 104.8861 | 105.3058 | 105.0195 | 105.4353 | |
| A3 (C2-C1-C22) | 104.6632 | 104.8093 | 104.8467 | 105.0548 | 104.7619 | 105.0065 | |
| A4 (C3-C1-C20) | 105.4487 | 104.9239 | 106.0693 | 105.3428 | 105.9491 | 105.1727 | |
| A5 (C3-C1-C22) | 110.0598 | 110.4677 | 109.3407 | 109.9326 | 109.4774 | 110.1062 | |
| A6 (C20-C1-C22) | 116.6507 | 116.5134 | 116.6409 | 116.4160 | 116.6212 | 116.4196 | |
| A7 (C1-C2-O7) | 122.6712 | 122.1731 | 122.5890 | 122.0461 | 122.6012 | 122.0599 | |
| A8 (C1-C2-C34) | 118.8294 | 119.0297 | 118.5520 | 118.8580 | 118.5112 | 118.8095 | |
| A9 (O7-C2-C34) | 118.3115 | 118.6060 | 118.6750 | 118.9135 | 118.6899 | 118.9368 | |
| A10 (C1-C3-C4) | 117.4677 | 117.2546 | 117.5179 | 117.3499 | 117.4703 | 117.2908 | |
| A11 (C1-C3-C40) | 120.4116 | 120.3391 | 120.5229 | 120.3696 | 120.4781 | 120.3201 | |
| A12 (C1-C3-O59) | 113.5239 | 113.6346 | 113.2288 | 113.4708 | 113.2740 | 113.5007 | |
| A13 (C4-C3-C40) | 119.7989 | 119.8618 | 119.6777 | 119.7275 | 119.7605 | 119.8264 | |
| A14 (C4-C3-O59) | 110.9192 | 111.3348 | 110.6687 | 111.0566 | 110.7288 | 111.1433 | |
| A15 (C3-C4-C5) | 108.2815 | 108.0767 | 108.5292 | 108.3020 | 108.4460 | 108.1898 | |
| A16 (C3-C4-C12) | 116.9097 | 116.9148 | 116.6545 | 116.8466 | 116.8336 | 117.0260 | |
| A17 (C3-C4-C36) | 107.3533 | 107.5825 | 107.2145 | 107.3890 | 107.2213 | 107.3820 | |
| A18 (C5-C4-C12) | 110.9502 | 111.2590 | 110.8879 | 111.1131 | 111.0310 | 111.3284 | |
| A19 (C5-C4-C36) | 108.2096 | 108.3900 | 108.2857 | 108.5557 | 108.0890 | 108.3471 | |
| A20 (C12-C4-C36) | 104.7402 | 104.2361 | 104.883 | 104.2585 | 104.7988 | 104.1530 | |
| A21 (C4-C5-C6) | 122.3963 | 122.5160 | 122.2095 | 122.2513 | 122.2181 | 122.2697 | |
| A22 (C4-C5-C46) | 126.1434 | 126.0858 | 126.2488 | 126.1993 | 126.1315 | 126.0739 | |
| A23 (C4-C5-O61) | 113.7557 | 113.5947 | 113.7382 | 113.6922 | 114.0173 | 113.9553 | |
| A24 (C6-C5-C46) | 108.4092 | 108.4312 | 108.2407 | 108.2667 | 108.2513 | 108.2900 | |
| A25 (C6-C5-O61) | 109.3436 | 109.1575 | 109.7850 | 109.6384 | 109.6935 | 109.5481 | |
| A26 (C5-C6-C26) | 106.9225 | 107.1323 | 107.1725 | 107.3025 | 107.1359 | 107.2931 | |
| A27 (C5-C6-C42) | 114.7934 | 114.8607 | 114.4807 | 114.5006 | 114.5313 | 114.5541 | |
| A28 (C5-C6-C51) | 101.8612 | 101.8830 | 101.9281 | 102.0115 | 101.8916 | 101.9777 | |
| A29 (C26-C6-C42) | 108.8679 | 108.6162 | 109.1102 | 108.9149 | 109.1443 | 108.9314 | |
| A30 (C26-C6-C51) | 113.8205 | 113.8653 | 113.9931 | 114.0014 | 113.9406 | 113.9367 | |
| A31 (C42-C6-C51) | 110.5307 | 110.4727 | 110.1102 | 110.0888 | 110.1443 | 110.1222 | |
| A32 (C16-C8-C20) | 117.8467 | 117.8806 | 117.5220 | 117.5381 | 117.3986 | 117.3974 | |
| A33 (C16-C8-C29) | 108.3950 | 108.5431 | 108.4117 | 108.5195 | 108.5270 | 108.6672 | |
| A34 (C16-C8-C32) | 109.5455 | 109.4283 | 109.5034 | 109.3293 | 109.6190 | 109.4415 | |
| A35 (C20-C8-C29) | 96.3773 | 96.4321 | 96.6032 | 96.6193 | 96.4146 | 96.4285 | 101.5c |
| A36 (C20-C8-C32) | 106.3315 | 106.2487 | 106.4280 | 106.3876 | 106.432 | 106.3732 | |
| A37 (C29-C8-C32) | 118.2843 | 118.2659 | 118.3155 | 118.4200 | 118.3462 | 118.4575 | |
| A38 (O11-C9-C12) | 113.2108 | 113.1065 | 113.2048 | 113.2060 | 113.1493 | 113.1724 | |
| A39 (O11-C9-C20) | 103.3360 | 103.1494 | 103.8285 | 103.6622 | 103.8971 | 103.7399 | 104.0c |
| A40 (C12-C9-C20) | 109.2549 | 109.4574 | 108.7908 | 108.9954 | 108.4814 | 108.6640 | |
| A41 (C9-O11-C29) | 111.1841 | 111.2217 | 109.8976 | 109.9018 | 109.8190 | 109.8362 | 110.6c |
| A42 (C4-C12-C9) | 110.4259 | 110.6951 | 110.0123 | 110.3980 | 109.8110 | 110.1418 | |
| A43 (C4-C12-O60) | 111.1499 | 111.4570 | 110.9644 | 111.4849 | 111.3257 | 111.9073 | |
| A44 (C9-C12-O60) | 109.0864 | 108.7044 | 108.7314 | 108.2508 | 108.4512 | 107.9972 | |
| A45 (C51-C14-C53) | 126.042 | 126.0928 | 126.1043 | 126.1692 | 126.2986 | 126.3771 | |
| A46 (C51-C14-C57) | 129.3418 | 129.1716 | 128.8385 | 128.6558 | 128.7371 | 128.5448 | |
| A47 (C53-C14-C57) | 104.5893 | 104.7043 | 105.0493 | 105.1666 | 104.9597 | 105.0728 | 106.14a |
| A48 (C55-O15-C57) | 107.1084 | 107.1499 | 106.7602 | 106.8013 | 106.8133 | 106.8678 | 106.74a |
| A49 (C1-C20-C8) | 121.1479 | 121.0073 | 120.9097 | 120.7705 | 120.9914 | 120.8439 | |
| A50 (C1-C20-C9) | 118.7226 | 118.5220 | 118.7478 | 118.3732 | 118.6818 | 118.2898 | |
| A51 (C8-C20-C9) | 103.8120 | 103.9439 | 104.2023 | 104.3600 | 104.0389 | 104.2216 | 104.4c |
| A52 (C6-C26-C40) | 111.4945 | 111.6304 | 111.4804 | 111.5216 | 111.4199 | 111.4969 | |
| A53 (C8-C29-O11) | 104.4386 | 104.4819 | 104.6594 | 104.594 | 104.6712 | 104.6043 | 107.5c |
| A54 (C8-C32-C34) | 120.4664 | 120.4528 | 120.5688 | 120.4387 | 120.4312 | 120.2925 | |
| A55 (C2-C34-C32) | 125.2907 | 124.9802 | 125.5569 | 125.2584 | 125.5114 | 125.1913 | |
| A56 (C3-C40-C26) | 124.7594 | 125.1561 | 124.3752 | 124.7373 | 124.3541 | 124.7241 | |
| A57 (C26-C40-O59) | 116.1404 | 115.9652 | 116.0868 | 116.0753 | 115.9905 | 115.9607 | |
| A58 (C5-C46-C48) | 110.0006 | 110.0212 | 109.8202 | 109.8537 | 109.6430 | 109.6699 | |
| A59 (C48-C46-O61) | 111.5740 | 111.5456 | 111.7313 | 111.7203 | 111.8859 | 111.8641 | |
| A60 (C46-C48-C51) | 102.6704 | 102.7788 | 102.8570 | 103.0253 | 102.6915 | 102.8703 | |
| A61 (C6-C51-C14) | 116.8638 | 116.8705 | 116.6829 | 116.6156 | 116.3993 | 116.3329 | |
| A62 (C6-C51-C48) | 104.4966 | 104.5425 | 104.2867 | 104.3539 | 104.3511 | 104.4332 | |
| A63 (C14-C51-C48) | 114.9685 | 114.8714 | 115.2826 | 115.1809 | 115.2757 | 115.1468 | |
| A64 (C14-C53-C55) | 106.1668 | 106.2381 | 106.7966 | 106.8606 | 106.6618 | 106.7168 | 106.14a |
| A65 (O15-C55-C53) | 110.7484 | 110.6455 | 110.3339 | 110.2350 | 110.4305 | 110.3331 | 110.49a |
| A66 (C14-C57-O15) | 111.3857 | 111.2607 | 111.0591 | 110.9356 | 111.1339 | 111.0086 | 110.49a |
| A67 (C12-O60-C62) | 123.1805 | 123.4264 | 122.4520 | 122.2629 | 121.8099 | 121.5920 | |
| A68 (O60-C62-C63) | 118.3342 | 119.1473 | 118.6681 | 119.4932 | 118.6273 | 119.3485 | |
| A69 (O60-C62-O65) | 118.3753 | 117.9395 | 117.5454 | 117.1467 | 117.6414 | 117.2568 | |
| A70 (C63-C62-O65) | 123.0766 | 122.6884 | 123.4720 | 123.0718 | 123.4069 | 123.1015 | |
| A71 (C62-C63-C64) | 116.9655 | 117.1950 | 116.2922 | 116.7661 | 116.1754 | 116.6519 | |
| A72 (C62-C63-C71) | 117.8479 | 117.3833 | 119.4971 | 118.5815 | 119.7175 | 119.0158 | |
| A74 (C64-C63-C71) | 125.0717 | 125.2904 | 124.1105 | 124.5124 | 123.9876 | 124.1815 | |
| A75 (C63-C64-C67) | 127.2664 | 127.2197 | 127.2301 | 127.2514 | 126.9123 | 126.7855 | |
| Total energy (Hartree) | -1719.15539 | -1719.17648 | -1729.82917 | -1729.84726 | -1729.17724 | -1729.19498 | |
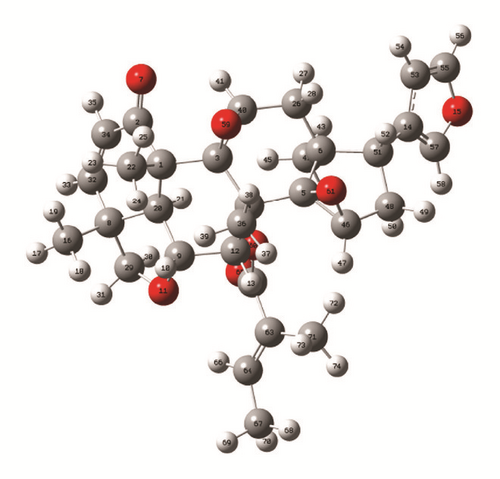
3.2. Structural Properties
A part of the optimized geometrical parameters (bond length, bond angle) and total electronic energy of the title molecule both in gas and in a solution of chloroform are given in Table 1 using the three levels and with the 6-311++G(d,p) basis set. The total description of the molecular geometry of Rubescin E molecule in gas phase and in a solution of chloroform using ab initio (RHF) and DFT (B3LYP and B3PW91) methods with the 6-311++G(d,p) basis set can be obtained from Supplementary Material S1.
The atom numbering scheme adopted for this purpose is the same as in Figure 1. The energy differences between the two used phases increase when we move from B3PW91 to B3LYP and to RHF and are found to be approximatively 0.48 eV, 0.49 eV, and 0.57 eV, respectively. The optimized bond length and bond angle of Rubescin E are also listed in Table 1 with some specific experimental values [12–14] found in the literature for some groups of compounds such as furan, ethylene oxide, and tetrahydrofuran present in our molecule. It can be observed from Table 1 that the values of the bond length obtained at B3LYP are slightly higher than those obtained at the B3PW91 level. These differences are found between 0.0034 Å and 0.0107 Å for C-C; 0.0061 Å and 0.0095 Å for C-O; and 0.0007 Å and 0.0013 Å for C=C in gas phase. The value of C=O bond length is better at the DFT methods since its values are closer to 2.10 Å found in literature [11]. It can also been observed that the calculated bonds length using Hartree Fock and DFT methods are very close to the values found in literature for the specific groups of compounds present in our molecule. These observed differences varied from 0.0012 Å at the B3LYP level to 0.0363 Å at the RHF level; from 0.0002 Å at the B3PW91 level to 0.0288 Å at the B3LYP level; and from 0.0019 Å at the B3LYP level to 0.0259 Å at the RHF level for C-C, C-O, and C=C bonds both in gas phase and in chloroform solution, respectively.
The bonds angles of the studied molecule are slightly different when we move from one phase to another at each level with larger values obtained at the RHF level. From our results, it can be seen that the C-C-C bond angle varies from 96.3773° to 129.3418°, from 96.6032° to 128.8385°, and from 96.4146° to 128.7371° at the gas phase, respectively, at the RHF, B3LYP, and B3PW91 level of the theory. In CDCl3, the C-C-C bond angles are similar to those obtained at the gas phase. The smallest value of C-C-C bond angle was C20-C8-C29 bond angle and the largest C51-C14-C57 bond angle. For the C-C-O angle, the smallest value was 104.4386° obtained at the RHF and the largest value was 123.472° obtained at the B3LYP level both in the gas phase. The C-O-C bond angle was found between 107.1084° and 123.4264° obtained at the RHF level. These bonds angles compared to some known values found in literature [12, 14] for specific compound present in our structure show good similarities. The little differences are found between 0.0268° and 1.5507° for C-C-C bond, between 0.0595° and 3.0614° for C-C-O bond, and between 0.0202° and 0.781° for C-O-C bond. These observed differences are due to the fact that these groups of compounds were not isolated.
3.3. Calculated 3JH-H Coupling Constant
The chemical 3JH-H proton-proton coupling constant was calculated using the original Karplus [10] equation in gas and solvent and its results compared to experimental values [1] obtained by extracting Rubescin E in a solution of chloroform. From our results, we found that the calculated parameters both in gas and in chloroform are all similar at all the levels used. These obtained results are also very close to experiment. As predicted in literature [10], we observed from Table 2 that when the angles between the two C-H vectors are close enough to 00 or 1800, the value of 3JH-H coupling constant is greater (with ) and is very small when the angle is close to 900.
| PARAMETERS | RHF | B3LYP | B3PW91 | EXP [1] | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gaz | CDCl3 | Gaz | CDCl3 | Gaz | CDCl3 | ||||||||
| Angles(°) | 3JH-H (Hz) | Angles(°) | 3JH-H (Hz) | Angles(°) | 3JH-H (Hz) | Angles(°) | 3JH-H (Hz) | Angles(°) | 3JH-H (Hz) | Angles(°) | 3JH-H (Hz) | ||
| H10-C9-C12-H13 | 45.5506 | 6.20 | 43.8143 | 6.49 | 48.1393 | 5.79 | 45.9537 | 6.14 | 48.3285 | 5.76 | 46.1662 | 6.10 | 4.0 |
| H10-C9-C20-H21 | 169.5395 | 12.65 | 169.8194 | 12.67 | 168.824 | 12.61 | 168.658 | 12.59 | 168.5 | 12.58 | 168.2201 | 12.56 | 12.0 |
| H27-C26-C40-H41 | -11.0718 | 10.65 | -12.0311 | 10.59 | -10.1794 | 10.70 | -10.89 | 10.66 | -10.4324 | 10.69 | -11.298 | 10.64 | 6.5 |
| H28-C26-C40-H41 | 105.3029 | 2.96 | 103.995 | 2.83 | 106.3433 | 3.07 | 105.3319 | 2.96 | 106.1668 | 3.05 | 104.964 | 2.92 | 1.3 |
| H33-C32-C34-H35 | -0.2873 | 11 | -0.123 | 11 | -0.5893 | 11 | -0.366 | 11 | -0.566 | 11 | -0.3331 | 11 | 10.0 |
| H47-C46-C48-H49 | -61.3614 | 3.82 | -61.1286 | 3.85 | -61.9356 | 3.74 | -61.8438 | 3.75 | -61.5482 | 3.79 | -61.4875 | 3.80 | 4.2 |
| H47-C46-C48-H50 | 58.7437 | 4.17 | 58.7503 | 4.17 | 58.0428 | 4.27 | 57.8579 | 4.30 | 58.534 | 4.20 | 58.3044 | 4.24 | 4.2 |
| H49-C48-C51-H52 | -42.5704 | 6.69 | -42.1786 | 6.75 | -43.9616 | 6.46 | -43.3642 | 6.56 | -44.5718 | 6.36 | -43.9227 | 6.47 | 4.2 |
| H50-C48-C51-H52 | -164.093 | 12.21 | -163.817 | 12.18 | -165.22 | 12.32 | -164.673 | 12.27 | -165.874 | 12.37 | -165.259 | 12.32 | 11 |
| H54-C53-C55-H56 | -0.3838 | 11 | -0.2856 | 11 | -0.3275 | 11 | -0.2429 | 11 | -0.3921 | 11 | -0.3074 | 11 | |
| H66-C64-C67-H68 | -177.906 | 12.99 | -177.979 | 12.99 | 178.4674 | 12.99 | 178.7874 | 13 | 178.4147 | 12.99 | 178.548 | 12.99 | |
| H66-C64-C67-H69 | -56.9125 | 4.43 | -56.9428 | 4.43 | -60.3746 | 3.95 | -59.9903 | 4 | -60.4007 | 3.95 | -60.1923 | 3.97 | 7.0 |
| H66-C64-C67-H70 | 60.6324 | 3.91 | 60.4696 | 3.94 | 56.6811 | 4.47 | 56.9449 | 4.42 | 56.6504 | 4.47 | 56.7234 | 4.46 | 7.0 |
3.4. Electronic Properties
3.4.1. Mulliken, ESP, and Natural Charge Distribution
The Mulliken atomic charges of our molecule calculated at all the levels in gas phase and chloroform show positive charge for all the hydrogen atoms. The net charge on all the atoms varies from -1.109653e to 1.980512e, from -1.164916e to 1.904034e, and from -0.891775e to 1.524787e, respectively, in gas phase at the RHF, B3PW91, and B3LYP levels. In a solution of chloroform, the charges varied from -1.064962e to 1.826589e, from -1.206706e to 1.904292e, and from -0.945041e to 1.550492e with some oxygen atoms charges being positive and can be explained by the fact that the oxygen is related to extremely negative carbon atoms. The most positive charge atoms are C63, C5, C8 and the most negative charge atoms are C71, C62, C67.
The electrostatic charges were evaluated in this work using the CHelpG scheme of Breneman model. We found from our results that the most positive charges atom is C4 followed by C62 and C2 and the most negative charge atom is C12 followed by C5 and C7. The observation made at all levels and basis set in gas phase and in a solution of chloroform is that the most positive charge atoms are directly related to the most negative charge atoms.
The natural atomic charges, obtained using the natural bonding orbital method, were also used to evaluate the atomic charge of Rubescin E. Positive and negative charges were found for all hydrogen and oxygen atoms, respectively. In this case, all carbon atoms directly linked to hydrogen atoms were found to have negative charges except for those linked to oxygen atoms. The most negative charge atom was calculated using HF method and was observed for O65 (-0.69456e) and O60 (-0.68330e), respectively, in chloroform and gas phase. The most positive charge atom was found to be C62 in both gas (0.97067e, 0.80601e, and 0.81407e, respectively, at the RHF, B3PW91, and B3LYP levels) and solvent (0.98887e, 0.81804e, and 0.82650e, respectively, at the RHF, B3PW91, and B3LYP levels); this is due to the fact that C62 is related to negative charge atoms (O65, O60, and C63). Mulliken, electrostatic, and natural atomic charge distributions are graphically shown in Figure 2. From Figure 2, one can observe that, for almost all the methods used for charge description, the most positive and negative charge atoms were calculated at the RHF level in both gas and chloroform and this is due to the fact that the effect of electron correlation is not well described in HF method.

3.4.2. Global Reactivity Descriptors
| RHF | B3LYP | B3PW91 | ||||
|---|---|---|---|---|---|---|
| Gas | Chloroform | Gas | Chloroform | Gas | Chloroform | |
| IP (eV) | 7.151 | 5.662 | 7.875 | 6.819 | 7.861 | 6.819 |
| EA (eV) | -0.841 | 0.684 | 0.461 | 1.804 | 0.450 | 1.825 |
| μcp (eV) | -3.155 | -3.173 | -4.168 | -4.312 | -4.156 | -4.322 |
| X (eV) | 3.155 | 3.173 | 4.168 | 4.312 | 4.156 | 4.322 |
| H (eV) | 3.996 | 2.489 | 3.707 | 2.508 | 3.706 | 2.497 |
| s (eV)−1 | 0.250 | 0.402 | 0.270 | 0.399 | 0.270 | 0.400 |
| ω (eV) | 1.245 | 2.022 | 2.343 | 3.707 | 2.330 | 3.740 |
The calculated vertical IP values in gas phase are bigger than their corresponding values in solvent. From Table 3, we also found that putting the molecule in solvent increases its electron affinity. From the calculated IP and EA values, one can conclude that solvent effect increases the capacity of molecule of gaining an electron compared to donating it. It also reduces the harness of our molecule and increases the softness. Hence, the presence of solvent increases the reactivity of the molecule Rubescin.
3.4.3. Frontier Molecular Orbitals
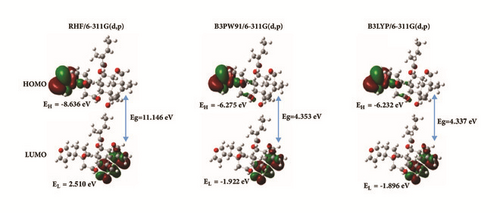
The frontier molecular orbitals of Rubescin E were evaluated using the ab initio and DFT methods. The 6-311G(d,p) and 6-311++G(d,p) basis sets were used for this purpose in gas phase and in chloroform solution. The results show that the energy gap of our molecule decreases when diffuse functions are added onto all the atoms. We also found that whenever the basis set and methods used, the energy gap is greater than 4, showing that our molecule is hard and can be used as insulator in many electronic devices. In Figure 3, the 3D plots of the HOMO and LUMO orbitals computed at the RHF, B3PW91, and B3LYP levels with the 6-311G(d,p) basis set are illustrated in gas phase. We observed that the HOMO of Rubescin E is located over the furan ring at the three levels and also at the C-C of cyclohexane ring and C-O of oxiran ring. By contrast, the LUMO orbital is located over the cyclohex-2-enone ring, C-C and C-O bond of tetrahydrofuran ring. We can therefore conclude that electron can easily be transferred from furan ring to tetrahydrofuran ring.
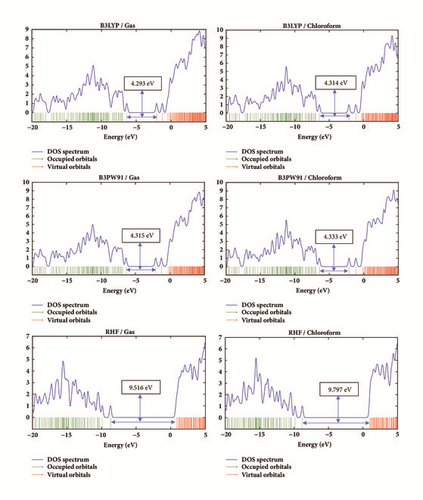
The total density of states (DOS) spectrum of Rubescin E at the gas phase and in chloroform is given in Figure 4 for each level at the 6-311++G(d,p) basis set. These DOSs spectra presented in Figure 4 were obtained from Gauss-Sum 3.0 program [18] which was used in order to show the contributions of different group to molecular orbital (HOMO and LUMO). From Figure 4, we observe that the HOMO-LUMO energy gap is smaller when we move from RHF to B3PW91 and from B3PW91 to B3LYP level, respectively, for both gas and chloroform phases, with larger values obtained in chloroform.
3.4.4. UV-Vis Spectra Analysis
Time dependent density functional theory (TD-DFT) was used in gas phase at the two levels B3PW91 and B3LYP with the 6-311++G(d,p) basis set in order to determine the first six excited states to investigate the UV-vis absorption spectra of the molecule. The excitation energy (E), wavelength (λ), and oscillator strength (f) along with their major contributions are given in Table 4 and their results are compared to experiment.
| Excited states | Exp [1] | B3PW91 | B3LYP | ||||||
|---|---|---|---|---|---|---|---|---|---|
| λ (nm) | λ (nm) | E (eV) | f | Major contributions | λ (nm) | E (eV) | f | Major contributions | |
| 1 | 365 | 360.27 | 3.4415 | 0.0014 | H-1 → L (93%) | 358.31 | 3.4603 | 0.0014 | H-1 → L (93%) |
| 2 | 312.18 | 3.9715 | 0.0000 | H → L (99%) | 313.69 | 3.9524 | 0.0000 | H → L (99%) | |
| 3 | 254 | 275.92 | 4.4934 | 0.0043 | H-4 → L (24%) | 274.77 | 4.5123 | 0.0041 | H-4 → L (28%) |
| 4 | 272.66 | 4.5473 | 0.0006 | H-4 → L (50%) | 272.27 | 4.5538 | 0.0004 | H-4 → L (44%) | |
| 5 | 269.56 | 4.5994 | 0.0001 | H-4 → L (19%) | 268.47 | 4.6182 | 0.0001 | H-4 → L (20%) | |
| 6 | 261.21 | 4.7465 | 0.0000 | H → L+1 (100%) | 263.16 | 4.7113 | 0.0000 | H → L+1 (100%) | |
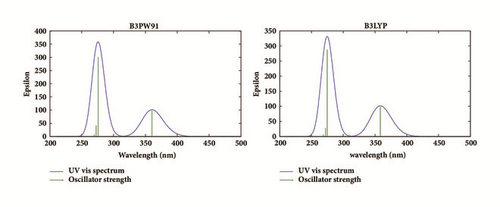
Two intense electronic transitions were predicted at 4.4934 eV (275.92 nm) and 3.4415 eV (360.27 nm) with oscillator strengths of 0.0043 and 0.0014, respectively, at the B3PW91 level and 4.5123 eV (274.77 nm) and 3.4603 eV (358.31 nm) with oscillator strengths of 0.0041 and 0.0014, respectively, at the B3LYP level. We observed from the spectra that the maximum absorption wavelength corresponds to the electronic transition from HOMO to LUMO+1 with 100% contribution followed by the electronic transition from HOMO to LUMO with 99% contribution at the two levels. The experimental absorption spectra of the title molecule predict two bands at 254 nm and 365 nm. The error between the theoretical and experimental results range from - 4.73 nm to 21.92 nm at the B3PW91 and from - 6.69 nm to 20.77 nm at the B3LYP level. These errors are due to the fact that only one molecule was considered for simulation. The theoretical UV-vis absorption spectra of Rubescin E in gas phase are shown in Figure 5.
3.4.5. Dipole Moment (μDM), Average Polarizability (α), First Static Hyperpolarizability (β), and Anisotropy of Polarization
| RHF | B3LYP | B3PW91 | ||||
|---|---|---|---|---|---|---|
| Gas | Chloroform | Gas | Chloroform | Gas | Chloroform | |
| μDM (D) | 5.3966 | 7.0953 | 5.2074 | 6.7654 | 5.1176 | 6.6663 |
| αxx | 352.266 | 421.425 | 387.992 | 470.193 | 384.258 | 465.488 |
| αxy | 17.3299 | 24.2341 | 19.6436 | 29.6995 | 19.3544 | 29.0512 |
| αyy | 336.148 | 424.889 | 374.795 | 479.493 | 371.091 | 475.445 |
| αxz | 1.50612 | 0.677331 | 0.715703 | -0.411779 | 0.795242 | -0.371934 |
| αyz | 3.39268 | -1.23142 | 4.44903 | 0.0306216 | 4.53244 | 0.450373 |
| αzz | 278.550 | 371.379 | 305.049 | 415.461 | 301.619 | 411.131 |
| αtot (∗10−24 esu) | 47.7036 | 60.0729 | 52.6799 | 67.3473 | 52.1438 | 66.7018 |
| Δα (∗10−24 esu) | 10.9240 | 9.8814 | 12.5387 | 11.6890 | 12.4723 | 11.5857 |
| βxxx | 58.5850 | 116.324 | 77.8905 | 117.687 | 82.0568 | 124.840 |
| βxxy | -34.3404 | -40.3762 | -33.9536 | -66.5203 | -29.0441 | -60.4155 |
| βxyy | 22.5993 | 15.4126 | -29.6091 | -106.843 | -36.6541 | -122.127 |
| βyyy | 92.3349 | 129.004 | 27.6922 | -58.5834 | 26.8972 | -63.6805 |
| βxxz | -16.3605 | -23.5326 | -55.0267 | -81.7313 | -58.0975 | -89.6785 |
| βxyz | -8.72859 | -0.242861 | -11.9414 | 10.3722 | -12.8764 | 6.24556 |
| βyyz | -38.9332 | -65.6523 | -107.633 | -207.304 | -108.216 | -214.866 |
| βxzz | -14.4537 | -58.3711 | -7.34826 | -70.3072 | -7.94692 | -69.1599 |
| βyzz | -50.8004 | -109.450 | -77.7921 | -196.200 | -71.2685 | -182.588 |
| βzzz | -6.38532 | 23.9632 | -16.7476 | -0.675756 | -9.68167 | 5.78764 |
| β (∗10−33 esu) | 787.4783 | 866.9154 | 1747.7167 | 3772.6270 | 1678.8815 | 3743.0498 |
3.4.6. Optoelectronic Properties
In order to recognize the optoelectronic nature of Rubescin E for different devices applications, some parameters such as electric field (E), electric polarization (P), electric susceptibility (χ), permittivity (ℰ), refractive index (η), and electric displacement (D) were calculated using equations given in the literature [23–25]. We observed from Table 6 that the results of the calculated parameters are slightly different when we move from one level to another and also when the medium changes. The value of electric field is greater in a solution of chloroform than its corresponding value in gas phase. This is because the polarizability increases in presence of a solvent. The values of electric susceptibility, dielectric constant, and refractive index are greater at B3LYP level compared to their corresponding value at the RHF. All the calculated parameters of optoelectronic properties obtained at the B3LYP level are similar to those obtained at the B3PW91 level. None of these parameters have been determined before either theoretically or experimentally.
| Parameters | RHF | B3LYP | B3PW91 | |||
|---|---|---|---|---|---|---|
| Gas | Chloroform | Gas | Chloroform | Gas | Chloroform | |
| E (V.m−1)∗ 109 | 3.3873 | 3.5365 | 2.9597 | 3.0078 | 2.9386 | 2.9924 |
| P (C.m−2)∗10−2 | 8.3339 | 10.7944 | 7.5778 | 8.6086 | 8.3117 | 7.9130 |
| χ | 2.7787 | 3.4473 | 2.8916 | 3.2324 | 3.1945 | 2.9865 |
| ∗10−11 | 3.3458 | 3.9377 | 3.4457 | 3.7475 | 3.7139 | 3.5297 |
| η | 1.9439 | 2.1089 | 1.9727 | 2.0573 | 2.0480 | 1.9966 |
| D (C.m−2)∗10−2 | 0.1133 | 0.1393 | 0.1020 | 0.1127 | 0.1091 | 0.1056 |
| MR (esu.mol−1) | 120.3345 | 151.5366 | 132.8875 | 169.8866 | 131.5351 | 168.2585 |
One of the central goals of this study is to understand the underlying structure–property relationships which might form the basis for a “molecular engineering” approach to electronics, optoelectronics, and photonics. The molar refractivity of our molecule, known to be an important parameter in quantitative structure–property relationship analysis was calculated for this purpose. The value of the molar refractivity was calculated at the three levels, in both gas and chloroform using the 6-311++G(d,p) basis set. The Lorenz-Lorentz equation was used for this calculation [26, 27] and its results are listed in Table 6.
The high values of molar refractivity, polarizability, anisotropy of polarizability, and first static hyperpolarizability of Rubescin E molecule show that the molecule has good quantitative structure–property relationship analysis and might therefore form the basis for a “molecular engineering” approach to electronics, optoelectronics, and photonics.
3.5. NMR Study of Rubescin E
The experimental and calculated chemical shifts of 1H along with their corresponding error are listed in Table 7. From our results we observed that all the methods provide results which are very close to experiment since the errors between the experimental and calculated results are smaller.
| Nuclei | Calculated δ (ppm) | Experimental δ (ppm) [1] | Nuclei | Calculated δ (ppm) | Experimental δ (ppm) [1] | ||||
|---|---|---|---|---|---|---|---|---|---|
| RHF | B3LYP | B3PW91 | RHF | B3LYP | B3PW91 | ||||
| H10 | 3,6354 | 4,4787 | 4,5162 | 4,44 | H41 | 3,2764 | 3,8070 | 3,7375 | 3,97 |
| H13 | 3,7599 | 4,5046 | 4,4656 | 5,5 | H43 | 0,0206 | 0,1390 | 0,1217 | - |
| H17 | 1,1735 | 1,3264 | 1,2850 | - | H44 | 0,5304 | 0,6752 | 0,6653 | 0,65 |
| H18 | 1,4006 | 1,4842 | 1,5205 | 1,34 | H45 | 1,1410 | 1,2581 | 1,2916 | - |
| H19 | 0,8843 | 0,9632 | 0,9055 | - | H47 | 2,9441 | 3,4299 | 3,3665 | 3,45 |
| H21 | 2,2212 | 3,1228 | 3,2220 | 2,9 | H49 | 1,8799 | 2,0794 | 2,0578 | 2,11 |
| H23 | 0,7480 | 0,8702 | 0,8499 | - | H50 | 1,6401 | 2,0098 | 2,0019 | 1,51 |
| H24 | 0,9682 | 1,2471 | 1,2747 | 1,43 | H52 | 2,1382 | 2,6231 | 2,6453 | 2,52 |
| H25 | 1,6905 | 1,7201 | 1,7225 | - | H54 | 6,4241 | 6,4756 | 6,5064 | 6,23 |
| H27 | 1,7833 | 2,0352 | 1,9975 | 1,9 | H56 | 7,6008 | 7,6737 | 7,6347 | 7,34 |
| H28 | 1,7575 | 2,1239 | 2,1319 | 1,9 | H58 | 7,2432 | 7,2352 | 7,1892 | 7,24 |
| H30 | 3,1956 | 3,7283 | 3,7158 | 3,77 | H66 | 6,5053 | 6,5963 | 6,7294 | 6,73 |
| H31 | 3,3513 | 3,5791 | 3,5410 | 3,55 | H68 | 1,9939 | 2,0486 | 2,0556 | - |
| H33 | 7,4298 | 7,4428 | 7,5055 | 7,07 | H69 | 1,6905 | 1,8891 | 1,9108 | 1,82 |
| H35 | 5,9894 | 6,1274 | 6,1740 | 5,95 | H70 | 1,7037 | 1,8508 | 1,8560 | - |
| H37 | 0,3741 | 0,4953 | 0,4827 | - | H72 | 1,3371 | 1,5726 | 1,5006 | - |
| H38 | 1,4776 | 1,8588 | 1,8632 | 1,22 | H73 | 1,7489 | 1,8289 | 1,8340 | 1,87 |
| H39 | 0,7281 | 1,2414 | 1,3276 | - | H74 | 2,1737 | 2,2617 | 2,2408 | - |
In order to compare experimental and theoretical results, a linear correlation of 1H-NMR chemical shifts was established as shown in Figure 6. The regression line was plotted using the following equations: δcal = 0.98880δexp − 0.17198, δcal = 0.97379δexp + 0.18796, and δcal = 0.97069δexp + 0.19387, respectively, at the RHF, B3PW91, and B3LYP levels of the theory. The theoretical results obtained from using the 6-311++G(d,p) basis set show good correlation with experiment since, and the calculated R-square values are found to be close to 1 at each level as shown by Figure 6.
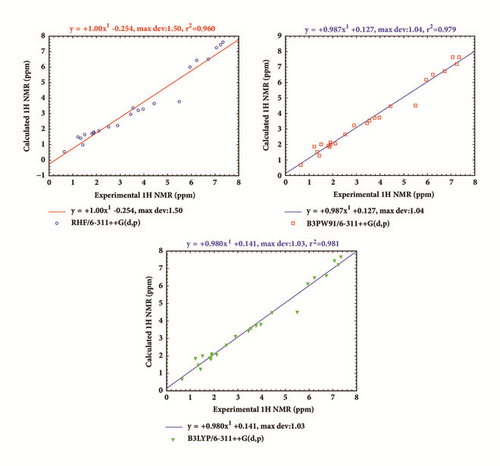
The calculated and experimental 13C chemical shifts of our molecule are given in Table 8 and their comparison can be found in Figure 7. The linear regression line plotted in Figure 7 shows that theoretical results are in good agreement with experiment. This is confirmed by the linear correlation coefficient calculated here as R-square at the RHF, B3PW91, and B3LYP levels using the 6-311++G(d,p) basis set.
| Nuclei | Calculated δ (ppm) | Experimental δ (ppm) [1] | Nuclei | Calculated δ (ppm) | Experimental δ (ppm) [1] | ||||
|---|---|---|---|---|---|---|---|---|---|
| RHF | B3LYP | B3PW91 | RHF | B3LYP | B3PW91 | ||||
| C1 | 44,217875 | 56,667075 | 53,80495 | 47,5 s | C34 | 134,341675 | 139,383575 | 138,51605 | 131,3 d |
| C2 | 206,549275 | 213,070575 | 210,62615 | 200,3 s | C36 | 21,545175 | 24,454275 | 24,23345 | 22,7 q |
| C3 | 56,393275 | 73,459075 | 70,54015 | 64,6 s | C40 | 53,124275 | 65,723775 | 64,21635 | 60,3 d |
| C4 | 43,854075 | 56,324675 | 52,83685 | 44,9 s | C42 | 22,468475 | 24,495375 | 24,17495 | 21,5 q |
| C5 | 60,103575 | 77,293875 | 74,30925 | 68,3 d | C46 | 48,923175 | 61,540375 | 59,53515 | 55,2 d |
| C6 | 39,115675 | 49,868075 | 47,23345 | 41,3 s | C48 | 29,511075 | 34,706875 | 33,33385 | 31,1 t |
| C8 | 39,020275 | 51,568975 | 49,31465 | 41,3 s | C51 | 38,272375 | 48,003275 | 46,38035 | 38,8 d |
| C9 | 65,951775 | 79,364675 | 77,38455 | 71,4 d | C53 | 117,347375 | 119,574075 | 118,57695 | 110,8 d |
| C12 | 72,763675 | 87,369975 | 84,63375 | 74,7 d | C55 | 149,815075 | 151,680375 | 149,71195 | 142,9 d |
| C14 | 130,650675 | 133,767875 | 131,73785 | 123,1 s | C57 | 144,528075 | 147,708875 | 145,91185 | 139,2 d |
| C16 | 21,641175 | 23,522875 | 22,88275 | 21,1 q | C62 | 178,475775 | 182,888075 | 180,33025 | 167,4 s |
| C20 | 44,504575 | 54,261975 | 53,16905 | 50,6 d | C63 | 132,986175 | 138,281375 | 136,47755 | 128,8 s |
| C22 | 16,680575 | 18,585575 | 18,72435 | 17,5 q | C64 | 148,221575 | 150,697975 | 151,11665 | 138,3 d |
| C26 | 34,988975 | 41,161875 | 39,99065 | 35,4 t | C67 | 15,275775 | 17,096475 | 17,51975 | 14,6 q |
| C29 | 71,816475 | 83,425975 | 81,35795 | 79,5 t | C71 | 13,518375 | 15,400475 | 15,47155 | 12,6 q |
| C32 | 164,415875 | 166,172275 | 165,17515 | 151,6 d | |||||
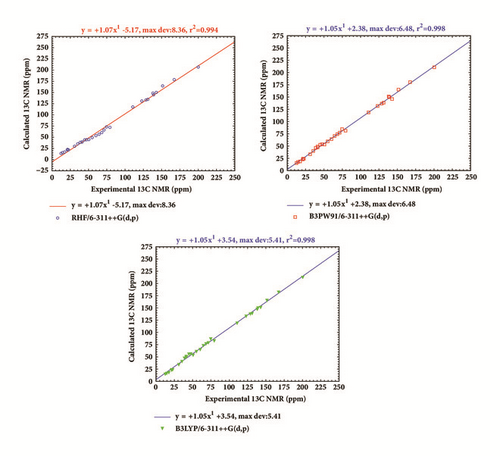
The following regression line plotted for each level using the general equation δcal = aδexp + b, where a and b are given in Figure 7, shows that the calculated 13C chemical shifts correlate very well with experiment. The linear correlation coefficient calculated as R-square found in Figure 7 also confirms this.
3.6. Vibrational Frequencies Analysis
The vibrational frequencies of our molecule were computed by using B3LYP/6-311G(d,p) method in both gas phase and chloroform. The experimental IR vibrational frequencies obtained for the two carbonyl moiety present in our structure along with the calculated scaled and unscaled vibrational frequencies, IR, and Raman frequencies with their approximate descriptions are given in Table 9. The rest of the vibrational parameter of Rubescin E molecule which is not described in Table 9 can be obtained from Supplementary Material S2. The scale factor was determined as the mean value of the scale factor that matches correctly for the C=O stretching and the given experimental value. The obtained scale factor was 0.9706. No imaginary frequencies were found showing that structure of the molecule Rubescin E is stable in both gas and solvent. Figure 8 gives the representation of the scaled IR intensity and Raman scattering activity.
| Gas phase | Chloroform solution | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Vibrational frequencies | Vibrational frequencies | ||||||||
| Exp. [1] | Unscaled | Scaled | IR | Raman | Unscaled | Scaled | IR | Raman | Approximate descriptions |
| 3277.8244 | 3179.489668 | 0.1483 | 154.454 | 3277.3381 | 3179.017957 | 0.2265 | 260.5952 | Sym νs C-H groups on furan ring | |
| 3272.9127 | 3174.725319 | 1.6469 | 66.8185 | 3272.4528 | 3174.279216 | 1.0819 | 83.7804 | Asym νs C-H groups on furan ring | |
| 3240.2105 | 3143.004185 | 0.9505 | 45.7116 | 3240.612 | 3143.39364 | 1.6053 | 100.3155 | Asym νs of (C53-H54; C55-H56) | |
| 3189.511 | 3093.82567 | 3.5332 | 66.4094 | 3189.3244 | 3093.644668 | 8.3712 | 160.0412 | νs C40-H41 | |
| 3175.4637 | 3080.199789 | 11.8025 | 201.1091 | 3175.3082 | 3080.048954 | 19.8811 | 372.2174 | Sym νs (C34-H35; C32-H33) | |
| 3172.7225 | 3077.540825 | 4.8286 | 43.2929 | 3170.4225 | 3075.309825 | 12.9561 | 111.1091 | Asym νs of CH3 (C36) | |
| 3164.5342 | 3069.598174 | 5.4628 | 42.0037 | 3160.4647 | 3065.650759 | 13.1398 | 103.7241 | νs C64-H66 | |
| 3140.7401 | 3046.517897 | 10.7253 | 48.1146 | 3141.8739 | 3047.617683 | 28.9110 | 111.4035 | Asym νs of CH3 (C36. C22) | |
| 3096.4047 | 3003.512559 | 37.8710 | 128.8493 | 3103.9325 | 3010.814525 | 53.3513 | 256.448 | Asym νs of (C29-H30; C29-H31) | |
| 3087.0614 | 2994.449558 | 18.8484 | 62.1458 | 3094.289 | 3001.46033 | 37.2141 | 110.584 | Asym νs of CH3 (C71); νs C12-H13 | |
| 3056.0169 | 2964.336393 | 13.0488 | 74.2148 | 3062.0737 | 2970.211489 | 17.9489 | 162.7148 | Sym νs of CH3 (C22) | |
| 3055.6408 | 2963.971576 | 14.4803 | 142.8654 | 3056.849 | 2965.14353 | 21.0392 | 234.8621 | Asym νs of (C67-H69; C67-H70) | |
| 3023.1661 | 2932.471117 | 14.1323 | 120.9272 | 3029.0714 | 2938.199258 | 23.4132 | 269.1079 | Sym νs of CH3 (C71) | |
| 3016.7818 | 2926.278346 | 23.9892 | 318.0136 | 3018.0608 | 2927.518976 | 25.8983 | 486.6073 | Sym νs of CH3 (C67) | |
| 2999.7383 | 2909.746151 | 1.0004 | 31.9507 | 2998.9246 | 2908.956862 | 3.4528 | 89.9972 | νs of C20-H21 | |
| 1720 | 1779.5912 | 1726.203464 | 172.5832 | 16.0679 | 1753.6214 | 1701.012758 | 326.2675 | 24.7567 | νs of C62=O65 and βs of C62-C63=C64-C67 |
| 1664 | 1742.8596 | 1690.573812 | 191.5410 | 32.6047 | 1719.1678 | 1667.592766 | 374.9763 | 96.2937 | νs of C2=O7 and βs of C1-C2-C34-H35 |
| 1699.8624 | 1648.866528 | 90.7515 | 127.5998 | 1692.7491 | 1641.966627 | 159.0973 | 264.4437 | νs C63=C64; βs H66-C64-C67-H68 and βs C62-C63-C71-H72 | |
| 1655.4051 | 1605.742947 | 20.9946 | 48.7257 | 1648.5716 | 1599.114452 | 54.0221 | 158.0979 | νs C34=C32; δs of H33-C32-C8 and δs of H35-C34-C2 | |
| 1627.2588 | 1578.441036 | 1.1593 | 11.251 | 1625.9499 | 1577.171403 | 1.4847 | 24.0532 | Asym νs of C=C on furan ring | |
| 1532.8277 | 1486.842869 | 17.3545 | 52.0428 | 1530.1712 | 1484.266064 | 23.5845 | 101.1704 | Sym νs of C=C on furan ring | |
| 1531.0536 | 1485.121992 | 4.3738 | 6.1013 | 1522.5028 | 1476.827716 | 5.4574 | 13.4777 | scis.s of (C29-H30; C29-H31) | |
| 1518.4514 | 1472.897858 | 13.9129 | 13.9129 | 1514.0912 | 1468.668464 | 12.9483 | 27.3727 | τs of CH3 (C22; C16) and scis.w of (C29-H30; C29-H31) | |
| 1503.6728 | 1458.562616 | 9.8386 | 5.7612 | 1498.5877 | 1453.630069 | 19.7850 | 13.2898 | τs of CH3 (C16; C22; C36) | |
| 1499.3956 | 1454.413732 | 5.1940 | 7.4533 | 1492.6161 | 1447.837617 | 9.3270 | 17.4033 | τs of CH3 (C42); scis.m of (C26-H27; C26-H28) and scis.w of (C48-H49; C48-H50) | |
| 1488.4029 | 1443.750813 | 0.9776 | 2.8672 | 1485.682 | 1441.11154 | 6.7043 | 7.8167 | τs of CH3 (C16; C22; C36) and δm of C20-H21 | |
| 1485.5561 | 1440.989417 | 2.9100 | 5.2938 | 1481.7402 | 1437.287994 | 4.3280 | 14.1082 | scis.s of (C48-H49; C48-H50) and τs of CH3 (C42) | |
| 1483.6563 | 1439.146611 | 0.4862 | 7.8554 | 1478.0624 | 1433.720528 | 1.4889 | 21.2082 | scis.s of (C26-H27; C26-H28) and τm of CH3 (C42) | |
| 1479.4465 | 1435.063105 | 7.9832 | 38.0149 | 1470.3189 | 1426.209333 | 12.7942 | 58.6094 | τs of CH3 (C67; C71) | |
| 1463.5075 | 1419.602275 | 2.5457 | 1.0126 | 1459.7847 | 1415.991159 | 4.0997 | 2.0734 | τs of H21-C20-C9-H10 and τw of CH3 (C22) | |
| 1442.8169 | 1399.532393 | 5.3126 | 6.5726 | 1441.0254 | 1397.794638 | 8.4482 | 14.8596 | νm of C3-C40; νm of C5-C46; rock.s of (C26-H27; C40-H41) and τm of H10-C9-C20-H21 | |
| 1422.4074 | 1379.735178 | 42.8712 | 4.011 | 1420.5762 | 1377.958914 | 63.3216 | 10.8875 | Sym CH3 umbrella mode | |
| 1418.7082 | 1376.146954 | 0.6510 | 1.2396 | 1416.3711 | 1373.879967 | 0.6332 | 11.5796 | Asym CH3 umbrella mode; rock.m (C34-H35;C32-H33); δm C51-H52 | |
| 1417.9087 | 1375.371439 | 6.7934 | 3.5193 | 1414.8341 | 1372.389077 | 5.2808 | 12.6492 | νm of C14-C53; δs of H52-C51 and sym CH3 umbrella mode | |
| 1411.6946 | 1369.343762 | 3.6967 | 24.766 | 1405.5801 | 1363.412697 | 6.3221 | 38.7377 | asym CH3 umbrella mode (C67; C71) and δm of H66-C64 | |
| 1404.0182 | 1361.897654 | 5.7921 | 1.3462 | 1402.0625 | 1360.000625 | 12.7684 | 4.8755 | rock.m of (H35-C34; C32-H33); CH3 umbrella mode (C22; C16) and τm of H21-C20-C9-H10 | |
| 1399.4114 | 1357.429058 | 7.3054 | 2.6928 | 1399.317 | 1357.33749 | 5.4113 | 6.6084 | τs of H10-C9-C20-H21; rock.m of (H35-C34; C32-H33) and δm of H13-C12-O60 | |
| 1392.7814 | 1350.997958 | 4.4872 | 7.7674 | 1393.9199 | 1352.102303 | 8.7259 | 13.1186 | τs of H10-C9-C20-H21; rock.s of (H35-C34; C32-H33) and δs of H13-C12-O6 | |
| 1381.3486 | 1339.908142 | 0.8619 | 1.6091 | 1378.5237 | 1337.167989 | 2.7575 | 3.5116 | wagg.s of (C29-H30; C29-H31); τs of H10-C9-C20-H21; δm of H13-C12-C9 and CH3 umbrella mode (C16) | |
| 1373.7055 | 1332.494335 | 4.3307 | 9.0916 | 1371.0783 | 1329.945951 | 5.0163 | 17.666 | νm of C63-C71; CH3 umbrella mode (C67; C71); δs of C64-H66 and τm of H10-C9-C20-H21 | |
| 1368.9888 | 1327.919136 | 4.4971 | 10.4931 | 1367.4102 | 1326.387894 | 5.4518 | 20.2257 | rock.s of (H56-C55; C53-H54); δs of C51-H52; wagg.s of (C48-H49; C48H50) and wagg.m of (C26-H27; C26H28) | |
| 1365.648 | 1324.67856 | 4.2088 | 1.0219 | 1364.8154 | 1323.870938 | 6.4354 | 2.7506 | τs of H10-C9-C12-H13; δm of C64-H66; rock.m (H35-C34; C32-H33); wagg.m of (C29-H30; C29H31) and CH3 umbrella mode (C16; C36) | |
| 1351.6819 | 1311.131443 | 2.3942 | 1.8233 | 1351.4078 | 1310.865566 | 3.8793 | 2.9367 | wagg.s of (C26-H27; C26-H28); δs of C51-H52 | |
| 1343.0612 | 1302.769364 | 0.8245 | 6.8235 | 1343.2284 | 1302.931548 | 0.0396 | 7.8405 | τm of H10-C9-C20-H21; δs of C12-H13; δs of C51-H52 | |
| 1326.3406 | 1286.550382 | 6.0965 | 5.2766 | 1322.4392 | 1282.766024 | 7.9781 | 13.8929 | νs of C3-C40; δs of C40-H41 | |
| 1301.2149 | 1262.178453 | 4.1883 | 6.2643 | 1301.7097 | 1262.658409 | 7.1261 | 6.9678 | νm of C5-C6; twist.s of (C26-H27; C26-H28); wagg.m of (C48-H49; C48-H50); δm of H47-C46-C5; rock.s of (H56-C55; C53-H54) | |
| 1297.0244 | 1258.113668 | 1.7948 | 7.1956 | 1297.4084 | 1258.486148 | 1.3878 | 21.5171 | νw of C9-C12; wagg.s of (C48-H49; C48-H50); δm of H47-C46-C48; δs of C51-H52; twist.m of (C26-H27; C26-H28) | |
| 1288.4675 | 1249.813475 | 3.5313 | 1.5262 | 1287.909 | 1249.27173 | 1.5765 | 14.1367 | δs of C46-H47; δs of C12-H13; τm of H10-C9-C20-H21 and twist.m of (C26-H27; C26-H28) | |
| 1278.2074 | 1239.861178 | 1.4763 | 18.6173 | 1278.0044 | 1239.664268 | 2.9774 | 29.5326 | νm of C14-C51; δs of C57-H58; twist.m of (C48-H49; C48-H50) and δs of C51-H52 | |
| 1273.4643 | 1235.260371 | 3.1680 | 10.1375 | 1271.8325 | 1233.677525 | 4.2401 | 20.9966 | δs of C46-H47; δs of C12-H13; δs of C57-H58; τs of H10-C9-C20-H21 and twist.m of (C26-H27; C26-H28) | |
| 1266.8541 | 1228.848477 | 3.8717 | 5.3878 | 1266.4233 | 1228.430601 | 6.8831 | 16.4996 | τs of H10-C9-C20-C8 and δm of C32-H33 | |
| 1253.2129 | 1215.616513 | 59.1657 | 19.3282 | 1253.6896 | 1216.078912 | 120.7089 | 57.0914 | scis.s of (C32-H33; C34-H35) and τm of C2-C1-C20-C9 | |
| 1252.2694 | 1214.701318 | 0.7185 | 4.8164 | 1251.9233 | 1214.365601 | 0.6008 | 8.7087 | δm of CH on furan ring; twist.s of (C48-H49; C48-H50); twist.m of (C26-H27; C26-H28) and τm of H52-C51-C6-C42 | |
| 1245.9092 | 1208.531924 | 177.9705 | 5.7457 | 1246.65 | 1209.2505 | 254.8417 | 9.1404 | νm of C62C63; τm of H66-C64-C67-H68; twist.s of (C29-H30; C29H31) | |
| 1237.0891 | 1199.976427 | 12.8957 | 8.0876 | 1236.5792 | 1199.481824 | 11.7625 | 18.8578 | twist.s of (C29-H30; C29-H31); τm of H21-C20-C8-C16 and rock.w of (C32-H33; C34-H35) | |
| 1220.0711 | 1183.468967 | 14.9312 | 3.1637 | 1219.3148 | 1182.735356 | 19.5929 | 7.8591 | twist.s of (C26-H27; C26-H28) and of (C48-H49; C48-H50); δs of C51-H52; δm of C55-H56 and τm of C6-C5-C4-C36 | |
| 1201.9071 | 1165.849887 | 3.4760 | 6.7455 | 1199.1897 | 1163.214009 | 8.0422 | 13.5718 | δs of C40-H41; δm of C46-H47 and τm of H13-C12-C4-C3 | |
| 1185.406 | 1149.84382 | 15.4074 | 0.3306 | 1180.1007 | 1144.697679 | 18.7873 | 1.4104 | twist.s of (C48-H49; C48-H50); τm of H52-C51-C14-C57; scis.s of (C55-H56; C53-H54) | |
| 1179.6911 | 1144.300367 | 1.9628 | 1.119 | 1178.2209 | 1142.874273 | 2.8925 | 1.7435 | twist.m of (C48-H49; C48-H50); τm of H28-C26-C40-H41; δm of C51-H52 and τm of C42-C6-C5-C4 | |
| 1166.7314 | 1131.729458 | 14.6259 | 5.1602 | 1164.8183 | 1129.873751 | 9.3342 | 9.3366 | τm C1-C20-C8-C32 twist.s of (C29-H30; C29-H31); τm C3-C4-C12-C9 | |
| 1157.5523 | 1122.825731 | 15.5290 | 4.7107 | 1156.1874 | 1121.501778 | 28.1722 | 11.6347 | Scis.m of (C32-H33; C34-H35); δs of C9-H10 and τm C12-C4-C5-C6 | |
| 1148.5582 | 1114.101454 | 146.5450 | 3.5872 | 1149.5402 | 1115.053994 | 200.0358 | 6.6811 | νm of C62-O60 and βs C63-C64-C67-H68 | |
| 1144.341 | 1110.01077 | 178416 | 3.5877 | 1144.4015 | 1110.069455 | 27.0332 | 7.8819 | twist.m of (C26-H27; C26-H28); τm C4-C5-C6-C4; τm C10-C9-C20-C8 | |
| 1136.9705 | 1102.861385 | 1.6907 | 9.6148 | 1134.337 | 1100.30689 | 2.0658 | 19.6536 | τs H28-C26-C40-H41; τm H37-C36-C46-C47; scis.s (C32-H33; C34-H35) | |
| 1122.8634 | 1089.177498 | 21.5468 | 4.0892 | 1120.5923 | 1086.974531 | 35.6177 | 10.2656 | τm H33-C32-C8-C20; τm C9-C12-C4-C36; τm C41-C40-C26-C28 and τm C42-C6-C51-C48 | |
| 1099.4941 | 1066.509277 | 48.0338 | 2.0757 | 1096.2182 | 1063.331654 | 62.1695 | 5.261 | νm C12-O60; δm of C46-H47; δm of C51-H52; τm C9-C20-C1-C22 and twist.m of (C48-H49; C48-H50) | |
| 1091.4985 | 1058.753545 | 28.1743 | 1.6861 | 1085.2223 | 1052.665631 | 29.9371 | 3.0875 | νm C57-O15 and scis.s of (C53-H54; C55-H56) | |
| 1080.7072 | 1048.285984 | 92.4087 | 0.7097 | 1080.9064 | 1048.479208 | 144.3970 | 1.9949 | νm C12-O60; sym δs CH3; scis.s of (C32-H33; C34-H35) and τm C2-C1-C3-C40 | |
| 1071.7177 | 1039.566169 | 123.1938 | 6.7128 | 1073.0176 | 1040.827072 | 197.5919 | 15.9455 | νm C62-O60; δs of C46-H47 and asym δs of CH3 (C71) | |
| 1068.3452 | 1036.294844 | 9.8016 | 1.8104 | 1067.1028 | 1035.089716 | 24.1877 | 5.7115 | τs C67C64C63C71 | |
| 1050.9373 | 1019.409181 | 13.3402 | 0.7713 | 1048.853 | 1017.38741 | 37.6705 | 1.8533 | δm of C46-H47; δm of C64-H66; τm C67-C64-C63-C71 | |
| 1045.5983 | 1014.230351 | 69.2901 | 6.619 | 1044.7341 | 1013.392077 | 62.2356 | 12.9459 | twist.m of (C71-H73; C71-H74); δm of C26-H27; δm of C53-H54; δm of C48-H50 | |
| 1027.1407 | 996.326479 | 1.7797 | 5.289 | 1027.2885 | 996.469845 | 30.2585 | 3.8663 | twist.s (C34H35; C32H33) | |
| 1022.4549 | 991.781253 | 0.9472 | 2.7037 | 1020.7406 | 990.118382 | 6.3182 | 4.1772 | νm of C48-C51; asym δs of CH3; βm H66-C64-C63-C62 and τm H13-C12-C4-C5 | |
| 1017.7638 | 987.230886 | 30.0425 | 3.9798 | 1015.3161 | 984.856617 | 43.5319 | 8.8798 | asym δs of CH3; rock.s of (C29-H30; C29-H31); τm C9-C20-C1-C3 | |
| 1011.5509 | 981.204373 | 4.8801 | 6.6943 | 1009.814 | 979.51958 | 6.3114 | 13.7312 | βs C51-C14-C53-H54; asym δm of CH3 (C42); βs H58-C57-O15-C55 | |
| 1002.0581 | 971.996357 | 12.1626 | 2.5574 | 998.7131 | 968.751707 | 27.5923 | 6.2284 | νm of C46-C48; τm H47-C46-C48-C49; βm C1-C3-C40-C26 | |
| 994.6222 | 964.783534 | 14.7581 | 1.7537 | 993.1115 | 963.318155 | 22.8186 | 4.3633 | asym δm of CH3 groups; τm C3-C4-C5-C46; τm C48-C51-C6-C26 | |
| 984.7888 | 955.245136 | 9.9824 | 2.1081 | 982.8653 | 953.379341 | 23.0630 | 4.4849 | τm C32-C8-C29-H31; asym δm of CH3 groups; τm H13-C12-C9-H10 | |
| 935.5082 | 907.442954 | 21.5974 | 1.5821 | 933.456 | 905.45232 | 35.1689 | 4.3679 | rock.s of (C26-H27; C26-H28); asym δm of CH3; τm C40-C3-C1-C22 | |
| 894.4122 | 867.579834 | 6.7651 | 6.1001 | 892.2404 | 865.473188 | 16.1490 | 13.2213 | twist.s (C67-H69; C67-H70) and δs C64-H66 | |
| 888.7652 | 862.102244 | 7.1646 | 2.8098 | 886.3304 | 859.740488 | 9.5352 | 6.1863 | δs C64-H66; rock.m (C48-H49; C48-H50); twist.s (C67-H69; C67-H70) | |
| 866.5271 | 840.531287 | 1.1709 | 0.6223 | 870.9888 | 844.859136 | 1.8110 | 2.3985 | twist.s of (C53-H54; C55-H56) | |
| 863.4892 | 837.584524 | 11.2475 | 6.7108 | 862.9942 | 837.104374 | 10.4041 | 13.1553 | τm H52-C51-C48-H49; rock.m (C26-H27; C26-H28); rock.m (C22-H23; C22-H24); τm H45-C42-C6-H5 | |
| 843.0488 | 817.757336 | 17.4461 | 2.5204 | 843.0694 | 817.777318 | 32.2094 | 5.1332 | wagg.s (C34-H35; C32-H33) and τw O7=C2-C1-C22 | |
| 834.8182 | 809.773654 | 8.7574 | 3.1907 | 831.3156 | 806.376132 | 15.1706 | 6.936 | τs H47-C46-C5-C4; τs C48-C51-C6-H42 | |
| 813.7477 | 789.335269 | 1.0138 | 6.0149 | 810.0882 | 785.785554 | 0.7347 | 13.0197 | τm C26-C40-C3-C4 | |
| 801.2001 | 777.164097 | 32.6376 | 0.9129 | 802.8851 | 778.798547 | 51.1580 | 3.2321 | Sym δs CH groups on furan ring | |
| 772.7524 | 749.569828 | 40.1779 | 4.4199 | 769.619 | 746.53043 | 62.4072 | 8.3682 | τs of C71-C63-C62-O60; τm of H66-C64-C67-H69 | |
| 765.4691 | 742.505027 | 7.1326 | 7.398 | 765.0018 | 742.051746 | 11.7201 | 14.1992 | Sym δm CH on furan ring and τm C42-C6-C51-C48 | |
| 751.3513 | 728.810761 | 2.6045 | 2.4905 | 750.9877 | 728.458069 | 5.0319 | 4.4818 | τm C5-C4-C12-C9 and τm C34-C32-C8-C29 | |
| 738.9121 | 716.744737 | 11.6448 | 0.2055 | 739.1239 | 716.950183 | 16.1963 | 0.0788 | Asym δs CH on furan ring | |
| 722.1832 | 700.517704 | 12.3489 | 2.6117 | 723.4458 | 701.742426 | 18.8683 | 4.4984 | τm C1-C2-C34-C32; τm C4-C12-O60-C62 | |
| 686.9578 | 666.349066 | 5.4224 | 1.4738 | 685.8912 | 665.314464 | 10.7183 | 2.8493 | τm H58-C57-C14-C53 and τm C48-C51-C6-C42 | |
| 668.865 | 648.79905 | 12.8788 | 0.9188 | 667.6324 | 647.603428 | 18.4726 | 1.8119 | τm C9-C12-C4-C36 | |
| 646.4378 | 627.044666 | 11.8100 | 0.5746 | 646.7719 | 627.368743 | 21.9688 | 1.442 | βm C67-C64-C63-C71 | |
| 619.5628 | 600.975916 | 14.5359 | 2.821 | 617.9459 | 599.407523 | 19.3158 | 4.5248 | τs C53-C55-O15-C57 | |
| 616.8961 | 598.389217 | 4.4856 | 1.6795 | 615.6735 | 597.203295 | 10.3745 | 2.8885 | τs C57-C14-C51-C48 | |
| 590.7602 | 573.037394 | 2.2255 | 8.0984 | 590.8644 | 573.138468 | 4.8686 | 15.7435 | τm O60-C62-C63-C71; τm C26-C6-C5-C46 | |
| 545.9651 | 529.586147 | 0.9299 | 3.7502 | 549.5733 | 533.086101 | 3.8923 | 7.7962 | τm C62-C63-C64-C67; δm of CH3 (C71) | |
| 538.3894 | 522.237718 | 17.1612 | 0.4714 | 536.6383 | 520.539151 | 25.1977 | 1.1212 | τm C4-C5-C6-C51 | |
| 508.9443 | 493.675971 | 1.2889 | 2.069 | 507.5983 | 492.370351 | 1.4410 | 4.1594 | τm C3-C4-C5-C46; rock.m (C26-H27; C26-H28) | |
| 475.643 | 461.37371 | 1.2962 | 4.5398 | 474.4059 | 460.173723 | 2.4947 | 10.7229 | δs C16-C8-C29 | |
| 461.5318 | 447.685846 | 2.3465 | 0.597 | 461.4543 | 447.610671 | 4.0236 | 0.9512 | τm C48-C46-C5-C4 | |
| 451.0159 | 437.485423 | 2.9275 | 4.0628 | 448.867 | 435.40099 | 4.9702 | 8.8493 | δs C32-H33; τm C29-C8-C32-C34 | |
| 437.1112 | 423.997864 | 1.4877 | 1.6801 | 437.3603 | 424.239491 | 4.9702 | 2.869 | τm O60-C62-C63-C64 and rock.m (C26-H27; C26-H28) | |
| 416.2717 | 403.783549 | 7.0349 | 2.9785 | 413.098 | 400.70506 | 9.3286 | 5.9324 | τm C62-C63-C64-C67 | |
| 376.4872 | 365.192584 | 0.6057 | 1.5014 | 375.9518 | 364.673246 | 0.8549 | 2.7432 | δs C36-C4-C12 | |
| 359.436 | 348.65292 | 1.0513 | 0.2212 | 357.6319 | 346.902943 | 0.4099 | 3.4574 | τm C22-C1-C3-C40 | |
| 347.1844 | 336.768868 | 0.2931 | 1.3363 | 346.0298 | 335.648906 | 0.6318 | 1.8682 | Asym δm of CH3 groups | |
| 309.437 | 300.15389 | 1.4908 | 0.891 | 306.2399 | 297.052703 | 1.5054 | 1.1169 | βm C67-C64-C63-C71 | |
| 231.0043 | 224.074171 | 3.5498 | 0.8619 | 229.9752 | 223.075944 | 7.8008 | 1.6674 | βm O60-C62-C63-C64 | |
| 42.7727 | 41.489519 | 0.3353 | 1.5162 | 39.5275 | 38.341675 | 0.5007 | 4.2131 | twist.m of (C14-C57; C14-C53) | |
- δ = bending; τ = out of plane deformation; β = in plane deformation; w = weak; m = medium; s = strong; wagg. = wagging; twist. = twisting; rock. = rocking; scis. = scissoring; ν = stretching; sym = symmetrical and asym = anti-symmetrical.
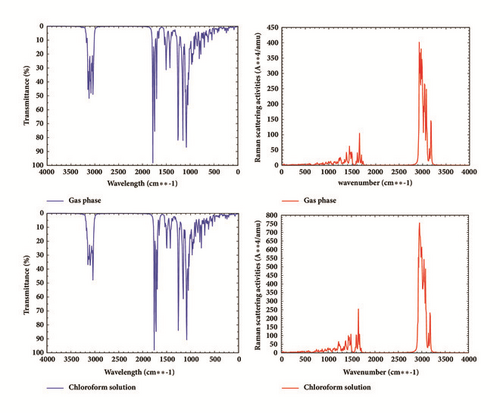
The C=O double bond gives rise to a very intense absorption band in IR spectrum. The position and intensity of this band range from 1870 cm−1 to 1540 cm−1 depending on the physical state, electronic, and mass effects of neighboring substituents, intra- and intermolecular interactions, and conjugations [29]. The C=O double bond absorption spectra were observed experimentally at 1720 cm−1 and 1664 cm−1 [1]. In this study, the vibrational mode of C=O was found at 1726.20 cm−1 and 1690.57 cm−1 gas phase and at 1701.01 cm−1 and 1667.59 cm−1 in chloroform. There is good agreement between the vibrational modes with experimental values.
4. Conclusion
In this study, the geometry optimization of Rubescin E has been carried out using ab initio HF and density functional theory DFT (B3LYP and B3PW91) methods in both gas phase and chloroform solution with the 6-311++G(d,p) basis set. The optimized parameters were compared to those of some existing groups of compound present in our molecule, since none of this have been done before for the title molecule and good agreement was found. In order to confirm the geometry of our molecule, the 3JH-H proton-proton coupling constant was evaluated and the results compared to experiment were similar. The calculated results have showed that Rubescin E possesses a HOMO-LUMO energy gap greater than 4, which indicate a hard molecule that can be used as an insulator in many electronic devices. We can also conclude from the HOMO-LUMO analysis that the electron can easily be transferred from the furan to tetrahydrofuran ring. The charge analysis performed using Mulliken population, CHepG, and NBO methods showed positive charge for all hydrogen atoms; it was observed that the most positive (respectively, negative) charge atoms were directly linked to the most negative (respectively, positive) charge atoms and also that all the carbon atoms linked to hydrogen were all negatively charged. The calculated first static hyperpolarizability was found to be more than four times greater than the reported value found in the literature for urea leading us to the conclusion that Rubescin E has very good NLO properties. The calculated optoelectronic properties show large values of refractive index, dielectric constant, and electrical susceptibility, leading us to the conclusion that Rubescin E has strong optical and phonon application. Good agreement was found between the calculated and experimental UV spectrum. The theoretical proton (1H) and carbon (13C) chemical shift values (with respect to TMS) were reported and compared with experimental data, showing a very good agreement for both 1H and 13C NMR. The calculated vibrational frequencies done using the B3LYP/6-311G(d,p) functional in both gas and chloroform solutions were all positive leading us to the conclusion that Rubescin E was stable. Approximate descriptions of the vibrational assignments were done in order to take out the different motions of atoms in the title molecule.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Acknowledgments
We are thankful to the Council of Scientific and Industrial Research (CSIR), India, for financial support through Emeritus Professor Scheme (Grant No. 21(0582)/03/EMR-II) to Prof. A.N. Singh of the Physics Department, Bahamas Hindu University, India, which enabled him to purchase the Gaussian Software. We are most grateful to Emeritus Prof. A.N. Singh for donating this software to Dr. Geh Wilson Ejuh, University of Dschang, IUT-FV Bandjoun, Cameroon.




