Volume 2019, Issue 1 4056204

Research Article

Open Access

Optimization on Nonlinear Dynamics of Gear Rattle in Automotive Transmission System

Mingxuan Liang,

Corresponding Author

Mingxuan Liang

[email protected]

orcid.org/0000-0001-6719-0126

College of Mechanical and Electrical Engineering, China Jiliang University, Hangzhou 310018, China cjlu.edu.cn

Search for more papers by this author

Ying Wang,

Ying Wang

College of Mechanical and Electrical Engineering, China Jiliang University, Hangzhou 310018, China cjlu.edu.cn

Search for more papers by this author

Tian Zhao,

Tian Zhao

College of Mechanical and Electrical Engineering, China Jiliang University, Hangzhou 310018, China cjlu.edu.cn

Search for more papers by this author

Mingxuan Liang,

Corresponding Author

Mingxuan Liang

[email protected]

orcid.org/0000-0001-6719-0126

College of Mechanical and Electrical Engineering, China Jiliang University, Hangzhou 310018, China cjlu.edu.cn

Search for more papers by this author

Ying Wang,

Ying Wang

College of Mechanical and Electrical Engineering, China Jiliang University, Hangzhou 310018, China cjlu.edu.cn

Search for more papers by this author

Tian Zhao,

Tian Zhao

College of Mechanical and Electrical Engineering, China Jiliang University, Hangzhou 310018, China cjlu.edu.cn

Search for more papers by this author

First published: 2019

https://doi.org/10.1155/2019/4056204

Citations: 9

Academic Editor: Chengzhi Shi

Share a link

Email
Wechat
Bluesky

Abstract

Recently, gear rattle noise is gradually becoming a nonignorable issue involving comfortableness in automotive transmission for a car. Generally, the rattle noise is influenced by nonlinear dynamic of multiple pairs of idler gears in the multistage gear transmission system. Optimization methods based on nonlinear rattle dynamic analysis are worthy of further study to control the noise. In this research, an equivalent rattle dynamic model of the idler gear is proposed, and the nonlinear rattle dynamic responses are solved based on the integral method. The effect laws of key factors on nonlinear dynamic performance are investigated by using a bifurcation diagram, spectrum map, and Poincaré map. Finally, the gear backlash, equivalent mass, and rotational speed are optimized based on Kriging surrogate model (KSM) and differential evolution (DE) algorithm by taking the minimization of the maximum rattle noise as the optimal object. It can be concluded that the rattle dynamics of the idler gear show rich nonlinear characteristics as the parameters change. The proposed method can not only reduce the sound pressure level of rattle noise but also provide a viable path and reference value for the low-noise design of the gear transmission system.

1. Introduction

The gear transmission system is one of the key components in power-train of the vehicle, and the low-noise design of the transmission is becoming a hot research issue [1]. In recent decades, as the reduction of meshing noise in the gear transmission system, the rattle noise problem is becoming more and more obvious, and it still needs to be studied in depth [2]. In an automotive transmission system, the unloaded idler gears are free in rotation and do not transmit any torque. They generally vibrate in a certain range of gear backlash when the rotational motion is transmitted from the output shaft of the engine to the input shaft of the gear transmission system, and they will impact with the active gears under some operating conditions, which can induce the impulsive phenomenon and rattle noise [3, 4]. Although the sound pressure of rattle noise is not as high as meshing noise, it is more likely to stimulate the hearing and affect the noise, vibration, and harshness (NVH) performance for their special frequency characteristics [5].

Although the impacts between the gears do not change the dynamic behavior of the driveline, it is widely believed that the rattle noise is particularly noticeable in the automotive multistage gear transmission system because of the influence of more nonlinear parameters. For one pair of the idler gear, the key factors affecting rattle noise are mainly gear backlash, moment of inertia of the idler gear, rotation speed of the active gear, and damping coefficient [6, 7]. The generation mechanism of rattle noise and corresponding suppression methods are still unclear so far in the automotive multistage transmission system. To study rattle dynamics between idler gears and at the same time reduce the sound pressure, on one hand, many efforts have focused on accurate description of rotation speed of active gears [8–10]. The fluctuation of rotation speed is usually affected by the change of engine power. The research studies are mainly to optimize the transfer function of the torsional excitation between the engine and the input shaft of gear transmission to make it more stable to reduce the vibration transmission through the driveline [11, 12]. Until now, the torsional excitation is often simplified as the 2nd order harmonic (H₂) excitation in most studies [13]. On the other hand, some investigations started from the equivalent dynamic model of impact effects between idler gears [14–16]. Rocca and Russo [14] elaborated the influence of gear backlash with periodic fluctuation on rattle noise based on a linear equivalent dynamic model. Fietkau and Bertsche [15] established a simplified model with Kelvin–Voigt method, and the influences of gear backlash and moment of inertia of idler gears on rattle noise were studied. The calculation functions of the resistance moment of lubricating oil on idler gears had been obtained theoretically and experimentally, and the relationship between resistance moment and rattle noise was analyzed in Brancati’s research [16]. Kadmiri et al. [17] and Shangguan et al. [18, 19] studied the mechanism of rattle noise through a gear rattle test rig, and the effects of lubricating oil damping on the gear impact were discussed deeply. Although these studies considered many other factors besides velocity fluctuation of driving gear, they mainly concerned the linear dynamics characteristics of related components. The influences of nonlinear factors between each parameter on rattle dynamic need to be studied in depth. Otherwise, some studies begun to pay attention to the nonlinear factors, but they were mainly based on the nonlinear dynamic model of single-pair gears by the numerical simulation method.

In fact, the total rattle noise for the multistage gear transmission system is not only produced by the single pair of gears but also it is derived from the superposition of several rattle noise sources with different sound levels in all pairs of idler gears, and some nonlinear factors between each pair of idler gears show coupling relationship. Therefore, it is necessary to analyze which kind of factor is more sensitive to the rattle noise in a multistage gear transmission system. Even if the influence of nonlinear factors on the rattle motion of idler gears is clarified, the mechanism of the total rattle noise is affected by many factors, and it is necessary to work on the whole driveline design in the multistage gear transmission system [20–22]. In order to deal with the influence of multiple coupling parameters, Harris et al. [23] established an impact dynamic model by using the elastic restorer between active gears and idler gears, in which the rattle threshold was verified, and the model can be applied for analysis of rattle noise in the transmission system. Johnson and Hirami [24] and Bozca and Fietkau [25] studied the effects of design parameters of idler gears on rattle noise based on the response surface model (RSM) of rattle noise. Rocca and Russo [14] established a gear impact dynamic model with 4 DOF, in which two factors of torsional stiffness of clutch and gear impact force were considered, and the influences of design parameters of clutch were simulated. The rattle dynamic model of impact effect with 5 DOF was established, and the influence of oil film squeezing of the idler gear was studied to reduce rattle noise in [26]. Although, the rattle noise can be decreased based on the dynamic model of a single pair of gear by optimizing design parameters, and the optimization research has laid foundation for the optimization of total rattle noise in the multistage transmission gear system. In fact, the mechanism of influence of nonlinear parameters on the total rattle is still unclear, and the optimization for a single pair of gear may affect the rattle noise of the other pairs of idler gears. Meanwhile, the multistage transmission gear system shows coupling nonlinear characteristics between each parameter, and the nonlinear optimization of coupling parameters needs to be further studied.

From the review of previous research work, it can be found that although the sound pressure level of rattle noise is not high compared to other meshing noises in a car, it is more likely to influence the NVH performance. Some nonlinear rattle dynamics can be explained based on linear dynamic of a single pair of gears by the simplified dynamic model. However, the total rattle noise of multistage gears is affected by all other pairs of idler gears. Furthermore, there is nonlinear coupling between the idler gears in each stage. In order to analyze and optimize multiple nonlinear coupling parameters to reduce the total rattle noise for the whole transmission system, an equivalent rattle dynamic model of a single pair of gears is established regarding the obvious rattle noise in a multistage transmission system in this paper. We intend to solve the modeling issue of nonlinear impact dynamics of the multistage gear transmission system and at the same time reduce the sound pressure level of rattle noise. The nonlinear rattle responses are solved by using the integral method, and the effect mechanisms of nonlinear parameters on rattle dynamics are described in depth by a bifurcation diagram, spectrum map, and Poincaré map. The surrogate model between total rattle noise and impact intensity is established based on KSM. Finally, the gear backlash, equivalent mass, and rotational speeds are optimized by taking the minimization of the maximum sound pressure level of total rattle noise as the optimal object by the DE algorithm, and the effects of the optimization algorithms are compared. The rest of the paper is organized as follows. In Section 2, the dynamic modeling approaches of gear rattle are outlined. In Section 3, we first introduce the specific parameter value of the gear rattle dynamic model, and then calculate nonlinear impact response and discuss the influence of each parameter in detail. Section 4 gives the optimization method on total rattle noise. Concluding remarks are summarized in Section 5.

2. Gear Rattle Modeling

A typical multistage gear transmission system in the vehicle is shown in Figure 1. When the transmission is working under a certain gear speed, the active gear for this gear speed will drive the corresponding idler gear rotating to transmit torque. The other active gears will drive the rest idler gears idling, and there is no torque transmission through these pairs of gears. With the speed fluctuation of the active gear and the change of gear backlash and other factors, the rattle noise will be generated when the teeth of active gear impact on the teeth surface of idler gears [1, 25]. The rattle dynamic model of the gears is established based on the following assumptions:

(1)
The rattle effects between gear teeth finish in a short moment, and the restitution coefficient is used to describe rattle action
(2)
The drag torque on the idler gear is constant when impact action is not occurred
(3)
The angular displacement of the active gear is simplified as harmonic excitation

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The typical structure of automotive transmission.

The equivalent dynamic model of a single pair of idler gear is established in Figure 2, in which R_b1 and R_b2 are the pitch radius of active gear and idler gear, respectively. I_g is the moment of inertia of the idler gear. y(t) is the equivalent displacement of active gear tooth. x(t) is the equivalent displacement of idler gear tooth. j is gear backlash.

The equivalent displacement along the tangential direction of pitch circle of the idler gear can be expressed as

\begin{matrix} x (t) = R_{b 2} θ (t), \end{matrix}

(1)

where θ(t) is the angular displacement of the idler gear. Before rattle effect occurs, the motion differential equation of the idler gear can be expressed as the following:

\begin{matrix} I_{g} \ddot{θ} (t) = - C, \end{matrix}

(2)

where C indicates drag torque of lubricating oil when the idler gear vibrates in the range of backlash of active gear teeth, which can be taken as a constant value. The motion differential equation of the idler gear in the range of backlash can also be expressed as

\begin{matrix} m \ddot{x} (t) = - F, \\ y (t) < x (t) < y (t) + j, \end{matrix}

(3)

where m is the equivalent mass of the idler gear,

m = I_{g} / R_{b 2}^{2}

and F is the equivalent resistance force of drag torque, F = C/R_b2. The impact effect of active gear tooth on idler gear tooth can be simplified to a harmonic excitation, and the excitation period is the ratio of rotation period of active gear to the number of gear teeth [26]. The displacement excitation y(t) of the active gear teeth can be expressed as

\begin{matrix} y (t) = H \cos (ω t - φ), \end{matrix}

(4)

where ω indicates gear-mesh frequency and H and φ are, respectively, equivalent amplitude and phase angle of angular displacement of the active gear. In this research, the impact effect between gear teeth is assumed to be a course of perfect elastic collision [27]. The relationship of rotational speed between active gear and idler gear can be expressed by restitution coefficient r as follows:

\begin{matrix} {\dot{x}}_{t^{+}} - {\dot{y}}_{t^{+}} = - r ({\dot{x}}_{t^{-}} - {\dot{y}}_{t^{-}}), \end{matrix}

(5)

where t⁻ and t⁺ are, respectively, instantaneous moments between active gear tooth and idler gear tooth before and after impact effect and r is the restitution coefficient. The impact intensity between gear teeth can be obtained as

\begin{matrix} I = m ({\dot{x}}_{t^{+}} - {\dot{x}}_{t^{-}}) . \end{matrix}

(6)

Compared with driving torque of the active gear, the impact force between gear teeth is very small, which can be assumed that it does not affect excitation function of the active gear, and the rotation speed of the active gear remains unchanged before and after impact effect occurs; thus,

{\dot{y}}_{t +} = {\dot{y}}_{t -}

. The relationship between impact intensity and rotation speed before and after impact effect occurs can be obtained as

\begin{matrix} I = m (1 + r) ({\dot{y}}_{t^{-}} - {\dot{x}}_{t^{-}}) . \end{matrix}

(7)

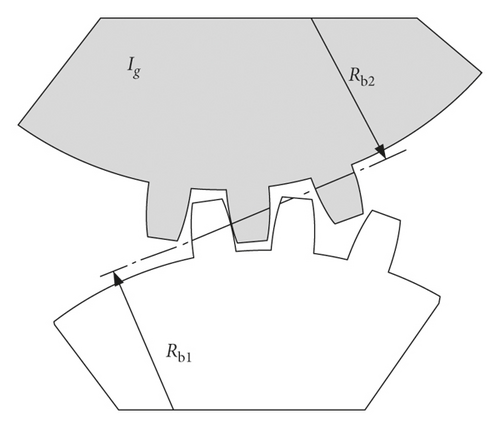
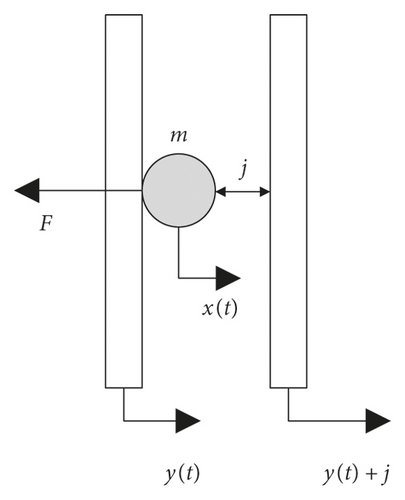
It can be seen from the above function that many factors may affect impact intensity of idler gears, in addition to rotation speed, equivalent mass of idler gear, and gear backlash, and drag torque of the idler gear may also influence impact intensity between the active gears and idler gears.

3. Nonlinear Rattle Dynamics

It is generally considered that a typical four-stroke engine has a stroke period of 80 ms under idle condition with rotation speed 1500 rpm in the vehicle system [28]. When the engine is disturbed by internal and external factor, the angular velocity and angular acceleration of active gears on the input shaft of the gear transmission system will fluctuate that are shown in Figure 3.

The fluctuation function of angular velocity of active gears on the input shaft can be expressed as

\begin{matrix} ω_{1} = \sum_{k = 1}^{\infty} H_{k} \sin (ω_{k n} t + ϕ_{k}), \end{matrix}

(8)

where H_k is the angular velocity amplitude of active gears, ω_kn is the fluctuation frequency, and ϕ_k is the phase angle. The angular acceleration can be obtained as follows:

\begin{matrix} α_{1} = \frac{d ω_{1}}{d t} . \end{matrix}

(9)

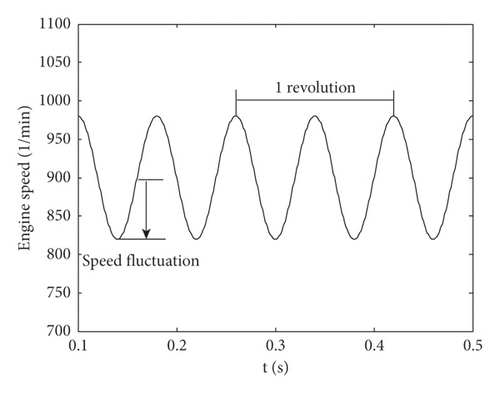
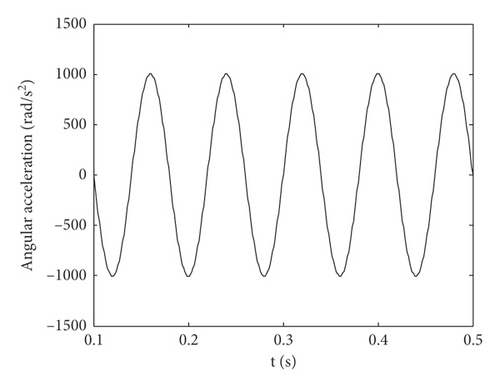
In this research, the restitution coefficient of idler gear teeth r = 0.65 is taken according to [27]. In order to analyze the nonlinear rattle mechanism of the idler gear, the first gear speed condition is taken as the research object, and the specific size and excitation parameter value are shown in Table 1.

Table 1. Parameter value under the first gear speed.

Parameters	R_b1 (mm)	R_b2 (mm)	I_g (kg·mm²)	r	j (mm)	Z₁	H₁ (rad/s)	T₁ (s)	ω_1n (rad/s)	φ₁ (mm)
Value	14.15	49.975	876	0.65	0.3	11	2π	0.08	2π/T	0

The numerical approaches are more effective to solve impact intensity for strong nonlinear characteristics of gear backlash and angular velocity fluctuation. To investigate the nonlinear behavior of impact intensity, the solutions of equation (7) are obtained by utilizing the integral method. Since the integral step size and initial parameters play an important role in the accuracy and efficiency of solution result, the iteration step size is defined as 10⁻⁶ sec after trial. The impact dynamic responses with different parametric values are solved, and the effects of parameters are obtained and analyzed comparatively in the following sections.

3.1. Effect of Gear Backlash

The gear backlash concerning the tooth gap between the active gear and idler gear is a common phenomenon in the gear transmission system. However, if the backlash size is out of the allowed value, the gear transmission system will be unstable in dynamic situations, and the position errors may appear in the gear chains. In this paper, the backlash is the shortest distance between nonworking tooth surfaces of two gears when they are about to contact with each other. The gear backlash usually tends to vary within a certain range in the automotive transmission system due to gear profile error and assembly error. In this study, the variation range of backlash is from 0.01 mm to 0.4 mm. We analyze the effect of gear backlash on rattle impact intensity and displacement. The bifurcation diagram of impact intensity I and equivalent displacement X of the idler gear with the change of gear backlash are obtained, as shown in Figures 4 and 5. In this study, the positive values of impact intensity represent that impact effects are on the right surface of active gear tooth, and the negative values representing impact are on the left surface. It can be seen that there are more than five times of impact effects in one period when gear backlash j is less than 0.06 mm, and the rattle impact actions are in an unordered state. With the increasing of gear backlash, the impact effects are decreased. There are four times of impact effects in one period for gear backlash j = [0.06, 0.1] mm, three times of impact effects for gear backlash j = (0.1, 0.18] mm, and two times of impact effects for gear backlash j = (0.18, 0.4] mm. Although the number of impact effects is decreasing, the impact intensity is enhanced, and the impact regularity is becoming more and more obvious with the increasing of gear backlash. As the gear backlash increases, the impact intensity is partially symmetrical to the zero position, but the impact displacement is asymmetrical. When the backlash is 0.4 mm, the impact displacement reaches the maximum.

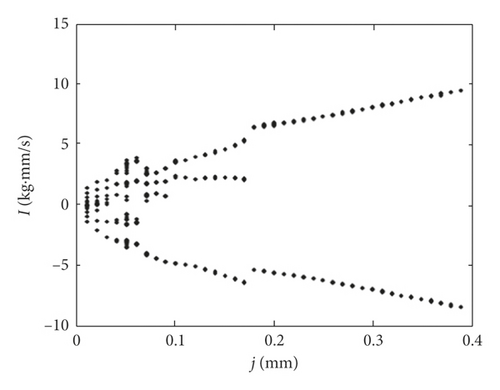
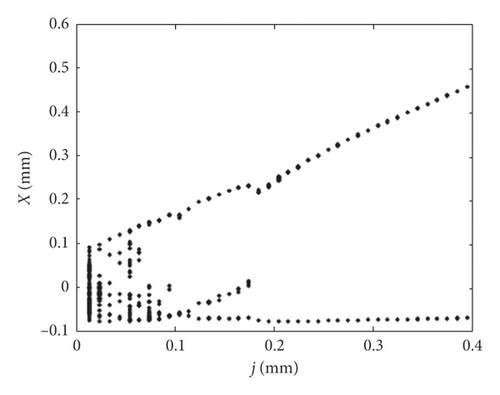
The equivalent displacement waveforms of active gear teeth and idler gear teeth are shown in Figure 6 for the gear backlash j = 0.2 mm, j = 0.15 mm, and j = 0.06 mm, respectively. Here, the sine waves in each figure indicate the equivalent displacements of the active gear teeth, and the upper sine waves represent the right surface of active gear tooth, and the lower sine waves represent the left surface. It can be seen that the equivalent displacements of idler gears fluctuate between the two surfaces of active gear teeth, and the number of impact effects increases obviously with the decreasing of gear backlash.

The motion frequency spectrograms of the idler gear under two different gear backlashes are shown in Figure 7. Since the stroke period T is 80 ms for the engine, according to the relationship between period and frequency, the base frequency f_base can be obtained as

\begin{matrix} f_{base} = \frac{1}{T} . \end{matrix}

(10)

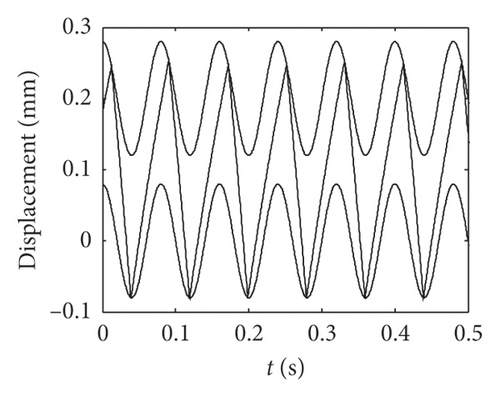
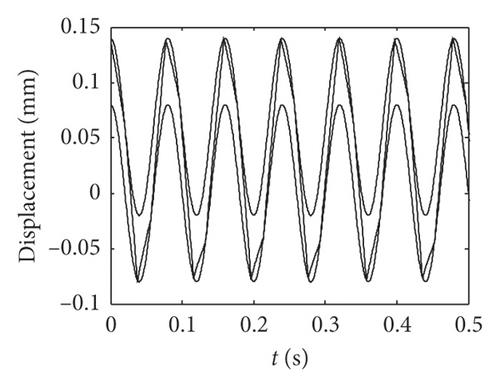
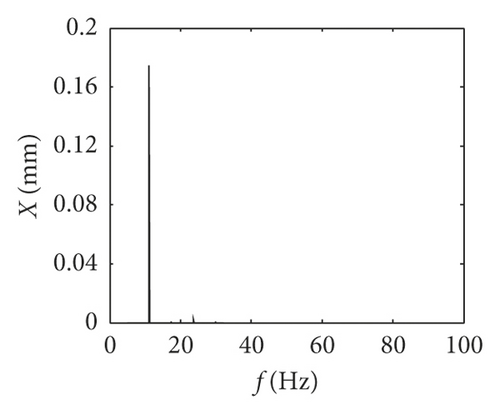
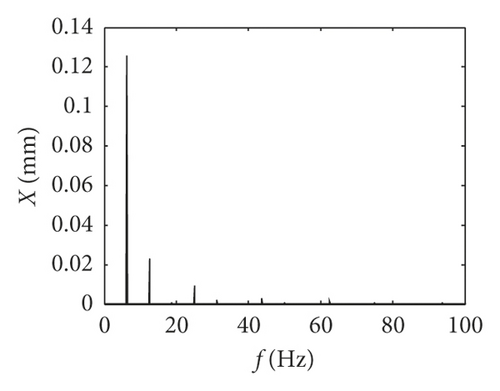
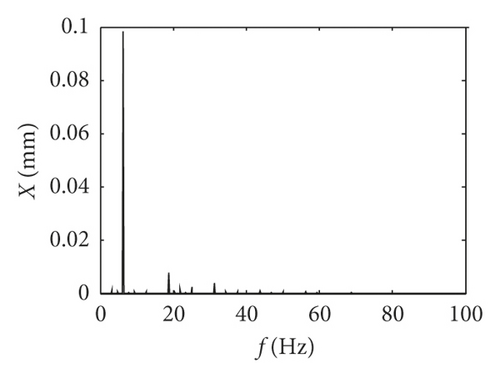
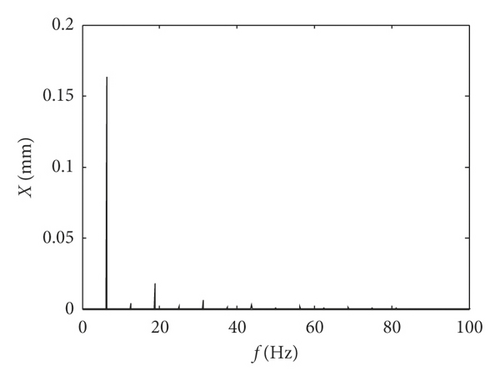
It can be seen from the equivalent displacement waveforms in Figure 6 and the frequency spectrogram in Figure 7 that when the gear backlash j = 0.2 mm, the idler gear tooth impacts only one time in one period, and the frequency components of idler gear tooth are mainly base frequency (12.5 Hz). When the gear backlash j = 0.15 mm, the idler gear tooth impacts three times in one period, and the main frequency components of idler gear tooth consist of base frequency (12.5 Hz), half frequency (6.25 Hz), and doubling frequency (25 Hz), as shown in Figure 7. When the gear backlash j = 0.06 mm, the idler gear tooth impacts four times in one period, the impact position is basically the same in each period, and the main frequency is half frequency of base frequency. Meanwhile, it can be seen that the equivalent displacements of the idler gear are gradually closer to the equivalent displacement of the active gear with the increasing in the number of impact effects by comparing the three equivalent displacements in Figure 6, and more frequency multiplier components will appear as the gear backlash decreases.

3.2. Effect of Idler Gear Mass

In order to analyze the effects of equivalent mass of the idler gear on nonlinear impact dynamic characteristics, the following constant parameter value is selected, the initial value of gear backlash j = 0.25 mm, and the initial design value of equivalent mass m of the idler gear for first gear speed is 0.35 kg according to Table 1 and equation (3). In this research, the equivalent mass of the idler gear can be adjusted according to the design requirements, and we change the equivalent mass of the idler gear from 0.1 kg to 2 kg to study the variation laws of impact dynamics. The bifurcation diagram of impact intensity and equivalent displacement of the idler gear with the change of equivalent mass are discussed when the equivalent mass changes from 0.1 kg to 2 kg, as shown in Figures 8 and 9. It can be seen that the impact intensities on left and right tooth surfaces enhance linearly with the increasing of equivalent mass of the idler gear, and the equivalent displacements of impact effect on both tooth surfaces remain at a relatively stable level, which means that there are very few influences of variation of equivalent mass on the equivalent displacement of the idler gear. Meanwhile, when the equivalent mass m = 0.1 kg, the impact motion state of the idler gear is period three, and with the increase of equivalent mass of the idler gear, the impact motion state changes to period two.

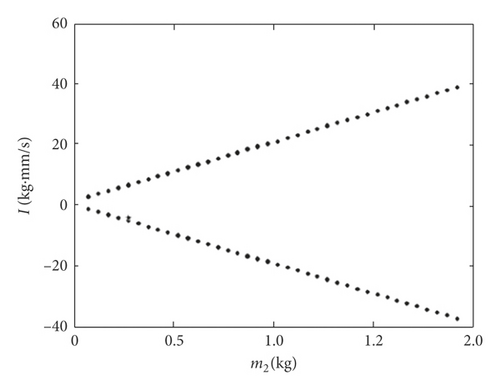
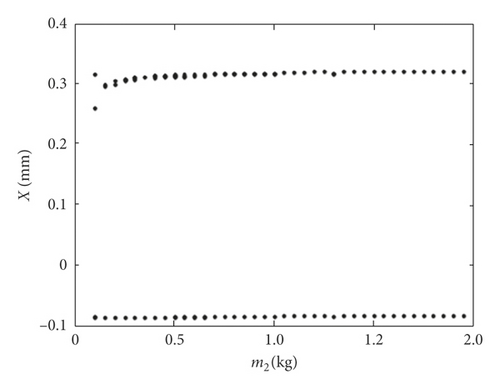
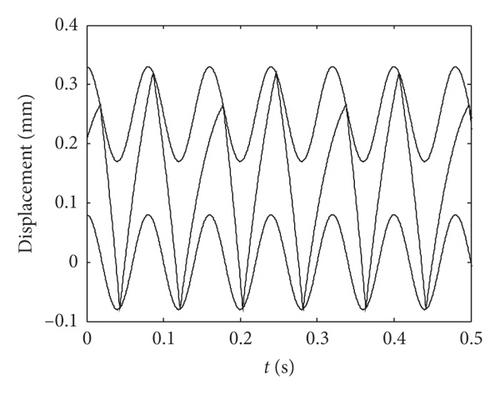
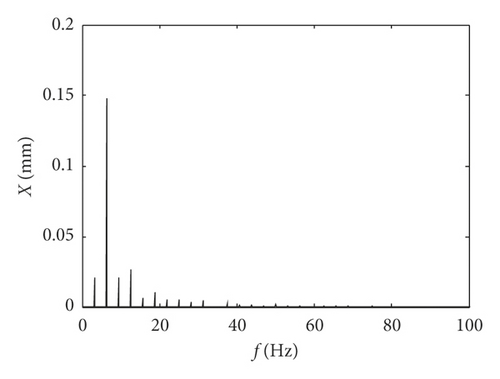
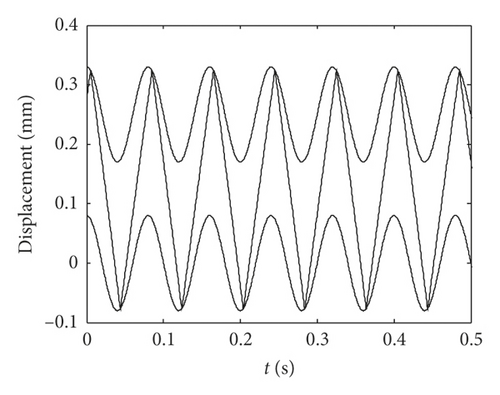
Figure 10 shows the impact equivalent displacement responses for the equivalent mass of the idler gear m = 0.1 kg, and it can be seen from the equivalent displacement diagram that the teeth of the idler gear impacts three times with the teeth of the active gear in each period. Although the idler gear impacts the same position on the left surface of idler gear teeth in the adjacent periods, it impacts different positions on the right surface, and the impact position on the right surface changes alternately, so it shows three different impact displacements when equivalent mass of the idler gear m = 0.1 kg in Figure 9. The impact displacement responses mainly consist of base frequency (12.5 Hz) and its harmonic frequencies. The impact equivalent displacement responses of the idler gear with the equivalent mass m = 1.5 kg are shown in Figure 11. Under this condition, there are also two times of impact effects in a period, and the corresponding impact positions for the adjacent periods are the same. The frequency spectrogram mainly contains half frequency (6.25 Hz), and the motion of idler gear is in the state of period two motion, and it shows two different impact displacements when m = (0.1, 2] kg in Figure 9.

3.3. Effect of Rotation Speed

The rotation speed of the active gear is not only affected by internal factors of the engine but also by external factors, such as air conditioning and headlights, and the rotation speed will fluctuate in certain range [29]. In order to analyze the influence of the fluctuation of rotation speed on rattle impact dynamics of the idler gear, we assume the amplitude of rotation speed H changes from 1 rad/s to 10 rad/s. The initial value of gear backlash j = 0.25 mm, and the initial design value of equivalent mass m of the idler gear is 0.35 kg. The change laws of impact intensity and impact displacement of the idler gear with the increasing of rotation speed of the active gear are shown in Figures 12 and 13. It can be seen that when the amplitude H of rotation speed varies in the range 1 rad/s-2 rad/s, the distributions of impact intensity I and displacement X all are like chaotic point clouds, which show that the system is in a random motion state. When H increases from 2 rad/s to 9 rad/s, there are two times of impact intensity and impact displacements in one period, and the system is in the period two motion state, and it is more suitable for the amplitude H to be controlled in this range. When H is in the range 9 rad/s-10 rad/s, the impact times are increased to 3 or 4 times in one period. From the general trend, the impact intensity and impact displacement increase gradually with the increasing of the amplitude of rotation speed.

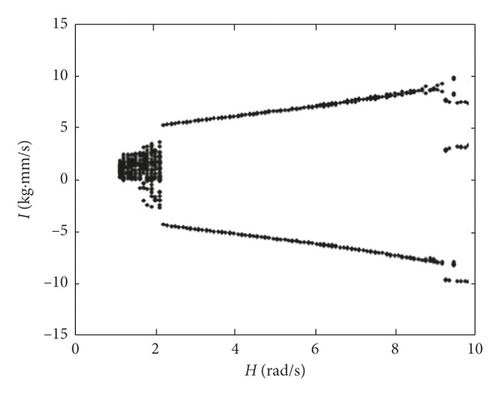
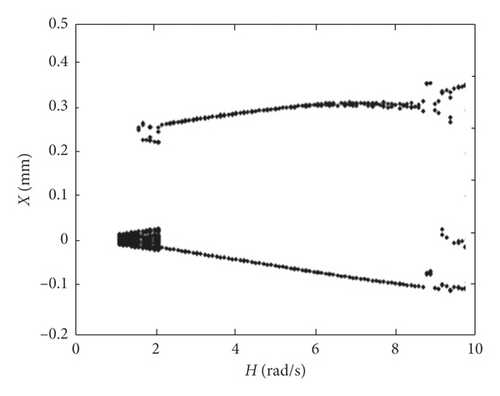
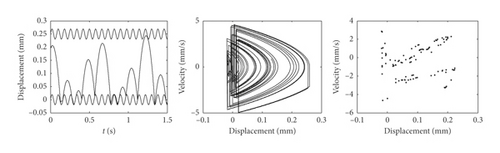
Figure 14 shows the nonlinear impact dynamic responses of the idler gear when the amplitude of rotation speed H = 1.5 rad/s. It can be found that in some periods, there is no impact effect between gear teeth, but there are multiple impact effects in some periods, and the number of impact effects on the left surface of the active gear teeth is significantly more than that on the right surface. The phase map shows infinite nonrepetition closed circles, and Poincaré map is a random scattered cloud distribution state, which can come to the conclusion that the impact of the idler gear is in a chaotic motion state.

4. Optimization on Total Rattle Noise

4.1. Rattle Noise Modeling of the Multistage Gear System

The schematic diagram of the automotive transmission system with multistage gears is shown in Figure 15. Z_1p, Z_2p, Z_3g, Z_4g, Z_5g, and Z_rp are six active gears under different gear speeds, and they are fixed on the input shaft or the output shaft, respectively, which can also be called fixed gears in this research. Z_1g, Z_2g, Z_3p, Z_4p, and Z_5p are the corresponding idler gears that are connected to the shafts by needle roller bearings, which can rotate freely around the gear shaft when they are in nonworking gear speed. The idler gears Z_3p and Z_4p will be fixed on the input shaft by the shift fork S₁ to transfer torque when they are in working gear speed, and the idler gears Z_1g, Z_2g, and Z_5p can also be controlled by the shift forks S₃ and S₂. When one of the idler gears is in the working gear speed, the other idler gears will idle, and rattle noise will be generated in the transmission system for the teeth of idler gears impacting on the surface of active gears. The relationship between sound pressure level of rattle noise l_p and impact intensity of the idler gear can be expressed as [1, 25]

\begin{matrix} l_{p} = 10 l g (k I + 10^{0.1 L_{basic}}), \end{matrix}

(11)

where k indicates the dimensionless correction factor. I is the impact intensity of the idler gear. L_basic indicates the basic sound pressure level. Table 2 shows the main parameter value of each gear in the transmission system.

Table 2. Structural parameter of each gear.

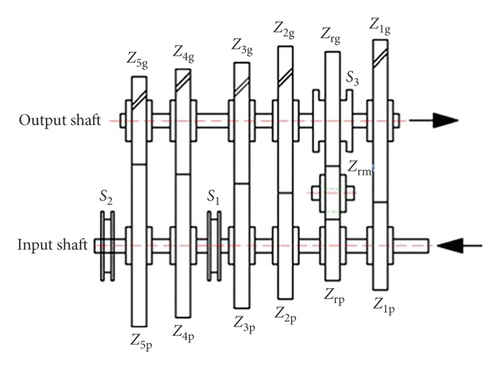
Gears	Z_1p	Z_2p	Z_3p	Z_4p	Z_5p	Z_1g	Z_2g	Z_3g	Z_4g	Z_5g
Number of teeth z	11	19	29	37	41	36	36	36	34	31
Equivalent mass of idler gear m (kg)	—	—	—	0.3608	0.3499	0.1659	0.1952	0.2473	—	—
Gear backlash j (mm)	0.20	0.20	0.20	0.20	0.20	—	—	—	—	—

4.2. Nonlinear Optimization of Rattle Noise

The maximum total rattle noise for a multistage gear system can be expressed as

\begin{matrix} Y_{r} = \max (l_{psumi}), \end{matrix}

(12)

where l_psumi is the total sound pressure level of rattle noise of the multistage gear under the ith working gear speed, n = 1,2, …, n and n represents the total number of working speeds in the transmission gear system. Here, the total sound pressure level of rattle noise l_psumi is superimposed by the rattle noise of all the idler gears, and it can be calculated according to the following function as [1, 25]

\begin{matrix} l_{psumi} = 10 l g (10^{0.1 l_{p 1}} + \dots + 10^{0.1 l_{p i - 1}} + 10^{0.1 l_{p i + 1}} + \dots + 10^{0.1 l_{p n}}), \end{matrix}

(13)

where l_pi indicates the sound pressure level of rattle noise in the meshing process of the ith idler gear, which can be obtained by the maximum impact intensity, as shown in equation (11).

It can be seen from the previous analysis that the total rattle noise in the automotive transmission system is affected by many coupling nonlinear factors, and it is difficult to be optimized directly. In this work, the Kriging surrogate model is built to describe the relationship between total rattle noise and nonlinear parameters, and the differential evolution algorithm is used to optimize the model. Figure 16 shows the general optimization procedure for determining the unknown parameters. Firstly, the initial Kriging surrogate model is generally built by samples of various idler gear parameters X and their corresponding maximum rattle noise response vector Y_r. Then, the optimization process can be characterized as follows based on the constructed Kriging surrogate model:

\begin{matrix} \{\begin{cases} find & X^{new} \\ Min & (Y_{r} (X^{new}) - Y_{r}^{true}) \\ s . t . & LB \leq X^{new} \leq UB and G (X^{new}) \leq 0, \end{cases} \end{matrix}

(14)

where Y_r represents the predicted rattle noise level based on the updated Kriging model.

Y_{r}^{true}

is the calculated response from equation (11). LB and UB are the upper and lower limits of design variables. The problem is to search the optimal value of design variables to minimize the objective function under the constraints of nonlinear inequality. Here, the equivalent mass vector m, gear backlash vector j of each pair of the idler gear, and the amplitude H of rotation speed of the active gear in the multistage gear system will be optimized in the process of design to reduce the maximum rattle noise level in the automotive transmission gear system. They can be synthesized into a single variable vector X as follows:

\begin{matrix} X = [m; j; H] . \end{matrix}

(15)

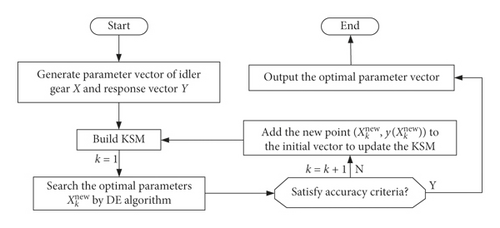
The complexity of the optimization model will increase obviously due to numerous nonlinear parameters in the multistage gear system, and the calculation cost will also be greatly increased. In order to search for the global optimal solution effectively, the DE algorithm is employed for the optimization of the updated Kriging model. Comparing to other evolutionary algorithms, DE algorithm is a more efficient global optimization algorithm by employing less stochastic approach in problem solving. The evolutionary process of the DE algorithm is similar to the genetic algorithm, including mutation, crossover, and selection operations, but the specific definitions of these operations are different from the genetic algorithm.

In the beginning of the DE algorithm, the population can be initialized as follows [30]:

\begin{matrix} \{X_{i} (0) |x_{i, j}^{L} \leq x_{i, j} (0) \leq x_{i, j}^{U}; i = 1,21,2, \dots, N; j =, \dots, D\}, \end{matrix}

(16)

where X_i(0) represents the ith individual and j represents the jth dimension. x_i,j(0) can be obtained as

\begin{matrix} x_{i, j} (0) = x_{i, j}^{L} + rand (0,1) (x_{i, j}^{U} - x_{i, j}^{L}), \end{matrix}

(17)

where

x_{i, j}^{U}

and

x_{i, j}^{L}

represents the upper and lower bounds of the jth dimension and rand(0,1) means taking random numbers between interval [0, 1].

The common difference strategy in the DE algorithm is to randomly select two different individuals in the population, and then the vector difference is scaled to perform vector synthesis with the individual to be mutated. For each target vector V_i(g + 1), the mutant vector can be produced by the following function:

\begin{matrix} V_{i} (g + 1) = X_{r 1} (g) + F (X_{r 2} (g) - X_{r 3} (g)), \end{matrix}

(18)

where i, r1, r2, r3 ∈{1,2, …, NP} and NP is the number of population. F is the scaling factor, which is usually taken in the range [0.5, 1]. g indicates the gth generation.

The purpose of the crossover operation is to randomly select individuals, which can generate a trial vector by replacing certain parameters of the target vector with the corresponding parameters of a randomly generated mutant vector:

\begin{matrix} U_{i, j} (g + 1) = \{\begin{cases} V_{i, j} (g + 1), & if rand (0,1) \leq C R, \\ V_{i, j} (g), & otherwise, \end{cases} \end{matrix}

(19)

where CR is the crossover probability, 0.85 ≤ CR ≤ 1, i = 1,2, …, M and M is the number of parameters to be optimized. The strategy of greedy selection is employed in the DE algorithm, which can ensure a better individual as a new individual to replace the target vector in the next generation.

\begin{matrix} X_{i, j} (g + 1) = \{\begin{cases} X_{i} (g + 1), & if f (U_{i} (g + 1)) \leq f (X_{i} (g)), \\ X_{i} (g) . \end{cases} \end{matrix}

(20)

Then, the model is continuously updated by adding new data point until it is sufficiently accurate criterion. The optimal parameter vector can be obtained to rebuild the Kriging model after some generations of mutation, crossover, and selection operations. In this paper, the traditional optimization algorithms for the nonlinear dynamics, such as general simulated annealing (SA) and genetic algorithm (GA), are employed to compare with the proposed method. The harmonic excitation parameters are selected as follows: the amplitude of angular velocity H = 2π rad/s, the phase angle φ₁ = 0, the restitution coefficient r = 0.65, and the drag force of the idler gear F = 14.5 N. Figure 17 shows the iterative convergence process of fitness value by using SA, GA, and DE, respectively, for the optimization of sound pressure level of rattle noise in the transmission system.

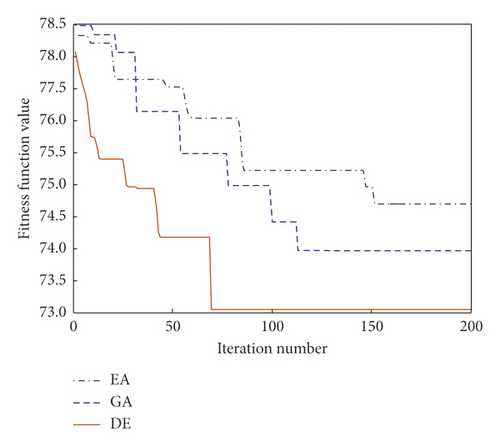
It can be found that the fitness values of the three optimization algorithms are close to each other in the beginning. Since the rattle noise of a multistage gear contains many coupling nonlinear factors, it require that the optimization algorithm should be designed to minimize time complexity and convergence speed, and more considerations should be given to the ability of the optimization algorithm to jump out of local optimal solution. However, the SA is insufficient in global searching ability, and it is not efficient. The GA is insufficient and precocious in local searching ability. Based on mutation and selection operator of the genetic algorithm, the solution group is constantly improved. The optimal solution is poorer by using SA, and the convergence speed is slower. Although the convergence speed is slightly faster by using GA, the algorithm will fall into local optimal solution after 110 iterations, and the optimization process is more likely to be precocious. In this research, the DE is adopted based on the aforementioned algorithm flow, which can availably avoid repeated search. Only after 65 iterations, the algorithm converges to a more optimal solution, which can meet the application conditions, and the ultimate solution obtained by DE is the most ideal in the three algorithms. It can be seen that the efficiency and accuracy of DE are greatly improved compared with common genetic algorithms.

The initial total sound pressure level of rattle noise under the first five gear speeds in the transmission system can be calculated based on initial design parameters in Table 1, and the obtained sound pressure level of rattle noise for first five idler gears is as follows: L_p = 75.49, 74.55, 77.41, 74.94, and 75.91 dB. It can be seen that the maximum sound pressure level of rattle noise is 77.41 dB, which is superimposed by the other idle gears when the system works under the third gear speed. After the initial design parameters are optimized, the total sound pressure level of gear rattle noise decreases obviously, and the optimal values of equivalent mass of each idler gear are m = 0.20, 0.15, 0.17, 0.14, and 0.13 kg, and the optimal values of gear backlash of each idler gear are j = 0.10, 0.13, 0.33, 0.14, and 0.15 mm. Although the reduction of equivalent mass and gear backlash can decrease sound pressure level of rattle noise of a single pair of gears, the total rattle noise of the whole transmission gear system is affected by complex impact of each pair of the idler gear. Under the optimal variable values, the total rattle noises of each idler gear are, respectively, equal to 73.21, 73.34, 73.40, 73.21, and 73.34 dB. Compared with the initial design parameters, the maximum reduction of rattle noise is near to 4 dB, and the relative declines are 3.0%, 1.6%, 5.2%, 2.1%, and 3.4% for each gear idler.

5. Conclusion

This research aims at tackling the issue of gear rattle mechanisms of the multistage transmission system. The nonlinear dynamic model of a single pair of idler gear is established, and the effect laws of gear parameters on nonlinear impact responses are analyzed by using the integral method, and the key influencing factors, including the gear backlash, equivalent mass of idler gear, and rotation speed of active gear, are discussed based on the bifurcation diagram, spectrum map, and Poincaré map. The Kriging surrogate model between total rattle noise and nonlinear parameters is presented, and the DE algorithm is employed to optimize the surrogate model by taking minimization of the maximum of sound pressure level of rattle noise as the optimal object. It can be concluded that the rattle dynamics of the idler gear show rich nonlinear characteristics as the parameters change. The achieved effect indicates that the proposed method can not only reduce the sound pressure level of rattle noise but also provide a viable path and reference value for the low-noise design of the gear transmission system.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (51705494) and the Natural Science Foundation of Zhejiang Province, China (Grant no. LQ17E050005).

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Bozca M., Transmission error model-based optimisation of the geometric design parameters of an automotive transmission gearbox to reduce gear-rattle noise, Applied Acoustics. (2018) 130, no. 15, 247–259, https://doi.org/10.1016/j.apacoust.2017.10.005, 2-s2.0-85030873228.
10.1016/j.apacoust.2017.10.005
Web of Science® Google Scholar
2 De la Cruz M., Theodossiades S., and Rahnejat H., An investigation of manual transmission drive rattle, Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-Body Dynamics. (2010) 224, no. 2, 167–181, https://doi.org/10.1243/14644193jmbd232, 2-s2.0-77953897576.
10.1243/14644193JMBD232
Web of Science® Google Scholar
3 Liu X.-L., Shangguan W.-B., Jing X., and Ahmed W., Vibration isolation analysis of clutches based on trouble shooting of vehicle accelerating noise, Journal of Sound and Vibration. (2016) 382, 84–99, https://doi.org/10.1016/j.jsv.2016.07.008, 2-s2.0-84979256977.
10.1016/j.jsv.2016.07.008
Web of Science® Google Scholar
4 Theodossiades S., De la Cruz M., and Rahnejat H., Prediction of airborne radiated noise from lightly loaded lubricated meshing gear teeth, Applied Acoustics. (2015) 100, 79–86, https://doi.org/10.1016/j.apacoust.2015.06.014, 2-s2.0-84941996239.
10.1016/j.apacoust.2015.06.014
Web of Science® Google Scholar
5 Baumann A., Fietkau P., Bertsche B. et al., Reduction of the gear-rattle noise level of automotive transmissions using innovative gear lubricants, Proceedings of the International VDI Congress Transmissions in Vehicles, 2010, Friedrichshafen, Germany, 373–393.
Google Scholar
6 Theodossiades S., Tangasawi O., and Rahnejat H., Gear teeth impacts in hydrodynamic conjunctions promoting idle gear rattle, Journal of Sound and Vibration. (2007) 303, no. 3-5, 632–658, https://doi.org/10.1016/j.jsv.2007.01.034, 2-s2.0-34247182078.
10.1016/j.jsv.2007.01.034
Web of Science® Google Scholar
7 Li L., Lu Z., Liu X.-L., Sun T., Jing X., and Shangguan W.-B., Modeling and analysis of friction clutch at a driveline for suppressing car starting judder, Journal of Sound and Vibration. (2018) 424, 335–351, https://doi.org/10.1016/j.jsv.2018.03.011, 2-s2.0-85044611943.
10.1016/j.jsv.2018.03.011
Web of Science® Google Scholar
8 Singh R., Xie H., and Comparin R. J., Analysis of automotive neutral grear rattle, Journal of Sound and Vibration. (1989) 131, no. 2, 177–196, https://doi.org/10.1016/0022-460x(89)90485-9, 2-s2.0-0024964708.
10.1016/0022-460X(89)90485-9
Web of Science® Google Scholar
9 Dogan S. N., Ryborz J., and Bertsche B., Design of low-noise manual automotive transmissions, Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics. (2006) 220, no. 2, 79–95, https://doi.org/10.1243/14644193jmbd10, 2-s2.0-33947599520.
10.1243/14644193JMBD10
Web of Science® Google Scholar
10 Baudin S., Rémond D., Antoni J., and Sauvage O., Non-intrusive rattle noise detection in non-stationary conditions by an angle/time cyclostationary approach, Journal of Sound and Vibration. (2016) 366, no. 31, 501–513, https://doi.org/10.1016/j.jsv.2015.11.044, 2-s2.0-84957430624.
10.1016/j.jsv.2015.11.044
Web of Science® Google Scholar
11 Yoon J.-Y. and Kim B., Gear rattle analysis of a torsional system with multi-staged clutch damper in a manual transmission under the wide open throttle condition, Journal of Mechanical Science and Technology. (2016) 30, no. 3, 1003–1019, https://doi.org/10.1007/s12206-016-0204-8, 2-s2.0-84961194244.
10.1007/s12206-016-0204-8
Web of Science® Google Scholar
12 Li L. and Singh R., Analysis of start-up transient for a powertrain system with a nonlinear clutch damper, Mechanical Systems and Signal Processing. (2015) 62-63, 460–479, https://doi.org/10.1016/j.ymssp.2015.03.001, 2-s2.0-84928612979.
10.1016/j.ymssp.2015.03.001
Web of Science® Google Scholar
13 Barthod M., Hayne B., Tébec J.-L., and Pin J.-C., Experimental study of dynamic and noise produced by a gearing excited by a multi-harmonic excitation, Applied Acoustics. (2007) 68, no. 9, 982–1002, https://doi.org/10.1016/j.apacoust.2006.04.012, 2-s2.0-34249025427.
10.1016/j.apacoust.2006.04.012
Web of Science® Google Scholar
14 Rocca E. and Russo R., Theoretical and experimental investigation into the influence of the periodic backlash fluctuations on the gear rattle, Journal of Sound and Vibration. (2011) 330, no. 20, 4738–4752, https://doi.org/10.1016/j.jsv.2011.04.008, 2-s2.0-79959949928.
10.1016/j.jsv.2011.04.008
Web of Science® Google Scholar
15 Fietkau P. and Bertsche B., Influence of tribological and geometrical parameters on lubrication conditions and noise of gear transmissions, Mechanism and Machine Theory. (2013) 69, 303–320, https://doi.org/10.1016/j.mechmachtheory.2013.06.007, 2-s2.0-84880287669.
10.1016/j.mechmachtheory.2013.06.007
Web of Science® Google Scholar
16 Brancati R., Rocca E., and Russo R., A gear rattle model accounting for oil squeeze between the meshing gear teeth, Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering. (2005) 219, no. 9, 1075–1083, https://doi.org/10.1243/095440705x34757, 2-s2.0-27444440355.
10.1243/095440705X34757
Web of Science® Google Scholar
17 Kadmiri Y., Rigaud E., Perret-Liaudet J., and Vary L., Experimental and numerical analysis of automotive gearbox rattle noise, Journal of Sound and Vibration. (2012) 331, no. 13, 3144–3157, https://doi.org/10.1016/j.jsv.2012.02.009, 2-s2.0-84859158821.
10.1016/j.jsv.2012.02.009
Web of Science® Google Scholar
18 Shangguan W.-B., Liu X.-L., Yin Y., and Rakheja S., Modeling of automotive driveline system for reducing gear rattles, Journal of Sound and Vibration. (2018) 416, no. 3, 136–153, https://doi.org/10.1016/j.jsv.2017.07.052, 2-s2.0-85044632653.
10.1016/j.jsv.2017.07.052
Web of Science® Google Scholar
19 Shangguan W.-B., Liu X.-L., Rakheja S., and Hou Q., Effective utilizing axial nonlinear characteristics of diaphragm spring and waveform plate to enhance breakaway performances of a clutch, Mechanical Systems and Signal Processing. (2019) 125, 123–141, https://doi.org/10.1016/j.ymssp.2018.05.060, 2-s2.0-85048419641.
10.1016/j.ymssp.2018.05.060
Web of Science® Google Scholar
20 Wu H. and Wu G., Driveline torsional analysis and clutch damper optimization for reducing gear rattle, Shock and Vibration. (2016) 2016, 24, 8434625, https://doi.org/10.1155/2016/8434625, 2-s2.0-84955498073.
10.1155/2016/8434625
Web of Science® Google Scholar
21 Liang M. X., Hu J. H., Li S. Q. et al., Topology optimization of transmission gearbox under multiple working loads, Advances in Mechanical Engineering. (2018) 10, no. 11, 1–7, https://doi.org/10.1177/1687814018813454, 2-s2.0-85057188874.
10.1177/1687814018813454
Web of Science® Google Scholar
22 Wu G. and Luan W., The impact of gear meshing nonlinearities on the vehicle launch shudder, SAE International Journal of Commercial Vehicles. (2015) 8, no. 1, 1–12, https://doi.org/10.4271/2015-01-0610, 2-s2.0-84952893488.
10.4271/2015-01-0610
Google Scholar
23 Haris A., Motato E., Mohammadpour M. et al., On the effect of multiple parallel nonlinear absorbers in palliation of torsional response of automotive drivetrain, International Journal of Non-linear Mechanics. (2017) 96, 22–35, https://doi.org/10.1016/j.ijnonlinmec.2017.06.008, 2-s2.0-85027887199.
10.1016/j.ijnonlinmec.2017.06.008
Web of Science® Google Scholar
24 Johnson O. and Hirami N., Diagnosis and objective evaluation of gear rattle, 911082, Proceedings of the 1991 SAE Noise and Vibration Conference, May 1991, Traverse City, Michigan, USA, 381–396.
Google Scholar
25 Bozca M. and Fietkau P., Empirical model based optimization of gearbox geometric design parameters to reduce rattle noise in an automotive transmission, Mechanism and Machine Theory. (2010) 45, no. 11, 1599–1612, https://doi.org/10.1016/j.mechmachtheory.2010.06.013, 2-s2.0-77957898665.
10.1016/j.mechmachtheory.2010.06.013
Web of Science® Google Scholar
26 Ottewill J. R., Neild S. A., and Wilson R. E., An investigation into the effect of tooth profile errors on gear rattle, Journal of Sound and Vibration. (2010) 329, no. 17, 3495–3506, https://doi.org/10.1016/j.jsv.2010.03.014, 2-s2.0-77951112821.
10.1016/j.jsv.2010.03.014
Web of Science® Google Scholar
27 Barthod M., Hayne B., Tébec J.-L., and Pin J.-C., Experimental study of gear rattle excited by a multi-harmonic excitation, Applied Acoustics. (2007) 68, no. 9, 1003–1025, https://doi.org/10.1016/j.apacoust.2006.04.011, 2-s2.0-34249026047.
10.1016/j.apacoust.2006.04.011
Web of Science® Google Scholar
28 Huang H. B., Li R. X., Huang X. R., Lim T. C., and Ding W. P., Identification of vehicle suspension shock absorber squeak and rattle noise based on wavelet packet transforms and a genetic algorithm-support vector machine, Applied Acoustics. (2016) 113, no. 1, 137–148, https://doi.org/10.1016/j.apacoust.2016.06.016, 2-s2.0-85008339642.
10.1016/j.apacoust.2016.06.016
Web of Science® Google Scholar
29 Johnsson R., Odelius J., and Rantatalo M., A new test track for automotive squeak and rattle (S&R) detection, Applied Acoustics. (2014) 80, 79–85, https://doi.org/10.1016/j.apacoust.2014.01.010, 2-s2.0-84894588012.
10.1016/j.apacoust.2014.01.010
Web of Science® Google Scholar
30 Tsai J.-T., Improved differential evolution algorithm for nonlinear programming and engineering design problems, Neurocomputing. (2015) 148, 628–640, https://doi.org/10.1016/j.neucom.2014.07.001, 2-s2.0-84908072432.
10.1016/j.neucom.2014.07.001
Web of Science® Google Scholar

Citing Literature

All articles

Optimization on Nonlinear Dynamics of Gear Rattle in Automotive Transmission System

Abstract

1. Introduction

2. Gear Rattle Modeling