1. Introduction

During the last decade, fractional calculus has emerged as a model for a broad range of nonclassical phenomena in the applied sciences and engineering [1–5]. Along with the expansion of numerous and even unexpected recent applications of the operators of the classical fractional calculus, the generalized fractional calculus is another powerful tool stimulating the development of this field [6–8]. The notion “generalized operator of fractional integration” appeared first in the papers of the jubilarian professor S. L. Kalla in the years 1969-1979 [9, 10]. A notable reference is the book by professor Kiryakova [11]. Later, generalized fractional operator was used successfully in papers of Mura and Mainardi [12] to model a class of self-similar stochastic processes with stationary increments, which provided models for both slow- and fast-anomalous diffusion. A brief review of generalized fractional calculus is surveyed in [8] and further generalizations of fractional integrals and derivatives are presented by Agrawal in [13]. In the definition of generalized fractional operator, more peculiar kernels are used, which include the classical power kernel function as a special case. Due to the special formulation, all known fractional integrals and derivatives and other generalized integration and differential operators, such as Hadamard operator and the Erdélyi-Kober operator, in various areas of analysis happened to fall in the framework of this generalized fractional calculus. It is shown in [13] that many integral equations can be written and solved in an elegant way using the generalized fractional operator.

Differential and integral equations with generalized fractional operators have been investigated by many authors from theoretical and application aspects [6, 11, 12, 14–16]. In [12, 17, 18], analytical form solutions of some of these differential and integral equations are given based on transmutation method, Mittag-Leffler function, Mainardi function, and H Fox functions. However, the analytical form solutions are very complicated with infinity serials or integrations, which makes them not suitable for fast computing, while numerical methods are more practical for these equations in applications. In [19], Xu proposes a finite difference scheme for time-fractional advection-diffusion equations with generalized fractional derivative [19]. Later, a finite difference scheme and an analytical solution are studied for generalized time-fractional diffusion equation by Xu and Argrawal [20, 21]. These schemes are based on finite difference discretization for first order derivative, which converge with order no more than 2.

Numerical methods with high order convergence have also been developed for fractional differential equations, e.g., spectral method [22], discontinuous Galerkin method [23], and wavelet method [24]. However, they have not yet been applied to fractional differential equations with generalized fractional operator. Among these, spectral method has been confirmed to be efficient and of high accuracy for some fractional differential equations. To name a few, in [25–27], Liu and his cooperators proposed a spectral approximation method to fractional derivatives and studied spectral methods for time-fractional Fokker-Planck equations, Riesz space fractional nonlinear reaction-diffusion equations. Li and Xu proposed a spectral method for time-space fractional diffusion equation [22]. Doha studied a spectral collocation method for multiterm fractional differential equations [28]. Zayernouri and Karniadakis proposed a spectral method for fractional ODEs based on polyfractonomials [29]. Zhao and Zhang studied the super-convergence property of spectral method for fractional differential equations [30]. Xu, Hesthaven, and Chen proposed multidomain spectral methods for space and time-fractional differential equations separately [23, 31]. Recently, efficient spectral-Galerkin algorithms are developed by Mao and Shen to solve multidimensional fractional elliptic equations with variable coefficients in conserved form as well as nonconserved form [32]. The classical fractional derivative of any power function can be expressed analytically. This indicates that fractional derivative of any function in polynomial spaces can be evaluated exactly. However, the definition of generalized fractional derivative is more complicated than classical fractional derivative. It is far more difficult to construct a direct spectral approximation to the generalized fractional derivative. In this paper, we firstly study fractional derivative of Jacobi polynomials and derive a general formula for fractional derivative of Jacobi polynomial of any order. Through a suitable variable transform technique, spectral approximation formulas are proposed for generalized fractional operators based on Jacobi polynomials. Then, operational matrices are constructed and efficient spectral collocation methods are proposed for the generalized fractional differential and integral equations appearing in the references and applications.

The rest of the current paper is organized as follows: In Section 2, we introduce the definitions of different generalized fractional operators, and some of their properties are also given. In Section 3, a general formula for fractional derivative of Jacobi polynomial of any order is derived. A spectral approximation method for generalized fractional operators is proposed and operational matrices are constructed. In Section 4, collocation methods are proposed for several differential and integral equations. Numerical experiments are carried out to verify the accuracy and efficiency of the methods. Finally, we draw our conclusions in Section 5.

2. Notations and Definitions

We first introduce some definitions and properties of fractional operators.

Based on the fractional integral, Riemann-Liouville and Caputo derivatives can be defined in the following way.

In investigations of dual integral equations in some applications, the modifications of Riemann-Liouville fractional integrals and derivatives are widely used. The important cases include Hadamard fractional operators and Erdélyi-Kober fractional operators.

Riemann-Liouville fractional integro-differentiation is formally a fractional power (d/dx)^α of the differentiation operator d/dx and is invariant relative to translation if considered on the whole axis. Hadamard suggested a construction of fractional integro-differentiation which is a fractional power of the type (x(d/dx)) ^α. This construction is well suited to the case of the half-axis and invariant relative to dilation [7, §18.3]. Thus Hadamard introduced fractional integrals of the following form.

The E-K fractional derivative of order α is defined in the following form.

In order to unify these definitions, Agrawal [13] proposed a new definition which includes most of them as special cases.

In this definition, if we set z(s) = s,   w(s) = 1, it reduces to the classical Riemann-Liouville fractional integral. Similarly, setting z(s) = log⁡(s), w(s) = s^μ will lead to Hadamard integral and z(s) = s^β,   w(s) = s^βγ will lead to E-K fractional integral with a factor t^βα.

3. Spectral Approximation of Generalized Fractional Operator

In this section, we will first study fractional derivative/integral of Jacobi polynomials and then derive a spectral approximation for generalized fractional operators based on Agrawal’s definitions. Fractional derivatives/integrals of others type can be obtained as special cases.

3.2. Spectral Approximation to Generalized Fractional Operators

We assume z(x) and w(x) are positive monotone functions and z, w ∈ C[a, b]. Obviously, z(x) and w(x) are invertible. The following lemmas can be derived for generalized fractional operators.

Lemma 21. Let g(ζ) = w(z⁻¹(ζ))f(z⁻¹(ζ)), 0 < α < 1; then the generalized fractional integral operator is equivalent to the following classical fractional integral:

$$ (41)

Here ζ₀ = z(a).

Proof. From the definition of generalized fractional integral, we have

$$ (42)

Since ζ = z(t) is positive monotone function, then ζ = z(t) is invertible, and we have t = z⁻¹(ζ),

$$ (43)

Let g(ζ) = w(z⁻¹(ζ))f(z⁻¹(ζ)); then the generalized fractional integral of f(x) is converted to classical fractional integral of g(ζ) in the following form:

$$ (44)

Lemma is proved.

Lemma 22. Let g(ζ) = w(z⁻¹(ζ))f(z⁻¹(ζ)),   0 < α < 1; then the generalized fractional derivative of order α is equivalent to the following classical fractional derivative:

$$ (45)

Here ζ₀ = z(a).

Proof. Similar to the proof of Lemma 21, we have

$$ (46)

Let g(ζ) = w(z⁻¹(ζ))f(z⁻¹(ζ)); then the generalized fractional derivative of f(x) is expressed through the classical fractional derivative of g(ζ),

$$ (47)

Lemma is proved.

Remark 23. These two lemmas establish important relation between classical and generalized fractional operators. With these lemmas, generalized fractional differential equations can be solved via classical fractional differential equations, and vice versa. Which kind of transform should be taken depends on characters of the problem to be solved.

In order to design a high order numerical approximation of the generalized fractional operator, we define a scaled space $$, such that

$$ (48)

where $$ is a polynomial space of up to order n.

Define a inner product and norm for space $$, such that

$$ (49)

Define projection Q_N into space $$, such that for any function u(x)

$$ (50)

Suppose Φ_j(x),   j = 0, …, N, are a set of orthogonal basis functions in space $$ satisfying

$$ (51)

Let N → ∞; then Φ_j(x),   j = 0,1, …, N, …, form a $$ space, and for any $$, the projection Q_Nu(x) can be written as

$$ (52)

Here $$ are expansion coefficients such that

$$ (53)

The weight function ω(x) plays an important role in the computational process and analysis of the method. Here, we choose a proper weight function to use properties of orthogonal polynomials and make the computation more efficient. Let p_j(z(x)) = w(x)Φ_j(x), and note that

$$ (54)

Take ω(x) = w²(x)z^′(x); then

$$ (55)

Since p_j(z) is polynomial of order j, the computation can be carried out easily through properties of orthogonal polynomials.

Suppose P_j,∗(x) is shifted Legendre polynomial defined on [z(a), z(b)]. Then, given any function $$ with weight ω(x) = w²(x)z^′(x), we have

$$ (56)

Recalling Lemmas 21 and 22, the generalized fractional integral and derivative can be obtained in the form

$$ (57)

$$ (58)

From Lemma 19, the following corollary can be obtained immediately.

Corollary 24. ζ(x) = z(x) is a monotone increasing function, w(x) > 0. 0 < α < 1, Q_N is a projection into space $$. $$; then there exists a constant C_α such that

$$ (59)

Here the weight function ω₁(ζ) = (ζ − a) ^−α(b − ζ) ^α,   ω₂(x) = ω₁(z(x))w²(x)z^′(x).

Remark 25. Unlike the convergence theory in classical polynomial space, the convergence order in space $$ depends on regularity of the function u(x) with respect to z(x). We will illustrate this through numerical examples.

Most of the time, it is more convenient to consider the problems in nodal form. We assume the given interpolation points are ζ_j = z(x_j)  (j = 0,1, …, N); then the Lagrange basis functions L_j(x)  (j = 0,1, …, N) can be defined as follows:

$$ (60)

The function u(x) can be expressed using both Jacobi polynomials and Lagrange polynomials. The following relation is derived:

$$ (61)

Considering the equivalence between Legendre basis and Lagrange basis, the following equality holds:

$$ (62)

where $$.

Then the nodal form expansion of u(x) is obtained

$$ (63)

From (57) and (58), the corresponding nodal form of generalized fractional integral and derivative are obtained

$$ (64)

$$ (65)

Example 26. Now we give an example to show the effectiveness and accuracy of the method. Assuming $$, we consider generalized fractional derivative of y(x) on the interval [0,1] with the following form:

$$ (66)

The exact generalized fractional derivative of y(x) is

$$ (67)

Numerical approximation to generalized fractional derivative of y(x) can be obtained using (58). We consider the maximum absolute error

$$ (68)

of the numerical derivative. Results for α = 0.2,0.5,0.8 are shown in Figure 1.

For this example, it is easy to check that $$. From theory of spectral approximation, the error would decrease exponentially when N < 10 and the numerical fractional derivative would be exact when N ≥ 10. Our numerical result coincides with the theory exactly.

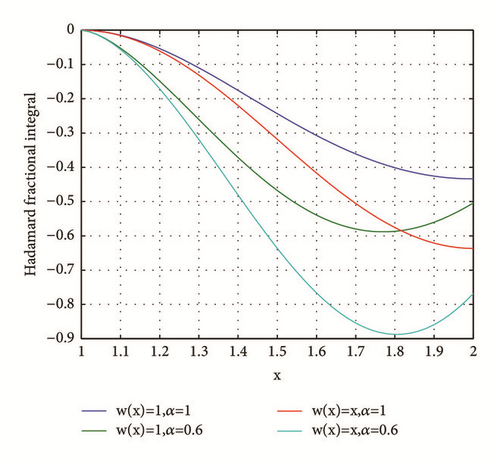
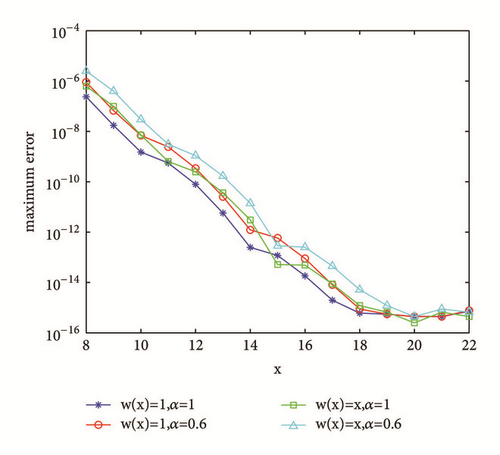
Example 27. In this example, we test the spectral approximation of Hadamard integral. Considering Hadamard-type fractional integral of y(x) = sin⁡(πx) on the interval [1,2], when w(x) = 1 and α = 1, the Hadamard integral of y(x) is Sine integral function, Si(πx) − Si(π); for more general w(x) and α, the exact Hadamard-type integral of y(x) is unknown. Here we consider several pairs of w(x) and α. Numerical Hadamard-type integral of y(x) would be computed using (57) with z(x) = log⁡(x). To evaluate the approximation accuracy, for the case w(x) = 1,   α = 1, the exact Hadamard fractional integral is computed using MATLAB built-in function sinint; for other cases, “exact” Hadamard fractional integral is computed using (57) with large N (e.g., N = 50), which is treated as reference solution. The results for numerical Hadamard integral and approximation error are shown in Figures 2 and 3.

For this example u is not in the space $$ for any n. Maximum error of approximated fractional integral converges exponentially until reaching machine accuracy.

4. Collocation Methods for Fractional Differential and Integral Equations

4.1. Fractional Ordinary Differential Equations

In this subsection, we consider collocation method for the generalized fractional ordinary differential equation of the form

$$ (85)

$$ (86)

Here 0 < α < 1,   w(x) > 0,   z(x) > 0 and z(x) is a monotone function in Ω.

We assume $$ is a numerical solution of the equation, x_i(i = 0,1, …, N) are the chosen interpolation points, $$. The following discretized equation is obtained:

$$ (87)

Let (87) hold on collocation points y_j  (j = 1, …, N); the matrix form is obtained:

$$ (88)

Here Λ is a diagonal matrix with Λ_ii = λ(y_i), F = (u₀, f(y₁), …, f(y_N)) ^T.

Considering the initial condition, we set $$ with the first row replaced by (1,0, …, 0), F^′ = F with its first element replaced by u₀. Then the solution U is obtained by solving the matrix equation $$.

Example 30. Consider the following example:

$$ (89)

$$ (90)

Here z(x) = x^2/3, w(x) = x, r is an arbitrary positive number.

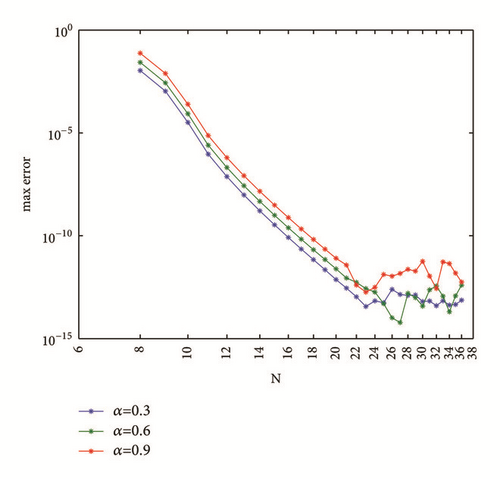
The exact solution of the ordinary differential equation is u(x) = x^r. Maximum absolute errors of numerical solutions for r = 6,7 and α = 0.3,0.6,0.9 are shown in Figures 4 and 5.

When z(x) = x^2/3,   w(x) = x, the scaled polynomial space $$ becomes

$$ (91)

For r = 7 the error converges exponentially and reaches machine accuracy at N = 12. It is faster than any finite difference method, while for r = 6 solution converges algebraically as N increases; however, it still reaches machine accuracy at N = 23. The major reason for this is that $$ and $$ for any $$.

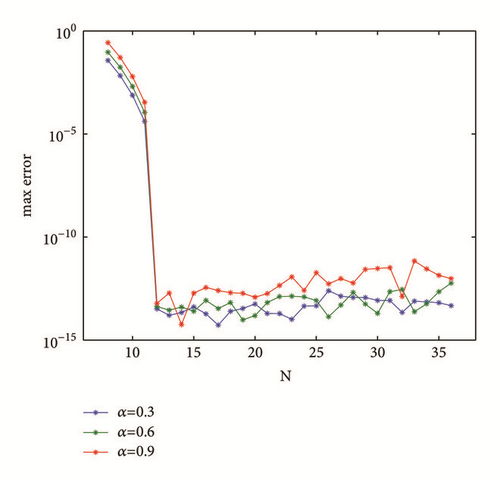
Remark 31. Since space $$ is transformed from classical polynomial space with respect to z(x), the convergence of spectral collocation method for ODEs with generalized fractional operators depends not only on the smoothness of the solution itself, but also on the scale function z(t).

4.2. Hadamard-Type Integral Equations

We consider the following Hadamard-type boundary value problem:

$$ (92)

In [42], Kilbas discussed the existence of the solution of (92). Explicit formulas for the solution f(t) were established in the following theorem.

Theorem 32 (see [42].)If x^μg(x) ∈ AC[a, b], then the Hadamard-type integral equation (92) with 0 < α < 1 is solvable in X_μ(a, b) and its solution may be represented in the form

$$ (93)

Here AC[a, b] is the set of absolutely continuous functions on [a, b] and X_μ(a, b) is space of those Lebesgue measurable functions f on [a, b] for which x^μ−1f(x) is absolutely integrable.

Solution of the Hadamard-type integral equation is exactly the same as generalized fractional derivative of Riemann-Liouville type with z(s) = log⁡(s),   w(s) = s^μ. The relationship between (93) and Caputo type generalized fractional derivative is

$$ (94)

Suppose x_j,   j = 0,1, …, N, are interpolation points; the discretized solution of equation (92) is

$$ (95)

Rewriting (95) in matrix form, we have

$$ (96)

where $$ is generalized fractional differential matrix; $$, F = (f_N(x₀), f_N(x₁), …, f_N(x_N)) ^T. $$ is a vector about the initial condition of the integral equation, defined by

$$ (97)

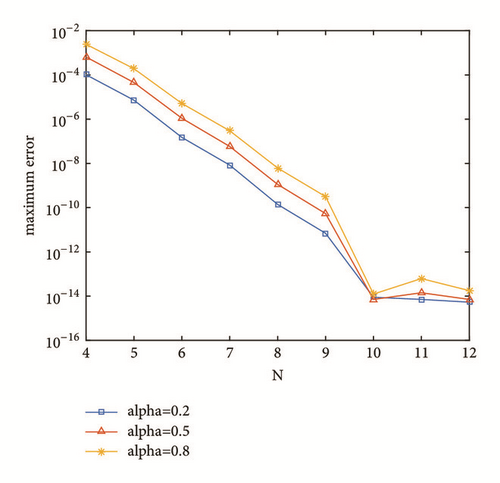
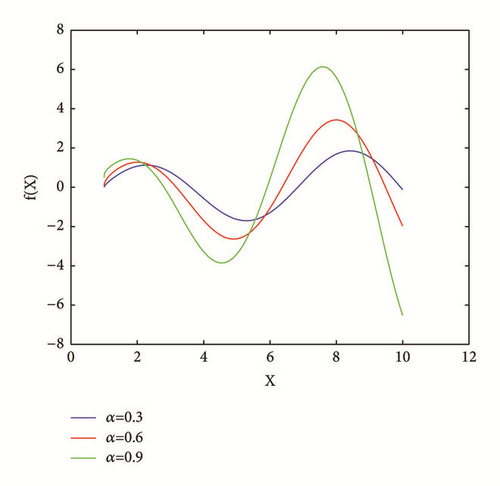
Example 33. Assume g(x) = sin⁡(x − 1),   μ = 1/3,   Ω = [1,10]. Solutions of (92) for α = 0.3,0.6,0.9 are shown in Figure 6.

4.3. Erdélyi-Kober Fractional Diffusion Equation

In this subsection, we consider the following Erdélyi-Kober fractional diffusion equation [12]:

$$ (98)

Erdélyi-Kober fractional diffusion equation, which is also called stretched time-fractional diffusion equation, is the master equation of a kind of generalized grey Brownian motion (ggBm). The ggBm is a parametric class of stochastic processes that provides models for both fast and slow anomalous diffusion. This class is made up of self-similar processes B_α,β(t) with stationary increments and it depends on two real parameters: 0 < α ≤ 2 and 0 < β ≤ 1. It includes the fractional Brownian motion when 0 < α ≤ 2 and β = 1, the time-fractional diffusion stochastic processes when 0 < α = β < 1, and the standard Brownian motion when α = β = 1. About the relationship between stochastic process B_α,β(t) and stretched time-fractional diffusion equation, the following proposition is presented in [12].

Proposition 34. The marginal probability density function f_α,β(x, t) of the process B_α,β(t), t ≥ 0, is the fundamental solution of the stretched time-fractional diffusion equation:

$$ (99)

Recalling the definition of generalized fractional integral and setting z(t) = t^α/β,   w(t) = 1, the equation can be rewritten as

$$ (100)

We use collocation method for both space and time discretization. We choose Legendre-Gauss-Lobatto (L-G-L) points x_i  (i = 0,1, …, M) as the space collocation points and choose t_j  (j = 0,1, …, N), such that z(t_j) are L-G-L points, as the time collocation points.

Define space collocation matrix $$, such that $$, and generalized fractional integral matrix, $$. Matrix $$ is computed through Theorem 28 and the space-time collocation matrices are obtained using Kronecker product  ^′⊗^′. Suppose $$ and $$ are space-time collocation matrices with dimension (M + 1)(N + 1)×(M + 1)(N + 1) for the second order derivative and fractional integral of order β separately. Then

$$ (101)

Suppose u_N(x, t) is the numerical solution of (98), defining $$, solution vector $$, and initial vector U₀, such that

$$ (102)

where, in the definition of U₀, each u₀(x_j) is repeated N + 1 times.

The matrix form discretized equation of (98) is obtained as

$$ (103)

In the discretized equation, initial condition is explicitly involved. After boundary condition added properly, numerical solution can be obtained by solving the matrix equation.

Example 35. Assume x ∈ Ω = (−1,1), t ∈ (0,0.5], $$, u(·,t)|_∂Ω = 0. Numerical solutions with M = N = 50 are shown in Figures 7–10.

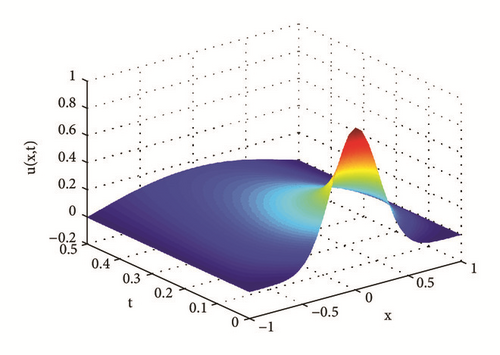
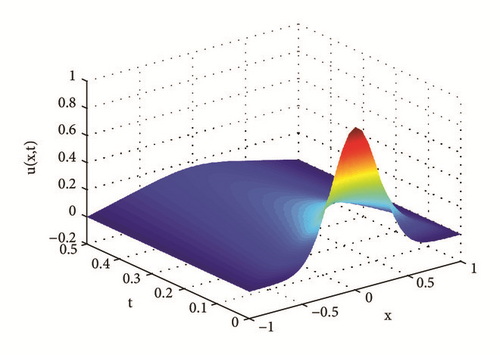
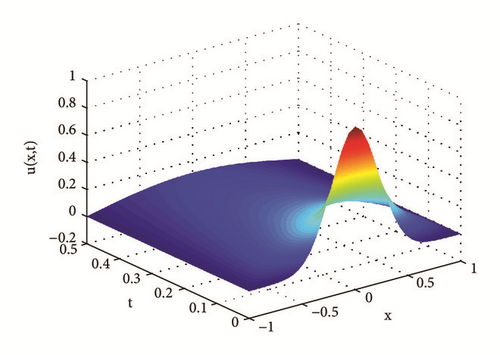
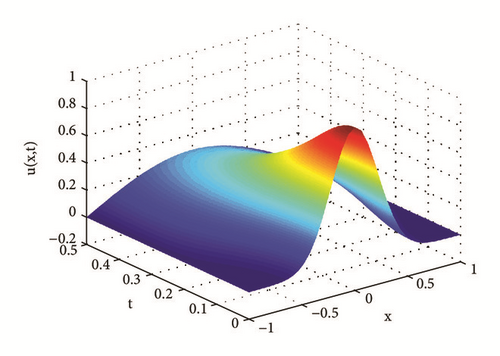
Erdélyi-Kober diffusion equation characterizes the marginal density function of the process B_α,β(t),   t ≥ 0. When α = β = 1, we recover the standard diffusion equation. When 0 < α = β < 1, we get the time-fractional diffusion equation of order β. When β = 1 and 0 < α < 2, we have the equation of the fractional Brownian motion marginal density.

As shown in Figures 7 and 8, when 1 < α < 2, the diffusion is fast, and the increments exhibit long-range dependence; when 0 < α < 1, the diffusion is slow, and the increments form a stationary process which does not exhibit long-range dependence. The results coincide with theoretical analysis in [12, 14].

5. Conclusion

In this paper, we propose a spectral collocation method for differential and integral equations with generalized fractional operators. To deal with the difficulty in designing spectral approximation scheme due to complexity of integral kernel and weight, a variable transform technique is applied to the generalized fractional operator, and a spectral approximation method is proposed for the generalized fractional operator. Operational matrices for generalized fractional operators are derived. Spectral collocation methods are designed for fractional ordinary differential equations, Hadamard-type integral equations, and Erdélyi-Kober diffusion equations separately. Numerical experiments are carried out to verify the accuracy and efficiency of the method and characteristics of the Erdélyi-Kober diffusion equation are analyzed based on numerical results.

Disclosure

An earlier version of this work was presented at the “8th International Congress on Industrial and Applied Mathematics (ICIAM 2015)”.

Conflicts of Interest

The authors declare that they have no conflicts of interest.