According to the performance degradation problem of feature extraction from higher-order statistics in the context of alpha-stable noise, a new feature extraction method is proposed. Firstly, the nonstationary vibration signal of rolling bearings is decomposed into several product functions by LMD to realize signal stability. Then, the distribution properties of product functions in the time domain are discussed by the comparison of heavy tails and characteristic exponent estimation. Fractional lower-order p-function optimization is obtained by the calculation of the distance ratio based on K-means algorithms. Finally, a fault feature dataset is established by the optimal FLOS and lower-dimensional mapping matrix of covariation to accurately and intuitively describe various bearing faults. Since the alpha-stable noise is effectively suppressed and state described precisely, the presented method has shown better performance than the traditional methods in bearing experiments via fractional lower-order feature extraction.

1. Introduction

Accurate condition monitoring of the key equipment parts is the main objective of intelligent diagnosis. As the most common and vulnerable support components of rotating machinery, rolling bearings have become the major monitoring objects. Therefore, feature extraction of bearing signals is a decisive factor for intelligent monitoring and diagnosis at present [1, 2].

The dynamic parameters, such as the driving force, damping force, and elastic force of the mechanical system, always demonstrate the nonlinear variation signals, especially during the emergency stage of equipment failure. Their vibration signals are non-Gaussian and nonstationary. Meanwhile, the complexity of institutions makes serious superimposing problems and same frequency interference phenomenon. Thus, the frequency of test signals is difficult to match the faulty frequency.

Aiming at this problem, the adaptive time-frequency analysis method is becoming the research hotspot of the existing vibration signal processing methods [3–5]. By further studying the relevant literatures, we have summarized the main types of traditional features. They include dimensionless parameters and various entropy values in the time domain [6–10], spectrum analysis in the frequency domain [11–14], and adaptive time-frequency analysis in the time-frequency domain [3, 15].

However, the conventional feature statistics usually ignores the distributing models of the adaptive signal components in engineering practice. For example, variance and high-order statistics of signal components are unbounded under alpha-stable noise conditions. Based on this finite statistics, the statistics mentioned above would show degradation performance of state description [16, 17].

Therefore, a new feature extraction method is introduced in this paper. The alpha-stable distribution model and signal processing method LMD are introduced in Sections 2 and 3. On the basis of further investigation of signal component distribution in Section 4, a new feature extraction method in fractional lower order is proposed in Section 5 and comparative analysis in Sections 6 and 7. Section 8 presents the analysis of computational complexity.

This new approach has three steps: First, LMD is chosen as the decomposition method of the nonstationary signals to achieve signal stability. Then, the signal pulse of the alpha-stable noise is effectively reduced by the optimal FLOS and lower-dimensional mapping matrix. Finally, the classification and identification of various faulty bearings are carried out precisely and intuitively. This new method solves the inaccurate description problem of various states in traditional methods by avoiding the infinite variance hypothesis.

2. Fractional Lower-Order Alpha-Stable Distribution

The alpha-stable distribution is an essential part of the non-Gaussian random distribution. The most striking characteristic is many samples far away from the mean value or the median, resulting in more peak pulses on the waveform in the time domain and thicker algebraic tails of those curves of probability density function PDF [18, 19].

Having four parameters, including characteristic exponent 0 < α ≤ 2, symmetry parameter −1 ≤ β ≤ 1, dispersion γ ≥ 0, and location parameter a, the impulsive signal X could be conveniently depicted by the characteristic function [20]:

\begin{matrix} φ (u) = \exp \{j a μ - γ {|u|}^{α} [1 + j β sgn (u) ω (u, α)]\}, \end{matrix}

(1)

where

\begin{matrix} ω (u, α) = \{\begin{cases} \tan π α / 2, & α \neq 1, \\ (2 / π) \log |u|, & α = 1, \end{cases} \\ sgn (u) = \{\begin{cases} 1, & u > 0, \\ 0, & u = 0, \\ - 1, & u < 0. \end{cases} \end{matrix}

(2)

The degree of the pulse characteristics is decided by characteristic exponent α. The smaller the value of α, the thicker the tails and the stronger the signal pulse. Figure 1 shows different PDF curves with different values of α. Gaussian distribution is the limiting case with α = 2, when φ(u) = exp{jaμ − σ²∣u∣²}; in addition, when 0 < α < 2, the random variable X is said to have fractional lower-order alpha-stable distribution, including Cauchy distribution (α = 1, β = 0) and Pearson distribution (α = 1/2, β = −1).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Different PDF curves with different α values.

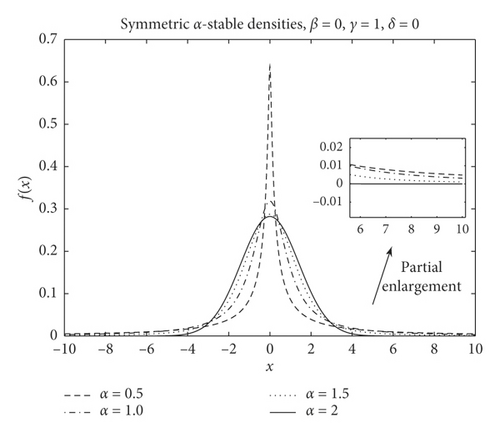
Undoubtedly, it is impossible that the probability density function PDF of fractional lower-order alpha-stable signals has the same convergence property of Gaussian signals. Because of the property of E|X|² = EX² = +∞, signal variance Var(X) = E(X²) − (EX)² is divergent. This is the basic reason for degradation performance of state description and the difficulty of intelligent monitoring of mechanical equipment.

In recent years, the alpha-stable noise and FLOS processing methods have shown better performance than the traditional methods. As a hottest research topic in the field of signal processing, FLOS processing methods have more extensive applicability in the processing of underwater sound, radar signals, and speech signals, time delay estimation, and biomedicine domain, for example, a new diagnosing method of noisy Greek folk music excerpts based on the alpha-stable noise assumption [21], description of various faulty bearing statuses through alpha-stable parameters and kurtosis values [22], a novel fault diagnosis model for axle box bearings based on symmetric alpha-stable distribution feature extraction and LS-SVM [23], the LOD fractional lower order matched filters and improved local optimum detector [24], and analytical parameter estimation by a hierarchical framework based on the skewed alpha-stable characteristic function [25].

3. Nonstationary Signal Processing

Local mean decomposition (LMD) is an adaptive time-frequency analysis method. LMD could solve the shortcomings of traditional methods: the false time-frequency information from the fixed basis functions, a great deal of calculation from the multiparameter optimization, the Heisenberg limitation in the time-frequency domain, and the overenvelope and underenvelope problems of the EMD method. Thus, LMD has potential application in bearing signal processing, becoming the research hotspot of the existing adaptive time-frequency analysis methods [26–30].

LMD could decompose a vibration signal x(t) into a series of components PF_i(t) and remainders u_i(t) through three loops:

\begin{matrix} x (t) = \sum {PF}_{i} (t) + u_{i} (t) . \end{matrix}

(3)

Signal components PF_i(t) represent the main frequency components of x(t). Combining with the maximum kurtosis criterion, PF₁(t) is often chosen as the main feature of the faulty bearings, which may imply abundant bearing fault state information [31].

To a certain extent, the LMD algorithm transforms the feature extraction problem of nonstationary signals into that of stationary components, increasing the description accuracy and reliability of various equipment states.

4. Analysis of Time-Domain Distribution Characteristics

However, when the noise is impulsive and modeled as a non-Gaussian process, variance and second- and higher-order statistical characteristics of PF₁(t) are infinite. This may reduce the accuracy and reliability of above statistics for the description of equipment states.

In order to investigate the distribution characteristics of bearing vibration signals, Yu et al. had contrasted the validity of the proposed statistical models [32]. It can be concluded that the alpha-stable distributed model is sufficient to thoroughly describe the statistical characteristics of faulty bearing signals with impulsive behaviors. In this paper, we have researched the noise-reducing ability of LMD in terms of tail heaviness and characteristic exponent α values of PF components.

4.1. Analog Vibration Signals

Vibration signal model of bearings (with the outer race fixed) is [33]

\begin{matrix} S = \sin (2 π f_{b} t) [1 + β \sin (2 π f_{r} t)] + v_{\partial}, \end{matrix}

(4)

where f_b is the frequency of the rolling ball passing through the inner race, f_r is the rotational frequency, β is the modulation ration, and v_∂ is the added noise. When the characteristic exponent is ∂ = 2, v_∂ becomes the Gaussian noise. Assuming f_b = 100 Hz, f_r = 25 Hz, β = 1, ∂₁ = 1.5, and ∂₂ = 2, we establish the vibration signals S₁ and S₂ under alpha-stable noise and Gaussian noise, respectively.

The vibration signals S₁ and S₂ are processed through the LMD algorithm to calculate the frequency function PDF of PF₁(t). Figure 2 shows the comparison of PDF tail heaviness.

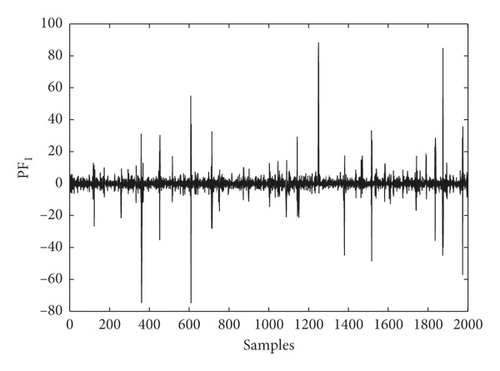
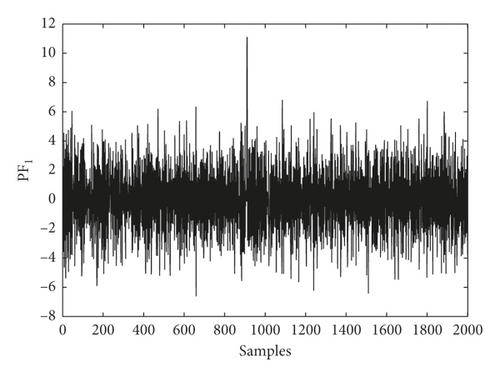
It is clear that PF₁(t) of S₁ has more evident pulse characteristics and thicker algebraic tails than that of S₂. This phenomenon proves the fact that LMD cannot effectively deal with the alpha distributed noise. The PDF tail still shows the characteristics of alpha distribution. Therefore, the adaptive time-scale decomposition of vibration signals exhibits a performance degradation problem.

4.2. Actual Vibration Signals

SKF6205-2RS bearing database from Case Western Reserve University is used as an example to study the distribution properties of the practical bearing signal component PF₁(t). This database includes normal bearings and faulty bearings with three faulty degrees ((a) 0.178 mm, (b) 0.356 mm, and (c) 0.533 mm): (A) normal condition, (B) rolling ball fault, (C) inner race fault, and (D) outer race fault. We record this database as X = {A, M.n}, where M.n represents the fault state M with the fault size n. It is clear that M ∈ {B,C,D} and n ∈ {a,b,c}. In this test, the rotational frequency f_r = 29.167 Hz, the sampling frequency f_s = 12000 Hz, the sample length N_h = 1024, and the number of samples N = 117.

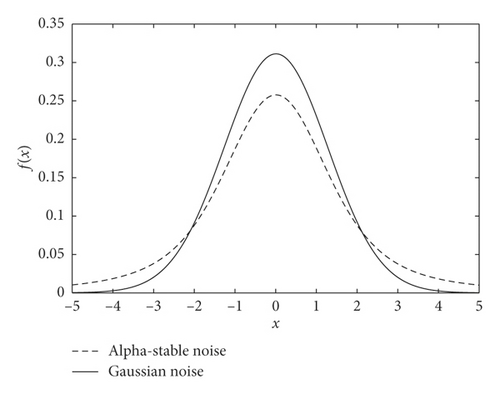
The most striking characteristic of the alpha-stable distributed signals is more peak pulses in the time domain and thicker algebraic tails of probability density function PDF. As shown in Figure 3, the dotted lines present the PDF tail heaviness of faulty bearing components PF₁(t) and the full lines of Gaussian components PF₁(t) (with the same parameters except characteristic exponents α). It can be seen that the PDF curve of normal bearings has a thicker tail than the Gaussian curve, meaning that the background noise obeys the fractional lower-order alpha distribution. In this context, both the faulty vibration signals display the same characteristics, including rolling ball fault, inner race fault, and outer race fault.

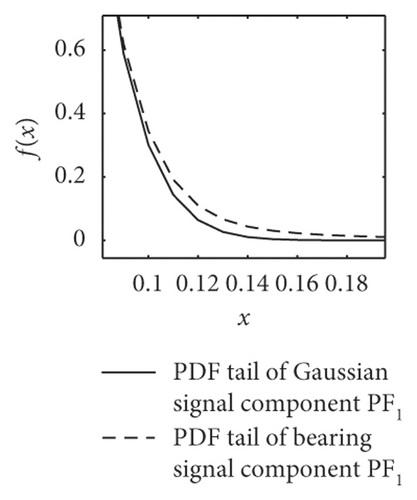
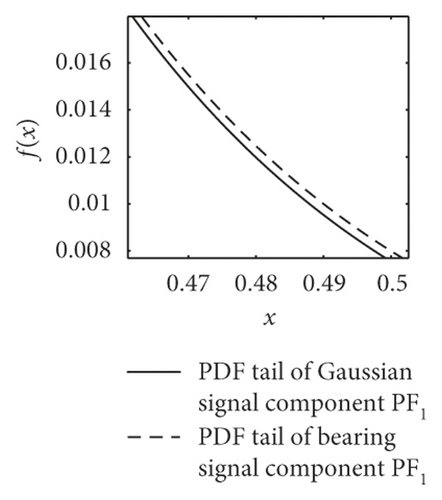
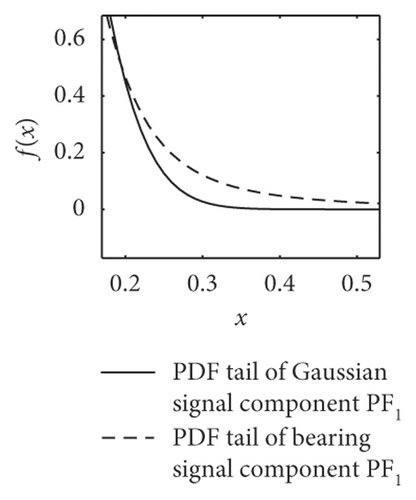
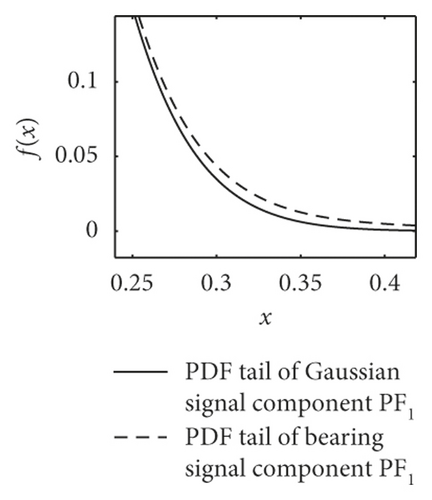
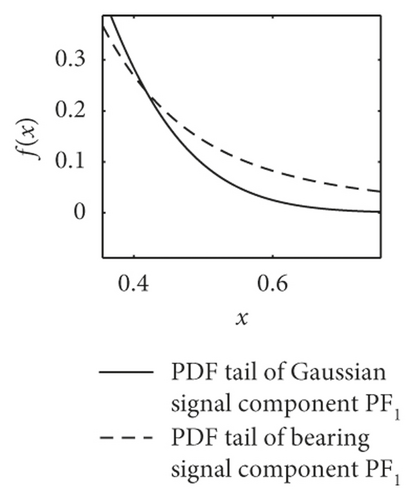
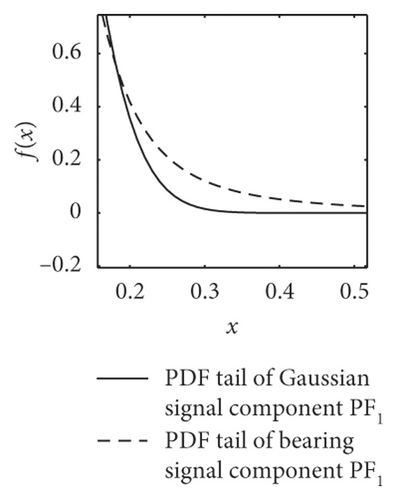
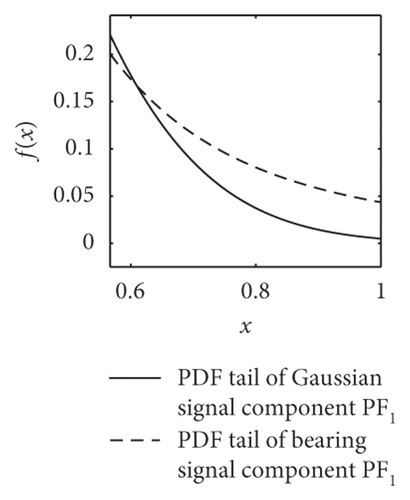
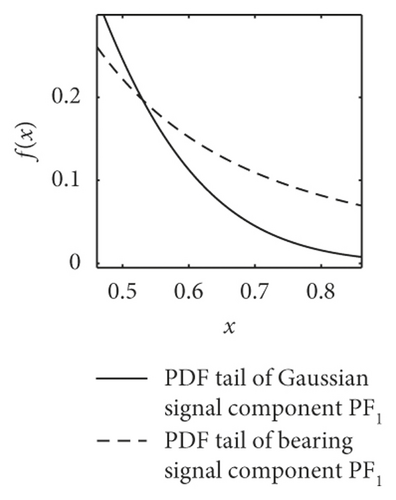
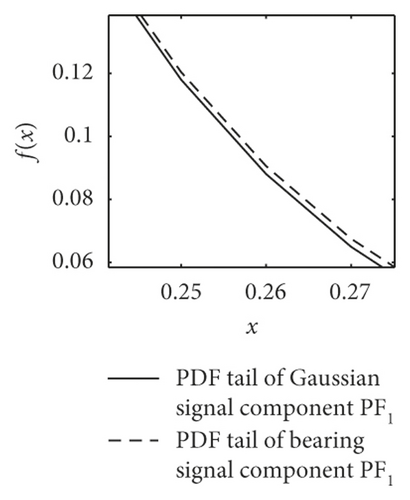
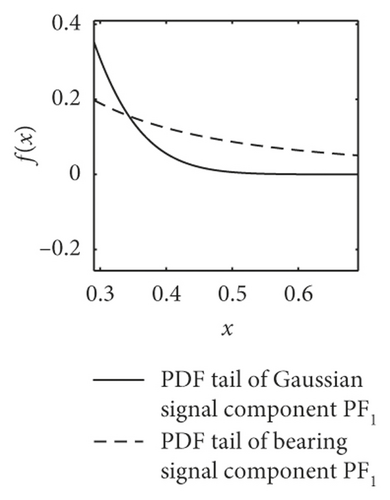
Furthermore, the mean values of characteristic exponents α of PF₁(t) components are estimated by the Koutrouvelis regression method, as shown in Table 1 [34]. It can be seen that the corresponding characteristic exponents α of the bearings are distinguished obviously. The value of rolling ball fault is in the range of 1.61–1.99, the inner race fault is in 1.43–1.53, and the outer race fault, except for D.b samples, is in 1.01–1.2. This phenomenon basically accords with the change law of PDF tails in Figure 3.

Table 1. Mean values of grouped samples (SKF6205-2RS).

Samples	A	B.a	B.b	B.c	C.a	C.b	C.c	D.a	D.b	D.c
Mean values	1.8971	1.9970	1.6187	1.9679	1.5221	1.5363	1.4333	1.1703	1.9899	1.0081

Figure 3 and Table 1 could easily prove the following:

(1)
There is no doubt that the alpha-stable distributed noise exists in the vibration signals under both normal and fault conditions.
(2)
When the noise is impulsive and modeled as a non-Gaussian process, PF₁(t) components fail to describe the vibration signals accurately, which has been a major drawback to the use of LMD.

Therefore, using the fractional lower-order features is more adaptive than the conventional second- and higher-order statistical moments to describe various signal states, effectively avoiding the invalid hypothesis.

5. Fractional Lower-Order Characteristics of Bearing Vibration Signals

Due to the impulsive noise and the nonstationary property, a fractional lower-order feature extraction method is introduced in this study. This new method adopts LMD to realize signal stability and obtains signal components with impulsive characteristic in the time domain. Then, the alpha-stable noise is weakened by the optimal fractional lower-order statistics (FLOS) and lower-dimensional mapping matrix. Finally, the feature matrix is constructed to effectively suppress the impulsive noise and accurately describe the equipment operational conditions. The algorithm flow is as follows (Figure 4).

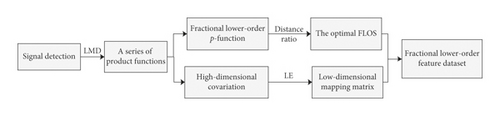
5.1. The Optimal FLOS

Unlike most statistical models, the α-stable distribution does not have closed-form probability density functions, except for a few known cases. In terms of the theory of alpha-stable distribution, the random variable X does not have finite second- or higher-order moments, when its statistic order is less than the value of characteristic exponent α. The formula of FLOS is

\begin{matrix} E [{∣ X ∣}^{p}] = \{\begin{cases} C (p, α) γ^{p / α}, & 0 < p < α, \\ \infty, & p \geq α, \end{cases} \end{matrix}

(5)

where Γ(⋅) is the gamma function and

C (p, α) = 2^{p + 1} Γ (p + 12 /) Γ (- p / α) / α \sqrt{π} Γ (- p / 2)

From formula (5), the selection of parameter p directly affects the estimation of FLOS, which is important for bearing state monitoring. In this paper, the optimal order value p_opt selection method is based on “maximum class separation distance and minimum intraclass distance.” First, we calculate FLOS with different p values to be the eigenvalue of each sample, described as

\begin{matrix} E^{i, j} (p) = \frac{2^{p + 1} Γ (p + 12 /) Γ (- p / α (i, j))}{α (i, j) \sqrt{π} Γ (- p / 2)} γ {(i, j)}^{p / α (i, j)} . \end{matrix}

(6)

The range of i is i ∈ {1,2, …, N} and j is j ∈ {1,2, …, J}. Here, N is the number of sample groups and J is the number of state types. Then, the best clustering center (x¹, x², …, x^J) of each state type is obtained by the K-means clustering algorithm. Finally, we could calculate the distance between E^i,j(p) and (x¹, x², …, x^J) in order to obtain the class separation distance D_b and intraclass distance D_i of each sample. At last, the optimal order p_opt could be selected by the maximum distance ratio ${\bar{D}}_{b} / {\bar{D}}_{i}$ .

5.2. Lower-Dimensional Mapping Matrix of Covariation

According to the infinite variance of alpha-stable signals, Miller put forward the concept of covariation in 1978. For the random variables X and Y of simultaneous distribution, the covariation of variables X and Y is given by formula (7), with characteristic exponents 1 < ∂ ≤ 2 and dispersion coefficient γ_y:

\begin{matrix} {[X, Y]}_{α} = \frac{E (X Y^{〈p - 1〉})}{E ({|Y|}^{p})} γ_{y}, 1 \leq p < \partial . \end{matrix}

(7)

Under certain conditions, the validity is similar to the covariance of the random variables of Gaussian signals, which could strengthen the common components of the signals to a certain extent. For the high-dimensional covariant matrix, the Laplacian eigenmaps algorithm is used to carry out the lower-dimensional mapping matrix. LE is suitable for nonlinear feature mining and dimensionality reduction of high-dimensional data, based on the principle that “the weight of the connection edge between the subgraphs is as low as possible and the weight of the connection edge in the subgraph is as high as possible.” Finally, it could easily realize the optimal embedding of high-dimensional manifolds by the mapping theory.

If there is an edge connection between the ith node x_i and the jth node x_j, the weight of the edge determined by the thermonuclear method is as follows:

\begin{matrix} W_{i j} = \exp (- \frac{{‖x_{i} - x_{j}‖}^{2}}{σ^{2}}) . \end{matrix}

(8)

The Laplace matrix is constructed by L = D − W. If the constructed nearest neighbor graph is connected, the problem of finding lower-dimensional embedding can be reduced to solve the generalized eigenvector problem:

\begin{matrix} L y = λ D y, \end{matrix}

(9)

where D is a diagonal weight matrix which satisfies D_ij = ∑_jW_ij. The low-dimensional embedded coordinate consists of the eigenvectors p₁, p₂, …, p_d+1, corresponding to the minimum d + 1 eigenvalues. The target dimension is determined by the number of fault types [35, 36].

6. Feature Accuracy Comparisons

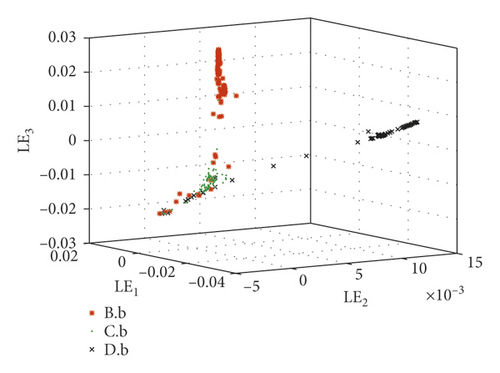
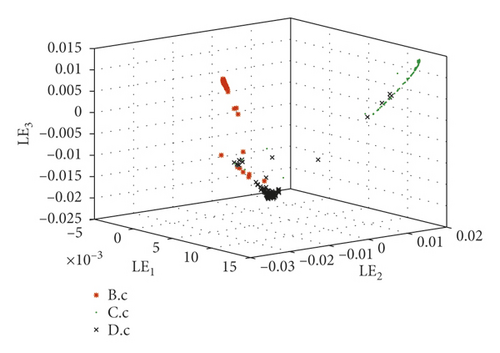
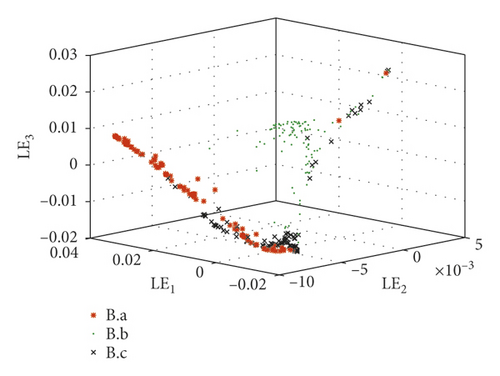
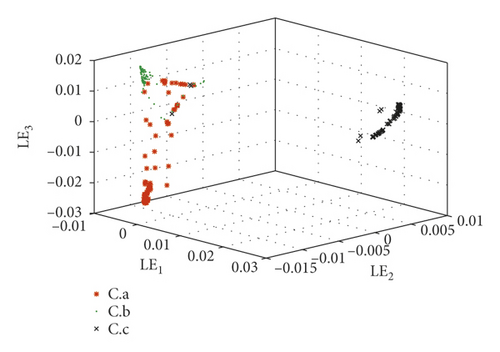
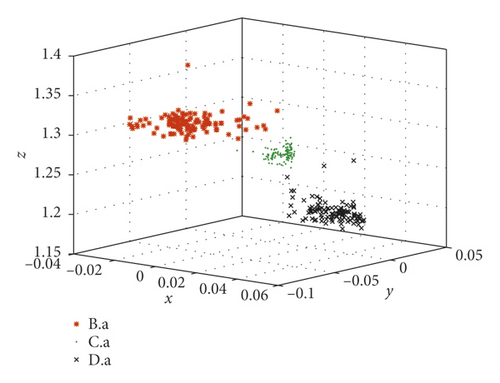
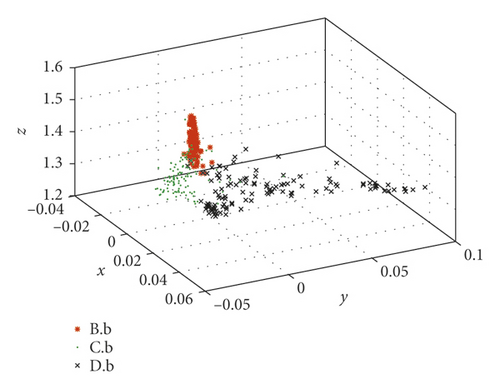
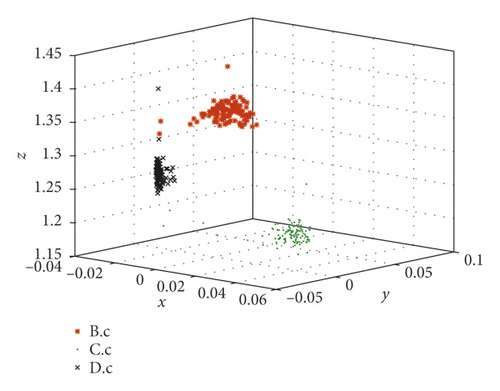
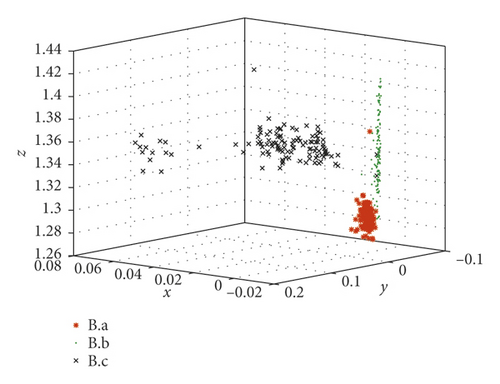
Take the SKF6205-2RS bearing signals as an example to compare the fractional lower-order features proposed in this paper with the multidimensional features in reference [30]. In reference [30], the same bearing signals, SKF6205-2RS bearing signals from the Case Western Reserve University Bearing Data Center, were processed by the same method LMD. Then, 23 conventional features such as variance, skewness, and kurtosis were considered to describe the status of bearings. As we know, they belong to second- and high-order statistics. The difference between reference [30] and this paper is the calculation of mapping matrix of PF₁(t). They are calculated from 23-dimensional time-domain characteristics in reference [30] and fractional low-order features proposed in this paper, respectively. Faulty bearing samples are divided into 6 groups in Table 2.

Table 2. Faulty samples divided into 6 groups.

No.	Groups	Description
1	X = {M.n\|M = B,C,D, n = a}	Three fault types in fault size a
2	X = {M.n\|M = B,C,D, n = b}	Three fault types in fault size b
3	X = {M.n\|M = B,C,D, n = c}	Three fault types in fault size c
4	X = {M.n\|M = B, n = a, b, c}	Rolling fault in different sizes
5	X = {M.n\|M = C, n = a, b, c}	Inner race fault in different sizes
6	X = {M.n\|M = D, n = a, b, c}	Outer race fault in different sizes

The range of parameter p is determined according to the minimum value of α. Take the variation of p as 0.1 and calculate the ratio value of ${\bar{D}}_{b} / {\bar{D}}_{i}$ . As shown in Table 3, the maximum ratio is 319.68 when the value p = 0.1.

Table 3. Ratio of different fault sets.

p	Ratio
0.1	319.68
0.2	288.63
0.3	85.61
0.4	253.99
0.5	195.63
0.6	126.25
0.7	205.08

The covariation matrices C_N×N of components PF₁(t) are calculated according to formula (7). Taking C_N×N to be the input matrix, we construct the Laplace characteristic matrix to enhance the fault components. Thus, we could obtain the lower-dimensional mapping matrix $C_{N \times 2}^{'}$ of each type of samples.

The characteristic 3D matrix CE_N×3 is formed by

C_{N \times 2}^{'}

and E_p matrices. The scattered plots are drawn in three-dimensional spaces with the feature matrix as the x, y, and z coordinate. Figure 5 shows the 3D scattered plots from 23-dimensional features in reference [30], except for the normal samples A. Figure 6 shows fractional lower-order features proposed in this paper. Lowercase roman letters (a)–(f) represent sample groups 1–6, respectively. Through 3D scattered plot comparisons of 6 fault sets between Figures 5 and 6, the effect of these two methods is quantified, respectively. There are some conclusions for different types of faulty bearings as follows:

(1)
The extracted features are constructed by just two types of statistics which are much fewer than those in reference [30].
(2)
These fault set samples are absolutely separated by the new features. It is proved that the fractional lower-order feature extraction proposed in this paper is more accurate for different state descriptions.

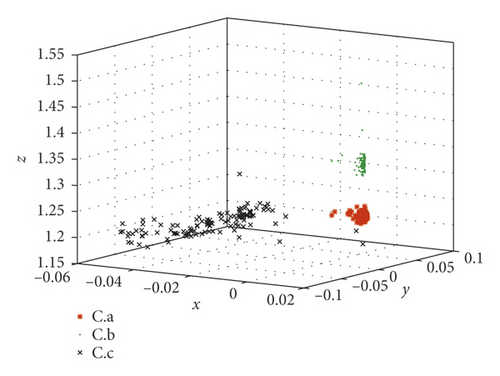
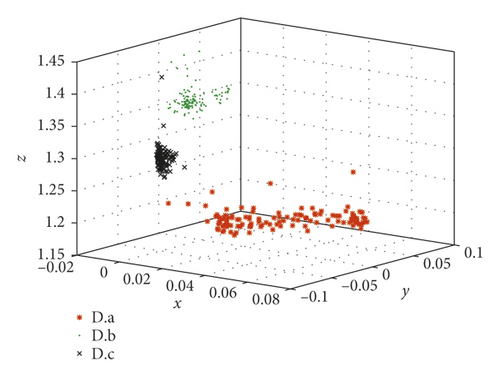
7. Feature Extractions of Form Roller Bearings

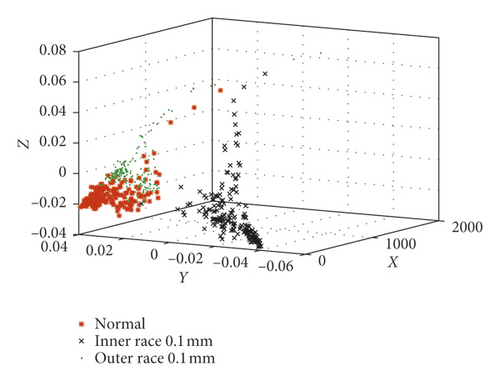
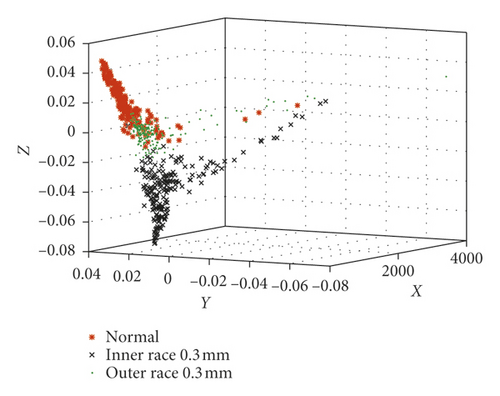
Offset printing press is a piece of high-precision industrial equipment that is designed to reproduce text and image at a high rate of speed and low cost. Accurate ink transfer is completed through the inking system and three-cylinder printing system. Form rollers ensure that the ink will uniformly overprint the image area of the plate. When their supporting bearing fails, it may cause oversize printing dots and inferior quality. Figure 7 shows different states of 6001 bearings. We had processed the inner race fault and outer race fault by line cutting. The fault sizes are 0.1 mm and 0.3 mm.

LMS test lab system is used to test and store the vibration signals of 6001 bearings (with the outer ring fixed). The model of acceleration sensors is PCB 333B30 (range is ±50 g and sensibility is 99.3 mV/g). In this real test, the rotational frequency of the form roller f_r = 4 Hz, the sampling frequency f_s = 6400 Hz, the sample length N_h = 2048, and the number of samples N = 190.

PDF curve comparison of normal and faulty signal components PF₁(t) is shown in Figure 8. Table 4 shows the mean estimation of characteristic exponent α. It could easily prove that the alpha-stable distributed noise exists in the vibration signals of form rollers, and signal components PF₁(t) yield the fractional lower-order alpha-stable distribution.

Table 4. Mean values of parameter α.

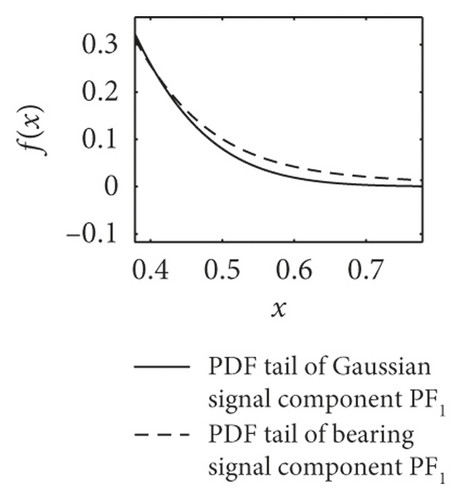
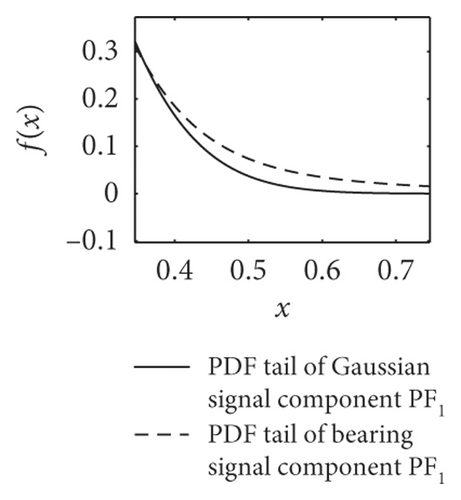
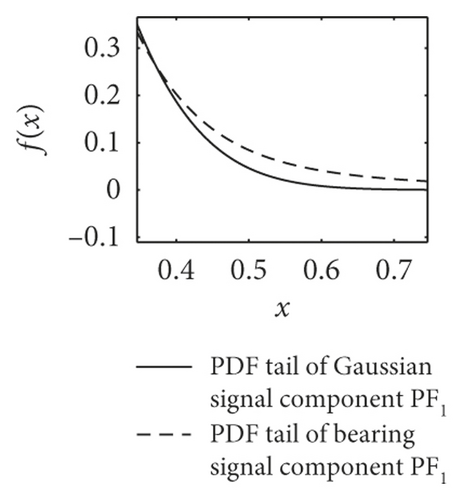
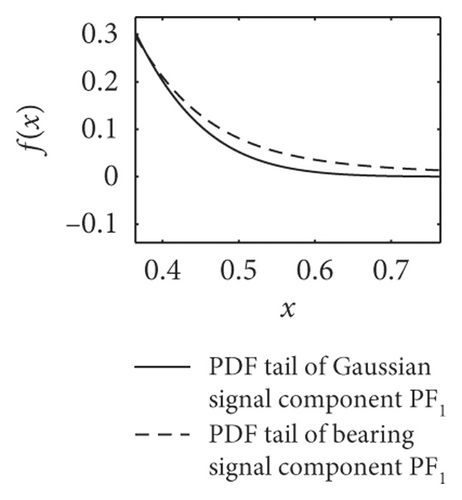
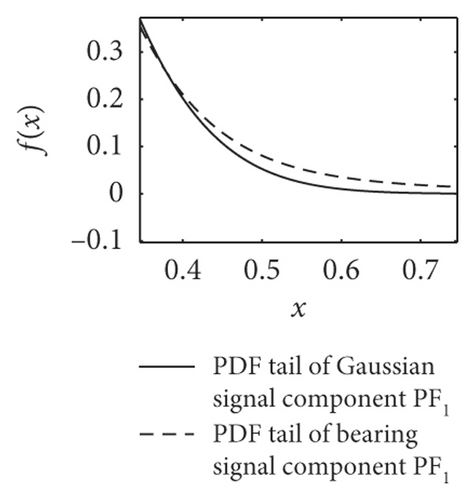
Sample	Normal	Inner race 0.1 mm	Inner race 0.3 mm	Outer race 0.1 mm	Outer race 0.3 mm
Mean	1.8192	1.7555	1.7307	1.7970	1.7960

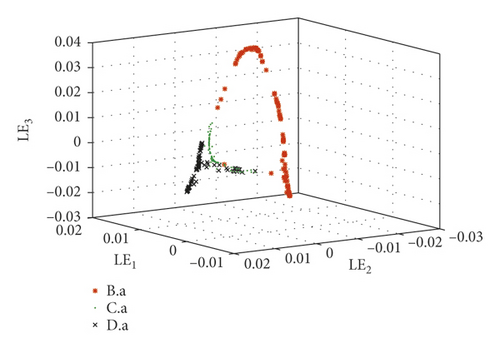
In order to fully compare and analyze the characteristics of each sample, these five kinds of bearing samples are divided into four groups in Table 5. Then, the optimal FLOS and mapped covariation matrices are calculated by algorithm flow in Figure 4 and formulas (5)–(9). Finally, fractional lower-order features are constructed to classify different fault types through 3D scattered plots. Figures 9 and 10 show the 3D scattered plots of the mapping matrix from 23-dimensional features in reference [30] and fractional lower-order features proposed in this paper. Lowercase roman letters (a)–(d) represent sample groups 1–4, respectively. In consideration of chaotic and rambling form bearing samples in Figure 9, the traditional feature extraction method degrades obviously in actual equipment status monitoring. On the contrary, with fractional lower-order noise suppressed by the new method in Figure 10, this vibration samples are distinguished much clearer in the three-dimensional space.

Table 5. Faulty samples divided into 4 groups (6001).

No.	Description
1	Normal, inner race fault 0.1 mm, and inner race fault 0.3 mm bearings
2	Normal, outer race fault 0.1 mm, and outer race fault 0.3 mm bearings
3	Normal, inner race fault 0.1 mm, and outer race fault 0.1 mm bearings
4	Normal, inner race fault 0.3 mm, and outer race fault 0.3 mm bearings

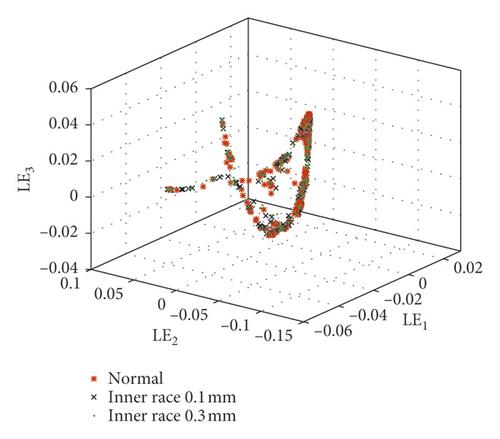
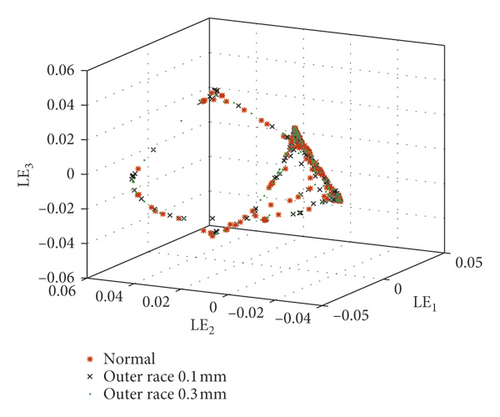
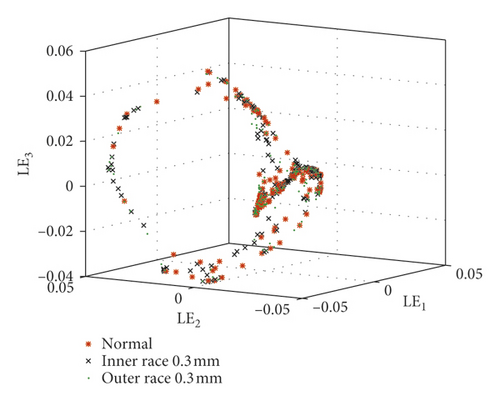
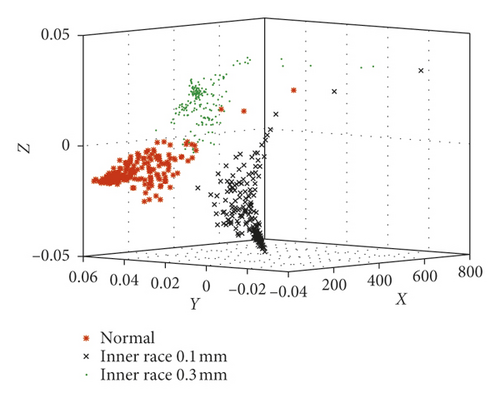
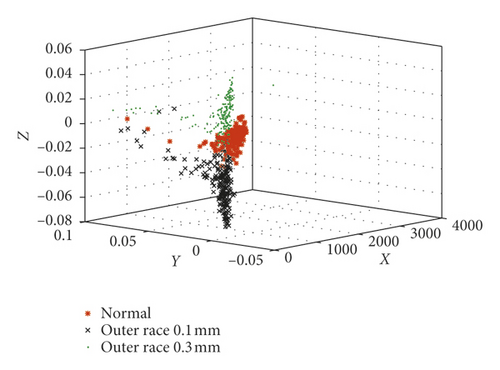
8. Analysis of Computational Complexity

Tables 6 and 7 show the computational complexity of programs. O(•) represents the time complexity of each algorithm. Here, l is the length of parameter p with the variation as 0.1. h is the iteration number of clustering centers. d is the complexity of distance calculation. t(23,3) is the complexity of the LE program in the reference, which has changed the dimension from 23 to 3. In a parallel manner, t(N, 2) represents the complexity of dimensional optimization from N to 2 via the LE program. It is obvious that O(max(J × N_h × N × l, N × l × h × d)) > O(J × N_h × N) and O(max(J∗N_h∗N², t(N, 2))) > O(t(23,3)). The running time is almost three times that of the comparison method in reference [30]. This phenomenon indicated that the proposed method is more complex.

Table 6. Computational complexity of programs in reference [30].

Program	Calculation of 23-dimensional features	Feature optimization program of 23-dimensional features	Running time (s) (SKF6205-2RS)	Running time (s) (6001)
Method in reference [31]	O(J × N_h × N)	O(t(23,3))	21.227	43.729

Table 7. Computational complexity of programs in this paper.

Program	Calculation of the optimal FLOS	Feature optimization program of covariation	Running time (s) (SKF6205-2RS)	Running time (s) (6001)
Proposed method	O(max(J × N_h × N × l, N × l × h × d))	O(max(J∗N_h∗N², t(N, 2)))	69.711	158.839

Significantly, this paper focuses on the description accuracy of bearing status. Figures 5 and 6 have shown the advantages of the proposed method in terms of description accuracy. Then, monitoring people could autonomously choose the adequate method according to time tolerance or description accuracy.

9. Conclusions

In this paper, a kind of fractional lower-order feature extraction method is specifically introduced so as to solve the degradation problem of conventional methods. According to the optimal FLOS and low-dimensional mapping matrix, the equipment operational conditions are described precisely and effectively.

The proposed method is validated by the bearing samples, and the results demonstrated the following:

(1)
The mixed vibration signal of the operation is an important class of α-stable distributed signals. On the basis of the aforementioned fact, the signals of faulty bearings, including rolling ball fault, inner race fault, and outer race fault, yield the characteristics of alpha-stable distribution.
(2)
When the noise is impulsive and modeled as a non-Gaussian process, the LMD algorithm does not process the vibration signals effectively for impulsive noise still existing in PF components. Especially in the actual equipment status-monitoring process, the noise interference in conventional methods becomes more obvious.
(3)
The improved performance is clearly demonstrated both theoretically and experimentally. In comparison with traditional methods related to Gaussian models, fractional lower-order features make more accurate description of bearings status. Monitoring people could autonomously choose the adequate method according to time tolerance or description accuracy.

This new method gives more insight into the distribution characteristics of the adaptively decomposed PF components. The present work could be applied to feature extraction of all signal components, and it would provide a certain theoretical support for further study of intelligent monitoring and diagnosis of the whole machine.

Conflicts of Interest

The authors declare that they have no conflicts of interest regarding the publication of this paper.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (No. 51275409), the National Science Foundation for Young Scientists of China (No. 51305340), and the Natural Science Project of Shaanxi Provincial Department of Education (No. 17JK0545).

Open Research

Data Availability

Data related to this paper have been given in Supplementary Materials. The SKF6205-2RS bearing fault database from Case Western Reserve University is from “http://csegroups.case.edu/bearingdatacenter/home.” Form roller bearing vibration data are from the offset printing press PZ650.

Supporting Information

References

1 Tang Y., Liu S. L., Liu Y. H., and Jiang R., Fault diagnosis based on nonlinear complexity measure for reciprocating compressor, Journal of Mechanical Engineering. (2012) 48, no. 3, 102–107, https://doi.org/10.3901/jme.2012.03.102, 2-s2.0-84863250966.
10.3901/JME.2012.03.102
Google Scholar
2 Lei Y., Jia F., Kong D. T., Lin J., and Xing S., Opportunities and challenges of machinery intelligent fault diagnosis in big data era, Journal of Mechanical Engineering. (2018) 54, no. 5, 94–104, https://doi.org/10.3901/jme.2018.05.094, 2-s2.0-85051349703.
10.3901/JME.2018.05.094
Google Scholar
3 Huang N. E., Shen Z., Long S. R. et al., The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis, Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. (1998) 454, no. 1971, 903–995, https://doi.org/10.1098/rspa.1998.0193, 2-s2.0-5444236478.
10.1098/rspa.1998.0193
Web of Science® Google Scholar
4 Zhang X. G., Song Z. Y., Li D. D., Zhang W., Zhao Z., and Chen Y., Fault diagnosis for reducer via improved LMD and SVM-RFE-MRMR, Shock and Vibration. (2018) 2018, 13, 4526970, https://doi.org/10.1155/2018/4526970, 2-s2.0-85050994404.
10.1155/2018/4526970
Web of Science® Google Scholar
5 Lv Y., Zhang H., and Yi C., Trivariate empirical mode decomposition via convex optimization for rolling bearing condition identification, Sensors. (2018) 18, no. 7, https://doi.org/10.3390/s18072325, 2-s2.0-85050824065.
10.3390/s18072325
Web of Science® Google Scholar
6 Jia F., Lei Y., Shan H., and Lin J., Early fault diagnosis of bearings using an improved spectral kurtosis by maximum correlated kurtosis deconvolution, Sensors. (2015) 15, no. 11, 29363–29377, https://doi.org/10.3390/s151129363, 2-s2.0-84947772934.
10.3390/s151129363
Web of Science® Google Scholar
7 He Z. J., Theories and Applications of Machinery Fault Diagnostics, 2010, Higher Education Press, Beijing, China.
Google Scholar
8 Kolmogorov A. N., A new metric invariant of transient dynamical systems and automorphisms in Lebesgue spaces, Dokl Akad Nauk SSSR. (1958) 119, no. 5, 861–864.
Web of Science® Google Scholar
9 Bandt C. and Pompe B., Permutation entropy: a natural complexity measure for time series, Physical Review Letters. (2002) 88, no. 17, 4, 174102, https://doi.org/10.1103/physrevlett.88.174102, 2-s2.0-84880568281.
10.1103/PhysRevLett.88.174102
CAS PubMed Web of Science® Google Scholar
10 Costa M., Goldberger A. L., and Peng C. K., Multiscale entropy analysis of complex physiologic time series, Physical Review Letters. (2002) 92, no. 8, 705–708.
Web of Science® Google Scholar
11 Randall R. B., Antoni J., and Chobsaard S., The relationship between spectral correlation and envelope analysis in the diagnostics of bearing faults and other cyclostationary machine signals, Mechanical Systems and Signal Processing. (2001) 15, no. 5, 945–962, https://doi.org/10.1006/mssp.2001.1415, 2-s2.0-0035456236.
10.1006/mssp.2001.1415
Web of Science® Google Scholar
12 Stack J. R., Harley R. G., and Habetler T. G., An amplitude modulation detector for fault diagnosis in rolling element bearings, IEEE Transactions on Industrial Electronics. (2004) 51, no. 5, 1097–1102, https://doi.org/10.1109/tie.2004.834971, 2-s2.0-5444230160.
10.1109/TIE.2004.834971
Web of Science® Google Scholar
13 ParkerB. E.Jr., Ware H. A., Wipf D. P. et al., Fault diagnostics using statistical change detection in the bispectral domain, Mechanical Systems & Signal Processing. (2000) 14, no. 4, 561–570, https://doi.org/10.1006/mssp.2000.1299.
10.1006/mssp.2000.1299
Web of Science® Google Scholar
14 Wang D., Tse P. W., and Tsui K. L., An enhanced Kurtogram method for fault diagnosis of rolling element bearings, Mechanical Systems & Signal Processing. (2013) 35, no. 1-2, 176–199, https://doi.org/10.1016/j.ymssp.2012.10.003, 2-s2.0-84870401853.
10.1016/j.ymssp.2012.10.003
Web of Science® Google Scholar
15 Smith J. S., The local mean decomposition and its application to EEG perception data, Journal of the Royal Society Interface. (2005) 2, no. 5, 443–454, https://doi.org/10.1098/rsif.2005.0058, 2-s2.0-33747100681.
10.1098/rsif.2005.0058
PubMed Web of Science® Google Scholar
16 Shao M. and Nikias C. L., Signal processing with fractional lower order moments: stable processes and their applications, Proceedings of the IEEE. (1993) 81, no. 7, 986–1010, https://doi.org/10.1109/5.231338, 2-s2.0-0027624516.
10.1109/5.231338
Web of Science® Google Scholar
17 Chen R. Q., Wang J., Lin R. Q., and Zhao X., Spectrum sensing based on nonparametric autocorrelation in wireless communication systems under alpha stable noise, Mobile Information Systems. (2016) 2016, 6, 6753830, https://doi.org/10.1155/2016/6753830, 2-s2.0-84973171196.
10.1155/2016/6753830
Web of Science® Google Scholar
18 Nolan J. P., Stable distributions: models for heavy-tailed data, 2005, https://fs2.american.edu/jpnolan/.
Google Scholar
19 Qiu T. S., Statistical Signal Processing (Processing and Application of Non-Gaussian Signals), 2004, Publishing House of Electronics Industry, Beijing, China.
Google Scholar
20 Ma X. Y. and Nikias C. L., Joint estimation of time delay and frequency delay in impulsive noise using fractional lower order statistics, IEEE Transactions on Signal Process. (1996) 44, no. 11, 2669–2687, https://doi.org/10.1109/78.542175, 2-s2.0-0030288337.
10.1109/78.542175
Web of Science® Google Scholar
21 Bassiou N., Kotropoulos C., and Koliopoulou E., Symmetric α-stable sparse linear regression for musical audio denoising, Proceedings of the International Symposium on Image & Signal Processing & Analysis, May 2013, Ljubljana, Slovenia.
Google Scholar
22 Xiong Q., Xu Y., Peng Y., Zhang W., Li Y., and Tang L., Low-speed rolling bearing fault diagnosis based on EMD denoising and parameter estimate with alpha stable distribution, Journal of Mechanical Science and Technology. (2017) 31, no. 4, 1587–1601, https://doi.org/10.1007/s12206-017-0306-y, 2-s2.0-85018494116.
10.1007/s12206-017-0306-y
Web of Science® Google Scholar
23 Li Y., Zhang W., Xiong Q., Lu T., and Mei G., A novel fault diagnosis model for bearing of railway vehicles using vibration signals based on symmetric alpha-stable distribution feature extraction, Shock and Vibration. (2016) 2016, 13, 5714195, https://doi.org/10.1155/2016/5714195, 2-s2.0-85008951548.
10.1155/2016/5714195
Web of Science® Google Scholar
24 Zheng Z. H. and Wang S. Y., Radar target detection method of fractional lower order matched filter in complex sea clutter background, ACTA Electronica Sinica. (2016) 44, no. 2, 319–326.
Google Scholar
25 Bibalan M. H., Amindavar H., and Amirmazlaghani M., Characteristic function based parameter estimation of skewed alpha-stable distribution: an analytical approach, Signal Processing. (2017) 130, 323–336, https://doi.org/10.1016/j.sigpro.2016.07.020, 2-s2.0-84979953945.
10.1016/j.sigpro.2016.07.020
Web of Science® Google Scholar
26 Ling X. and Yan X. A., A self-adaptive time-frequency analysis method based on local mean decomposition and its application in defect diagnosis, Journal of Vibration and Control. (2016) 22, no. 4, 1049–1061, https://doi.org/10.1177/1077546314538992, 2-s2.0-84958225638.
10.1177/1077546314538992
Web of Science® Google Scholar
27 Yang Y., Cheng J., and Zhang K., An ensemble local means decomposition method and its application to local rub-impact fault diagnosis of the rotor systems, Measurement. (2012) 45, no. 3, 561–570, https://doi.org/10.1016/j.measurement.2011.10.010, 2-s2.0-84856763171.
10.1016/j.measurement.2011.10.010
Web of Science® Google Scholar
28 Huang C., Meng Y. J., Lei W. P., and Zhao J., Full vector envelope technique based on complex local mean decomposition and its application in fault feature extraction for rotor system, Journal of Mechanical Engineering. (2016) 52, no. 7, 69–78, https://doi.org/10.3901/jme.2016.07.069, 2-s2.0-84965032319.
10.3901/JME.2016.07.069
Google Scholar
29 Wang J., Li J., and Wan X. D., Fault feature extraction method of rolling bearings based on singular value decomposition and local mean decomposition, Journal of Mechanical Engineering. (2015) 51, no. 3, 104–110, https://doi.org/10.3901/jme.2015.03.104, 2-s2.0-84924812092.
10.3901/JME.2015.03.104
Google Scholar
30 Xu Q. Q., Liu K., Hou H. P. et al., Diagnosis method of fault bearings based on LMD and LE, China Mechanical Engineering. (2016) 27, no. 22, 3075–3081.
Google Scholar
31 Li H., Zhao C. S., Zhou S., and Guo Y., Fault feature enhancement method for rolling bearing based on wavelet packet-coordinate transformation, Journal of Mechanical Engineering. (2011) 47, no. 19, 74–80, https://doi.org/10.3901/jme.2011.19.074, 2-s2.0-80855153825.
10.3901/jme.2011.19.074
CAS Google Scholar
32 Yu G., Li C. N., Zhang J. F. et al., A new statistical modeling and detection method for rolling element bearing faults based on alpha-stable distribution, Mechanical Systems and Signal Processing. (2013) 41, no. 1-2, 155–175, https://doi.org/10.1016/j.ymssp.2013.08.015, 2-s2.0-84885624558.
10.1016/j.ymssp.2013.08.015
Web of Science® Google Scholar
33 Li Z. N., Lv Y. P., and Han J., Bland sepraration of non-stationary signals in the mechanical equipment based on time-frequency analysis, Journal of Mechanical Strength. (2008) 30, no. 3, 354–358.
CAS Google Scholar
34 Koutrovelis I. A., Regression type estimation of the parameters of stable laws, Journal of the American Statistical Association. (1980) 75, no. 372, 918–928, https://doi.org/10.1080/01621459.1980.10477573, 2-s2.0-84893895320.
10.1080/01621459.1980.10477573
Web of Science® Google Scholar
35 He Q., Vibration signal classification by wavelet packet energy flow manifold learning, Journal of Sound and Vibration. (2013) 332, no. 7, 1881–1894, https://doi.org/10.1016/j.jsv.2012.11.006, 2-s2.0-84872776720.
10.1016/j.jsv.2012.11.006
Web of Science® Google Scholar
36 He Q. B., Time-frequency manifold for nonlinear feature extraction in machinery fault diagnosis, Mechanical Systems and Signal Processing. (2013) 35, no. 1-2, 200–218, https://doi.org/10.1016/j.ymssp.2012.08.018, 2-s2.0-84870468265.
10.1016/j.ymssp.2012.08.018
Web of Science® Google Scholar

Citing Literature

All articles

A New Feature Extraction Method for Bearing Faults in Impulsive Noise Using Fractional Lower-Order Statistics

Abstract

1. Introduction

2. Fractional Lower-Order Alpha-Stable Distribution

3. Nonstationary Signal Processing