Volume 2019, Issue 1 2670836

Research Article

Open Access

Calibration of Numerical Simulation Methods for Underwater Explosion with Centrifugal Tests

Qiusheng Wang

Institute of Geotechnical and Underground Engineering, Beijing University of Technology, Beijing 100124, China bjut.edu.cn

Search for more papers by this author

Shicong Liu,

Corresponding Author

Shicong Liu

[email protected]

orcid.org/0000-0002-2339-0908

Institute of Geotechnical and Underground Engineering, Beijing University of Technology, Beijing 100124, China bjut.edu.cn

Search for more papers by this author

Haoran Lou,

Haoran Lou

Institute of Geotechnical and Underground Engineering, Beijing University of Technology, Beijing 100124, China bjut.edu.cn

Search for more papers by this author

Qiusheng Wang,

Qiusheng Wang

Institute of Geotechnical and Underground Engineering, Beijing University of Technology, Beijing 100124, China bjut.edu.cn

Search for more papers by this author

Shicong Liu,

Corresponding Author

Shicong Liu

[email protected]

orcid.org/0000-0002-2339-0908

Institute of Geotechnical and Underground Engineering, Beijing University of Technology, Beijing 100124, China bjut.edu.cn

Search for more papers by this author

Haoran Lou,

Haoran Lou

Institute of Geotechnical and Underground Engineering, Beijing University of Technology, Beijing 100124, China bjut.edu.cn

Search for more papers by this author

First published: 2019

https://doi.org/10.1155/2019/2670836

Citations: 2

Academic Editor: Mickaël Lallart

Share a link

Email
Wechat
Bluesky

Abstract

The centrifugal underwater explosion tests and corresponding numerical simulations were carried out to study the laws of shock wave and bubble pulsation. A semiempirical method to determine JWL state equation parameters was given. The influence on numerical results caused by factors such as state equation of water, boundary condition, and mesh size was analyzed by comparing with the centrifugal underwater explosion test results. The results show that the similarity criterion is also suitable in numerical simulation; the shock wave peak pressure calculated by polynomial state equation is smaller than that of shock state equation. However, the maximum bubble radius and the pulsation period calculated by the two equations are almost the same. The maximum bubble radius is mainly affected by the boundary simulating the test model box, and the pulsation period is mainly affected by the artificial cutoff boundary. With the increase of standoff distance of measuring point, the mesh size required for the numerical calculation decreases; the size of the two-dimensional model is recommended to take 1/30 ∼ 1/10 explosion radius. In three-dimensional models, when mesh size is 2 times larger than explosion radius, the bubble motion change in the second pulsation period is not obvious. When mesh size is smaller than 1 time explosive radius, the full period of bubble pulsation can be well simulated, but calculation errors increase slowly and computation time greatly increases, so the three-dimensional mesh size is suggested to take the charge radius. Shock wave peak pressure is basically unaffected by gravity. As the gravity increases, the bubble maximum radius and the first pulsation period both decrease.

1. Introduction

Underwater explosion plays a vital role in military and civil construction. The load of underwater explosion mainly consists of two parts: shock wave and bubble pulsation, each of which accounts for about 50% of the total energy of explosion [1]. Researches of underwater explosion are mostly focused on these two aspects. There are two kinds of test methods widely used to study underwater explosion in the beginning of study, so called small equivalent charge explosion tests [2, 3] and mechanism tests [4–7]. In recent years, the two tests have also been highly developed. Zhang et al. [8] used the small charge explosion to study bubble dynamics with the technology of high-speed camera. Zhang et al. [9] studied the bubble motion near a raised free boundary in the small charge explosion test. However, the effects of buoyancy and gravity need to be ignored in most small equivalent charge explosion tests and mechanism test studies. Gel’Fand and Takayama [10] pointed out that, in the underwater explosion test, the shock wave can ignore the gravity effect but the bubble pulsation must consider that. According to the similarity criterion of underwater explosion model tests [11], Mach and Froude similitudes can be achieved simultaneously only when the gravity effect is considered. So, the centrifugal test is a good way to study underwater explosion. The China Institute of Water Resources and Hydropower Research has conducted some underwater explosion tests in centrifuge, and some of the test results can be found in references [12–14]. The similarity criterion and the laws of shock wave and bubble pulsation with the change of centrifugal acceleration were given.

Numerical simulation is a more convenient method to study underwater explosion problem. However, the accuracy is deeply affected by some factors such as state equation of water, boundary condition, and mesh size. Some studies have been conducted for numerical influence factors. Li et al. [15] analyzed different state equations of water in theory, proposed the applicable range of each state equation, and verified the theoretical results by numerical simulation. Chisum and Matsumoto [16, 17] studied the bubble pulsation by finite element software called MSC.DYTRAN. They pointed out that the pulsation period, the bubble center position, and the bubble deformation were deeply affected by the boundary condition in the first bubble period. Mu et al. [18] summarized the influence of different boundary conditions on bubble and proposed the range that the bubble can be regarded as spherical shape. Shi et al. [19] compared the numerical results of the shock wave specific impulse and peak pressures under different mesh sizes in air explosion models and presented a method to reduce the error caused by the mesh size. Zhang et al. [20] summarized a method to determine the mesh size through air and underwater explosion numerical simulation. However, there is a huge gap between experimental and numerical methods up to date. Many numerical researches lack the experimental verification. Calibration of numerical simulation methods for underwater explosion with test results is needed.

In this paper, the centrifugal underwater explosion tests of spherical explosive RDX were introduced, and the corresponding numerical simulations were conducted. In the process of numerical simulation, the calibration of the similarity criterion in numerical simulation was conducted, and a method to determine parameters of the JWL state equation was given. On the basis of 1g RDX explosive underwater explosion tests, different finite element models were used to study the influences of various factors, including the state equation of water, the boundary condition, and the mesh size. Finally, combining the numerical results of the optimal numerical model and centrifugal underwater explosion test results, some rules of shock wave and bubble pulsation were summarized.

2. Centrifugal Model Experiments of Underwater Explosion

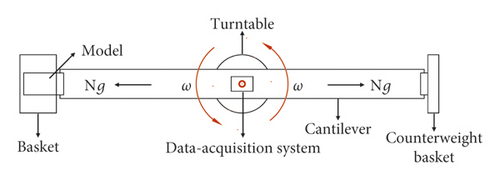
The underwater centrifugal explosion tests were performed on LXJ-4-450 centrifuge (Figure 1) in IWHR laboratory (the China Institute of Water Resources and Hydropower Research). The centrifuge can provide a maximum acceleration of 300g, which has a maximum rotation radius of 5.03 m and payload of 1.5 t. The dimensions of the centrifugal basket are 1500 × 1000 × 1500 mm. The centrifugal basket and model placed in it gradually become horizontal when rotating. Therefore, a centrifugal acceleration Ng, which is dozen times larger than the gravity acceleration, is formed along the cantilever direction. Neglecting the earth gravity and assuming the centrifugal acceleration remaining uniform, the small-scale model will have same gravity field as the prototype.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

The LXJ-4-450 centrifuge.

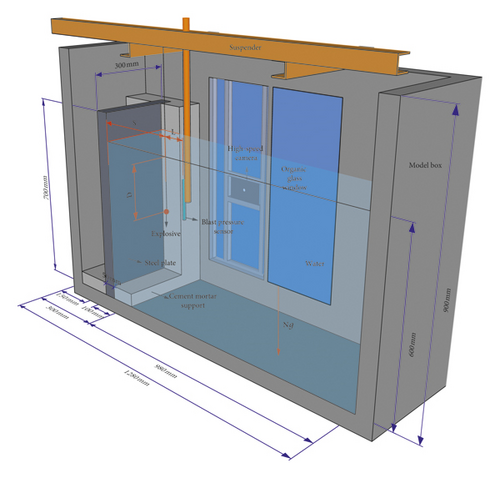
As shown in Figure 2, the test model container has a size of 1280 × 720 × 900 mm and is made of aluminum alloy. On the side of the container, there is an organic glass observation window, near which the high-speed camera (FASTCAM-ultima APX) is placed to capture the bubble. The high-speed camera has a frequency of 2000 fps and resolution of 1024 × 1024. The dimension of the steel plate is 700 × 600 × 50 mm, which is fixed by a cement mortar support with thickness of 50 mm. It is used to study the dynamic responses of the structure caused by underwater explosion, which is only regarded as the shell of model container in this paper. The explosive is in the same longitudinal plane and underwater depth D as the water pressure sensor (ICP138A25). The depth of water in the model box is 600 mm. All data are collected through a system with 32 acquisition channels on the top of the centrifugal shaft. The test cases are shown in Table 1, and it includes the different distances between the explosive and the sensor L and the distance between the explosive and the steel plate S.

Table 1. Experiment scheme.

No.	Ng	W (g)	D (mm)	S (mm)	L (mm)	Filmed	P_m (MPa)	R_m (mm)	T (ms)
UE-Exp-01	40	1.010	300	150	175		36.98
UE-Exp-02	40	1.024	300	250	250		25.46
UE-Exp-03	40	1.015	300	200	300		21.49
UE-Exp-04	40	1.023	300	300	350	√	17.61	131.25	18
UE-Exp-05	40	1.025	300	300	350	√	18.21	131.52	18.5
UE-Exp-06	20	1.020	300	300	350	√	19.43	141.26	24
UE-Exp-07	30	1.021	300	300	350	√	18.30	134.17	21
UE-Exp-08	50	1.038	300	300	350	√	19.35	123.67	16.5
UE-Exp-09	20	1.016	200	200	300		20.20
UE-Exp-10	40	1.040	200	200	300		21.29
UE-Exp-11	1	0.050	300	300	350	√	3.5	62.4	11.5
UE-Exp-12	20	0.050	300	300	350	√	3.47	53.3	8.5
UE-Exp-13	30	0.050	250	300	354	√	3.08	49.6	7.5
UE-Exp-14	40	0.050	300	300	350	√	4.99	45.6	6.0
UE-Exp-15	20	0.150	375	300	358		4.98
UE-Exp-16	40	0.150	300	300	350	√	3.31	69.6	9.5

Note. P_m is the shock wave peak pressure, R_m is the maximum bubble radius in the first pulsation period, and T is the size of the first bubble pulsation period.

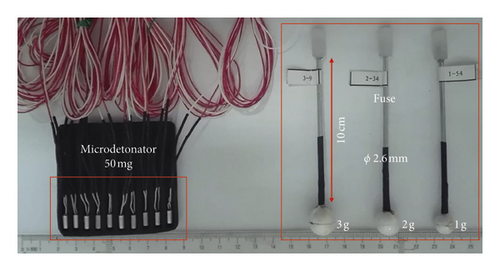
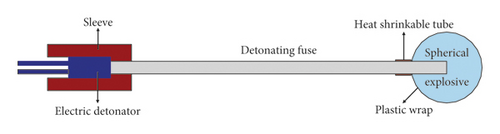
In order to improve the accuracy of model tests, the explosive used was a self-made RDX spherical explosive, and it took the way of a central detonation. The microdetonator detonates the detonating fuse, and then, the detonating fuse detonates the center of the charge. RDX spherical explosives and microdetonators are shown in Figure 3. The RDX spherical explosive consists of two separated hemispherical explosives. The 10 cm long detonating fuse with diameter of 2.6 mm has a dose (TNT equivalent) of 48 mg/m, and the dose of a microdetonator (RDX equivalent) is 50 mg. Sleeve, heat shrinkable tube, and plastic wrap are added to reinforce and protect the entire detonating device. The explosive has a density of 1.65 g/cm³ and a detonation velocity of 8160 m/s. As shown in Table 1, UE-Exp-11∼14 are underwater explosion test cases caused by a single 50 mg detonator, while UE-Exp-15∼16 are caused by three 50 mg detonators in series, which is used to simulate a 150 mg detonator.

3. Similarity Criterion for Centrifuge Underwater Explosion Tests

The similarity criterion is the theoretical basis of underwater explosion model test, which can be easily deduced by the tool of dimensional analysis. References [11, 13] have been given more elaborate research. The rationality of the similarity criterion also has been calibrated by a series of centrifugal underwater explosion tests [11].

When studying underwater explosion shock wave and bubble pulsation, the water viscosity is ignored, and it is assumed that the explosion process is adiabatic. The shock wave parameters that need to be calculated include the shock wave peak pressure P_m and the time parameter θ, while the bubble parameters include the maximum bubble radius R_m and the pulsation period T. Beyond that, the parameters affecting the explosion process are considered: explosive parameters including explosive mass W, explosive radius R_e, detonation velocity U, explosive density ρ_e, explosive energy per unit mass E, and explosive depth D; water medium parameters including water density ρ₀, sound velocity in water C₀, and flow velocity of water μ; and other parameters including gravity acceleration g, atmospheric pressure P₀, and standoff distance L. Therefore, choosing the density of the water ρ₀, the explosive depth D, and the flow velocity of water μ which are the basic parameters. Applied by the p theorem, all the above parameters can be expressed by the nondimensionalized implicit function equations. The nondimensionalized implicit function equations are as follows:

\begin{matrix} \{\begin{cases} \frac{P_{m}}{ρ_{0} μ^{2}} = f_{1} (\frac{μ^{2}}{D g}, \frac{C_{0}}{μ}, \frac{P_{0}}{ρ_{0} μ^{2}}, \frac{W}{ρ_{0} D^{3}}, \frac{E}{μ^{2}}, \frac{R_{e}}{D}, \frac{U}{μ}, \frac{L}{D}), \\ \frac{θ}{D μ^{- 1}} = f_{2} (\frac{μ^{2}}{D g}, \frac{C_{0}}{μ}, \frac{P_{0}}{ρ_{0} μ^{2}}, \frac{W}{ρ_{0} D^{3}}, \frac{E}{μ^{2}}, \frac{R_{e}}{D}, \frac{U}{μ}, \frac{L}{D}), \\ \frac{R_{m}}{D} = f_{3} (\frac{μ^{2}}{D g}, \frac{C_{0}}{μ}, \frac{P_{0}}{ρ_{0} μ^{2}}, \frac{W}{ρ_{0} D^{3}}, \frac{E}{μ^{2}}, \frac{R_{e}}{D}, \frac{U}{μ}), \\ \frac{T}{D μ^{- 1}} = f_{4} (\frac{μ^{2}}{D g}, \frac{C_{0}}{μ}, \frac{P_{0}}{ρ_{0} μ^{2}}, \frac{W}{ρ_{0} D^{3}}, \frac{E}{μ^{2}}, \frac{R_{e}}{D}, \frac{U}{μ}) . \end{cases} \end{matrix}

(1)

Because the fluid and explosive used in the model are the same as the prototype, W, U, E, ρ₀, C₀, μ, and P₀ are constants, and then, equation (1) is further rewritten as

\begin{matrix} \{\begin{cases} P_{m} = f_{1} (\frac{1}{D g}, \frac{W}{D^{3}}, \frac{R_{e}}{D}, \frac{L}{D}), \\ \frac{θ}{D} = f_{2} (\frac{1}{D g}, \frac{W}{D^{3}}, \frac{R_{e}}{D}, \frac{L}{D}), \\ \frac{R_{m}}{D} = f_{3} (\frac{1}{D g}, \frac{W}{D^{3}}, \frac{R_{e}}{D}), \\ \frac{T}{D} = f_{4} (\frac{1}{D g}, \frac{W}{D^{3}}, \frac{R_{e}}{D}) . \end{cases} \end{matrix}

(2)

In the experiment, to satisfy the similarity theorem, each dimensionless parameter in equation (2) should be equal correspondingly. For example, if to make (θ/D)_m/(θ/D)_p = 1 (subscripts m represents model and p represents prototype), then

\begin{matrix} {(\frac{1}{D g})}_{m} = {(\frac{1}{D g})}_{p}, \\ {(\frac{W}{D^{3}})}_{m} = {(\frac{W}{D^{3}})}_{p}, \\ {(\frac{R_{e}}{D})}_{m} = {(\frac{R_{e}}{D})}_{p}, \\ {(\frac{L}{D})}_{m} = {(\frac{L}{D})}_{p} . \end{matrix}

(3)

Combining the same type of parameters, then

\begin{matrix} \frac{D_{m}}{D_{p}} = \frac{g_{p}}{g_{m}}, \\ \frac{W_{m}}{W_{p}} = {(\frac{D_{m}}{D_{p}})}^{3}, \\ \frac{D_{m}}{D_{p}} = \frac{{(R_{e})}_{m}}{{(R_{e})}_{p}}, \\ \frac{D_{m}}{D_{p}} = \frac{L_{m}}{L_{p}} . \end{matrix}

(4)

Given the geometric length scale is λ, namely, D_m/D_p = λ, the remaining scales in the above equations should satisfy that

\begin{matrix} \frac{g_{p}}{g_{m}} = λ, \\ \frac{W_{m}}{W_{p}} = λ^{3}, \\ \frac{{(R_{e})}_{m}}{{(R_{e})}_{p}} = λ, \\ \frac{L_{m}}{L_{p}} = λ . \end{matrix}

(5)

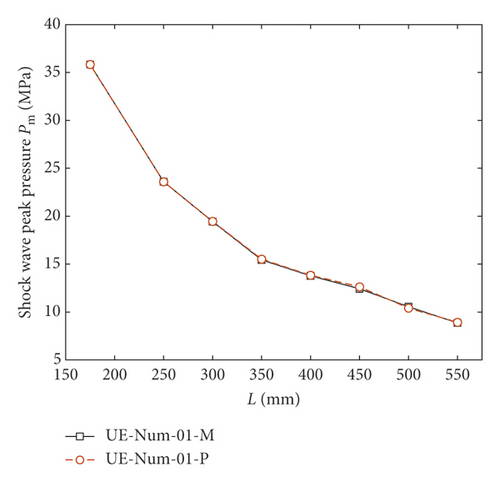
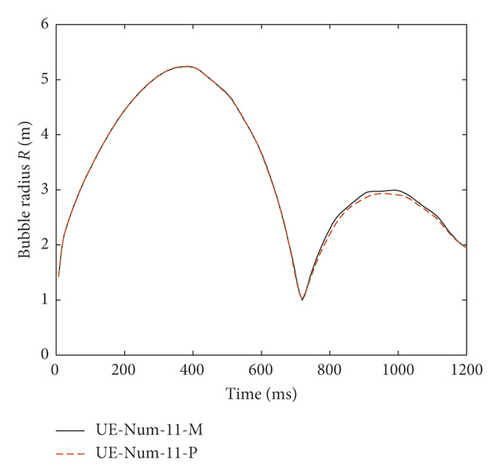
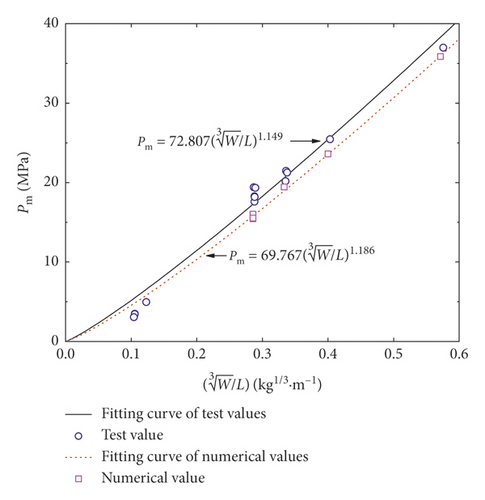
Table 2 lists the centrifugal similarity relation between the prototype and the model. Actually, the similarity criterion can also be deduced by balance and state equations and can automatically be satisfied in numerical simulation. This can be verified by two simple calculations (UE-Num-01 and UE-Num-11 in Table 3). The UE-Num-01 was used to calculate the shock wave, while the UE-Num-11 was used to calculate the bubble pulsation. The prototypes of the UE-Num-01 and UE-Num-11 were created through the similarity relation in Table 2. As it can be seen in Figure 4, the calculated variation of the shock wave peak pressure and the bubble radius are almost the same.

Table 2. The centrifugal similarity relation.

Parameters	Dimension	Prototype	Model	Scale
Explosive mass	M	W	λ³W	λ³
Explosive radius	L	R_e	λR_e	λ
Standoff distance		L	λL
Bubble radius		R	λR
Depth of explosive		D	λD
Time constant	T	θ	λθ	λ
Period	T	T	λT	λ
Gravity acceleration	LT⁻²	g	g/λ	λ
Water destiny	ML⁻³	ρ₀	ρ₀	1
Explosive destiny	ML⁻³	ρ_e	ρ_e	1
Atmosphere pressure	ML⁻¹T⁻²	P₀	P₀	1
Shock wave peak pressure	ML⁻¹T⁻²	P_m	P_m	1
Flow velocity of water	LT⁻¹	μ_p	μ_p	1
Sound velocity		C₀	C₀
Detonation velocity		U	U
Explosive energy per unit mass	ML²T⁻²	E	E	1

Table 3. Scheme of numerical models.

No.	Symmetry	Ng	SEW	Mesh sizes (mm)	Boundary 1	Boundary 2
UE-Num-01	2D	40	Shock	0.5	Flow out	Rigid
UE-Num-02	2D	40	Polynomial	0.5	Flow out	Rigid
UE-Num-03	2D	40	Shock	0.5	Flow out	STEEL 4340
UE-Num-04	2D	40	Shock	0.5	Rigid	Rigid
UE-Num-05	2D	40	Shock	0.5	Rigid	STEEL 4340
UE-Num-06	2D	20	Shock	0.5	Flow out	Rigid
UE-Num-07	2D	30	Shock	0.5	Flow out	Rigid
UE-Num-08	2D	50	Shock	0.5	Flow out	Rigid
UE-Num-09	3D	20	Shock	5	Flow out	Rigid
UE-Num-10	3D	30	Shock	5	Flow out	Rigid
UE-Num-11	3D	40	Shock	5	Flow out	Rigid
UE-Num-12	3D	40	Shock	5	Flow out	STEEL 4340
UE-Num-13	3D	40	Shock	5	Rigid	Rigid
UE-Num-14	3D	40	Shock	5	Rigid	STEEL 4340
UE-Num-15	3D	50	Shock	5	Flow out	Rigid
UE-Num-16	3D	50	Shock	5	Flow out	STEEL 4340
UE-Num-17	3D	50	Shock	5	Rigid	Rigid
UE-Num-18	3D	50	Shock	5	Rigid	STEEL 4340
UE-Num-19	3D	50	Polynomial	5	Flow out	Rigid
UE-Num-20	3D	50	Shock	5	Flow out	Rigid
UE-Num-21	3D	50	Shock	5	Flow out	Rigid
UE-Num-22	3D	50	Shock	5	Flow out	Rigid

Note. SEW is the state equation of water.

4. Numerical Simulation of Underwater Explosion

Among the available commercial finite element packages such as ANSYS LS-DYNA, ABAQUS, ANSYS AUTODYN, and MSC DYTRAN, ANSYS AUTODYN is a nonlinear explicit finite difference software with many solvers such as Lagrange, Euler, ALE (arbitrary Lagrange–Euler), Shell, and SPH, among whom coupling calculations can be performed, so that the high-order nonlinear problems caused by the interaction of solids, gases, and fluids can be addressed, and it can also solve the large deformation problems, such as explosive expansion and bubble pulsation involved in underwater explosion. ANSYS AUTODYN has good computational stability and provides material models and data. It also has techniques such as mesh redivision, mesh coarsening and refinement, and remap that creates a mapping between low-dimensional calculation results and high-dimensional models, which can greatly shorten modeling and calculating time.

The two-dimensional finite element method was used to study the shock wave. The models were established by the axisymmetric method. The mass of explosive is 1 g, and the radius of explosive is 5.25 mm. Centrifugal acceleration environment, model sizes, arrangements of charge measuring points, and boundary type are shown in Figure 5. The three-dimensional finite element method was used to study the bubble pulsation. The basic models are shown in Figure 6. Figure 6(a) is a model using rigid boundary to simulate the outer shell of the test model, while Figure 6(b) illustrates using STEEL 4340 model shell to simulate the outer shell of the test model. In the three-dimensional modeling, the remap technique was applied, in which the shock wave just touching the boundary in the two-dimensional model is mapped to the three-dimensional model to continue the computation.

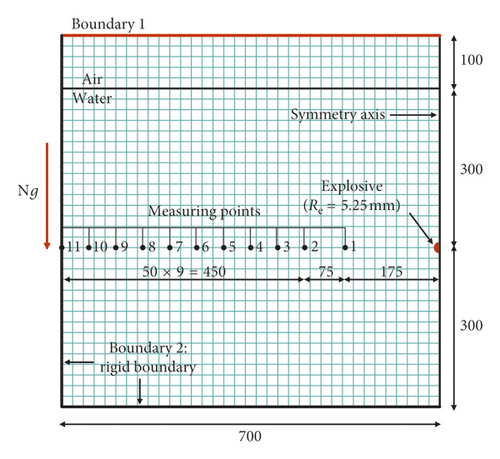
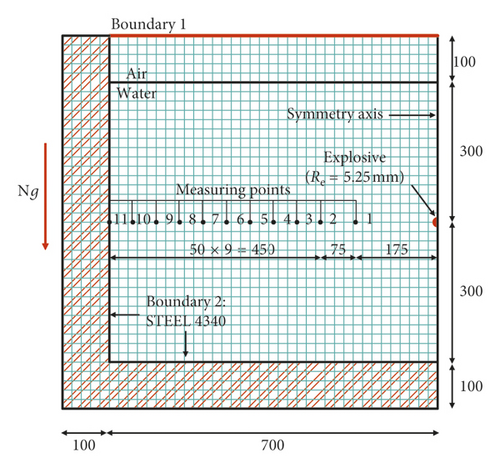
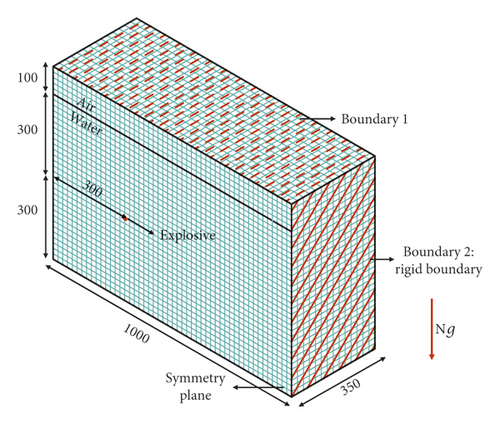
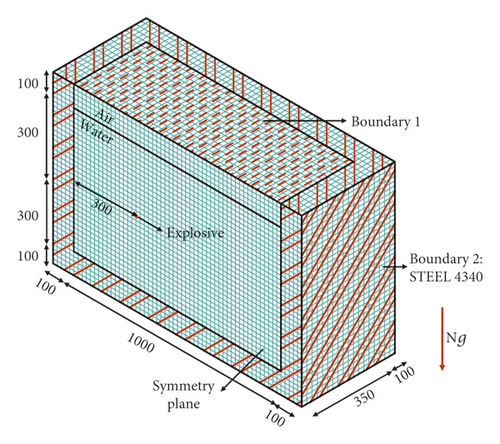
The numerical cases are shown in Table 3. The model UE-Num-01 was used to simulate the shock wave of test cases UE-Exp-01∼05. The models UE-Num-06, 07, and 08 were used to simulate the shock wave of test cases UE-Exp-06, 07, and 08, respectively. The models UE-Num-09, 10, 11, and 15 were used to simulate the bubble pulsation of test cases UE-Exp-04, 06, 07, and 08, respectively. The factors influencing the numerical results accuracy are as follows.

4.1. The State Equation Used in the Numerical Analysis

State equation is a functional relation characterized by object pressure, density, and internal energy. The main parameters in state equation are determined by tests. The state equations of each material can have different forms [21, 22] and are generally semiempirical and semitheoretical formulas. The materials involved in this paper are air, STEEL 4340, explosive, and water.

4.1.1. The State Equation of Air

The ideal gas state equation is usually used for air [23]. The pressure is defined as

\begin{matrix} P = (γ - 1) \frac{ρ}{ρ_{0}} E_{0}, \end{matrix}

(6)

where γ = 1.4 is the adiabatic exponent, ρ₀ = 1.225 kg/m³ is the initial air density, ρ is the air density, and E₀ is the internal energy of air.

4.1.2. The State Equation of STEEL 4340

The test model box selects STEEL 4340 material model and the linear state equation. The linear state equation [24] is written as

\begin{matrix} P = K μ, \end{matrix}

(7)

where μ = ρ/ρ₀ − 1 is the compression ratio, ρ₀ = 7.83 g/cm³ is the initial density, ρ is the density, and K = 159 GPa is the bulk modulus.

4.1.3. The State Equation of Explosive

The state equation used in the RDX explosive is the JWL equation [23], which can be expressed as

\begin{matrix} P = A (1 - \frac{ω}{R_{1} V}) e^{- R_{1} V} + B (1 - \frac{ω}{R_{2} V}) e^{- R_{2} V} + \frac{ω E_{0}}{V}, \end{matrix}

(8)

where A, B, R₁, R₂, and ω are the materials parameters, P is the detonation products pressure, V is the relative volume of detonation products, and E₀ is the initial internal energy per unit volume of explosive. The three items contained in the right end of the formula successively play a major role in high-, medium-, and low-pressure regions.

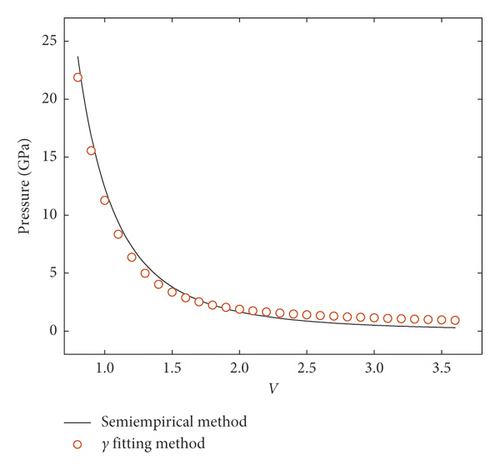
Because the explosives used in this test were developed specially, the parameters in the JWL equation should be determined first. The parameters can be determined by a semiempirical method and verified by the γ-fitting method [25].

The relationship between explosive detonation velocity and charge density can be written as follows [26, 27]:

\begin{matrix} D = a + K ρ_{0}, \end{matrix}

(9)

where D is the explosive detonation velocity in km/s, ρ₀ is the initial charge density in g/cm³, and a and K are the empirical coefficients related to the explosive type with a = 2.395 and K = 3.589 for RDX charge [25]. ρ₀ = 1.65 g/cm³ for RDX charge. So, the explosive detonation velocity is 8.317 km/s in this case.

Using D and ρ₀, the polytropic index of the detonation products γ [28] and E₀ [29] can be expressed as

\begin{matrix} γ = \frac{ρ_{0}}{(0.140.26 + ρ_{0})}, \end{matrix}

(10)

\begin{matrix} E_{0} = (0.2040.0734 - ρ_{0}) ρ_{0} D^{2} . \end{matrix}

(11)

The isentropic curve equation corresponding to the JWL equation is

\begin{matrix} P_{S} = A e^{- R_{1} V} + B e^{- R_{2} V} + C V^{- (ω + 1)}, \end{matrix}

(12)

where C is an undetermined coefficient and the subscript S represents the isentropic process. According to the thermodynamic relations, the internal energy on the isentropic curve can be obtained by

\begin{matrix} E_{S} = \frac{A}{R_{1}} e^{- R_{1} V} + \frac{B}{R_{2}} e^{- R_{2} V} + \frac{C}{ω} V^{- ω} . \end{matrix}

(13)

In accordance with the CJ [25] condition of explosive detonation,

- {(\partial P_{S} / \partial V)}_{V_{CJ}} = ρ_{0} D

, and it can be deduced that

\begin{matrix} A R_{1} e^{- R_{1} V_{CJ}} + B R_{2} e^{- R_{2} V_{CJ}} + C (ω + 1) V_{CJ}^{- (ω + 2)} = ρ_{0} D, \end{matrix}

(14)

where V_CJ is the relative specific volume of detonation products at the CJ point.

The CJ isentropic curve is through the CJ point, so

\begin{matrix} A e^{- R_{1} V_{CJ}} + B e^{- R_{2} V_{CJ}} + C V_{CJ}^{- (ω + 1)} = P_{CJ}, \end{matrix}

(15)

where P_CJ is the detonation pressure of explosive.

From the Hugoniot relation of detonation products, it is given by

\begin{matrix} \frac{A}{R_{1}} e^{- R_{1} V} + \frac{B}{R_{2}} e^{- R_{2} V} + \frac{C}{ω} V^{- ω} = E_{0} + \frac{1}{2} P_{CJ} (1 - V_{CJ}) . \end{matrix}

(16)

V_CJ and P_CJ are expressed as

\begin{matrix} V_{CJ} = \frac{γ}{(γ + 1)}, \end{matrix}

(17)

\begin{matrix} P_{CJ} = \frac{ρ_{0} D^{2}}{(γ + 1)} . \end{matrix}

(18)

The ω value could be 0.33, and R₂ ≈ 0.27 R₁(4 ≤ R₁ ≤ 5) [28–30]. The parameters A, B, and C can be calculated by equations (14)–(16). The computed results of parameters are listed in Table 4.

Table 4. Parameters of the JWL state equation of RDX charge.

ρ₀ (g/cm³)	D (km/s)	E₀ (GPa)	γ	P_CJ (GPa)	A (GPa)	B (GPa)	C (GPa)	R₁	R₂	ω
1.65	8.317	9.536	2.9	29.266	565.295	1.21711	2.202399	4.2139	1.13775	0.35

The γ fitting method [25] is a simple way to get unknown parameters of the JWL equation by plotting the P-V curve with ρ₀, D, and γ. The formula is defined as

\begin{matrix} P = \frac{γ^{γ}}{{(γ + 1)}^{γ + 1}} \frac{ρ_{0} D^{2}}{V^{γ}} . \end{matrix}

(19)

Figure 7 is a P-V plot based on equations (6) and (17), which used the parameters of Table 4. The values obtained by the two methods are very close, so the data in Table 4 are verified to be reasonable.

4.1.4. The State Equation of Water

When studying high-pressure problems caused by explosion, the Mie–Grüneisen state equation was often used as the state equation of water. There are two state equations for water, namely, the shock state equation and the polynomial state equation. The shock state equation is the Mie–Grüneisen high-pressure state equation that is expressed by Hugoniot points (P_H, μ) [15]. The pressure is given by

\begin{matrix} P = P_{H} (1 - Γ μ) + Γ (1 + μ) ρ_{0} E, \end{matrix}

(20)

where μ = ρ/ρ₀ − 1 is the compression ratio, ρ₀ = 1 g/cm³ is the initial density of water, ρ is the density of water, E is the internal energy per unit mass, P_H is the Hugoniot pressure of shock, which is an unknown function containing μ and is determined by the Hugoniot curve of impact, and Г is the Grüneisen coefficient, which is an unknown function containing μ and is determined by Г₀ (the Grüneisen coefficients at normal temperature and pressure) and its physical properties at high pressure. The Г formula is simplified as

\begin{matrix} Γ = Γ_{0} + a μ, \end{matrix}

(21)

where a is the modified constant of Г₀.

In the shock state equation, shock wave velocity of water U has the linear relationship with the particle velocity after shock wave μ_p, that is, S₂ = 0 and S₃ = 0 in the following equation [31]:

\begin{matrix} U = C_{0} + S_{1} μ_{p} + S_{2} \frac{μ_{p}^{2}}{U} + S_{3} \frac{μ_{p}^{3}}{U^{2}}, \end{matrix}

(22)

where S₁, S₂, and S₃ are the undetermined constants and C₀ is the sound velocity at normal temperature and pressure. The formula of P_H can be obtained as follows:

\begin{matrix} ρ_{0} U = ρ (U - μ_{p}), \end{matrix}

(23)

\begin{matrix} P_{H} = ρ_{0} D μ_{p}, \end{matrix}

(24)

\begin{matrix} P_{H} = \frac{ρ_{0} C_{0}^{2} μ (μ + 1)}{{[1 - (S_{1} - 1) μ]}^{2}} . \end{matrix}

(25)

For the Grüneisen coefficient Г, the shock state equation makes Г = Г₀. There are two kinds of Shock state equations, HULL and SNL state equations [32–34]. The parameters of the above two equations are shown in Table 5. In the SNL state equation, Г equals to 0, namely, the pressure is only determined by the density. This paper adopted the HULL state equation; in other words, the influence of internal energy was considered.

Table 5. Parameters of two shock state equations.

Equation types	C₀ (Km/s)	S₁	S₂	S₃	Г₀	a
HULL	1.483	1.75	0	0	0.28	0
SNL	1.647	1.92	0	0	0	0

The polynomial state equation of water [24] has different formulas, and it is determined by the state of compression.

When the water is compressed (μ > 0), its state equation is written as

\begin{matrix} P = A_{1} μ + A_{2} μ^{2} + A_{3} μ^{3} + (B_{0} + B_{1} μ) ρ_{0} E . \end{matrix}

(26)

When the water expands (μ < 0), its state equation is written as

\begin{matrix} P = T_{1} μ + T_{2} μ^{2} + B_{0} ρ_{0} E, \end{matrix}

(27)

where E is the internal energy per unit mass of water; A₁, A₂, A₃, T₁, and T₂ are pressure dimension constants; and B₀ and B₁ are dimensionless constants. Comparing equation (17) and compression state equation of water (equation (23)), P_H and Г are expressed as

\begin{matrix} P_{H} = \frac{2 (A_{1} μ + A_{2} μ^{2} + A_{3} μ^{3})}{2 - μ (B_{0} + B_{1} μ) / (μ + 1)}, \end{matrix}

(28)

\begin{matrix} Γ = \frac{(B_{0} + B_{1} μ)}{(1 + μ)} . \end{matrix}

(29)

The parameters of polynomial state equation are shown in Table 6.

Table 6. Parameters of polynomial state equation of water.

A₁ GPa	A₂ (GPa)	A₃ (GPa)	B₀	B₁	T₁ (GPa)	T₂
2.2	9.54	14.57	0.28	0.28	2.2	0

The state equation of water was set to different forms to study the influence on the numerical results of shock wave and bubble pulsation. UE-Num-01 and UE-Num-02 were used to study the shock wave, and UE-Num-15 and UE-Num-19 were used to study the bubble pulsation (Table 3).

4.2. The Boundary Condition Used in the Numerical Analysis

Due to the limitation of computing power, numerical simulation should avoid the large size calculation models. The boundary condition affects numerical simulation results greatly. In numerical simulation, boundary conditions should meet the need of calculation.

There are three kinds of boundary in numerical simulation, namely, transmitting boundary, flow out, and rigid boundary. Different boundary has different reflection on stress wave. In terms of reflection ability, the strongest one is rigid boundary and the weakest one is transmitting boundary. Transmitting boundary cannot be applied in the three-dimensional model, because three-dimensional model’s calculation consumes too much time, and if the transmitting boundary is applied, the model will lose too much energy, and it may lead to the break of computation. This paper focuses on the study of flow out and rigid boundary.

The influence of boundary condition was studied with two-dimensional models UE-Num-01, 03, 04, and 05 and three-dimensional models UE-Num-11∼18. As shown in Figures 5 and 6, Boundary 1 of the artificial cutoff boundary was used because of the limitation of model size, which is at the top of the air. Boundary 2 was used to simulate the test model shell. In addition to the rigid boundary, a 100 mm thick STEEL 4340 shell was also used. The boundary selection of each model is presented in Table 3. To make the results of boundary condition more universe, the bubble radius R and the bubble pulsation T are dimensionless processing:

\begin{matrix} R^{'} = \frac{R_{num}}{R_{m}}, \end{matrix}

(30)

\begin{matrix} T^{'} = \frac{t}{T}, \end{matrix}

(31)

where R ^′andT ^′ are the dimensionless bubble radius and dimensionless pulsation period; R_num and t are the numerical bubble radius and numerical time; and R_m and T are test maximum bubble radius and test bubble pulsation.

4.3. The Mesh Size

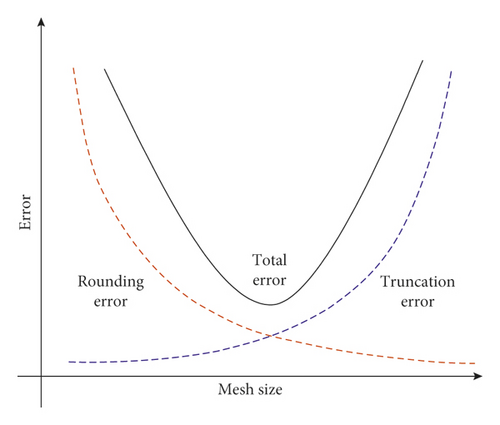
The mesh size must be small enough for improving the accuracy of computation. For large-size model computation, it is unreasonable to utilize the small mesh size. Firstly, it is because of the limitation of computing power. Secondly, when solving the difference equation in numerical computation, the limitation of computer’s word length causes the last significant digit of the floating-point number in the calculation process to be rounded up; thus, it can result in the accumulation of rounding error. Figure 8 shows the relationship between the error and the mesh size. Too small mesh size reduces the truncation errors caused by the differential equations being discrete into difference equations and increases the rounding errors caused by the rise of node’s number; therefore, it may contribute to an increase in the total error [35]. The mesh size must be within compass.

The explosive radius R_e is an important length parameter in computation. It defines the parameterless λ to describe the density of the mesh size, which is defined as follows:

\begin{matrix} λ = \frac{R_{e}}{L}, \end{matrix}

(32)

where R_e is the explosive radius and L is the mesh size.

The mesh size influence was studied by changing the mesh size of UE-Num-01 and UE-Num-11 in Table 3. The mesh size of UE-Num-01 was set to 2 mm, 1.5 mm, 1.25 mm, 1 mm, 0.8 mm, 0.5 mm, 0.25 mm, 0.2 mm, and 0.15 mm, and the corresponding λ is 2.625, 3.5, 4.2, 5.25, 6.5625, 10.5, 21, 26.25, and 35. The mesh size of UE-Num-11 is, respectively, set to 20 mm, 15 mm, 12 mm, 10 mm, 7.5 mm, 5 mm, and 2.5 mm, and the corresponding λ is 0.2625, 0.35, 0.4375, 0.525, 0.7, 1.05, and 2.1.

5. Results and Discussion

5.1. The Influence Factors on Numerical Results

5.1.1. The Influence of State Equation of Water on Numerical Results

Figure 9 illustrates the influence of state equation of water on the shock wave peak pressure P_m. Table 7 illustrates the comparison between test results and numerical results of shock wave peak or bubble pulsation. The values of P_m calculated by the shock state equation are closer to the test values. R_m and T are almost unaffected by the state equation of water. The water peak pressures calculated by the polynomial state equation are slightly smaller than that calculated by the shock state equation, so R_m would be slightly larger, but the difference of the state equation did not affect the pulsation period T. It can also be concluded that the shock state equation is more suitable for the case when the compression ratio μ is larger, but results calculated with the two state equations are close in the lower compression state. That is, when in the initial stage of explosion, the compression ratio μ of water is very large, which may result in higher P_m calculated by the shock state equation. In the later bubble pulsation phase, the water is in a lower compression state, and R_m and T calculated by the two state equations are similar.

Table 7. Comparison between numerical results of bubble pulsation with different water state equations and test results.

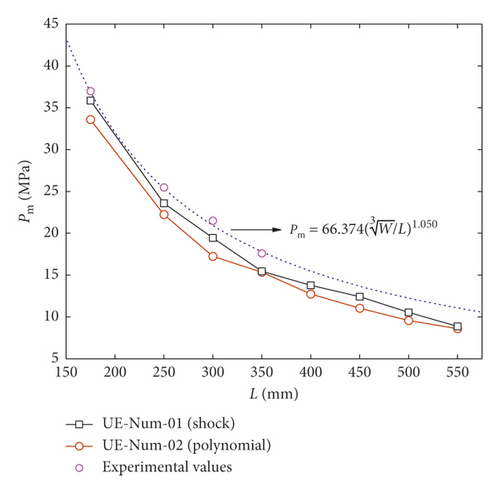
Types	Test values	UE-num-15 (shock)	UE-num-19 (polynomial)
R_m (mm)	123.67	125.08	125.27
T (ms)	16.50	16.18	16.18

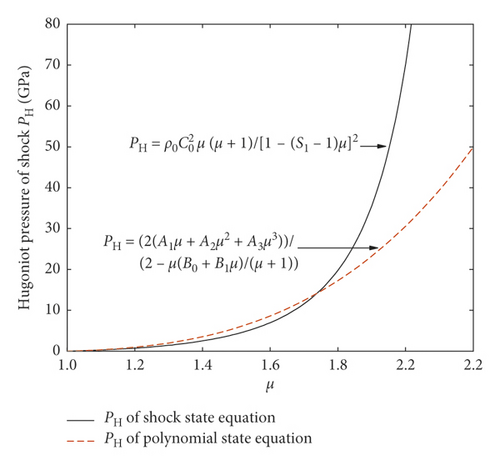
The reasons for different results need to be explained from the state equation itself. It can be seen from equation (17) that the water pressure is mainly dominated by two parts, the Hugoniot pressure of shock P_H and the Grüneisen coefficient Г. In this paper, Г = 0.28 is in the shock state equation directly, and substituting B₀ = B₁ = 0.28 into equation (26) of the polynomial state equation yields Г = 0.28, which indicates that the Hugoniot pressure P_H becomes the only influencing factor for comparative analysis. Figure 10 shows the relation between P_H and the compression ratio μ under two different state equations. It can be found from Figure 10 that the calculation results of the polynomial state equation are much smaller than that of the shock state equation in the high compression state, but they have the same P_H in the low compression state. Therefore, the shock waves cause high compression to the water, so the P_m calculated by the shock state equation is larger than that of the polynomial. When the bubble pulsation occurs, namely, the low compression state, R_m and T calculated by the two state equations are the same.

5.1.2. The Influence of Boundary Condition on Numerical Results

Figure 11 is a graph of P_m values varying with standoff distance L, which were calculated by models with different boundaries. Table 8 shows the P_m values of different measuring points, which were also computed by models with different boundaries. UE-Num-01 uses the flow out boundary as the artificial truncation boundary and also utilizes the rigid boundary to simulate the test model box. UE-Num-03 uses the flow out boundary as the artificial truncation boundary and the STEEL 4340 to simulate the test model box. UE-Num-04 uses the rigid boundary as the artificial truncation boundary and the rigid boundary to simulate the test model box. UE-Num-05 uses the rigid boundary as the artificial truncation boundary and the STEEL 4340 boundary to simulate the test model box. As shown in Table 8, UE-Num-01 has the same P_m value as the UE-Num-04, and the two models have the same Boundary 2 to simulate the test model but different Boundary 1 on the artificial truncation boundary, and the same situation can also be found in UE-Num-03 and UE-Num-05, so it can be concluded that the artificial truncation boundary (Boundary 1) has less influence on the shock wave peak pressure P_m. As shown in Figure 11, when L > 550 mm, the P_m does not decrease by law; in other words, P_m is obviously affected by the boundary condition; and the measuring point closer to the explosive center will be less affected from the boundary. As it can be seen from the measuring point 11 on the Boundary 2, P_m calculated by models with STEEL 4340 is larger than that of rigid boundary. That is, the reflection ability of STEEL 4340 is stronger.

Table 8. P_m of different measuring points at different boundary models.

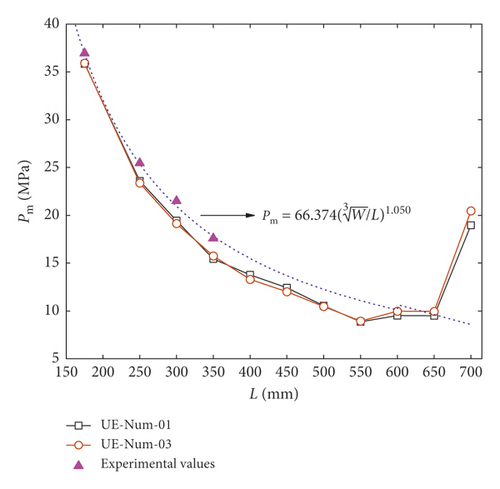
No.	L (mm)	Numerical results (MPa)
No.	L (mm)	UE-num-01	UE-num-03	UE-num-04	UE-num-05
1	175	35.85	35.89	35.85	35.89
2	250	23.60	23.36	23.60	23.36
3	300	19.45	19.13	19.45	19.13
4	350	15.45	15.76	15.45	15.76
5	400	13.78	13.30	13.78	13.30
6	450	12.42	12.01	12.42	12.01
7	500	10.55	10.47	10.55	10.47
8	550	8.87	8.94	8.87	8.94
9	600	9.52	9.98	9.52	9.98
10	650	9.50	9.95	9.50	9.95
11	700	18.96	20.44	18.96	20.44

Figure 12 is a plot of the bubble radius R ^′ varying with time in the first pulsation period, which was calculated by models with different boundaries at hypergravity accelerations of 40g and 50g. Figure 13 has four pressure cloud maps at the moment that each of bubbles had the maximum radius under 50g.

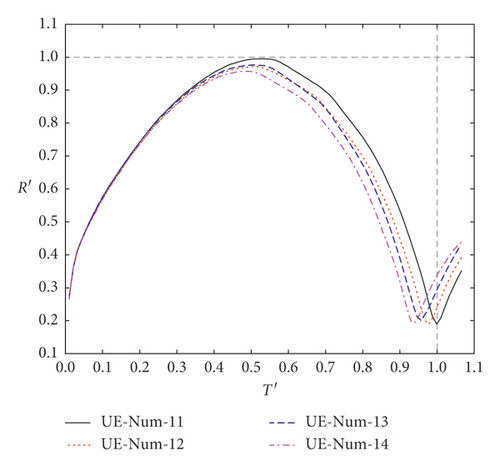
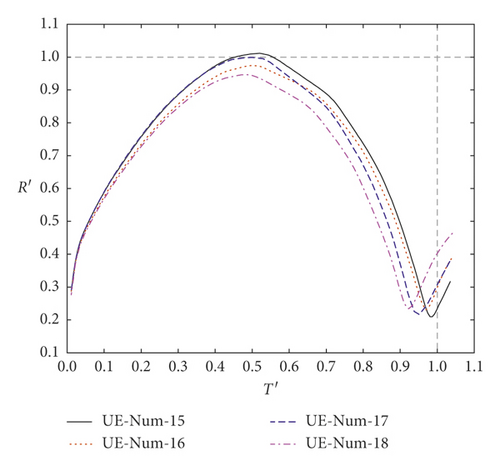
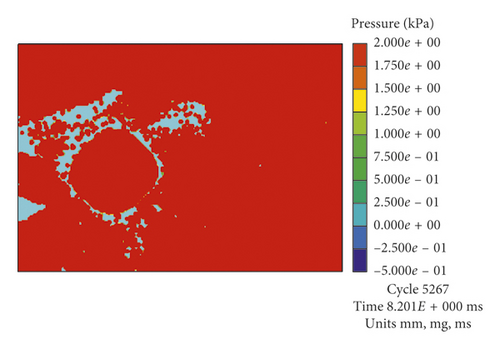
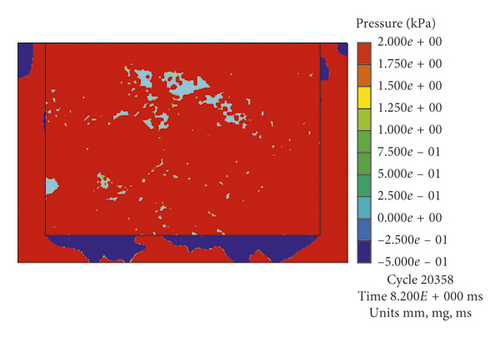
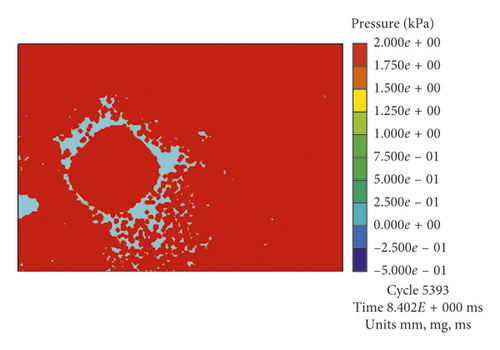
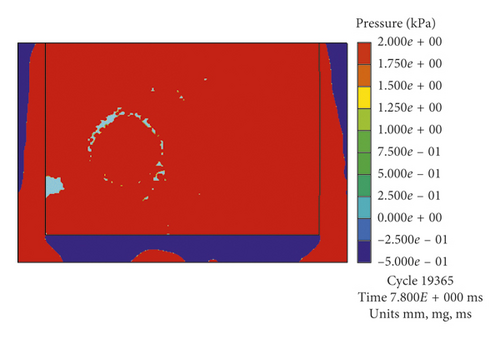
As shown in Figure 12(b), the values of R ^′ calculated by the models UE-Num-15 and UE-Num-17 are larger than that calculated by the models UE-Num-16 and UE-Num-18. UE-Num-15 has the same Boundary 2 to simulate the test model box but different Boundary 1 on the artificial truncation boundary from UE-Num-17, which indicates that the R_m is mainly affected by Boundary 2. The STEEL 4340 has stronger reflection ability than the rigid boundary, so the R_m of UE-Num-15 and UE-Num-17 is larger than that of R_m of UE-Num-16 and UE-Num-18. In addition to the influence of Boundary 1, UE-Num-15 has the smallest water pressure and the largest R_m, while UE-Num-18 has the largest water pressure and the smallest R_m. It also can be found from Figure 13 that when using STEEL 4340 that simulates the test model box, the water pressure around the bubble is larger than that of using the rigid boundary, which results in the smaller bubble radius; namely, the maximum radius of UE-Num-15 and UE-Num-17 are larger than that of UE-Num-16 and UE-Num-18.

From Figure 12(b), the T of UE-Num-15 and UE-Num-16 is larger than that of UE-Num-17 and UE-Num-18, which indicates that the length of the bubble pulsation period is controlled by both Boundary 1 and Boundary 2, and Boundary 1 is the dominant one. The rigid boundary was applied to Boundary 1, which leads to the water pressure being larger at the same moment; that is, it made the bubble to shrink faster. In addition to the influence of Boundary 2, the order of the four model bubble pulsation periods is as follows: UE-Num-15 > UE-Num-16 > UE-Num-17 > UE-Num-18. The same relations described above can also be found in Figure 12(a). According to Figure 12, the R ^′ and T ^′ of UE-Num-11 and UE-Num-15 are closer to 1. That is to say, it is better to use the rigid boundary to simulate the test model box and use the flow out boundary to simulate the artificial truncation boundary.

5.1.3. The Influence of Mesh Size on Numerical Results

Figure 14(a) illustrates the relationship between P_m and λ at different measuring points, 14(b) shows the P_m absolute errors between numerical results and test results, and the absolute error is written as

\begin{matrix} absolute error = \frac{|{(value)}_{num} - {(value)}_{\exp}|}{{(value)}_{\exp}} \times 100 %, \end{matrix}

(33)

where (value)_num is the numerical calculation result and (value)_exp is the test calculation result.

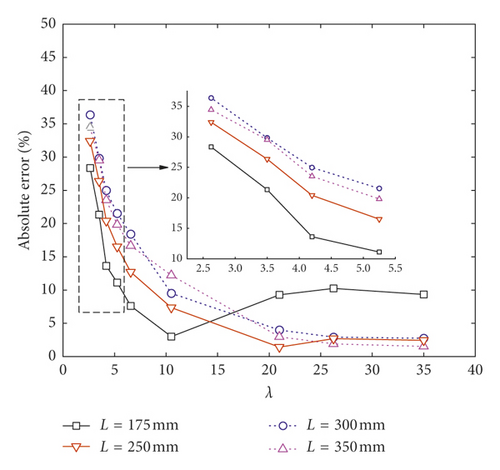
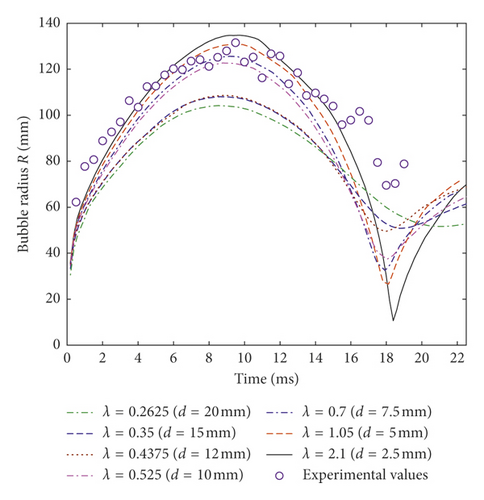
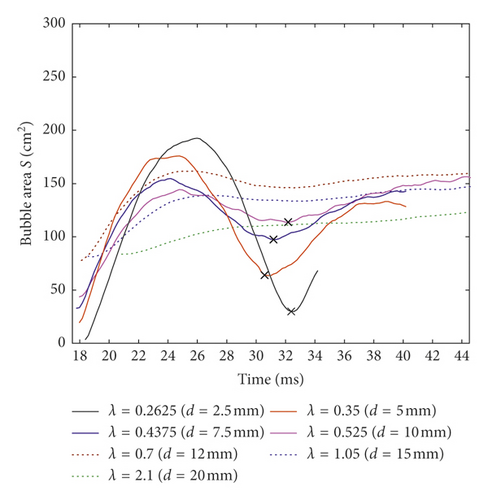
Figure 15(a) illustrates the relation between R under different λ in the first pulsation period and time, while 15(b) illustrates the R_m and T absolute errors. Figure 16 is a plot of the bubble area S varying with time in the second pulsation period under different λ. Table 9 illustrates the basic characteristics and computing time of different mesh size models. Numerical computing time in Table 9 means the time taken for each two-dimensional model to simulate 0.4 ms explosion, or for each three-dimensional model to simulate 30 ms explosion.

Table 9. The characteristics and calculation time of different mesh size models.

λ	d (mm)	Symmetry	Cells/elements	Nodes	Numerical computing time
2.625	2	2D	122500	123201	6 min
3.5	1.5	2D	218089	219024	14 min
4.2	1.25	2D	313600	314721	17 min
5.25	1	2D	490000	491401	33 min
6.5625	0.8	2D	765625	767376	1 h·4 min
10.5	0.5	2D	1960000	1962801	4 h·17 min
21	0.25	2D	7840000	7845601	30 h·55 min
26.25	0.2	2D	12250000	12257001	59 h·17 min
35	0.15	2D	21780899	21790224	207 h·33 min
0.2625	20	3D	31500	34884	2 h·1 min
0.35	15	3D	75576	81600	4 h·2 min
0.4375	12	3D	148680	158100	8 h·4 min
0.525	10	3D	245000	258156	12 h·6 min
0.7	7.5	3D	592012	615600	20 h·10 min
1.05	5	3D	1960000	2012211	36 h·18 min
2.1	2.5	3D	15680000	15888021	493 h·50 min

It can be seen from Figure 14(a) that, as the λ increases, P_m increases, and this tends to be stable gradually. When λ is 35, because the P_m of the measuring point 1 (L = 175 mm) begins to reduce, this is mainly because the effective data points to be saved under this model have exceeded the limitation of finite element software. It can be found from Figure 14(b) that, when λ is 10.5, the error of measuring point 1 has the smallest value; in other words, whenever λ increases or decreases from the value, the error both increases. The measuring point 2 (L = 250 mm) has the smallest error when λ = 21. When λ = 35, the measuring point 3 (L = 300 mm) and 4 (L = 350 mm) have the smallest error according to the present calculation. Therefore, different measuring points have different requirements on the mesh size. The error of measuring point closer to the explosive can reach allowed scope when the mesh size is relatively small. With the increase of L, the mesh size should decrease to meet requirement for numerical computation accuracy. As it can be seen from Table 9, the computing time of λ = 35 was 3.5 times greater than λ = 26.25, but the mesh size was only reduced by 0.05 mm. Thus, by reference to the error and computing time, if the shock wave is studied by the two-dimensional model, it is recommended that the mesh size can take (1/30–1/10) R_e.

In the first bubble pulsation, as the mesh size L decreases, the R_m increases, and the error is the smallest when λ = 0525 (Figures 15(a) and 15(b)); i.e., the mesh size is about twice larger than the explosive radius. The T error is the smallest when λ = 1.05; i.e., the mesh size is about equal to the explosive radius. In the second bubble pulsation period, because the bubble shape is no longer approximately circular, the statistics were based on the bubble occupied area. It can be concluded from Figure 16 that the maximum bubble area S_m increases with the decrease of the mesh size. When λ < 0.525 (the mesh size is 2 times larger than the charge radius), the variation of the bubble area was little during the second period, and the critical point between the second and third pulsation period is not obvious. When λ > 0.525, the variation of bubble size can be clearly observed, and the critical point of different periods can be found, but the computing time will be prolonged greatly with the increase of mesh size. As shown in Table 9, the computing time of λ = 2.1 (the mesh size is about 1/2 times of the charge radius) is 13 times larger than that of λ = 1.05. Combining the error and the computing time, if the three-dimensional model is used to study the bubble pulsation, it is suggested that the mesh size can be the same as the explosive radius R_e.

5.2. Test and Numerical Results on Shock Wave and Bubble Pulsation

The shock wave pressure is unusually determined by the Cole empirical formula (equation (31)):

\begin{matrix} P_{m} = k_{P} {(\frac{\sqrt[3]{W}}{L})}^{α_{P}}, \end{matrix}

(34)

where K_p and α_p are empirical coefficients, which are related to the type of charge. The fitting data were taken from all P_m test values and numerical simulation of 1g explosive. Table 10 illustrates the numerical calculation values of P_m. Relative error in Table 10 is expressed as

\begin{matrix} relative error = \frac{{(value)}_{num} - {(value)}_{\exp}}{{(value)}_{\exp}} \times 100 % . \end{matrix}

(35)

Table 10. Shock wave peak pressures under different working conditions.

Experiment scheme	UE-exp-01	UE-exp-02	UE-exp-03	UE-exp-04	UE-exp-06	UE-exp-07	UE-exp-08
Numerical values (MPa)	35.85	23.60	19.45	15.45	16.02	15.53	15.66
Relative error (%)	−3.06	−7.31	−9.49	−12.27	−17.55	−15.14	−19.07

The shock wave pressures of UE-Exp-01, 02, 03, 04, 06, 07, and 08 are listed in Figure 17. From Figure 17, the results of UE-Exp-1, 2, 3, and 4 are obtained under 40g centrifugal acceleration, but their standoff distances are different. So, it can be concluded that, with the increase of standoff distance L, the shock wave peak pressure P_m decreases. UE-Exp-4, 6, 7, and 8 have the same standoff distance L but different centrifugal accelerations, and their shock wave pressures are almost the same, so it can be concluded that the influence of gravity can be ignored when studying the shock wave peak pressure.

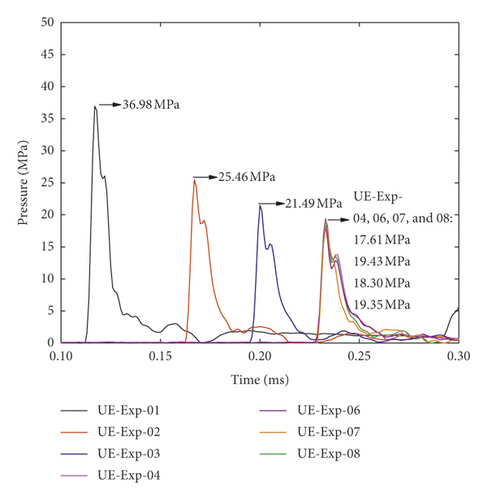
Through the above analysis of numerical influence factors, UE-Num-01, 06, 07, and 08 are used in simulating UE-Exp-04, 06, 07, and 08 and UE-Num-01 is used in simulating UE-Exp-01, 02, 03, and 04. From Table 10, the same shock wave change trends are also drawn in numerical simulation. As shown in Figure 18, the test values of P_m are a little larger than numerical values of P_m, but they have the same change trend varying with proportional distance.

Through the above analysis of numerical influence factors, UE-Num-11 is used in simulating UE-Exp-04. Bubble pulsation pictures in the first period including the test case of UE-Exp-04 and its numerical simulation results are displayed in Figure 19. The results of the maximum bubble radius R_m and the pulsation period T under different test conditions are shown in Table 1. Due to the limitation of the shooting range of high-speed camera, some bubbles have exceeded the shooting range during the expansion process, but the bubble shape is still processed in a complete circle. In the contraction phase, the bubble is moved upwards, so the second pulsation period bubble pictures are incomplete. As shown in Figure 19, the experimental bubble expanded to the maximum at 9.5 ms under 40g, while numerical bubble at 9.58 ms. The bubble shape was still spherical during expansion, but gradually became spindle-shaped when contracted whenever it was in a test or numerical condition. The bubble contracted to the minimum at 18.0 ms in test and at 17.98 ms in numerical simulation.

Figure 20 shows the bubble pulsation results of test cases UE-Exp-04, 06, 07, and 08 and their numerical simulation. The R_m and T numerical results of UE-Exp-04, 06, 07, and 08 are shown in Table 11. It can be seen that the difference between numerical value and test value of R_m or T is minute, the errors of which are both within 3%. However, in the bubble shrinking phase, the radius curve gradually deviates from the test results, which is mainly due to larger energy loss in the test process, numerical mesh size, and other reasons. Furthermore, it can be concluded that, bubble pulsation must consider the effect of gravity, which confirms the conclusion of Gel’Fand and Takayama [10]. With the increase of gravity acceleration, the R_m and T both decrease. Figure 21 shows the R_m and T formulas fitted by equations (36) and (37) deduced by Cole [2]:

\begin{matrix} R_{m} = K_{R} \sqrt[3]{\frac{W}{D + D_{0}}}, \end{matrix}

(36)

\begin{matrix} T = K_{T} \frac{\sqrt[3]{W}}{{(D + D_{0})}^{56 /}}, \end{matrix}

(37)

where D₀ = 10.34 m is the equivalent water depth of atmospheric pressure and K_R and K_T are empirical coefficients. The points in the figure are test and numerical results in prototype condition, which were obtained by converting results in model condition to result in prototype condition using the similarity relation in Table 2. It can be seen that the fitting formula of test or numerical simulation has the same formula type, and the determination coefficients R² are both above 99.9%, so the numerical calculation is reasonable and the centrifugal test is feasible. Namely, the small equivalent charge under hypergravity field can simulate the bubble pulsation law of large equivalent charge under normal gravity field.

Table 11. Comparison of test and numerical results of R_m and T under various gravity conditions.

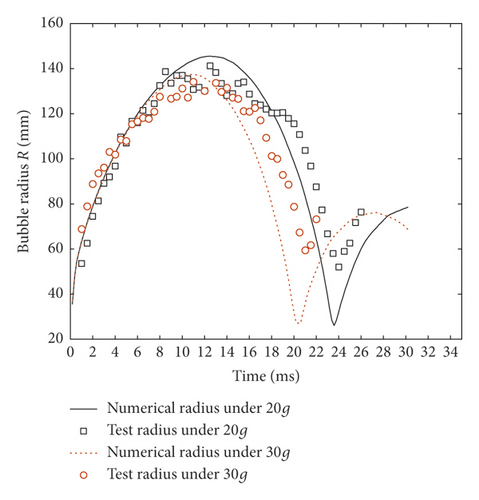
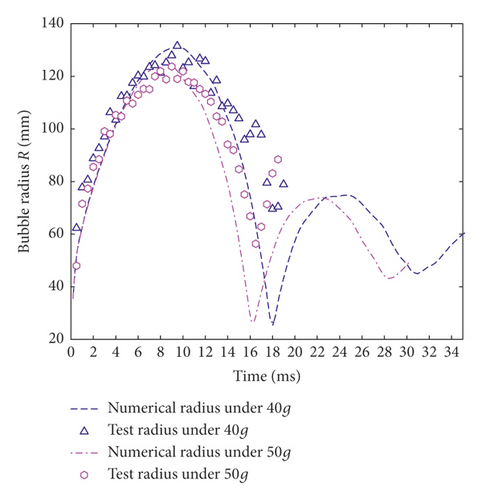
No.	Numerical results		Relative errors (%)
No.	R_m (mm)	T (ms)	R_m (mm)	T (ms)
UE-exp-04	145.49	23.58	2.99	−1.75
UE-exp-06	137.45	20.38	2.44	−2.95
UE-exp-07	130.93	17.98	−0.45	−0.11
UE-exp-08	125.08	16.18	1.14	−1.94

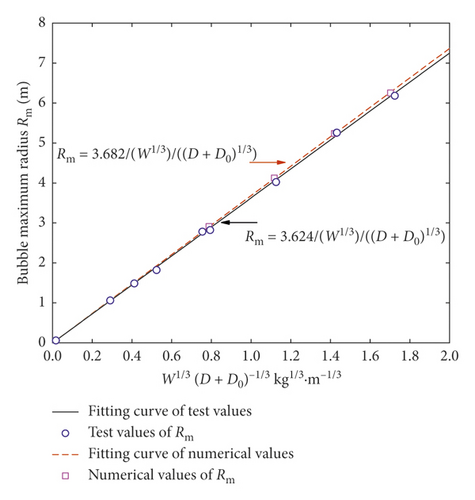
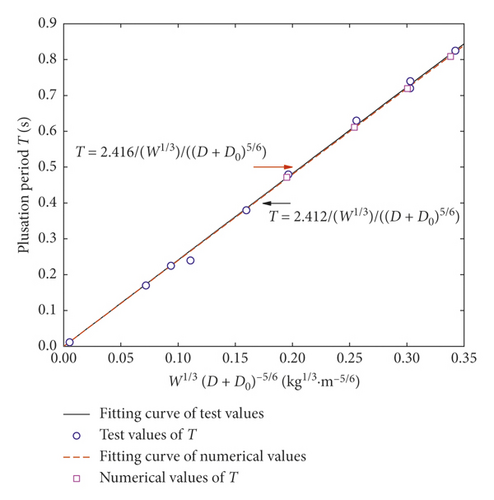
6. Conclusions

Centrifugal underwater explosion and corresponding numerical simulation have been conducted. Some factors influencing the numerical result accuracy were analyzed based on the centrifugal underwater explosion. A method to determine JWL state equation parameters of a special explosive was given. According to the test and numerical results, conclusions can be drawn as follows:

(1)
The shock wave peak pressure calculated by the polynomial state equation is smaller than that calculated by the shock state equation. The difference in state equation of water has less effect on the bubble maximum radius and the pulsation period.
(2)
The boundary simulating model box affects R_m more. The T is influenced both by the boundary simulating model box and the artificial truncation boundary, but the dominant one is the artificial truncation boundary.
(3)
As the mesh size decreases, the shock wave peak pressure increases and tends to be stable gradually. It is recommended that the mesh size of the two-dimensional model takes (1/30 ∼ 1/10) explosive radius. In the first bubble pulsation period, when the mesh size takes about the explosive radius, the errors of the maximum radius and the bubble pulsation period are both the smallest. In the second bubble pulsation period, when the mesh size is twice larger than the explosive radius, it is impossible to see the dynamic change of bubble shape clearly. The mesh size of the three-dimensional model is recommended to take the 1 time explosive radius.
(4)
The centrifugal underwater explosion tests and the corresponding numerical simulation prove that the shock wave peak pressure is not affected by the gravity effect, and the maximum radius and the bubble pulsation period decrease with the increase of gravity acceleration.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

The research reported in this paper was supported by research grants from the State Key Program of National Natural Science Foundation of China (nos. 51339006 and 51679003) and the Project of Beijing Education Commission (Grant number: KM201610005010).

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Snay H. G., Hydrodynamics of underwater explosions, 515, Proceedings of the Symposium on Naval Hydrodynamics, May 1957, Washington, DC, USA.
Google Scholar
2 Cole R. H., Underwater Explosions, 1948, Princeton University Press, New Jersey, NJ, USA.
10.5962/bhl.title.48411
Google Scholar
3 Klaseboer E., Hung K. C., Wang C. et al., Experimental and numerical investigation of the dynamics of an underwater explosion bubble near a resilient/rigid structure, Journal of Fluid Mechanics. (2005) 537, no. 537, 387–413, https://doi.org/10.1017/s0022112005005306, 2-s2.0-23944522571.
10.1017/S0022112005005306
Web of Science® Google Scholar
4 Tipton R. E., Steinberg D. J., and Tomita Y., Bubble expension and collapse near a rigid wall, JSME International Journal. Ser. 2, Fluids Engineering, Heat Transfer, Power, Combustion, Thermophysical Properties. (1992) 35, no. 1, 67–75, https://doi.org/10.1299/jsmeb1988.35.1_67, 2-s2.0-0026817564.
10.1299/jsmeb1988.35.1_67
CAS Google Scholar
5 Ishida H., Nuntadusit C., Kimoto H. et al., Cavitation bubble behavior near solid boundaries, Proceedings of the CAV 2001: Fourth International Symposium on Cavitation, June 2001, Pasadena, CA, USA.
Google Scholar
6 Benjamin T. B. and Ellis A. T., The collapse of cavitation bubbles and the pressures thereby produced against solid boundaries, Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. (1966) 260, no. 1110, 221–240, https://doi.org/10.1098/rsta.1966.0046.
10.1098/rsta.1966.0046
Web of Science® Google Scholar
7 Dadvand A., Khoo B. C., and Shervani-Tabar M. T., A collapsing bubble-induced microinjector: an experimental study, Experiments in Fluids. (2009) 46, no. 3, 419–434, https://doi.org/10.1007/s00348-008-0568-3, 2-s2.0-59849122628.
10.1007/s00348-008-0568-3
Web of Science® Google Scholar
8 Zhang A.-M., Wang S.-P., Huang C., and Wang B., Influences of initial and boundary conditions on underwater explosion bubble dynamics, European Journal of Mechanics-B/Fluids. (2013) 42, no. 2, 69–91, https://doi.org/10.1016/j.euromechflu.2013.06.008, 2-s2.0-84882455344.
10.1016/j.euromechflu.2013.06.008
Web of Science® Google Scholar
9 Zhang S., Wang S. P., and Zhang A. M., Experimental study on the interaction between bubble and free surface using a high-voltage spark generator, Physics of Fluids. (2016) 28, no. 3, 032109, https://doi.org/10.1063/1.4944349, 2-s2.0-84962030372.
10.1063/1.4944349
Web of Science® Google Scholar
10 Gel’Fand B. E. and Takayama K., Similarity criteria for underwater explosions, Combustion, Explosion, and Shock Waves. (2004) 40, no. 2, 214–218, https://doi.org/10.1023/b:cesw.0000020144.55275.df, 2-s2.0-3543078020.
10.1023/B:CESW.0000020144.55275.df
Web of Science® Google Scholar
11 Hu J., Chen Z., Zhang X. et al., Underwater explosion in centrifuge part I: validation and calibration of scaling laws, Science China Technological Sciences. (2017) 60, no. 11, 1638–1657, https://doi.org/10.1007/s11431-017-9083-0, 2-s2.0-85029423097.
10.1007/s11431-017-9083-0
Web of Science® Google Scholar
12 Long Y., Zhou H. Y., Liang X. Q. et al., Underwater explosion in centrifuge part II: dynamic responses of defensive steel plate, Science China Technological Sciences. (2017) 60, no. 11, 1941–1957, https://doi.org/10.1007/s11431-017-9107-2, 2-s2.0-85034211861.
10.1007/s11431-017-9107-2
CAS Web of Science® Google Scholar
13 Song G., Chen Z. Y., Long Y. et al., Experiment and numerical investigation of the centrifugal model for underwater explosion shock wave and bubble pulsation, Ocean Engineering. (2017) 142, 523–531, https://doi.org/10.1016/j.oceaneng.2017.04.035, 2-s2.0-85030470099.
10.1016/j.oceaneng.2017.04.035
Web of Science® Google Scholar
14 Wu J. Y., Long Y., Zhong M. S. et al., Centrifuge experiment and numerical study on the dynamic response of air-backed plate to underwater explosion, Journal of Vibroengineering. (2017) 19, 5231–5247.
10.21595/jve.2017.18646
Web of Science® Google Scholar
15 Li X. J., Zhang C. J., Wang X. H. et al., Numerical study on the effect of equations of state of water on underwater explosions, Engineering Mechanics. (2014) 31, no. 8, 46–52, in Chinese.
Google Scholar
16 Chisum J. E., Simulation of the Dynamic Behavior of Explosion Gas Bubble in a Compressible Fluid Medium, 1996, Storming Media, Washington, DC, USA.
Google Scholar
17 Matsumoto K., Boundary Curvature Effects on Gas Bubble Oscillations in Underwater Explosion, 1996, Storming Media, Washington, DC, USA.
Google Scholar
18 Mu J., Zhu S., Diao A. M. et al., Analysis on the characteristics of UNDEX bubbles under different boundary conditions, Journal of Vibration and Shock. (2014) 33, no. 13, 92–97, in Chinese.
Google Scholar
19 Shi Y., Li Z., and Hao H., Mesh size effect in numerical simulation of blast wave propagation and interaction with structures, Transactions of Tianjin University. (2008) 14, no. 6, 396–402, https://doi.org/10.1007/s12209-008-0068-9, 2-s2.0-57249115141.
10.1007/s12209-008-0068-9
Google Scholar
20 Zhang S. R., Li H. B., Wang G. H. et al., Comparative analysis of mesh size effects on numerical simulation of shock wave in air blast and underwater explosion, Journal of Hydraulic Engineering. (2015) 46, no. 3, 298–306, in Chinese.
Google Scholar
21 Liu M. B., Liu G. R., and Lam K. Y., Investigations into water mitigation using a meshless particle method, Shock Waves. (2002) 12, no. 3, 181–195, https://doi.org/10.1007/s00193-002-0163-0, 2-s2.0-0036877437.
10.1007/s00193-002-0163-0
Web of Science® Google Scholar
22 Saito T., Marumoto M., Yamashita H. et al., Experimental and numerical studies of underwater shock wave attenuation, Shock Waves. (2003) 13, no. 2, 139–148, https://doi.org/10.1007/s00193-003-0201-6, 2-s2.0-0141574088.
10.1007/s00193-003-0201-6
Web of Science® Google Scholar
23 Larcher M., Simulation of the Effects of an Air Blast Wave, Pubsy JRC41337, 2007, JRC Technical Note, Ispra, Italy.
Google Scholar
24 Century Dynamic Inc., AUTODYN Theory Manual Version 4.3, 2005, Century Dynamic Inc, Concord, CA, USA.
Google Scholar
25 Shen F., Wang H., and Yuan J., A simple method for determining parameters of JWL EOS, Journal of Vibration and Shock. (2014) 33, no. 9, 107–110, in Chinese.
Google Scholar
26 Johansson C. H. and Persson P. A., Detonics of High Explosives, 1970, Academic Press, Cambridge, MA, USA.
Google Scholar
27 Chirat R. and Pittion-Rossillon G., A new equation of state for detonation products, The Journal of Chemical Physics. (1981) 74, no. 8, 4634–4642, https://doi.org/10.1063/1.441653, 2-s2.0-0007963966.
10.1063/1.441653
CAS Web of Science® Google Scholar
28 Urtiew P. A. and Hayes B., Parametric study of the dynamic JWL-EOS for detonation products, Combustion, Explosion, and Shock Waves. (1991) 27, no. 4, 505–514, https://doi.org/10.1007/bf00789568, 2-s2.0-0026692571.
10.1007/BF00789568
Web of Science® Google Scholar
29 Johansson C. H. and Persson P. A., Density and pressure in the Chapman-Jouguet plane as functions of initial density of explosives, Nature. (1996) 212, no. 5067, 1230–1231, https://doi.org/10.1038/2121230a0, 2-s2.0-25444465010.
10.1038/2121230a0
Google Scholar
30 Urtiew P. A. and Hayes B., Empirical estimate of detonation parameters in condensed explosives, Journal of Energetic Materials. (1991) 9, no. 4, 297–317, https://doi.org/10.1080/07370659108018630, 2-s2.0-0345149882.
10.1080/07370659108018630
CAS Google Scholar
31 Nellis W. J., Radousky H. B., Hamilton D. C. et al., Equation-of-state, shock-temperature, and electrical-conductivity data of dense fluid nitrogen in the region of the dissociative phase transition, The Journal of Chemical Physics. (1991) 94, no. 3, 2244–2257, https://doi.org/10.1063/1.459895, 2-s2.0-36449006696.
10.1063/1.459895
CAS Web of Science® Google Scholar
32 Liu M. B., Liu G. R., Lam K. Y., and Zong Z., Smoothed particle hydrodynamics for numerical simulation of underwater explosion, Computational Mechanics. (2003) 30, no. 2, 106–118, https://doi.org/10.1007/s00466-002-0371-6, 2-s2.0-0037218965.
10.1007/s00466-002-0371-6
CAS Web of Science® Google Scholar
33 Shin Y. S., Lee M., Lam K. Y., and Yeo K. S., Modeling mitigation effects of watershield on shock waves, Shock and Vibration. (1998) 5, no. 4, 225–234, https://doi.org/10.1155/1998/782032, 2-s2.0-0032314692.
10.1155/1998/782032
Web of Science® Google Scholar
34 Stenberg D. J., Spherical Explosions and the Equation of State of Water, UCID-2097, 1987, Lawrence Livermore National Laboratory, Livermore, CA. USA.
10.2172/6766676
Google Scholar
35 Pang C. J., Numerical Simulation of Bubble Pulsation Produced by Underwater Explosion, 2008, National University of Defense Technology, Changsha, China, in Chinese.
Google Scholar

Citing Literature

All articles

Calibration of Numerical Simulation Methods for Underwater Explosion with Centrifugal Tests

Abstract

1. Introduction

2. Centrifugal Model Experiments of Underwater Explosion

3. Similarity Criterion for Centrifuge Underwater Explosion Tests

4. Numerical Simulation of Underwater Explosion

4.1. The State Equation Used in the Numerical Analysis

4.1.1. The State Equation of Air

4.1.2. The State Equation of STEEL 4340

4.1.3. The State Equation of Explosive

4.1.4. The State Equation of Water

4.2. The Boundary Condition Used in the Numerical Analysis

4.3. The Mesh Size

5. Results and Discussion

5.1. The Influence Factors on Numerical Results

5.1.1. The Influence of State Equation of Water on Numerical Results

5.1.2. The Influence of Boundary Condition on Numerical Results

5.1.3. The Influence of Mesh Size on Numerical Results

5.2. Test and Numerical Results on Shock Wave and Bubble Pulsation

6. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Calibration of Numerical Simulation Methods for Underwater Explosion with Centrifugal Tests

Abstract

1. Introduction

2. Centrifugal Model Experiments of Underwater Explosion

3. Similarity Criterion for Centrifuge Underwater Explosion Tests

4. Numerical Simulation of Underwater Explosion

4.1. The State Equation Used in the Numerical Analysis

4.1.1. The State Equation of Air

4.1.2. The State Equation of STEEL 4340

4.1.3. The State Equation of Explosive

4.1.4. The State Equation of Water

4.2. The Boundary Condition Used in the Numerical Analysis

4.3. The Mesh Size

5. Results and Discussion

5.1. The Influence Factors on Numerical Results

5.1.1. The Influence of State Equation of Water on Numerical Results

5.1.2. The Influence of Boundary Condition on Numerical Results

5.1.3. The Influence of Mesh Size on Numerical Results

5.2. Test and Numerical Results on Shock Wave and Bubble Pulsation

6. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information