1. Introduction

Many studies on the CH equation have assumed that the mobility is constant; however, the equation was originally formulated with degenerate mobility [1]. Numerical methods and simulations with variable mobility can be easily found (for example [8–11]). Kim [12] showed the effect of space-dependent mobility (M(x, y) = 0.01 + 0.99y) on phase separation through a numerical example, which is shown in Figure 1.

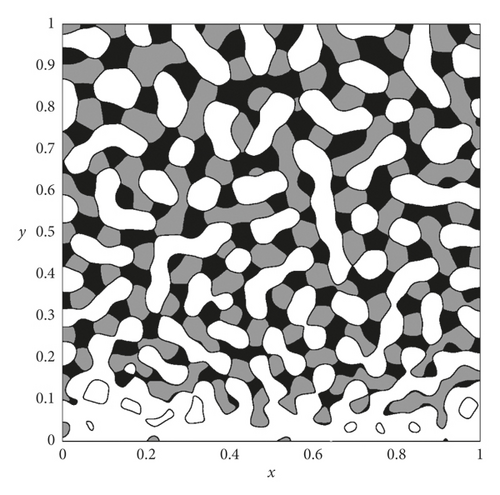
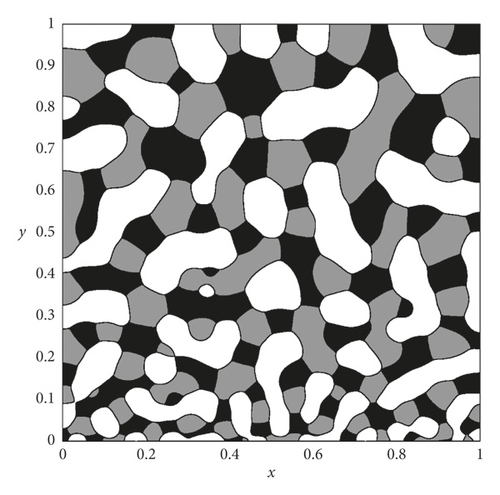
Variable mobility changes the rate of phase separation and the coarsening process. This observation motivated us to employ space-dependent mobility to the manufacturing of a biomedical scaffold because many researchers have recently demonstrated that adaptive porosity and pore size are important requirements for a scaffold [13, 14]. A general scaffold has been constructed with a uniform pattern [15–17]. However, various types of biomedical scaffolds have also been proposed to provide reinforcing features [18, 19].

To numerically design a biomedical scaffold, we require an algorithm that can deal with complex geometry. Thus, we consider a simple and efficient method that was proposed in [20]. In this paper, we completely prove the energy stability of the proposed method with variable mobility. Applying space-dependent mobility, we have a concrete result for a cylindrical scaffold with control of both porosity and pore size.

The remainder of this paper is organized as follows. In Section 2, we describe our numerical method for the CH equation with variable mobility in arbitrarily shaped domains. In Section 3, several numerical experiments are reported. Finally, conclusions are presented in Section 4.

2. Numerical Methods

For simplicity, we describe the numerical algorithm in the two-dimensional space, and then its three-dimensional discretization is analogously defined. To solve the given equations in the complex domain, we use the boundary control function G introduced in [20], which we have described below. The summation by parts formula is shown with the proposed inner products. Owing to this formula, we can simply prove the mass conservation and the decreasing of the energy functional.

2.1. Boundary Control Function

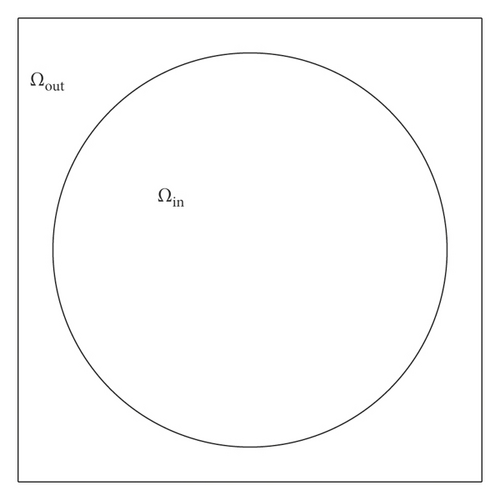
Given an arbitrary domain Ω_in and its boundary Γ = ∂Ω_in, we take a rectangular domain Ω = (0, L_x) × (0, L_y) embedding Ω_in. Let Ω_out = Ω/Ω_in be outside of Ω_in (see Figure 2(a)).

Let Δx = L_x/N_x and Δy = L_y/N_y be the space step sizes with even integers N_x and N_y, respectively; we consider a uniform mesh h = Δx = Δy. We define a set of cell centers as Ω^h = {(x_i, y_j) : 1 ≤ i ≤ N_x, 1 ≤ j ≤ N_y}, where x_i = (i − 0.5)h and y_j = (j − 0.5)h. Let $$ and $$ be approximations of c(x_i, y_j, t_n) and μ(x_i, y_j, t_n), respectively, where t_n = nΔt and Δt is a time step size. We define the inner and outer grid domains as $$ and $$, respectively, see Figure 2(b). We denote Γ^h by the numerical interface, which is a staggered line between $$ and $$. At the cell center, the boundary control function G is defined as

$$ (3)

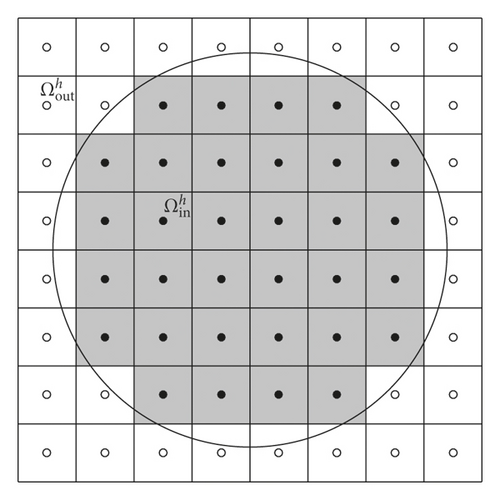
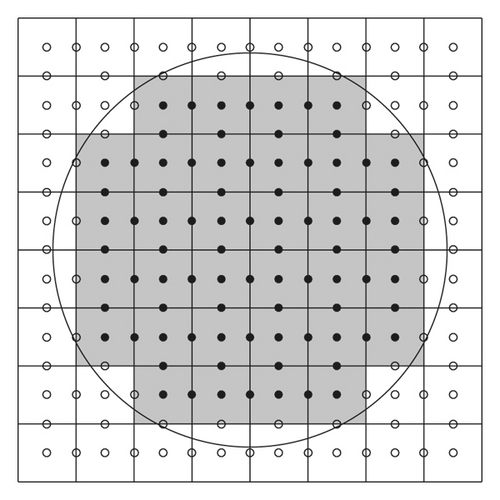
At the edge, G is defined as G_i+(1/2),j = G_ijG_i+1,j and G_i,j+(1/2) = G_ijG_i,j+1, see Figure 2(c). By defining the boundary control function G, we can reuse the multigrid algorithm which is natural to the rectangular domain.

Here, we consider a zero Neumann boundary condition on the staggered boundary Γ^h:

$$ (4)

where n is the outward normal vector at the cell edge. In this paper, we focus on the method with guaranteed mass conservation and energy stability. Because the value of G at the boundary Γ^h is defined to be zero, G has the information for the boundary condition. For example, if x_i+(1/2),j or x_i,j+(1/2) is the edge point of the boundary, then

$$ (5)

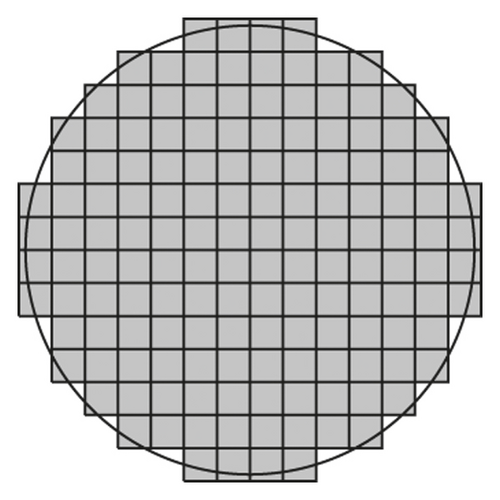
Figure 3 shows that $$, which is an approximation of the circular disk domain Ω_in, converges to Ω_in as we refine the mesh size.

We define the discrete differentiation of c as

$$ (6)

The discrete divergence operator is denoted as

$$ (7)

Now, we present the fully discrete scheme for the CH equation with variable mobility in a complex domain, which is based on the convex splitting method [21]. A semi-implicit time and centered difference space discretization of equations (1) and (2) are as follows:

$$ (8)

$$ (9)

where F_c(c) and F_e(c) are convex functions. The boundary conditions are included in the function G.

3. Numerical Experiments

First, we report a two-dimensional simulation to numerically demonstrate the mass conservation and energy dissipation. Next, we present the numerical results which highlight different evolutions with constant and space-dependent mobilities in a rectangular domain. Finally, we report the numerical experiments on spinodal decomposition in the spherical and cylindrical domains.

The system is solved via the multigrid method [23]. For details on the restriction and prolongation operators in the complex domain with the multigrid method, please refer to [20].

3.1. Mass Conservation and Energy Dissipation

To demonstrate that the numerical scheme inherits the energy decreasing property in a complex domain, we display the evolution of the discrete total energy. The variable mobility is taken as M(c) = |c(1 − c)|. The initial state is taken to be

$$ (21)

in a domain Ω = (0,1) × (0,1). The interface Γ is a disk whose radius is 0.45 and center is located at (0.5, 0.5). Other numerical parameters are taken as h = 1/256, ϵ = 0.002, and Δt = 0.05 h.

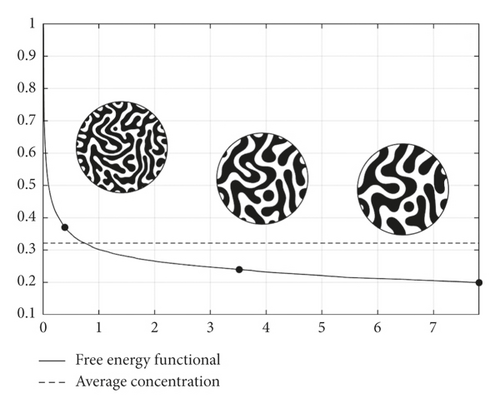
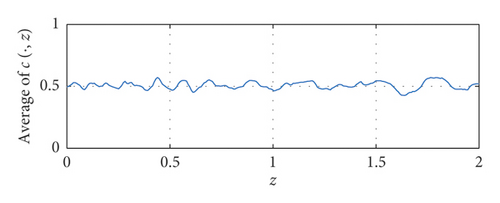
Figure 4 shows the evolution of the scaled energy functional and average concentration, which implies that the total discrete energy is nonincreasing and the mass is preserved. The insets show the evolution of the concentration field at the times marked by closed circles.

3.2. Rectangular Domain with a Space-Dependent Mobility

We show an example of the phase separation to compare the effect of space-dependent mobility. Figure 5 shows the temporal evolution of the spinodal decomposition of a binary mixture with a constant mobility M(x, y) = 1 and space-dependent mobility M(x, y) = 0.25x². In these simulations, the initial condition is

$$ (22)

where rand(x, y) is a random number selected from a random distribution between −1 and 1. A 512 × 128 mesh grid is used on the rectangular domain Ω = (0,4) × (0,1). For the numerical parameters, Δt = 10⁻⁵ and ϵ = 0.0025 are employed. For the phase separation, Figures 5(a) and 5(b) show the solutions at t = 0.01 and t = 0.5, respectively, with constant mobility M = 1. Figure 5(c) shows the different evolution after converting from constant mobility M = 1 to space-dependent mobility M = 0.25x² from t = 0.01. For the constant mobility case, uniform coarsening and domain growth are observed. For the space-dependent mobility case, nonuniform coarsening and domain growth are observed, i.e., smaller- and larger-scale coarsening occurs for small and large values of mobility, respectively.

3.3. Stability Test

To demonstrate the energy stability of the proposed scheme, we calculate the numerical solution for large time steps with the initial condition:

$$ (23)

The domain Ω_in is a disk whose radius is 0.45 and center is (0.5, 0.5). Variable mobility M(x, y, cⁿ) = x²|cⁿ(1 − cⁿ)| is employed in the computational domain Ω = (0,1) × (0,1). Other parameters are taken as h = 1/256, ϵ = 0.002, and T = 8.

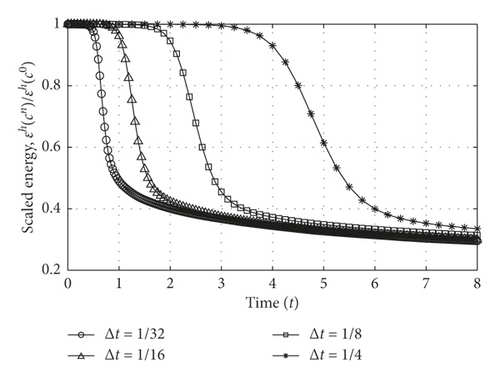
Figure 6 shows the evolution of the scaled discrete energy for various time steps. All the curves are nonincreasing and imply that the numerical solutions are energy stable. We note that a time delay occurs if we use a large time step, as shown in Figure 7.

3.4. Spherical Domain with a Space-Dependent Mobility

We now report a numerical experiment in a spherical domain. The surface Γ is a sphere with radius 0.45 and center (0.5, 0.5, 0.5) on the computational domain Ω = (0,1)³ and Ω_in is the inside of Γ. The initial condition is taken to be

$$ (24)

on Ω_in. The mobility function is defined as M = |c(1 − c)|(32d⁵ + 0.01), where $$. For the computation, we set h = 1/128, ϵ = 0.005, and Δt = h. Figure 8 shows the isosurfaces of the evolution of c. For visibility, we plot the longitude and latitude of the boundary of the domain Γ. The typical phase separation and coarsening procedure is observable; however, the growth rates of the inner and outer regions are quite different.

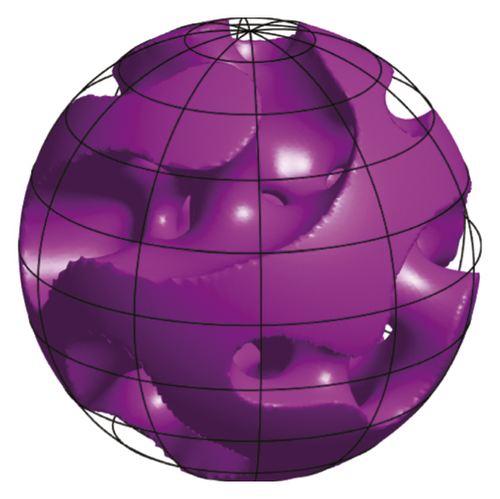
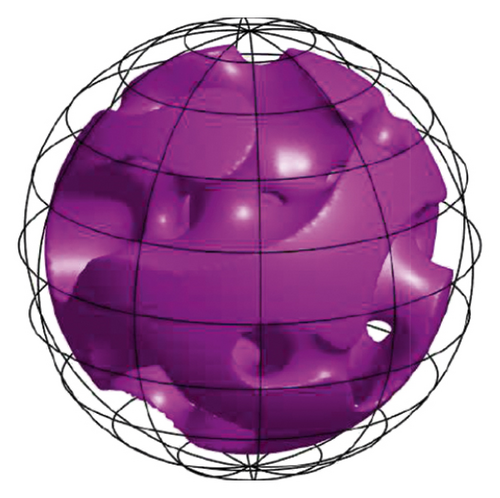
Figure 9 shows the isosurfaces of internal domains with various radii at t = 4. We can show that the phase domain is getting thinner; however, the local average concentration is almost completely preserved.

3.5. Application to Design the Scaffold

In this section, we consider manufacturing a cylindrically shaped biomedical scaffold for the application of space-dependent mobility. This is motivated by [13] which indicates that a proper spatial gradient of concentration is required for effective regeneration of tissues and organs. Figure 10(a) shows the PCL/F127 cylindrical scaffold, which has a gradient on the concentrations along the longitudinal direction. As shown in Figures 5 and 9, the space-dependent mobility in the CH equation gives the ability to control both the porosity and pore size of the scaffold.

Adaptively changing the pore size is not a new concept in the field of biomedical scaffold manufacturing [24–26]. For example, we can consider the design in Figure 10(b) as the PDLLA in [25]; however, they could not control the porosity of the scaffold. Figure 10(b) is obtained by the isosurface of

$$ (25)

within the region of x² + y² ≤ 3.24π² and 0 ≤ z ≤ 8π.

We now consider the design of a specific cylindrical scaffold by applying the variable mobility M = |c(1 − c)|M^s(x) with

$$ (26)

which is gradually increasing along the longitudinal direction. We examine the evolution of a random perturbation with a small magnitude about mean composition

$$ (27)

on the domain Ω = (0,1) × (0,1) × (0,2). For the simulation parameters, we take h = 1/128, ϵ = 0.003, and Δt = h.

To highlight the variation of pore size in Figure 10(c), we also present cross-sectional images at various heights in Figure 11. In this figure, the red, green, and blue regions indicate c = 1, 0.5, and 0, respectively.

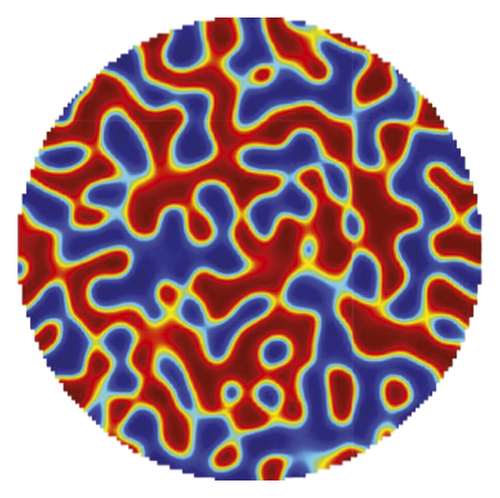
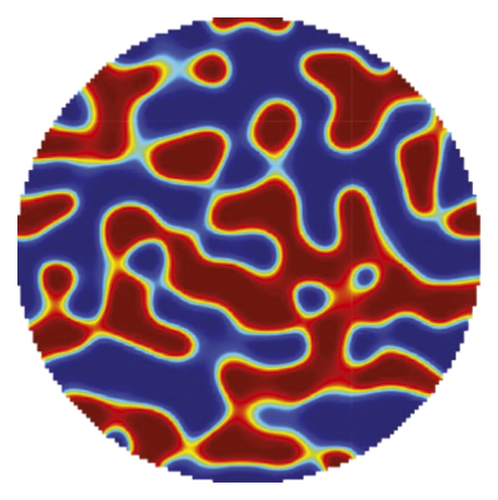
While Figure 11 shows the dynamical variation of the pore size, Figure 12 shows that the porosity of all cross sections is near 50%. Consequently, both the porosity and pore size can be simultaneously controlled by applying phase separation with space-dependent mobility, as shown in Figure 10(c).

4. Conclusions

We proposed a conservative and stable finite difference method to solve the CH equation with variable mobility in complex geometries. We proved that the numerical scheme is conservative and energy dissipative for any time step size. In addition, the CH equation with space-dependent mobility was considered. The two- and three-dimensional numerical results show that local length scale in phase separations can be controlled by using space-dependent mobilities. We expect that space-dependent mobility can be applied to the fabrication of scaffolds to control both local pore size scale and porosity.

Conflicts of Interest

The authors declare that they have no conflicts of interest.