Vibration Isolation of Existing Buildings in Microvibration Traffic Environment
Abstract
In order to explore the impact of traffic environmental microvibration on buildings, this paper studies indoor vibration isolation, a method applicable to existing buildings. The vibration isolation scheme is designed based on the residential buildings adjacent to metro lines in Shanghai. By using the dynamic theory, the effective range of vibration isolation stiffness is analyzed. The effectiveness of the indoor vibration isolation method is verified through theoretical calculations and comparison of field measurements before and after isolation. A detailed numerical model is established to analyze the indoor isolation and the effect after parameter optimization from the slab thickness, filling material, and isolator stiffness. The results show that the isolation effect is proportional to the thickness of the total slab thickness of the isolation system and inversely proportional to the stiffness of the isolator. And when concrete is used as the filling material, the isolation effect is best. The isolation effect of the midspan position is better than that of the wall-floor junction. The vibration isolation effect is more obvious after the parameters are optimized. With its convenient construction technology, short cycle, and low cost, this method is worth promoting.
1. Introduction
The impact of rail transit vibration on the work and life of residents in its surrounding buildings, as well as its influence on the normal use of precision instruments, has attracted extensive attention from academic and engineering circles [1, 2]. Recent studies on vibration isolation technology in existing buildings focus mainly on the application and research of several isolation methods. Each has its own advantages and problems. The floating floor vibration isolation technology [3] and the room-in-room vibration isolation technology [4] have high headroom requirements on the houses. They are mainly used in buildings with considerable headroom such as concert halls and theaters. The overall vibration isolation technology [5, 6] has good effect, but costs are high for the existing buildings. It is mostly used for planned buildings or existing buildings with historic value. Because of such factors as headroom and cost, none of the three technologies is applicable to common existing buildings, especially those with the old-fashioned masonry residential structure. The indoor vibration isolation method proposed in this paper is specifically designed for existing buildings and can meet the headroom requirements. Qu Wenjun and Xia Qian’s research team first proposed this method conducted preliminary research [7, 8] and discovered its significant isolation effect. So far, no better method has been proposed by other research teams which is more suitable for existing buildings nor has any team conducted researches to improve this method. By analyzing the vibration reduction effect, combined with structural dynamics theory, this paper analyzes the effective range of vibration isolation stiffness and has proved the effectiveness of the indoor vibration isolation method practically and theoretically. The isolation effect of the method is analyzed in terms of three factors: floor thickness, filling material, and isolator stiffness, so as to provide data support for the promotion of the method in the future.
2. Determination of the Vibration Isolation Scheme
2.1. Overview of the Test Buildings
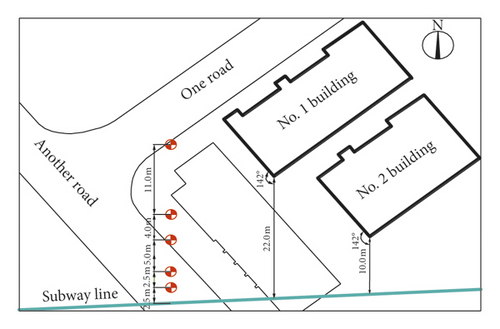
A section of metro lines in Shanghai is chosen for the test, with two common masonry-structured residential buildings on the site. This paper takes Building 2 as the research object, as shown in Figure 1. The building is a 5-storey masonry structure, 10 meters from the subway central line. Built in the 1960s, it is light in weight and poor in structural integrity, so it will have strong response to external vibrations. The planimetric relationship between the building and the tunnel is shown in Figure 2.


2.2. Introduction to the Vibration Isolation Method
- (1)
The bottom layer is the core layer composed of the rubber vibration isolator which may as well be made of special compounded rubber synthesized from high-strength metal thin layers (laminated). The static stiffness Kzs of the rubber is calculated according to equation (1), with rubber height greater than 30 mm and width greater than 150 mm × 150 mm. The number of vibration isolators and layout spacing are determined by the specific project (the recommended vibration isolator spacing is less than 500 mm). The overall height of the core layer is greater than 30 mm:
-
where W1, N, and ρ stand for the indoor dynamic load, the number of vibration isolators, and the ground subsidence control displacement, respectively.
- (2)
The middle layer is a C20 plain concrete layer with thickness greater than 100 mm.
- (3)
The top layer is the ordinary indoor floor, which should be built 24 hours after the pouring of the middle layer.
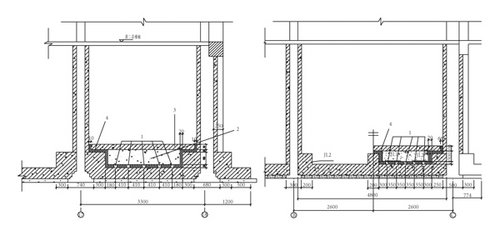
The gaps between the three structural layers are filled with polymer foam boards. Based on the dynamic principle of vibration isolation, with the balance and stability of the structure considered, a ground vibration isolation scheme is proposed, as shown in Figure 3. Each room is an independent isolation system consisting of a floor and a set of isolators.
2.2.1. Characteristics and Difficulties in the Vibration Isolation
2.2.2. Vibration Isolation Technology Selection and Arrangement of Isolators
- (1)
According to the stability requirement of the structure, it is not advisable to use steel springs and fiberglass as the vibration isolation material.
- (2)
Air springs are not suitable for vibration isolation of ordinary houses because of their complicated structure and high price.
- (3)
Considering the practical use and the convenience of material processing, we have selected artificial rubber to make isolation devices for the test building.
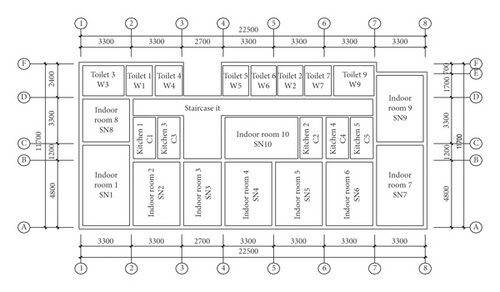
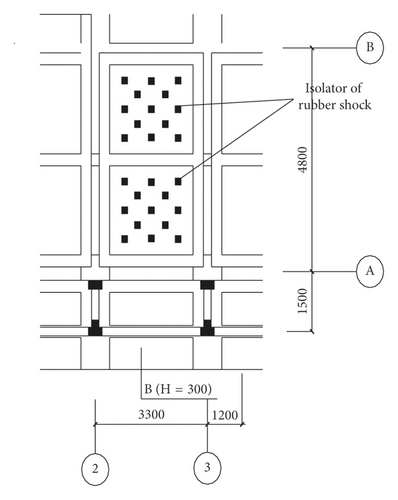
The number of isolators and their spacing are determined by specific projects. It is recommended that the spacing between isolators be less than 500 mm and the overall height of the core layer be greater than 30 mm. Based on the above parameters, the isolators are arranged in every room of the test building (the name and location of each room are shown in Figure 4). Figure 5 shows the layout of the isolators in Room SN2.
3. Theoretical Basis of Vibration Isolation
3.1. Parameter Calculation
The indoor ground vibration isolation system of existing buildings is a single-degree-of-freedom system. Its main characteristic parameters include the system’s natural vibration frequency, static stiffness, and mass. The above parameters are determined after considering the external vibration characteristics, the dynamic performance, and the structural characteristics of the vibration isolation material. The detailed theoretical analysis is as follows.
3.1.1. Dynamic Range of Natural Vibration Frequency and Vibration Isolation Coefficient
3.1.2. System Mass M and Isolator Height H
Taking Room SN2 as an example, based on its net size, S1 = 13.9 m2, D = 0.2 m, S2 = 13.9, and d = 0.1 m. The ground material is supposed to be concrete, and the corresponding γc = 2100 kg/m3. When H takes the typical value of 3 cm, M is calculated to be around 7.9 × 103 kg according to equation (12). Each vibration isolator in the system is subjected to a weight of 7.9 × 103 kg/26 = 303.8 kg (26 vibration isolators are arranged in Room SN2).
3.1.3. Static Stiffness of the Vibration Isolation System KZS
According to equation (13), we find Kzs = 3.02 × 104 N/cm (minimum value). As shown in Figure 5, there are 26 isolators arranged in the room.
3.1.4. Dynamic Stiffness Kz and System Natural Frequency fn
Substituting the value of Kz and the weight borne by each isolator (303.8 kg) into equation (2) yields fn = 25.1 Hz, which clearly satisfies the requirements of equation (6).
3.1.5. Vibration Isolation Effect of the System
After adopting the vibration damping scheme, the maximum acceleration level of 1/3 octave with a center frequency of 50 Hz is 38 dB lower than the corresponding limit (86 dB) in Standards for Indoor Vibration Limits and Measurement Methods for Residential Buildings (GB/50355-2005) [12] (Level 1 daytime limit). As can be seen, this method improves the vibration isolation effect obviously in the frequency range with 50 Hz as the center.
3.2. Stiffness Check
Equation (19) shows a reasonable range of stiffness per unit area when the vibration isolation system based on relevant parameters of the test buildings meets isolation requirements.
Room SN2 with a net size of 2.9 m × 4.8 m, as shown in Figure 5, is equipped with 26 vibration isolators. Theoretical calculations show that the dynamic stiffness of each isolator is 7.54 kN/mm and the stiffness per unit area is 14.1 kN/mm/m2. Therefore, the arrangement of the rubber isolators used in the vibration isolation measures and the selection of isolation parameters are reasonable and meet the related requirements.
4. Comparative Analysis of Vibration Tests before and after Isolation
The indoor vibration isolation method is applied to test buildings. Under the same environment, the research team conducts on-site testing of the buildings and compares the data of each test room before and after the application of the isolation method.
4.1. Arrangement of the Test Points
In order to compare the vibration isolation effect, three typical rooms (indoor room 2 (SN2), bathroom 2 (W2), and kitchen room 2 (C2)) are selected on each floor for testing, and their locations are shown in Figure 4. Sensors are installed on the floor of each room to test the vertical (Z-direction) and horizontal (X along the longitudinal direction of the house and Y along the lateral direction of the house) isolation. SN2 and C2 are precast slab rooms, and W2 is a cast-in-place slab room. Because of the limited number of sensors, group tests are performed on vertical and horizontal vibrations of the buildings.
French Lens piezoelectric acceleration sensors (LC0132T) with a sensitivity coefficient of 49 V/g and an intelligent data acquisition system are used in the tests. All instruments and sensors have been debugged and calibrated before testing.
The test data are filtered, and acceleration signals are recorded. The vibration response of buildings is analyzed by evaluating the parameter vibration acceleration and the acceleration level.
4.2. Analysis of Vibration Isolation Effects
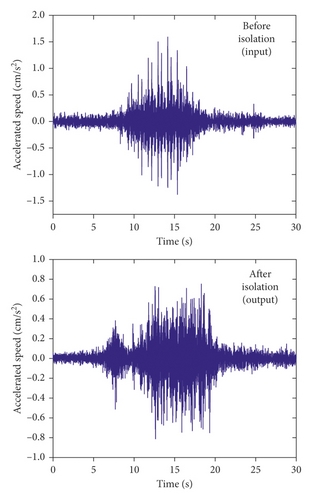
Because of space limitations, Figure 6 only shows the comparison of vertical vibration between the slab midspan and the junction of Room SN2. For the midspan, the vertical vibration level of the floor before isolation increases with the floor height, and the vertical vibration level of each floor after isolation is slightly attenuated as compared with that before isolation. The maximum vibration isolation is 3.26 dB on the top floor (Figure 6(a)). For the junction, the vertical vibration level of each floor after isolation is slightly attenuated as compared with that before isolation, and the isolation decreases with the floor height (Figure 6(b)). The isolation of the third to fifth floors is significantly smaller than that of the corresponding midspan, and the maximum isolation is 2.31 dB on the ground floor. It can be seen that both the midspan and the junction show obvious isolation effects. The higher the floor, the more obvious the vibration isolation effect of the midspan position as compared with the junction.
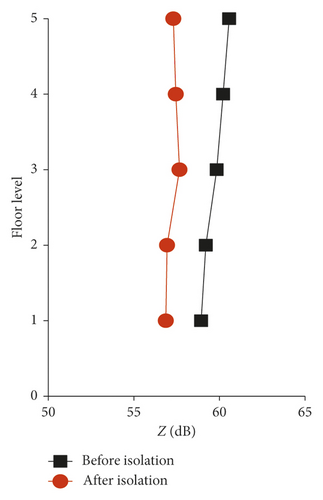
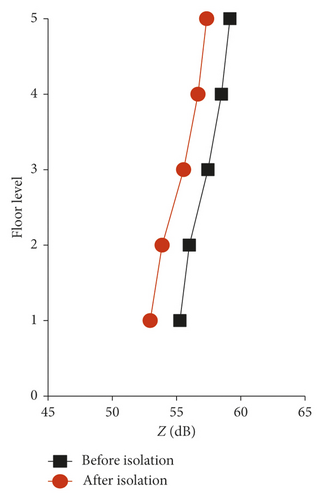
The vertical vibration levels of the three rooms are listed in Table 1. The vertical vibration levels of each floor before and after isolation can be visually observed. In indoor rooms, the vertical isolation of the midspan increases with the floor height, while it is opposite for the junction. In the kitchen room, the vertical isolation of the midspan and the junction decreases as the floor height increases. In bathrooms, the vertical isolation of the midspan and junction increases with the floor height.
| Room | Midspan | Wall-floor junction | ||||
|---|---|---|---|---|---|---|
| Floor | Before isolation | After isolation | Reduction | Before isolation | After isolation | Reduction |
| SN2 | ||||||
| First | 58.93 | 56.87 | 2.06 | 55.26 | 52.95 | 2.31 |
| Second | 59.20 | 56.94 | 2.26 | 56.00 | 53.88 | 2.11 |
| Third | 59.84 | 57.67 | 2.17 | 57.44 | 55.55 | 1.89 |
| Fourth | 60.22 | 57.45 | 2.77 | 58.50 | 56.67 | 1.83 |
| Fifth | 60.57 | 57.31 | 3.26 | 59.16 | 57.35 | 1.81 |
| C2 | ||||||
| First | 58.31 | 54.28 | 4.03 | 55.04 | 52.72 | 2.32 |
| Second | 58.56 | 55.45 | 3.11 | 56.58 | 54.29 | 2.29 |
| Third | 59.89 | 57.47 | 2.42 | 58.30 | 56.18 | 2.12 |
| Fourth | 61.04 | 58.62 | 2.41 | 59.35 | 57.26 | 2.09 |
| Fifth | 61.66 | 59.30 | 2.36 | 59.89 | 57.82 | 2.08 |
| W2 | ||||||
| First | 56.07 | 54.59 | 1.48 | 54.96 | 53.86 | 1.10 |
| Second | 56.71 | 54.89 | 1.82 | 55.66 | 54.00 | 1.65 |
| Third | 57.78 | 55.72 | 2.06 | 56.77 | 54.87 | 1.90 |
| Fourth | 58.38 | 55.54 | 2.84 | 57.67 | 55.64 | 2.04 |
| Fifth | 59.14 | 55.96 | 3.18 | 58.32 | 56.20 | 2.12 |
The comparison of the vibration isolation of each floor is shown in Table 2. It can be seen that, on each floor, the vibration levels of different positions in the room are obviously different. For indoor rooms with a large span and kitchens and bathrooms with a small span, the isolation level of the midspan is greater than that of the wall-floor junction. The span has no obvious impact on the difference in the isolation level of each floor, and the same is true for the floor material.
| Isolation difference of each floor | Midspan | Wall-floor junction | Evaluation of isolation effects |
|---|---|---|---|
| Indoor room | 0.1 dB∼0.6 dB | 0.06 dB∼0.22 dB | The isolation level of each floor at the midspan differs greatly, and the difference is small at the junction |
| Kitchen (precast slab) | 0.1 dB∼0.9 dB | 0.03 dB∼0.17 dB | The isolation level of each floor at the midspan differs greatly, and the difference is small at the junction |
| Bathroom (cast-in-place slab) | 0.24 dB∼0.78 dB | 0.08 dB∼0.55 dB | The isolation level of each floor at the midspan differs greatly, and the difference is relatively large at the junction |
The horizontal vibration level of the slab is small before and after isolation, mostly below 2 dB. Therefore, the specific values of the horizontal vibration level are not detailed here.
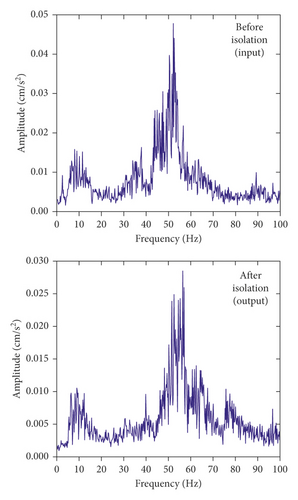
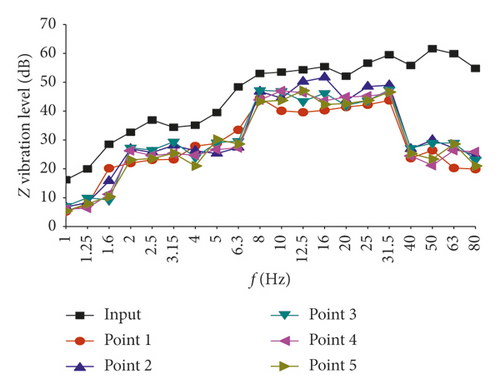
In order to further understand the frequency range of the damping effect and clearly reflect the isolation effect at different frequencies, the vertical vibration acceleration levels (VALs) before and after isolation are listed in Figure 7. Because of space limitations, only the information on Room SN2 on the second floor is presented.
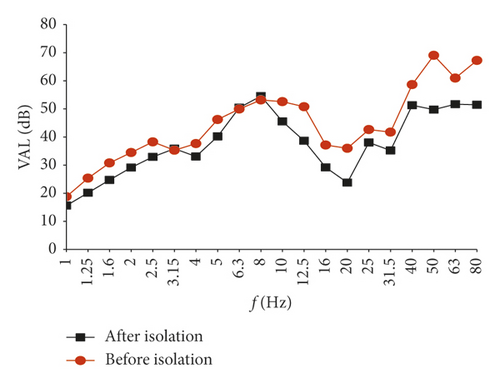
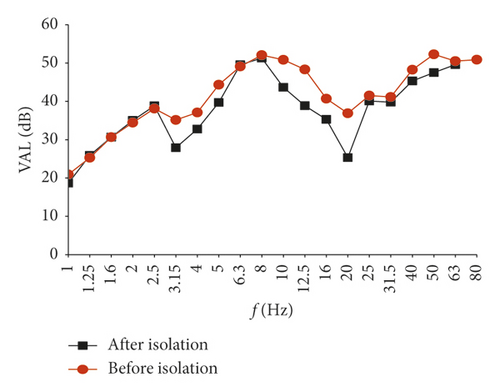
It can be seen that the vibration reduction at the midspan position is obvious in each frequency range, with the maximum being 15.8 dB. The vibration reduction at the wall-floor junction is obvious in the frequency ranges of 2.5∼6.3 Hz and 10 Hz∼25 Hz, with the maximum being 11.6 dB, which is slightly smaller than that of the midspan position. Therefore, the isolation effect of the method is obvious.
5. Numerical Study of Various Parameters of the Vibration Isolation Method
In order to further analyze the effect of the indoor vibration isolation method, Room SN2 is selected as the research object; the location of the room is 10 m away from the middle line of the tunnel with its finite element model established by using ANSYS. The isolation effect is studied from slab thickness, filling material, and isolator stiffness. The vibration isolation system floor uses the SHELL181 unit, which gives the corresponding backfill material properties. The vibration intensity of the surface (10 m away from the center line of the tunnel) of the No. 2 test building is used as the model excitation, as shown in Figure 8, and the vertical vibration level is 54.8 dB [8].
The calculation of the vibration isolation floor is shown in Figure 9. The concrete slab thickness on the rubber support consists of two parts: (1) the excavation depth (cast slab thickness), which is 0.2 m, i.e., D = 0.2 m in equation (12), and (2) the floor thickness, which is 0.1 m, i.e., d = 0.1 m in equation (12). In order to simplify the calculation, the excavation area is approximated to be the same as the room area and the slab uses the axis size. The vertical stiffness of the isolator is 7.54, which is calculated according to the theory in Section 2.1. Because of space limitations, only the numerical model of the isolation floor with a total thickness of 0.3 m is presented, as shown in Figure 10.
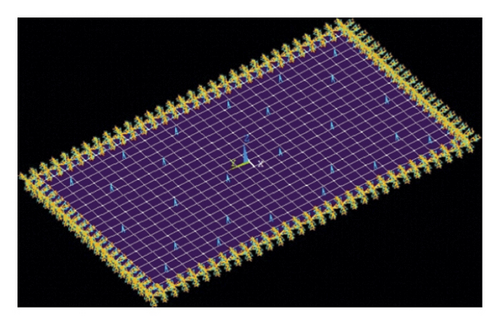
The concrete strength is Grade C20, and the compressive strength takes the designed value fc = 9.6 MPa. The material properties are shown in Table 3.
| Material | Initial elastic modulus (MPa) | Poisson’s ratio | Density (kg/m3) | Damping ratio | Strength (MPa) |
|---|---|---|---|---|---|
| Concrete | 0.912 × 104 | 0.2 | 2500 | 0.1 | 9.6 |
5.1. Analysis of the Isolation Effect for Different Thickness
A numerical model of the concrete slab with a total thickness of 0.25 m, 0.3 m, and 0.4 m is established.
Take the isolation floor with a total thickness of 0.3 m as an example. The vibration characteristics of the midspan, the upper junction, the lower junction, the left junction, and the right junction (numbered 1, 2, 3, 4, and 5) are analyzed, respectively. Figure 8 shows the comparison of excitation and response at Position 1. It can be seen that the isolation effect of the scheme is obvious, mainly in the frequency range of 40∼60 Hz, while in the range of 10∼20 Hz, the effect is not obvious because it is close to the natural frequency of the system.
Figure 11 shows that the vibration reduction at the midspan position with a center frequency of 50 Hz is 35 dB, similar to the calculated value in Section 2.1. For both the midspan and the wall-floor junctions, the isolation effect of the 40∼60 Hz frequency band is better than that of medium- and low-frequency bands.
The Z vibration level at different positions of the floor is shown in Table 4. The results show that the isolation effect is better at the midspan position, while the effect is worse at the junctions. From the perspective of the rubber support arrangement, there are more supports at the center positions. Therefore, the more vertical constraints the floor is subjected to, the better the isolation effect. The slab at the wall-floor junction is subject to little constraint, and thus, the isolation effect is poor. When the slab thickness is less than 0.4 m, the isolation effect at the midspan and wall junctions is both proportional to the thickness, and the vibration reduction is 5.3∼13.2 dB and 2.5∼9.3 dB, respectively.
| Point | Input position | 1 (midspan) | 2 (upper junction) | 3 (lower junction) | 4 (left junction) | 5 (right junction) |
|---|---|---|---|---|---|---|
| Thickness of 0.25 m | 54.8 | 49.5 | 52.3 | 51.7 | 50.9 | 49.4 |
| Thickness of 0.3 m | 54.8 | 47.0 | 52.1 | 50.6 | 49.6 | 48.5 |
| Thickness of 0.4 m | 54.8 | 41.6 | 47.1 | 46.3 | 46.1 | 45.5 |
5.2. Analysis of the Isolation Effect for Different Filling Materials
Table 5 lists the material parameters under three working conditions. Reference [13] is referred to for the concrete parameters, and the Shanghai soft soil parameters are referred to for the soil parameters, as shown in Table 6. Slabs with a total thickness of 0.3 m are used in all the three working conditions. It should be noted that the filling materials in working condition 3 are concrete and soil, which are filled in two layers with a thickness of 0.1, as shown in Figure 12. The excitation applied is the same as that in Section 4.1 when the isolation effect for different slab thickness is discussed.
| Working condition no. | 1 | 2 | 3 |
|---|---|---|---|
| Filling material | Concrete | Soil | Concrete and soil |
| Poisson’s ratio | 0.2 | 0.29 | Respective Poisson’s ratio |
| Damping ratio | 0.1 | 0.02 | Respective damping ratio |
| Elastic modulus (N/mm2) | 0.912 × 104 | 54.4 | Respective elastic modulus |
| Density (kg/m3) | 2000 | 1800 | Respective density |
| Soil name | Bottom layer depth (m) | Gravity (KN/m3) | Poisson’s ratio | Average velocity of shear wave (m/s) | Elasticity modulus (MPa) | Shear modulus (MPa) |
|---|---|---|---|---|---|---|
| Soil filling | 1.53 | 19.0 | 0.29 | 110 | 54.4 | 21.1 |
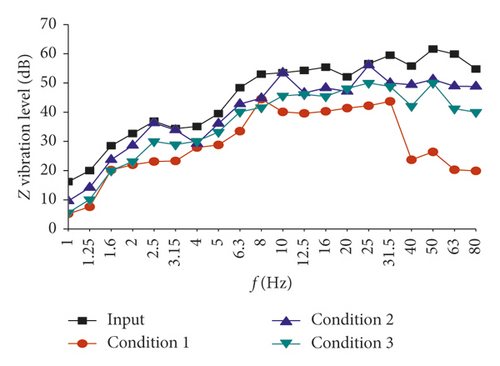
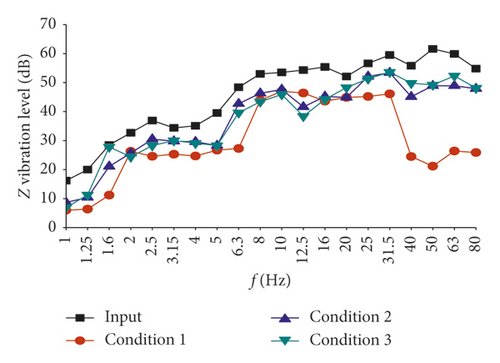
Five positions of the slab are selected (the same as those in Section 4.1) to analyze the isolation effect under different working conditions. The results of vibration level distribution are shown in Table 7. It is found that, in condition 1 and condition 3, the isolation effect at the midspan is better than that at the wall junction. The difference in the isolation effect between the two positions under condition 1 is between 2.7 and 7.8 dB, and the difference is between 3.3 and 4.6 dB under condition 3. Under condition 2, the isolation effect at the midspan is not as obvious as that at the wall junction, but the difference is not large, ranging from 1.5 to 5.1 dB.
| Point | Input position | 1 (midspan) | 2 (upper junction) | 3 (lower junction) | 4 (left junction) | 5 (right junction) |
|---|---|---|---|---|---|---|
| Condition 1 | 54.8 | 47.0 | 52.1 | 50.6 | 49.6 | 48.5 |
| Condition 2 | 54.8 | 54.8 | 51.3 | 52.5 | 51.9 | 53.9 |
| Condition 3 | 54.8 | 50.2 | 51.5 | 51.1 | 50.6 | 51.4 |
Because of space limitations, only Point 1 and Point 4 vibration acceleration levels of the midspan and wall junction under various working conditions are listed here, as shown in Figure 13. As can be seen from Figure 13(a), the isolation effect is best when the filling material is concrete in condition 1, mainly between 40 and 80 Hz. The worst one is when the filling material is soil in condition 2, and the isolation effect is not significantly different in each frequency band. Even in the range of the 10∼25 Hz intermediate frequency, vibration amplification occurs. According to Figure 13(b), in the high-frequency band (40∼80 Hz), condition 1 shows the best isolation effect. In the intermediate- and low-frequency bands, the isolation effect under the three conditions is similar, with condition 1 showing the highest effect. At the center frequency of 12.5 Hz, the isolation effect in conditions 2 and 3 is slightly higher than that in condition 1. The reason might be that the frequency is close to the natural frequency of the isolation system in condition 1, which causes the resonance of the vibration isolation system.
5.3. Analysis of the Isolation Effect for Different Stiffness
The slab size of Room SN2 is 2.9 m × 4.8 m. The reasonable stiffness of a single isolator is calculated to be in the range of 0.95∼12.0 kN/mm. We take 3 kN/mm, 7.54 kN/mm, and 12 kN/mm for comparative analysis, which are numbered Stiffness 3, Stiffness 7.54, and Stiffness 12. The total thickness of the slab selected is 0.3 m, and the filling material is concrete. The same five positions as before are analyzed.
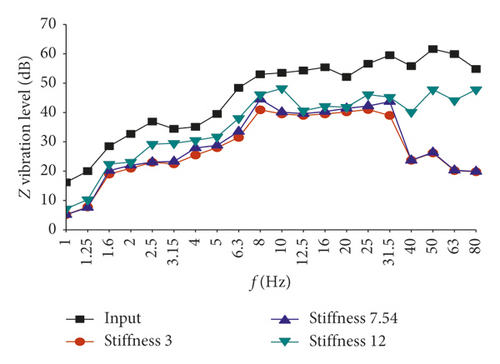
The results of the vibration level distribution under various conditions are shown in Table 8. As can be observed, the smaller the stiffness, the better the isolation effect. When the stiffness is 3 kN/mm, the isolation at the midspan is 10.1 dB and the isolation at the junction positions is 6.4∼9.8 dB. When the stiffness is 12 kN/mm, the isolation at the midspan is 4.4 dB and the isolation at the junction positions is 2∼4.2 dB. From the perspective of the rubber support arrangement, there are more supports at the center positions. Therefore, the more vertical constraints the floor is subjected to, the better the isolation effect.
| Point | Input position | 1 (midspan) | 2 (upper junction) | 3 (lower junction) | 4 (left junction) | 5 (right junction) |
|---|---|---|---|---|---|---|
| Stiffness 3 | 54.8 | 44.7 | 48.3 | 48.4 | 45.4 | 45.0 |
| Stiffness 7.54 | 54.8 | 47.0 | 52.1 | 50.6 | 49.6 | 48.5 |
| Stiffness 12 | 54.8 | 50.5 | 52.6 | 52.8 | 51.3 | 50.6 |
Because of space limitations, only Point 1 and Point 4 vibration acceleration levels of the midspan and wall junction under different stiffness are listed here, as shown in Figure 14. As can be seen in Figure 14(a), Stiffness 3 has the best isolation effect, mainly between 40 and 80 Hz, and the worst is Stiffness 12. According to Figure 14(b), in the high-frequency band (40∼80 Hz), Stiffness 3 and Stiffness 7.54 show good isolation effect, with no major difference. For Stiffness 12, its isolation effect decreases considerably. In the intermediate- and low-frequency bands below 40 Hz, Stiffness 3 has the best isolation effect, but the difference between the three is not large.

5.4. Effect Analysis of the Isolation Method after Parameter Optimization
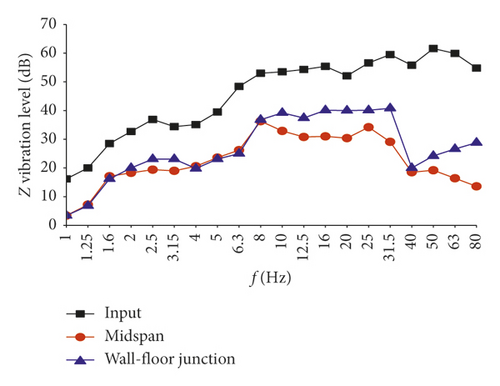
Based on the preceding three-parameter analysis, Room SN2 is taken as the research object. The optimized parameters are selected; that is, the total slab thickness of the room is 0.4 m (including the thickness of the slab d = 0.1 m and the cast slab thickness D = 0.3 m; the variable names are shown in equation (12)). The filling material is concrete, and the stiffness of the isolator is 3 kN/mm (26 isolators are arranged in the room, and the reasonable stiffness of a single isolator is 1.3∼16.4 kN/mm; see Section 2.2 for the calculation method). The calculation results before and after isolation are shown in Table 9, and the numbering of the five positions is the same as before. It can be seen that the indoor vibration isolation has remarkable effect. The vibration isolation at the midspan position is 16 dB, and the vibration isolation at the junction is between 10 and 12.4 dB. The isolation effect of each frequency band is shown in Figure 15. As can be seen, the vibration isolation effect of the midspan and the wall-floor junction mainly occurs in the frequency band of 40∼80 Hz. The vibration isolation at the midspan position in each frequency band is higher than that at wall-floor junctions. The vibration isolation under 10 Hz in the low-frequency band is reduced, and the difference in vibration isolation between the two positions is small.
| Input | 1 (midspan) | 2 (upper junction) | 3 (lower junction) | 4 (left junction) | 5 (right junction) |
|---|---|---|---|---|---|
| 54.8 | 38.8 | 43.7 | 44.1 | 42.8 | 42.4 |
6. Conclusions
- (1)
After adopting the vibration damping scheme, the maximum acceleration level of 1/3 octave with a center frequency of 50 Hz is 38 dB lower than the corresponding limit (86 dB) in Standards for Indoor Vibration Limits and Measurement Methods for Residential Buildings (GB/50355-2005) (Level 1 daytime limit). As can be seen, this method improves the vibration isolation effect obviously in the frequency range with 50 Hz as the center, and the effect at the midspan position is better than that at wall-floor junctions.
- (2)
By comparing the effects before and after isolation, the following has been found: (1) in indoor rooms, the vertical isolation of the midspan increases with the floor height, while it is opposite for the wall-floor junction; (2) in kitchen rooms, the vertical isolation of the midspan and the junction decreases as the floor height increases; and (3) in bathrooms, the vertical isolation of the midspan and junction increases with the floor height. On each floor, the vibration levels of different positions in the room are obviously different. For indoor rooms with a large span and kitchens and bathrooms with a small span, the isolation level of the midspan is greater than that of the junction. The span has no obvious impact on the difference in the isolation level of each floor, and the same is true for the floor material.
- (3)
The isolation effect is directly proportional to the total thickness of the vibration isolation system, and the system of concrete filling material has the best effect. The stiffness of the isolator is inversely proportional to the effect. The smaller the stiffness, the better the isolation effect, which is mainly concentrated in the range of 40∼80 Hz.
- (4)
The optimized parameters are applied to Room SN2 with remarkable results. The vibration reduction at the midspan is 16 dB, and the vibration isolation at wall-floor junctions is between 10 and 12.4 dB. With its convenient construction technology, short cycle, and low cost, the method has wide application prospects especially for existing buildings.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Acknowledgments
This work was supported by the National Natural Science Fund (51708450), China Postdoctoral Science Foundation Project (2018M643702), Basic Research Project of Natural Science in Shaanxi Province (2018JQ5169), Shaanxi Provincial Postdoctoral Foundation Project (2018BSHEDZZ22), Ph.D. Research Start-Up Project (107-451115002), and School-Level Scientific Research Project (2016CX025).
Open Research
Data Availability
All data used to support the findings of this study are included within the supplementary information files. Details can be found in annex 2.




