Volume 2019, Issue 1 1012987

Research Article

Open Access

Wind-Induced Vibration Response of an Inspection Vehicle for Main Cables Based on Computer Simulation

Lu Zhang,

Corresponding Author

Lu Zhang

[email protected]

orcid.org/0000-0002-4997-0046

School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China swjtu.edu.cn

Technology and Equipment of Rail Transit Operation and Maintenance Key Laboratory of Sichuan Province, Chengdu 610031, China

Search for more papers by this author

Shaohua Wang,

Shaohua Wang

School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China swjtu.edu.cn

Technology and Equipment of Rail Transit Operation and Maintenance Key Laboratory of Sichuan Province, Chengdu 610031, China

Search for more papers by this author

Peng Guo,

Corresponding Author

Peng Guo

[email protected]

orcid.org/0000-0001-5520-7701

School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China swjtu.edu.cn

Technology and Equipment of Rail Transit Operation and Maintenance Key Laboratory of Sichuan Province, Chengdu 610031, China

Search for more papers by this author

Qunsheng Wang,

Qunsheng Wang

orcid.org/0000-0002-1270-3921

State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China swjtu.edu.cn

Search for more papers by this author

Lu Zhang,

Corresponding Author

Lu Zhang

[email protected]

orcid.org/0000-0002-4997-0046

School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China swjtu.edu.cn

Technology and Equipment of Rail Transit Operation and Maintenance Key Laboratory of Sichuan Province, Chengdu 610031, China

Search for more papers by this author

Shaohua Wang,

Shaohua Wang

School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China swjtu.edu.cn

Technology and Equipment of Rail Transit Operation and Maintenance Key Laboratory of Sichuan Province, Chengdu 610031, China

Search for more papers by this author

Peng Guo,

Corresponding Author

Peng Guo

[email protected]

orcid.org/0000-0001-5520-7701

School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China swjtu.edu.cn

Technology and Equipment of Rail Transit Operation and Maintenance Key Laboratory of Sichuan Province, Chengdu 610031, China

Search for more papers by this author

Qunsheng Wang,

Qunsheng Wang

orcid.org/0000-0002-1270-3921

State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China swjtu.edu.cn

Search for more papers by this author

First published: 2019

https://doi.org/10.1155/2019/1012987

Academic Editor: Evgeny Petrov

Share a link

Email
Wechat
Bluesky

Abstract

This paper presents a simulation approach based on the finite element method (FEM) to analyze the wind-induced vibration response of an inspection vehicle for main cables. First, two finite element (FE) models of a suspension bridge and a main cable-inspection vehicle coupled system are established using MIDAS Civil software and ANSYS software, respectively. Second, the mean wind speed distribution characteristics at a bridge site are analyzed, and the wind field is simulated based on the spectral representation method (SRM). Third, a modal analysis and a wind-induced vibration response transient analysis of the suspension bridge FE model are completed. Fourth, the vibration characteristics of the inspection vehicle are analyzed by applying fluctuating wind conditions and main cable vibration displacements in the main cable-inspection vehicle coupled FE model. Finally, based on the ISO2631-1-1997 standard, a vehicle ride comfort evaluation is performed. The results of the suspension bridge FE modal analysis are in good accordance with those of the experimental modal test. The effects of the working height, number of nonworking compressing wheels, and number of nonworking driving wheels during driving are discussed. When the average wind speed is less than 13.3 m/s, the maximum total weighted root mean square acceleration (a_v) is 0.1646 m/s² and the vehicle ride comfort level is classified as “not uncomfortable.” This approach provides a foundation for the design and application of inspection vehicles.

1. Introduction

As the most important component of a suspension bridge, the main cable is corroded by the long-term exposure to natural factors (e.g., wind, rain, freezing temperatures, temperature changes, and humidity changes), which can endanger the security and reduce the service life of the bridge [1–3]. Therefore, it is necessary to inspect and maintain the main cable regularly. The traditional method of inspecting the main cable is artificial climbing, which has many shortcomings, such as having blind inspection areas, difficulty in climbing at high altitudes, low efficiency, and potential safety hazards. To improve the efficiency of cable inspection, various types of crawling robots have been developed [4–6]. These light crawling robots can perform unmanned inspections of the sling and the cable, but it is difficult to inspect the main cable of a suspension bridge with cable bands and other ancillary structures or provide a suitable maintenance platform. Therefore, it is of great significance to develop an inspection vehicle suitable for large main cables.

To inspect the main cable of a suspension bridge, an inspection vehicle is designed and manufactured, as shown in Figure 1. The inspection vehicle adopts the wheeled walking scheme of “10 sets of driving wheels +3 pairs of compressing wheels (driven wheels)” to surround the main cable. The vehicle body is a Π-shaped steel frame, and the other parts are aluminum alloy trusses. The whole vehicle weighs 8.5 t, including a 1 t live load. Three sets of lock devices are installed on each pair of revolving plates at the bottom of the vehicle body to increase the rigidity of the vehicle body. The inspection vehicle adopts automatic control technology to perform the alternate lifting and lowering of the driving wheels, the advancing and retracting of the compressing wheels, the rotating of flaps, and the switching of lock devices by controlling the hydraulic cylinders to straddle obstacles such as cable bands and hangers. The vehicle can identify cable bands automatically, climb cable bands actively, and crawl at a large angle (30°) when manned.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

(a) An inspection vehicle for a main cable. (b) Structure of the vehicle.

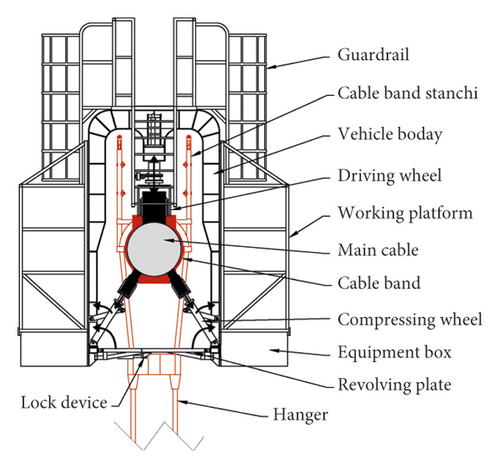
The inspection vehicle drives on the main cable, which is a typical wind-sensitive structure. Wind-induced vibration directly affects the security of equipment and the efficiency of workers [7]. Therefore, the dynamic properties of the main cable-inspection vehicle coupled system under wind loads should be studied when the inspection vehicle is designed. Researchers have conducted numerous field measurements to investigate the wind-induced vibration characteristics of suspension bridges [8–10]. Field measurement is the most direct and reliable method to obtain site wind data [11–13]. However, this approach requires a long period and is easily affected by environmental conditions. Li et al. [14], Chen et al. [15], and Li et al. [16] investigated the wind characteristics of different bridge sites through wind tunnel tests to provide a basis for bridge design. Although this method is not affected by the geographical environment, accurate models must be built, and the cost can be extremely expensive. With the development of theoretical studies and computer technology, simulation experiments have been increasingly used to study the effects of various factors on bridge components at the initial stage of the research work to reduce the number of field measurements and tunnel tests [17, 18]. Field measurements and tunnel tests are usually used for final validation. Bai et al. [19] and Helgedagsrud et al. [20] performed and validated simulation experiments by comparing different simulation results with those of wind tunnel tests. However, these studies focused on the wind-induced vibration of suspension bridges, and few studies have focused on the wind-induced vibration of mobile devices on the main cable.

The inspection vehicle was developed in the specialized field of mobile robots. In most previous studies, researchers focused on the design and vibration caused by the climbing of robots. Kim et al. [4] and Cho et al. [5] manufactured a wheel-based robot and a caterpillar-based robot for the inspection of a hanger rope, and the climbing abilities of both robots were validated in indoor experimental environments. Xu et al. [6] designed a cable-climbing robot for cable-stayed bridges, and the obstacle-climbing performance of each robot was simulated and validated in the laboratory. However, these robots are all tiny unmanned robots, and only structural safety must be considered. For a manned inspection vehicle, the vibration of the vehicle may cause discomfort or annoy the workers and influence performance [21]. These factors must be studied in the design process. The wind-induced vibration of the inspection vehicle is a complicated solid-wind-cable interaction problem, and the corresponding action mechanism has not yet been effectively studied.

The simulation of a random wind field is essential for time-domain vibration analysis of the inspection vehicle under wind loads. Based on the Monte Carlo method, the digital filtering method and the spectral representation method (SRM) [22] are two basic approaches used to simulate the random wind field. SRM, the method adopted in this paper, has been widely used in the engineering community due to its accuracy and simplicity [23, 24]. In order to improve the efficiency of SRM for the simulation of multidimensional wind fields, Tao et al. [23, 25], Huang et al. [24], and Xu et al. [26] proposed different optimization methods for solving. With the development of sensor technology, the study of wind fields has gradually been extended from stationary fields to nonstationary fields, especially for extreme wind [27, 28]. However, no empirical model is available for nonstationary winds due to the difficulties in mathematical treatments and nonergodic characteristics [28]. Therefore, stationary wind is the objective of this paper.

The purpose of this paper is to propose a method of assessing the vibration response of a main cable-inspection vehicle coupled system under fluctuating wind conditions. This paper is organized as follows: In Section 2, the process for establishing a suspension bridge finite element (FE) model and a main cable-inspection vehicle coupled FE model is introduced in detail. Taking the Qingshui River Bridge as an example, the mean wind speed distribution characteristics at the bridge site are analyzed and the wind field is simulated in Section 3. Section 4 presents the ride comfort evaluation method based on the ISO 2631-1-1997 standard [21]. A modal analysis of the suspension bridge FE model, transient analysis of both FE models, and ride comfort evaluation of the vehicle are conducted in Section 5. Finally, the conclusions and future work are discussed in Section 6.

2. Finite Element Model

The unit length mass of the inspection vehicle is much smaller than that of the suspension bridge. The inspection vehicle has little influence on the vibration amplitude and acceleration of the cable [29]. Therefore, the influence of the inspection vehicle on the vibration response of the bridge is not considered in this study. In order to simplify the study, the suspension bridge FE model and the main cable-inspection vehicle coupled FE model are established. MIDAS Civil software is used for the suspension bridge FE Model because of the accuracy and accessibility of its built-in formulas. For the main cable-inspection vehicle coupled FE model, ANSYS software is used due to the variety of its element types and the flexibility of its ANSYS Parametric Design Language (APDL). The dynamic displacement of the main cable which is recorded over time from the suspension bridge FE model is taken as the excitation source for the main cable-inspection vehicle coupled FE model to realize one-way coupling between two FE models.

2.1. Suspension Bridge FE Model

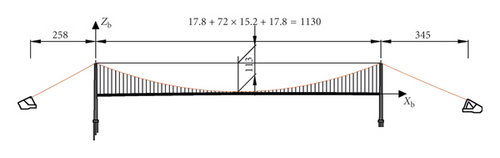
The Qingshui River Bridge, located in Guizhou Province, China, is 27 m wide with a main span of 1130 m. The structure is a single-span steel truss suspension bridge located in a mountainous area, connecting the expressway from Guizhou to Weng’an, as shown in Figure 2x_b is the axial direction of the bridge, y_b is the direction of the bridge width, and z_b is the vertical direction.

The FE model of the Qingshui River Bridge was built using MIDAS Civil software, as presented in Figure 3. Beam elements are used for the bridge deck and towers. Truss elements are used for the main cable and hangers and are tension-only elements. The structural parameters of the bridge FE model are listed in Table 1. The bottom of each tower and each anchorage are fixed. The bridge deck is connected to two main towers by elastic contacts in both the y and z directions, with ratings of 1000000 kN/m. One end of the bridge deck is constrained in the x direction. The weight of the bridge deck, two main cables, and all hangers are added to the nodes of the bridge deck and main cables in the form of a uniformly distributed mass load. Fluctuating wind loads are applied to the bridge deck and the main cables simultaneously on the elasticity center nodes in a given time sequence. The damping ratio is defined as 0.005.

Table 1. Parameters of the suspension bridge.

Part	A (m²)	I_y (m⁴)	I_z (m⁴)	ρ (kg/m³)	W (kN/m)	E (GPa)
Main tower	56.0	752.6	762.3	2500	—	34.5
Bridge deck	4.594	6.78	223.41	—	256.0	205
Main cable	0.3526	—	—	—	27.679	192
Hanger	0.0017	—	—	—	0.134	192

A, cross-sectional area; I_y, vertical section moment of inertia; I_z, transverse section moment of inertia; E, Young’s modulus; ρ, density; W, weight per unit length.

2.2. Main Cable-Inspection Vehicle Coupled FE Model

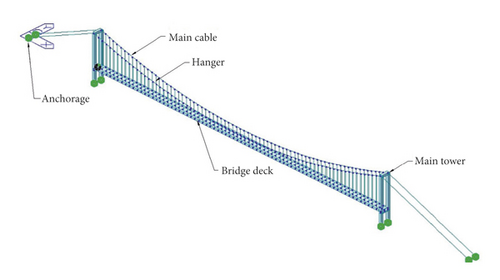
The structure of the main cable-inspection vehicle coupled system is shown in Figure 4x_v is the width direction of the bridge deck, y_v is the direction perpendicular to the tangential direction of the main cable centerline, and z_v is the tangential direction of the main cable centerline.

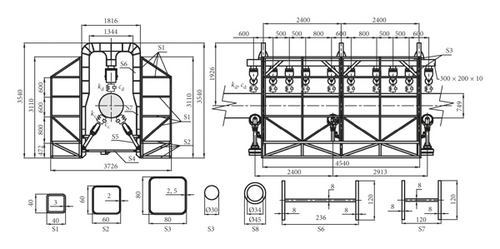
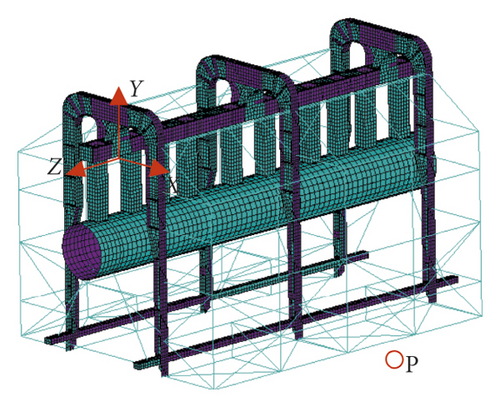
The FE model of the main cable-inspection vehicle coupled system was established in ANSYS software, as shown in Figure 5. The main cable is defined as a rigid body. SHELL 63 elements are used for the vehicle body, and BEAM 188 elements are used for working platforms, compressing wheel brackets, and the equipment box truss. The guardrail, compressing wheels, driving wheels, power system, and control system are omitted, and the weight of each part is added to the model by adjusting the material density of the local structure. The parameters of the material are shown in Table 2. Between the driving wheels and main cable or the compressing wheels and main cable are viscoelastic contacts, which are defined as spring-damping contacts. The parameters of the spring-damping contacts are shown in Table 3. Fluctuating wind loads are applied to the vehicle on the windward nodes in a given time sequence. The dynamic displacement of the main cable that is recorded over time from the suspension bridge FE model is taken as the excitation source.

Table 2. The parameters of the material used in the coupled FE model.

Part	E (MPa)	ν	ρ (kg/m³)
Main cable	Rigid body	—	—
Vehicle body	2.05 × 10⁵	0.3	7850
Driving/compression wheel	2.05 × 10⁵	0.3	60000
Working platform	6.9 × 10⁴	0.33	4000
Equipment box	6.9 × 10⁴	0.33	85000

E, Young’s modulus; ν, Poisson’s ratio; ρ, density.

Table 3. The parameters of the spring-damping contacts used in the coupled FE model.

Parameters	k_d (N/mm)	c_d (N·s/mm)	k_c (N/mm)	c_c (N·s/mm)
Value	285.3	0.2	1500	0.2

k_d and c_d are the spring stiffness and viscous damping coefficient of the contact between the driving wheels and main cable, respectively; k_c and c_c are the spring stiffness and viscous damping coefficient of the contact between the compressing wheels and main cable, respectively.

For consistency in the comparison of results, the vibration of node P, located at the bottom of the middle of the working platform on the windward side (see Figure 5), is investigated in the following analysis.

2.3. Coordinate Relationship

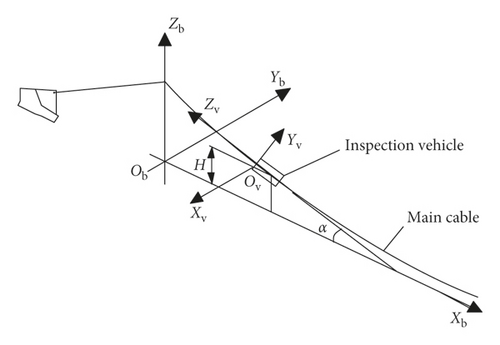
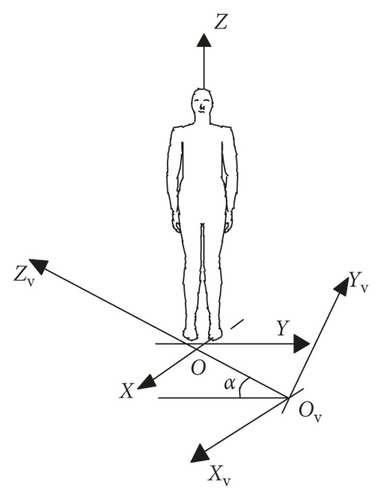
The inspection vehicle drives along the main cable during work, which results in changes in both the inclination angle (α) and working height (H) of the inspection vehicle. According to the different heights of the main cable from the bridge deck, H is set at 5 m, 35 m, 65 m, 95 m, and 113 m. The relation between H and α is shown in Table 4. According to the selected coordinate system when establishing the FE models, the coordinate relationships between the suspension bridge and inspection vehicle and the vehicle and a worker are shown in Figure 6.

Table 4. The relation between H and α.

H	5 m	35 m	65 m	95 m	113 m
α	0°	12.1°	16.8°	20.2°	21.3°

The displacements obtained from the transient analysis of the suspension bridge FE model need to be transferred to the main cable-inspection vehicle coupled FE model. The displacement relations in the two coordinate systems are as follows:

\begin{matrix} D_{x v} = - D_{y b}, \\ D_{y v} = D_{x b} \cdot \sin α + D_{z b} \cdot \cos α, \\ D_{z v} = - D_{x b} \cdot \cos α + D_{z b} \cdot \sin α, \end{matrix}

(1)

where D_xv, D_yv, and D_zv are the displacements of the main cable in the X, Y, and Z directions of the vehicle coordinate system O_v—X_vY_vZ_v, respectively. Additionally, D_xb, D_yb, and D_zb are the displacements of the main cable in the X, Y, and Z directions of the bridge coordinate system O_b—X_bY_bZ_b, respectively.

The acceleration obtained from the transient analysis of the main cable-inspection vehicle coupled FE model is transferred to the foot of the worker. The acceleration relations in the two coordinate systems are as follows:

\begin{matrix} a_{x} = a_{x v}, \\ a_{y} = a_{y v} \cdot \sin α - a_{z v} \cdot \cos α, \\ a_{z} = a_{z v} \cdot \sin α + a_{y v} \cdot \cos α, \end{matrix}

(2)

where a_xv, a_yv, and a_zv are the accelerations of the inspection vehicle (node P) in the X, Y, and Z directions of the vehicle coordinate system O_v—X_vY_vZ_v, respectively. In addition, a_x, a_y, and a_z are the accelerations transferred to the foot of the worker in the X, Y, and Z directions of the worker coordinate system O—XYZ, respectively.

3. Wind Speed and Wind Load Simulation

3.1. Wind Speed Simulation

The wind speed V(t) in nature over a given time interval is considered to be the sum of mean wind speed

\bar{V}

and fluctuating wind speed v(t):

\begin{matrix} V (t) = \bar{V} + v (t) . \end{matrix}

(3)

To obtain the mean wind speed distribution characteristics for the Qingshui River Bridge, a wind measurement tower was built approximately 100 m away from the main tower of the bridge close to Guizhou. An NRG 40C anemometer (produced by NRG Systems company) was mounted 10 m above the bridge deck to record 10-min mean wind speeds (

{\bar{V}}_{10}

). Based on the records from 33 months (from January 2014 to September 2016), the frequency of each mean wind speed interval was calculated, as shown in Figure 7. The lognormal probability density distribution, which is extensively used to fit the wind speed distribution over land [30], is used to fit these wind speed data and is given as follows [31]:

\begin{matrix} f (\bar{V}) = \frac{1}{\bar{V} σ \sqrt{2 π}} \exp \{- \frac{{(\ln (\bar{V}) - μ)}^{2}}{2 σ^{2}}\}, \end{matrix}

(4)

where σ and μ are the shape and scale parameters, respectively.

According to the maximum likelihood estimator (MLE) method, the shape and scale parameters are calculated as follows [31]:

\begin{matrix} μ = \frac{1}{M} \sum_{i = 1}^{M} \ln (v_{i}), \\ σ = \sqrt{\frac{1}{M} \sum_{i = 1}^{M} {[\ln (v_{i})]}^{2},} \end{matrix}

(5)

where M is the total number of wind speed values and i = 1, 2, …, and v_i is the wind speed at time step.

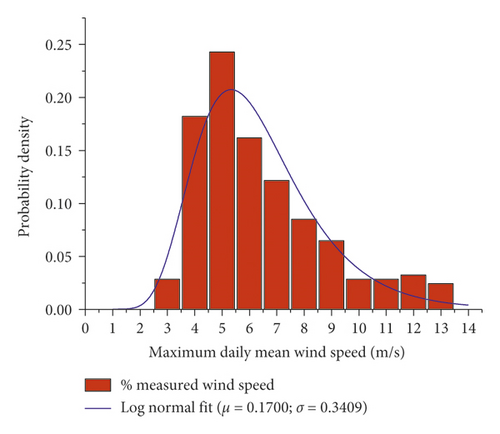
Figure 7 shows that the maximum daily mean wind speed is 13.3 m/s. Because a real-time wind speed alarm system is installed on the inspection vehicle, the influence of height on wind speed is neglected. Therefore, the design maximum working mean wind speed of the inspection vehicle is 13.3 m/s ( ${\bar{V}}_{\max} = 13.3 m / s$ ).

The Davenport power spectrum [32] is used to simulate the fluctuating wind field along the bridge because the influence of height on wind speed is neglected. The Davenport power spectrum is expressed as follows [32]:

\begin{matrix} S_{v} (n) = 4 k {\bar{V}}_{10}^{2} \frac{x^{2}}{n {(1 + x^{2})}^{43 /}}, \end{matrix}

(6)

where

x = 1200 n / {\bar{V}}_{10}

, k is a coefficient that depends on the roughness of the surface, and n is the fluctuating wind frequency.

The wind field of suspension bridges in each direction can be considered as a one-dimensional m-variable (1D-mV) zero-mean homogeneous random process V(t) =

{[V_{1} (t), V_{2} (t), \dots, V_{m} (t)]}^{T}

[23], where T is a transpose indicator. The cross power spectral density (CPSD) matrix of V(t) can be described as follows:

\begin{matrix} S (n) = [\begin{matrix} S_{11} (n) & S_{12} (n) & \dots & S_{1 m} (n) \\ S_{21} (ω) & S_{22} (n) & \dots & S_{2 m} (n) \\ ⋮ & ⋮ & ⋱ & ⋮ \\ S_{m 1} (n) & S_{m 2} (n) & \dots & S_{m m} (n) \end{matrix}] . \end{matrix}

(7)

The CPSD between any two components V_j(t) and V_p(t) can be expressed as

\begin{matrix} S_{i q} (n) = \sqrt{S_{j} (n) S_{q} (n)} γ_{j q} (n) e^{i θ_{j q} (n)}, \end{matrix}

(8)

where γ_jq(n) is the coherence function, the Davenport empirical function [33] is used, j, q = 1, 2, …, m, and θ_jq(n) is the corresponding phase angle [34].

The CPSD matrix can be factorized into the following product with the Cholesky decomposition:

\begin{matrix} S (n) = H (n) H^{T^{*}} (n), \end{matrix}

(9)

where the superscript ^∗ indicates the matrix should be conjugate and H(n) is a lower triangular matrix.

According to SRM, the fluctuating wind speed for any point v_j(t) is given as follows [22]:

\begin{matrix} v_{j} (t) = 2 \sqrt{Δ n} \sum_{l = 1}^{j} \sum_{k = 1}^{N} |H_{j l} (n_{l k})| \cos [n_{l k} t - θ (n_{l k}) + ϕ_{l k}], \\ n_{l k} = k Δ n - (1 - \frac{l}{m}) Δ n, \\ θ (n_{l k}) = \tan^{- 1} \{\frac{Im [H_{l k} (n_{l k})]}{Re [H_{l k} (n_{l k})]}\}, \end{matrix}

(10)

where N is the total number of frequency intervals, Δn = n_u/N, n_u is the cutoff frequency, n_lk is the double-index frequency, H_jl = (n_lk) are the elements of matrix H(n), θ(n_lk) is the phase angle of the complex element in H(n) at frequency n_lk, and ϕ_lk is a random phase angle uniformly distributed from 0 to 2π.

Referring to the JTG/T D60-01-2004 standard [35], the bridge site is classified as Class D, k is taken as 0.01291, and the ground roughness index is taken as 0.3. Using fast Fourier transform (FFT) and the random number generator in MATLAB, wind speed curves in the time domain can be simulated. Thirty-seven simulation points are uniformly distributed along the length of the bridge deck. This paper only considers the effect of the cross-bridge wind, and the angle between the incoming wind direction and primary flow plane is taken as 0°. The simulated fluctuating wind speed time history at the middle-span position (z = 10 m; ${\bar{V}}_{10}$ = 13.3 m/s) for the bridge is presented in Figure 8.

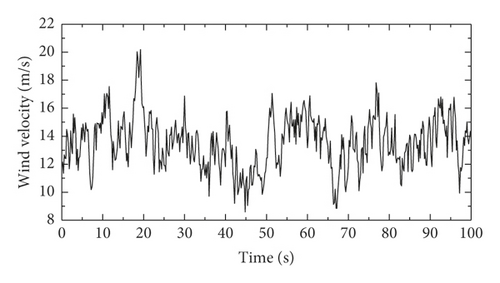
3.2. Wind Load Simulation

Wind load on a bridge can be classified into three parts: static wind load, buffeting load, and self-excited load. Chen et al. found that the effect of the self-excited force is limited when the wind speed is lower than the design basic wind speed [36]. Therefore, only static wind load and buffeting load on the bridge are considered in this paper.

The wind loads per unit length including the static wind and buffeting loads acting at the elasticity center of the bridge deck/cable or acting on the windward nodes of the inspection vehicle are defined as follows:

\begin{matrix} L_{w} (t) = \frac{1}{2} ρ H C_{L} V {(t)}^{2}, \\ D_{w} (t) = \frac{1}{2} ρ B C_{D} V {(t)}^{2}, \\ M_{w} (t) = \frac{1}{2} ρ B^{2} C_{M} V {(t)}^{2}, \end{matrix}

(11)

where L_w(t), D_w(t), and M_w(t) are the lift, drag, and torque wind force, respectively, ρ is the air density, H is the height of the bridge deck or diameter of the main cable or windward projection height of the inspection vehicle, and C_L, C_D, and C_M are the lift, drag, and torque wind force coefficients, respectively. All three forces are considered for the deck, but only drag force is considered for the cables and the vehicle. According to the section model tests of the bridge deck in the wind tunnel completed by Wang et al. [37], C_L, C_D, and C_M for the deck are taken as 0.2, 1.5, and 0.02, respectively. Referring to the JTG/T D60-01-2004 standard [35], C_L for the cables and the vehicle are taken as 0.7 and 1.8, respectively.

4. Comfort Evaluation

With the increasing awareness of human physiological and behavioral responses to vibration, the comfort problem in the vibration environment has extended from the ride comfort of automobiles to the operating comfort of engineering equipment and has received increased attention [38, 39]. In this paper, the evaluation method recommended by the ISO2631-1-1997 standard [21] is used to evaluate the perception and ride comfort of a worker driving an inspection vehicle under vibration. According to the standard, the acceleration time history signals in all directions transmitted from the working platform floor to a worker through the feet are transformed into the frequency domain using FFT. The frequency-weighted root mean square (rms) acceleration a_w is determined by weighting and the appropriate addition of one-third octave band data as follows [21]:

\begin{matrix} a_{w} = {[\sum_{k} {(W_{k} a_{k})}^{2}]}^{12 /}, \end{matrix}

(12)

where W_k is the weighting factor of the kth one-third octave band given by the ISO 2631-1-1997 standard and a_k is the rms acceleration of the kth one-third octave band.

In orthogonal coordinates, the vibration total value of the weighted rms acceleration a_v is calculated by a_w in three directions as follows [21]:

\begin{matrix} a_{v} = {(k_{x}^{2} a_{w x}^{2} + k_{y}^{2} a_{w y}^{2} + k_{z}^{2} a_{w z}^{2})}^{12 /}, \end{matrix}

(13)

where a_wx, a_wy, and a_wz are the frequency-weighted accelerations with respect to orthogonal coordinate axes x, y, and z, respectively, and k_x, k_y, and k_z are the multiplying factors given by the ISO 2631-1-1997 standard [21].

The relationship between a_v and subjective sensory comfort is shown in Table 5 [21]. After calculating a_v, it is convenient to quantitatively evaluate the ride comfort of the inspection vehicle.

Table 5. Subjective criteria for ride comfort.

a_v (m/s²)	Comfort level
<0.315	Not uncomfortable
0.315∼0.63	A little uncomfortable
0.5∼1.0	Fairly uncomfortable
0.8∼1.6	Uncomfortable
1.25∼2.5	Very uncomfortable
>2.0	Extremely uncomfortable

5. Results and Analysis

5.1. Suspension Bridge FE Model Verification

The block-Lanczos method was used in the modal analysis of a suspension bridge to verify the correctness of the proposed suspension bridge FE model. To measure the modal characteristics of the suspension bridge, a full-bridge aeroelastic model was constructed that was scaled to C = 1/100 of the original. According to the similarity criterion suggested in the JTG/T D60-01-2004 standard [35], the major design parameters of the model are listed in Table 6. The full-bridge aeroelastic elastic model was composed of the bridge deck, main towers, main cables, hangers, and bases. The model main beam adopted aluminum chords and plastic diagonals. The bridge deck consisted of 37 sections with a 2 mm gap between each section and a U connection between two sections. Each tower contained a steel core beam and wooden boards that provided an aerodynamic shape. Steel strand provided stiffness of cable, and an iron block was enwrapped outside the cable to control the weight. Each hanger consisted of a steel wire without shear stiffness but with high tension stiffness. Lead blocks were used to adjust the weight of the model and were installed inside the bridge deck model. Plastic boards were used to simulate the aeroelastic shape of the deck rail. The test was conducted in the Industrial Wind Tunnel (XNJD-3) of Southwest Jiaotong University, as shown in Figure 9. The dynamic response of the model was measured by the forced oscillation method [14]. Two laser displacement sensors were used to obtain the vibration signal in the test. A comparison of the results of the FE modal analysis and experiment modal test of the first 4 vibration modes is presented in Table 7. The table shows that the modes of vibration are fully consistent, and the difference in frequency values is less than 5%. Therefore, the FE model of the suspension bridge has high accuracy and can effectively reflect the dynamic characteristics of the suspension bridge.

Table 6. Major design parameters of the full-bridge aeroelastic model.

Parameter	Unit	Similarity ratio	Value of the real bridge	Value of the model
Length
Total length of bridge deck (L)	m	C	1130	11.3
Width of bridge deck (B)			27	0.27
Height of bridge deck (H)			7	0.07
Height of main tower (H_t)			230	2.3
Stiffness
Vertical stiffness of bridge deck, EI_y	Nm²	C⁵	1.39 × 10¹²	1.39 × 10²
Transverse stiffness of bridge deck, EI_z			4.58 × 10¹³	4.58 × 10³
Along-bridge direction stiffness of the bottom of main tower, EI_y			2.63 × 10¹³	2.63 × 10³
Transverse stiffness of the bottom of main tower, EI_z			12.60 × 10¹³	12.60 × 10³

Table 7. Comparison of vibration modes.

Mode no.	Frequency			Mode of vibration	Remark
Mode no.	Experiment modal test (Hz)	FE modal analysis (Hz)	Difference (%)	Mode of vibration	Remark
1	0.0844	0.0818	3.1		Symmetric lateral vibration
2	0.1660	0.1608	3.1		Antisymmetric vertical vibration
3	0.1777	0.1812	2.0		Symmetric vertical vibration
4	0.2435	0.2542	4.4		Antisymmetric lateral vibration

5.2. Wind-Induced Vibration Response of the Main Cable

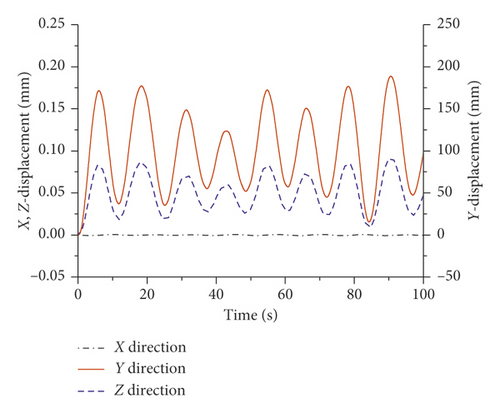
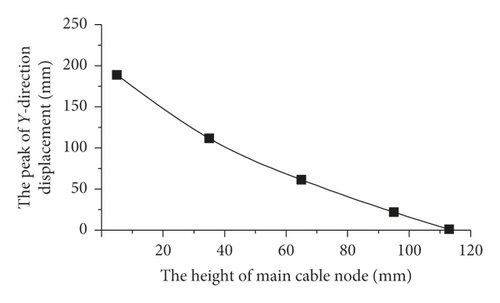
After validation, the suspension bridge FE model can be used to analyze the vibration characteristics of the main cable with fluctuating winds as the excitation source. Figure 10 shows the vibration displacement history of the node at the middle-span position, which is 5 m above the bridge deck surface in the bridge coordinate system O_b—X_bY_bZ_b. The vibration frequency of the main cable is 0.0815, which is consistent with the first-order frequency of the suspension bridge. The results are also consistent with the conclusion of Huang et al. [40]. The main vibration direction of the main cable is the Y direction (lateral direction). The peak value of the Y-direction vibration displacement is 188.7 mm, and the peak values of X-direction and Z-direction vibration displacement are less than 0.1 mm. Therefore, only the Y-direction vibration of the main cable node is considered in the study of the wind-induced vibration response in the main cable-inspection vehicle coupled FE model. As the height of the main cable node increases, the constraint on the node from the cable saddle becomes stronger and the peak value of the Y-direction vibration displacement of the node gradually decreases, as shown in Figure 11.

5.3. Wind-Induced Vibration Response of the Inspection Vehicle

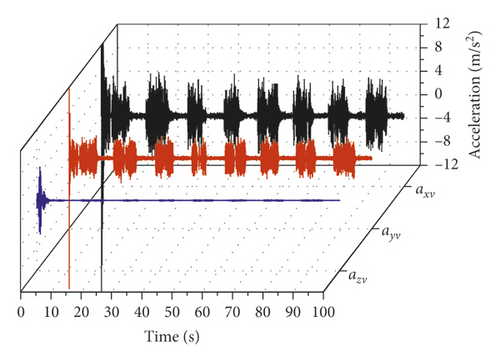
The transient analysis of the main cable-inspection vehicle coupled FE model was performed with the fluctuating wind and the displacement of the main cable node as the excitation sources. Figure 12 shows the vibration acceleration time history of the inspection vehicle node P at a height of 5 m in the moving coordinate system O_v—X_vY_vZ_v. At this time, all the driving wheels and compressing wheels of the inspection vehicle are in contact with the main cable. The vibration of the inspection vehicle has a large impact from 0 s to 10 s, which is due to the impact of gravity applied during simulation. This phenomenon will not occur during the operation of the inspection vehicle. Therefore, all subsequent acceleration statistics start from 10 s to maintain accuracy. The peak value of the X-direction vibration acceleration (a_xv) at node P at a height of 5 m is the largest at 7.86 m/s², and the peak value of the Z-direction vibration acceleration (a_zv) is the smallest at 0.55 m/s². The peak value of the Y-direction vibration acceleration (a_yv) is 3.81 m/s². Therefore, the main vibrations of the inspection vehicle are X-direction vibration and Y-direction vibration.

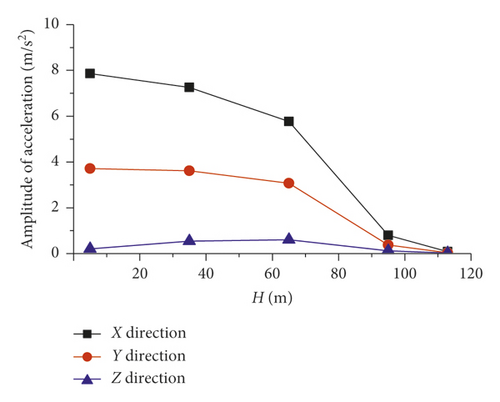
When the inspection vehicle climbs along the main cable, the working height (H) and inclination angle (α) of the inspection vehicle increase simultaneously. Due to the influence of the constraint on the nodes of the cable from the main cable saddle strength and the increase in the gravity component in the Z direction of the inspection vehicle, the peak values of the X-direction and Y-direction vibration acceleration of the inspection vehicle gradually decrease and the peak value of the Z-direction vibration acceleration initially increases and then decreases, as shown in Figure 13.

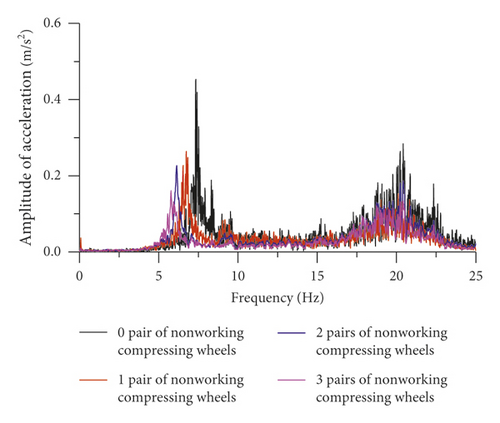
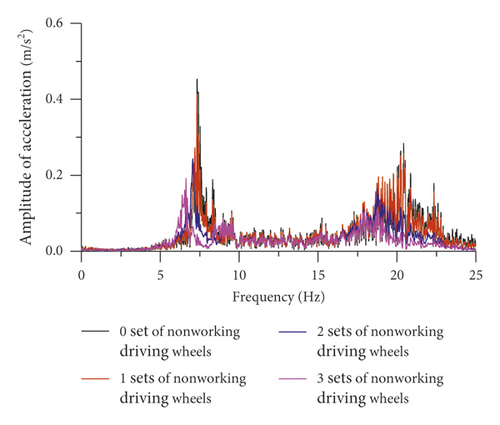
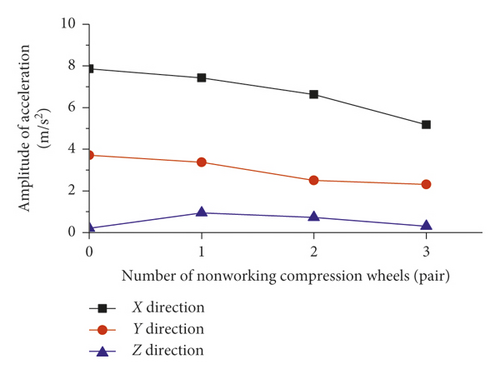
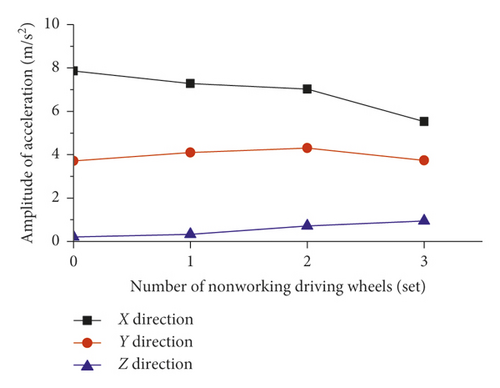
When the inspection vehicle crosses the cable band, the driving wheels need to be lifted and the compressing wheels need to be alternately opened. Lifting the driving wheels or opening the compressing wheels will change the coupling relationship between the inspection vehicle and the main cable and will reduce the contact stiffness between them, resulting in simultaneous reductions in the main frequency and the main frequency amplitude, as shown in Figure 14. As the number of nonworking compression wheels increases, the vertical and lateral contact stiffness values between the inspection vehicle and the main cable simultaneously decrease, resulting in a gradual decrease in the peak values of both the X-direction and Y-direction vibration acceleration of the inspection vehicle and an initial increase and subsequent decrease in the peak value of the Z-direction vibration acceleration, as shown in Figure 15. As the number of nonworking driving wheels increases, the vertical contact stiffness between the inspection vehicle and the main cable decreases, resulting in a gradual decrease in the peak value of the X-direction vibration acceleration of the inspection vehicle, a nonobvious change in the peak value of the Y-direction vibration acceleration, and a slow increase in the peak value of the Z-direction vibration acceleration, as shown in Figure 16.

5.4. Ride Comfort Evaluation of the Inspection Vehicle

The inspection vehicle is a type of aerial work equipment. Vibration of the vehicle can not only induce psychological panic in workers but also affect the work efficiency and health of workers [21]. Therefore, it is necessary to analyze the ride comfort of the vehicle. Through coordinate transformation, the vibration acceleration transmitted to the foot of a worker in the inspection vehicle is obtained and the vehicle ride comfort is further analyzed. Figure 17 illustrates the variation curves of the vibration total values of the weighted rms acceleration (a_v).

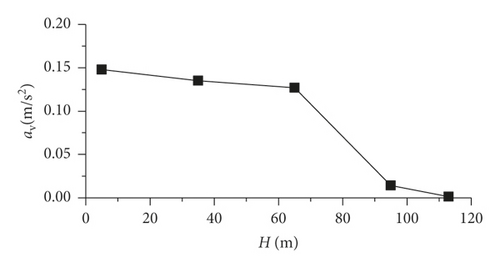
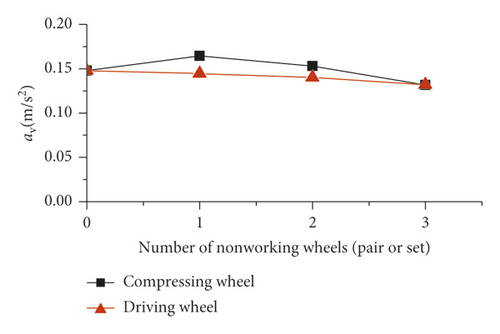
Figure 17(a) shows that as the working height of the inspection vehicle increases, the value of a_v decreases slowly first and then sharply and the maximum reduction ratio of a_v is 99.0%. The ride comfort of the inspection vehicle is improved due to the vehicle acceleration change described in Section 5.3. When the inspection vehicle works at the middle-span position (H = 5 m), the value of a_v reaches a maximum of 0.1478 m/s², which is less than 0.315 m/s², and the vehicle ride comfort level is “not uncomfortable.”

Figure 17(b) shows that when one pair of compressing wheels at the end of the vehicle is opened, the value of a_v reaches a maximum of 0.1646 m/s², which is less than 0.315 m/s². Thus, the vehicle comfort level is “not uncomfortable” because as the number of open compressing wheel pairs increases, the main frequency of vehicle vibration decreases. In this case, the frequency gradually approaches the sensitive frequency of the human body and the vehicle acceleration changes as described in Section 5.3. As the number of nonworking driving wheels increases, the value of a_v slowly decreases, and the vehicle ride comfort improves due to the decreases in the main frequency and amplitude of the main frequency described in Section 5.3. When all the driving wheels contact the main cable, the value of a_v is the largest at 0.1478 m/s², less than 0.315 m/s². Therefore, the vehicle ride comfort level is “not uncomfortable.”

6. Conclusions

In this paper, an FE model of a suspension bridge and a coupled FE model of a main cable-inspection vehicle coupled system were established by MIDAS Civil software and ANSYS software, respectively, and the two systems were connected by the vibration displacement of the main cable. An experimental modal test of the suspension bridge was completed, and the dynamic responses of both the suspension bridge and the inspection vehicle were analyzed using two FE models under fluctuating wind conditions simulated by MATLAB software. The main conclusions drawn from the study results are as follows:

(1)
By comparing the results of the FE modal analysis and modal test of the first 4 vibration modes, the vibration modes are fully consistent and the difference in frequency values between them is less than 5%. The validity of the FE model of the suspension bridge is verified.
(2)
Through the transient analysis under fluctuating wind conditions, the main vibration direction of the main cable is the lateral direction and the main vibration directions of the inspection vehicle are the X direction and Y direction. The increase in the working height will lead to a significant reduction in the vibration displacement amplitude of the main cable node and a significant reduction in the vibration response of the inspection vehicle. An increase in the number of nonworking compressing wheels or nonworking driving wheels will result in a decrease in the main frequency and slowly reduce the vibration response of the inspection vehicle.
(3)
The vehicle ride comfort evaluation under different working conditions shows that an increase in the working height improves the vehicle ride comfort due to the reduction in the vibration response of the inspection vehicle. The increase in the number of nonworking compressing wheels affects the vibration amplitude and frequency of the vehicle, which results in an initial deterioration and subsequent improvement in vehicle ride comfort. The increase in the number of nonworking driving wheels will lead to improved vehicle ride comfort.
(4)
The vehicle ride comfort analysis shows that when the average wind speed of the inspection vehicle is below 13.3 m/s, the maximum value of a_v for the vehicle is 0.1646 m/s² and the vehicle ride comfort level is “not uncomfortable,” which meets the users’ requirements.

The simulation results presented demonstrate that the numerical analysis method proposed in this paper can be implemented to evaluate wind-induced vibration characteristics for other similar devices working on the main cable. However, comparisons and experimental tests on the influence of the long-term driving of the inspection vehicle on the main cable protective layer have yet to be achieved. These issues remain potential topics of future work.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This research was supported by the National Natural Science Foundation of China (no. 51675450) and the Guizhou Science and Technology Special Project (no. 20156001).

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Cocksedge C., Hudson T., Urbans B., and Baron S., M48 severn bridge—main cable inspection and rehabilitation, Proceedings of the Institution of Civil Engineers—Bridge Engineering. (2010) 163, no. 4, 181–195, https://doi.org/10.1680/bren.2010.4.181, 2-s2.0-79951507978.
10.1680/bren.2010.4.181
Google Scholar
2 Bloomstine M. L., Main cable corrosion protection by dehumidification: experience, optimization and new development, 2115, Proceedings of the 6th New York City Bridge Conference, July 2011, New York City, NY, USA.
Google Scholar
3 Mayrbaurl R. M. and Camo S., NCHRPV Report 534: Guidelines for Inspection and Strength Evaluation of Suspension Bridge Parallel Wire Cables, 2004, Transportation Research Board of the National Academies, Washington, DC, USA.
Google Scholar
4 Kim H. M., Cho K. H., Jin Y. H., Liu F., Koo J. C., and Choi H. R., Development of cable climbing robot for maintenance of suspension bridges, 415, Proceedings of 2012 IEEE International Conference on Automation Science and Engineering, August 2012, Seoul, Republic of Korea, https://doi.org/10.1109/coase.2012.6386375, 2-s2.0-84872518417.
10.1109/coase.2012.6386375
Google Scholar
5 Cho K. H., Jin Y. H., Kim H. M., Moon H., Koo J. C., and Choi H. R., Caterpillar-based cable climbing robot for inspection of suspension bridge hanger rope, 217, Proceedings of 2013 IEEE International Conference on Automation Science and Engineering, August 2013, Madison, WI, USA, 1059–1062, https://doi.org/10.1109/coase.2013.6653913, 2-s2.0-84891542574.
10.1109/coase.2013.6653913
Google Scholar
6 Xu F., Shen J., and Jiang G., Kinematic and dynamic analysis of a cable-climbing robot, International Journal of Advanced Robotic Systems. (2015) 12, no. 7, 1–17, https://doi.org/10.5772/60865, 2-s2.0-84938631057.
10.5772/60865
Web of Science® Google Scholar
7 Xu F., Wang X., and Jiang G., Experimental studies on the dynamic behaviour of a robot cable-detecting system, Transactions of the Institute of Measurement and Control. (2016) 38, no. 3, 338–347, https://doi.org/10.1177/0142331215592950, 2-s2.0-84958529918.
10.1177/0142331215592950
Web of Science® Google Scholar
8 Petersen Ø. W., Øiseth O., and Lourens E.-M., The use of inverse methods for response estimation of long-span suspension bridges with uncertain wind loading conditions: practical implementation and results for the Hardanger Bridge, Journal of Civil Structural Health Monitoring. (2019) 9, no. 1, 21–36, https://doi.org/10.1007/s13349-018-0319-y, 2-s2.0-85060922087.
10.1007/s13349-018-0319-y
Web of Science® Google Scholar
9 Wang H., Li A., Guo T., and Tao T., Establishment and application of the wind and structural health monitoring system for the Runyang Yangtze River Bridge, Shock and Vibration. (2014) 2014, 15, 421038, https://doi.org/10.1155/2014/421038, 2-s2.0-84929635319.
10.1155/2014/421038
Web of Science® Google Scholar
10 Xu Y. L., Zhu L. D., Wong K. Y., and Chan K. W. Y., Field measurement results of Tsing Ma suspension bridge during typhoon Victor, Structural Engineering and Mechanics. (2000) 10, no. 6, 545–559, https://doi.org/10.12989/sem.2000.10.6.545.
10.12989/sem.2000.10.6.545
Web of Science® Google Scholar
11 Li Q. S., Li X., He Y., and Yi J., Observation of wind fields over different terrains and wind effects on a super-tall building during a severe typhoon and verification of wind tunnel predictions, Journal of Wind Engineering and Industrial Aerodynamics. (2017) 162, 73–84, https://doi.org/10.1016/j.jweia.2017.01.008, 2-s2.0-85009962775.
10.1016/j.jweia.2017.01.008
Web of Science® Google Scholar
12 Wang H., Tao T., Gao Y., and Xu F., Measurement of wind effects on a kilometer-level cable-stayed bridge during typhoon Haikui, Journal of Structural Engineering. (2018) 144, no. 9, 04018142, https://doi.org/10.1061/(asce)st.1943-541x.0002138, 2-s2.0-85049023149.
10.1061/(ASCE)ST.1943-541X.0002138
Web of Science® Google Scholar
13 Tao T., Wang H., and Wu T., Comparative study of the wind characteristics of a strong wind event based on stationary and nonstationary models, Journal of Structural Engineering. (2017) 143, no. 5, 04016230, https://doi.org/10.1061/(asce)st.1943-541x.0001725, 2-s2.0-85017023239.
10.1061/(ASCE)ST.1943-541X.0001725
Web of Science® Google Scholar
14 Li G. H., Wang W. J., Ma X. C., Zuo L. B., Wang F. B., and Li T. Z., Wind tunnel test study on pipeline suspension bridge via aeroelastic model with π connection, Journal of Pipeline Systems Engineering and Practice. (2019) 10, no. 1, 04018025, https://doi.org/10.1061/(asce)ps.1949-1204.0000333, 2-s2.0-85054077541.
10.1061/(ASCE)PS.1949-1204.0000333
Web of Science® Google Scholar
15 Chen Z., Zhang C., Wang X., and Ma C., Wind tunnel measurements for flutter of a long-afterbody bridge deck, Sensors. (2017) 17, no. 2, https://doi.org/10.3390/s17020335, 2-s2.0-85012260327.
10.3390/s17020335
Web of Science® Google Scholar
16 Li Y., Xu X., Zhang M., and Xu Y., Wind tunnel test and numerical simulation of wind characteristics at a bridge site in mountainous terrain, Advances in Structural Engineering. (2017) 20, no. 8, 1123–1223, https://doi.org/10.1177/1369433216673377, 2-s2.0-85027118183.
10.1177/1369433216673377
Web of Science® Google Scholar
17 Yang Y., Gang Y., Wei F., and Qin W., Buffeting performance of long-span suspension bridge based on measured wind data in a mountainous region, Journal of Vibroengineering. (2018) 20, no. 1, 621–635, https://doi.org/10.21595/jve.2017.18737, 2-s2.0-85042261150.
10.21595/jve.2017.18737
Google Scholar
18 Zhao L. and Ge Y., Cross-spectral recognition method of bridge deck aerodynamic admittance function, Earthquake Engineering and Engineering Vibration. (2015) 14, no. 4, 595–609, https://doi.org/10.1007/s11803-015-0048-8, 2-s2.0-84949570100.
10.1007/s11803-015-0048-8
Web of Science® Google Scholar
19 Bai Y., Zhang Y., Liu T., Liu T., Kennedy D., and William F., Numerical predictions of wind-induced buffeting vibration for structures by a developed pseudo-excitation method, Journal of Low Frequency Noise Vibration and Active Control. (2019) 38, no. 2, 510–526, https://doi.org/10.1177/1461348419828248, 2-s2.0-85061635777.
10.1177/1461348419828248
Web of Science® Google Scholar
20 Helgedagsrud T. A., Akkerman I., Bazilevs Y., ASCE, Mathisen K. M., and Øiseth O. A., Isogeometric modeling and experimental investigation of moving-domain bridge aerodynamics, Journal of Engineering Mechanics. (2019) 145, no. 5, 04019026, https://doi.org/10.1061/(asce)em.1943-7889.0001601, 2-s2.0-85062183910.
10.1061/(ASCE)EM.1943-7889.0001601
Web of Science® Google Scholar
21 International Organization for Standardization, ISO, 2631-1:1997, Mechanical Vibration and Shock-Evaluation of Human Exposure to Whole-Body Vibration-Part 1: General Requirements, 1997, International Organization for Standardization, Geneva, Switzerland.
Google Scholar
22 Shinozuka M. and Jan C.-M., Digital simulation of random processes and its applications, Journal of Sound and Vibration. (1972) 25, no. 1, 111–128, https://doi.org/10.1016/0022-460x(72)90600-1, 2-s2.0-0039400744.
10.1016/0022-460X(72)90600-1
Web of Science® Google Scholar
23 Tao T., Wang H., Yao C., He X., and Kareem A., Efficacy of interpolation-enhanced schemes in random wind field simulation over long-span bridges, Journal of Bridge Engineering. (2018) 23, no. 3, 04017147, https://doi.org/10.1061/(asce)be.1943-5592.0001203, 2-s2.0-85039871923.
10.1061/(ASCE)BE.1943-5592.0001203
Web of Science® Google Scholar
24 Huang G., Liao H., and Li M., New formulation of Cholesky decomposition and applications in stochastic simulation, Probabilistic Engineering Mechanics. (2013) 34, 40–47, https://doi.org/10.1016/j.probengmech.2013.04.003, 2-s2.0-84879108885.
10.1016/j.probengmech.2013.04.003
CAS Web of Science® Google Scholar
25 Tao T., Wang H., and Kareem A., Reduced-Hermite bifold-interpolation assisted schemes for the simulation of random wind field, Probabilistic Engineering Mechanics. (2018) 53, 126–142, https://doi.org/10.1016/j.probengmech.2018.08.002, 2-s2.0-85052843851.
10.1016/j.probengmech.2018.08.002
Web of Science® Google Scholar
26 Xu Y.-L., Hu L., and Kareem A., Conditional simulation of nonstationary fluctuating wind speeds for long-span bridges, Journal of Engineering Mechanics. (2014) 140, no. 1, 61–73, https://doi.org/10.1061/(asce)em.1943-7889.0000589, 2-s2.0-84891365539.
10.1061/(ASCE)EM.1943-7889.0000589
Web of Science® Google Scholar
27 Tao T. and Wang H., Modelling of longitudinal evolutionary power spectral density of typhoon winds considering high-frequency subrange, Journal of Wind Engineering and Industrial Aerodynamics. (2019) 193, 103957, https://doi.org/10.1016/j.jweia.2019.103957.
10.1016/j.jweia.2019.103957
Web of Science® Google Scholar
28 Huang G., Zheng H., Xu Y., and Li Y., Spectrum models for nonstationary extreme winds, Journal of Structural Engineering. (2015) 141, no. 10, 04015010, https://doi.org/10.1061/(asce)st.1943-541x.0001257, 2-s2.0-84931055853.
10.1061/(ASCE)ST.1943-541X.0001257
Web of Science® Google Scholar
29 Xu F., Wang L., Wang X., and Jiang G., Dynamic performance of a cable with an inspection robot—analysis, simulation, and experiments, Journal of Mechanical Science and Technology. (2013) 27, no. 5, 1479–1492, https://doi.org/10.1007/s12206-013-0328-2, 2-s2.0-84878152988.
10.1007/s12206-013-0328-2
Web of Science® Google Scholar
30 Alavi O., Sedaghat A., and Mostafaeipour A., Sensitivity analysis of different wind speed distribution models with actual and truncated wind data: a case study for Kerman, Iran, Energy Conversion and Management. (2016) 120, 51–61, https://doi.org/10.1016/j.enconman.2016.04.078, 2-s2.0-84964659483.
10.1016/j.enconman.2016.04.078
Web of Science® Google Scholar
31 brano V. L., Orioli A., Ciulla G., and Culotta S., Quality of wind speed fitting distributions for the urban area of Palermo, Italy, Renewable Energy. (2011) 36, no. 3, 1026–1039, https://doi.org/10.1016/j.renene.2010.09.009, 2-s2.0-77958198848.
10.1016/j.renene.2010.09.009
Web of Science® Google Scholar
32 Davenport A. G., The spectrum of horizontal gustiness near the ground in high winds, Quarterly Journal of the Royal Meteorological Society. (2010) 88, no. 376, 197–198, https://doi.org/10.1002/qj.49708837618, 2-s2.0-84979329166.
10.1002/qj.49708837618
Google Scholar
33 Davenport A. G., The dependence of wind load upon meteorological parameters, Proceedings of the International Research Seminar on Wind Effects on Building and Structures, September 1968, Ottawa, Canada, University of Toronto Press, 19–82.
Google Scholar
34 Di Paola M. and Gullo I., Digital generation of multivariate wind field processes, Probabilistic Engineering Mechanics. (2001) 16, no. 1, 1–10, https://doi.org/10.1016/s0266-8920(99)00032-6, 2-s2.0-0035198883.
10.1016/S0266-8920(99)00032-6
Web of Science® Google Scholar
35 Ministry of Transport of the People′s Republic of China, JTG/T-D60-01: 2004, Wind-Resistent Design Specification for Highway Bridges, 2014, Ministry of Transport of the People's Republic of China, Beijing, China.
Google Scholar
36 Chen Z. Q., Han Y., Hua X. G., and Luo Y. Z., Investigation on influence factors of buffeting response of bridges and its aeroelastic model verification for Xiaoguan Bridge, Engineering Structures. (2009) 31, no. 2, 417–431, https://doi.org/10.1016/j.engstruct.2008.08.016, 2-s2.0-57749197808.
10.1016/j.engstruct.2008.08.016
Web of Science® Google Scholar
37 Wang K., Liao H. L., and Li M. S., Flutter performances of a long-span suspension bridge with steel trusses based on wind tunnel testing, Journal of Vibration and Shock. (2015) 34, no. 15, 175–194.
Google Scholar
38 Abdelkareem M. A., Makrahy M. M., Abd-El-Tawwab A. M., EL-Razaz A., Kamal Ahmed Ali M., and Moheyeldein M., An analytical study of the performance indices of articulated truck semi-trailer during three different cases to improve the driver comfort, Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-Body Dynamics. (2018) 232, no. 1, 84–102, https://doi.org/10.1177/1464419317709895, 2-s2.0-85042531041.
10.1177/1464419317709895
Web of Science® Google Scholar
39 Stanković M., Mićović A., Sedmak A., and Popović V., Analysis of comfort parameters in special purpose vehicles from technological development point of view, Tehnicki vjesnik—Technical Gazette. (2018) 25, no. 2, 502–509, https://doi.org/10.17559/tv-20171007101611, 2-s2.0-85045903829.
10.17559/tv-20171007101611
Web of Science® Google Scholar
40 Huang G. Q., Shu Y. W., Peng L. L., Ma C. M., Liao H. L., and Li M. S., Response analysis of long-span suspension bridge under mountainous winds, Journal of Southwest Jiaotong University. (2015) 50, no. 4, 610–616.
Google Scholar

All articles

Wind-Induced Vibration Response of an Inspection Vehicle for Main Cables Based on Computer Simulation

Abstract

1. Introduction