DFT Calculations of Hydrogen Adsorption inside Single-Walled Carbon Nanotubes
Abstract
DFT calculations have been performed to study noncovalent interactions of a hydrogen molecule and single-walled carbon nanotubes (SWCNTs) of various diameters. Understanding these interactions is crucial for the development of systems for hydrogen storage and delivery. The barrier and barrier-free introduction of a hydrogen molecule into SWCNTs is observed. It has been found that hydrogen molecules bind differently onto SWCNTs, depending on their diameters and the orientation of an H2 molecule inside the SWCNT. The binding inside SWCNTs with small diameters ((3,3); (4,4)) is very unfavorable; the opposite situation is in the case of larger ((5,5); (6,6)) SWCNTs. Finally, in the case of ((7,7); (8,8)) SWCNTs, the hydrogen binding energies decrease, and their values approach to those of graphene.
1. Introduction
In recent years, numerous studies on the potential applications of single-walled carbon nanotubes (SWCNTs) [1] in various fields including the development of novel organic electronic materials, chemical sensors, and vehicles for organ-specific drug delivery and other therapeutic processes have been carried out [2–10]. Noncovalent interactions of small molecules and SWCNTs are pivotal to many of these applications [11–13].
The ultimate exploiting the noncovalent functionalization of SWCNTs will require detailed information on the factors that affect these interactions. Therefore, many experimentalists and theorists have examined noncovalent interactions of small molecules with the exterior walls of SWCNTs and the encapsulation of molecules inside SWCNTs [14–16]. Among these molecules, one of the most important is hydrogen. Hydrogen is a perfect alternative energy source. It is abundant in nature, has low environmental effects, and finally, its combustion produces only water and heat. Recently, the scientific efforts have been focused on finding the efficient, safe, and cheap method to store hydrogen for the possible usage in large-scale applications [17–20]. There are different technologies for hydrogen storage such as liquefaction, metal hybrids, and physisorption. An effective method of keeping is relied on both the ability to simply place hydrogen in the “tank” and the facility to release it for potential use. From this point of view, it is worth studying SWCNTs, hollow nanocontainers, to ascertain whether it is possible to use them efficiently for hydrogen storage. Although some papers study hydrogen adsorption onto outer walls of SWCNTs [21], lead(II)- and aluminium-based metal-organic framework [22, 23], and boron nitride nanotubes [24], there is only one paper, to the best of our knowledge, which studies hydrogen confined into carbon nanotubes with very small diameters [25]. Thus, there exists a demand to study interactions of hydrogen molecules and interior surfaces of SWCNTs of various diameters.
Inspired by the above considerations, in this paper, we quantify the noncovalent interactions between hydrogen molecules and the inner walls of SWCNTs as well as graphene by techniques based on the dispersion-corrected density functional theory (DFT-D3), which has been successfully applied to predict adsorption properties of many systems with high reliability and low computational efforts [26–28].
2. Computational Methods
All calculations were carried out using Orca 3.0.3 program package [29]. The dispersion-corrected (as proposed by Grimme) GGA PBE-D3 functional [30–32] together with the SVP basis set [33] was employed. This functional has been demonstrated to be reliable and commonly used in the studies of adsorption phenomena [34, 35]. We consider various armchair nanotubes as models of (n,n) SWCNTs, n = 3–8. The following models of SWCNTs are used: C48H12 (3,3), C64H16 (4,4), C80H20 (5,5), C96H24 (6,6), C112H28 (7,7), and C138H32 (8,8). It was earlier predicted that the (2,2) armchair SWCNT is the carbon nanotube with the smallest possible diameter of 3 Å [36]. However, that type of nanotubes was formed inside a MWCNT of a larger diameter. Therefore, in this study, we use the (3,3) model as the smallest one as predicted in [37]. The coronene molecule (C24H12) is adopted as a graphene model system (Figure 1). It was stated that coronene is the smallest molecule that resembles the properties of graphene [38].
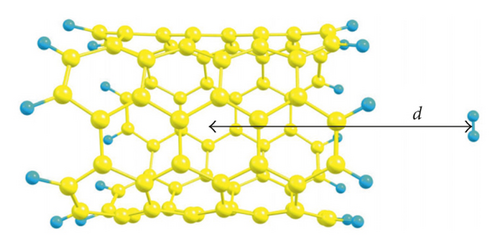
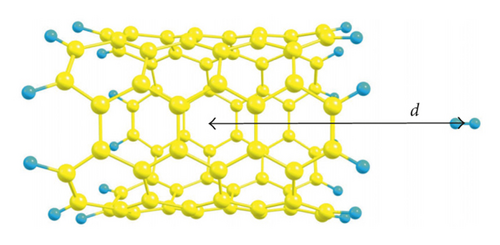
3. Results and Discussions
3.1. Introduction of a Hydrogen Molecule inside a Series of SWCNTs
In order to understand the fundamental interactions between hydrogen molecules and SWCNTs, we introduce a single H2 molecule inside a series of nanotubes with different diameters (from 4.140 to 10.907 Å) to have the opportunity to point out all phenomena that appear inside SWCNTs of small and large diameters. For this aim, we theoretically study a step-by-step insertion of a hydrogen molecule along the nanotube axis in two orientations relative to the axis (parallel and perpendicular ones), using PBE-D3 (Figure 1). Here, we (1) quantify the energetics for the entry of hydrogen into SWCNTs under study to figure out the possibility of SWCNTs loading as well as the feasibility of formation of endohedral complexes, (2) evaluate the noncovalent interactions between hydrogen molecules and inner walls of SWCNTs as well as graphene, and (3) show the differences in H2 behavior upon interactions with SWCNTs of various diameters.
The interaction energies (Ei,m) as a function of distance (d) from the center of studied SWCNTs to the center of mass of a hydrogen molecule are plotted for the two aforementioned orientations (Figure 1). The d value of zero corresponds to the center of a SWCNT. For the (3,3) and (4,4) SWCNTs, we can see that there exists an entry barrier for an H2 encapsulation in either orientation. The d of 7 Å for the (3,3) SWCNT and 6.5 Å for (4,4) SWCNT corresponds to the local minima caused by the van der Waals interactions between hydrogen and SWCNTs. As is expected, the energy barrier for the hydrogen introduction is larger for the (3,3) SWCNT which has lower diameter compared with the (4,4) counterpart. For (3,3) and (4,4) SWCNTs, at the distances from 0 to 5 Å (i.e., inside the SWCNTs), one can see the oscillations of Ei,m values. As a whole, the orientation of an H2 molecule parallel with the axis of (3,3) and (4,4) SWCNTs is more energetically favorable (Figure 2). For the larger SWCNTs, the entering of H2 is a barrier-free one (Figure 2) for either orientation.
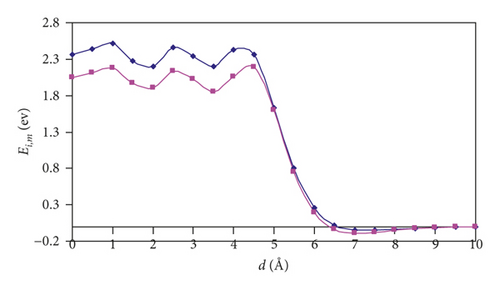
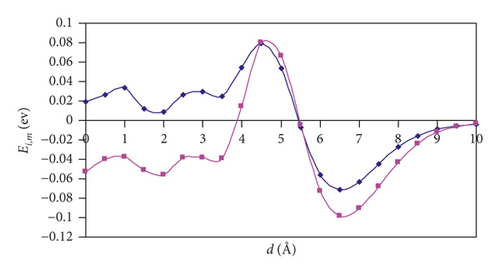
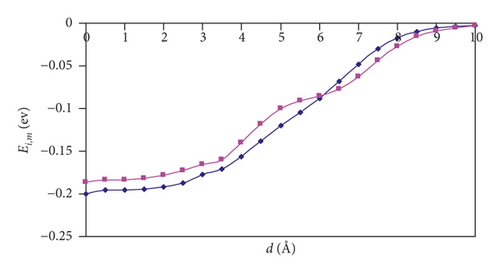
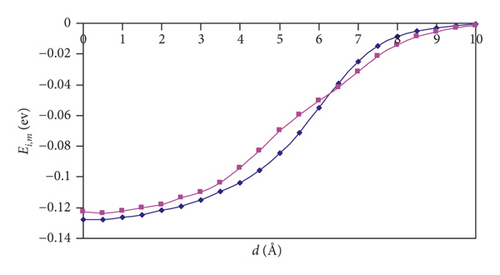
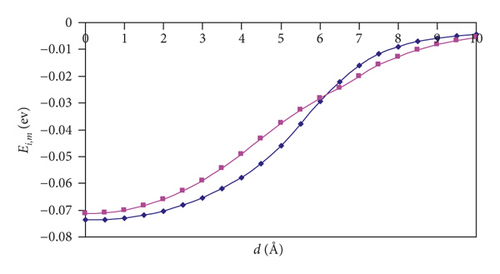
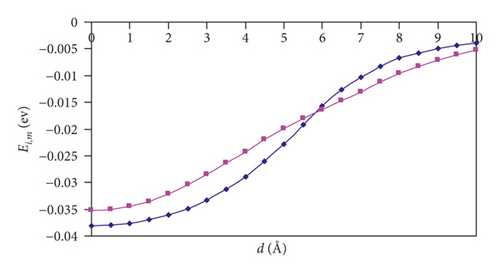
For (n,n) SWCNTs (n = 5–8), the Ei,m versus d graphs adopt the “S-shape” character, and we can see that, for the parallel orientation of an H2 molecule, the curve acquires a more slanted shape than for the perpendicular orientation. At a distance of 6 Å, there is a point of intersection of the two curves. Thus, one can observe the interesting feature: namely, the hydrogen approaching the nanotubes is more favorable in the parallel orientation, and the introduction is more favorable in the perpendicular orientation.
3.2. Endohedral Complexes of Hydrogen with SWCNTs and Graphene
Table 1 lists predicted binding and interaction energies as well as equilibrium distances between H2 and SWCNTs (or graphene).
There is no sufficient internal space in the smallest considered SWCNTs, (3,3) and (4,4), to effectively adsorb hydrogen molecules. Therefore, Eb values are considerably less favorable than those for SWCNTs of larger diameters (Table 1). The R values of 2.00 and 2.75 Å for the parallel orientation of H2 in (3,3) and (4,4) SWCNTs, respectively, are much smaller than those for larger SWCNTs and graphene. The H–H bond lengths in the hydrogen molecule disturbed significantly on H2 introduction into (3,3) and (4,4) SWCNTs. Thus, for example, for the H2 molecule which is perpendicularly introduced into (3,3) SWCNT, the changes in the H–H bond length are of 0.04 Å (5 per cent), whereas for the in-parallel introduced molecule, the variation is of 0.02 Å (2.5 per cent). For (5,5)–(8,8) SWCNTs, there are no such large deviations. For (4,4) SWCNT, the parallel orientation of H2 is more energetically favorable than the perpendicular one, although the binding is weak. The reverse situation can be observed for larger SWCNT, where the perpendicular orientations become energy minima. Again, for (8,8) SWCNT, the parallel orientation is more favorable. However, the two orientations are of almost equal energies, and it is possible they both exist.
| System | Parallel orientation | Perpendicular orientation | ||||
|---|---|---|---|---|---|---|
| Eb | Ei | R1 | Eb | Ei | R | |
| (3,3) SWCNT | 1.906 | 2.048 | 2.00 | 2.149 | 2.360 | 2.00 |
| (4,4) SWCNT | −0.057 | −0.053 | 2.75 | 0.010 | 0.019 | 2.78 |
| (5,5) SWCNT | −0.195 | −0.187 | 3.05 | −0.199 | −0.200 | 3.28 |
| (6,6) SWCNT | −0.135 | −0.123 | 3.07 | −0.141 | −0.128 | 3.04 |
| (7,7) SWCNT | −0.110 | −0.071 | 3.06 | −0.113 | −0.074 | 3.05 |
| (8,8) SWCNT | −0.077 | −0.035 | 3.54 | −0.076 | −0.038 | 3.62 |
| Graphene | −0.066 | −0.067 | 3.10 | —2 | −0.068 | 3.10 |
- 1The equilibrium distances (R) are measured between an H2 molecule and the closest wall of a SWCNT; 2for graphene, there is only one value of Eb as the initial parallel and perpendicular orientations converge to one equilibrium configuration.
As a whole, one may observe the increase in Eb on going from (3,3) to (5,5) SWCNTs and the following decrease on going from (5,5) to (8,8) SWCNTs, with the maximal Eb of −0.195 (parallel orientation) and −0.199 eV (perpendicular orientation) (Table 1). It can be explained by the very small diameters of the (3,3) and (4,4) SWCNTs which complicate the introduction of hydrogen. Eb is unfavorable for the perpendicular orientation of H2 even in the case of (4,4). The larger tubes provide more space for H2 molecules to introduce into and adsorb onto the internal walls of SWCNTs. Besides this, (5,5) SWCNT represents the best diameter/number of neighbor carbon atoms ratio. Indeed, the comprehensive work of Okamoto and Miyamoto [39] showed that the Eb values depend significantly on the carbon nanotubes’ curvature or, in other words, on the number of neighbor carbon atoms. The ease of the H2 introduction into SWCNTs of large diameters is accompanied by the gradual decline in Eb. The observed trends in Eb changes were also found in the paper of Munusamy and Wheeler [14] on substituted benzenes and in works of Tournus et al. [15, 16] on benzene. Finally, the Eb values for (8,8) SWCNT, which has the largest diameters and the smallest curvature among studied nanotubes, approach to the values for graphene.
In terms of practical applications, we propose to utilize a number of uniform SWCNTs for hydrogen storage. The methods of the scalable synthesis and separation of SWCNTs can be found elsewhere [40, 41]. Compared with flat graphene-based materials for H2 storage, the (5,5) and (6,6) SWCNTs have the improved Eb values. Therefore, these nanotubes require comparatively low pressures to achieve a reasonable storage capacity. The usage of the uniform materials can promote the hydrogen uptake and thus modify the relatively harsh operation mode of existing carbon-based hydrogen storage systems. Our predictions can be used as a guiding reference in employment of high-capacity hydrogen storage materials based on SWCNTs for practical usage.
4. Conclusions
We have examined the introduction of hydrogen molecules into SWCNTs, calculated Eb and Ei values of H2/SWCNT complexes, and compared the results with those on graphene. Overall, we reached the following four main conclusions: (i) Hydrogen interacts stronger with the inside of SWCNTs than with graphene. Moreover, for all but the smallest nanotubes, there is a barrier-free energy pathway for formation of these endohedral complexes. (ii) For small (3,3) and (4,4) SWCNTs, Eb values are unfavorable owing to very small diameters of these nanotubes; besides this, there are strong interactions between the walls of SWCNTs and hydrogen molecules affecting H–H bonds. (iii) SWCNTs of middle diameters ((6,6) and especially (5,5) SWCNTs) are the most effective ones in terms of hydrogen storage. (iv) For larger SWCNTs, which have smaller curvatures, the Eb values approach to those for graphene.
Conflicts of Interest
The author declares that there are no conflicts of interest.
Acknowledgments
This work was partially supported by the base part of the Government Assignment for Scientific Research from the Ministry of Education and Science of Russia (project code: 13.7232.2017/8.9). The author thanks the joint center “Baikal Center of Nanotechnologies” for its facilities.




