Volume 2018, Issue 1 9769150

Research Article

Open Access

A New Method of Hypothesis Test for Truncated Spline Nonparametric Regression Influenced by Spatial Heterogeneity and Application

Sifriyani

orcid.org/0000-0002-4616-775X

Department of Mathematics, Faculty of Mathematics and Natural Sciences, Mulawarman University, Samarinda, Indonesia unmul.ac.id

Search for more papers by this author

I. N. Budiantara,

Corresponding Author

I. N. Budiantara

[email protected]

orcid.org/0000-0001-6572-4083

Department of Statistics, Faculty of Mathematics, Computing and Data Sciences, Sepuluh Nopember Institute of Technology, Surabaya, Indonesia its.ac.id

Search for more papers by this author

S. H. Kartiko,

S. H. Kartiko

Department of Mathematics, Faculty of Mathematics and Natural Sciences, Gadjah Mada University, Yogyakarta, Indonesia ugm.ac.id

Search for more papers by this author

Gunardi,

Gunardi

Department of Mathematics, Faculty of Mathematics and Natural Sciences, Gadjah Mada University, Yogyakarta, Indonesia ugm.ac.id

Search for more papers by this author

Sifriyani,

Sifriyani

orcid.org/0000-0002-4616-775X

Department of Mathematics, Faculty of Mathematics and Natural Sciences, Mulawarman University, Samarinda, Indonesia unmul.ac.id

Search for more papers by this author

I. N. Budiantara,

Corresponding Author

I. N. Budiantara

[email protected]

orcid.org/0000-0001-6572-4083

Department of Statistics, Faculty of Mathematics, Computing and Data Sciences, Sepuluh Nopember Institute of Technology, Surabaya, Indonesia its.ac.id

Search for more papers by this author

S. H. Kartiko,

S. H. Kartiko

Department of Mathematics, Faculty of Mathematics and Natural Sciences, Gadjah Mada University, Yogyakarta, Indonesia ugm.ac.id

Search for more papers by this author

Gunardi,

Gunardi

Department of Mathematics, Faculty of Mathematics and Natural Sciences, Gadjah Mada University, Yogyakarta, Indonesia ugm.ac.id

Search for more papers by this author

First published: 12 September 2018

https://doi.org/10.1155/2018/9769150

Citations: 12

Academic Editor: Giovanni P. Galdi

Share a link

Email
Wechat
Bluesky

Abstract

This study developed a new method of hypothesis testing of model conformity between truncated spline nonparametric regression influenced by spatial heterogeneity and truncated spline nonparametric regression. This hypothesis test aims to determine the most appropriate model used in the analysis of spatial data. The test statistic for model conformity hypothesis testing was constructed based on the likelihood ratio of the parameter set under H₀ whose components consisted of parameters that were not influenced by the geographical factor and the set under the population parameter whose components consisted of parameters influenced by the geographical factor. We have proven the distribution of test statistics V and verified that each of the numerators and denominators in the statistic test V followed a distribution of χ². Since there was a symmetric and idempotent matrix S, it could be proved that . Matrix D(u_i, v_i) was positive semidefinite and contained weighting matrix W(u_i, v_i) which had different values in every location; therefore matrix D(u_i, v_i) was not idempotent. If and D(u_i, v_i) was not idempotent and also was a N(0, I) distributed random vector, then there were constants k and r; hence ; therefore it was concluded that test statistic V followed an F distribution. The modeling is implemented to find factors that influence the unemployment rate in 38 areas in Java in Indonesia.

1. Introduction

This study examines theoretically the multivariate nonparametric regression influenced by spatial heterogeneity with truncated spline approach. The model is the development of truncated spline nonparametric regression that takes into account geographic or spatial factors. Truncated spline is a function constructed on the basis of polynomial components and truncated components; i.e., polynomial pieces that have knot points, which can overcome the pattern of changes in data behavior. Truncated spline approach is used as a solution to solve the problem of spatial data analysis modeling; that is, the relationship between the response variable and the predictor variable does not follow a certain pattern and there is a changing pattern in certain subintervals. The response variable in the model contains the predictor variables whose respective regression coefficients depend on the location where the data is observed, due to differences in environmental and geographic characteristics between the observation sites; therefore each observation has different variations (spatial heterogeneity). Spatial is one type of dependent data, where data at a location is influenced by the measurement of data at another location (spatial dependency).

This study determines the model conformity hypothesis test between multivariable nonparametric regression that is influenced by spatial heterogeneity with truncated spline approach and multivariable nonparametric regression in general. This hypothesis test aims to determine the model that is most suitable for spatial data analysis. The test statistic was derived using the maximum likelihood ratio test (MLRT) method. The first step in this study was formulating the hypothesis to be tested and then defining the set of parameters under H₀ whose components consist of parameters that are not influenced by geographical factors and the set under population parameters whose components consist of parameters influenced by geographical factors. Likelihood ratio Λ was constructed based on the maximum ratio of the likelihood function under H₀ as the numerator and set under the population as a denominator. Based on the likelihood ratio test statistic V was obtained. Furthermore, the distribution of test statistic V was determined. To prove the distribution of test statistic V, we first proved that each numerator and denominator are chi square distributed.

The purpose of this study is to obtain a new method for the determination of hypothesis test of model conformity between multivariate nonparametric truncated spline regression influenced by spatial heterogeneity versus multivariate nonparametric truncated spline regression in general. This hypothesis test aims to determine what model is most suitable for spatial data analysis.

2. Truncated Spline Nonparametric Regression Influenced by Heterogeneity Spatial

Truncated spline nonparametric regression influenced by spatial heterogeneity is the development of nonparametric regression for spatial data with parameter estimators local to each location of observation. Truncated spline approach is used to solve spatial analysis problems whose regression curve is unknown [1]. The assumption of the regression model used is the normal distributed error with mean zero and variance σ²(u_i, v_i) at each location (u_i, v_i). Location coordinates (u_i, v_i) are an important factor in determining the weights used to estimate the parameters of the model. Given data (x_1i, x_2i, …, x_li, y_i) and relationship between (x_1i, x_2i, …, x_li) and y_i, it is assumed to follow multivariate nonparametric regression model as follows:

(1)

y_i is response variable and f(x_1i, x_2i, …, x_li) is unknown regression curve and assumed to be additive. If f(x_1i, x_2i, …, x_li) is approached with a truncated spline function. Mathematically, the relation between response variable y_i and the predictor variable (x_1i, x_2i, …, x_li) at i-th location for the multivariate nonparametric truncated spline regression model can be expressed as follows [2]:

(2)

with truncated function:

(3)

Equation (2) is a multivariate nonparametric truncated spline regression model of degree m with n area. The components in (2) are described as follows:

y_i is a response variable at i-th location, where i = 1,2, …, n.

x_pi is a p-th predictor variable at i-th location with p = 1,2, …, l.

K_ph is an h-th knot point in p-th predictor variable component with h = 1,2, …, r.

β_pk(u_i, v_i) is a polynomial component parameter of a multivariate nonparametric truncated spline regression. β_pk(u_i, v_i) is a k-th parameter from p-th predictor variable at i-th location. δ_p,m+h(u_i, v_i) is a truncated component from multivariate nonparametric truncated spline regression. δ_p,m+h(u_i, v_i) is an l + h-th parameter in h-th knot point and p-th predictor variable at i-th location.

Multivariate nonparametric truncated spline regression in (2) is described as follows:

(4)

Equation (4) can also be expressed as follows:

(5)

Thus (5) can be expressed by

(6)

whose vector

contains of truncated spline function with geographical weighting sized n × 1; response variable and error, respectively, are given by vectors as follows:

(7)

Vectors

and

are, respectively, sized n × 1.

Meanwhile matrices X and P are, respectively, given by

(8)

Vectors

and

are, respectively, given by

(9)

Matrix X is sized n × (1 + lm); matrix P contains predictor variable of truncated function sized n × lr. Vector

is a parameter vector sized (1 + lm) × 1. Vector

is a parameter vector containing truncated function sized lr × 1. The estimator forms

, and

are complete in Theorem 1 and Corollary 2 [2].

Theorem 1. If the regression model (2) with an error ε_i normally distributed with zero mean and variance σ²(u_i, v_i) was given Maximum Likelihood Estimator (MLE), it is used to obtain estimator and as follows.

(10)

where

(11)

Corollary 2. If and are given by Theorem 1, then the estimator for the regression curve is given by

(12)

where

(13)

Estimator of regression curve contains the polynomial components represented by matrix X and truncated components represented by matrix P [3]. If the matrix P = 0, then the estimator multivariable of nonparametric regression curve in the Geographically Weighted Regression (GWR) models with truncated spline approach, , will change to estimator polynomial parametric regression curve in the GWR model. Furthermore, if P = 0 and matrix X contains a linear function, the estimator of the multivariable spline nonparametric regression curve in the GWR model, , will change to estimator of linear parametric regression curves in the GWR model or multiple linear regression in the GWR model developed by many researchers such as Brusdon and Fotheringham [4], Fotheringham, Brunsdon, and Charlton (2003), Demsar, Fotheringham, and Charlton [5], Yan Li, Yan Jiao, and Joan A. Browder [6], Shan-shan Wu, Hao Yang, Fei Guo, and Rui -Ming Han [7], and Benassi and Naccarato [8].

This study continued the previous research [2]; in this study the test statistics that will be used in the truncated spline nonparametric regression influenced by spatial heterogeneity modeling will be found; further research continued the distribution of test statistics and rejection areas.

3. Method

The hypothesis test for model conformity between multivariate nonparametric truncated spline regression influenced by spatial heterogeneity with nonparametric truncated spline regression is derived.

Step 1. Formulating hypothetical model:

H₀: β_pk(u_i, v_i) = β_pk and δ_p,m+h(u_i, v_i) = δ_p,m+h,
- p = 1,2, …, l; k = 1,2, …, m; h = 1,2, …, r; i = 1,2, …, n
H₁: at least, there is one of β_pk(u_i, v_i) ≠ β_pk or δ_pm+h(u_i, v_i) ≠ δ_p,m+h,
- p = 1,2, …, l; k = 1,2, …, m; h = 1,2, …, r; i = 1,2, …, n.

Step 2. Defining the set of parameters under population Ω.

Step 3. Determining estimators and which are parameters in the space under population (Ω).

Step 4. Obtaining maximum likelihood function under population (Ω).

Step 5. Defining parameter space under H₀, i.e., ω.

Step 6. Determining estimators and which are parameters under H₀.

Step 7. Obtaining maximum likelihood function under space H₀.

Step 8. Obtaining likelihood ratio Λ.

Step 9. Obtaining test statistic V from model conformity testing.

Step 10. Specifying the distribution of numerator τ from test statistic V.

Step 11. Specifying the distribution of denominator τ^∗ from test statistic V.

Step 12. Specifying the distribution of test statistic V.

Step 13. Deciding the rejection area of H₀ and writing the conclusion.

4. Parameter Estimation under Space H₀ and Space Population in the Model

A hypothesis testing of model conformity for nonparametric spline regression with spatial heterogeneity was designed by using hypothesis formulation:

H₀: β_pk(u_i, v_i) = β_pk and δ_p,m+h(u_i, v_i) = δ_p,m+h,
H₁: at least, there is one of β_pk(u_i, v_i) ≠ β_pk or δ_pm+h(u_i, v_i) ≠ δ_p,m+h.

This hypothesis test was derived using maximum likelihood ratio test method by defining the parameter spaces under H₀(ω) and under population (Ω). The parameter space under H₀(ω) is given by

(14)

where

(15)

While the parameter space under the population (Ω) is given by

(16)

Obtaining the test statistic of hypothesis above required some lemmas as follows.

Lemma 3. If is a parameter under population (Ω) from nonparametric spline regression with spatial heterogeneity (2), then estimator is given by

(17)

Proof. To obtain estimator we form likelihood function under population parameter space L(Ω). Therefore y_i has normal distribution with mean

(18)

and variance

; then probability functions y₁, y₂, …, y_n are given by

(19)

Obtained likelihood function is as follows:

(20)

Equation (20) in matrix form is

(21)

Estimator

is obtained on the basis of the following derivative results:

(22)

Then the following is obtained:

(23)

Therefore,

(24)

Furthermore, estimator is shown in Lemma 4.

Lemma 4. If is a parameter in space under population (Ω) from nonparametric spline regression with spatial heterogeneity spatial (2), then estimator which is obtained from likelihood function:

(25)

is given by

(26)

Proof. Estimator is obtained using likelihood function:

(27)

The ln likelihood function is given by

(28)

Furthermore, estimator

is obtained on the basis of the following derivative results:

(29)

Then the following was obtained:

(30)

Therefore,

(31)

Based on estimators

and

which are given by Lemmas 3 and 4 the following is obtained:

(32)

Lemma 5. If and are parameters under H₀ from multivariate nonparametric truncated spline influenced by spatial heterogeneity model (2), then estimator for is given by

(33)

and estimator for

is given by

(34)

Proof. To obtain estimators and we form likelihood function under parameter space H₀L(ω). Therefore y_i has normal distribution with mean

(35)

and variance

; then probability functions y₁, y₂, …, y_n are given by

(36)

The following likelihood functions were obtained:

(37)

The equation is in the form of a matrix

(38)

Estimators

and

are obtained:

(39)

Based on Lemma 5, maximum likelihood function is obtained as follows:

(40)

and

are parameters estimator of under H₀ from multivariate nonparametric regression with truncated spline approach.

5. Statistics Test for Truncated Spline Nonparametric Regression with Spatial Heterogeneity

The test statistic for the model conformity hypothesis test can be obtained by using Lemmas 3, 4, and 5. In the next step, we show the likelihood ratio for test statistic presented in Lemma 6.

Lemma 6. If and , respectively, are given by (32) and (40), then the likelihood ratio Λ is given by

(41)

where

(42)

Proof. Based on Lemmas 3, 4, and 5, and also (32) and (40), the likelihood ratio is obtained:

(43)

Based on (3) and (5), the likelihood ratio

(44)

Given test statistic for model conformity hypothesis is presented by Theorem 7.

Theorem 7. If likelihood ratio Λ is given by Lemma 6, then test statistic for H₀ versus H₁ in (2) is given by

(45)

Proof. Based on Lemma 6, the likelihood ratio is as follows:

(46)

Based on MLRT method, H₀ is rejected if

(47)

For a constant c, (43) is equivalent to

(48)

In the two sections of the inequality above, each numerator is divided by n − lm − 1 and each denominator is divided by tr((I − ξ)^T(I − ξ)); then the following inequality is obtained:

(49)

Based on (44), the test statistic for H₀ versus H₁ is given by

(50)

Furthermore, the distribution of statistics test V will be found.

The statistics test given in Theorem 7 is test statistics developed from the spline truncated approach in the GWR model, different from the one developed by Leung, Mei, and Zhang [9], Leung, Mei, and Zhang [10], and Mennis and Jordan [11] using GWR without using the Truncated Spine approach.

6. Distribution of Test Statistic and Critical Area of Hypothesis

To prove the distribution of test statistic V, we first prove and . The proofs are presented in Theorems 8 and 9 as follows.

Theorem 8. If S is a matrix given by Lemma 6 then statistic is

(51)

Proof. To prove this Lemma, the following steps are taken.

Matrix S is shown which is a symmetric and idempotent matrix as follows:

(52)

Based on equation above, it is proved that matrix S is symmetric.

(53)

It is proved that matrix S is idempotent. Furthermore, tr(S) is calculated as follows:

(54)

Therefore, it is proved that

(55)

Theorem 9. If D(u_i, v_i) is a matrix given by Lemma 6 then statistic is

(56)

Proof. Based on (24), we obtain

(57)

And estimator is obtained:

(58)

in which

(59)

Further, error vector is given as follows:

(60)

Sum Square of Error (SSE) of model is obtained by squaring the following error vectors:

(61)

Furthermore,

(62)

Since SSE is a quadratic form from random variable:

(63)

hence, matrix (I − ξ)^T(I − ξ) is positive semidefinite but not idempotent. Next, we obtain

(64)

Since

, hence

, and since matrix (I − ξ)^T(I − ξ) is not idempotent, the distribution of statistic is

(65)

For constants k and r, based on (55), we obtain

(66)

Since (I − ξ)^T(I − ξ) is symmetric and positive semidefinite, hence there is an orthogonal matrix Θ; therefore,

(67)

Λ is a diagonal matrix in which λ₁, λ₂, …, λ_n are eigenvalues from matrix (I − ξ)^T(I − ξ). Hence

(68)

in which

. Random variables

are independent, identical, and normal distributed; therefore

(69)

with mean 1 and variance 2; therefore

(70)

Since

(71)

Hence the values of k and r are as follows:

and

; as a result,

(72)

Hence

(73)

Corollary 10. If statistic V is given by Theorem 7, then

(74)

Proof. Based on Theorem 8, statistic is obtained:

(75)

Based on Theorem 9, statistic is obtained:

(76)

Hence

(77)

The critical area for the model conformity hypothesis is derived which is given by Lemma 11.

Lemma 11. If given test statistic V is as in Theorem 7, then the critical area for H₀ is given by

(78)

A constant c is obtained according to

(79)

in which α is a determined level of significance and

(80)

Proof. Based on Theorem 7, the following relationship is obtained:

(81)

for a constant c^∗. According to Corollary 10, statistic is obtained:

(82)

for a level of significance α given by H₀ which is rejected if

(83)

After finding the hypothesis test formulation, the suitability of the model between the truncated spline nonparametric regression model which is influenced by spatial heterogeneity and nonparametric regression (global) will then be implemented on unemployment rate data in 38 regions in Java Indonesia.

7. Empirical Study on Unemployment Rate in Java Indonesia

7.1. Description of Research Data

In this study, the nonparametric truncated spline regression model influenced by spatial heterogeneity was applied to Open Unemployment Rate (OUR) data in province of Java, Indonesia, and some predictor variables that were suspected to affect it, i.e., population density (X₁), percentage of the poor (X₂), percentage of population with low education (X₃), percentage of population working in agriculture sector (X₄), area of agricultural land (X₅), economic growth rate (X₆), regional minimum wage (X₇), and ratio number of large industries being number of labor force (X₈). The amount of data used is 382 from 38 provinces and 8 predictor variables. Table 1 shows the description of our research data and the predictor variables.

Table 1. Description of our research data and the predictor variables.

Variable	Data	Minimum	Maximum	Rata-rata	Standard Deviation
Y	38	0,61	8,59	4,3939	1,81385
X₁	38	4,59	25,80	12,0963	4,99263
X₂	38	0,2105	7,6445	2,631579	1,6160512
X₃	38	0,07	7,19	5,5747	1,22772
X₄	38	35,10	33.548,70	3.378,7658	6.497,23435
X₅	38	851582	2507632	1516816.21	420415.074
X₆	38	0,0074281	0,1640892	0,052024430	0,0474488599
X₇	38	0,0405726	12,4704588	2,631578947	2,8535682531
X₈	38	474	85122	28730,32	22372,865

Source: BPS (2017a, 2017b, and 2017c).

The spread of Open Unemployment Rate in East Java is shown by Figure 1. It shows the percentage of East Java unemployment rate in 2015.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Open Unemployment Mapping in province of Java, Indonesia.

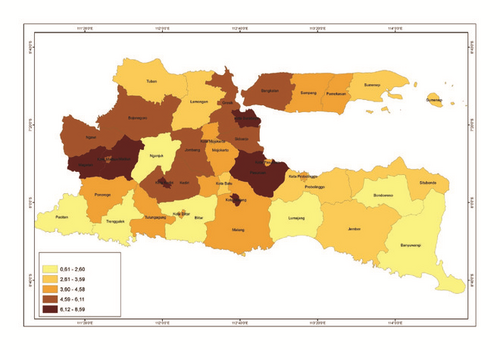
7.2. Spatial Heterogeneity Test

Each region has different characteristics and different parameters, as well as different functional forms; this is what proves spatial aspect. Breusch-Pagan testing is used to see the spatial heterogeneity of each location. Table 2 shows the Breusch-Pagan test.

Table 2. Breusch-Pagan test.

Test	Significance Value	Decision
Breusch-Pagan	0.002414	Reject H₀

Since spatial effect testing is fulfilled, i.e., there are effects of spatial heterogeneity, then the case can be solved by using the point approach. Furthermore, an analysis was performed using nonparametric truncated spline regression model influenced by spatial heterogeneity.

7.3. Model Conformity Test

Hypotheses for model conformity test between multivariate nonparametric truncated spline regression model influenced by heterogeneity spatial and multivariate nonparametric truncated spline regression model (global) are as follows:

H₀: β_pk(u_i, v_i) = β_pk and δ_p,m+h(u_i, v_i) = δ_p,m+h,
- p = 1,2, …, 8; k = 1; h = 1,2, 3; i = 1,2, …, 38
H₁: at least, there is one of β_pk(u_i, v_i) ≠ β_pk or δ_pm+h(u_i, v_i) ≠ δ_p,m+h,
- p = 1,2, …, 8; k = 1; h = 1,2, 3; i = 1,2, …, 38

The test statistic is given by Theorem 7 as follows:

(84)

Matrix S was constructed by multivariate nonparametric truncated spline. Matrix D(u_i, v_i) was constructed by multivariate nonparametric truncated spline regression. Hence, the numerator is obtained:

(85)

with degree of freedom n − lm − 1 = 29. Meanwhile the denominator is obtained:

(86)

with degree of freedom tr((I − ξ)^T(I − ξ)) = 27,0762. Test statistic V = 2,06 with level of significance α = 0,05 was obtained and concluded to reject H₀ since V > F_{(0,05; 29,27)} = 1,88. Therefore, there is a significant difference between multivariate nonparametric truncated spline regression influenced by spatial heterogeneity and nonparametric truncated spline regression. Due to the influence of geographical factors on the model, the appropriate model used is multivariate nonparametric truncated spline regression influenced by spatial heterogeneity.

The modeling application used Open Unemployment Rate (OUR) data in 38 districts/cities in East Java. The results of the empirical study showed that the OUR data has a geographical influence, namely, spatial heterogeneity, and based on the results of the model conformity hypothesis test, the appropriate model used is a multivariable nonparametric truncated spline regression model influenced by spatial heterogeneity with the weighted Gaussian kernel function. The modeling produced a coefficient of determination of 80.42%.

8. Conclusion

Multivariate nonparametric regression with truncated spline approach influenced by spatial heterogeneity is given as follows:

(87)

Based on the results of the discussion and data analysis, some conclusions can be drawn as follows:

(1)
The hypotheses for model conformity between multivariate nonparametric truncated spline regression model influenced by spatial heterogeneity and nonparametric truncated spline regression (global) are as follows:
- H₀: β_pk(u_i, v_i) = β_pk and δ_p,m+h(u_i, v_i) = δ_p,m+h,
  - p = 1,2, …, l; k = 1,2, …, m;h = 1,2, …, r; i = 1,2, …, n
- H₁: at least, there is one of β_pk(u_i, v_i) ≠ β_pk or δ_pm+h(u_i, v_i) ≠ δ_p,m+h,
  - p = 1,2, …, l; k = 1,2, …, m;h = 1,2, …, r; i = 1,2, …, n
Test statistic derived using Maximum Likelihood Ratio Test (MLRT) is obtained as follows:
(88)
(2)
The distribution of multivariate nonparametric truncated spline regression model influenced by spatial heterogeneity is as follows:
(89)
with level of significance α; therefore H₀ is rejected if
(90)

Conflicts of Interest

The authors of this work declare that there are no conflicts of interest regarding the publication of this paper.

Acknowledgments

The authors thank The Ministry of Research, Technology and Higher Education, Republic of Indonesia/Kementerian Riset, Teknologi dan Pendidikan Tinggi Republik Indonesia (Kemenristekdikti RI) for funding this work.

Open Research

Data Availability

The data of 38 districts/cities in East Java used to support the findings of this study have been deposited in https://www.bps.go.id/.

References

1 Sifriyani, Haryatmi, Budiantara I. N., and Gunardi, Geographically weighted regression with spline approach, Far East Journal of Mathematical Sciences. (2017) 101, no. 6, 1183–1196, https://doi.org/10.17654/MS101061183, 2-s2.0-85015967548.
10.17654/MS101061183
Google Scholar
2 Sifriyani, Sri Haryatmi Kartiko, Nyoman Budiantara I., and Gunardi, Development of nonparametric geographically weighted regression using truncated spline approach, Songklanakarin Journal of Science and Technology. (2018) 40, no. 4, 909–920.
Google Scholar
3 Sifriyani, Multivariable Nonparametric Regression Truncated Spline in the Geographically Weighted Regression Models, [Dissertation], 2018, Universitas Gadjah Mada.
Google Scholar
4 Brunsdon C., Fotheringham A. S., and Charlton M., Some notes on parametric significance tests for geographically weighted regression, Journal of Regional Science. (1999) 39, no. 3, 497–524, 2-s2.0-0000722130, https://doi.org/10.1111/0022-4146.00146.
10.1111/0022-4146.00146
Web of Science® Google Scholar
5 Demšar U., Fotheringham A. S., and Charlton M., Exploring the spatio-temporal dynamics of geographical processes with geographically weighted regression and geovisual analytics, Information Visualization. (2008) 7, no. 3-4, 181–197, https://doi.org/10.1057/PALGRAVE.IVS.9500187.
10.1057/PALGRAVE.IVS.9500187
Web of Science® Google Scholar
6 Li Y., Jiao Y., and Browder J. A., Modeling spatially-varying ecological relationships using geographically weighted generalized linear model: A simulation study based on longline seabird bycatch, Fisheries Research. (2016) 181, 14–24, 2-s2.0-84962732587, https://doi.org/10.1016/j.fishres.2016.03.024.
10.1016/j.fishres.2016.03.024
Web of Science® Google Scholar
7 Wu S.-S., Yang H., Guo F., and Han R.-M., Spatial patterns and origins of heavy metals in Sheyang River catchment in Jiangsu, China based on geographically weighted regression, Science of the Total Environment. (2017) 580, 1518–1529, 2-s2.0-85009423243, https://doi.org/10.1016/j.scitotenv.2016.12.137.
10.1016/j.scitotenv.2016.12.137
CAS PubMed Web of Science® Google Scholar
8 Benassi F. and Naccarato A., Households in potential economic distress. A geographically weighted regression model for Italy, 2001--2011, Spatial Statistics. (2017) 21, no. part B, 362–376, https://doi.org/10.1016/j.spasta.2017.03.002, MR3693949.
10.1016/j.spasta.2017.03.002
Web of Science® Google Scholar
9 Leung Y., Mei C.-L., and Zhang W.-X., Statistical tests for spatial nonstationarity based on the geographically weighted regression model, Environment and Planning A. (2000) 32, no. 1, 9–32, https://doi.org/10.1068/a3162, 2-s2.0-0034094265.
10.1068/a3162
Web of Science® Google Scholar
10 Leung Y., Mei C.-L., and Zhang W.-X., Testing for spatial autocorrelation among the errors of the geograhically weighted regression, Environment and Planning A. (2000) 32, no. 1, 871–890.
10.1068/a32117
Web of Science® Google Scholar
11 Mennis J. L. and Jordan L., The distribution of environmental equity: Exploring spatial nonstationarity in multivariate models of air toxic releases, Annals of the Association of American Geographers. (2005) 95, no. 2, 249–268, 2-s2.0-27844474193, https://doi.org/10.1111/j.1467-8306.2005.00459.x.
10.1111/j.1467-8306.2005.00459.x
Web of Science® Google Scholar

Citing Literature

All articles

A New Method of Hypothesis Test for Truncated Spline Nonparametric Regression Influenced by Spatial Heterogeneity and Application

Abstract

1. Introduction

2. Truncated Spline Nonparametric Regression Influenced by Heterogeneity Spatial

3. Method

4. Parameter Estimation under Space H₀ and Space Population in the Model

5. Statistics Test for Truncated Spline Nonparametric Regression with Spatial Heterogeneity

6. Distribution of Test Statistic and Critical Area of Hypothesis