We consider the following nonlinear parabolic equation: u_t − div(|∇u|^p(x)−2∇u) = f(x, t), where and the exponent of nonlinearity p(·) are given functions. By using a nonlinear operator theory, we prove the existence and uniqueness of weak solutions under suitable assumptions. We also give a two-dimensional numerical example to illustrate the decay of solutions.

1. Introduction

Let Ω be a bounded domain in

with a smooth boundary ∂Ω. We consider the following initial and boundary value problem:

where

and

are given functions. The exponent p(·) is a given measurable function on

such that

(1)

with

(2)

We also assume that p(·) satisfies the log-Hölder continuity condition:

(3)

where A > 0 and 0 < δ < 1 are constants. The term div(|∇u|^p(·)−2∇u) is called the p(·)-Laplacian and denoted by Δ_p(·)u.

The study of partial differential equations involving variable-exponent nonlinearities has attracted the attention of researchers in recent years. The interest in studying such problems is stimulated and motivated by their applications in elastic mechanics, fluid dynamics, nonlinear elasticity, electrorheological fluids, and so forth. In particular, parabolic equations involving the p(·)-Laplacian are related to the field of image restoration and electrorheological fluids which are characterized by their ability to change the mechanical properties under the influence of the exterior electromagnetic field. The rigorous study of these physical problems has been facilitated by the development of the Lebesgue and Sobolev spaces with variable exponents.

Regarding parabolic problems with nonlinearities of variable-exponent type, many works have appeared. We note here that most of the results deal with blow-up and global nonexistence. Let us mention some of these works. For instance, Alaoui et al. [1] considered the following nonlinear heat equation:

(4)

in a bounded domain in

(n ≥ 1) with a smooth boundary ∂Ω. Under appropriate conditions on the exponent functions m, p and for f = 0, they showed that any solution with nontrivial initial datum blows up in finite time. They also gave a two-dimensional numerical example to illustrate their result. Pinasco [2] studied the following problem:

(5)

where

is a bounded domain with a smooth boundary ∂Ω, and the source term is of the following form:

(6)

with p, q: Ω → (1, ∞) and the continuous function a:

being given functions satisfying specific conditions. They established the local existence of positive solutions and proved that solutions with initial data sufficiently large blow up in finite time. Parabolic problems with sources like the ones in (5) appear in several branches of applied mathematics and they have been used to model chemical reactions, heat transfer, or population dynamics.

Recently, Shangerganesh et al. [3] studied the following fourth-order degenerate parabolic equation:

(7)

in a bounded domain

(n ≥ 1) with a smooth boundary ∂Ω, and proved the existence and uniqueness of weak solutions of (7) by using the difference and variation methods under suitable assumptions on f, g and the exponents p.

Equation (P) is a nonlinear diffusion equation which has been used to study image restoration and electrorheological fluids (see [4–11]). In particular, Bendahmane et al. [12] proved the well-posedness of a solution, for L¹-data. Akagi and Matsuura [13] gave the well-posedness for L² initial datum and discussed the long-time behaviour of the solution using the subdifferential calculus approach. In our paper, we give an alternative proof of the well-posedness of (P) which is simpler than that in [13] using a theory of nonlinear evolution equations. In addition, we give a numerical example in 2D to illustrate the decay result obtained in [13].

This paper consists of three sections in addition to the introduction. In Section 2, we recall the definitions of the variable-exponent Lebesgue spaces, L^p(·)(Ω), the Sobolev spaces, W^1,p(·)(Ω), as well as some of their properties. We also state, without proof, a proposition to be used in the proof of our main result. In Section 3, we state and prove the well-posedness of solution to our problem. In Section 4, we give a numerical verification of the decay result.

2. Preliminaries

We present some preliminary facts about the Lebesgue and Sobolev spaces with variable exponents (see [1, 14–16]). Let p:Ω → [1, ∞] be a measurable function, where Ω is a domain of

. We define the Lebesgue space with a variable-exponent p(·) by

(8)

where

(9)

is called a modular. Equipped with the Luxembourg-type norm,

(10)

L^p(·)(Ω) is a Banach space (see [10]).

Lemma 1 (Hölder’s inequality [10]). Let p, q, s ≥ 1 be measurable functions defined on Ω such that

(11)

for a.e. y ∈ Ω. If f ∈ L^p(·)(Ω) and g ∈ L^q(·)(Ω), then fg ∈ L^s(·)(Ω) and

(12)

Lemma 2 (see [10].)Let p be a measurable function on Ω. Then,

(a)
‖f‖_p(·) ≤ 1 if and only if ϱ_p(·)(f) ≤ 1;
(b)
for f ∈ L^p(·)(Ω), if ‖f‖_p(·) ≤ 1, then ϱ_p(·)(f) ≤ ‖f‖_p(·); and if ‖f‖_p(·) ≥ 1, then ‖f‖_p(·) ≤ ϱ_p(·)(f);
(c)
‖f‖_p(·) ≤ 1 + ϱ_p(·)(f).

Lemma 3 (see [10].)If (1) holds, then

(13)

for any u ∈ L^p(·)(Ω).

We next define the variable-exponent Sobolev space W^1,p(·)(Ω) as follows:

(14)

This space is a Banach space with respect to the norm

. Furthermore,

is the closure of

in W^1,p(·)(Ω). The dual of

is defined as

, by the same way as the usual Sobolev spaces where 1/p(·) + 1/p^′(·) = 1.

Lemma 4 (see [10].)Let Ω be a bounded domain of and p(·) satisfies (1) and (3), and then

(15)

where the positive constant C depends on p(·) and Ω. In particular, the space

has an equivalent norm given by

Lemma 5 (see [10].)If , q:Ω → [1, ∞) is a continuous function and

(16)

Then the embedding

is continuous and compact.

Definition 6 (see [17].)Let V be a separable Banach space and H be a Hilbert space such that V ⊂ H ⊂ V^′ with continuous embedding and V is dense in H. Let A:V → V^′ be a nonlinear operator.

(1)
A is said to be monotone if If, in addition, we have
(17)
then A is said to be strictly monotone.
(2)
A is said to be bounded, if A(S) is bounded in V^′, whenever S is bounded in V.
(3)
A is said to be hemicontinuous, if the real function
(18)
is continuous from to , for any fixed u, v, w ∈ V.

We end this section with a proposition which is exactly like Theorem 7.1 [17].

Proposition 7. Let u₀ ∈ H and . Suppose that A: V → V^′ is a bounded monotone and hemicontinuous (nonlinear) operator satisfying, for some α, β > 0 and for some p > 1,

(19)

Then the following problem

(20)

has a unique weak solution:

(21)

where 1/p + 1/p^′ = 1.

3. Well-Posedness

In this section, we state and prove the well-posedness of our problem.

Theorem 8. Let . Assume that (1) and (3) hold. Then (P) has a unique weak solution:

(22)

where 1/p(·) + 1/p^′(·) = 1.

Proof. We verify the conditions of Proposition 7. Let , and equip it with the norm,

(23)

So,

. Define A : V → V^′ by

(24)

Boundedness of A. For all u, v ∈ V,

(25)

Hölder inequality gives

(26)

Combining (25) and (26), we obtain

(27)

Then, Lemma 2 implies

(28)

Combining (27) and (28), we arrive at

(29)

Let S ⊂ V such that ‖u‖_V ≤ M, for all u ∈ S. That is, ‖∇u‖_p(·) ≤ M.

If M ≤ 1, then Lemma 2 implies ϱ_p(·)(∇u) ≤ 1 and (29) gives .

If M > 1, then . Thus, (29) implies .

Hence A is bounded.

Monotonicity of A. Let u, v ∈ V. Then

(30)

By using the inequality,

(31)

for all

and a.e. x ∈ Ω. Thus we obtain 〈A(u) − A(v), u − v〉 ≥ 0.

Hence, A is monotone.

To verify (19), we note that, for all u ∈ V, we have

(32)

If ‖u‖_V = ‖∇u‖_p(·) > 1, then by Lemma 3, we get

(33)

Combining (32) and (33), we easily see that

(34)

If ‖u‖_V = ‖∇u‖_p(·) ≤ 1, then by Lemma 2, we obtain

(35)

Therefore, we have

(36)

Hemicontinuity of A. Let u, v, w ∈ V be fixed. Let

(37)

Let λ_k → λ (real) and consider

(38)

Since

(39)

for a.e. x ∈ Ω and

(40)

where

, then, by the classical dominated convergence theorem,

(41)

Hence, A is hemicontinuous.

Therefore, conditions of Proposition 7 are satisfied and problem (P) has a unique solution.

4. Numerical Study

In this section, we present some numerical results and applications of the problem:

which is a well-posed problem due to Theorem 8. Our objective is to provide a numerical verification of the following decay result:

Proposition 9 (see [13].)Assume that (1) and (3) hold. Then the solution of (P∗) satisfies the following:

(i)
If p₂ = 2, then there exists a constant c₂ > 0 such that
(42)
(ii)
If p₂ > 2, there exists a constant c₁ > 0 and t₁ ≥ 0 such that
(43)

We consider two applications to illustrate numerically an exponential decay for the case p(x, y) = 2 and a polynomial decay for an exponent function p(·) satisfying conditions (1)–(3).

For this purpose, we introduce a numerical scheme for (P∗), prove its convergence in Section 4.1, and show the decay results in Section 4.2.

4.1. Numerical Method

In this part, we present a linearized numerical scheme to obtain the numerical results of the system (P∗) and confirm the decay results. The system is fully discretized through a finite difference method for the time variable and a finite element Galerkin method for the space variable. Useful background about the numerical and error analysis of these methods is found in [18]. More interestingly in [19], Li and Wang introduced a numerical scheme to solve strongly nonlinear parabolic systems and proved unconditional error estimates of the scheme. Our problem (P∗) is highly nonlinear due to the presence of the gradient and nonlinear exponent in the diffusivity coefficient, which can be zero inside the spatial domain. Below, we introduce our numerical scheme for the purpose of confirming the decay results.

The parabolic equation

(44)

is discretized using finite differences for the time derivative and a finite element method for the p(·)−Laplacian term. For this, we divide the time interval [0, T] into N equal subintervals by

(45)

and denote by

(46)

The term u_t is approximated using the first-order forward finite difference formula:

(47)

Semidiscrete Problem. A linear semidiscrete formulation of (P∗) takes the following form: given p and u₀, find {u¹, u², …, uⁿ⁺¹} such that

(48)

This problem is elliptic and admits a unique solution [20], for every n = 0,1, …, N. Also, the Rothe approximation u⁽ⁿ⁾ to the exact solution u, given by

(49)

is well defined and u⁽ⁿ⁾ → u in L²(Ω) as τ → 0, see [1].

Full-Discrete Problem. The variable uⁿ⁺¹ is discretized in space by a finite element method. For this, let Ω_h be a triangulation of Ω with a maximal element size h. Let also v_h be a test function in the linear Lagrangian space P₁(Ω_h) such that v_h = 0 on ∂Ω_h.

The semidiscrete problem is then written in a weak form to define the full-discrete problem: given p_h, uⁿ ∈ P₁(Ω_h), find

such that

(50)

For p_h ≥ 2, the above problem has a unique solution

for every nontrivial

. This follows from the Lax-Milgram Lemma, and the Galerkin approximation

converges to uⁿ⁺¹ in

as h → 0; see [18].

4.2. Numerical Results

In this subsection, we present the following numerical applications of (P∗):

(1)
Exponential decay: for p_h(x, y) = 2, we show, for some c > 0, that
(51)
(2)
Polynomial decay: for p_h(x, y) = (1/5)⌈x⌉² + 2.5, we show, for some c > 0 and t₀ > 0, that
(52)
Here, ⌈·⌉ denote the greatest integer function.

In both applications, we set the following parameters:

(53)

Figure 1 shows the mesh used for Ω_h, which involves 23702 triangles and 12052 vertices.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Mesh of the domain [−5,5]×[−5,5].

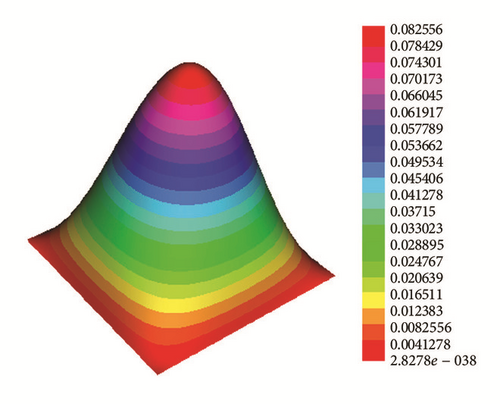
The initial condition is taken to be and projected into P₁(Ω_h); see Figure 2.

The numerical results are obtained using the noncommercial software, FreeFem++ [21].

Application 1. p_h(x, y) = 2 satisfies the required conditions (1)–(3). Figure 3 shows the numerical solutions for t = 5, t = 10, t = 20, and t = 50.

With c = 0.1, Figure 4(a) shows that

decays exponentially as

(54)

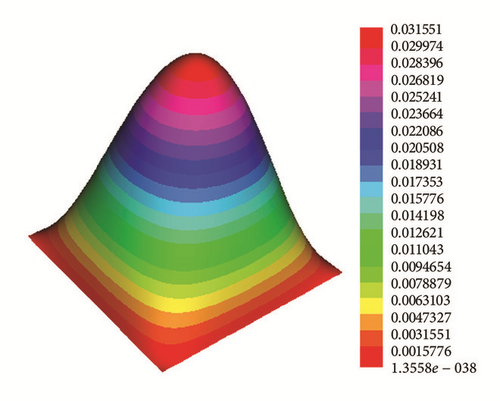
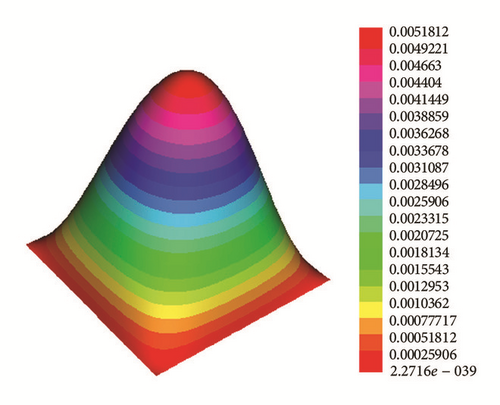
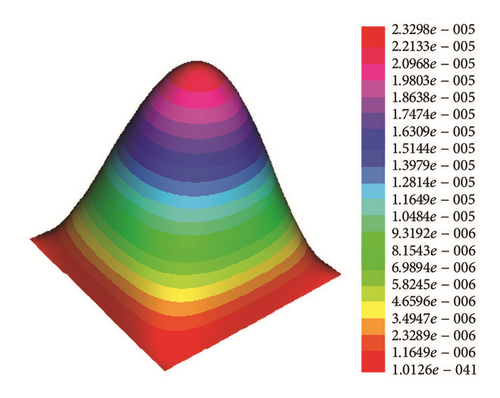
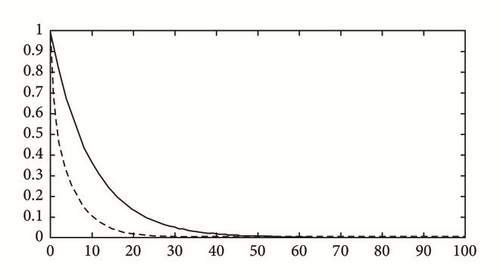
This is also confirmed by Figure 4(b) that shows the ratio y = g₁(t)/e^−0.1t is less than one and remains decreasing for a large value of T.

Application 2. The exponent function p_h(x, y) = (1/5)⌈x⌉² + 2.5, in Figure 5, satisfies the required conditions (1)–(3) as

(i)
p₁ = 2.5, p₂ = 7.5;
(ii)
for |x − y | < δ with 0 < δ < 1.

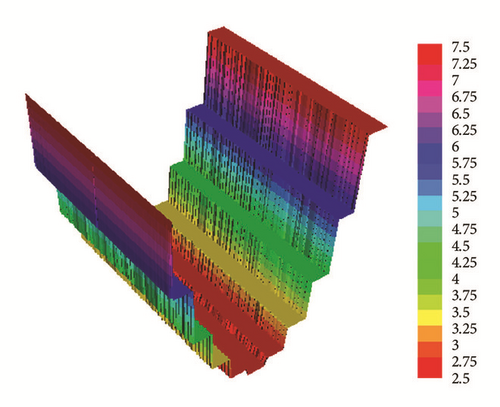
Figure 6 shows the numerical solutions for t = 5, t = 10, t = 20, and t = 50.

In this case, the solution

has a polynomial decay. With c = 1, Figure 7(a) shows that

(55)

This is also confirmed by Figure 7(b), which shows that the ratio y = g₂(t)/(1 + t) ^−2/11 remains less than one and decreasing until T.

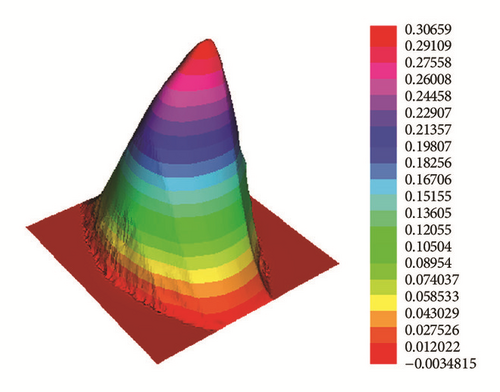
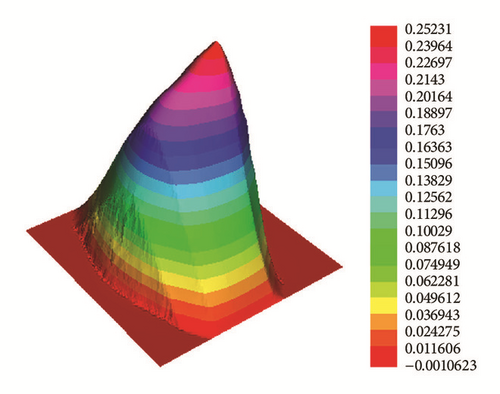
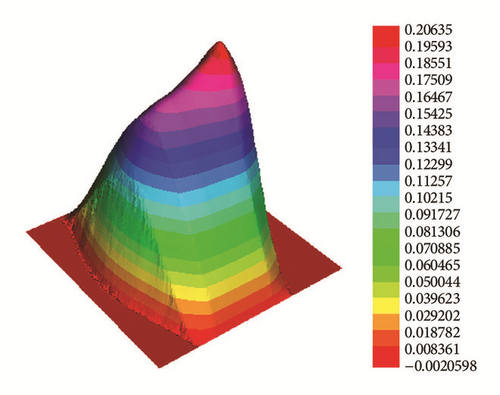
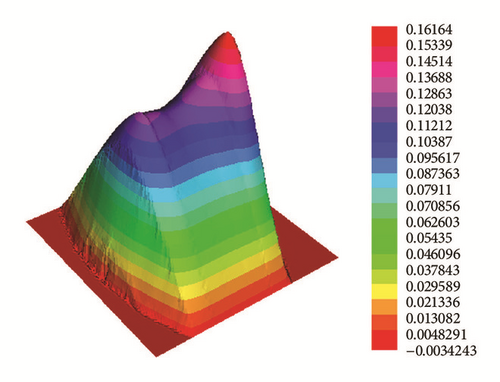
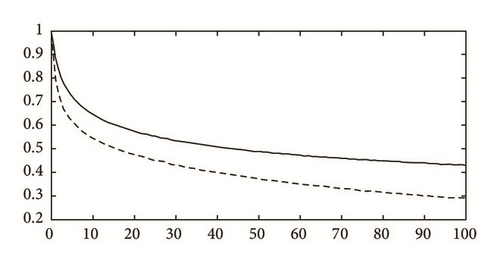
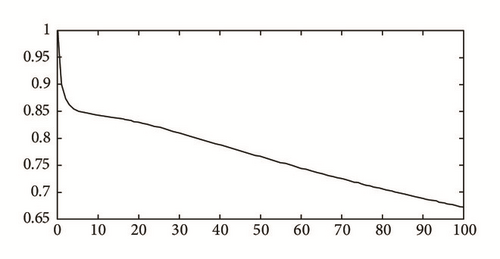
We conclude that the numerical results in above applications verify Proposition 9.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

The authors acknowledge King Fahd University of Petroleum and Minerals for its support. This work is sponsored by KFUPM under Project no. FT 161004.

References

1 Alaoui M. K., Messaoudi S. A., and Khenous H. B., A blow-up result for nonlinear generalized heat equation, Computers & Mathematics with Applications. An International Journal. (2014) 68, no. 12, part A, 1723–1732, https://doi.org/10.1016/j.camwa.2014.10.018, MR3283362.
10.1016/j.camwa.2014.10.018
Web of Science® Google Scholar
2 Pinasco J. P., Blow-up for parabolic and hyperbolic problems with variable exponents, Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. (2009) 71, no. 3-4, 1094–1099, https://doi.org/10.1016/j.na.2008.11.030, MR2527528.
10.1016/j.na.2008.11.030
Web of Science® Google Scholar
3 Shangerganesh L., Gurusamy A., and Balachandran K., Weak solutions for nonlinear parabolic equations with variable exponents, Communications in Mathematics. (2017) 25, no. 1, 55–70, MR3667076, 2-s2.0-85022089992, https://doi.org/10.1515/cm-2017-0006.
10.1515/cm-2017-0006
Google Scholar
4 Acerbi E. and Mingione G., Regularity results for a class of functionals with non-standard growth, Archive for Rational Mechanics and Analysis. (2001) 156, no. 2, 121–140, MR1814973, https://doi.org/10.1007/s002050100117, Zbl0984.49020, 2-s2.0-0035579913.
10.1007/s002050100117
Web of Science® Google Scholar
5 Acerbi E. and Mingione G., Regularity results for stationary electro-rheological fluids, Archive for Rational Mechanics and Analysis. (2002) 164, no. 3, 213–259, MR1930392, https://doi.org/10.1007/s00205-002-0208-7, Zbl1038.76058, 2-s2.0-0036768849.
10.1007/s00205-002-0208-7
Web of Science® Google Scholar
6 Chen Y., Levine S., and Rao M., Variable exponent, linear growth functionals in image restoration, SIAM Journal on Applied Mathematics. (2006) 66, no. 4, 1383–1406, MR2246061, https://doi.org/10.1137/050624522, Zbl1102.49010, 2-s2.0-33747163537.
10.1137/050624522
Web of Science® Google Scholar
7 Diening L., Ettwein F., and Ruzicka M., C1,α-regularity for electrorheological fluids in two dimensions, Nonlinear Differential Equations and Applications NoDEA. (2007) 14, no. 1-2, 207–217, https://doi.org/10.1007/s00030-007-5026-z, MR2346460.
10.1007/s00030-007-5026-z
Web of Science® Google Scholar
8 Ettwein F. and Ruzicka M., Existence of local strong solutions for motions of electrorheological fluids in three dimensions, Computers & Mathematics with Applications. An International Journal. (2007) 53, no. 3-4, 595–604, https://doi.org/10.1016/j.camwa.2006.02.032, MR2323712.
10.1016/j.camwa.2006.02.032
Web of Science® Google Scholar
9 Guo Z., Liu Q., Sun J., and Wu B., Reaction-diffusion systems with p(x)-growth for image denoising, Nonlinear Analysis: Real World Applications. (2011) 12, no. 5, 2904–2918, https://doi.org/10.1016/j.nonrwa.2011.04.015, MR2813233.
10.1016/j.nonrwa.2011.04.015
Web of Science® Google Scholar
10 Diening L., Harjulehto P., Hästö P., and Růžička M., Lebesgue and Sobolev spaces with variable exponents, Lecture Notes in Mathematics. (2011) 2017, 1–518, 2-s2.0-79953877824, https://doi.org/10.1007/978-3-642-18363-8_1, Zbl1222.46002.
10.1007/978-3-642-18363-8_1
Web of Science® Google Scholar
11 Ružička M., Electrorheological Fluids: Modeling and Mathematical Theory, 2000, 1748, Springer, Berlin, Germany, Lecture Notes in Mathematics, https://doi.org/10.1007/BFb0104029, MR1810360.
10.1007/BFb0104029
Web of Science® Google Scholar
12 Bendahmane M., Wittbold P., and Zimmermann A., Renormalized solutions for a nonlinear parabolic equation with variable exponents and L¹-data, Journal of Differential Equations. (2010) 249, no. 6, 1483–1515, https://doi.org/10.1016/j.jde.2010.05.011, MR2677803.
10.1016/j.jde.2010.05.011
Web of Science® Google Scholar
13 Akagi G. and Matsuura K., Well-posedness and large-time behaviors of solutions for a parabolic equation involving p(x)-Laplacian, Discrete and Continuous Dynamical Systems - Series A, Dynamical systems, differential equations and applications. 8th AIMS Conference. Suppl. Vol. I. (2011) 22–31, MR3012130.
Google Scholar
14 Edmunds D. E. and Rakosnik J., Sobolev embeddings with variable exponent, Studia Mathematica. (2000) 143, no. 3, 267–293, MR1815935.
10.4064/sm-143-3-267-293
Web of Science® Google Scholar
15 Edmunds D. E. and Rakosnik J., Sobolev embeddings with variable exponent, II, Mathematische Nachrichten. (2002) 246/247, 53–67, https://doi.org/10.1002/1522-2616(200212)246:1<53::AID-MANA53>3.0.CO;2-T, MR1944549.
10.1002/1522-2616(200212)246:1<53::AID-MANA53>3.0.CO;2-T
Web of Science® Google Scholar
16 Fan X. and Zhao D., On the spaces L^p(x)(Ω) and W^m,p(x)(Ω), Journal of Mathematical Analysis and Applications. (2001) 263, no. 2, 424–446, https://doi.org/10.1006/jmaa.2000.7617, MR1866056.
10.1006/jmaa.2000.7617
Web of Science® Google Scholar
17 Simon L., Application of Monotone Type Operators to Nonlinear PDEs, 2013, Prime Rate Kft., Budapest, Hungary.
Google Scholar
18 Quarteroni A. and Valli A., Numerical approximation of partial differential equations, 1994, 23, Springer-Verlag, Berlin, Germany, Springer Series in Computational Mathematics, MR1299729.
10.1007/978-3-540-85268-1
Google Scholar
19 Li D. and Wang J., Unconditionally optimal error analysis of Crank-Nicolson Galerkin {FEM}s for a strongly nonlinear parabolic system, Journal of Scientific Computing. (2017) 72, no. 2, 892–915, MR3673699, https://doi.org/10.1007/s10915-017-0381-3, Zbl06805231, 2-s2.0-85012863881.
10.1007/s10915-017-0381-3
Web of Science® Google Scholar
20 Leray J. and Lions J.-L., Quelques résulatats de Visick sur les problémes elliptiques nonlinéaires par les méthodes de Minty-Browder, Bulletin de la Société Mathématique de France. (1965) 93, 97–107, MR0194733.
10.24033/bsmf.1617
Google Scholar
21 Hecht F., Freefem++ manual, http, http://www.freefem.org.
Google Scholar

Citing Literature

All articles

Well-Posedness and Numerical Study for Solutions of a Parabolic Equation with Variable-Exponent Nonlinearities

Abstract

1. Introduction

2. Preliminaries

3. Well-Posedness

4. Numerical Study

4.1. Numerical Method

4.2. Numerical Results

Conflicts of Interest

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Well-Posedness and Numerical Study for Solutions of a Parabolic Equation with Variable-Exponent Nonlinearities

Abstract

1. Introduction

2. Preliminaries

3. Well-Posedness

4. Numerical Study

4.1. Numerical Method

4.2. Numerical Results

Conflicts of Interest

Acknowledgments

References

Citing Literature

Figures

References

Related

Information