Global Sensitivity Analysis of High Speed Shaft Subsystem of a Wind Turbine Drive Train

1. Introduction

Nowadays wind turbine industry is growing very fast and wind power has become one of the most cost effective of all renewable energy sources because of environmental concerns and finite resource of fossil fuels [1]. Therefore, it has attracted political and business interest and extensive research is carried out at different universities and institutes [2].

It is very important to reduce the costs of design, manufacturing, and maintenance and optimize the power performance of wind turbines in order to be cost competitive in the current market. A better understanding and consequently improvement of wind turbine drive train dynamics performance could lead to overall cost efficiency in wind turbine operations. This is done by advanced system modelling, identifying the reasons for premature failures and fault diagnoses [3] in different components in drive train of wind turbines. Examples of multibody dynamic analysis to predict the components’ loads in wind turbine drive trains are in [4–6]. Generally, the dynamic performance of wind turbine drive train can be investigated based on different points of view, such as power performance, operational speeds, loads in specific components like coupling and bearings in both healthy and faulty situations, and misalignment parameters [7–14]. Different structural dynamic parameters can directly influence a wind turbine ultimate performance and in terms of loading, high speed shaft components are the most important since the components experience major extreme loads during different regimes, especially in transient one.

The current research deals with mathematical modelling of high speed shaft drive train test rig. A typical wind turbine drive train is composed of a generator as an electrical part with a control set, flexible couplings, a speed-up gearbox, a main shaft, and a wind rotor as an air-operated system [15]. The power from the rotor is transferred through main shaft, gearbox, and high speed shaft to the generator.

We propose the global sensitivity analysis (GSA) as a tool to better investigate wind turbine drive train dynamics, more specifically, high speed shaft drive train models. The aim is to quantify the input structural parameters’ effect to objective functions of the system dynamics (interaction quantification set [16]). From GSA the most influential design parameters on objective functions of wind turbines can be determined, which could ease the optimization process by narrowing down the number of input design parameters.

Methodology of sensitivity analysis is various and it has been used for different applications. Reviews on different GSA methods can be found in [16–20]. Some examples of sensitivity analysis are derivative-based Morris one-at-a-time (OAT) local sensitivity method [21] and Sobol/Saltelli method providing the variance based sensitivity [22, 23], whereas the Sobol/Saltelli variance based sensitivity method provides indices that quantify the relative contribution of each input structural parameter to set of objective functions [22, 23]. In the variance based GSA, input variables are chosen randomly in a proper range. Then, the contribution of input parameter to objective functions is investigated via the sensitivity indices. These sensitivity indices are quantifying the contribution of a random variable to the total variance of the response, which is basis of variance based global sensitivity analysis in [23].

Computational effort when design analysis requires a large set of loading conditions to be evaluated, such as wind turbine drive trains, is very important. As one of the most common methods for GSA, Monte Carlo simulation for these systems is not efficient since it is computationally expensive. On the other hand, GSA within analysis of variance decomposition (ANOVA) or high dimensional model representation (HDMR) theory is suitable method in terms of being cost effective. It decomposes the response function of a high dimensional system into combination of low dimensional system set. This reduces the computational effort. A multiplicative dimensional reduction method (M-DRM) for GSA was proposed by Zhang and Pandey [24] entailing simple representation of GSA indices. The method has proved to be as accurate as Monte Carlo with much less computational effort [22].

Several works have been done within sensitivity analysis of rigid and flexible multibody systems with respect to structural parameters such as mass, moment of inertia, stiffness, and damping values [25–28]. In [29] extended Fourier amplitude sensitivity test method was used and the results of a single turbine and a set of large group of turbines was compared by GSA. Sensitivity analysis to perform a large set of data analysis for a wind farm was reported in [30].

Considering that the faults occur in high speed shaft drive trains, this could be a subject of study [31, 32]. The test rig for high speed shaft drive train as subsystem of wind turbine has been constructed in order to do experimental study and acquire data for validation of developed mathematical model. Another purpose of the test rig is to investigate strategies to detect faults. Early fault detection is important since it can reduce the cost of maintenance drastically.

Ultimately, by introducing faults and defects and different components of high speed shaft drive train, we investigate the detectability of faults and failures within GSA. Such an analysis could lead to fault diagnose in components of wind turbine drive train and prevent failures in early stages.

In the following sections, the proposed mathematical model of high speed shaft drive train test rig with the experimental setup at the lab is presented. Then, input variables and different operational scenarios and objective functions are introduced. Different sources of faults and failures such as defect in the bearing, backlash in the coupling, and torque ripple in the motor are introduced and modelled. Ultimately, the GSA indices for the validated model have been investigated. Results of GSA allow one to understand the priorities in contribution of system parameters for any specific objective function and lead one to focus on the areas of operation that show greatest opportunities for optimization. The outcome of the current research leads to useful information regarding wind turbine drive train dynamics behaviour on different operational scenarios which not only provide possibility to reduce the number of input parameters for optimization and speed up the process, but also give insight to design functional components in proper ranges and in a smarter way. In particular, the main aim of the paper is to apply the GSA for the proposed mathematical model of high speed shaft drive train including aforementioned fault sources. Quantifying the faults effects on the drive train objective functions could be applied as a methodology to contribute to virtual condition monitoring in order to detect and predict faults and prevent failures in early stages in different components of drive trains.

2. High Speed Shaft Drive Train System Test Rig

The most common wind turbine is of lateral (horizontal) axis type, which entails main supporting tower upon which sits a nacelle and rotor. Inside the nacelle sits a main shaft supported by bearings on which the rotor hangs. The main shaft is connected to a gearbox, which, in turn, is connected to the generator with control system (Figure 1). The high speed shaft subsystem is one part where faults in bearing are often observed.

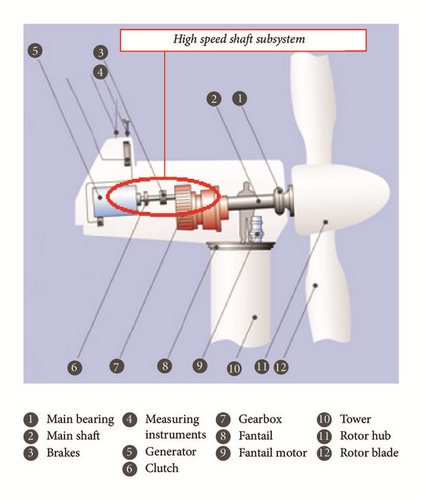
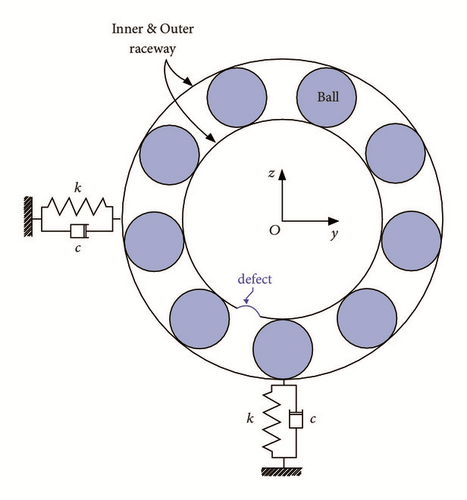
To support experimental and numerical studies of wind turbine drive train dynamics, a scaled down test rig has been built and instrumented as reported in [33, 34]. It entails a motor, rotor disk with shaft, where the rotor shaft is passing through the bearing housing and connected to the motor by a coupling. A small eccentric mass can be added on the rotor disk to give a varying load. The setup of the drive train test rig is represented in Figure 2.

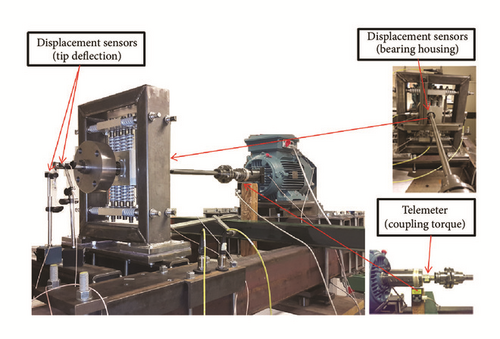
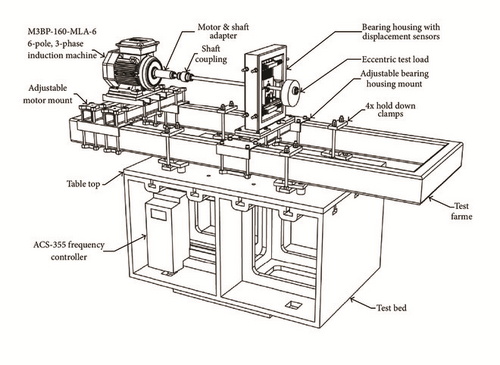
The test rig is driven by ABB motor model M3BP160 MLA 6 (6 pole, 75 kW) with a variable frequency controller (ACS355 from ABB providing speed up to 1000 rpm). In addition, the test rig entails motor shaft adapter, shaft’s coupling, bearing housing with flexible support, a disk on which an eccentric mass can be added, and bedplate on which all the components are mounted.

The data acquisition system is SKF @ptitude Observer; SKF offers under its Windcon 3.0 condition monitoring system. The set of sensors comprise accelerometers and Eddy probes displacement sensors, which detect vibrations in the test rig and deflection at both tip and bearing housing. Additionally, in order to measure the torque in coupling, full bridge strain gauges are put on the motor shaft, and the signal is acquired using a telemeter system (TEL 1-PCM).

In previous works [33, 34], the coupling torque, deflection fields in both lateral and vertical directions in tip, and bearing housing have been measured and used for model validation. To support future studies of defect detection, the objective functions derived in this paper are based on these sensors.

2.1. Mathematical Model of Drive Train System Test Rig

An engineering abstract of the test rig is shown in Figure 3. The mathematical model has been developed based on both rigid and flexible shaft assumption in bending modes, considering that the torsional flexibility is concentrated at coupling. The motor is rigidly attached to the bedplate.

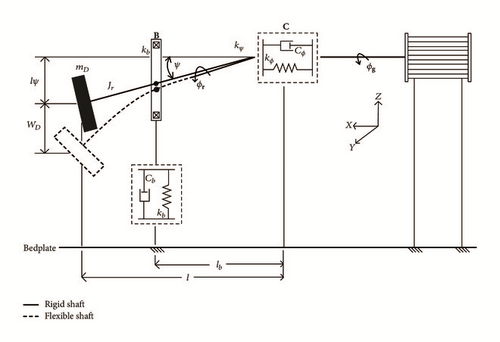
2.1.1. Governing Equations

The kinetic, potential, and dissipative energies and nonconservative forces are derived considering that the shaft is rotating, and its bending deflection w(x) is assumed to occur in the radial direction only. The disk is seen as a rigid body, and the shaft torsional flexibility is concentrated in coupling as well as linear along the shaft length. A linear spring model is adopted to simplify the flexibility of structure of the bearings [35].

$$ ()

Here $$ is the contribution of the shaft bending to potential energy and the indices sh and D denotes for shaft and disk, respectively. The complete list of structural parameters is given in Table 1. The shaft torsion is parametrized by ϕ_D, ϕ_s, and ϕ_g, as an angle of rotation in the disk (rotor tip), shaft, and motor, respectively.

Table 1. Test rig nominal and randomized input parameters.

Parameter	Symbol	Nominal value (X⋆)	Xmin/X⋆	Xmax/X⋆
Motor inertia with respect to x axis	Jg	0.087 kgm2	0.5	2
Rotor inertia with respect to x axis	Jr	0.095 kgm2	0.5	2
Rotor shaft inertia with respect to x axis	Jsh	0.0003 kgm2
Rotor inertia with respect to ψ (minor axis)	Ir	19.083 kgm2	0.5	2
Disk inertia with respect to y axis	ID	18 kgm2
Shaft inertia with respect to y axis	$$	0.5 kgm2
Disk mass	mD	14.52 kg	0.75	1.5
Rotor shaft mass	msh	3.85 kg
Eccentric mass value mounted in the rotor disk	me	74.4 gr	0	4
Distance of eccentric mass from center	re	8 cm
Rotor shaft and disk mass	mr	18.35 kg
Length from coupling to the tip	l	0.85 m	0.8	1.2
Length from coupling to bearing housing	lb	0.72 m	0.8	1.2
Length from coupling to CG of disk and rotor shaft	l0	0.75 m
Damping factor	ζd	0.01 s
Coupling torsional stiffness	kϕ	2600 Nm/rad	0.75	5
Coupling bending stiffness	kψ	56 kNm/rad	0.75	5
Bearing mount lateral and vertical stiffness coefficients	$$	4308 kN/m	0.75	5
Bearing hub bending stiffness	$$	0.1kψ	0.75	5
Coupling torsional damping	Cϕ	26 kNm/rad	0.5	10
Coupling bending damping	Cψ	56 kNm s/rad	0.5	10
Bearing mount lateral and vertical damping coefficients	Cb	4308 kN s/m	0.5	10
Bearing friction damping coefficient	Cbf	0.0023 Ns/m	0.8	3
Rotor torsional damping coefficient plus bearing friction	$$	0.006 Ns/m	0.8	3
Motor torsional damping coefficient	Cbg	0.006 Ns/m	0.5	10
Shaft bending stiffness	EI	7.6699 kNm2	0.5	10
Angle dependency factor of kb	αb	1	0.8	1.5
Torque ripples parameters	$$	10 Nm	0	3
Backlash gap	BL	0.002 m	0	3
Backlash regularization parameter	σ	40
Bearing torque disturbance zone for defect	ε	0.1
Maximum value of rotational bearing defect torque	$$	30 Nm	0	5
Maximum value of radial bearing defect torque	$$	30 Nm	0	5

Applying Lagrange formalism, the nonlinear set of equations of motion can be written as matrix equation with time variant coefficients as follows:

$$ ()

where M is the inertia matrix, B is the vector related to internal forces acting on the test rig, and q is the vector of generalized coordinate to be defined in Section 2.1.2.

F is an external load vector and it is a combination of $$, $$, and $$ which applies to specific degree of freedom.

$$ corresponds to external forces due to the disturbance of the bearing defects imposed to the system (described in Section 2.2.3). The defect may impose the disturbance torque into bending and torsional degrees of freedom (• = {ψ, ϕ_r}).

$$ refers to the backlash of the coupling which appears as an internal load in the governing equations. The backlash has a contribution in the potential energy since it is modelled as a spring with gap.

$$ is torque ripples imposed by the motor, a source of faults in drive train dynamics representing electromechanical interaction between components.

2.1.2. Parametrization of the Model

Since the coupling is assumed to be very stiff in torsion (apart from its backlash), the shaft torsional flexibility and coupling play are here added and included in k_ϕ, and $$. We introduce ϕ_r as the rotor (disk plus shaft) angle, such that the shaft twist is represented by $$ where ϕ_g is the motor shaft angle. Hence, ϕ_s and ϕ_D are both replaced by ϕ_r in the governing equations in Section 2.1.1. We assume that the shaft inertia and coupling are abstracted as J_r = J_sh + J_C. Coupling torsional stiffness is represented in a way that includes both shaft and coupling torsional stiffness’s. Similarly, the shaft and coupling damping, $$ and $$, are represented by C_ϕ.

The shaft deflection is parametrized in terms of rigid and flexible contribution to total deflection as w(x) = ψx + w_Dφ(x), where ψ is the angular deflection at the coupling, w_D is the rotor shaft tip deflection due to shaft flexibility, and φ(x) is taken as the shape of the fundamental bending eigenmode as described in [33]. In [33], we developed and validated the mathematical model of high speed shaft drive train test rig considering the shaft flexibility in terms of bending. To obtain a suitable shape function φ(x), the Euler-Bernoulli beam theory is applied [36]. Only radial vibration amplitudes of the beam were considered. The fundamental bending eigenmode based on structural parameters in Table 1 was found at β = 0.8734 and its shape function φ for a shaft rotating at speed Ω = 1000 rpm gives the eigenfrequency at ω^⋆ = 109.4608 rad/s. The next eigenmode was found at ω^⋆ = 6151 rad/s, which is much higher than relevant excitation frequency. The deflection fields in two locations, namely, tip (x = l) and bearing hub (x = l_b), are assessed within the aforementioned assumptions. Thus, the tip radial deflection would be ψl + w_Dφ(l), and the bearing housing radial deflection becomes ψl_b + w_Dφ(l_b). The displacements in vertical and lateral directions become mirrored by rotational angle ϕ_r. Note that we simplify the deflection field in the bearing hub. For more realistic model, shaft prebending and relative motion of inner ring with respect to the bearing hub frame must be considered.

To conclude, the vector of generalized coordinate is defined as $$.

2.2. Faults Modelling in the Drive Train

2.2.1. Electromechanical Modelling of the Motor: Motor Torque with Ripple

Considering that wind turbine drive train contains both mechanical and electrical components, it is of important concern to have a model which studies electromechanical interactions. In induction motors, many kinds of excitation occur such as electromagnetic forces exist, that is, unbalanced magnetic pull. Torsional vibration of drive train system could lead to significant fluctuation of motor speed. Such oscillation of the angular speed superimposed on the average motor angular speed causes severe oscillation of electric currents in motor windings [37]. In this section, we model torque ripple as source of this fluctuations in motor speed.

In the current mathematical model, we assume the motor as a 6-pole induction machine with rated power 7.5 kW at speed 975 rpm. The speed is set from a frequency converter, such that the torque is given by the difference from set speed $$ and actual speed $$. A cycle of ramp startup-steady state-shutdown can thus be described by

$$ ()

where

$$ ()

where Δω_mark = 25/60 × 2π rad/s, M_mark = 73.4561 Nm, t₀ is the startup-time, and t₁ is the instance of time when motor is turned off (without braking). From electrical measurement of the voltage from the frequency converter, it was found that, in addition to M_mech, there is a small periodic torque (ripple) acting on the generator rotor at frequencies $$, and $$. Hence, the following electrical torque is considered:

$$ ()

where $$ are coefficients that contribute to torque ripple with corresponding frequencies and have been obtained based on comparison of the torque ripple range in steady state in simulation and experiments.

2.2.2. Backlash Modelling of the Coupling

Here, we propose backlash as nonlinear stiffness properties to the system structure, which is common source of faults in transmission system dynamics (Figure 4). This phenomenon affects the governing equations. Properly functioning mechanical systems need to have a certain clearance (gap, play) between the components transmitting motion under load. As part of internal forces, T_int is defined as follows [38]:

$$ ()

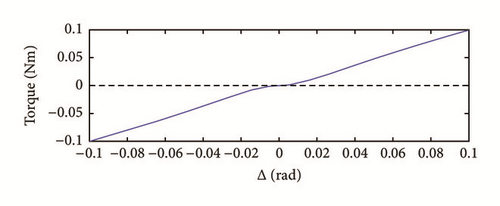
2.2.3. Modelling of Defects in Rolling Elements (Bearing): Disturbance Torque from Bearing Inner Ring

Bearing fault diagnosis is important in condition monitoring of any rotating machine. Early fault detection is one of the concerns within the wind turbine system modelling. To this end, we need to model source of faults in the bearing. Dynamic modelling and vibration response simulation of rolling bearings with surface defects is a common assumption within fault modelling. When bearing balls roll over defects, shock pulses with high frequency are generated with excessive vibration leading the whole system to failure. This characteristic impulse-response signal is detected by the vibration monitor. An inner raceway rotates with shaft’s rotation and goes through the loaded zone of bearing every rotation. This mechanism shows that the vibration of inner raceway with defect is modulated by the shaft rotation [39–41].

Here we propose a simple modelling of surface defect for bearing which imposes a disturbance torque in certain angles in the inner raceway connected to the rotor shaft (similar to when a ball passes from the defects and causes a excitation to the system). Figure 5 shows the external torque imposed in radial and rotational directions. As part of external forces, $$ is defined based on impulse factor ε and maximum torque $$ as shown in Figure 5(a).

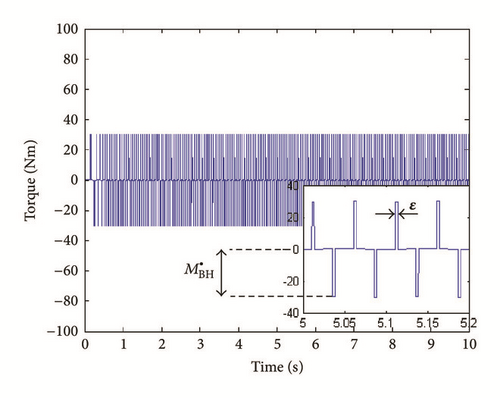
Proper value for maximum disturbance is $$ Nm. ε(=0.1) is the angular length of active contact zone, where the defect is assumed (Figure 5).

Depending on the rolling elements number included in the bearing structure, the geometric relationship among its components, and shaft rotational speed, characteristic rotational frequencies initiating from respective bearing elements could be obtained. In this regard, the characteristic passing frequency in the inner ring is defined as follows:

$$ ()

where f_r is the rotor rotational frequency (=$$), N_b is number of rolling balls (N_b = 9), D_b(=72 mm) and D_c(=53.5 mm) are the balls diameter and bearing pitch ((D_o + D_i)/2) diameters, respectively. φ is the contact angle (φ = 0 rad). The bearing defect location (here, the inner race) will determine that f_i(≈10.55f_r) will be exhibited in the machine vibration signal.

2.2.4. Uneven Mounting Stiffness

For subsequent study of excitation of uneven mounting stiffness, the bearing mount stiffness has been defined as function of rotor shaft angle ϕ_r(t) as follows:

$$ ()

where α_b is a parameter corresponding to angle dependency of k_b and defines different loads in vertical and lateral directions imposed to the bearing springs.

2.5. System Model Response for the Nominal Values

Here, we present the simulation response of the mathematical model based on structural parameters nominal values represented in Table 1. The displacement fields in both lateral and vertical direction with their FFT have been presented.

The deflection fields include three different operational scenarios based on Figure 6 with steady state of $$ sec and shutdown starting at t = 6 sec. The tip deflection fields in both vertical and lateral directions are presented with zoom in steady state ($$ sec) and shutdown ($$ sec) in Figure 7.

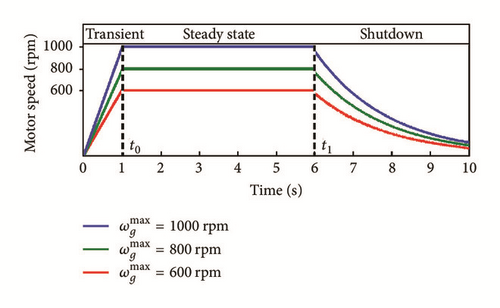
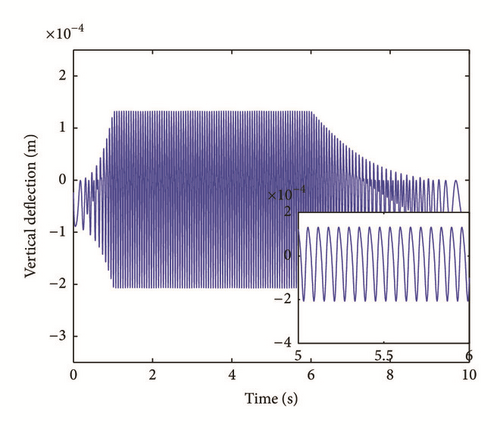
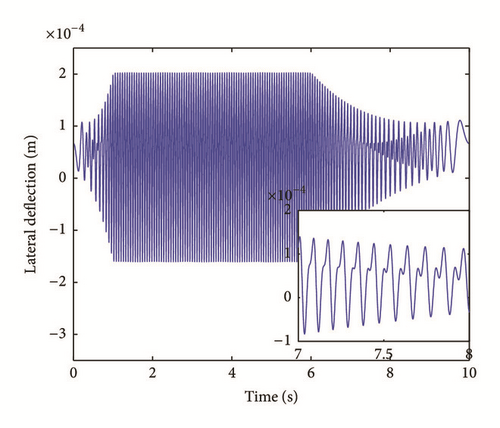
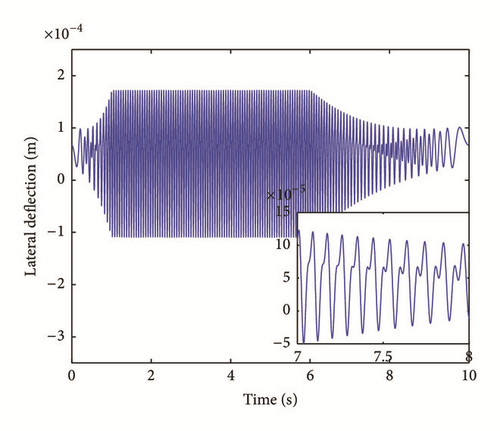
The bearing housing deflection fields in both vertical and lateral directions are presented with zoom in steady state ($$ sec) and shutdown ($$ sec) are shown in Figure 8.

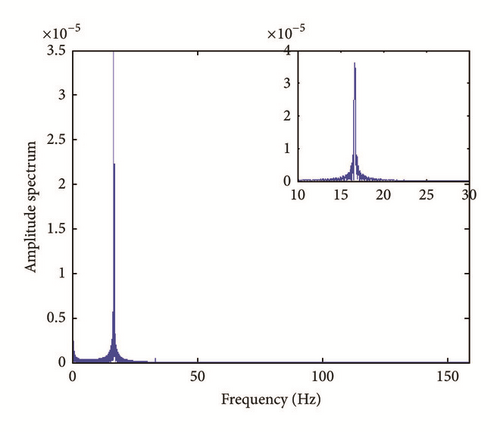
The frequency response functions of the tip deflection in both vertical and lateral directions are presented with zoom on the dominant frequency in Figure 9.

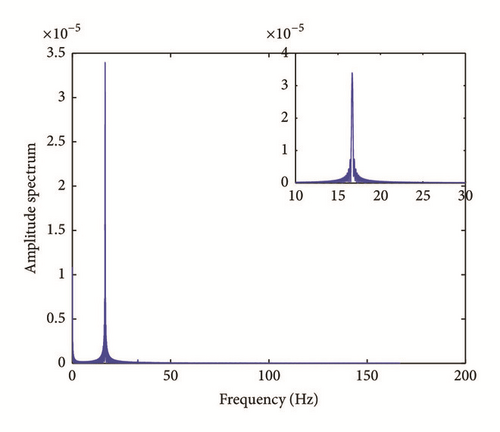
The coupling torque with its frequency response is presented here in Figure 10.

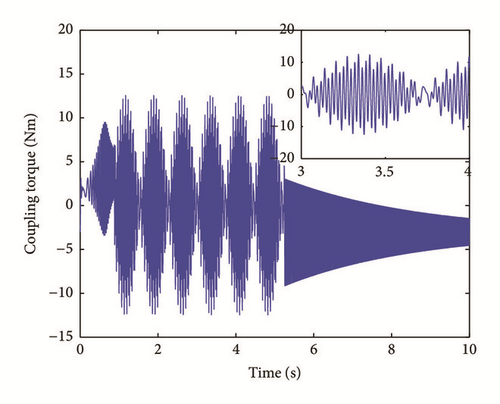
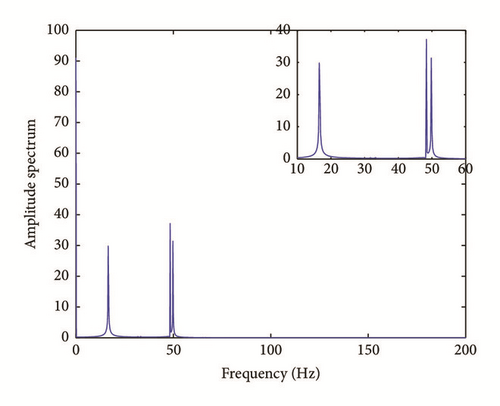
The equations of motion have been solved using Newmark numerical procedure method implemented in Matlab software. In order to satisfy the convergence criteria, the proper time step has been chosen as Δt = 10⁻⁴.

3. Objective Functions

In this section we introduce the set of objective functions. The introduced objective functions are assessed in order to evaluate the dynamic performance of the developed high speed shaft models.

(i) Tip Deflection in Both Vertical and Lateral Directions in Steady State and Shutdown Regimes $$. The RMS values of the tip deflection in both lateral and vertical in two operational scenarios (steady state and shutdown) (RMS(Y^std), RMS(Z^std) and RMS(Y^SD), RMS(Z^SD), resp.) are obtained within the mathematical model and the sensitivity indices based on the structural inputs have been defined for these objective functions.

(ii) Bearing Hub Deflection in Both Vertical and Lateral Directions in Steady State and Shutdown Regimes $$. RMS value of the bearing housing bending in both lateral and vertical directions in two operational scenarios (steady state and shutdown) ($$, $$ and $$, $$, resp.) is obtained within the mathematical model and the sensitivity indices based on the structural inputs have been defined for these objective functions. A model of gearbox is required to consist of shaft and bearing housing stiffness, which allows interaction between housing and the internal components to be investigated.

(iii) Frequency Response of the Tip Deflection in Lateral and Vertical Directions in Steady State and Shutdown $$. These are the desired objective function representations: FFT(Y^std), FFT(Z^std) and FFT(Y^SD), FFT(Z^SD), respectively. The modal sensitivity analysis allows one to recognize the eigenfrequency response to design parameters changes. It can also help for the better identification of important dynamic properties.

(iv) Coupling Torque in Different Operational Scenarios Transient, Steady State, and Shutdown Cases $$. In order to determine the influence of the design parameters in torsional vibration model, RMS values of the coupling torque in different operational scenarios transient, steady state, and shutdown cases are investigated as objective functions (RMS(CT^tr), RMS(CT^std), and RMS(CT^SD), resp.). The coupling torque is defines as M_ϕ = k_ϕΔ.

Coupling torque in transient regime is very important to measure and quantify the parameters which have the most effect, since the component experiences the most severe loadings due to this regime nature. By shutting down the motor, there is not any load imposed by motor side and the range of the coupling torque is decreased from steady state value to zero in short period of time.

(v) The First and Second Peaks in FFT Diagram of Coupling Torque in Steady State $$. There are several picks in the coupling torque frequency response, of which the most dominant one is of interest to study, and investigating the most influential parameter would give valuable conclusion form the vibrational point of view. Studying the torsional model, we came up with a conclusion that some peaks in FFT are related to the ripple due to motor. Quantifying those peaks would give the contribution of the fault source to the objective function, which is very valuable information in terms of optimization.

(vi) The Peak in FFT Diagram of Coupling Torque in Shutdown Regime $$. During shutdown we expect that only torsional eignefrequency of the structure plays the role in FFT.

4. Global Sensitivity Analysis of High Speed Shaft Test Rig

The efficiency and applicability of global sensitivity analysis is already proven by some mathematical and mechanical examples [24]. The aim here is to apply this method to the high speed shaft drive train dynamics with respect to the structural parameters.

5. Results from GSA of High Speed Shaft (HSS) Model

In this section, the global sensitivity analysis of the developed mathematical models corresponding to high speed shaft drive train system has been presented. Both torsional and bending models are examined under three different operational scenarios with different motor speeds in steady state ($$ Hz).

The analysis presented here focuses on the response characteristics particular to chosen objective functions. It is expected that the operational scenarios will influence the dynamics and structural response to different input variables.

5.0.1 Convergence Study. The number of function evaluations using M-DRM method is N_X × N. For specific set of input variables and on each operational scenario, all objective functions are evaluated at the same time by a single time integration of the model. In order to achieve an acceptable approximation of the sensitivity analysis indices using the M-DRM method, it is important to assess the convergence of the results by increasing number of Gaussian quadrature integration abscissas denoted by N in (18).

The convergence study shows that for a nonlinear system such as high speed shaft drive train with system input parameters prescribed in Section 5, sufficient level of accuracy for the sensitivity analysis can be obtained with 21 × 20 = 420 (N_X = 21 design parameters and N = 20 integration abscissas) function evaluations. This is one of the most prominent aspects of the global sensitivity analysis using this approach, which could reduce the computational effort drastically.

5.1. GSA of Drive Train High Speed (HSS) Shaft Subsystem Model

In this section we apply GSA to the total model which comprises bending and torsional parameters all together. The input parameters are defined in (20).

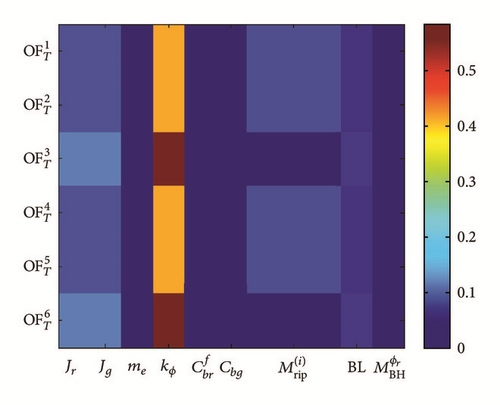
For the model containing all bending and torsional parameters, the primary and total sensitivity indices are as shown in Figure 11.

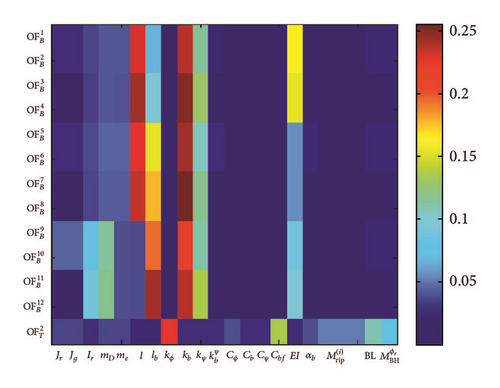
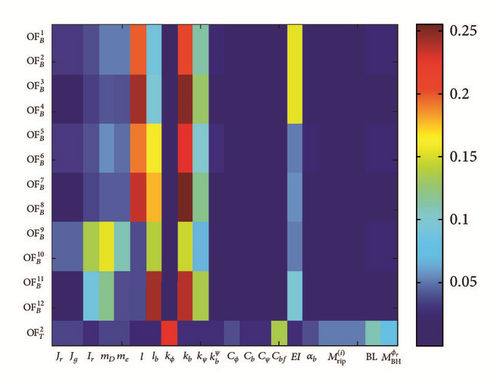
It can be concluded from this that the torsional input parameters (coupling torsional stiffness k_ϕ and bearing damping due to friction C_bf and motor torque ripples $$, backlash parameter BL, and bearing impact disturbance $$) do not have significant influence to the bending objective functions ($$). The same conclusion could be made based on the bending input parameters (coupling bending stiffness k_ψ and bearing mounting stiffness k_b and shaft bending stiffness EI) which do not seem to have major effect on torsional objective function ($$).

Based on this analysis, we conclude that the torsional and bending response of the model can be analysed separately, which allows for substantially simpler analysis, which will discussed next.

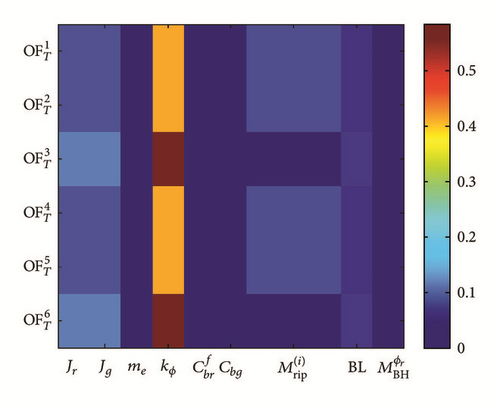
5.2. HSS Bending Model

After separating the two models, we analyse the sensitivity of HSS within the frame of bending model based on bending objective functions such as deflection field in bearing hub and tip in both lateral and vertical directions and the corresponding frequency domains.

Considering the separation of model, the simulation results of the bending model have been obtained based on semi-inverse dynamics approach (“perfect” speed control), by prescribing the motor angular speed, where it constitutes the input to the system and is prescribed as a ramp loading expressed by Heaviside function:

$$ ()

where t₀ and t₁ denote the instant of time of the end of transient and instant of time of the start of the shutdown operations, respectively. t_end is duration of the operational scenarios (see Figure 6).

In order to investigate the bending model sensitivity, the input parameter appearing in the governing equations corresponding to the model is chosen as follows:

$$ ()

Here, the sensitivity analysis has been performed for bending model for 3 different operational scenarios with different motor speeds in steady state regime.

It was shown that within these 3 different motor frequencies, the contribution of the input parameters is not changing drastically. The obtained results of GSA are presented in Figure 12. The results indicates that the most influential structural parameters which have the major effect to the objective functions are coupling bending stiffness k_ψ and bearing mounting stiffness k_b, shaft bending stiffness EI, and bearing hub and tip locations l_b, l. Also, the damping parameters do not have significant effect on both primary and total sensitivity indices.

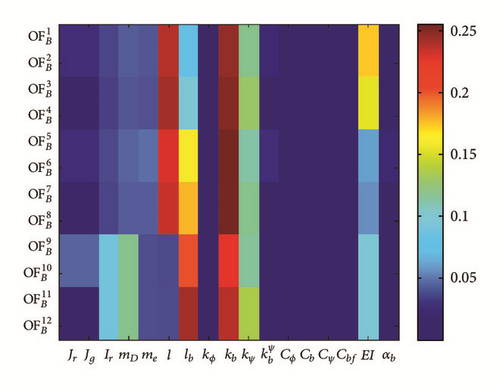
More detailed analysis of the results based on each objective functions and influence of the input parameters is presented as follows.

(i) Tip Deflection in Vertical and Lateral Directions in Steady State $$ and Shutdown Scenarios $$. It is illustrated that the coupling bending stiffness k_ψ and bearing hub mounting stiffness k_b are the most dominant influential parameters, respectively.

It could be seen from Figure 12 that the shaft bending stiffness EI has more influence in tip deflection field compared to the other objective function. This is somehow logical since the first bending mode shape is higher in tip (x = l) compared to bearing hub (x = l_b) [33].

Moreover, the geometric locations of bearing hub and tip (l_b, l) are influential parameters in terms of deflection field in both bearing hub and tip.

(ii) Bearing Hub Deflection in Vertical and Lateral Directions in Steady State $$ and Shutdown Scenarios $$. In bearing deflection field the influence of l_b is more than l. In tip deflection field the influence of l is more than l_b.

The bearing bending stiffness $$ does not have a major effect to the system objective functions.

It could be seen that the angle dependency of the bearing stiffness α_b is not having a major effect to all of objective functions, since the realistic range for α_b is small.

(iii) Frequency Response of the Tip Deflection in Vertical and Lateral Directions in Steady State $$ and Shutdown Scenarios $$. The influences of stiffness parameters k_ψ and k_b and EI and l_b and also inertia parameters I_r, m_D, and m_e are the most dominant parameters, respectively. This tells that aforementioned parameters are the most important ones in terms of frequency response of the tip deflection.

Among the mass inertia parameters, I_r, m_e, and m_D affect most of the bending objective functions.

It could be also seen form Figure 12 that the damping input parameters have the least influences on both primary and total sensitivity indices.

To sum up the conclusion related to the GSA of HSS subsystem within the frame of bending model, k_b and k_ψ and EI and I_r and m_D and m_e have the major effects on both primary and total sensitivity indices.

However, according to the sensitivity analysis results, rest of parameters stated in the system modelling do not have a remarkable effect on the mentioned objective functions. Such information would be particularly useful in attenuating the number of design parameters for optimization applications of wind turbine drive trains setups which leads to cost efficient simulations.

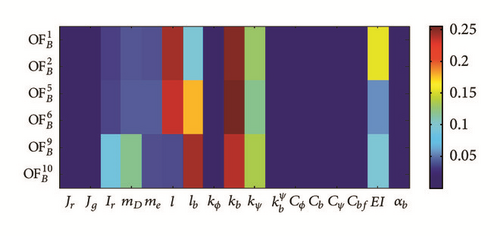
5.3. Bending Model with Bearing Defect: Detection of Faults in Inner Ring

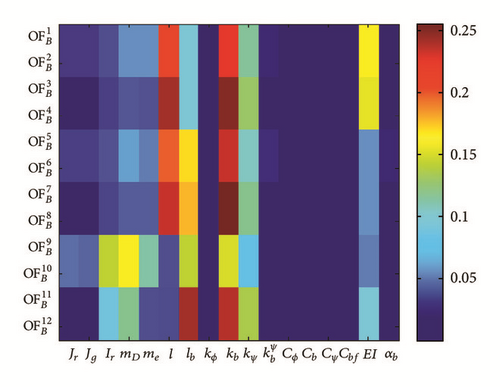
Here, we study the bearing defect influence to the objective functions. The aim is to investigate the sensitivity indices with respect to the bearing defect parameter $$ imposing a radial load to the bearing housing and seek its effect to the bearing deflection and loads.

It is hypothesized that if the sensitivity index with respect to parameter $$ is comparable to other sensitivities in certain OF, we can expect that a sensor measuring this OF is able to detect defects of size related to the magnitude of $$. The obtained results on GSA with bearing defect are presented in Figure 13 and summarized below.

The minimum value of $$ which makes the sensitivity indices to be detectable has been investigated.

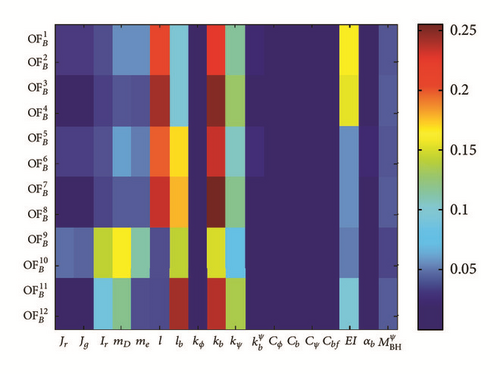
• (i)

  Deflection fields in vertical and lateral directions in steady state and shutdown scenarios for the tip ($$) and bearing hub ($$), respectively: in Figure 13, comparing $$ sensitivity indices for objective functions tip and bearing hub deflections ($$ versus $$), the influence of the bearing defect $$ in bearing hub is more than the tip. This is due to direct influence of the defect in the bearing by imposing the defect torque, which means that the bearing may experience more damage by introducing a defect in the inner ring.

• (ii)

  Frequency response of the tip deflection in steady state ($$) and shutdown ($$) scenarios: in FFT of tip deflection, bearing defect has shown different influence compared to the healthy case (no defect). This means that the frequency response of structure in both healthy and faulty conditions is different and by studying FFT of system response and investigating their sensitivity indices, we could detect some faults sources in specific components.

5.4. HSS Torsional Model

The torsional model has been studied based on the faults sources introduced in the previous sections. Backlash effects on coupling creating nonlinearities to the system structure, motor torque ripple with specific peaks in the frequency domain, and bearing defect disturbance torque imposing on the rotor angular direction are applied within system modelling. In order to optimize the design and upgrade the structural performance, the system response must be studied based on these assumptions and compared with the healthy conditions. This gives a better insight to understand the faults sources and could facilitate the way to prevent the failures in drive train by creating structures which are less sensitive with respect to these faults sources. This could be studied within GSA by investigating and optimizing the sensitivity indices.

The sensitivity analysis for torsional model has been performed based on 3 different operational scenarios (see Figure 6) for motor speeds in steady state regime. In order to investigate the torsional model sensitivity analysis, the input parameters appearing in the governing equations corresponding to the model are chosen as follows:

$$ ()

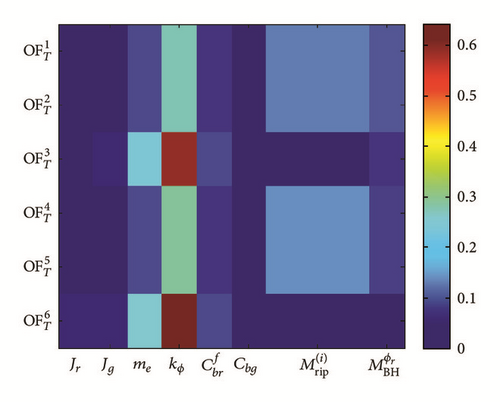
5.4.1. Torsion Vibration Model of Drive Train Test Rig with Backlash

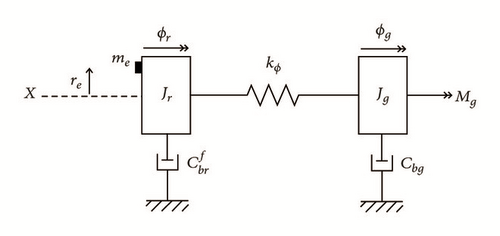
Upon considering only the torsional response of the test rig, the complete model in Section 2.1 is reduced, a lumped torsion vibration model. An engineering abstract of the model is depicted in Figure 14 and entails two inertias, disk J_r and generator rotor J_g, respectively. Each of these inertias is supported by bearings. The shaft and coupling flexibility is lumped together and represented by a torsion spring. Due to gravity and eccentric mass, there will be an external torque M_r(=m_er_egcos⁡ϕ_r) acting on the disk, and the induced electrical torque from the motor M_g acts on the generator rotor.

Hence, we have the following set of equations to describe the test rig torsional vibration response:

$$ ()

Here, we define $$ as combination structural damping in rotor and the bearing damping due to the friction.

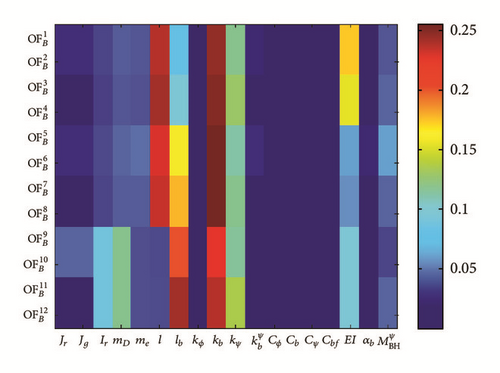
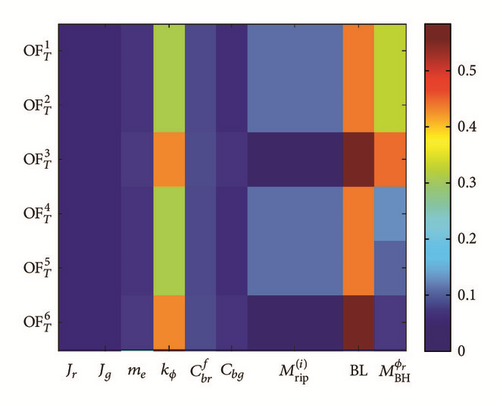
Based on the results (see Figure 15), it could be demonstrated that the most influential input parameters to the torsional objective functions are coupling torsional stiffness k_ϕ and backlash in coupling BL, motor torque ripples $$, and bearing defect parameter $$. Also, the structural damping of the rotor and bearing friction coefficient $$ has some effects to both primary and total sensitivity indices. The effects of damping coefficient (except the bearing damping) and rotor and motor mass inertia values (J_r and J_g) are not significant compared to the other aforementioned parameters. In total sensitivity $$, also eccentric mass has shown some impact which is expectable since it imposes an external torque to the structure.

More detailed analysis of the results based on each objective functions and influence of the input parameters is stated as follows.

(i) Coupling Torque in Transient and Steady State Regimes $$. The coupling torque has strong sensitivity in terms of torque ripple parameters $$ arising from the motor. This tells the significance of motor ripple assumption in drive trains as one type of fault source.

(ii) Coupling Torque and Its FFT in Shutdown Regime $$. It is clear that in shutdown regime there is no any torque ripple imposed by the motor, of which objective functions $$ and $$ sensitivity indices for torque ripples are identically zero.

In FFT, coupling torque influence is more than steady state case, since there is no ripple imposed by the motor. Also eccentric mass has some contribution especially in total sensitivity index.

(iii) Frequency Response of the Coupling Torque in Steady State Regime $$. In FFT of the coupling torque in steady state regime, the most dominant parameter is k_ϕ. Then the backlash and motor torque ripples have significant contribution. This tells that in vibration analysis it is very important to identify the vibration faults sources namely here backlash and ripple, which may affect the system structure in a severe way.

(iv) Bearing Defect Maximum Value $$. By increasing the bearing defect maximum torque (Figure 5), we could investigate its contribution to the sensitivity indices. The aim is to define the minimum value of defect parameter $$ such that the sensitivity indices related to this parameter would be larger than a specific value ($$ Nm). This methodology contributes to detect, predict, and prevent the faults and failures in bearings.

Summing up the results of GSA for torsional model, we could state that the most influential parameters are k_ϕ and faults sources BL and $$ and also C_bf, respectively.

For disturbance torque coming from bearing housing $$, we notice that its influence is more in total sensitivity index rather than primary one. This means that $$ influence is more when the other parameters are changed. The same conclusion could be made for ripple parameters $$.

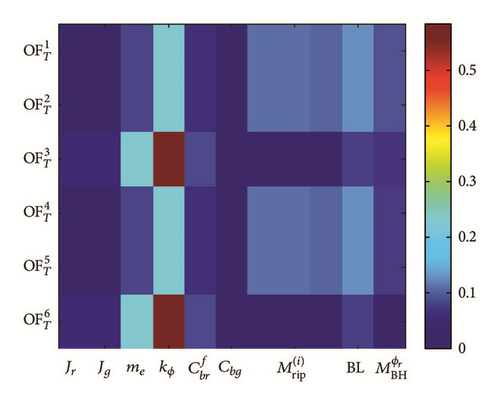
5.4.2. Torsional Model with No Backlash

In order to emphasize into the bearing fault detection, we study the system structure response based on no backlash (Figure 16). Then, we investigate the influence of the input parameters to the objective functions in case when the shaft coupling has a backlash.

The obtained results have led to the following conclusions:

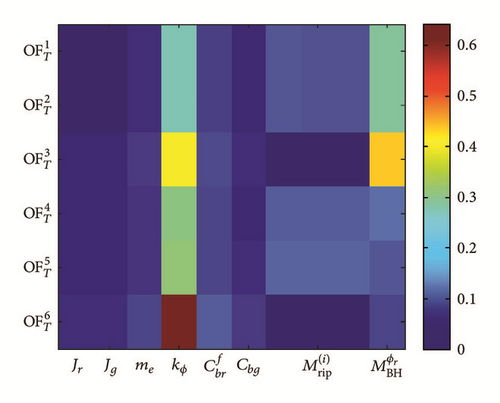
• (i)

  The bearing defect (quantified in terms of $$) could be detected easier in case where no backlash compared to with backlash (more contribution sensitivity indices especially the primary one). This is very important conclusion and means that, in the systems with a couple of sources of faults, the detectability of each fault may not be easy and it get more complex by introducing more complex system and assuming more faults.

• (ii)

  The influence of bearing defect in the FFT for first peak and the second peaks is small, though recognizable. This draws the same conclusion for the bending model with defect, which tells that some specific peaks in the FFT correspond to the system structural faults.

5.5. Special Cases: Resonance Investigation

The operating speed ranges in wind turbines and system excitation frequency have a wide range. The system may encounter resonances leading to severe vibration and affect the normal operation of the machine. Thus, the drive train dynamics must be studied with more focus in excitation ranges.

To focus on the excitation ranges, we investigate the primary and secondary sensitivity indices within the case in which the input parameters leads to resonance. It means that we only take the randomized input parameters which are near to the resonance frequency of the system in terms of bending and torsion:

$$ ()

where SYS(X) and SYS(c) denote for the system eigenvalue based on randomized set of X and nominal structural parameters presented in Table 1, respectively. Also TOL = 1 Hz is considered as a tolerance for frequency fluctuation.

Some conclusions could be made based on aforementioned cases, and the results are presented in Figures 17 and 18.

• (i)

  By selecting those randomized variables which based on them the eigenfrequency of the structure is near to specific value (50 Hz), the sensitivity of eigenfrequency variables takes the most contribution. This is expectable since in the resonance points the system influential parameters are only the ones which the eigenfrequency of the system is based on them.

• (ii)

  In optimum case, where the randomized values are identical to the bending and torsional eigenfrequencies, we expect that only the input parameters have influence that they are in the eigenfrequency definition.

6. Conclusion and Outlook

The global sensitivity analysis for both torsional and bending models of high speed shaft drive train test rig with respect to its structural parameters has been carried out using M-DRM method.

The current study showed the feasibility and efficiency of the M-DRM for global sensitivity analysis of nonlinear dynamical system (high speed shaft drive train), which provided the results in a computationally efficient framework. The M-DRM applied here revealed practical significant results which can reduce the number of input design parameters for optimization of wind turbine drive train systems.

By comparing the sensitivity of objective functions with respect to different input structural parameters, a better understanding of drive train system dynamics is obtained. Vertical and lateral deflections in bearing housing and tip, coupling torque in 3 different operational scenarios, FFT of these functions, have been introduced as the objective functions to represent the test rig dynamic performance. To reflect the effect of operational scenarios, the aforementioned outputs have been evaluated within transient, steady state, and shutdown cases in 3 different motor speeds. The effect of the fundamental structural parameters on the dynamic response of the HSS drive train test rig has been recognized. By comparing the sensitivity indices of corresponding objective functions, a better understanding of drive train system dynamics is obtained.

The global sensitivity analysis provided a useful method to deeply understand some aspects of the initial structural parameters to the dynamic outputs. At this stage, a preliminary assessment of the key parameters has been performed. Moreover, fault modelling in functional components such as motor ripples, bearing defects, coupling backlash, and their detectability within GSA has been investigated. This facilitates understanding the faults sources and their effect to other functional components, which leads to better design and optimize drive trains more efficiently with less failure.

Conflicts of Interest

The authors declare that they have no conflicts of interest.