Reentry Trajectory Optimization for a Hypersonic Vehicle Based on an Improved Adaptive Fireworks Algorithm

1. Introduction

In recent decades, global strike and space transportation have spurred more and more interests in hypersonic vehicles (HVs) [1] for both military and civilian applications. The development of advanced guidance and control technologies for HV is promoted to meet the need for an effective and reliable access to the space. With aerodynamic control, the unpowered HV has the ability of reentering and gliding through the atmosphere. In order to steer an efficient and safety flight in the complex conditions, the reentry trajectory optimization problem of HV has been widely of concern. The aim of reentry trajectory optimization is to find an optimal solution under the reentry flight dynamics and physics, given the aerodynamics, structural strength, and the thermal protection system [2]. Besides, as the reentry dynamics is highly nonlinear, the reentry trajectory optimization is a nonconvex problem with multiple constraints, such as the control ability, heating rate, dynamic pressure, and aerodynamic load. Thus, it is difficult to solve these problems analytically, and numerical techniques are required to determine an approximation to the continuous solution.

There are two main kinds of numerical methods to solve trajectory optimization problems: indirect methods and direct methods [3]. In indirect methods [4], the original problem is transformed into a two-point boundary problem by applying the calculus of variations or the Pontryagin maximum principle. It has high accuracy, and it ensures that the solution satisfies the necessary optimality conditions. However, in indirect methods, it is quite complicated to derive the necessary optimality conditions. Besides, the radius of convergence is small, and it is difficult to guess the initial value of costate variable [5].

In order to overcome the disadvantages of indirect methods, direct methods have been developed, which are classified into two main types: direct shooting method and collocation methods. In the direct shooting method, only the control variables are parameterized and explicit numerical integration is used to satisfy the differential equation constraints. As an improvement, collocation methods [6–9] discretize both the states and control variables, and they use piecewise or global polynomials to approximate the differential equations at collocation points. Pseudospectral methods (PMs) are frequently used collocation methods, which include Gauss PM (GPM) [10, 11], Legendre PM (LPM), Radau PM (RPM) [12], and Chebyshev PM (CPM) [13]. By direct methods, the reentry trajectory optimization problem with infinite dimensions is transformed into the nonlinear programming problem (NLP) with finite dimensions, which is usually a high-dimensional multimodal nonsmooth problem. Some deterministic methods, such as sequential quadratic programming (SQP) [6, 14], second-order cone programming (SOCP) [15], and sequential convex programming method [16], are used to solve it. However, deterministic algorithms are sensitive, and they are easy to be stagnated at a local optimal point.

In the recent years, intelligent algorithms with the global searching ability, which are easy to implement, have been applied to solve the reentry trajectory optimization problems with the development of computational technology [14, 17–24]. In [17], a hybrid genetic algorithm (GA) collocation method was introduced for trajectory optimization, in which the initial guesses for the state and control variables are interpolated by the best solution of GA. Zhao and Zhou employed the particle swarm optimization (PSO) to obtain the end-to-end trajectory for hypersonic reentry vehicles in a quite simple formulation [19]. Zhang et al. applied the ant colony algorithm (ACO) to generate the optimal reentry trajectory for a reusable launch vehicle (RLV) [20]. Additionally, differential evolution (DE) [21, 22] that mimicked the process of nature evolution and simulated annealing (SA) inspired by annealing in metallurgy was also introduced to deal with reentry trajectory optimization problems.

Among these intelligent algorithms, the fireworks algorithm (FWA) is a relatively new swarm intelligence method firstly proposed by Tan and Zhu [25]. Inspired by the fireworks explosion, the algorithm selects some locations as the fireworks in space, each for exploding to generate a shower of sparks. Through the explosion procedure of the FWA, the diversity of population is enhanced. Besides, owing to the powerful local search capabilities and distributed parallel search mechanism, the FWA has a faster convergence speed compared with other intelligent algorithms.

The enhanced fireworks algorithm (EFWA) [26] is an improved version of the FWA in some operators. To improve the EFWA, the adaptive fireworks algorithm (AFWA) [27] was proposed with an adaptive explosion amplitude, which is calculated according to the fitness of individuals adaptively. Afterwards, some improved FWA were proposed and applied in solving various practical optimization problems. For example, Gao and Ming [28] combined the cultural algorithm (CA) with the FWA for the digital filter design. Zheng et al. [29] developed a hybrid FWA with DE operators to improve the diversity and avoid prematurity. Based on a self-adaption principle and bimodal Gaussian function, Xue et al. [30] proposed an advanced FWA to design the PID controllers with high-quality performances. From the previous research, it is recognized that the information interaction among all individuals of the FWA is relatively poor, whereas the interaction is vital in swarm intelligence algorithms. Thus, when solving complex multimodal problem of the optimal reentry trajectory generation, it may be easy to get trapped in a local optimum. As far as we are concerned, the application of the FWA for reentry trajectory optimization is scarce and has not been found in the published literature.

In this paper, we focus on the improvement of the AFWA and its application to the reentry trajectory optimization problems. Firstly, an improved version of the AFWA (I-AFWA) is developed by combining the standard AFWA (S-AFWA) with a new mutation strategy. In each iteration of the algorithm, the new mutation operator and auxiliary mutation individual selection strategy are applied to make Gaussian fireworks learn from more individuals (not only the best individual) and generate diverse sparks from all fireworks and explosion sparks. The interactions of the fireworks and sparks are enhanced to further improve the diversity of the population and avoid being trapped in local optima too early. Then, the I-AFWA is applied to the reentry trajectory optimization problems. The problem is transformed into NLP by using Chebyshev polynomial interpolation to discretize the angle of attack (AOA) and bank angle simultaneously, and the scope of the AOA is figured out by path constraints to simplify the problem. Next, a constraint-handling technique based on the adaptive penalty function and the distance measure is proposed to incorporate with the I-AFWA and used to deal with the multiconstrained parameter optimization problem. Finally, two reentry scenarios are given to illustrate the validity and effectiveness of the proposed I-AFWA method on the reentry trajectory optimization problem.

The remainder of this paper is organized as follows. The general reentry trajectory optimization problem is formulated in Section 2. Section 3 proposes the I-AFWA with a new mutation strategy, and a constraint-handling technique is incorporated with the I-AFWA for the reentry trajectory optimization. In Section 4, two different reentry tasks for HV are presented to evaluate the proposed algorithm. A few conclusions are made in Section 5.

2. Problem Formulation

2.1. Reentry Dynamics

Using a spherical rotating Earth model, the three-degree-of-freedom (3DOF) point mass dynamics equations [31] of a hypersonic reentry vehicle are described as follows:

$$ (1)

$$ (2)

$$ (3)

$$ (4)

$$ (5)

$$ (6)

where r is the radial distance from the center of the Earth to the vehicle. θ and ϕ are the longitude and latitude, respectively. v is the Earth-relative velocity. γ is the velocity flight path angle and ψ is the velocity heading angle measured from the North in a clockwise direction. σ is the bank angle, which is the angle between the vehicle longitudinal symmetry plane and the vertical plane [2]. ω_e is the Earth’s self-rotation angular velocity, and g = μ/r² is the gravitational acceleration where μ is the gravitational constant. L and D are the aerodynamic lift force and drag force, respectively, which are given as follows:

$$ (7)

where ρ = ρ₀exp(−h/h_s) is the density of atmosphere, with ρ₀ as the density of atmosphere at sea level, h_s as the scalar height coefficient, and h as the altitude from the sea level. h = r − r_e, where r_e denotes the Earth’s radius. S_ref and m are the aerodynamic reference area and mass of the vehicle, respectively. C_L and C_D are the lift and drag coefficients determined by the AOA α and Mach number M_a = v/V_s(r). α denotes the angle between the relative velocity and a reference line fixed with respect to the vehicle body [2], which does not occur explicitly in the equations and appear through the aerodynamic forces L and D. Given the altitude h, velocity v, and the AOA α, the Mach number M_a is calculated, and then the corresponding lift and drag coefficient C_L and C_D values are found by looking up the table functions with the value of M_a and α. The independent variable is the time t, and control variables are α and σ. The geometric sketch of reentry flight is shown in Figure 1.

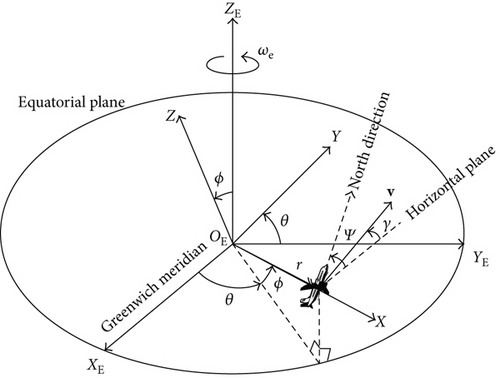
2.2. Multiple Constraints

2.2.1. Heating Rate

$$ indicates the heating rate at a specified point on the surface of the reentry vehicle, which normally chooses the stagnation point on the nose. It is determined by the atmospheric density and Earth-relative velocity [31], which must be limited as follows:

$$ (8)

where k_Q is the heating rate normalization constant. c is the constant coefficient that typically takes the value of 3.0, 3.15, or 3.25. $$ represents the maximum allowable value of heating rate.

2.2.2. Dynamic Pressure

The dynamic pressure q is a typical path constraint, and it is limited to control the hinge moment of an actuator in a reasonable range. The peak value of the dynamic pressure must be less than the maximum value q_max as follows:

$$ (9)

2.2.3. Aerodynamic Load

In order to protect the mechanical system, the instantaneous value of aerodynamic load in the body-normal direction n_T is given lower than the maximum value n_Tmax as follows:

$$ (10)

2.2.4. Quasi-Equilibrium Glide Condition

As the flight path angle is small and varies relatively slowly in a major portion of the lifting reentry trajectory [32], we set $$ and ignore the Earth’s self-rotation in (5), and it generates

$$ (11)

This is the so called quasi-equilibrium glide condition (QEGC) [32], which guarantees that the reentry trajectory does not oscillate acutely for the convenience of the attitude controller design. It is a soft condition that forms the upper boundary of altitude-velocity reentry corridor. Additionally, hard constraints including heating rate, dynamic pressure, and aerodynamic load form the lower boundary of altitude reentry corridor. Therefore, the altitude-velocity reentry corridor is illustrated in Figure 2.

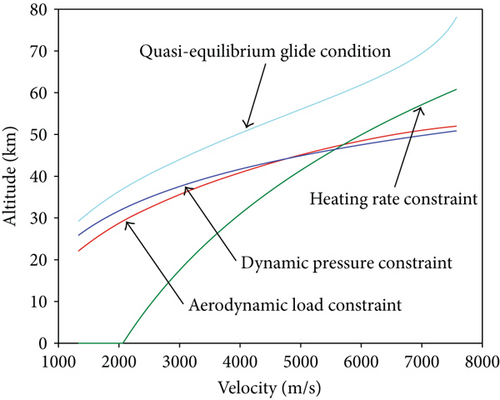
2.2.5. Control Boundary

To maintain the stability of the reentry vehicle, it is necessary to limit the two control variables of AOA and bank angle as follows:

$$ (12)

2.2.6. Terminal Conditions

Given the different reentry flight missions and conditions, the terminal states, including terminal altitude, position, velocity, flight path angle, and heading angle, are restrained as follows:

$$ (13)

where t_f is the terminal time of the reentry phase, and r_f, θ_f, ϕ_f, v_f, γ_f, and ψ_f represent the ideal reentry terminal states, respectively.

3. Trajectory Optimization Algorithm Description

Reentry trajectory optimization problem is a continuous optimal control problem with infinite dimensions, so it is difficult to solve directly. To solve this problem, we first transform it to a finite dimensional NLP by the discretization of control curves with Chebyshev polynomial interpolation. However, it is also difficult to optimize the AOA and bank angle simultaneously, so we obtain the scope of AOA by path constraints ((8), (9), (10), and (11)). Subsequently, a constraint-handling technique based on an adaptive penalty function and a distance measure is proposed to deal with multiple constraints. Finally, a new improved AFWA with a new mutation strategy is developed to solve the NLP.

3.4. Improved Adaptive Fireworks Algorithm

Although there are some variants for the AFWA, premature convergence when solving complex multimodal problems of the optimal reentry trajectory generation is still the main deficiency of the AFWA. The search process of the AFWA indicates that the diversification mechanism is not very flexible, and in particular it does not utilize more information about other better quality solutions in the swarm. Especially, the interaction of fireworks in the explosion operator is not sufficient when obtaining the number and amplitude of the fireworks, which can be easily polarized. In other words, the best firework may generate an overwhelming number of sparks, while the other fireworks produce very few sparks. In the mutation operator, the interaction between the explosion sparks is ignored, and thus the diversity of sparks is reduced. Besides, the mutation sparks can hardly be passed down to the next generation [35]. For a D-dimensional optimization problem, the fitness of an individual may be determined by values in all dimensions, and an individual that has discovered the region corresponding to the global optimum in some dimensions may have a low fitness value because of the poor solutions in the other dimensions [36]. Thus, it is vital to generate more diverse sparks in all dimensions.

In order to make use of the beneficial information in the population more effectively to generate better quality solutions, a new mutation strategy is proposed to improve the S-AFWA, which can enhance the diversity of the population and improve the global search capability. In the new mutation strategy, the location of the mutation spark X_j is generated by the selected firework X_i in all dimensions as follows:

$$ (42)

where a_i = [a_i(1), a_i(2), …, a_i(D)] defines which individual the selected firework X_i should follow; that is, X_i stretches along the direction between the selected individual and itself. $$ is the corresponding kth dimension of any individual (all fireworks and explosion sparks, including itself), and the decision depends on the mutation probability P_i, which can take different values for different fireworks.

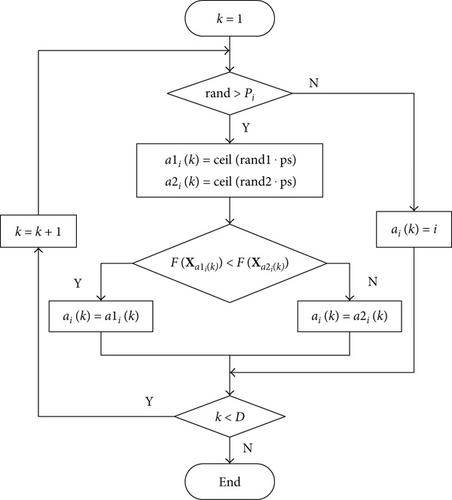
For each dimension of the firework X_i, a random number is generated. If the random number is greater than P_i, the corresponding dimension will learn from another individual; otherwise, it will learn from itself. We employ a selection procedure of a_i(k) when the dimension of the firework learns from another individual as follows.

Firstly, two individuals (excluding the selected firework X_i) are randomly selected among the population. Subsequently, compare the fitness values of the two individuals and select the better one. At last, the winner is used as the exemplar to learn from for that dimension.

After the above selection procedure, if all exemplars in different dimensions of the firework are itself (i.e., a_i(k) = i in all dimensions; due to that, all generated random numbers above are less than P_i), we will randomly choose one dimension to learn from the corresponding dimension of another individual. The detailed procedure of choosing a_i in (42) is given in Figure 3, where the ceil operator obtains the smallest integer greater than or equal to the specified expression and ps = n + m − 1 is the population size.

The new mutation strategy can generate new spark in the search space using the information from all the individuals, and thus the interaction between the fireworks and sparks is enhanced, not limited to the selected firework and the best firework. The proposed mutation strategy exhibits a larger potential search space for mutation sparks than that of the S-AFWA, and thus the diversity is also enhanced. Especially when the best firework falls into the local optimum region, the mutation sparks have the increasing ability to jump out of the local optimum via the cooperative behavior of the whole population.

In order to address optimization problems in a general manner, each firework has a different mutation probability P_i. Therefore, fireworks have different levels of exploration and exploitation ability in the population, and they are able to solve diverse problems. We empirically set the mutation probability for each firework as follows:

$$ (43)

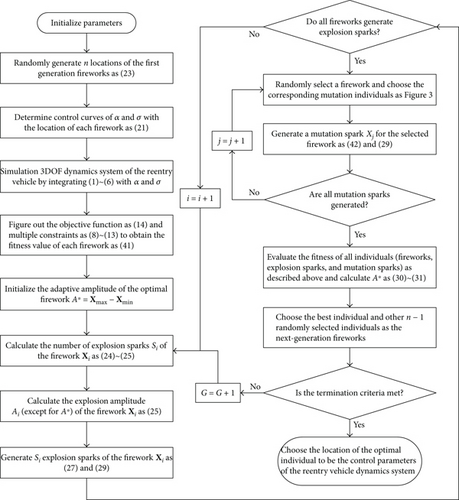
In detail, the procedure of reentry trajectory optimization based on the I-AFWA with a new mutation strategy is depicted in Figure 4.

4. Simulation and Results

In order to verify the effectiveness of the proposed algorithm, the I-AFWA is tested in comparison with the S-AFWA, DE, PSO, GA, and FWA. These algorithms all run 20 times repeatedly based on a similar simulation environment. The population size (spark size in the I-AFWA, S-AFWA, and FWA and particle number in DE, PSO, and GA) is set as 50, and the maximum number of function evaluations G_max = 100000 for all algorithms. The AOA discrete point number N_α = 5, and bank angle discrete point number N_σ = 10. Besides, other main parameters are shown in Table 1.

In order to deal with multiple constraints, these six algorithms all adopt the constraint-handling technique proposed in this paper. The simulation of reentry trajectory optimization is conducted on two cases using different objective functions: minimum downrange and minimum total heat.

4.1. Minimum Downrange Trajectory

For convenience of description, the definition of the standard reentry longitudinal plane and related concepts is given. The schematic diagram of the downrange is presented in Figure 5, where r₀ and v₀ are the position vector and velocity vector, respectively, of the reentry point. O_E is the center of the Earth, and r_f is the position vector of the reentry terminal point. The standard reentry longitudinal plane is a plane composed of r₀ and v₀, and r_b is the projection of r_f on this plane. The vector n is the unit normal vector of the plane. The motion in the standard longitudinal plane is called the longitudinal motion, and the motion deviating from the plane is called the lateral motion. Therefore, the reentry downrange Z is defined as the arc length of a circle with the radius of r_f corresponding to the angle δ_Z between vectors r_b and r₀, which is formulated as follows:

$$ (46)

where the relevant parameters are defined as

$$ (47)

where r₀, θ₀, ϕ₀, v₀, γ₀, and ψ₀ represent the initial states of the reentry phase.

In the minimum downrange reentry trajectory optimization, the terminal constraints of the longitude, latitude, and heading angle need not be considered, and the objective function is given as

$$ (48)

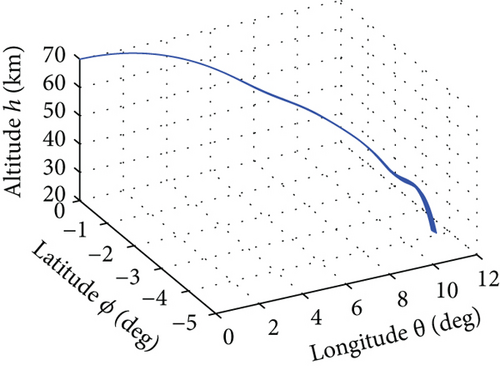
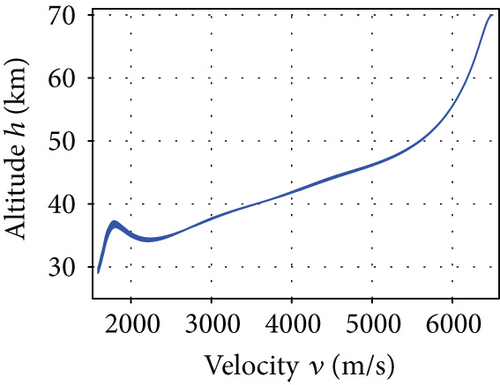
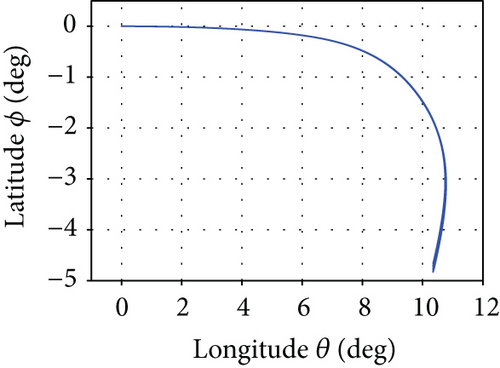
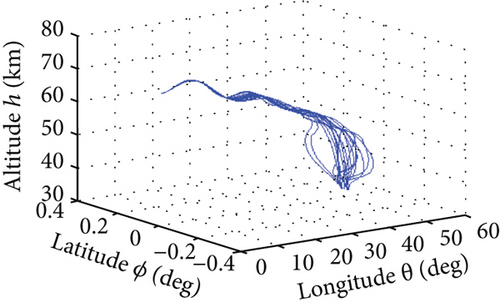
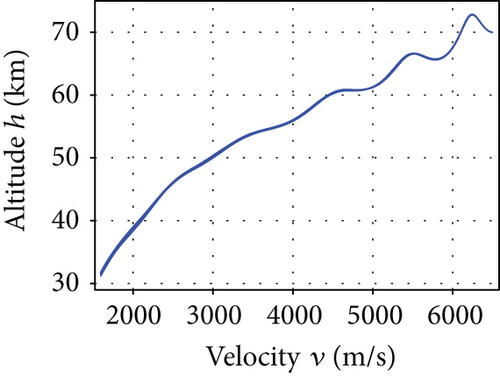
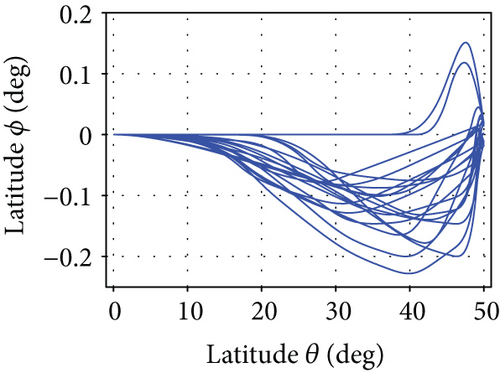
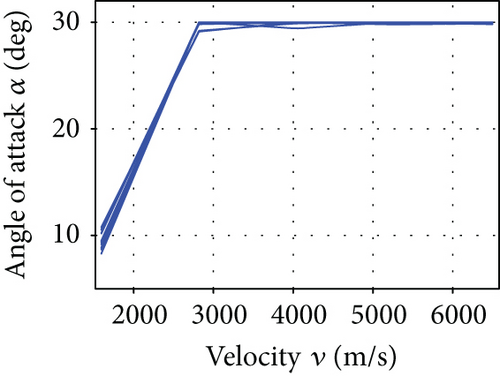
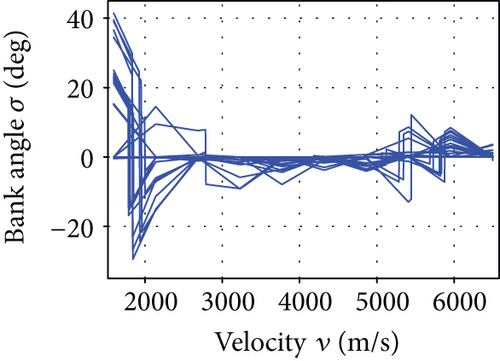
The average convergence curves of the six comparative algorithms are illustrated in Figure 6. As we can see, in the minimum downrange reentry trajectory optimization, both the convergence speed and the final optimization result of our I-AFWA are better, when compared with those of the other five algorithms. Figure 7 presents the simulation results under running the I-AFWA 20 times, including the 3D trajectory, ground trajectory, control curves, and path constraint curves. It can be found that all constraints are satisfied and the reentry trajectory and control profiles are smooth throughout the flight, which indicate that our algorithm is quite efficient in handling multiple constraints.

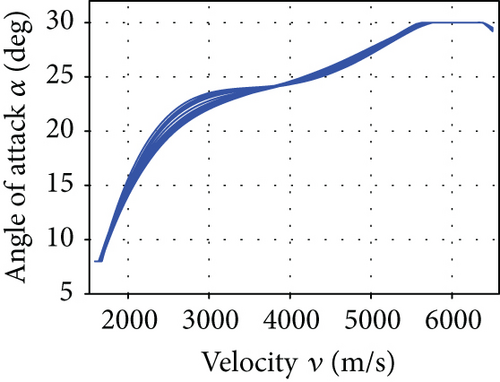
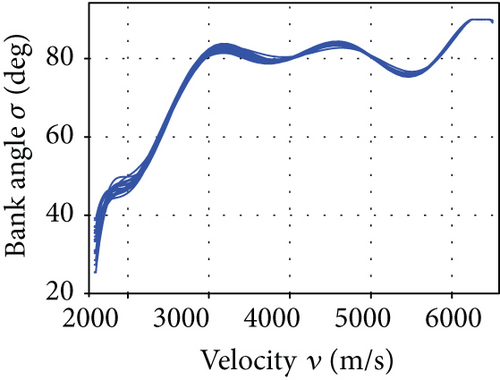
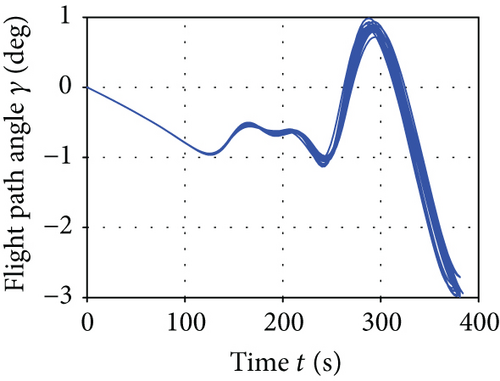
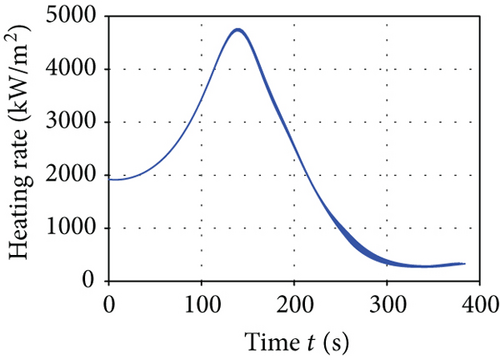
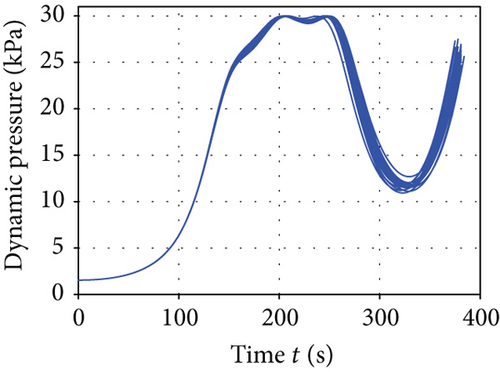
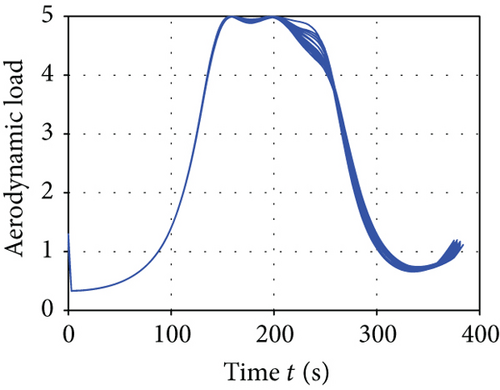
The mean and standard deviation of the optimization performance index, path constraints, and terminal constraints of minimum downrange reentry trajectory obtained by the six intelligent algorithms are presented in Table 2. The performance index of the minimum downrange generated by the I-AFWA is much better than that generated by the S-AFWA, DE, PSO, GA, and FWA, which demonstrates that the optimization precision of the I-AFWA is higher and our improvement strategy is effective. Besides, the distribution range of the minimum downrange is very small, which shows that the I-AFWA achieves better performance and robustness.

Table 2. Performance index and constraints in minimum downrange reentry trajectory optimization with the six comparative algorithms.

Evaluation index	I-AFWA		S-AFWA		DE		PSO		GA		FWA
	Mean	Std	Mean	Std	Mean	Std	Mean	Std	Mean	Std	Mean	Std
Zf (km)	1152.1	0.8	1182.6	2.2	1155.8	1.5	1187.5	26.1	1240.3	1.8	1522.8	63.5
$$ (kW/m2)	4974.1	9.8	4745.3	12.5	4899.3	38.1	4699.6	113.9	4830.5	59.2	4720.4	150.8
max(q) (kPa)	29.991	7e − 3	29.469	0.036	29.840	0.071	29.955	0.121	29.535	0.096	28.737	0.334
max(nT) (g)	4.995	1e − 3	4.967	0.118	4.999	3e − 4	4.996	3e − 3	4.984	0.047	4.835	0.686
|Δr(tf)| (km)	0.96	0.07	0.89	0.53	0.75	0.46	1.32	0.41	1.05	0.38	1.18	0.77
|Δv(tf)| (m/s)	9.82	0.18	9.95	0.09	9.96	0.10	9.81	0.60	9.89	0.21	8.84	1.08
|Δγ(tf)| (°)	0.197	0.102	0.784	0.173	0.879	0.084	0.886	0.124	0.913	0.236	0.656	0.455
Run time (s)	78.3	—	76.5	—	91.5	—	70.6	—	87.5	—	74.2	—

The minimum downrange of the reentry vehicle is 1151.8 km, and the corresponding trajectory has a larger AOA, which can increase the aerodynamic drag force and decrease the lift-drag ratio, thus consuming more energy and reducing the maneuver capacity of reentry vehicles, resulting in smaller flight downrange.

4.2. Minimum Total Heat Trajectory

The objective function of minimum total heat reentry trajectory optimization problem is given as follows:

$$ (49)

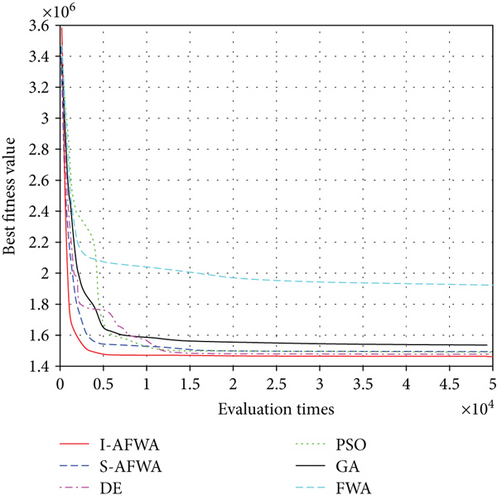
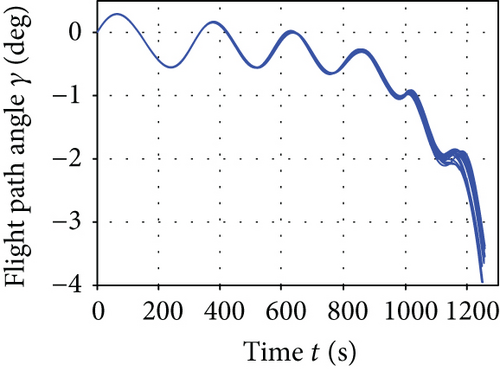
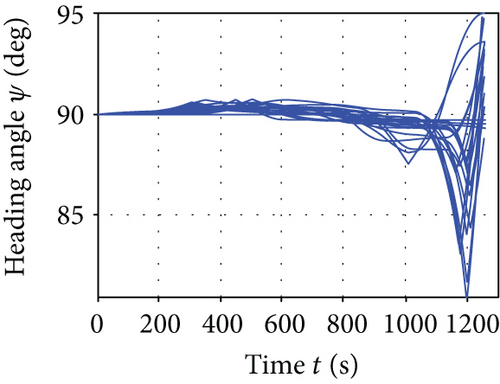
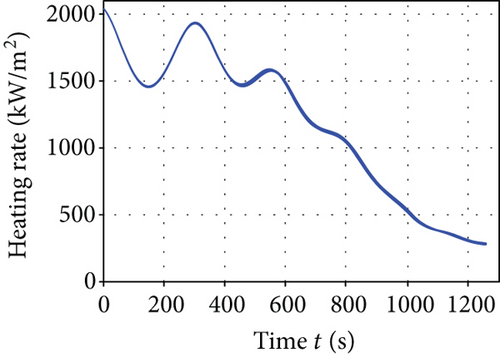
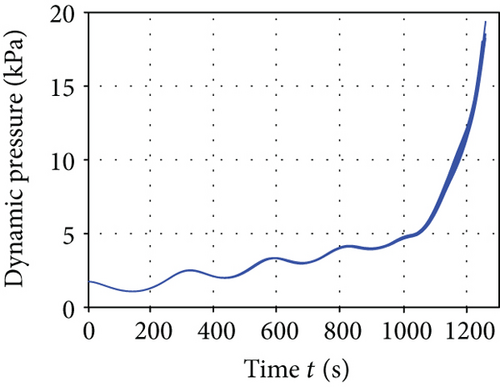
Figure 8 presents the average convergence curves of the comparative algorithms. It can be seen that the I-AFWA also has the fastest convergence speed in the six algorithms. The simulation results using the I-AFWA, including the state and control profiles, are depicted in Figure 9. The minimum total heat and constraints of minimum total heat reentry trajectory with the six algorithms are compared in Table 3. The terminal constraints, such as the final altitude, longitude, latitude, velocity, flight path angle, and heading angle, are satisfied accurately. The heating rate, dynamic pressure, and aerodynamic load are less than the maximum allowable values strictly. The minimum total heat of the I-AFWA is much smaller than that of the other five algorithms, which proves once again that the optimization results of the I-AFWA are better. Additionally, the variance of the performance index is also relatively small.

Table 3. Performance index and constraints of minimum total heat reentry trajectory optimization with the six comparative algorithms.

Evaluation index	I-AFWA		S-AFWA		DE		PSO		GA		FWA
	Mean	Std	Mean	Std	Mean	Std	Mean	Std	Mean	Std	Mean	Std
Q (kJ)	1.472e6	2.1e3	1.489e6	8.0e3	1.482e6	1.5e3	1.493e6	6.5e3	1.535e6	4.3e3	1.922e6	9.7e3
$$ (kW/m2)	2037.9	7.8e − 3	2452.2	8.2	2448.5	1.3	2532.8	11.8	2483.2	4.8	2756.5	32.8
max(q) (kPa)	18.053	0.342	24.439	3.0e − 2	19.854	0.771	20.955	1.210	21.386	1.005	24.852	2.363
max(nT) (g)	1.081	2.3e − 2	2.883	0.375	1.975	0.126	2.293	0.531	2.132	0.154	2.379	0.612
|Δr(tf)| (km)	1.70	0.12	0.95	0.61	1.78	0.06	1.03	0.55	1.43	0.23	1.15	0.64
|Δθ(tf)| (°)	2.50e − 2	1.14e − 2	3.78e − 2	6.73e − 3	3.52e − 2	1.24e − 2	3.89e − 2	1.33e − 2	4.06e − 2	8.57e − 3	3.12e − 2	1.81e − 2
|Δϕ(tf)| (°)	1.53e − 2	4.14e − 3	3.34e − 2	8.35e − 3	2.48e − 2	1.15e − 2	3.14e − 2	1.85e − 2	4.37e − 2	1.02e − 2	2.89e − 2	1.44e − 2
|Δv(tf)| (m/s)	5.52	0.28	7.95	2.23	7.63	0.87	8.32	0.43	6.68	0.95	7.32	1.76
|Δγ(tf)| (°)	0.598	0.199	0.753	0.272	0.680	0.142	0.833	0.105	0.768	0.176	0.712	0.235
|Δψ(tf)| (°)	2.432	1.691	2.833	1.125	3.435	0.693	3.236	1.135	3.585	0.937	4.018	1.244
Run time (s)	258.4	—	250.5	—	287.1	—	232.8	—	274.6	—	242.7	—

From the simulation results, it can be seen that the minimum total heat of this reentry scenario is about 1.47 × 10⁶ kJ, maybe smaller in fact. The reentry trajectory with minimum total heat corresponds to larger AOA and smaller bank angle, where the aerodynamic lift force of the vehicle is relatively large, the flight altitude is higher, and the atmospheric density is lower, thus reducing the heating rate (in terms of (8)) and decreasing the total heat; when the velocity is lower (close to the end of the reentry phase), pull down the AOA, so that the flight height drops rapidly, and meanwhile lateral maneuver is carried out to consume excess energy, making the vehicle reach the reentry terminal states and complete the flight mission.

Tables 2 and 3 also give the run time of each algorithm in the last row. On the two objective functions, we can see that the run time of the I-AFWA is typically a little more than that of the S-AFWA, which is mainly because the I-AFWA takes more computational time on the selection of auxiliary mutation individuals. Note that the run time of PSO is the smallest and that of DE is the largest. However, for reentry trajectory optimization problem, compared with the long flight time, the little gap between the run times of the I-AFWA and S-AFWA is almost negligible. Although PSO runs much faster, the optimization result is relatively poor; DE is just the opposite. The running speed of the FWA is second only to that of PSO, but its optimization result is the worst. GA presents relatively poor performances in both two aspects.

In summary, the results of the numerical simulations demonstrate that the proposed new mutation strategy, which enhances the information interactions between the fireworks and sparks to a great extent, can greatly improve the population diversity and thus avoid premature convergence during the search. Consequently, the I-AFWA can achieve a much better balance of exploration and exploitation than S-AFWA, DE, PSO, GA, and FWA and thus improve convergence speed and solution accuracy effectively.

5. Conclusion

In this paper, based on the AFWA and a new mutation strategy, a new optimization algorithm called the I-AFWA is proposed to generate an optimal trajectory for a hypersonic reentry vehicle under multiple constraints. By incorporating the new mutation operator and auxiliary mutation individual selection strategy to the S-AFWA, the information sharing among the fireworks and sparks is enhanced to generate more diverse individuals, and thus the global search capability is improved. Additionally, based on the distance measure and adaptive penalty function, a constraint-handling technique is developed to deal with all path and terminal constraints. The I-AFWA-based optimal reentry trajectory generation method takes all control variables into consideration, which makes it have high fidelity.

The simulation results of two different reentry missions are used to validate the reentry trajectory optimization algorithm, and some analyses are conducted. It is indicated that the I-AFWA exhibits better search efficiency and achieves better optimization performance than S-AFWA, DE, PSO, GA, and FWA. Besides, the convergence speed of the I-AFWA is also the fastest. The I-AFWA can also be applied to other optimization functions and other optimization problems. However, due to the increased computational cost caused by the selection process of auxiliary mutation individuals, the running speed of the I-AFWA is not the fastest one among all the algorithms. In the future research, the proposed algorithm will be further studied and tested on more complicated reentry scenarios involving waypoint and no-fly zone constraints.

Conflicts of Interest

The authors declare that there is no conflict of interests regarding the publication of this paper.