The Existence and Structure of Rotational Systems in the Circle
Abstract
By a rotational system, we mean a closed subset X of the circle, , together with a continuous transformation f : X → X with the requirements that the dynamical system (X, f) be minimal and that f respect the standard orientation of . We show that infinite rotational systems (X, f), with the property that map f has finite preimages, are extensions of irrational rotations of the circle. Such systems have been studied when they arise as invariant subsets of certain specific mappings, . Because our main result makes no explicit mention of a global transformation on , we show that such a structure theorem holds for rotational systems that arise as invariant sets of any continuous transformation with finite preimages. In particular, there are no explicit conditions on the degree of F. We then give a development of known results in the case where F(θ) = d · θmod1 for an integer d > 1. The paper concludes with a construction of infinite rotational sets for mappings of the unit circle of degree larger than one whose lift to the universal cover is monotonic.
1. Introduction
In what follows, denotes the unit circle with the standard orientation.
Definition 1. Let . A continuous transformation f : X → X preserves cyclic order if, for any A, B, C ∈ X with distinct images, the arcs ABC and f(A)f(B)f(C) have the same orientation.
Definition 2. A rotational system is a subset and a continuous transformation f : X → X, with the properties that
- (i)
the dynamical system (X, f) is minimal,
- (ii)
the transformation f : X → X preserves cyclic order.
In this situation, we will simply say that (X, f) is rotational.
We need to recall one more definition, before stating the main theorem.
Definition 3. Let fi : Xi → Xi be continuous transformations of compact metric spaces for i = 1,2. The dynamical system (X1, f1) is an extension of (X2, f2) if there is a continuous, surjective function ϕ : X1 → X2 such that ϕ∘f1 = f2∘ϕ.
Our main result is as follows.
Theorem 4. Let (X, f) be a rotational system such that X is an infinite, proper subset of . In addition, suppose that the continuous mapping f : X → X has finite preimages, that is, |T−1x| < ∞ for each x ∈ X. Then,
- (i)
the dynamical system (X, f) is an extension of an irrational rotation of the circle via a map that is compatible with the cyclic ordering on both X and T;
- (ii)
the function ϕ has preimages of cardinality one except at countably many points of . The preimages of these exceptional points have cardinality two and are the endpoints of gaps of the set X in ;
- (iii)
(X, f) has a unique ergodic measure μ and ϕ∗μ is the standard Lebesgue measure on .
The angle of the rotation of in the preceding theorem is called the rotation number of (X, f).
Such systems are of particular interest when they arise as invariant subsets of a continuous mapping on the whole circle, . Recall that a closed subset X of is invariant with respect to F if F(X)⊆X. In this situation, we may set f = F|X and consider the dynamical system (X, f). Such a system, (X, f), is a subsystem of .
Our main theorem has the following obvious corollary.
Corollary 5. Let be a continuous mapping with finite preimages. Suppose, moreover, that X is a closed, infinite, proper subset of that is invariant with respect to F. If (X, f) is rotational, then all three conclusions of Theorem 4 hold.
In the case where is given by F(θ) = d · θ mod1 for an integer d > 1, Corollary 5 has an extensive history. Ideas related to the d = 2 case were studied by Morse and Hedlund [1] in their work on Sturmian trajectories. The problem was taken up later by several authors, including Gambaudo et al. [2], Veerman [3, 4], Goldberg [5], Goldberg and Milnor [6], and Bullett and Sentenac [7]. The d > 2 case was studied by Goldberg and Tresser [8], Blokh et al. [9], and Bowman et al. [10]. In sum, these works provide a complete characterization of the rotational subsystems, with rational and irrational rotation number, for the uniform cover of with positive degree.
In this paper, we point out that parts of the analysis of rotational systems with irrational rotation number can be done without explicit reference to an ambient transformation on the unit circle. This leads to a structure result for rotational subsystems of a wide class of continuous transformations , those with finite preimages.
The proof of Theorem 4 will be accomplished over the next two sections. An important step is to solve the functional equation found in Proposition 16. This equation is mentioned in the appendix in [8] where an analytical approach to the uniform cover case is sketched. (In particular, for the direction we are interested in, a solution to the functional equation is claimed but not given.) We provide a solution to this problem in our more general setting using the existence of an invariant measure together with the Mean Ergodic Theorem. Sections 4 and 5 then revisit the known d-fold cover case (see [3, 4, 8, 9]) from our point of view.
For a given continuous , Theorem 4 and its corollary shed no light on how to determine which irrational numbers can be realized by rotational subsystems of . When degF = 1, it is well known that there can be at most one such rotation number. In the uniform cover case with d > 1, every irrational number in [0,1 can be achieved. In the last section, we consider degree d > 1 mappings of that are monotonic with respect to the usual orientation. Mappings of this type can have intervals of constancy or an arbitrary number of fixed points (many of which may be attractive). In particular, they are not conjugate to the uniform cover case via a homeomorphism. We show that, with at most countable exceptions, every irrational rotation number can be realized when the degree is two. When the degree is larger than 2, there are examples for every irrational rotation number.
2. Structure of Rotational Subsets
- (i)
(X, f) is a rotational system.
- (ii)
X is an infinite, proper subset of .
- (iii)
f : X → X has finite preimages.
Proposition 6. The set X is a Cantor set; that is, it is a compact set that is perfect and has empty interior.
Proof. Suppose θ0 ∈ X is an isolated point of such a dynamical system. Minimality implies that the orbit, , is dense in X. As a consequence, we have that fn(θ0) = θ0 for some positive integer n. The set must then be finite as well as dense. Therefore, X = {fn(θ0) : n > 0}. This contradiction implies that X cannot have any isolated points. Thus, X is a perfect subset of ; that is, it is closed and has no isolated points.
Now, consider the possibility that X contains a closed interval of positive length. Since X is closed and a proper subset of , we may choose a closed interval I⊆X of maximal length. The set I cannot be left invariant by any power of f. If n were such a power, then fn|I would have a fixed point. The orbit of this fixed point would be a finite invariant subset of X, which is impossible. Next, fix θ0 ∈ I. Since the orbit of this point is dense and I has a nonempty interior, there must be a positive integer n such that fn(θ0) ∈ I. On the other hand, there must a point θ1 ∈ I with fn(θ1) ∉ I. Let θt, 0 ≤ t ≤ 1, be the linear path in I that connects θ0 to θ1. Then fn(θt) connects fn(θ0) ∈ I with fn(θ1) ∉ I. But the range of fn is contained in X. An argument using the intermediate value theorem shows that this contradicts the maximality of I. We have shown that X has empty interior.
Remark 7. The properties of the dynamical system (X, f) used in the above result are that (X, f) is minimal and that X is an infinite, closed, proper subset of .
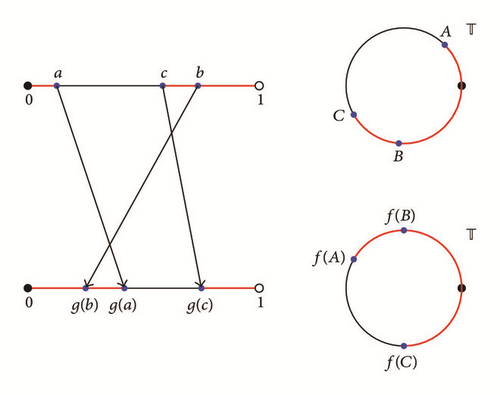
There is also a useful reformulation of the condition that f preserves cyclic order. Let A, B and C be three distinct points in with distinct images under f. Then, the points a = χ−1(A), b = χ−1(B), and c = χ−1(C) have distinct images under g. The action of g on this triple can be conveniently encoded by an arrow diagram as in Figure 2. That the arcs ABC and f(A)f(B)f(C) have the same orientation in is equivalent to saying that the corresponding arrow diagram has an even number (zero or two) of crossings. This elementary fact is easy to check and will be convenient in the proof of Proposition 9.
Lemma 8. Suppose x, y ∈ Ξ and g(x) = y. Then, there are sequences an and bn in Ξ such that
- (i)
an and bn are strictly monotone sequences,
- (ii)
g(an) = bn for all ,
- (iii)
limn→∞an = x and limn→∞bn = y.
Proof. The proof uses the following elementary fact: suppose one is given a convergent sequence of real numbers whose terms are distinct from the limit. Then, there is a subsequence which is strictly monotonic.
Now, since Ξ is perfect, one can construct a sequence an ∈ Ξ such that an ≠ x for all and an → x as n → ∞. By passing to a subsequence, one can further arrange an to be strictly monotonic. Moreover, by the continuity of g, g(an) → g(x) = y. Set bn = g(an). Since g has finite preimages, g(an) ≠ y for all but finitely many n. By once again passing to a subsequence, if necessary, we may arrange that bn is strictly monotone.
Proposition 9. The preimages of g : Ξ → Ξ have cardinality at most two.
Proof. Suppose, to the contrary, that x0, x1, x2 ∈ Ξ are three distinct points with the same image under g. So g(xi) = y for i = 0,1 and 2. We may assume that x0, x1, and x2 are arranged in increasing order in [0,1[. Let and , i = 0,1, 2 be the sequences in Ξ obtained by applying Lemma 8 to x0, x1, and x2, respectively.
The proof proceeds according to how and approach y.
Case and Approach y from the Same Side. We give the argument when both sequences approach y from below; the other possibility is dealt with similarly. In this case, we can use the properties of sequence to find indices k and l so that
Case and . Choose n sufficiently large so that
Case and . By invoking Lemma 8 again, we construct an x′ that is sufficiently close to x1 so that x0 < x′ < x2 and g(x′) ≠ y. We treat the case where g(x′) < y = g(x)—the other case is handled similarly. In this situation, there is a sufficiently large n with the property that . So,
Thus, the arrow diagram for has an odd number (one) of crossings.
Hence, in all three cases, we have a contradiction.
Proposition 10. The inequality
Proof. Suppose that α′ > β′. Minimality ensures that β′ > α. By using Lemma 8, we can find x near α such that α < g(x) < β. However, this would lead to an arrow diagram for the triple x, β′, α′ with an odd number of crossings.
Now, consider x ∈ Ξ with α′ < x < β′. By the definition of α′ and β′, g(x) must be distinct from α or β. Hence g(x) must be strictly between α and β. This is a contradiction due to an impossible arrow diagram—this time for the triple α′, x, β′.
Finally, since Ξ has no isolated points, α′ ≠ α and β′ ≠ β.
Lemma 11. Let x, y ∈ Ξ. If x < y and g(x) < g(y), then, for any z ∈ Ξ with x < z < y, we must have g(x) ≤ g(z) ≤ g(y).
Proof. Failure of the conclusion clearly leads to an impossible arrow diagram for the triple x, z, y.
Proposition 12. α < g(β) ≤ g(α) < β.
Proof. Minimality rules out the possibilities that g(α) = α and g(β) = β.
If g(β) = α, then by Lemma 8 there is x ∈ Ξ near β such that g(α) > g(x) > α. This means that the arrow diagram for α, x, β is not allowed. In a similar way, g(α) = β can also be ruled out.
Only the middle inequality remains. Suppose, to the contrary, that g(β) > g(α). The previous proposition implies that g(α) ≤ g(x) ≤ g(β), for any x ∈ Ξ that is strictly between α and β. Thus, Im g is a proper subset of X. This violates the minimality assumption.
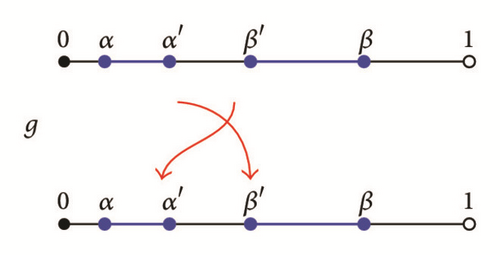
Proposition 13. g is monotone increasing on the sets and . Moreover,
Proof. Let x, y ∈ Ξ ∩ [α, α′] with x < y. Suppose g(y) < g(x). Since y < β′, the definition of β′ forces α = g(β′) < g(y). Thus, the arrow diagram for the triple x, y, β′ is impossible. This contradiction shows that g is monotonic increasing on [α, α′]. A similar argument applies to Ξ ∩ [β′, β].
Next, let x ∈ Ξ∩[α, α′] and suppose g(x) ≤ x. Since g has no fixed points, g(x) < x. For the same reason, α < g(α). Appealing to the monotonicity property proved in the previous paragraph, we have α < g(α) ≤ g(x) < x. Lemma 11 then implies that Ξ∩[α, x] is a nonempty, proper, closed invariant subset of Ξ—a contradiction. Thus g(x) > x for x ∈ Ξ∩[α, α′]. The last inequality can be verified similarly. See Figure 3 for a diagram of the structure of g.
3. Coding by Irrational Rotations of the Circle
Proposition 14. (i) If x0, x1 ∈ Ξ and Ξ∩(x0, x1) = ∅, then γ(x0) = γ(x1).
(ii) On the other hand, if Ξ∩(x0, x1) ≠ ∅, then γ(x0) > γ(x1).
Proof. The first statement follows directly from the facts that spt μ⊆Ξ and μ contains no point masses.
To prove the second statement, first put U = Ξ∩(x0, x1) and
The above result can be restated as follows: for any distinct pair x, x′ ∈ Ξ, γ(x) = γ(x′) if and only if x and x′ are endpoints of a gap of Ξ ⊂ ]0,1[. A further useful corollary of this is that any nonempty open subset of Ξ has positive μ-measure.
Lemma 15. One has
Proof. It is enough to show that
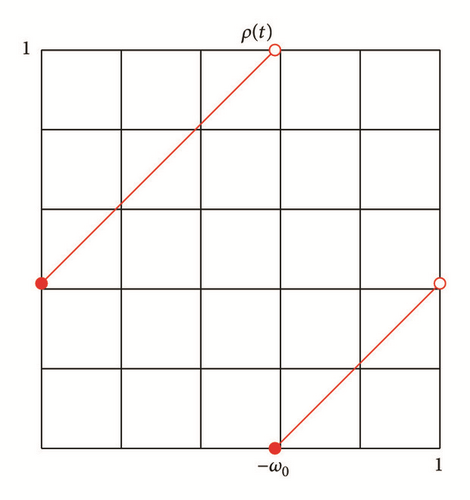
Proposition 16. There is an ω0 ∈ (0,1) such that
Proof. Put ω0 = μ([β′, β]). If x ∈ Ξ∩[α, α′], then the g invariance of the measure μ implies that
Remark 17. In the appendix to the article by Goldberg and Tresser [8], an analytic argument for characterizing rotational subsystems for the map F(θ) = d · θ mod1 (where d > 1) is sketched. The preceding proposition is claimed, but no argument is given. In addition, the authors then start with data equivalent to what is given in Section 5 and solve this functional equation to produce rational systems with a given rotation number.
Proposition 18. ω0 is irrational.
Proof. If ω0 were rational, the set
Lemma 19. Let Z0 be those points x ∈ Ξ with the property that for every δ > 0, the intervals (x, x + δ) and (x, x − δ) contain infinitely many points of Ξ. Then Z0 is a dense, uncountable subset of Ξ.
Proof. A point is in the complement of Z0 in Ξ precisely when it is the endpoint of a gap, that is, a maximal open interval contained in [α, β]\Ξ. Since there are at most countably many such open intervals, we conclude that Ξ\Z0 is countable. Since the perfect set Ξ is uncountable, Z0 is uncountable as well.
The density follows from a small modification of the standard argument that a perfect subset of a complete metric space is uncountable. Suppose U⊆Ξ is a nonempty open set with U∩Z0 = ∅. Then, U is countable. Let U = {x1, x2, …}. Write Ui = Ξ\{xi} and note that Ui is dense and open in Ξ for each i. Baire’s theorem yields that is dense in Ξ. But, by construction, —a contradiction. So, Z0 is dense.
Theorem 20. The dynamical system (Ξ, g) is uniquely ergodic.
Proof. Let x0 ∈ Z0. By Proposition 14 and Lemma 19,
- (i)
x ∈ Ξ and x < x0⇒γ(x) < γ(x0),
- (ii)
x ∈ Ξ and x > x0⇒γ(x) > γ(x0).
Therefore, for any y ∈ Ξ and n ≥ 0,
With this last result, we have completed the proof of Theorem 4. Indeed, the analysis of this section transfers over to the dynamical system (X, f) by means of the isomorphism, χ−1, of dynamical systems. In particular, one sets ϕ = Γ∘χ−1.
4. The Uniform d-Fold Cover
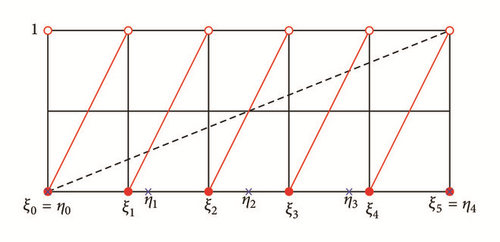
(See Figure 4 for the d = 5 case.) Under our operating assumptions, Ξ is infinite and minimal. Hence, none of ξi and ηi can lie in Ξ. In particular, any point in Ξ must lie in the interior of precisely one of the intervals I0, …, Id−1.
Proposition 21. The map is a homeomorphism from Ξ to .
Proof. Since Ξ is compact, it is enough to show that is continuous on Ξ. Suppose xi, x ∈ Ξ and xi → x as i → ∞. For any n, we must have that gnx lies in an open interval of the form . Since g is continuous on [0,1)\{ξ0, ξ1, …, ξd−1},
In summary, this discussion shows how any rotational subsystem (X, g) of the uniform d-fold cover of the unit circle must arise from the symbolic flow of an irrational rotation of relative to a suitable partition. The next section shows that this process can be reversed.
5. The Inverse Process
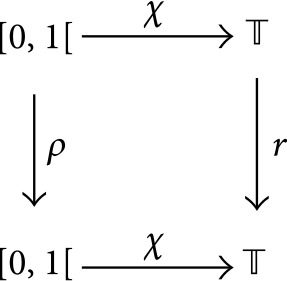
Remark 22. It is well known that is a minimal dynamical system. Hence, for any non-empty open there is an N > 0 with the following property: for every ,
It follows easily that the analogous statement holds for ([0,1[, ρ) and any non-empty open U ⊂ ]0,1[. (Simply apply the previous observation to V = χ(U).)
As before, let be the set of t ∈ [0,1[ satisfying ρn(t) = {t + nω0} ≠ ti for all and . In other words, consists of those points of whose forward orbit does not contain any of the nodes ti. is invariant under the map ρ.
Proposition 23. (i) The complement of in [0,1[ is countable.
(ii) For every t ∈ [0,1[, there is an integer n ≥ 0 with the property that .
Proof. The map ρ is invertible. The complement of is just the countable set:
For the proof of the second claim, fix t ∈ [0,1[. If the orbit of t hits the infinitely often, then there must be an index i such that
Proposition 24. The map is a continuous, injective, strictly monotonic increasing and
Proof. Kronecker’s theorem also implies injectivity of E: Let t and t′ be distinct points in with t′ > t. Set Δ = t′ − t and note that there must be an s with the property that s and s′ = s + Δ lie in the interior of different Ji’s. Note that if |ρnt − s| is sufficiently small, then |ρnt − s | = |ρnt′ − s′|. In particular, by choosing n so that |ρnt − s| is sufficiently small, we may insure that ρnt and ρnt′ will be in different Ji’s. Hence the d-adic encodings of t and t′ are different. Since neither of these encodings can end with an infinite string of d − 1’s, E(t) ≠ E(t′).
Equation (52) follows directly from (51) and the ensuing discussion.
Let and tn be a sequence in that converges to t. Then, since ρkt is in the interior of one of Ji, ρktn must eventually have this property as well. Thus, E must be continuous.
It only remains to prove that E is monotone increasing. Let t, with t < t′. Write E(t) = a0a1a2… and . Because E is injective, there is a first index i ≥ 0 for which . If i = 0, t < t′ implies . This in turn yields E(t) < E(t′). If i > 0, then entails that both ρi−1t and ρi−1t′ are in interior of the same Jk. Since ρ is increasing on the interior of any Jn, we must have . As a consequence, E(t) < E(t′) in this case as well.
Write Ξ0 for the image of under the map E and let Ξ be its closure in [0,1[. It is straightforward to check that Ξ0 is invariant under G. Establishing this for its closure is complicated by the possibility that G might not be continuous on Ξ. Most of the effort in the proof of the next result is to rule this out.
Proposition 25. Ξ is a compact subset of ]0,1[ and is invariant under G.
Proof. By Remark 22, there is an N with the property that for each t ∈ [0,1[, the set
By examining G explicitly, it is easy to check that G−1[m, M] is a compact subset of [0,1[ that does not contain any of the points ξ0, …, ξd−1. Since these are precisely the points of discontinuity of G, G is continuous on G−1[m, M]. Because Ξ0 is invariant, GΞ0⊆Ξ0 ⊂ [m, M]. Consequently, and G is continuous on Ξ.
Let x ∈ Ξ. Then xn → x for a sequence xn ∈ Ξ0. By the observations in the previous paragraph, G(xn) → G(x). Since, Ξ0 is G invariant, this proves that .
As before, define g : Ξ → Ξ by g = G|Ξ.
Theorem 26. The dynamical system (Ξ, g) is rotational.
Proof. We first prove the minimality of (Ξ, g).
Consider a point x0 ∈ Ξ0. An y ∈ Ξ can be approximated to within an arbitrary accuracy by an element of y0 ∈ Ξ0. Write t0, s0 for the elements of with E(t0) = x0 and E(s0) = y0. By Kronecker’s theorem, there is a sequence ni of indices such that . The continuity of E together with Proposition 24 yields
Now let x ∈ Ξ\Ξ0. It suffices to prove that an element in the forward orbit of x is in Ξ0. We may write x as a limit of a sequence xi in Ξ0. Write ti for the elements of [0,1[ with E(ti) = xi. By passing to a subsequence, if needed, we may assume that χ(ti) converges to an element of , say χ(t). By Proposition 23, there is m such that . By continuity of r, we have that χ(ρm(ti)) = rm(χ(ti)) → rm(χ(t)) = χ(ρm(t)). Since , . Since χ−1 is continuous on the latter set, ρm(ti) → ρm(t). We may apply E to both sides of this last limit to get
The only point left is to prove that g respects cyclic order on Ξ. To this end, let x0, x1, and x2 be an increasing triple of points in Ξ with distinct images under g. We may approximate each of these points by elements of Ξ0 without changing the number of crossings in the arrow diagram. Hence, we may assume that x0, x1, and x2 are in Ξ0. Let t0, t1, and t2 be the preimages under E of x0, x1, and x2, respectively. The ti’s are in increasing order due to Proposition 24. This monotonicity property of E together with the identity in that proposition, also force the arrow diagram for t0, t1, and t2 under the map ρ to have the same number of crossings as that for x0, x1, and x2 under g. But it is easy to verify that ρ respects cyclic order. Hence, so does g.
6. Examples for a Class of Continuous Maps
As the last two sections show, every irrational ω0 ∈ [0.1) arises as the rotation number of some rotational system with respect to a standard cover of degree d > 1. (This is true for rational ω0 ∈ [0,1) as well.) It is tempting to ask if this is true for any continuous transformation of degree d > 1.
- (i)
H is monotone increasing function on each half-open interval [sk, sk+1),
- (ii)
H(sk) = 0 and .
Applying a piecewise linear change of coordinates, we may assume that si = i/d for i = 0, …, d.
Definition 27. A finite word v is a prefix of a word w if v⋆u where ⋆ means concatenation of words.
We collect some useful remarks that are easy to check.
Remark 28. (i) Aw are half-open intervals that are closed on the left.
(ii) Let w and v be finite words. Suppose that w is a prefix for the word v. Then Av⊆Aw. In addition, if vk ≠ d − 1 for some k > j, then .
(iii) For any fixed w and n≥|w|, the collection
(iv) If w = i1i2 … in and w′ = i2 … in, then
(v) If w and v are of the same length and w precedes v in lexicographical order, then
Remark 29. The lexicographical ordering on and the usual order on [0,1[ are also compatible with the factor map ι. In particular, for any x, y ∈ [0,1[,
- (i)
x < y implies ι(x) ≤ ι(y),
- (ii)
ι(x) < ι(y) implies x < y.
Thus, for any , the preimage ι−1{w} is either empty, a singleton, or an interval of positive length. In particular, the cardinality of ι−1{w} exceeds one for only countable many words .
Lemma 30. Let xn be a sequence in [0,1) with the property that ι(xk) converges in to w. Suppose, in addition, that the infinite word w does not end with an infinite sequence of d − 1’s. Then any convergent subsequence with a limit, say x, has the property that x ∈ [0,1) with ι(x) = w.
Proof. Let w = i0i1i2… and set wn = i0i1 … in for each . Since ι(xi) → w, we have that, for each m, for all sufficiently large k. By Remark 28 and the hypothesis on w, we have that for any n there is an m > n with the property that
Remark 31. If the infinite word does not terminate with an infinite sequence of d − 1’s, there is an x ∈ [0,1[ with the property that ι(x) = w. To see this, first construct a sequence xn by the requirement that for each . (Here wn is defined as in the previous proof.) By construction, ι(xn) → w as n → ∞. Let x be any limit point of this sequence in . By Lemma 30, x ∈ [0,1) and ι(x) = w.
The map ι is not continuous everywhere on [0,1). However, one can characterize the points of continuity.
Lemma 32. Let x0 ∈ [0,1) be a point with the property that ι(x0) does not terminate with an infinite sequence of 0’s. Then x0 is a point of continuity for the map .
Proof. Write w = i0i1i2… for ι(x0) and let wn = i0i1 … in. The hypothesis entails that x0 does not lie on the left endpoint of any of the . In other words, x0 is in the interior of all the . Suppose xk → x0 as k → ∞. For any , for all sufficiently large k. For such k, ι(xk) will have wn as a prefix. Since is arbitrary, ι(xn) → w = ι(x0) as n → ∞.
Now choose an irrational number ω0 ∈ [0,1) and a compatible partition as in (43) of the last section. Let (X, f) be the rotational system constructed from this data and write (Ξ, g) for the associated system on [0,1).
Let Z ⊂ [0,1) consist of those points z with the property that the associated word ι(z) is in . The word associated with an x ∈ Ξ cannot end with an infinite sequence of d − 1’s; this would contradict the minimality of the infinite system (Ξ, g), for instance. Hence, by Remark 31, for any x ∈ Ξ there is a z ∈ Z with .
We next claim that Z is (sequentially) compact in [0,1). Indeed, recall that is compact (see Proposition 21). Let zn be any sequence in Z. By passing to a subsequence, we may assume that zn converges in and ι(zn) converges to a . By Lemma 30, we have that z = lim zi satisfies z ∈ [0,1) and ι(z) = w.
Another feature is that no z ∈ Z can have the property that ι(z) ends with an infinite string of 0’s. (The same statement holds for any where x ∈ Ξ.) Consequently, by Lemma 32, ι is continuous on Z.
Consider the composition . The function ψ : Z → Ξ assigns to a z ∈ Z the element in Ξ with the same symbolic representation. In view of Proposition 21 and the previous paragraph, ψ is continuous. It is also clear that it is a map between the dynamical systems (Z, H|Z) and (Ξ, g), that is, ψ∘H = g∘ψ.
Let (Y, H|Y) be a compact, minimal subsystem of (Z, H) and write h = H|Y. The factor map ψ restricts to Y in a natural way: ψ∘h = g∘ψ. Since (Ξ, g) is minimal as well, ψ maps Y to Ξ surjectively. In particular, Y is infinite.
The only point left open is whether (Y, h) preserves cyclic order. We do not know if this is true in general, but it is true generically as will now be shown.
Proposition 33. In the d = 2 case, (Y, h) is a rotational system for all irrational ω0 ∈ [0,1 except for a countable number of possible exceptions.
Proof. In this case, the choice of ω0 determines the partition in (43). We will write for the associated rotational system. Note that, for distinct choices ω0 and , the corresponding sets, and must be disjoint. Indeed, because of minimality, the orbit of any common point would have to be dense in both sets. This would imply that , which yields .
Thus, the family of sets, , is an uncountable collection of disjoint sets. By Remark 29, ι is injective on all but countably many of . For such ω0, h = hω is a continuous bijection between compact sets. So h is a homeomorphism. Since h respects the ordering of [0,1), (Y, h) preserves cyclic order.
The d > 2 case differs in that, for each ω0, there are uncountably many choices for the partition, , described in (43). Let denote the rotational system uniquely associated with ω0 and , according to the method of Section 5. For distinct partitions and compatible with θ0, and are disjoint. Thus, ι will be injective on for all but countably many of the partitions compatible with ω0. This yields the following.
Proposition 34. If d > 2 and ω0 is an irrational number in [0,1, there are uncountable many rotational systems (Y, h) with rotation number ω0.
Conflicts of Interest
The author declares that he has no conflicts of interest regarding the publication of this paper.
Acknowledgments
This work was supported in part by a Faculty Research Fellowship from Eastern Michigan University (Fall 2016).




