International Journal of Differential Equations
Volume 2018, Issue 1 8686502
Research Article
Open Access

Computational Optimization of Residual Power Series Algorithm for Certain Classes of Fuzzy Fractional Differential Equations

Mohammad Alaroud, 

Mohammad Alaroud

School of Mathematical Sciences, Faculty of Science and Technology, Universiti Kebangsaan Malaysia, 43600 Bangi, Selangor, Malaysia ukm.my

Search for more papers by this author
Mohammed Al-Smadi, 

Mohammed Al-Smadi

Department of Applied Science, Ajloun College, Al-Balqa Applied University, Ajloun 26816, Jordan bau.edu.jo

Search for more papers by this author
Rokiah Rozita Ahmad, 

Corresponding Author

Rokiah Rozita Ahmad

School of Mathematical Sciences, Faculty of Science and Technology, Universiti Kebangsaan Malaysia, 43600 Bangi, Selangor, Malaysia ukm.my

Search for more papers by this author
Ummul Khair Salma Din, 

Ummul Khair Salma Din

School of Mathematical Sciences, Faculty of Science and Technology, Universiti Kebangsaan Malaysia, 43600 Bangi, Selangor, Malaysia ukm.my

Search for more papers by this author
First published: 02 July 2018
https://doi.org/10.1155/2018/8686502
Citations: 22
Academic Editor: Carla Pinto

Abstract

This paper aims to present a novel optimization technique, the residual power series (RPS), for handling certain classes of fuzzy fractional differential equations of order 1 < γ ≤ 2 under strongly generalized differentiability. The proposed technique relies on generalized Taylor formula under Caputo sense aiming at extracting a supportive analytical solution in convergent series form. The RPS algorithm is significant and straightforward tool for creating a fractional power series solution without linearization, limitation on the problem’s nature, sort of classification, or perturbation. Some illustrative examples are provided to demonstrate the feasibility of the RPS scheme. The results obtained show that the scheme is simple and reliable and there is good agreement with exact solution.

1. Introduction

Fuzzy fractional differential equation is hot and important branch of mathematics. It has attracted much attention recently due to potential applications in artificial intelligence, industrial engineering, physics, chemistry, and other fields of science. Parameters and variables in many of the nature studies and technological processes that were designed utilizing the fractional differential equation (FDE) are specific and completely defined. Indeed, such information may be vague and uncertain because of experimentation and measurement errors that then lead to uncertain models, which cannot handle these studies. The process of analyzing the relative influence of uncertainty in inputs information to outputs led us to study solutions to the qualitative behavior of equations. Therefore, it is necessary to obtain some mathematical tools to understand the complex structure of uncertainty models [1–5]. On the other hand, the theory of fractional calculus, which is a generalization of classical calculus, deals with the discussion of the integrals and derivatives of noninteger order, has a long history, and dates back to the seventeenth century [6–10]. Different forms of fractional operators are introduced to study FDEs such as Riemann–Liouville, Grunwald-Letnikov, and Caputo. Out of these forms, the Caputo concept is an appropriate tool for modeling practical situations due to its countless benefits as it allows the process to be performed based on initial and boundary conditions as is traditional and its derivative is zero for constant [11–17].

The residual power series (RPS) method developed in [18] is considered as an effective optimization technique to determine and define the power series solution’s values of coefficients of first- and second-order fuzzy differential equations [19–22]. Furthermore, the RPS is characterized as an applicable and easy technique to create power series solutions for strongly linear and nonlinear equations without being linearized, discretized, or exposed to perturbation [23–27]. Unlike the classical power series method, the RPS neither requires comparing the corresponding coefficients nor is a recursion relation needed as well. Besides that, it calculates the power series coefficients through chain of equations of one or more variables and offers convergence of a series solution whose terms approach quickly, especially when the exact solution is polynomial.

The remainder of this paper is organized as follows. In Section 2, essential facts and results related to the fuzzy fractional calculus will be shown. In Section 3, the concept of Caputo’s H-differentiability will be presented together with some closely related results. In Section 4, basic idea of the RPS method will be presented to solve the fuzzy FDEs of order 1 < γ ≤ 2. In Section 5, numerical application will be performed to show capability, potentiality, and simplicity of the method. Conclusions will be given in Section 6.

2. Preliminaries

In this section, necessary definitions and results relating to fuzzy fractional calculus are presented. For the fuzzy derivative concept, the strongly generalized differentiability will be adopted, which is considered H-differentiability modification.

A fuzzy set v in a nonempty set U is described by its membership function v : U → [0,1]. So, for each η ∈ U the degree of membership of η in v is defined by v(η).

Definition 1 ([28]). Suppose that v is a fuzzy subset of ℝ. Then, v is called a fuzzy number such that v is upper semicontinuous membership function of bounded support, normal, and convex.

If v is a fuzzy number, then [v]σ = [v1(σ), v2(σ)], where v1(σ) = min⁡{η∣η ∈ [v]σ} and v2(σ) = max⁡{η∣η ∈ [v]σ} for each σ ∈ [0,1]. The symbol [v]σ is called the σ-level representation or the parametric form of a fuzzy number v.

Theorem 2 ([29]). Suppose that satisfy the following conditions:

  • (1)

    v1 is a bounded nondecreasing function.

  • (2)

    v2 is a bounded nonincreasing function.

  • (3)

    v1(1) ≤ v2(1).

  • (4)

    for each k ∈ 0,1], and .

  • (5)

    and .

Then given by v(x) = sup⁡{σ∣v1(σ) ≤ x ≤ v(σ)} is a fuzzy number with parameterization [v1(σ), v2(σ)].

Definition 3 ([29]). Let . If there exists an element such that , then we say that is the Hukuhara difference (H-difference) of v and w, denoted by v ⊖ w.

The sign ⊖ stands always for Hukuhara difference. Thus, it should be noted that v ⊖ w ≠ v + (−1)w. Normally, v + (−1)w is denoted by v − w. If the H-difference v ⊖ w exists, then [v ⊖ w] σ = [v1(σ) − w1(σ), v2(σ) − w2(σ)].

Definition 4 ([30]). The complete metric structure on is given by the Hausdorff distance mapping such that

()
for arbitrary fuzzy numbers v = (v1, v2) and w = (w1, w2).

Definition 5 ([30]). Let . Then the function φ is continuous at x0 ∈ [a, b] if for every ϵ > 0, ∃δ = δ(x0, ϵ) > 0 such that DH(φ(x), φ(x0)) < ϵ, for each x ∈ [a, b], whenever |x − x0| < δ.

Remark 6. If the function φ(x) is continuous for each x ∈ [a, b], where the continuity is one-sided at endpoints of [a, b], then φ(x) is continuous function on [a, b]. This means that φ(x) is continuous on [a, b] if and only if φ1σ and φ2σ are continuous on [a, b].

Definition 7 ([28]). For fixed x0 ∈ [a, b] and , the function φ is called a strongly generalized differentiable at x0, if there is an element such that either

  • (i)

    the H-differences φ(x0 + ξ) ⊖ φ(x0), φ(x0) ⊖ φ(x0 − ξ) exist, for each ξ > 0 sufficiently tends to 0 and , or

  • (ii)

    the H-differences φ(x0) ⊖ φ(x0 + ξ), φ(x0 − ξ) ⊖ φ(x0) exist, for each ξ > 0 sufficiently tends to 0 and ,

where the limit here is taken in the complete metric space

Theorem 8 ([31]). Suppose that , where [φ(x)] σ = [φ1σ(x), φ2σ(x)],     ∀ σ ∈ [0,1], then

  • (1)

    the functions φ1σ and φ2σ are two differentiable functions and , when φ is (1)-differentiable;

  • (2)

    the functions φ1σ and φ2σ are two differentiable functions and , when φ is (2)-differentiable.

Definition 9 ([31]). Suppose that . One can say that φ is (n, m)-differentiable at x0 ∈ (a, b), if exists on a neighborhood of x0 as a fuzzy function and it is (m)-differentiable at x0. The second-order derivatives of φ at x are indicated by for n, m = {1,2}.

Theorem 10 ([32]). Let and , where [φ(x)] σ = [φ1σ(x), φ2σ(x)] for each σ ∈ [0,1]:

  • (1)

    If is (1)-differentiable, then and are differentiable functions and ,

  • (2)

    If is (2)-differentiable, then and are differentiable functions and ,

  • (3)

    If is (1)-differentiable, then and are differentiable functions and ,

  • (4)

    If is (2)-differentiable, then and are differentiable functions and .

Definition 11 ([32]). Let and . One can say that φ is Caputo fuzzy H-differentiable at x when exists, where 0 < γ ≤ 1. Also, we say that φ is Caputo [(1) − γ]-differentiable if φ is (1)-differentiable and φ is Caputo [(2) − γ] differentiable if φ is (2)-differentiable, where and stand for the space of all continuous and Lebesque integrable fuzzy-valued functions on [a, b], respectively.

Theorem 12 ([33]). Let 0 < γ ≤ 1 and Then, for each σ ∈ [0,1], the Caputo fuzzy fractional derivative exists on (a, b) such that

()
for (1)-differentiable and
()
for (2)-differentiable.

The next characterization theorem shows a way to convert the FFDEs into a system of ordinary fractional differential equations (OFDEs), ignoring the fuzzy setting approach.

Theorem 13 ([34]). Consider the below fuzzy fractional IVPs

()
subject to
()
where f: such that

(i) [f(t, φ(t))] σ = [f1σ(t, φ1σ(t), φ2σ(t)), f2σ(t, φ1σ(t), φ2σ(t))].

(ii) for any ϵ > 0 there exist δ > 0 such that |f1σ(t, s, u) − f1σ(t1, s1, u1)| < ϵ and |f2σ(t, s, u) − f2σ(t1, s1, u1)| < ϵ,   ∀ σ ∈ [0,1], whenever (t, s, u) and and f1σ, f2σ are uniformly bounded on any bounded set.

(iii) there is a constant (say) such that

()
and
()
Therefore, there are two systems of OFDEs that are equivalent to FFDEs (4) and (5) as follows:

Case 1. When φ(t) is Caputo [(1)-γ]-differentiable

()
with φ1σ(t0) = φ01σ, φ2σ(t0) = φ02σ.

Case 2. When φ(t) is Caputo [(2)-γ]-differentiable

()
with φ1σ(t0) = φ01σ, φ2σ(t0) = φ02σ.

3. Formulation of Fuzzy Fractional IVPs of Order 1 < γ ≤ 2

Consider the below fuzzy fractional differential equation
()
subject to fuzzy initial conditions
()
where is a linear or nonlinear continuous fuzzy-valued function, g(t) is a continuous real valued function with nonnegative values on [a, b], and φ(t) is unknown analytical fuzzy function to be determined. We assume that the fuzzy fractional IVPs (10) and (11) have unique smooth solution on the domain of interest.

Next, some theorems and definitions which are used later in this paper are presented.

Definition 14. Let be fuzzy function such that . Then, for 1 < γ ≤ 2, Caputo’s H-derivative of φ at x ∈ (a, b) is defined as

()

Also, we say that φ is Caputo [(n, m) − γ]-differentiable for n, m ∈ {1,2}, when exists, and φ is (n, m)-differentiable.

Theorem 15. Let , such that [φ(x)] σ = [φ1σ(x), φ2σ(x)],    ∀ σ ∈ [0,1]. Caputo’s H-derivative of order 1 < γ ≤ 2 exists on (a, b) such that

(i) If φ is (1,1)-differentiable, then , .

(ii) If φ is (1,2)-differentiable, then .

(iii) If φ is (2,1)-differentiable, then .

(iv) If φ is (2,2)-differentiable, then , where M = 1/Γ(2 − γ).

The (n, m)-solution of fuzzy fractional IVPs (10) and (11) is a function that has Caputo [(n, m) − γ]-differentiable and satisfies the FFIVPs (10) and (11). To compute it, we firstly convert the fuzzy problem into equivalent system of second OFDEs, called correspondence (n, m)-system, based upon the type of derivative chosen. Then, by utilizing the σ-cut representation of φ(t), f(t, φ(t)), and the initial data in (11) such that [φ(t)]σ = [φ1σ(t), φ2σ(t)], [f(t, φ(t))]σ = [f1σ(t,φ1σ(t), φ2σ(t)), f2σ(t,φ1σ(t), φ2σ(t))], [φ(a)]σ = [φ1σ(a), φ2σ(a)] = [α1σ, α2σ], and , the following corresponding (n, m)-systems will be hold:

(i) (1,1)-system such that
()
(ii) the (1,2)-system such that
()
(iii) the (2,1)-system such that
()
(iv) the (2,2)-system such that
()
subject to initial conditions
()

Theorem 16 ([33]). Let n, m ∈ {1,2} and let [φ(t)] σ = [φ1σ(t), φ2σ(t)] be an (n, m)-solution of FFIVPs (10) and (11) on [a, b]. Then, φ1σ(t) and φ2σ(t) will be a solution to the associated (n, m)-system.

Theorem 17 ([33]). Let n, m ∈ {1,2} and let φ1σ(t) and φ2σ(t) be the solution of (n, m)-system for each σ ∈ [0,1]. If [φ(t)] σ = [φ1σ(t), φ2σ(t)] has valid level sets and φ(t) is Caputo [(n, m) − γ]-differentiable, then φ(t) is an (n, m)-solution of FFIVPs (10) and (11) on [a, b].

The aim of the next algorithm is to perform a strategy to solve the FFIVPs (10) and (11) in terms of its σ-cut representation form. Indeed, there are four cases that depend on type of differentiability.

Algorithm 18. To determine the solutions of FFIVPs (10) and (11), do the following:

Case (I). If φ(t) is Caputo [(1,1)-γ]-differentiable and the FFIVPs (10) and (11) will be converted to crisp system described in (13) and (17), then do the following steps:

  •  

    Step 1: Solve the required system.

  •  

    Step 2: Ensure that and are valid level sets for each σ ∈ [0,1].

  •  

    Step 3: Construct (1,1)-solution φ(t) whose σ-cut representation is [φ1σ(t), φ2σ(t)].

Case (II). If φ(t) is Caputo [(1,2)-γ]-differentiable and the FFIVPs (10) and (11) will be converted to crisp system described in (14) and (17), then do the following steps:

  •  

    Step 1: Solve the required system.

  •  

    Step 2: Ensure that and are valid level sets for each σ ∈ [0,1].

  •  

    Step 3: Construct (1,2)-solution φ(t) whose σ-cut representation is [φ1σ(t), φ2σ(t)].

Case (III). If φ(t) is Caputo [(2,1)-γ]-differentiable and the FFIVPs (10) and (11) will be converted to crisp system described in (15) and (17), then do the following steps:

  •  

    Step 1: Solve the required system.

  •  

    Step 2: Ensure that and are valid level sets for each σ ∈ [0,1].

  •  

    Step 3: Construct (2,1)-solution φ(t) whose σ-cut representation is [φ1σ(t), φ2σ(t)].

Case (IV). If φ(t) is Caputo [(2,2)-γ]-differentiable and the FFIVPs (10) and (11) will be converted to crisp system described in (16) and (17), then do the following steps:

  •  

    Step 1: Solve the required system.

  •  

    Step 2: Ensure that and are valid level sets for each σ ∈ [0,1].

  •  

    Step 3: Construct (2,2)-solution φ(t) whose σ-cut representation is [φ1σ(t), φ2σ(t)].

4. Description of Fractional RPS Method

In this section, the RPS scheme is presented for constructing an analytical solution of FFIVPs (10) and (11) through substituting the expansion of fractional power series (FPS) among the truncated residual functions. In view of that, the resultant equation helps us to derive a recursion formula for the coefficients’ computation, where the coefficients can be computed recursively through the recurrent fractional differentiating of the truncated residual function.

Definition 19 ([35]). A fractional power series (FPS) representation at t0 has the following form:

()
where 0 ≤ m − 1 < γ ≤ m, t ≥ t0, and cn’s are the coefficients of the series.

Theorem 20 ([35]). Suppose that f has the following FPS representation at t0:

()
where f(t) ∈ C[t0, t0 + R) and for n = 0,1, 2, …; then the coefficients cn will be in the form such that (n-times).

Conveniently, for obtaining (n, m)-solution of FFIVPs (10) and (11) utilizing the solution of the corresponding (n, m)-system, we will explain the fashion to determine (1,1)-solution equivalent to the solution for the system of OFDEs (13) and (17). Further, same manner can be applied to construct other type of (n, m)-solutions. To achieve our goal, assume that the solution of OFDEs (13) and (17) at t0 = 0 has the following form:
()
Since φ1σ(t) and φ2σ(t) satisfy the initial conditions in (17), then the following polynomials φ1σ(t) = α1σ + β1σt and φ2σ(t) = α2σ + β2σt will be the initial guesses for the system and the solutions can also be represented by
()
Consequently, the kth-truncated series solutions can be given by
()
The residual functions Res1σ(t) and Res2σ(t) are defined as follows:
()
and the kth-residual functions Resk,1σ(t) and Resk,2σ(t) for k = 1,2, 3, …n are defined as follows:
()

From (23), we have Resnσ(t) = 0 and limk→∞⁡Resk,nσ(t) = Resnσ ≡ 0 for n = 1,2 and each t ≥ 0, which leads to . Also, the fractional derivatives and are equivalent at t = 0 for each m = 0,1, 2, …, k, that is, . However, holds for n = 1,2.

Regarding employing the RPS algorithm to obtain the 1st unknown coefficients, c1and d1, substitute the 1st approximations φ1,1σ(t) = α1σ + β1σt + c1(tγ/Γ(1 + γ)) and φ1,2σ(t) = α2σ + β2σt + d1(tγ/Γ(1 + γ)) into the 1st residual functions Res1,1σ(t) and Res1,2σ(t) of (24) such that
()
and based upon the facts Res1,1σ(0) = Res1,2σ(0) = 0, we have and . Therefore, the 1st RPS approximate solutions can be written as
()
Currently, for the 2nd unknown coefficients, c2 and d2 substitute and into the 2nd residual functions, Res2,1σ(t) and Res2,2σ(t) of (24) such that
()
Then, by applying the fractional derivative on both sides of Res2,1σ(t) and Res2,2σ(t), using the facts as well, the values of c2 and d2 will be given by
()
For the 3rd unknown coefficients, c3 and d3 substitute and into the 3rd residual functions, Res3,1σ(t) and Res3,2σ(t) of (24), and then by computing and and using the facts , the coefficients, c3 and d3, will be given such that
()

Using similar argument, the 4th unknown coefficients, c4 and d4, will be given utilizing the facts . The same manner can be repeated until we obtain on the coefficients’ arbitrary order of the FPS solution for the OFDE (13).

5. Numerical Simulation and Discussion

This section aims to verify the efficiency and applicability of the proposed algorithm by applying the RPS method to a numerical example. Here, all necessary calculations and analysis are done using Mathematica 10.

For this purpose, let us consider the fuzzy fractional differential equation
()
with the fuzzy initial conditions
()
where γ ∈ 1,2] and μ, α, β are the fuzzy numbers whose σ-cut representation is [σ − 1,1 − σ].

Based on the type of differentiability, the FFIVPs (30) and (31) can be converted into one of the following systems.

Case 1. If φ(t) is (1,1)-solution, then the corresponding (1,1)-system will be

()
If γ = 2, then the exact solution of (32) is [φ(t)] σ = [σ − 1,1 − σ](1 + t + tγ/Γ(γ + 1)), t ∈ [0,1]. In finding the fuzzy (1,1)-solution of FFDEs (30), let φ(t) be Caputo [(1,1)-γ]-differentiable. Sequentially, after selecting the initial guesses as φ0,1σ(t) = (σ − 1) + (σ − 1)t and φ0,2σ(t) = (1 − σ) + (1 − σ)t, the FPS expansion of solutions for OFDEs (32) can be represented as follows:
()

To determine the 1st RPS approximate solution for OFDEs (32), substitute the 1st-truncated series φ1,1σ(t) = (σ − 1) + (σ − 1)t + c1(tγ/Γ(1 + γ)) and φ1,2σ(t) = (1 − σ) + (1 − σ)t + d1(tγ/Γ(1 + γ)) into the 1st-residual functions Res1,1σ(t) and Res1,2σ(t) such that Res1,1σ(t) = 1 − σ + c1 and Res1,2σ(t) = σ − 1 + d1. Thus, based upon the facts Res1,1σ(0) = 0 and Res1,2σ(0) = 0, we have c1 = σ − 1 and d1 = 1 − σ. Hence, the 1st RPS approximate solution for OFDEs (32) can be written in the form of

()

Similarly, to find out the 2nd RPS approximate solution for OFDEs (32), substitute the 2nd truncated series φ2,1σ(t) = (σ − 1) + (σ − 1)t + c1(tγ/Γ(1 + γ)) + c2(t2γ/Γ(1 + 2γ)) and φ2,2σ(t) = (1 − σ) + (1 − σ)t + d1(tγ/Γ(1 + γ)) + d2(t2γ/Γ(1 + 2γ)) into the 2nd residual functions Res2,1σ(t) and Res2,2σ(t) such that and . Now, applying the fractional derivative on both sides of Res2,1σ(t) and Res2,2σ(t) yields the following: and . So, the 2nd unknown coefficients are c2 = 0 and d2 = 0 through using the facts Therefore, the 2nd RPS approximate solution for OFDEs (32) is given by

()

Accordingly, the unknown coefficients cn and dn will be vanished for n ≥ 3 by continuing in the similar approach, that is, and . Hence, the RPS approximate solutions corresponding to (1,1)-system are coinciding well with the exact solutions φ1σ(t) = (1 + t + (tγ/Γ(1 + γ)))(σ − 1) and φ2σ(t) = (1 + t + tγ/Γ(1 + γ))(1 − σ). Here, [φ1σ(t), φ2σ(t)], , and are valid level sets for σ ∈ [0,1] and t ∈ [0,1]. Moreover,φ(t) = μ(1 + t + tγ/Γ(1 + γ)) is a (1,1)-solution for FFIVPs (30) and (31) on [0,1].

Case 2. If φ(t) is (1,2)-solution, then the corresponding (1,2)-system will be

()
If γ = 2, then the exact solution of (36) is [φ(t)] σ = [σ − 1,1 − σ](1 + t − tγ/Γ(γ + 1)), t ∈ [0,1]. In finding the fuzzy (1,2)-solution of FFDEs (30), let φ(t) be Caputo [(1,2)-γ]-differentiable. Sequentially, after selecting the initial guesses as in case 1, the FPS expansion of solutions for OFDEs (36) can be represented by
()

To determine the 1st RPS approximate solution for OFDEs (36), substitute the 1st truncated series φ1,1σ(t) = (σ − 1) + (σ − 1)t + c1(tγ/Γ(1 + γ)) and φ1,2σ(t) = (1 − σ) + (1 − σ)t + d1(tγ/Γ(1 + γ)) into the 1st residual functions Res1,1σ(t) and Res1,2σ(t) such that Res1,1σ(t) = σ − 1 + c1 and Res1,2σ(t) = 1 − σ + d1. Thus, based upon the facts Res1,1σ(0) = Res1,2σ(0) = 0, we have c1 = 1 − σ and d1 = σ − 1. Hence, the 1st RPS approximate solution for OFDEs (36) can be written in the form of

()

Similarly, to find out the 2nd RPS approximate solution for OFDEs (36), substitute the 2nd truncated series φ2,1σ(t) = (σ − 1) + (σ − 1)t + c1(tγ/Γ(1 + γ)) + c2(t2γ/Γ(1 + 2γ)) and φ2,2σ(t) = (1 − σ) + (1 − σ)t + d1(tγ/Γ(1 + γ)) + d2(t2γ/Γ(1 + 2γ)) into the 2nd residual functions Res2,1σ(t) and Res2,2σ(t) such that Res2,1σ(t) = 1 − σ + c1 + c2(tγ/Γ(1 + γ)) and Res2,2σ(t) = −1 + σ + d1 + d2(tγ/Γ(1 + γ)). Then, applying the fractional derivative on both sides of Res2,1σ(t) and Res2,2σ(t)yields the following: and . So, the 2nd unknown coefficients are c2 = 0 and d2 = 0 through using the facts Therefore, the 2nd RPS approximate solution for OFDEs (36) is given by

()

By continuing in the similar manner, the unknown coefficients cn and dn will be vanished for n ≥ 3, that is, and . Hence, the RPS approximate solutions corresponding to (1,2)-system are coinciding well with the exact solutions φ1σ(t) = (1 + t − tγ/Γ(1 + γ))(σ − 1) and φ2σ(t) = (1 + t − tγ/Γ(1 + γ))(1 − σ). Here, [φ1σ(t), φ2σ(t)], , and are valid level sets for σ ∈ [0,1] and t ∈ [0,1]. On the other hand, φ(t) = μ(1 + t − tγ/Γ(1 + γ)) is a (1,2)-solution for FFIVPs (30) and (31) on [0,1].

Case 3. If φ(t) is (2,1)-solution, then the corresponding (2,1)-system will be

()
If γ = 2, then the exact solution of (40) is [φ(t)] σ = [σ − 1,1 − σ](1 − t − tγ/Γ(1 + γ)), . To obtain the fuzzy (2,1)-solution of FFDEs (30), let φ(t) is Caputo [(2,1)-γ]-differentiable. By using the same manner in previous cases, the solutions for (2,1)-system can be obtained such as φ1σ(t) = (1 − t − tγ/Γ(1 + γ))(σ − 1) and φ2σ(t) = (1 − t − tγ/Γ(1 + γ))(1 − σ). It is easy to check that and are also valid level sets for σ ∈ [0,1] and . Thus, φ(t) = μ(1 − t − tγ/Γ(1 + γ)) is a (2,1)-solution for FFIVPs (30) and (31) on .

Case 4. If φ(t) is (2,2)-solution, then the corresponding (2,2)-system will be

()
If γ = 2, then the exact solution of OFDEs (41) is [φ(t)] σ = [σ − 1,1 − σ](1 − t + tγ/Γ(γ + 1)), t ∈ [0,1]. Finally, to determine the fuzzy (2,2)-solution of FFDEs (30), let φ(t) be Caputo [(2,2)-γ]-differentiable. By using the same manner in previous cases, the solutions for (2,2)-system can be obtained such as φ1σ(t) = (σ − 1)(1 − t + tγ/Γ(1 + γ)) and φ2σ(t) = (1 − σ)(1 − t + tγ/Γ(1 + γ)). Here, and are also valid level sets for σ ∈ [0,1] and t ∈ [0,1]. However, φ(t) = μ(1 − t + tγ/Γ(γ + 1)) defines as a (2,2)-solution for FFIVPs (30) and (31) on (0,1].

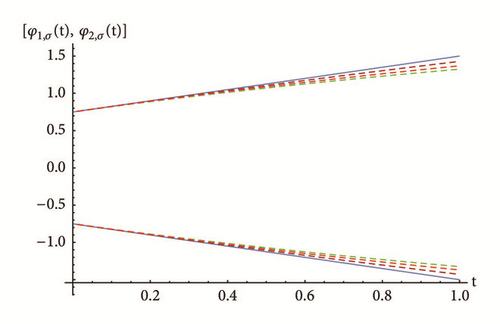
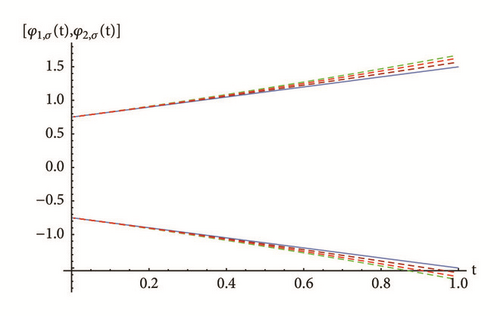
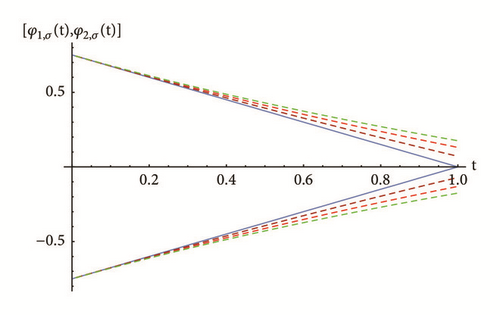
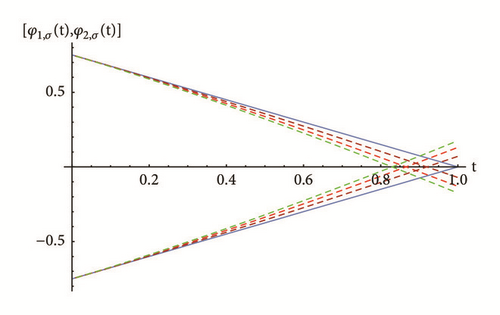
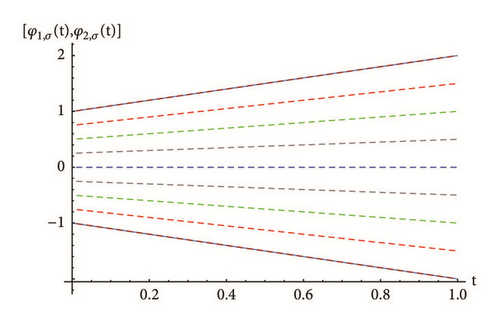
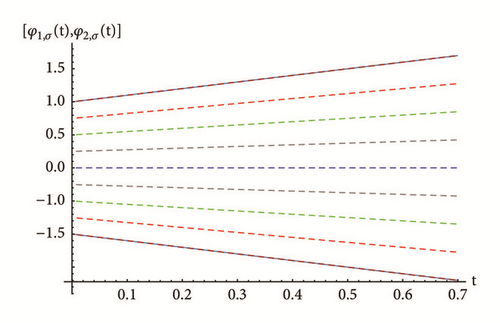
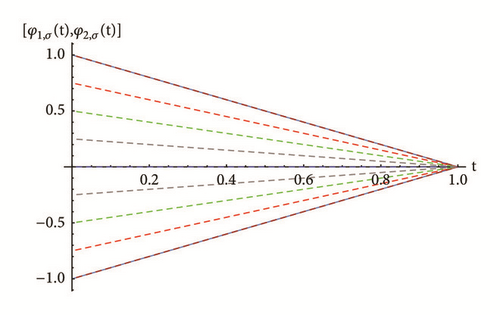
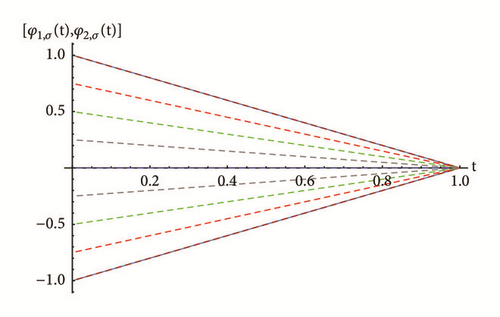
To demonstrate the agreement between the exact and approximate solution, Table 1 shows the absolute error of the 10th PRS approximate solution for FFIVPs (30) and (31) obtained for different values of σ-cut representations and nodes with fractional order γ = 1.9. Some graphical results are also presented in Figures 1 and 2. The numerical results obtained indicate that the RPS approximate solutions are in good agreement with each other and with the exact solutions for all cases of differentiability.

Table 1. The absolute error of 10th approximation of FFIVPs (30) and (31).
(n, m)-solution t σ = 0 σ = 0.25 σ = 0.5 σ = 0.75
(1,1)-system  0.2 2.0578567 × 10−4 1.5433927 × 10−4 1.0289283 × 10−4 5.1446419 × 10−5
 0.4 3.8465419 × 10−4 2.8849064 × 10−4 1.9232709 × 10−4 9.6163547 × 10−5
 0.6 5.5428820 × 10−4 4.1571615 × 10−4 2.7714410 × 10−4 1.3857205 × 10−4
 0.8 7.1821803 × 10−4 5.3866352 × 10−4 3.5910901 × 10−4 1.7955450 × 10−4
  
(1,2) -system  0.2 2.9676224 × 10−4 2.2257168 × 10−4 1.4838112 × 10−4 5.1446419 × 10−5
 0.4 4.7033136 × 10−4 3.5274852 × 10−4 2.3516568 × 10−4 9.6163547 × 10−5
 0.6 6.3684312 × 10−4 4.7763234 × 10−4 2.7714410 × 10−4 1.3857205 × 10−4
 0.8 7.9857642 × 10−4 5.3866352 × 10−4 3.5910901 × 10−4 1.7955450 × 10−4
  
(2,1) -system  0.2 2.0578567 × 10−4 1.5433925 × 10−4 1.0289283 × 10−4 5.1446419 × 10−5
 0.4 3.8465419 × 10−4 2.8849064 × 10−4 1.9232709 × 10−4 9.6163547 × 10−5
 0.6 5.5428820 × 10−4 4.1571615 × 10−4 2.7714410 × 10−4 1.3857205 × 10−4
 0.8 6.3684312 × 10−4 5.3746353 × 10−4 3.5910901 × 10−4 1.7955450 × 10−4
  
(2,2) -system  0.2 2.0578567 × 10−4 1.5433925 × 10−4 1.0289283 × 10−4 5.1446419 × 10−5
 0.4 3.8465419 × 10−4 2.8849064 × 10−4 1.9232709 × 10−4 9.6163547 × 10−5
 0.6 5.5428820 × 10−4 4.1571615 × 10−4 2.7714410 × 10−4 1.3857205 × 10−4
 0.8 7.1821803 × 10−4 5.3866352 × 10−4 3.5910901 × 10−4 1.7955450 × 10−4
Details are in the caption following the image
Figure 1 (a) RPS solution of (1,1)-system
Open in figure viewerPowerPoint
Plots of α-cut representations of φk,1σ(t), φk,2σ(t) with k = 10, σ = 0.25, and different values of γ ∈ {2,1.9,1.8,1.7} (- - - Exact, ⋯ RPS-approximation).
Details are in the caption following the image
Figure 1 (b) RPS solution of (1,2)-system
Open in figure viewerPowerPoint
Plots of α-cut representations of φk,1σ(t), φk,2σ(t) with k = 10, σ = 0.25, and different values of γ ∈ {2,1.9,1.8,1.7} (- - - Exact, ⋯ RPS-approximation).
Details are in the caption following the image
Figure 1 (c) RPS solution of (2,1)-system
Open in figure viewerPowerPoint
Plots of α-cut representations of φk,1σ(t), φk,2σ(t) with k = 10, σ = 0.25, and different values of γ ∈ {2,1.9,1.8,1.7} (- - - Exact, ⋯ RPS-approximation).
Details are in the caption following the image
Figure 1 (d) RPS solution of (2,2)-system
Open in figure viewerPowerPoint
Plots of α-cut representations of φk,1σ(t), φk,2σ(t) with k = 10, σ = 0.25, and different values of γ ∈ {2,1.9,1.8,1.7} (- - - Exact, ⋯ RPS-approximation).
Details are in the caption following the image
Figure 2 (a) σ-levels of (1,1)-system
Open in figure viewerPowerPoint
Plots of exact and RPS-approximation at γ = 2 with different values of σ-levels, σ ∈ {0,0.25,0.5,0.75,1} (- - - Exact, ⋯ RPS-approximation).
Details are in the caption following the image
Figure 2 (b) σ-levels of (1,2)-system
Open in figure viewerPowerPoint
Plots of exact and RPS-approximation at γ = 2 with different values of σ-levels, σ ∈ {0,0.25,0.5,0.75,1} (- - - Exact, ⋯ RPS-approximation).
Details are in the caption following the image
Figure 2 (c) σ-levels of (2,1)-system
Open in figure viewerPowerPoint
Plots of exact and RPS-approximation at γ = 2 with different values of σ-levels, σ ∈ {0,0.25,0.5,0.75,1} (- - - Exact, ⋯ RPS-approximation).
Details are in the caption following the image
Figure 2 (d) σ-levels of (2,2)-system
Open in figure viewerPowerPoint
Plots of exact and RPS-approximation at γ = 2 with different values of σ-levels, σ ∈ {0,0.25,0.5,0.75,1} (- - - Exact, ⋯ RPS-approximation).

6. Conclusion

In this paper, the RPS algorithm is successfully developed, investigated, and applied to solve the fuzzy differential equation of fractional order 1 < γ ≤ 2 with fuzzy initial constraints under the fuzzy concept of Caputo H-differentiability. The fuzziness is represented using upper semicontinuous membership function of bounded support, convex, and normalized fuzzy numbers based on its single parametric form. The behavior of approximate solution for different values of fractional order γ is discussed quantitatively as well as graphically. The numerical results in this paper demonstrate the efficiency of the algorithm. We conclude that the proposed scheme is highly accurate in solving widely array of fuzzy fractional issues.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This research was financially supported by the UKM (Grant no. GP-K007788 and GP-K006926).

    Data Availability

    The data used to support the findings of this study are available from the corresponding author upon request.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.