In this paper, the coupled Schrödinger-Boussinesq equations (SBE) will be solved by the sech, tanh, csch, and the modified simplest equation method (MSEM). We obtain exact solutions of the nonlinear for bright, dark, and singular 1-soliton solution. Kerr law nonlinearity media are studied. Results have proven that modified simple equation method does not produce the soliton solution in general case. Solutions may find practical applications and will be important for the conservation laws for dispersive optical solitons.

1. Introduction

All optical communications are being used for transcontinental and transoceanic data transfer, through long-haul optical fibers, at the present time. There are various aspects of soliton communication that still need to be addressed. One of the features is the dispersive optical solitons. In presence of higher order dispersion terms, soliton communications are sometimes a hindrance as these dispersion terms produce soliton radiation. Nonlinear evolution equations have a major role in various scientific and engineering fields, such as optical fibers. Nonlinear wave phenomena of dispersion, dissipation, diffusion, reaction, and convection are very important in nonlinear wave equations. In recent years, quite a few methods for obtaining explicit traveling and solitary wave solutions of nonlinear evolution equations have been proposed. In recent years, exact homoclinic and heteroclinic solutions were proposed for some NEEs like nonlinear Schrödinger equation, Sine-Gordon equation, Davey-Stewartson equation, Zakharov equation, and Boussinesq equation [1–7].

In particular, the study of the coupled Schrödinger-Boussinesq equations has attracted much attention of mathematicians and physicists [8–10]. The existence of the global solution of the initial boundary problem for the equations was investigated in [8]. The existence of a periodic solution for the equations was considered in [9]. Kilicman and Abazari [10] used the (G^′/G)-expansion method to construct periodic and soliton solutions for the Schrödinger-Boussinesq. The investigation of nonlinear partial differential equations plays an important role in the study of nonlinear physical phenomena [9–12].

The nonlinear coupled Schrödinger-Boussinesq equation (SBE) governs the propagation of optical solitons in a dispersive optical fiber and is a very important equation in the area of theoretical and mathematical physics. This paper is going to take a look at the bright, dark, and singular soliton solutions for Kerr law nonlinearity media.

2. Governing Equations

Consider the coupled Schrödinger-Boussinesq equations (SBE). They appeared in [13] as a special case of general systems governing the stationary propagation of coupled nonlinear upper hybrid and magneto sonic waves in magnetized plasma. These equations were in the form [14]

(1)

where α₁, α₂ are real constants, E(x, t) is a complex function, and N(x, t) is a real function. The complete integrability of (1) was studied by Chowdhury et al. [15], and N-soliton solution, homoclinic orbit solution, and rogue solution were obtained by Hu et al. [16], Dai et al. [17–19], and Mu and Qin [20].

3. The Traveling Solution

Consider the nonlinear partial differential equation in the form

(2)

where u(x, t) is a traveling wave solution of nonlinear partial differential equation (2). We use the transformations

(3)

where ξ = x − ρt + χ. This enables us to use the following changes:

(4)

Using (4) to transfer the nonlinear partial differential equation (2) to nonlinear ordinary differential equation,

(5)

The ordinary differential equation (5) is then integrated as long as all terms contain derivatives, where we neglect the integration constants.

4. Hyperbolic Function Methods

The solutions of many nonlinear equations can be expressed in the following form.

4.1. Sech Function Method (Bright Soliton) [21]

(6)

4.2. Tanh Function Method (Dark Soliton) [22]

(7)

4.3. Csch Function Method (Singular Soliton) [21, 22]

(8)

where A represent the amplitudes of the solitons and μ represents the solitons width.

We substitute (6), (7), or (8) into the reduced equation (5), balance the terms of the sech, tanh, and csch functions, and solve the resulting system of algebraic equations by using computerized symbolic packages. We next collect all terms with the same power in sech^k⁡(μξ), tanh^k⁡(μξ), or csch^k⁡(μξ), set to zero their coefficients to get a system of algebraic equations among the unknowns A, μ, and β, and solve the subsequent system.

5. The Application

The starting hypothesis for solving (1) by the aid of traveling waves solution is as follows: introduce the transformations

(9)

where

(10)

where k, ω, ρ, ϵ₀, and χ are real constants. The parameter ρ represents the soliton velocity.

Substituting (9) and (10) into (1) and decomposing into real and imaginary parts leads to

(11)

(12)

(13)

Substitute (12) in (10), then

(14)

Integrating (13) twice with zero constant, (13) can be written as

(15)

5.1. Bright Soliton

Seeking the solution by sech function method as in (6)

(16)

the system of equations in (11) and (15) becomes, respectively,

(17)

(18)

Equating the exponents and the coefficients of each pair of the sech functions, we find

(19)

Thus setting coefficients of (17)-(18) to zero yields set system of equations:

(20)

Solving the system of equations in (20), we get

(21)

(22)

(23)

(24)

For k = α₁ = 1, α₂ = 4, ϵ₀ = χ = 0, the real part of E₁(x, t) = 48cos⁡(x + 16t) sech²⁡{2(x − 2t)}, and N₁(x, t) = 24 sech²⁡{2(x − 2t)}.

Figures 1 and 2 represent the solitary wave of the real part of E₁(x, t) in (23) and N₁(x, t) in (24), respectively, for −5 ≤ x ≤ 5, 0 ≤ t ≤ 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The solitary wave of the real part of E₁(x, t) in (23) for −5 ≤ x ≤ 5, 0 ≤ t ≤ 1.

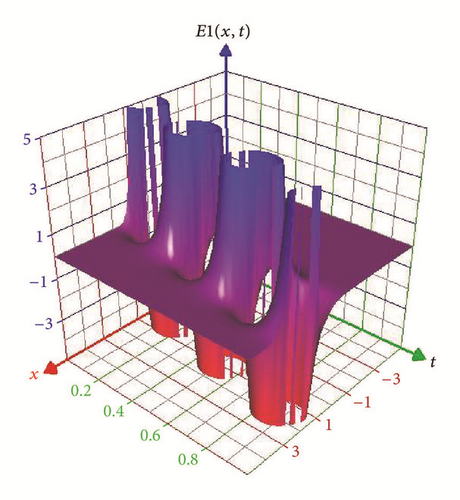
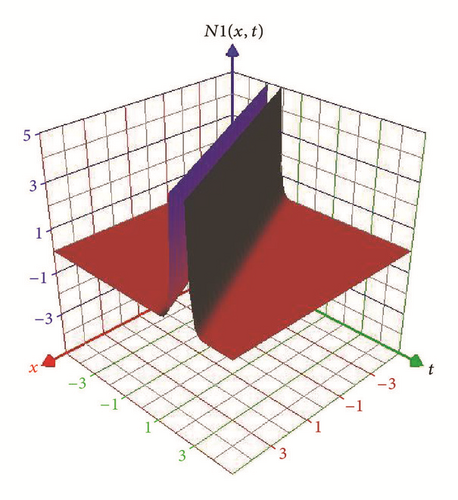
5.2. Dark Soliton

Seeking the solution by tanh function method as in (7)

(25)

the system of equations in (11) and (15) becomes, respectively,

(26)

(27)

Equating the exponents and the coefficients of each pair of the sech functions, we find

(28)

Thus setting coefficients of (26)-(27) to zero yields set system of equations:

(29)

Solving the system of equations in (29), we get

(30)

(31)

(32)

(33)

For k = α₁ = 1, α₂ = 4, ϵ₀ = χ = 0, the real part of

, and

Figures 3 and 4 represent the solitary wave of the real part of E₂(x, t) in (32) and N₂(x, t) in (33) for −5 ≤ x ≤ 5, 0 ≤ t ≤ 1.

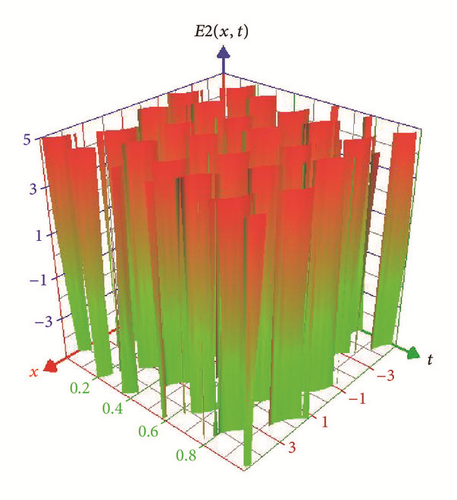
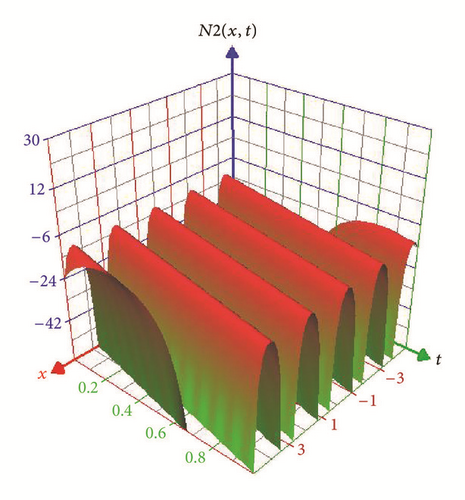
5.3. Singular Soliton

Seeking the solution by sech function method as in (8)

(34)

the system of equations in (11) and (15) becomes, respectively,

(35)

(36)

Equating the exponents and the coefficients of each pair of the sech functions, we find

(37)

Thus setting coefficients of (35)-(36) to zero yields set system of equations:

(38)

Solving the system of equations in (38), we get

(39)

(40)

(41)

For k = α₁ = 1, α₂ = 4, ϵ₀ = χ = 0, the real part of

, and

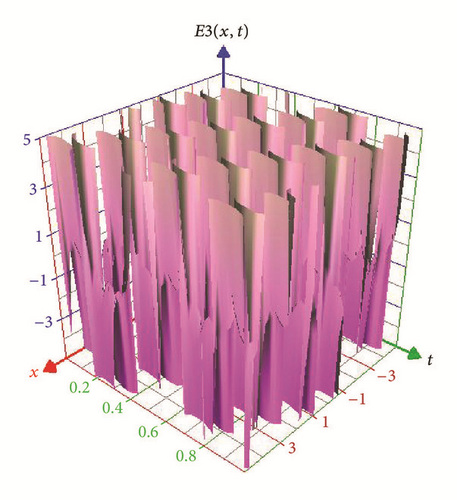
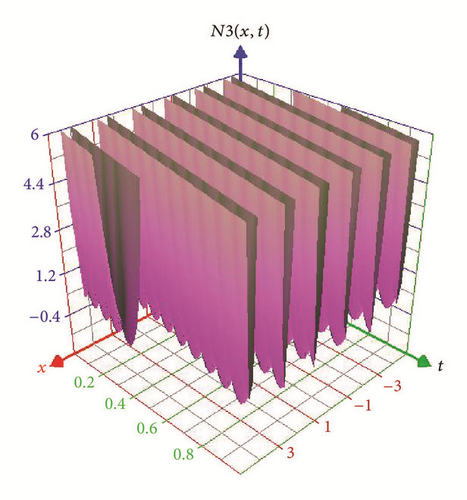
Figures 5 and 6 represent the solitary wave of the real part of E₃(x, t) in (40) and N₃(x, t) in (41) for −5 ≤ x ≤ 5, 0 ≤ t ≤ 1.

5.4. Modified Simple Equation Method

This section will analyze (11) and (15) by the modified simple equation method; assume that solutions are of the form [23]

(42)

where the parameters m, n can be found by balancing the highest-order linear term with the nonlinear terms in (11) and (15), respectively.

In (11), we balance u^′′ with uv, to obtain m + 2 = m + n, and then n = 2. While in (15), We balance v^′′ with u², to obtain n + 2 = 2m, and then m = 2.

Then

(43)

where A₀, A₁, A₂, B₀, B₁, and B₂ are constants to be calculated.

Substitute (43) in (11) and (15), respectively, to get

(44)

In (44) equating expressions at (ψ^j j = 0, −1, −2, −3, −4) to zero, we get the following system of equations:

(45)

Obviously when solving the system of (45), we conclude that equations can be satisfied simultaneously for the following constraints. Hence, the modified simple equation method does not produce the soliton solution in general case:

(46)

Then we will solve the following ordinary differential equation:

(47)

and therefore

(48)

where a₀, a₁ are arbitrary constants.

And

(49)

Finally solutions become

(50)

6. Conclusion

In this paper the dispersive bright, dark, and singular soliton solutions to SBE with Kerr law of nonlinearity were studied. The sech, tanh, csch, and the modified simplest equation method have been successfully applied to find solitons solutions for the coupled Schrödinger-Boussinesq equations. Several constraint conditions were assuring the existence of such solitons with Kerr law nonlinearity. The modified simple equation method does not produce the soliton solution in general case. Solutions by three methods are plotted in figures for the real and imaginary parts for E(x, t) and N(x, t). Compatibility in figures shape between the solutions of E(x, t) and N(x, t) by the same method sometimes appeared. Solutions may be important for the conservation laws for dispersive optical solitons. Those research outcomes will be soon disseminated.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Acknowledgments

This work was supported by Al-Rafidain University College.

References

1 Ablowitz M. J. and Herbst B. M., On homoclinic structure and numerically induced chaos for the nonlinear Schrödinger equation, SIAM Journal on Applied Mathematics. (1990) 50, no. 2, 339–351, https://doi.org/10.1137/0150021, MR1043590.
10.1137/0150021
Web of Science® Google Scholar
2 Ercolani N., Forest M. G., and McLaughlin D. W., Geometry of the modulational instability. III. Homoclinic orbits for the periodic sine-Gordon equation, Physica D: Nonlinear Phenomena. (1990) 43, no. 2-3, 349–384, https://doi.org/10.1016/0167-2789(90)90142-C, MR1067917.
10.1016/0167-2789(90)90142-C
Web of Science® Google Scholar
3 Dai Z. and Huang J., Homoclinic tubes for the Davey-Stewartson {II} equation with periodic boundary conditions, Chinese Journal of Physics. (2005) 43, no. 2, 349–356, MR2150328, 2-s2.0-20144375348.
Web of Science® Google Scholar
4 Dai Z., Huang J., Jiang M., and Wang S., Homoclinic orbits and periodic solitons for Boussinesq equation with even constraint, Chaos, Solitons & Fractals. (2005) 26, no. 4, 1189–1194, 2-s2.0-19144365922, https://doi.org/10.1016/j.chaos.2005.02.025.
10.1016/j.chaos.2005.02.025
Web of Science® Google Scholar
5 Dai Z., Huang J., and Jiang M., Explicit homoclinic tube solutions and chaos for Zakharov system with periodic boundary, Physics Letters A. (2006) 352, no. 4-5, 411–415, MR2210330, https://doi.org/10.1016/j.physleta.2005.12.026, Zbl1187.37112, 2-s2.0-33644971190.
10.1016/j.physleta.2005.12.026
CAS Web of Science® Google Scholar
6 Jawad A. J. M., Soliton Solutions for Nonlinear Systems (2+1)-Dimensional Equations, IOSR Journal of Mathematics. (2012) 1, no. 6, 27–34, https://doi.org/10.9790/5728-0162734.
10.9790/5728-0162734
Google Scholar
7 Hase Y. and Satsuma J., An N-soliton solution for the nonlinear Schrödinger equation coupled to the Boussinesq equation, Journal of the Physical Society of Japan. (1988) 57, no. 3, 679–682, https://doi.org/10.1143/JPSJ.57.679, MR941447.
10.1143/JPSJ.57.679
Web of Science® Google Scholar
8 Guo B. L. and Shen L. J., The global solution of initial value problem for nonlinear Schrödinger-Boussinesq equation in 3-dimensions, Acta Mathematicae Applicatae Sinica. English Series. (1990) 6, no. 1, 11–21, https://doi.org/10.1007/BF02014711, MR1049630.
10.1007/BF02014711
CAS Google Scholar
9 Guo B. and Du X., Existence of the periodic solution for the weakly damped Schrödinger–Boussinesq equation, Journal of Mathematical Analysis and Applications. (2001) 262, no. 2, 453–472, https://doi.org/10.1006/jmaa.2000.7455, MR1859319, Zbl1040.35114, 2-s2.0-0035888613.
10.1006/jmaa.2000.7455
Web of Science® Google Scholar
10 Kilicman A. and Abazari R., Travelling wave solutions of the SchröDinger-Boussinesq system, Abstract and Applied Analysis. (2012) 2012, 11, 198398, https://doi.org/10.1155/2012/198398, 2-s2.0-84870028415.
10.1155/2012/198398
Google Scholar
11 Lai S. Y. and Wiwatanapataphe B., The asymptotics of global solutions for semilinear wave equations in two space dimensions, Dynamics of Continuous, Discrete & Impulsive Systems. Series B. Applications & Algorithms. (2011) 18, no. 5, 647–657, MR2884524.
Google Scholar
12 Lai S., Wu Y. H., and Wiwatanapataphee B., On exact travelling wave solutions for two types of nonlinear k(n, n) equations and a generalized KP equation, Journal of Computational and Applied Mathematics. (2008) 212, no. 2, 291–299, https://doi.org/10.1016/j.cam.2006.12.008, MR2383021.
10.1016/j.cam.2006.12.008
Web of Science® Google Scholar
13 Conte R. and Musette M., Link between solitary waves and projective Riccati equations, Journal of Physics A: Mathematical and General. (1992) 25, no. 21, 5609–5623, https://doi.org/10.1088/0305-4470/25/21/019, MR1192020, Zbl0782.35065, 2-s2.0-21144479106.
10.1088/0305-4470/25/21/019
Web of Science® Google Scholar
14 Huang X., The investigation of solutions to the coupled Schrödinger-Boussinesq equations, Abstract and Applied Analysis. (2013) 2013, 5, 170372, https://doi.org/10.1155/2013/170372, MR3068178.
10.1155/2013/170372
Google Scholar
15 Chowdhury A. R., Dasgupta B., and Rao N. N., Painléve analysis and Backlund transformations for coupled generalized Schrödinger-Boussinesq system, Chaos, Solitons & Fractals. (1998) 9, no. 10, 1747–1753, 2-s2.0-0032182477, https://doi.org/10.1016/S0960-0779(98)00005-8, Zbl0934.35168.
10.1016/S0960-0779(98)00005-8
Web of Science® Google Scholar
16 Hu X.-B., Guo B.-L., and Tam H.-W., Homoclinic orbits for the coupled Schrödinger-Boussinesq equation and coupled higgs equation, Journal of the Physical Society of Japan. (2003) 72, no. 1, 189–190, 2-s2.0-0037214772, https://doi.org/10.1143/JPSJ.72.189.
10.1143/JPSJ.72.189
CAS Web of Science® Google Scholar
17 Dai Z.-D., Liu Z.-J., and Li D.-L., Exact periodic solitary-wave solution for KdV equation, Chinese Physics Letters. (2008) 25, no. 5, 1531–1533, https://doi.org/10.1088/0256-307x/25/5/003, 2-s2.0-46749099413.
10.1088/0256-307X/25/5/003
Web of Science® Google Scholar
18 Dai Z., Liu J., and Li D., Applications of {HTA} and {EHTA} to {YTSF} equation, Applied Mathematics and Computation. (2009) 207, no. 2, 360–364, MR2489107, https://doi.org/10.1016/j.amc.2008.10.042, Zbl1159.35408, 2-s2.0-58349086009.
10.1016/j.amc.2008.10.042
Web of Science® Google Scholar
19 Dai Z., Li Z., Liu Z., and Li D., Exact homoclinic wave and soliton solutions for the 2D Ginzburg-Landau equation, Physics Letters A. (2008) 372, no. 17, 3010–3014, https://doi.org/10.1016/j.physleta.2008.01.015, MR2404757, Zbl1220.35168, 2-s2.0-41349092706.
10.1016/j.physleta.2008.01.015
CAS Web of Science® Google Scholar
20 Mu G. and Qin Z., Rogue waves for the coupled schrödinger-boussinesq equation and the coupled higgs equation, Journal of the Physical Society of Japan. (2012) 81, no. 8, 2-s2.0-84864675978, https://doi.org/10.1143/JPSJ.81.084001, 084001.
10.1143/JPSJ.81.084001
Web of Science® Google Scholar
21 Jawad A. J. M., Mirzazadeh M., and Biswas A., Solitary wave solutions to nonlinear evolution equations in mathematical physics, Pramana—Journal of Physics. (2014) 83, no. 4, 457–471, 2-s2.0-84908013253, https://doi.org/10.1007/s12043-014-0818-2.
10.1007/s12043-014-0818-2
Web of Science® Google Scholar
22 Jawad A. J., Three Different Methods for New Soliton Solutions of the Generalized NLS Equation, Abstract and Applied Analysis. (2017) 2017, 8, 5137946, https://doi.org/10.1155/2017/5137946.
10.1155/2017/5137946
Google Scholar
23 Mohamad Jawad A. J., Petkovi\′c M. D., and Biswas A., Modified simple equation method for nonlinear evolution equations, Applied Mathematics and Computation. (2010) 217, no. 2, 869–877, MR2678603, https://doi.org/10.1016/j.amc.2010.06.030, 2-s2.0-77955664465, Zbl1201.65119.
10.1016/j.amc.2010.06.030
Web of Science® Google Scholar

Citing Literature

All articles

Soliton Solutions of the Coupled Schrödinger-Boussinesq Equations for Kerr Law Nonlinearity

Abstract

1. Introduction

2. Governing Equations

3. The Traveling Solution

4. Hyperbolic Function Methods

4.1. Sech Function Method (Bright Soliton) [21]

4.2. Tanh Function Method (Dark Soliton) [22]

4.3. Csch Function Method (Singular Soliton) [21, 22]