Application of Residual Power Series Method to Fractional Coupled Physical Equations Arising in Fluids Flow
Abstract
The approximate analytical solution of the fractional Cahn-Hilliard and Gardner equations has been acquired successfully via residual power series method (RPSM). The approximate solutions obtained by RPSM are compared with the exact solutions as well as the solutions obtained by homotopy perturbation method (HPM) and q-homotopy analysis method (q-HAM). Numerical results are known through different graphs and tables. The fractional derivatives are described in the Caputo sense. The results light the power, efficiency, simplicity, and reliability of the proposed method.
1. Introduction
Fractional differential equations (FDEs) have found applications in many problems in physics and engineering [1, 2]. Since most of the nonlinear FDEs cannot be solved exactly, approximate and numerical methods must be used. Some of the recent analytical methods for solving nonlinear problems include the Adomian decomposition method [3, 4], variational iteration method [5], homotopy perturbation method [6, 7], homotopy analysis method [8, 9], spectral collocation method [10], the tanh-coth method [11], exp-function method [12], Mittag-Leffler function method [13], differential quadrature method [14], and reproducing kernel Hilbert space method [15, 16].
The RPSM was first devised in 2013 by the Jordanian mathematician Omar Abu Arqub as an efficient method for determining values of coefficients of the power series solution for first and the second-order fuzzy differential equations [40]. The RPSM is an effective and easy to construct power series solution for strongly linear and nonlinear equations without linearization, perturbation, or discretization. In the last few years, the RPSM has been applied to solve a growing number of nonlinear ordinary and PDEs of different types, classifications, and orders. It has been successfully applied in the numerical solution of the generalized Lane-Emden equation [41], which is a highly nonlinear singular differential equation, in the numerical solution of higher-order regular differential equations [42], in approximate solution of the nonlinear fractional KdV-Burgers equation [43], in construct and predict the solitary pattern solutions for nonlinear time-fractional dispersive PDEs [44], and in predicting and representing the multiplicity of solutions to boundary value problems of fractional order [45]. The RPSM distinguishes itself from various other analytical and numerical methods in several important aspects [46]. Firstly, the RPSM does not need to compare the coefficients of the corresponding terms and a recursion relation is not required. Secondly, the RPSM provides a simple way to ensure the convergence of the series solution by minimizing the related residual error. Thirdly, the RPSM is not affected by computational rounding errors and does not require large computer memory and time. Fourthly, the RPSM does not require any converting while switching from the low-order to the higher-order and from simple linearity to complex nonlinearity; as a result, the method can be applied directly to the given problem by choosing an appropriate initial guess approximation.
2. Fundamental Concepts
Definition 1 (see [43].)The Caputo time-fractional derivatives of order α > 0 of u(x, t) is defined as
Definition 2 (see [47], [48].)A power series representation of the form
Theorem 3 (see [47], [48].)Suppose that f has a fractional power series representation at t0 of the form
Definition 4 (see [43].)A power series representation of the form
Theorem 5 (see [43], [44].)Suppose that u(x, t) has a multiple fractional Power series representation at t0 of the form
Corollary 6 (see [44].)Suppose that u(x, y, t) has a multiple fractional Power series representation at t0 of the form
3. Basic Idea of RPSM
As in [40, 41], since the fractional derivative of a constant in the Caputo sense is zero and the fractional derivatives of Res(x, t) and Resk(x, t) are matching at t = 0 for each n = 0,1, 2, …., k.; that is, , n = 0,1, 2, …., k.
4. Applications
To illustrate the basic idea of RPSM, we consider the following two time-fractional Gardner and Cahn-Hilliard equations.
4.1. Time-Fractional Gardner Equation
4.2. Time-Fractional Cahn-Hilliard Equation
5. Numerical Results
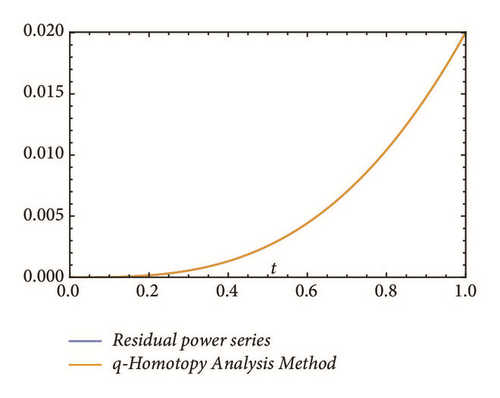
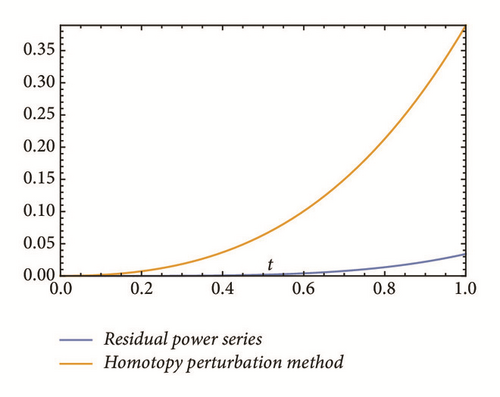
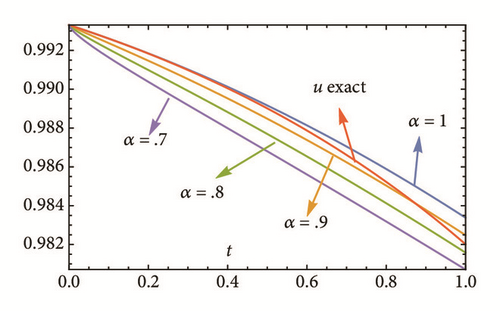
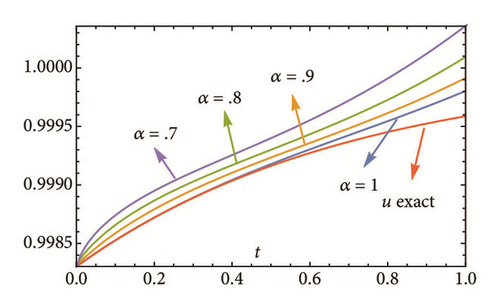
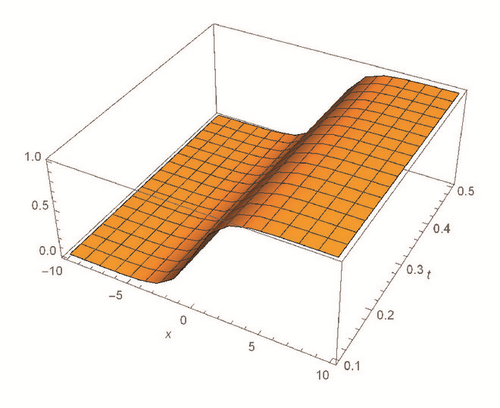
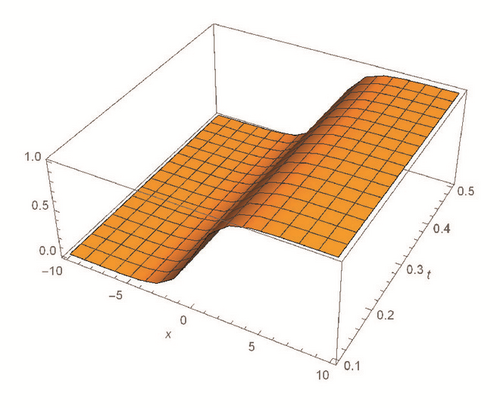
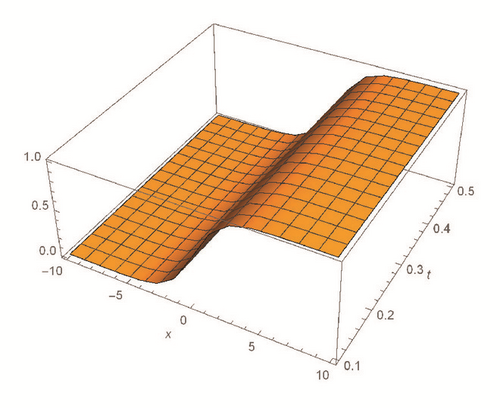
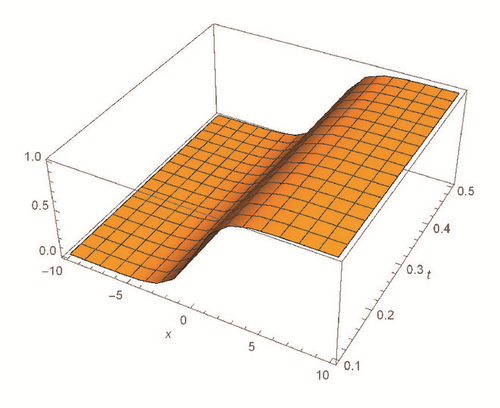
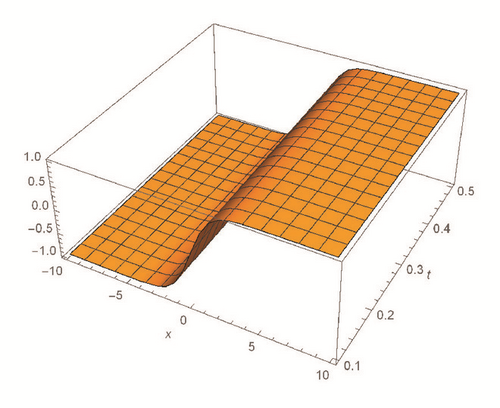
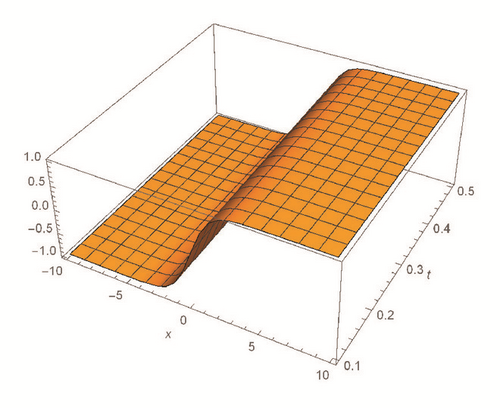
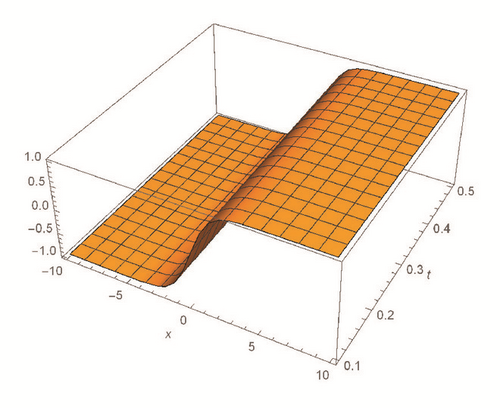
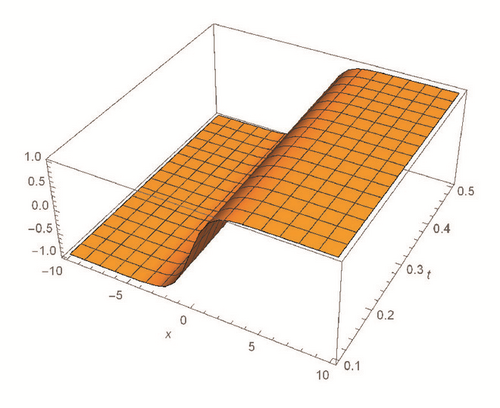
This section deals with the approximate analytical solutions obtained by RPSM for Gardner and Cahn-Hilliard equations. In classical case(α → 1), Figure 1 and Tables 1 and 2 describe the comparison between RPSM with q-HAM [28] and HPM [36]. In fractional case, Figures 2, 3, and 4 describe the geometrical behavior of the solutions obtained by RPSM for different fractional value α of the two equations.
| x | |uexact − uRPS| | |uexact − uqHAM| |
|---|---|---|
| .1 | 166.002 × 10−6 | 166.002 × 10−6 |
| .2 | 162.707 × 10−6 | 162.707 × 10−6 |
| .3 | 156.257 × 10−6 | 156.257 × 10−6 |
| .4 | 146.917 × 10−6 | 146.917 × 10−6 |
| .5 | 135.064 × 10−6 | 135.064 × 10−6 |
| x | |uexact − uRPS| | |uexact − uHPM| |
|---|---|---|
| .1 | 25.5541 × 10−6 | 4.68338 × 10−3 |
| .2 | 41.5291 × 10−6 | 7.28902 × 10−3 |
| .3 | 54.2246 × 10−6 | 9.6162 × 10−3 |
| .4 | 62.8898 × 10−6 | 11.5931 × 10−3 |
| .5 | 67.2637 × 10−6 | 13.174 × 10−3 |
6. Conclusions
This work has used the RPSM for finding the solution of the time-fractional Gardner and Cahn-Hilliard equations. A very good agreement between the results obtained by the RPSM and q-HAM [28] was observed in Figure 1(a) and Table 1. Figure 1(b) and Table 2 indicate that the mentioned method achieves a higher level of accuracy than HPM [36]. Consequently, the work emphasized that the method introduces a significant improvement in this field over existing techniques.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Open Research
Data Availability
[1] The [approximate solution obtained by q-homotopy analysis method] data used to support the findings of this study have been deposited in the [article] repository ([doi.org/10.1016/j.asej.2014.03.014]) [28]. [2] The [approximate solution obtained by homotopy perturbation method] data used to support the findings of this study have been deposited in the [article] repository ([doi.org/10.1080/10288457.2013.867627]) [36].




