Robust Exponential Stability of Switched Complex-Valued Neural Networks with Interval Parameter Uncertainties and Impulses
Abstract
In this paper, dynamic behavior analysis has been discussed for a class of switched complex-valued neural networks with interval parameter uncertainties and impulse disturbance. Sufficient conditions for guaranteeing the existence, uniqueness, and global robust exponential stability of the equilibrium point have been obtained by using the homomorphism mapping theorem, the scalar Lyapunov function method, the average dwell time method, and M-matrix theory. Since there is no result concerning the stability problem of switched neural networks defined in complex number domain, the stability results we describe in this paper generalize the existing ones. The effectiveness of the proposed results is illustrated by a numerical example.
1. Introduction
It is of great importance to study complex-valued neural networks because of their extensive application in many fields, such as filtering, speech synthesis, remote sensing, signal processing, and others, which cannot be analyzed comprehensively with only their real-valued counterparts [1, 2]. Complex-valued neural networks are not only the simple extensions of real-valued systems due to their more complicated properties and research methods for dynamic behavior analysis, including stability, synchronization, and periodicity of system states. Therefore, there have been a great number of important studies published in the last few years that investigate dynamic behavior analysis of complex-valued neural networks.
Ever since the authors in [3, 4] studied the stability problems of several kinds of neural networks defined in complex number domain, scholars have presented plenty of significant conclusions about the stability of various complex-valued neural networks. Considering that time delay is unavoidable in the practice model of artificial neural networks, which could lead to instability of systems, Hu [5] established a class of delayed complex-valued neural networks and obtained sufficient conditions for assuring the equilibrium point stability of the system with two classes of complex-valued activation functions. With respect to complex-valued neural networks with various delays, the corresponding achievements can be referred in [6–12]. The impulsive effect inevitably exists in practical neural networks. For instance, system states are subject to instantaneous perturbations and experience abrupt changes in certain instances, which may be caused by the switching phenomenon, a frequency change or another sudden noise, and exhibits an impulsive effect [13]. Authors [13] established some sufficient conditions for assuring the exponential stability of a class of delayed complex-valued neural networks with impulsive disturbance by using the vector Lyapunov function method and the mathematical induction method. In [14], the global exponential convergence of T-S fuzzy complex-valued neural networks with time-varying delays and impulsive effects was discussed, and some sufficient conditions were obtained in terms of a complex-valued linear matrix inequality for assuring the global exponential convergence of the system states. Song [15, 16] also considered the impulsive effect in two tapes of complex-valued neural networks with time delays.
Recently, fruitful results on dynamic behavior analysis of nonlinear systems including neural networks with switching signals have been reported in the existing literatures [17–29]. As pointed out in [17], the nodes of a neural network in reality may encounter a connection failure or a new connection build-up; the structure of a neural network is inevitably designed to change abruptly with some internal or external incentives. This usually obligates neural networks to exhibit a special characteristic, network mode switching. Modeling this behavior by using the technique of the Markov process [2] or the switched system [18, 19] is more natural and generally accepted in the practical application of neural networks. However, the stability results proposed in [17–27] are only suitable to neural networks defined in the real number domain. In [2], a class of delayed complex-valued neural networks with Markova jumping parameters was established. The existence, uniqueness, and stochastic exponential robust stability of the equilibrium point of the addressed system were studied by coupling the M-matrix theory with the vector Lyapunov function method. Thus far, there are no stability results with respect to complex-valued neural networks with switching signal. In addition to the impulsive effects, parameter uncertainties have been considered in the form of delayed neural networks including real-valued systems [20, 30, 31] and complex-valued systems [2, 32–34], which were named interval systems. With respect to the stability problem of switched neural networks, there are two main problems that need to be generalized further. The switched neural networks defined in the real number domain can be extended to switched systems defined in the complex number domain. Moreover, the switched activation functions and self-feedback coefficients were not considered in the models of switched real-valued neural networks in the most of existing results, such as [19, 20, 26], which can be assumed to be switch signals.
Motivated by the above discussion, in this paper we will investigate the robust exponential stability of a class of switched complex-valued neural networks with interval parameter uncertainties and impulsive disturbance. The advantages and contributions can be described as follows. (1) The switched neural networks are defined in the complex number domain which including real-valued neural networks. (2) The interconnected matrices, self-feedback coefficients, and activation functions in the model are with different forms in different switched subsystems. (3) Both impulsive disturbances and interval parameter uncertainties are considered in the systems. (4) The sufficient conditions for ensuring the robust exponential stability of the equilibrium point are expressed in terms of the simple forms of inequalities, which are easy to check in practice.
This paper is organized as follows. In Section 2, a model description and preliminaries are given, including definitions, assumed conditions, and lemmas. In Section 3, a theorem and several corollaries are proposed for the stability judgment of the complex-valued neural networks addressed in this paper. In Section 4, a numerical example with simulation results is given to verify the effectiveness of the main results. Finally, the conclusion is drawn and future work is proposed in Section 5.
2. Model Description and Preliminaries
Notations, herein defined, will be used throughout the whole paper. Let R, C, and Z+ denote a real number set, a complex number set, and a positive integer set, respectively. Assuming that u = x + yi; here x, y ∈ R and i denotes the imaginary unit. Let |u| be the module; i.e., . Denote as the conjugate complex number of u. For complex number vector u ∈ Cn, let |u | = (|u1 | , |u2 | , …, |un | ) T, when (·) T denotes the transpose of the vector. Define the norm of the complex number vector u as . For the complex number matrix A = (ajm) n×n ∈ Cn×n, let |A | = (|ajm | ) n×n ∈ Rn×n, where and Re(·) and Im(·) represent the real and the imaginary parts of a complex number, respectively.
Assumption 1. Each function is globally Lipschitz with Lipschitz constant ; i.e., the inequality holds for all uj(t), vj(t) ∈ C, j = 1,2, …, n, h ∈ Ξ. Let .
Remark 2. Activation functions in complex number domains that satisfy Assumption 1 are actually the extensions of the real-valued functions that satisfy the Lipschitz continuity condition. As demonstrated in [2, 7, 14, 34, 35], it is easy to verify that assumptions concerning the conditions of the decomposition of a complex-valued activation function into its real and imaginary parts in [8, 10, 13] are strong constraints, and that, in this case, shows a special case of Assumption 1. In order to unify the research approach using real-valued systems and complex-valued systems, it is assumed that complex-valued activation functions are not explicitly expressed by separating real and imaginary parts, but by satisfying the Lipschitz continuity condition.
Assumption 3. It is assumed that, for all uj(t), vj(t) ∈ C, there exists a positive number such that holds, and j = 1,2, …, n, k = 1,2, ….
It is obvious that Assumption 3 implies that the impulsive function is bounded.
Let be the equilibrium point of (2).
Definition 4. The equilibrium point u# of (2) is defined to be robustly exponentially stable if there exists M ≥ 1 and λ > 0 such that the following inequality holds for all Ah ∈ AhI, Bh ∈ BhI ( h ∈ Ξ) and t ≥ t0 ≥ 0,
Definition 5 (see [36], [37].)It is supposed that Nσ(t1, t2) denotes the switching numbers on time-interval (t1, t2), here t1 > 0. If there exists Γ > 0 such that, for any t2 ≥ t1 ≥ 0 and N0 ≥ 0, the inequality Nσ(t1, t2) ≤ N0 + ((t2 − t1)/Γ) holds, then Γ is called the average dwell time.
In order to obtain results, the following lemmas are given in this paper.
Lemma 6 (see [6].)Let Q = (qjm) n×n ∈ Rn×n be a matrix with qjm ≤ 0(j, m = 1,2, ⋯, n, j ≠ m). The following statements are equivalent: (i) Q = (qjm) n×n is an M-matrix; (ii) the real parts of all eigenvalues of Q are positive; and (iii) there exists a positive vector ξ ∈ Rn such that Qξ > 0.
Denote Ω(Q) = {ξ ∈ Rn∣Aξ > 0, ξ > 0} if Q is an M-matrix.
Lemma 7 (see [6].)If H(z) is a continuous function on Cn and satisfies the following conditions, (i) H(z) is univalent injective on Cn, and (ii) lim‖z‖→∞‖H(z)‖ → ∞, then H(z) is a homeomorphism of Cn into itself.
3. Main Results
In this section, we will give several sufficient conditions for judging the robust exponential stability of u#of (2).
Theorem 8. Suppose that Assumptions 1 and 3 hold. If the following conditions are satisfied, then the equilibrium point u# of (2) exists and is unique and robustly exponentially stable for all Ah ∈ AhI, Bh ∈ BhI, and arbitrary input O(t) ∈ Cn:
(I) Every matrix is a M-matrix, where
(II) For any given ξh ∈ Ω(Qh), the average dwell time satisfies Γ > Γ∗ = (lnυ)/ε; here ε > 0 satisfies the following inequalities:
Proof. First, the existence and uniqueness of u#of (2) will be proven for every subsystem by Lemmas 6 and 7.
The map which is associated with (2), is defined, i.e., for all j = 1,2, …, n and h ∈ Ξ,
It is well known that if Hh(u) is a homeomorphism map, then there is a unique equilibrium point u# for (2).
We prove that Hh(u) is a univalent injective on Cn under Assumption 1.
According to Lemma 6, it can be concluded that there exists a positive vector ξh such that the following inequalities hold for all j = 1,2, …, n, h ∈ Ξ:
Moreover, it follows from (9) that there exists a sufficient small positive number μ > 0 such that the following inequalities hold for all j = 1,2, …, n, h ∈ Ξ:
It is assumed that there exist u, v ∈ Cn with u ≠ v such that , j = 1,2, …, n, h ∈ Ξ; i.e.,
Considering (4) and (5) as well as Assumption 1, for all j = 1,2, …, n, h ∈ Ξ, we get
Furthermore, (14) can be rewritten as where , , j = 1,2, …, n, j ≠ m. Because the matrix Qh is an M-matrix, it is obvious that the matrix is also an M-matrix. We know that holds and exists obviously. Furthermore, it can be concluded that |u − v | = 0; i.e., u = v. It is an obvious contradiction with the assumption u ≠ v. Hence, Hh(u) is a univalent injective on Cn, h ∈ Ξ.
Next, we will prove that lim‖u‖→∞‖Hh(u)‖ → ∞.
Let , j = 1,2, …, n, h ∈ Ξ; i.e.,
After multiplying by the conjugate complex number of uj on both sides of (15), then for all j = 1,2, …, n, h ∈ Ξ, we get
Taking the conjugate operation on both sides of (16), for all j = 1,2, …, n, h ∈ Ξ, we have
After combining (16) and (17) and considering (4), (5), Assumption 1, for all j = 1,2, …, n, h ∈ Ξ, we obtain
After multiplying by (j = 1,2, …, n, h ∈ Ξ) on both sides of (18), taking the sum, and considering (12), we get
Furthermore, it can be concluded that
That is ; i.e., . Therefore, holds. Obviously, we have that as ‖u‖ → ∞. It means that ‖Hh(u)‖ → ∞ as ‖u‖ → ∞.
In summation, it follows from Lemma 7 that Hh(u) is a homeomorphism on Cn, h ∈ Ξ. Therefore, (2) has a unique equilibrium point u#.
Next, the robust exponential stability of the equilibrium point u# will be proved by applying the scalar Lyapunov function method.
From (11), it can be obtained that
Define a function as follows:
Due to Fj(0) < 0 and Fj(·) is a continuous function, there exists such that ; i.e.,
Choose a candidate scalar Lyapunov function as follows:
Calculating the right upper derivation along the zero solution of (7), we obtain
Considering (23), we get
Because σ(t): [0, ∞) → Ξ = {1,2, …, N} is a piecewise constant function, taking , we can get
Furthermore, when t ∈ [tk, tk+1), holds.
Next, we will prove the convergence of system state at the impulsive instant. Suppose that σ(t) = mh ∈ Ξ as t ∈ [tk−1, tk), which means the subsystem mh is activated. When t ∈ [tk, tk+1), σ(t) = jh ∈ Ξ, this means that the subsystem jh is activated at , k = 1, 2, …. Furthermore, we have
According to the conditions given below (9) and Assumption 3, we have
Combining (27) and (29), we have ; here υ ≥ 1; i.e.,
Using this analogy, we have , where Nσ(t0, t) denotes the switching number. Because the impulses only occur at the switching moment, Nσ(t0, t) also denotes the impulse number.
Furthermore, according to integral mean value theorem, we have
Then
That is, .
In addition, it is obvious that holds. Let , so we have .
That is,
Let ; μ = ε − ((lnυ)/Γ); thus, we get . It is obvious that θ > 0 when Γ > (lnυ)/ε.
According to Definition 4, it can be concluded that the zero solution of (7) is robustly exponentially stable, which means the equilibrium point of (2) is robustly exponentially stable. The proof is completed.
Remark 9. Robust stability of impulsive complex-valued neural networks with time delays was studied by applying Lyapunov-Krasovskii functional method and the complex-valued matrix inequality skills in [34]. Switching signal was not considered in the model addressed in there. In addition, in most of papers concerning switched neural networks defined in real number domain, such as [19, 20, 26], only interconnected matrices were supposed to be switched signals. Obviously, the impulsive complex-valued system with switched signals including both self-feedback functions and activation functions in this paper includes the models established in [19, 20, 26, 34].
When there is no impulse effect in (2), the corresponding corollary can be stated as follows.
Corollary 10. Suppose that Assumption 1 holds. If the following conditions are satisfied, then the equilibrium point u# of (2) is with existence, uniqueness, and robustly exponential stability for all Ah ∈ AhI, Bh ∈ BhI (h ∈ Ξ), and arbitrary input O(t) ∈ Cn:
(I) Every matrix is an M-matrix, where
(II) The average dwell time satisfies Γ > Γ∗ = (lnυ)/ε, with ; here ε, , and are defined as Theorem 8.
Because the proof of Corollary 10 is similar to that of Theorem 8, it is omitted here.
It is well known that complex-valued neural networks can be viewed as extensions of real-valued neural networks. In the following explanation, we will present some conditions guaranteeing the robust exponential stability of switched neural networks with impulses and delays under the condition that all variables and functions in (2) and Assumptions 1 and 3 are defined in the real number domain.
Corollary 11. Suppose that Assumptions 1 and 3 hold. If the following conditions are satisfied, then the equilibrium point u# of (2) is with existence, uniqueness, and robustly exponential stability for all Ah ∈ AhI, Bh ∈ BhI and arbitrary input O(t) ∈ Rn:
(I) Every matrix is an M-matrix, where
(II) For any given ξh ∈ Ω(Qh), the average dwell time satisfies Γ > Γ∗ = (lnυ)/ε; here, ε > 0 satisfies the following inequality:
Proof. Choose the candidate scalar Lyapunov function as follows:
By using similar analysis to that used as proof for Theorem 8, the conclusion of Corollary 11 can be obtained directly. The proof is completed.
When comparing Theorem 8 and Corollary 11, it can be seen that the stability conditions for judging complex-valued neural networks are more complicated and conservative due to the more complicated properties of complex-valued systems.
Remark 12. In addition to impulse disturbances [13–15, 34, 35] and parameter uncertainties [2, 31, 34], stochastic disturbances [10, 38] also exist in real complex-valued neural networks. Additionally, the stability problem and the synchronization problem of fractional-order systems have become a hot research topic [39, 40]. The research in this paper can be extended further to the study of the stability of the mentioned systems.
4. Example
In this section, an example with simulation results is given to illustrate the effectiveness of the sufficient conditions established in the preceding section.
Table 1 shows the self-feedback coefficients, activation functions, and impulsive functions of three subsystems in (2), respectively.
| Functions | Subsystem 1 | Subsystem 2 | Subsystem 3 |
|---|---|---|---|
| ωj | 4.5 | 9 | 8 |
| fj(uj(t)) | 0.25uj(t) + 0.25sin(uj(t)) | 0.75uj(t) + 0.75sin(uj(t)) | |
|
|
|
|
|
It can be determined from Table 1 that , , , , , , k = 1,2, ….
Let ε = 1, ξ1 = [1.05, 0.95] T, ξ2 = [1.1, 1] T, and ξ3 = [1, 1.2] T. Through calculations, we can drive that Γ∗ = (lnυ)/ε = 2.434s. According to the condition in Theorem 8, the average dwell time is taken as Γ = 3s > Γ∗. Therefore, the switching time sequence (or impulse moment of occurrence) is described as tk ∈ {3s, 6s, 9s, …}. Assume that the external inputs of the three subsystems are zero. Let the delays be defined as τjm = 0.6s, j, m = 1,2.
It follows from Lemma 6 that matrices Q1, Q2, and Q3 are all M-matrix.
Additionally, we need to verify (9) of condition (II) in Theorem 8. For the three subsystems, we obtain the calculated results in Table 2.
| Subsystem 1 | Subsystem 2 | Subsystem 3 | |
|---|---|---|---|
| Neuron 1 | −0.993 | −0.105 | −1.929 |
| Neuron 2 | −1.924 | −2.254 | −3.174 |
It can be determined from Table 2 that inequalities (9) hold in all three subsystems.
In conclusion, all conditions in Theorem 8 are satisfied. According to Theorem 8, we can conclude that the equilibrium point of (2) with above assumptions possesses existence, uniqueness, and exponential robust stability.
Tables 3 and 4 show the initial conditions and the interconnected matrices of each of the three subsystems in (2), respectively. They will be used in simulation.
| Subsystem 1 | Subsystem 2 | Subsystem 3 | |
|---|---|---|---|
| u1(s) | 2+1.5i | 1.3+i | 0.2-0.5i |
| u2(s) | -1-1.2i | -1-0.2i | -0.7+1.1i |
| Subsystem 1 | Subsystem 2 | Subsystem 3 | |
|---|---|---|---|
| A |
|
|
|
| B |
|
|
|
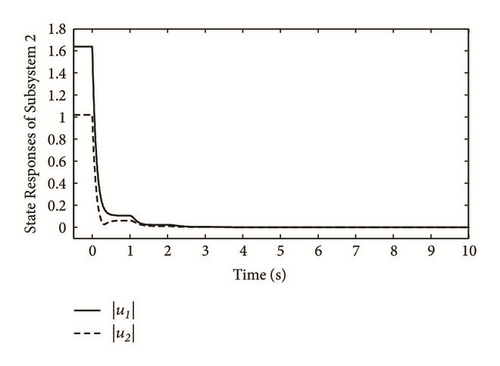
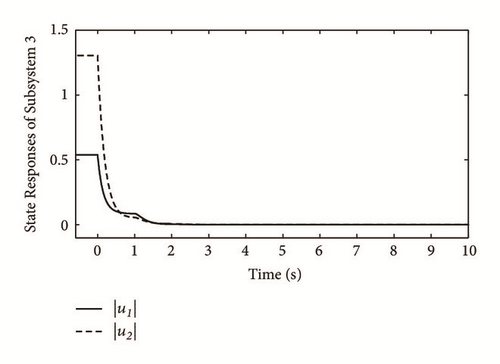
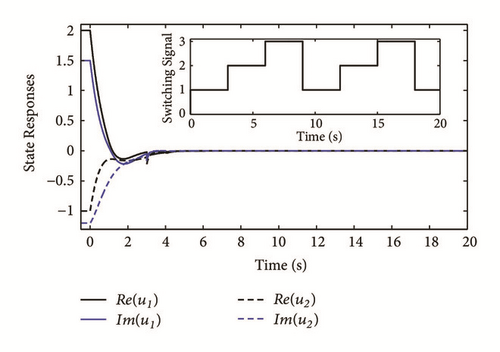
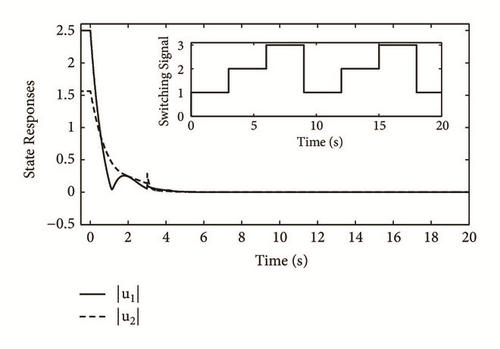
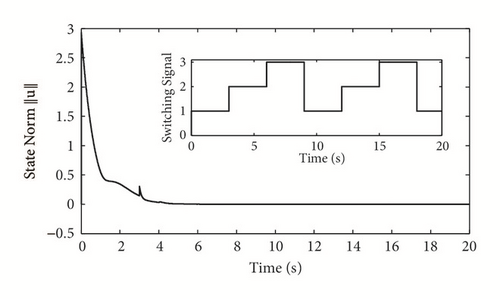
The state curves of (2) with the three subsystems are, respectively, given in Figures 1–6. It follows from the simulation results that the equilibrium point of (2) is existent, unique, and stable, verifying the correctness of Theorem 8.

5. Conclusion and Future Work
The existence, the uniqueness, and the robust exponential stability of the equilibrium point of a class of switched complex-valued neural networks with interval parameter uncertainties and impulses are investigated in this paper. By employing homomorphism mapping theorem, the scalar Lyapunov function method, the average dwell time method, and M-matrix theory, several sufficient conditions are established for guaranteeing the existence, the uniqueness, and the robust exponential stability of the system. Finally, a numerical example with simulation results has been provided to show the effectiveness of the obtained results.
Based on the research presented in this paper, we will try to study the dynamic behavior of a class of switched complex-valued neural networks with mixed delays (including both time-varying delays and continuously distributed delays) and impulsive effect which do not only occur at the switching moment between subsystems, but also when transferring inside subsystems.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Acknowledgments
This work was supported in part by the Scientific Research Foundation of the Education Department of Sichuan Province [Grants nos. 17ZA0364 and 16ZB0163], in part by the National Natural Science Foundation of China [Grants nos. 11572264 and 11402214], in part by the Foundation for Distinguished Young Talents in Higher Education of Guangdong [Grant no. 2016KQNCX103], in part by the Open Research Subject of Key Laboratory of Fluid and Power Machinery (Xihua University), Ministry of Education [Grant no. szjj2016-007], in part by the Open Research Fund of Key Laboratory of Automobile Measurement and Control & Safety (Xihua University), Sichuan Province [Grant no. szjj2017-074], in part by the “Chunhui Plan” Cooperative Research for Ministry of Education [Grant no. Z2016133], and in part by the Open Research Subject of Artificial Intelligence Key Laboratory of Sichuan Province [Grant no. 2017RYJ03]. The authors deeply appreciate Yang Xiang, Yan Yan, and Ling Zhao of Xihua University and the American Journal Experts services for their helpful constructive suggestions concerning the language revision of this manuscript.
Open Research
Data Availability
No data were used to support this study.




