The article establishes a seven-degree-of-freedom projectile trajectory model for a new type of spinning projectile. Based on this model, a numerical analysis is performed on the ballistic characteristics of the projectile, and the trajectory of the dual-spinning projectile is filtered with the unscented Kalman filter algorithm, so that the measurement information of projectile onboard equipment is more accurate and more reliable measurement data are provided for the guidance system. The numerical simulation indicates that the dual-spinning projectile is mainly different from the traditional spinning projectile in that a degree of freedom is added in the direction of the axis of the projectile, the forebody of the projectile spins at a low speed or even holds still to improve the control precision of the projectile control system, while the afterbody spins at a high speed maintaining the gyroscopic stability of the projectile. The trajectory filtering performed according to the unscented Kalman filter algorithm can improve the accuracy of measurement data and eliminate the measurement error effectively, so as to obtain more accurate and reliable measurement data.

1. Introduction

With the technical development of weapons, basic requirements of modern weapon systems are low collateral damage and accuracy. Currently, the great stocks of uncontrolled spin-stabilized projectiles in various countries are gradually being converted to precision-guided and controlled projectiles. Spin-stabilized projectiles maintain stability in flight through high-speed spinning. In order to deal with the challenges to measurement and control systems caused by high-speed spinning, drag increasing mechanisms, spinning reducing mechanisms, pulse engines and built-in sliders, and similar components are currently used as actuators to reduce fall point dispersion effectively. However, the drawback is that a continuous control force cannot be applied and precision strikes are difficult to achieve.

At present, a canard-guided dual-spinning projectile [1–11] has been converted to a controlled spinning projectile with great development potential. It can be used for continuous control to realize precision strikes. Furthermore, the great amount of uncontrolled projectiles currently stored can be modified into precise missiles only if fuzes of the traditional uncontrolled spin-stabilized projectiles are changed into canard-guided despinning fuzes. The dual-spinning projectile consists of two parts, that is, a forebody (with canards) and an afterbody, and the two parts are connected through a ball bearing. During flight, the forebody spins at a low speed (several or about a dozen turns per second), and the afterbody spins at a high speed (hundreds of turns per second) around the vertical axis, which gives rise to the term “dual-spin.” The low spinning speed of the forebody can make the measurement of related parameters and design of the control system more precise, and the high spinning speed of the afterbody allows maintaining the gyroscopic stability of the projectile, achieving a stable flight. A structural diagram of a dual-spinning projectile is shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Structural diagram of dual-spinning projectile.

During flight, since the projectile is affected by factors such as the environment, certain errors will inevitably be caused in the measurement system. With accumulation of these errors, the precision of the control system will be greatly affected. Trajectory filtering based on flight measurement data is an important means to understand the actual flight status of the projectile. It is widely applied in fields such as simulated flight model validation, emplacement reconnaissance amending, and trajectory prediction and filtering [12, 13]. At present, extended Kalman filtering (EKF) is widely applied in fields such as trajectory reconstruction and filtering. EKF is a linearization method for the nonlinear estimation problem. The linearization process will produce certain errors; it is difficult to find out the Jacobi matrix in its analytical form for the dual-spinning projectile model; there also has a heavy calculation burden. In order to overcome the shortcomings of EKF and avoid the error-prone and calculation-heavy Jacobi matrix, reconstruction and filtering of the dual-spinning projectile’s trajectory in this article is performed using the unscented Kalman filter (UKF) [14–16].

2. Seven-Degree-of-Freedom Mathematical Model of Dual-Spinning Projectile

Since the spinning speeds of the forebody and the afterbody of a dual-spinning projectile are different in the direction of the axis of the projectile, one degree of freedom (DOF) is added to the six-DOF rigid body dynamic model, which is used as a basis. Therefore, a seven-DOF dynamic model of the dual-spinning projectile is established in this article. This model comprises a centroid motion caused by the resultant force and rotation around the centroid caused by the resultant moment.

2.1. Coordinate System

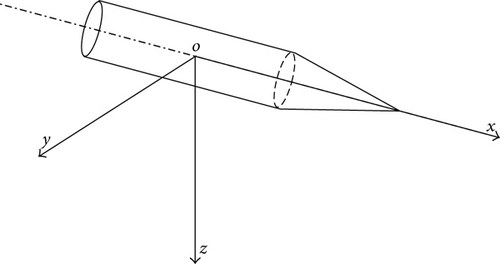
The coordinate system of the axis of the projectile is as follows: The origin o is the location of the centroid, the axis direction along the nose of the projectile is the ox axis, the axis pointing rightward at a right angle to the axis of the projectile is the oy axis, and the oz axis is determined according to the right-hand rule. Figure 2 is the schematic diagram of the coordinate system.

2.2. Dynamic Model

This article establishes a dynamic model of the dual-spinning projectile under the coordinate system of the axis of the projectile. This model comprises a dynamic model of the centroid motion and a dynamic model of the rotation around the centroid. The model of the centroid’s motion is shown as (1), and the model of rotation around the centroid is shown as (2).

(1)

(2)

In (1) and (2), m is the total mass of the projectile; (u, v, w) are the velocity components, respectively; (X, Y, Z) are the resultant force components of the aerodynamic force, the canard-guided control force, and the resultant force of the Magnus force and gravity, respectively; (p_f, p_a, q, r) are the rotation speed components, where p_f is the rotation speed of the forebody and p_a is the rotation speed of the afterbody; (L_f, L_a, M, N) are the moment components of the afterbody, where L_f indicates the rolling moment of the forebody and L_a indicates the rolling moment subjected contributed by the afterbody; while I is the moment of inertia matrix.

2.3. Kinematic Model

In the kinematic equation set of the dual-spinning projectile, kinematic equations of the movement of the centroid and the attitude change of the projectile body relative to the ground coordinate system are established. Equation (3) is a kinematic model of the centroid of the dual-spinning projectile, and (4) is a kinematic model of the attitude influenced by rotation around the centroid.

(3)

(4)

In (3) and (4), (x_e, y_e, z_e) are the coordinate components in the ground coordinate system and (ϕ_f, ϕ_a, θ, ψ) are the roll angle of the forebody, the roll angle of the afterbody, the pitch angle, and the yaw angle of the projectile body, respectively.

2.4. Force and Moment on Projectile

2.4.1. Force on Projectile

Resultant force is calculated as follows:

(5)

Aerodynamic force from the projectile is calculated as follows:

(6)

Aerodynamic force from the canard wing is calculated as follows:

(7)

Magnus force is calculated as follows:

(8)

Gravity is calculated as follows:

(9)

2.4.2. Moment on Projectile

Resultant moment is calculated as follows:

(10)

Moment from the projectile is calculated as follows:

(11)

Moment from the canard wing is calculated as follows:

(12)

Magnus moment is calculated as follows:

(13)

Damping moment is calculated as follows:

(14)

Control/friction moment is calculated as follows:

(15)

where L_m is the control moment of the coaxial motor and L_f-a is the friction moment between the forebody and the afterbody, which can be expressed as

(16)

where k_s is the static friction coefficient and k_v is the viscous friction coefficient.

In (5), (6), (7), (8), (9), (10), (14), (15), and (16),

is the total velocity of the missile body’s centroid, d is the radius of the projectile, S is the reference area,

is the dynamic pressure, and ρ is the air density; C_A is the axial force coefficient, C_Yβ and C_Nα are the normal force coefficients of the projectile body, C_Yδ and C_Nδ are the canard wing lift coefficients, C_ypα is the Magnus force coefficient, and g is the gravitational acceleration; C_mα and C_mβ are the normal moment coefficients of the projectile’s body, C_mδ and C_nδ are the canard wing moment coefficients, C_npα is the Magnus moment coefficient, C_lpf and C_lpa are the roll damping moment coefficients of the forebody and the afterbody, respectively, and C_mq and C_nr are the equator damping moment coefficients. δ_y and δ_z are the virtual equivalent rudder angles, and the relationships between them and the real rudder angles are expressed with the following equations:

(17)

where δ_m and δ_n are the pitch rudder angle and yaw steering angle, respectively. α is the angle of attack, β is the angle of sideslip, and α^′ is the angle of total attack, and their equations are as follows:

(18)

3. Trajectory Characteristics

3.1. Trajectory Characteristics Simulation

According to the above model, a computer simulation program was developed to perform trajectory simulation. The basic physical parameters and aerodynamic parameters of the projectile are shown in Table 1. Launching conditions are as follows: the initial velocity was 930 m/s, the firing angle was 65°, and the canards opened at the 30th second. The trajectory characteristics simulation in this part was chosen so as to validate the correctness of the seven-DOF projectile trajectory model and form the basis for the subsequent analysis, and thus, only simulation results of coordinate and velocity data are presented herein. In order to distinguish the difference from traditional projectiles, simulation data of spinning speeds of the forebody and the afterbody are provided in this part.

Table 1. Projectile parameters.

Parameter	Value	Parameter	Value
m	45.5 kg	C_ypα	−0.039
D	155 mm	C_mα	4.102
L	909 mm	C_mδ	0.351
	0.012 kg·m⁻²	C_npα	0.006
	0.133 kg·m⁻²	C_lpf	−0.023
I_y	1.800 kg·m⁻²	C_lpa	−0.002
C_A	0.352	C_mq	−1.125
C_Yβ	−2.012	k_s	0.001
C_Nδ	3.121	k_v	0.00001

3.2. Trajectory Characteristics Analysis

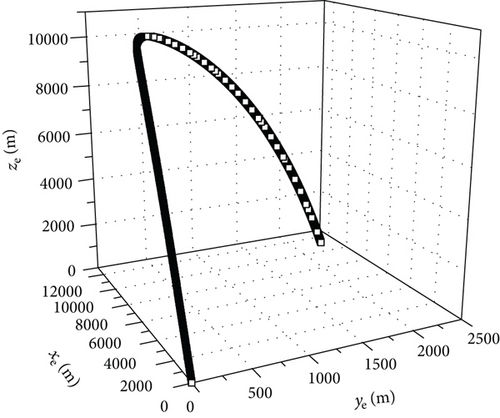
Figures 3–7 show curves of the velocity component, ballistic trajectory, and spinning speed characteristics, respectively. It can be clearly seen from Figures 3–7 that the established model is correct. The canard wing opened at the 30th second of the flight time, and certain changes occur in the speed data, so that the ballistic trajectory of the controlled trajectory is affected, which indicates that the canard wing can correct the trajectory. If the canard wing performs actions according to a certain control input, the trajectory can be corrected, so as to realize precision strikes to the target.

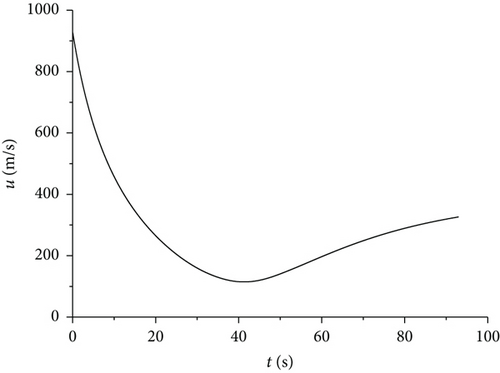
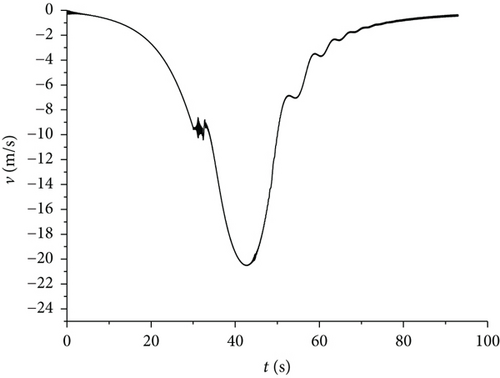
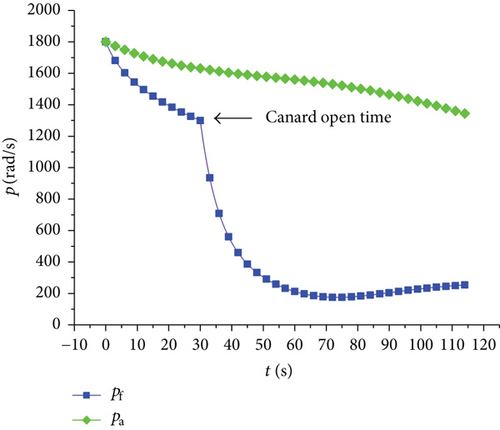
In order to illustrate the distinction between the dual-spinning projectile and the traditional spinning projectile, Figure 7 in particular provides the curve of speed data of the dual-spinning projectile. It can be seen from Figure 7 that speed of the afterbody shows free decay as the flight time passes, and it still maintains a high speed by the end of the flight, so as to guarantee the gyroscopic stability of the projectile during flight, allowing the projectile to be stable throughout the flight. The spinning speed of the forebody decays freely until the canard opened. Since the moment of inertia of the forebody is considerably less than that of the afterbody, the decrease in spinning speed in the free flight phase before the canard wing bounces off is greater than that of the afterbody. When the canard wing bounces off, the roll damping moment of the forebody increases rapidly, so that the spinning speed of the forebody decays rapidly. The low speed of the forebody is quite beneficial to the normal operation of the measurement and control systems, which is the expected result.

4. Trajectory Filtering

4.1. Construction of UKF Equation

The system model of the dual-spinning projectile is strongly nonlinear. If a linear filtering method, for example, KF or EKF, is applied, large linearization error will be caused. Moreover, system equations of seven-DOF are very complex, and it is hard to obtain the Jacobi matrix in analytical form, so in this article, the UKF is used to perform online trajectory reconstruction.

Depending on the actual engineering needs, online data filtering is mainly performed on coordinates (x_e, y_e, z_e) in this article, so

is selected as the state parameter, and the measurement parameters are the measured coordinates’ information. According to (1), (2), (3), and (4), the UKF state equation and measurement equation can be built, which are shown as

(19)

where W is the system noise, v is the measurement noise, G is the system noise driving matrix, and y is the vector of the measurement value.

The steps for trajectory reconstruction using the UKF are the following.

4.1.1. Initialization

The weighting factor

of sigma point, the weighting factor

of the corresponding variance, and the associated scale factor are shown in the following equations:

(20)

(21)

(22)

(23)

In (20), (21), (22), and (23), subscripts 0 and i of the weighting factor correspond to 2n_a + 1 sigma points. n_a is the dimension of state vector, λ is the parameter of the composite scale, η is the major scale factor determining distribution scope of sigma points around the priori mean, and the typical value is (10⁻³, 1), while ε is the second scale factor for stressing weights of the zero-order sigma points for calculation of posterior covariance (for Gaussian distribution, the optimal is ε = 2), and κ is the third scale factor, which is usually taken as 0. In this article, we assume that the process noise and measurement noise are both zero-mean Gaussian white noise, the process noise covariance matrix is Q, and the measurement noise covariance matrix is R.

4.1.2. Calculating Sigma Point and Updating

Since approximating the state distribution is easier than approximating the nonlinear function, the nonlinear propagation of random state variables can be completed through a determined sample group. It is assumed that the external stimulation, the estimated value of the state vector x, and the variance matrix of estimated error at time k − 1 are known as u_k−1,

, and P_k−1. In order to simplify the calculation process and separate the process noise, the continuous state equation integral form is used for the sigma point predicted value. The calculation process of 2n_a + 1 group sample sigma point χ_k−1 and its predicted value χ_k/k−1, predicted mean

, and predicted value of the variance of the state parameter P_k/k−1 at time k are shown in

(24)

4.1.3. Measurement Updating

Predicted measurement value γ_k/k−1 at the time of k − 1, mean value of predicted measurement y_k/k−1, and state parameter and measurement prediction error variance matrix at time k − 1 are

, the measurement prediction error variance matrix is

, the state variable correction coefficient matrix is K_k, the state error variance matrix at time k is P_k, and the state estimated value at time k is

. The computational equations of the above physical parameters are as follows:

(25)

4.2. Simulation Verification

The trajectory filtering method based on the algorithm given in this article was validated. The validation conditions were as follows: the projectile initial speed was 930, the firing angle was 65°, and the projectile weight was 45.5 kg. The measured trajectory value was simulated by adding Gaussian white noise to the theoretical calculating value of the trajectory. Based on this measured value, the effectiveness of the UKF algorithm in the process of trajectory filtering was verified. Figures 8–10 show comparison curves of measurements and reconstruction values of x_e, y_e, and z_e, respectively. It can be seen from Figures 8–10 that the precision of measurement data of the ballistic trajectory filtering through the UKF algorithm was significantly improved and is suitable for engineering applications.

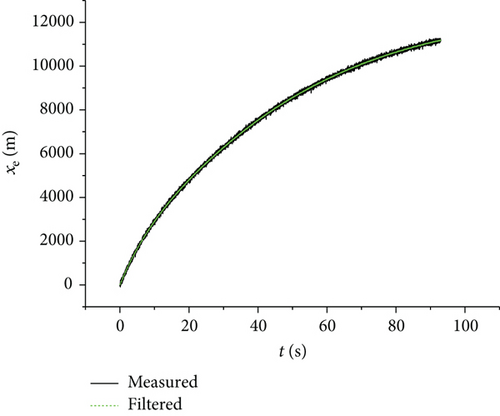
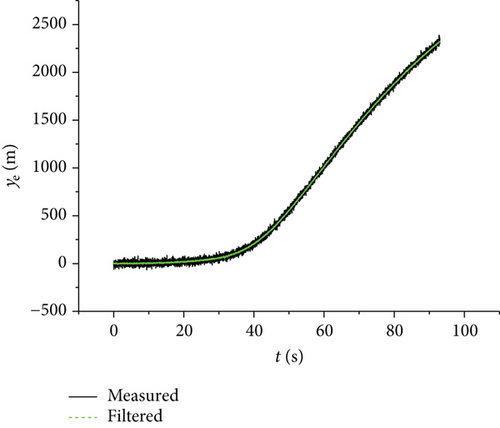
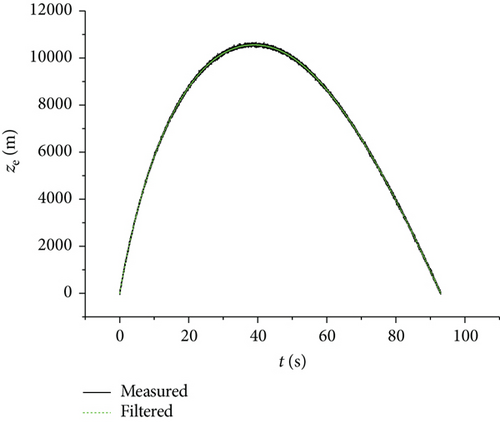
5. Conclusions

The article establishes a seven-DOF projectile trajectory model of a dual-spinning projectile. After analyzing the ballistic characteristics of the dual-spinning projectile with the method of numerical simulation, it can be seen that the major distinction between the dual-spinning projectile and the traditional spinning projectile is that the forebody and the afterbody show different spinning speed characteristics. This article specifically analyzes the reason causing this phenomenon and advantages for using such a structure. Furthermore, in this article, filtering the trajectory of the dual-spinning projectile is performed by using the UKF algorithm. Based on the comparison of the ballistic trajectory data before and after filtering, it can be seen that the precision of the measurement data is further improved, which can provide more accurate and reliable basic data for engineering applications.

Conflicts of Interest

The authors declare that they have no competing interests.

Acknowledgments

This work is supported by the National Natural Science Foundation of China under grant number 11472136.

References

1 Costello M. and Peter A., Linear theory of a dual-spin projectile in atmospheric flight, Journal of Guidance, Control, and Dynamics. (2000) 23, no. 5, 789–797, https://doi.org/10.2514/2.4639, 2-s2.0-0034273221.
10.2514/2.4639
Web of Science® Google Scholar
2 Wernert P., Stability Analysis for Canard Guided Dual-Spin Stabilized Projectiles, AIAA-2009-5843, 2009, AIAA, Reston.
Google Scholar
3 Chang S. J. and Wang Z. Y., Analysis of spin-rate property for dual-spin-stabilized projectiles with canards, Journal of Spacecraft and Rockets. (2014) 51, no. 3, 958–966, https://doi.org/10.2514/1.A32830, 2-s2.0-84903560348.
10.2514/1.A32830
Web of Science® Google Scholar
4 Zhu D. L. and Tang S. J., Flight stability of a dual-spin projectile with canards, Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering. (2015) 229, no. 4, 703–716, https://doi.org/10.1177/0954410014539293, 2-s2.0-84924916685.
10.1177/0954410014539293
Web of Science® Google Scholar
5 Chang S., Dynamic response to canard control and gravity for a dual-spin projectile, Journal of Spacecraft and Rockets. (2016) 53, no. 3, 558–566, https://doi.org/10.2514/1.A33485, 2-s2.0-84971455002.
10.2514/1.A33485
Web of Science® Google Scholar
6 Philippe W. and Spilios T., Modelling and stability analysis for a class of 155 mm spin-stabilized projectiles with course correction fuse (CCF), Proceedings of the AIAA Atmospheric Flight Mechanics Conference, 2011, Portland, Oregon, https://doi.org/10.2514/6.2011-6269.
10.2514/6.2011-6269
Google Scholar
7 Theodoulis S., Gassmann V., Wernert P., Dritsas L., Kitsios I., and Tzes A., Guidance and control design for a class of spin-stabilized fin-controlled projectiles, Journal of Guidance, Control, and Dynamics. (2013) 36, no. 2, 517–531, https://doi.org/10.2514/1.56520, 2-s2.0-84875713437.
10.2514/1.56520
Web of Science® Google Scholar
8 Zhang Y. and Xiao L., Simulation research on flight control system of dual-spin projectile with fixed wing canards, Computer Simulation. (2016) 33, no. 3, 80–85.
Google Scholar
9 Lee C.-H. and Jun B.-E., Guidance algorithm for projectile with rotating canards via predictor-corrector approach, 2014 IEEE Conference on Control Applications(CCA), 2014, Antibes, Fance, 2072–2077, https://doi.org/10.1109/CCA.2014.6981608, 2-s2.0-84920516489.
10.1109/CCA.2014.6981608
Google Scholar
10 Spagni J., Theodoulis S., and Wernert P., Flight control for a class of 155 mm spin-stabilized projectile with reciprocating canards, AIAA Guidance, Navigation and Control Conference, 2012, Minnesota, https://doi.org/10.2514/6.2012-4685.
10.2514/6.2012-4685
Google Scholar
11 Rogers J. and Costello M., Design of a roll-stabilized mortar projectile with reciprocating canards, Journal of Guidance, Control, and Dynamics. (2010) 33, no. 4, 1026–1034, https://doi.org/10.2514/1.47820, 2-s2.0-77956374134.
10.2514/1.47820
Web of Science® Google Scholar
12 Yang R. J. and Wang L. M., Trajectory reconstruction using radar measured data, Journal of Ballistics China. (2011) 23, no. 3, 43–46.
Google Scholar
13 Wang Y. and Zhou D. Y., Real-time trajectory data processing algorithm based on adaptive UKF, Journal of Huazhong University of Science & Technology. (2014) 42, no. 9, 68–71.
Google Scholar
14 Julier S. J. and Uhlmann J. K., Unscented filtering and non-linear estimation, Proceeding of the IEEE. (2004) 92, no. 3, 401–422, https://doi.org/10.1109/JPROC.2003.823141, 2-s2.0-21244437999.
10.1109/JPROC.2003.823141
Web of Science® Google Scholar
15 Julier S. J. and Uhlman J. K., A new method for nonlinear transformation of means and covariance in filters and estimators, IEEE Transactions on Automatic Control. (2000) 45, no. 3, 477–482, https://doi.org/10.1109/9.847726, 2-s2.0-0033723743.
10.1109/9.847726
Web of Science® Google Scholar
16 Julier S. J., The scaled unscented transformation, Proceeding of the 2002 American Control Conference, 2002, Anchorage, https://doi.org/10.1109/ACC.2002.1025369.
10.1109/ACC.2002.1025369
Google Scholar

Citing Literature

All articles

Modeling of Dual-Spinning Projectile with Canard and Trajectory Filtering

Abstract

1. Introduction