International Journal of Aerospace Engineering

Volume 2018, Issue 1 1752815

Research Article

Open Access

Dynamics Analysis of Deployable Structures considering a Two-Dimensional Coupled Thermo-Structural Effect

Qi’an Peng,

Corresponding Author

Qi’an Peng

[email protected]

orcid.org/0000-0003-2323-5569

School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an, China nwpu.edu.cn

Search for more papers by this author

Sanmin Wang,

Sanmin Wang

orcid.org/0000-0003-1410-3097

School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an, China nwpu.edu.cn

Search for more papers by this author

Bo Li,

Bo Li

orcid.org/0000-0002-8587-8044

School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an, China nwpu.edu.cn

Search for more papers by this author

Changjian Zhi,

Changjian Zhi

orcid.org/0000-0003-4096-064X

School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an, China nwpu.edu.cn

Search for more papers by this author

Jianfeng Li,

Jianfeng Li

orcid.org/0000-0003-2397-1072

School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an, China nwpu.edu.cn

Search for more papers by this author

Qi’an Peng,

Corresponding Author

Qi’an Peng

[email protected]

orcid.org/0000-0003-2323-5569

School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an, China nwpu.edu.cn

Search for more papers by this author

Sanmin Wang,

Sanmin Wang

orcid.org/0000-0003-1410-3097

School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an, China nwpu.edu.cn

Search for more papers by this author

Bo Li,

Bo Li

orcid.org/0000-0002-8587-8044

School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an, China nwpu.edu.cn

Search for more papers by this author

Changjian Zhi,

Changjian Zhi

orcid.org/0000-0003-4096-064X

School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an, China nwpu.edu.cn

Search for more papers by this author

Jianfeng Li,

Jianfeng Li

orcid.org/0000-0003-2397-1072

School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an, China nwpu.edu.cn

Search for more papers by this author

First published: 04 October 2018

https://doi.org/10.1155/2018/1752815

Citations: 1

Academic Editor: Yue Wang

Share a link

Email
Wechat
Bluesky

Abstract

The deployment accuracy of deployable structures is affected by temperature and flexibility. To obtain the higher accuracy, various measures such as the optimization design and the control process are employed, and they are all based on deployment dynamics characteristics of deployable structures. So a precise coupled thermo-structural deployment dynamics analysis is important and necessary. However, until now, only a one-dimensional thermal effect is considered in the literatures because of simplicity, which reduces the accuracy of the model. Therefore, in this paper, a new model coupling mechanical field with a temperature field is presented to analyze the deployment dynamics of a deployable structure with scissor-like elements (SLEs). The model is based on the absolute nodal coordinate formulation (ANCF) and is established via a new locking-free beam element whose formulation is extended to account for the two-dimensional thermally induced stresses due to the heat expansion for the first time. Namely, in the formulation, the thermal influences are along two-dimensional directions, the axial direction and the transverse direction, rather than along a one-dimensional direction. The validity and precision of the proposed model are verified using a flexible pendulum example. Finally, the dynamics of a linear deployable structure with three SLEs modeled by the element is simulated under a temperature effect.

1. Introduction

Over the past three decades, deployable structures have been extensively used in space missions because they own the properties of high stiffness, low mass, and small folding volume [1–4]. And with the rapid development of aerospace industry, higher demands for these structures have been proposed. One of the most important is higher deployment accuracy, which is affected by thermal and flexible effects [5].

In order to achieve higher accuracy, the precise deployment dynamics characteristic of deployable structures is essential because it is fundamental to the optimization design [6] and the control process [7]. However, due to the high cost of the imitated space environment on the ground, it is difficult to predict the dynamic capability of these structures by experiment. So some practical methods are developed for dynamic analysis of these flexible structures. The most classical approach is the floating frame of reference formulation [8], but it is deficient in dynamic stiffening and will lead to an imprecise simulation result. To overcome this drawback, Shabana presented a new approach called the absolute nodal coordinate formulation (ANCF) [9], which can satisfy the dynamic stiffening automatically [10, 11] and leads to a constant mass matrix and zero centrifugal and Coriolis forces [12]. Because of these advantages, several beam elements [11, 13–16], plate elements [17], and brick elements [18] applied to analyze various objects of study have been developed within this formulation. A two-dimensional shear beam element proposed by Omar and Shabana [11] to consider the shear deformation effect is among them. However, in a later research, it was found out that this beam element deriving elastic forces on the basis of the nonlinear elastic theory suffers from volumetric Poisson’s locking, thickness locking, and shear locking, which influence the accuracy and computational efficiency of ANCF greatly [19, 20]. In order to avoid the Poisson’s locking, an exact description of elastic forces is presented by Sopanen and Mikkola [21], but the simplest way is setting the Poisson ratio to zero directly. Possible alternatives to solve other locking problems are selective reduced integration [22–24] and the redefinition of elastic forces based on the Hellinger-Reissner principle [20, 25].

As the absolute nodal coordinate formulation grows and is verified in many fields [26, 27], some researchers start to apply it in space deployable structures. Li et al. [28] use ANCF to simulate the deployment dynamics of the deployable antenna reflector. Tian et al. [29] simulate the deployment dynamics of two types of deployable structures based on ANCF and find a good agreement between simulations and experiments. In these simulations, all of researchers do not take into account the temperature effect and only investigate the deployable systems under the normal temperature. Li and Wang [30] fill the gap by discussing the deployable driving torque at the lowest and highest temperature within ANCF, but their model is based on a simple Euler–Bernoulli beam element and only the axial thermal effect is pondered. As mentioned above, however, a precise dynamics analysis is important and necessary for deployable structures. Besides, several high-profile examples have verified that the temperature effect has a great influence on deployable structures [31, 32]. So the multidimensional coupled thermo-structural effect on the deployment process of deployable structures must be considered.

To this end, a new model coupling mechanical field with a temperature field of a deployable structure with scissor-like elements (SLEs) based on ANCF is presented. The model is established by a new planar locking-free shear deformable beam element inspired from the gradient-deficient element which alleviates the thickness locking. In order to simulate the deployment dynamics characteristic accurately, the formulation of the shear deformable beam element is extended to contain the thermal stress due to heat expansions. Note that the temperature field is uniform and the heat expansions are along two-dimensional directions; that is to say, the thermal loads are applied in an axial direction and a transverse direction, which is a great improvement compared with that of Li and Wang [30]. Also, the heat expansion coefficients are equal in two-dimensional directions because of the isotropic material in the model. This formulation is verified by ANSYS with a simple pendulum driven by gravity. In the end, on the basis of the new model, the simulation results of deployment dynamics of the deployable structure considering the coupled thermo-structural effect are calculated out and compared with results of only flexible analysis of the same structure to discuss the temperature effects.

This paper is organized as follows. The coupled thermo-structural formulation of the locking-free shear deformable beam element with two-dimensional thermal loads is discussed in Section 2. In Section 3, the formulation is demonstrated and a model of the deployable structure consisting of SLEs is established with the formulation. Also, the coupled thermo-structural analysis of other deployable structures comprising rods can be created by using this formulation. The simulation results of the deployable structure with SLEs are illustrated in Section 4. Finally, some valuable conclusions are drawn in Section 5.

2. A Locking-Free Shear Deformable Beam Element under the Thermo Effect

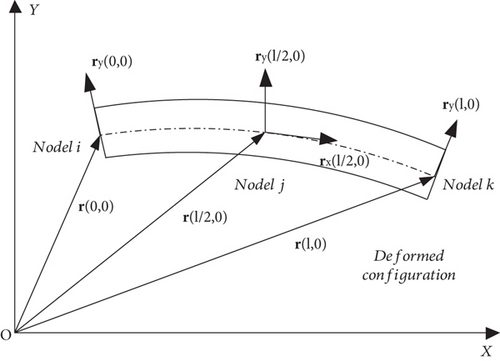
In this paper, using a two-dimensional shear deformable beam element [11] to model the rods is appropriate because motions and forces of the deployable structure with SLEs are in plane and no torsion occurs. However, the beam element suffers from the locking phenomena. So a new locking-free shear deformable beam element is presented in Figure 1. In the improved beam kinematics, an additional slope vector r_x is added in the middle of the gradient-deficient element [19].

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The position vector of an arbitrary point on the beam element.

An arbitrary point p on the beam element can be expressed as

(1)

where S is the additional shape function compared with [19]

(2)

The matrix I is a 2 × 2 identity matrix, the elements S_i(i = 1, 2, …, 7) are given as follows, and their detailed derivation process is shown in the appendix.

(3)

where a = x/l, b = y/l, l is the length of the beam element, and x, y are the element coordinates in the element local coordinate system. So the nodal coordinate vector can be written as

(4)

where

, and

are the global positions of nodes and

, and

are the global slopes of the element nodes.

The velocity at any material point can be obtained:

(5)

Thus, the kinetic energy of the beam element is expressed as follows:

(6)

where M is the mass matrix and is constant.

(7)

where V is the volume of the beam element and ρ is the material density of the beam.

Before deducing the strain energy, in order to bring the thermal effect into the formulation of the beam element, some assumptions are introduced. The material is isotropous, and the temperature field is homogeneous along the beam element. So the strain vector due to the change of temperature can be written as [33]

(8)

where α_T is the coefficient of thermal expansion and ΔT is the change in the temperature field. According to continuum mechanics theory, the strain vector due to the deformation can be derived as follows. First, the deformation gradient is defined as

(9)

where S_i is the ith row of the element shape function and e₀ is the absolute nodal coordinate vector of the beam element in the initial configuration. Hence, the Lagrangian strain tensor due to flexibility can be written as

(10)

where

(11)

The strain tensor can be written as a vector form because of its symmetry:

(12)

where ε₁ and ε₂ are normal strains along the x, y direction, respectively, and ε₃ is the shear strain.

(13)

So the strain vector considering the coupled thermo-structural effect can be obtained:

(14)

In terms of constitutive relation, the stress vector related to the strain vector is given by

(15)

where D indicates the coefficient matrix of material elasticity, and it can be written as follows because of the isotropic homogenous material:

(16)

where

(17)

where E and ν indicate the elastic modulus and Poisson’s ratio of the beam material, respectively, and μ indicates the shear modulus. So the strain energy is

(18)

The elastic forces can be deduced by using the strain energy U.

(19)

where K is the stiffness matrix.

(20)

where

(21)

Finally, according to Lagrange’s equation [9], the equation of motion for the beam element affected by temperature is given by

(22)

where Q_w is the generalized external forces applied in the element.

3. Validation

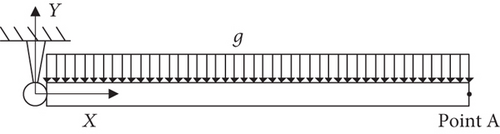
A simple example that a rectangular pendulum moves from the horizontal rest position under the effect of gravity (g = 9.8 m/s²), as shown in Figure 2, is examined to validate the proposed model with a two-dimensional thermal load based on ANCF. And the thermal load is applied by changing the temperature from 0°C to 200°C suddenly. And other simulation parameters such as the material property and geometry size of the pendulum are given in Table 1.

Table 1. Material properties and geometry sizes of the pendulum.

Characteristic parameters	Values
Length L (m)	1
Cross-sectional area A (m²)	0.02 × 0.02
Material density ρ (kg/m³)	7750
Elasticity modulus E (N/m³)	2 × 10⁸
Poisson’s ratio ν	0
Thermal expansion coefficient α_T (K⁻¹)	2.85 × 10⁻⁵

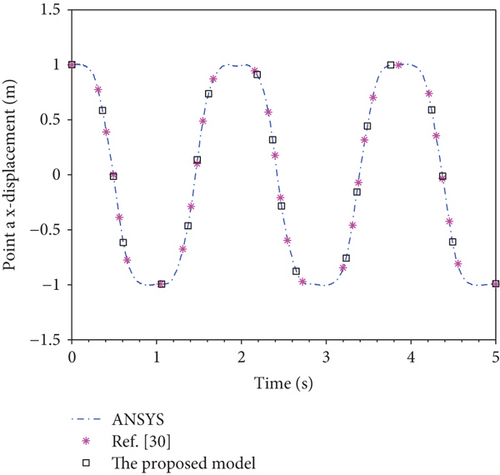
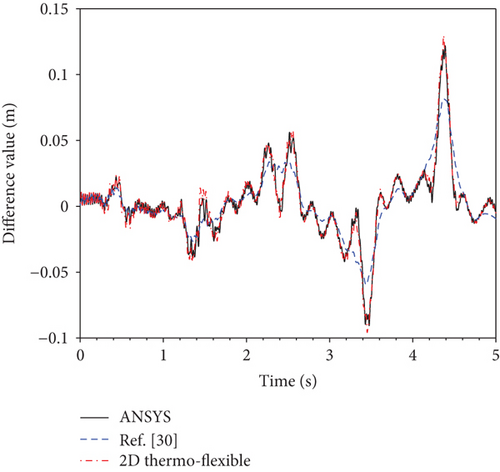
Figure 3 shows the curves of displacement of point a which are evaluated by ANSYS, the 1D thermo-structural model [30], and the proposed model, respectively. The two models are in good agreement with ANSYS within a large overall motion. It demonstrates that the proposed beam element is free of locking phenomena. Further, in order to observe the difference among three results clearly, a margin calculation is carried out. The difference between ANSYS and the flexible model, the difference between the 1D thermo-structural model and the flexible model, and the difference between the proposed model and the flexible model are compared in Figure 4. Here, the flexible model implies no temperature effect. It is clear from the difference value present in Figure 4 that the proposed model is in good agreement with ANSYS, whereas the 1D thermo-structural model has a huge gap with ANSYS. So the proposed model has higher precision. Therefore, the development of the new two-dimensional thermo-structural model is significant.

So the proposed model is used to assemble the deployable structure with SLEs under the thermal effect. The dynamics equations with the constraint conditions can be expressed as follows:

(23)

where q is the generalized coordinate vector of the deployable structure, m and k are the mass matrix and the stiffness matrix, respectively, f is the generalized force vector, λ is the Lagrange multipliers, Φ is the constraint equation, and Φ_q is the derivative matrix of Φ with respect to q. Note that the stiffness matrix k is the function of the temperature T besides the generalized coordinate vector q.

4. Numerical Results

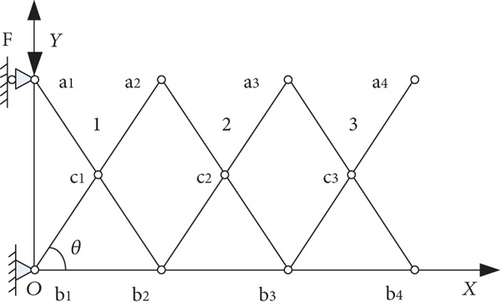
In this section, a deployable structure with three scissor-like elements considering the coupled thermo-structural effect is discussed. As shown in Figure 5, a scissor-like element is assembled by two rods which can be treated as beams with a pin, and the three scissor-like elements are connected to a deployable system with pins. A driving force equal to 50 N is applied at point a₁. The material property and geometry size of the structure are given in Table 2. And the motion simulation is carried out within the time interval t ∈ [0, 3]s, where the system is uniformly revelational to the temperature profile presented in Figure 6 with a maximum temperature of 150°C and a minimum temperature of −150°C [30]. In order to demonstrate the temperature influence on the dynamics of the mechanism, the simulation results are compared with the same system only considering the flexible effect.

Table 2. Material properties and geometry sizes of the deployable structure.

Characteristic parameters	Values
Length L (m)	2
Cross-sectional area A (m²)	0.02 × 0.02
Material density ρ (kg/m³)	2750
Elasticity modulus E (N/m²)	7 × 10¹⁰
Poisson’s ratio ν	0
Thermal expansion coefficient α_T (K⁻¹)	2.3 × 10⁻⁵

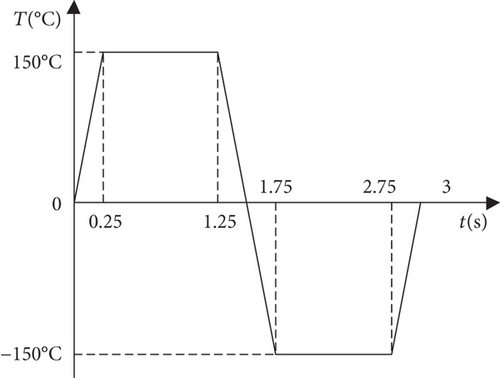
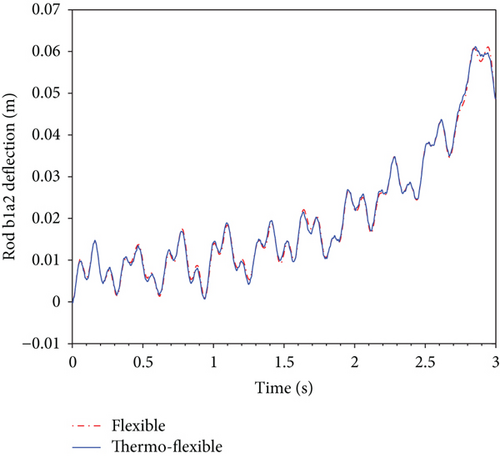
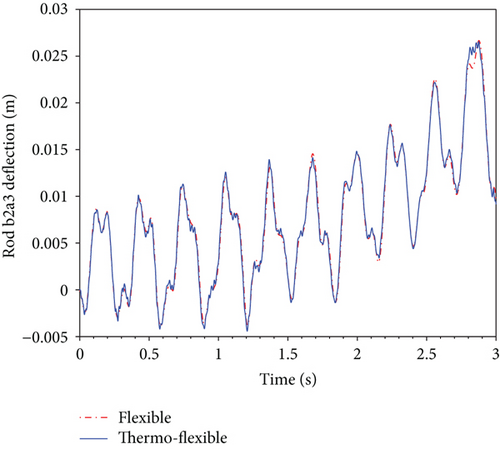
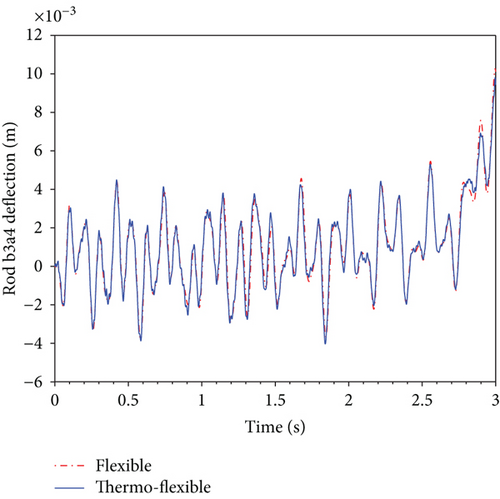
Figure 7 shows the deflection curves of rod b₁a₂, rod b₂a₃, and rod b₃a₄ in the changing temperature field as shown in Figure 6 and in the constant temperature field. Referring to Figure 7, it can be seen that the time-dependent temperature leads to many small vibrations which can be observed 2.7 s after clearly when the two curves differ greatly at the moment. These small vibrations which will influence the deployment accuracy greatly arise because thermally induced transverse strain results in varying moment of inertia related to the cross-sectional area besides the change of the length of rods resulting from thermally induced axial stress. Another notable point from the pictures is that the temperature influence on the deflection of the rods seems to weaken in this time period of 2 s to 2.5 s. A probable reason is that the lowest temperature effect on the deployable structure partly offsets the highest temperature effect in the earlier period.

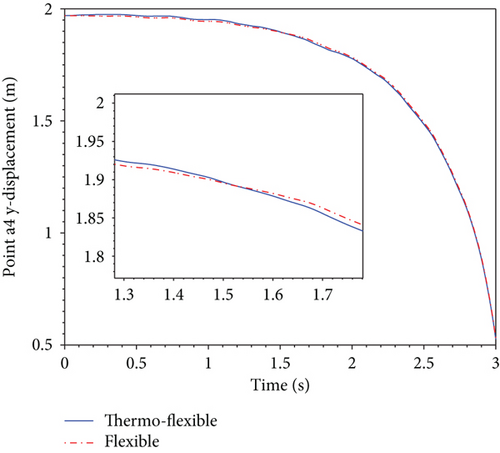
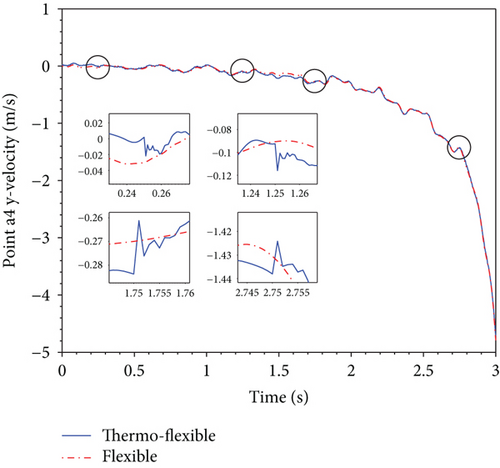
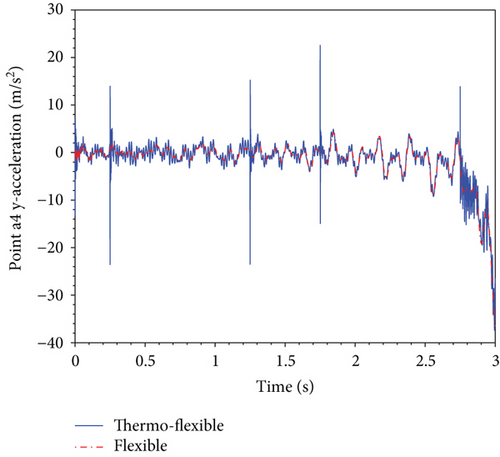
The motion diagrams of a representative point a₄ selected to stand for the dynamics characteristics of the deployable structure are shown in Figure 8. Referring to Figure 8, the temperature impacting on deployment displacement and velocity is not obvious, but there is a huge influence on deployment acceleration of point a₄. The thermal effect results in additional vibrations emerging in acceleration, which can be observed by comparing the thermo-flexible curve with the flexible curve. Besides, referring to Figures 6 and 8(c), it is found that acceleration vibrations become larger perspicuously at inflection points of the temperature profile such as 0.25 s, 1.25 s, 1.75 s, and 2.75 s. These vibrations may lead to unexpected collision and impact which might result in the invalidation of the deployable structure or even mission failure.

5. Conclusions

In this paper, the dynamics analysis of the deployable structure with three SLEs considering the coupled thermo-structural effect based on ANCF is presented.

(1)
In order to establish the precise model coupling of the mechanical field with the temperature field of the mechanism, the formulation of a new locking-free beam element with the additional slope vector is extended to account for the thermally induced stresses in two-dimensional directions, that is, the axial direction and transverse direction
(2)
It shows that the new beam element is free of locking phenomena as a result of a good agreement between the calculating results of the simple pendulum and the simulation results of the ANSYS within a large overall motion. Then, the validity and the precision of the proposed thermo-structural model are demonstrated through the further margin calculation: the difference of the proposed model is approximately identical to the difference of ANSYS, whereas the difference of the 1D thermo-structural model has a relatively large gap with the difference of ANSYS. Therefore, the proposed model is more precise than the 1D thermal-structural model. On the other hand, it also demonstrates that the development of the new two-dimensional thermo-structural model is significant
(3)
In the final simulations of the deployable structure, by contrasting the thermo-flexible deflection with the flexible deflection, it is found that the main influence of temperature is that the change of temperature leads to many vibrations: for the deflection of rods, many small vibrations arise because thermally induced transverse strain results in varying moment of inertia related to the cross-sectional area besides the change of the length of rods resulting from thermally induced axial stress. On the other hand, for the deployment dynamics characteristics, temperature has a huge impact on deployment acceleration. The thermal effect will result in additional vibrations emerging in acceleration of an arbitrary point on the deployable structure, and these vibrations will become larger perspicuously at inflection points of temperature change

Conflicts of Interest

The authors declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (grant number 51175422).

Appendix

For the new beam element, the displacement field is defined as

(A.1)

where a_i, b_i(i = 1, 2, ⋯, 7) are the polynomial coefficients.

The nodal displacement conditions shown in Figure 1 can be expressed as

(A.2)

Thus, the polynomial coefficients can be derived from (A.2):

(A.3)

By substituting (A.3) into (A.1), the displacement field is rewritten with nodal displacement:

(A.4)

where

(A.5)

Open Research

Data Availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 You Z. and Pellegrino S., Deployable mesh reflector, The International Symposium on Spatial, Lattice, and Tension Structures, 1994, 103–112.
Google Scholar
2 Cherniavsky A. G., Gulyayev V. I., Gaidaichuk V. V., and Fedoseev A. I., Large deployable space antennas based on usage of polygonal pantograph, Journal of Aerospace Engineering. (2005) 18, no. 3, 139–145, https://doi.org/10.1061/(ASCE)0893-1321(2005)18:3(139), 2-s2.0-22944441937.
10.1061/(ASCE)0893-1321(2005)18:3(139)
Web of Science® Google Scholar
3 Wang Y., Liu R., Yang H., Cong Q., and Guo H., Design and deployment analysis of modular deployable structure for large antennas, Journal of Spacecraft and Rockets. (2015) 52, no. 4, 1101–1111, https://doi.org/10.2514/1.A33127, 2-s2.0-84940769662.
10.2514/1.A33127
Web of Science® Google Scholar
4 Li B., Wang S. M., Yuan R., Xue X. Z., and Zhi C. J., Dynamic characteristics of planar linear array deployable structure based on scissor-like element with joint clearance using a new mixed contact force model, Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science. (2016) 230, no. 18, 3161–3174, https://doi.org/10.1177/0954406215607903, 2-s2.0-84991821827.
10.1177/0954406215607903
Web of Science® Google Scholar
5 Tang Y., Li T., Wang Z., and Deng H., Surface accuracy analysis of large deployable antennas, Acta Astronautica. (2014) 104, no. 1, 125–133, https://doi.org/10.1016/j.actaastro.2014.07.029, 2-s2.0-84906318627.
10.1016/j.actaastro.2014.07.029
Web of Science® Google Scholar
6 Sun J., Tian Q., and Hu H., Structural optimization of flexible components in a flexible multibody system modeled via ANCF, Mechanism and Machine Theory. (2016) 104, 59–80, https://doi.org/10.1016/j.mechmachtheory.2016.05.008, 2-s2.0-84973279178.
10.1016/j.mechmachtheory.2016.05.008
Web of Science® Google Scholar
7 Zhang Y., Duan B., and Li T., A controlled deployment method for flexible deployable space antennas, Acta Astronautica. (2012) 81, no. 1, 19–29, https://doi.org/10.1016/j.actaastro.2012.05.033, 2-s2.0-84865300745.
10.1016/j.actaastro.2012.05.033
Web of Science® Google Scholar
8 García de Jalón J. and Bayo E., Kinematic and Dynamic Simulation of Multibody Systems, 1994, Springer, New York, Mechanical Engineering Series, https://doi.org/10.1007/978-1-4612-2600-0.
10.1007/978-1-4612-2600-0
Google Scholar
9 Shabana A. A., Dynamics of Multibody Systems, 2005, Cambridge University Press, https://doi.org/10.1017/CBO9780511610523, 2-s2.0-84926162148.
10.1017/CBO9780511610523
Google Scholar
10 Berzeri M. and Shabana A. A., Study of the centrifugal stiffening effect using the finite element absolute nodal coordinate formulation, Multibody System Dynamics. (2002) 7, no. 4, 357–387, https://doi.org/10.1023/A:1015567829908, 2-s2.0-0036575666.
10.1023/A:1015567829908
Web of Science® Google Scholar
11 Omar M. A. and Shabana A. A., A two-dimensional shear deformable beam for large rotation and deformation problems, Journal of Sound and Vibration. (2001) 243, no. 3, 565–576, https://doi.org/10.1006/jsvi.2000.3416, 2-s2.0-0035821826.
10.1006/jsvi.2000.3416
Web of Science® Google Scholar
12 Shabana A. A., Computational Continuum Mechanics, 2012, Cambridge University Press.
Google Scholar
13 Berzeri M. and Shabana A. A., Development of simple models for the elastic forces in the absolute nodal co-ordinate formulation, Journal of Sound and Vibration. (2000) 235, no. 4, 539–565, https://doi.org/10.1006/jsvi.1999.2935, 2-s2.0-0034710526.
10.1006/jsvi.1999.2935
Web of Science® Google Scholar
14 Shabana A. A. and Yakoub R. Y., Three dimensional absolute nodal coordinate formulation for beam elements: theory, Journal of Mechanical Design. (2001) 123, no. 4, 606–613, https://doi.org/10.1115/1.1410100, 2-s2.0-13644283164.
10.1115/1.1410100
Web of Science® Google Scholar
15 Yakoub R. Y. and Shabana A. A., Three dimensional absolute nodal coordinate formulation for beam elements: implementation and applications, Journal of Mechanical Design. (2001) 123, no. 4, 614–621, https://doi.org/10.1115/1.1410099, 2-s2.0-13644282674.
10.1115/1.1410099
Web of Science® Google Scholar
16 von Dombrowski S., Analysis of large flexible body deformation in multibody systems using absolute coordinates, Multibody System Dynamics. (2002) 8, no. 4, 409–432, https://doi.org/10.1023/A:1021158911536, 2-s2.0-0036862161.
10.1023/A:1021158911536
Web of Science® Google Scholar
17 Dmitrochenko O. N. and Pogorelov D. Y., Generalization of plate finite elements for absolute nodal coordinate formulation, Multibody System Dynamics. (2003) 10, no. 1, 17–43, https://doi.org/10.1023/A:1024553708730, 2-s2.0-0041695378.
10.1023/A:1024553708730
Web of Science® Google Scholar
18 Kübler L., Eberhard P., and Geisler J., Flexible multibody systems with large deformations using absolute nodal coordinates for isoparametric solid brick elements, ASME 2003 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, September 2003, Chicago, Illinois, USA, 31–52, https://doi.org/10.1115/DETC2003/VIB-48303.
10.1115/DETC2003/VIB-48303
Google Scholar
19 García-Vallejo D., Mikkola A. M., and Escalona J. L., A new locking-free shear deformable finite element based on absolute nodal coordinates, Nonlinear Dynamics. (2007) 50, no. 1-2, 249–264, https://doi.org/10.1007/s11071-006-9155-4, 2-s2.0-34548293312.
10.1007/s11071-006-9155-4
Web of Science® Google Scholar
20 Hussein B. A., Sugiyama H., and Shabana A. A., Coupled deformation modes in the large deformation finite-element analysis: problem definition, Journal of Computational and Nonlinear Dynamics. (2007) 2, no. 2, https://doi.org/10.1115/1.2447353, 2-s2.0-34248330012.
10.1115/1.2447353
Web of Science® Google Scholar
21 Sopanen J. T. and Mikkola A. M., Description of elastic forces in absolute nodal coordinate formulation, Nonlinear Dynamics. (2003) 34, no. 1/2, 53–74, https://doi.org/10.1023/B:NODY.0000014552.68786.bc.
10.1023/B:NODY.0000014552.68786.bc
Web of Science® Google Scholar
22 Kerkkänen K. S., Sopanen J. T., and Mikkola A. M., A linear beam finite element based on the absolute nodal coordinate formulation, Journal of Mechanical Design. (2005) 127, no. 4, 621–630, https://doi.org/10.1115/1.1897406, 2-s2.0-23044460435.
10.1115/1.1897406
Web of Science® Google Scholar
23 Gerstmayr J., Matikainen M. K., and Mikkola A. M., A geometrically exact beam element based on the absolute nodal coordinate formulation, Multibody System Dynamics. (2008) 20, no. 4, 359–384, https://doi.org/10.1007/s11044-008-9125-3, 2-s2.0-52549126470.
10.1007/s11044-008-9125-3
Web of Science® Google Scholar
24 Nachbagauer K., Pechstein A. S., Irschik H., and Gerstmayr J., A new locking-free formulation for planar, shear deformable, linear and quadratic beam finite elements based on the absolute nodal coordinate formulation, Multibody System Dynamics. (2011) 26, no. 3, 245–263, https://doi.org/10.1007/s11044-011-9249-8, 2-s2.0-80051546313.
10.1007/s11044-011-9249-8
Web of Science® Google Scholar
25 Sugiyama H. and Suda Y., A curved beam element in the analysis of flexible multi-body systems using the absolute nodal coordinates, Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics. (2007) 221, no. 2, 219–231, https://doi.org/10.1243/1464419JMBD86, 2-s2.0-34547146339.
10.1243/1464419JMBD86
Web of Science® Google Scholar
26 Yoo W. S., Lee J. H., Park S. J., Sohn J. H., Pogorelov D., and Dmitrochenko O., Large deflection analysis of a thin plate: computer simulations and experiments, Multibody System Dynamics. (2004) 11, no. 2, 185–208, https://doi.org/10.1023/B:MUBO.0000025415.73019.bb, 2-s2.0-3543124075.
10.1023/B:MUBO.0000025415.73019.bb
Web of Science® Google Scholar
27 Yoo W. S., Kim M. S., Mun S. H., and Sohn J. H., Large displacement of beam with base motion: flexible multibody simulations and experiments, Computer Methods in Applied Mechanics and Engineering. (2006) 195, no. 50-51, 7036–7051, https://doi.org/10.1016/j.cma.2005.02.035, 2-s2.0-33748034402.
10.1016/j.cma.2005.02.035
Web of Science® Google Scholar
28 Li P., Liu C., Tian Q., Hu H., and Song Y., Dynamics of a deployable mesh reflector of satellite antenna: parallel computation and deployment simulation 1, Journal of Computational and Nonlinear Dynamics. (2016) 11, no. 6, article 061005, https://doi.org/10.1115/1.4033657, 2-s2.0-84978698669.
10.1115/1.4033657
PubMed Web of Science® Google Scholar
29 Tian Q., Zhao J., Liu C., Zhou C., and Hu H., Dynamics of space deployable structures, ASME 2015 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, ASME, 2015, Boston, USA, V006T010A010.
Google Scholar
30 Li T. and Wang Y., Deployment dynamic analysis of deployable antennas considering thermal effect, Aerospace Science and Technology. (2009) 13, no. 4-5, 210–215, https://doi.org/10.1016/j.ast.2009.04.005, 2-s2.0-67649306041.
10.1016/j.ast.2009.04.005
Web of Science® Google Scholar
31 Thornton E. and Foster R., Dynamic response of rapidly heated space structures, Computational Nonlinear Mechanics in Aerospace Engineering, 2013, 33rd Structures, Structural Dynamics and Materials Conference, Dallas, TX, USA, 451–477.
Google Scholar
32 Foster C. L., Tinker M. L., Nurre G. S., and Till W. A., Solar-array-induced disturbance of the Hubble Space Telescope pointing system, Journal of Spacecraft and Rockets. (1995) 32, no. 4, 634–644, https://doi.org/10.2514/3.26664, 2-s2.0-0029341697.
10.2514/3.26664
Web of Science® Google Scholar
33 Boley B. A., Weiner J. H., and Dill E. H., Theory of thermal stresses, Physics Today. (1961) 14, no. 3, 58–60, https://doi.org/10.1063/1.3057466.
10.1063/1.3057466
Google Scholar

Citing Literature

All articles

Dynamics Analysis of Deployable Structures considering a Two-Dimensional Coupled Thermo-Structural Effect

Abstract

1. Introduction

2. A Locking-Free Shear Deformable Beam Element under the Thermo Effect

3. Validation

4. Numerical Results

5. Conclusions

Conflicts of Interest

Acknowledgments

Appendix

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Dynamics Analysis of Deployable Structures considering a Two-Dimensional Coupled Thermo-Structural Effect

Abstract

1. Introduction

2. A Locking-Free Shear Deformable Beam Element under the Thermo Effect

3. Validation

4. Numerical Results

5. Conclusions

Conflicts of Interest

Acknowledgments

Appendix

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information