International Journal of Differential Equations

Volume 2018, Issue 1 1019242

Research Article

Open Access

A Fractional Order Model for Viral Infection with Cure of Infected Cells and Humoral Immunity

Adnane Boukhouima

Laboratory of Analysis, Modeling and Simulation (LAMS), Faculty of Sciences Ben M’sik, Hassan II University, P.O Box 7955 Sidi Othman, Casablanca, Morocco univh2c.ma

Search for more papers by this author

Khalid Hattaf,

Corresponding Author

Khalid Hattaf

[email protected]

orcid.org/0000-0002-5032-3639

Laboratory of Analysis, Modeling and Simulation (LAMS), Faculty of Sciences Ben M’sik, Hassan II University, P.O Box 7955 Sidi Othman, Casablanca, Morocco univh2c.ma

Centre Régional des Métiers de l’Education et de la Formation (CRMEF), 20340 Derb Ghalef, Casablanca, Morocco crmef-casablanca.net

Search for more papers by this author

Noura Yousfi,

Noura Yousfi

orcid.org/0000-0001-8435-5981

Laboratory of Analysis, Modeling and Simulation (LAMS), Faculty of Sciences Ben M’sik, Hassan II University, P.O Box 7955 Sidi Othman, Casablanca, Morocco univh2c.ma

Search for more papers by this author

Adnane Boukhouima,

Adnane Boukhouima

Laboratory of Analysis, Modeling and Simulation (LAMS), Faculty of Sciences Ben M’sik, Hassan II University, P.O Box 7955 Sidi Othman, Casablanca, Morocco univh2c.ma

Search for more papers by this author

Khalid Hattaf,

Corresponding Author

Khalid Hattaf

[email protected]

orcid.org/0000-0002-5032-3639

Laboratory of Analysis, Modeling and Simulation (LAMS), Faculty of Sciences Ben M’sik, Hassan II University, P.O Box 7955 Sidi Othman, Casablanca, Morocco univh2c.ma

Centre Régional des Métiers de l’Education et de la Formation (CRMEF), 20340 Derb Ghalef, Casablanca, Morocco crmef-casablanca.net

Search for more papers by this author

Noura Yousfi,

Noura Yousfi

orcid.org/0000-0001-8435-5981

Laboratory of Analysis, Modeling and Simulation (LAMS), Faculty of Sciences Ben M’sik, Hassan II University, P.O Box 7955 Sidi Othman, Casablanca, Morocco univh2c.ma

Search for more papers by this author

First published: 02 December 2018

https://doi.org/10.1155/2018/1019242

Citations: 3

Guest Editor: Nurcan B. Savaşaneril

Share a link

Email
Wechat
Bluesky

Abstract

In this paper, we study the dynamics of a viral infection model formulated by five fractional differential equations (FDEs) to describe the interactions between host cells, virus, and humoral immunity presented by antibodies. The infection transmission process is modeled by Hattaf-Yousfi functional response which covers several forms of incidence rate existing in the literature. We first show that the model is mathematically and biologically well-posed. By constructing suitable Lyapunov functionals, the global stability of equilibria is established and characterized by two threshold parameters. Finally, some numerical simulations are presented to illustrate our theoretical analysis.

1. Introduction

The immune response plays an important role to control the dynamics of viral infections such as human immunodeficiency virus (HIV), hepatitis B virus (HBV), hepatitis C virus (HCV), and human T-cell leukemia virus (HTLV). Therefore, many mathematical models have been developed to incorporate the role of immune response in viral infections. Some of these models considered the cellular immune response mediated by cytotoxic T lymphocytes (CTL) cells that attack and kill the infected cells [1–5] and the others considered the humoral immune response based on the antibodies which are produced by the B-cells and are programmed to neutralize the viruses [6–11]. However, all these models have been formulated by using ordinary differential equations (ODEs) in which the memory effect is neglected while the immune response involves memory [12, 13].

Fractional derivative is a generalization of integer derivative and it is a suitable tool to model real phenomena with memory which exists in most biological systems [14–16]. The fractional derivative is a nonlocal operator in contrast to integer derivative. This means that if we want to compute the fractional derivative at some point t = t₁, it is necessary to take into account the entire history from the starting point t = t₀ up to the point t = t₁. For these reasons, modeling some real process by using fractional derivative has drawn attention of several authors in various fields [17–22]. In biology, it has been shown that the fractional derivative is useful to analyse the rheological proprieties of cells [23]. Furthermore, it has been deduced that the membranes of cells of biological organism have fractional order electrical conductance [24]. Recently, much works have been done on modeling the dynamics of viral infections with FDEs [25–31]. These works ignored the impact of the immune response and the majority of them deal only with the local stability.

In some viral infections, the humoral immune response is more effective than cellular immune response [32]. For this reason, we improve the above ODE and FDE models by proposing a new fractional order model that describes the interactions between susceptible host cells, viral particles, and the humoral immune response mediated by the antibodies; that is,

()

where x(t), l(t), y(t), v(t), and w(t) are the concentrations of susceptible host cells, latently infected cells (infected cells which are not yet able to produce virions), productive infected cells, free virus particles, and antibodies at time t, respectively. Susceptible host cells are assumed to be produced at a constant rate λ, die at the rate dx, and become infected by virus at the rate f(x, v)v. Latently infected cells die at the rate ml and return to the uninfected state by loss of all covalently closed circular DNA (cccDNA) from their nucleus at the rate ρl. Productive infected cells are produced from latently infected cells at the rate γl and die at the rate ay. Free virus particles are produced from productive infected cells at the rate ky, cleared at the rate μv, and are neutralized by antibodies at the rate qvw. Antibodies are activated against virus at the rate gvw and die at the rate hw.

In system (1), D^α represents the Caputo fractional derivative of order α defined for an arbitrary function φ by

()

with 0 < α ≤ 1 [33]. Further, the infection transmission process in (1) is modeled by Hattaf-Yousfi functional response [34] which was recently used in [35, 36] and has the form f(x, v) = βx/(α₀ + α₁x + α₂v + α₃xv), where α₀, α₁, α₂, α₃ ≥ 0 are the saturation factors measuring the psychological or inhibitory effect and β > 0 is the infection rate. In addition, this functional response generalizes many common types existing in the literature such as the specific functional response proposed by Hattaf et al. in [37] and used in [2, 31] when α₀ = 1; the Crowley-Martin functional response introduced in [38] and used in [39] when α₀ = 1 and α₃ = α₁α₂; and the Beddington-DeAngelis functional response proposed in [40, 41] and used in [3, 4, 10] when α₀ = 1 and α₃ = 0. Also, the Hattaf-Yousfi functional response is reduced to the saturated incidence rate used in [9] when α₀ = 1 and α₁ = α₃ = 0 and the standard incidence function used in [27] when α₀ = α₃ = 0 and α₁ = α₂ = 1, and it was simplified to the bilinear incidence rate used in [5, 6] when α₀ = 1 and α₁ = α₂ = α₃ = 0.

On the other hand, system (1) becomes a model with ODEs when α = 1, which improves and generalizes the ODE model with bilinear incidence rate [42], the ODE model with saturated incidence rate [43], and the ODE model with specific functional response [44].

The rest of the paper is organized as follows. The next section deals with some basic proprieties of the solutions and the existence of equilibria. The global stability of equilibria is established in Section 3. To verify our theoretical results, we provide some numerical simulations in Section 4, and we conclude in Section 5.

2. Basic Properties and Equilibria

In this section, we will show that our model is well-posed and we discuss the existence of equilibria.

Since system (1) describes the evolution of cells, then we need to prove that the cell numbers should remain nonnegative and bounded. For biological considerations, we assume that the initial conditions of (1) satisfy

()

Then we have the following result.

Theorem 1. Assume that the initial conditions satisfy (3). Then there exists a unique solution of system (1) defined on [0, +∞. Moreover, this solution remains nonnegative and bounded for all t ≥ 0.

Proof. First, system (1) can be written as follows:

()

where

()

It is important to note that when α = 1, (4) becomes a system with ODEs. In this case, we refer the reader to [45] for the existence of solutions and to the works [46–50] for the stability of equilibria. In the case of FDEs, we will use Lemma 2.4 in [31] to prove the existence and uniqueness of solutions. Hence, we put

()

We discuss four cases:

(i)
If α₀ ≠ 0, F(X) can be formulated as follows:
()
- where
  ()
- Hence,
  ()
(ii)
If α₁ ≠ 0, we can write F(X) in the form
()
- where
  ()
- Moreover, we get
  ()
(iii)
If α₂ ≠ 0, we have
()
- where
  ()
- Further, we obtain
  ()
(iv)
If α₃ ≠ 0, we have
()
- where
  ()
- Then
  ()

Hence, the conditions of Lemma 2.4 in [31] are verified. Then system (1) has a unique solution on [0, +∞. Now, we show the nonnegativity of solutions. By (1), we have

()

As in [31, Theorem 2.7], we deduce that the solution of (1) is nonnegative.

Finally, we prove the boundedness of solutions. We define the function

()

Then, we have

()

where δ = min⁡{d, m, a/2, μ, h}. Thus, we obtain

()

Since 0 ≤ E_α(−δt^α) ≤ 1, we get

()

This completes the proof.

Now, we discuss the existence of equilibria. It is clear that system (1) has always an infection-free equilibrium E₀(λ/d, 0,0, 0,0). Then the basic reproduction number of (1) is as follows:

()

To find the other equilibria, we solve the following system:

()

From (29), we get w = 0 or v = h/g. Then we discuss two cases.

If w = 0, by (25)-(28), we have l = (λ − dx)/(m + γ), y = γ(λ − dx)/a(m + γ), v = kγ(λ − dx)/aμ(m + γ), and

()

Since l ≥ 0, y ≥ 0, and v ≥ 0, then x ≤ λ/d. Consequently, there is no equilibrium when x > λ/d.

We define the function h₁ on [0, λ/d] by

()

We have h₁(0) = −aμ(m + ρ + γ)/kγ < 0,

, and h₁(λ/d) = (aμ(m + ρ + γ)/kγ)(R₀ − 1).

Hence if R₀ > 1, (30) has a unique root x₁ ∈ (0, λ/d). As a result, when R₀ > 1 there exists an equilibrium E₁(x₁, l₁, y₁, v₁, 0) satisfying x₁ ∈ (0, λ/d), l₁ = (λ − dx₁)/(m + γ), y₁ = γ(λ − dx₁)/a(m + γ), and v₁ = kγ(λ − dx₁)/aμ(m + γ).

If w ≠ 0, then v = h/g. By (25)-(27), we obtain l = (λ − dx)/(m + γ), y = γ(λ − dx)/a(m + γ), w = kγg(λ − dx)/aqh(m + γ) − μ/q, and

()

Since l ≥ 0, y ≥ 0, and w ≥ 0, we have x ≤ λ/d − ahμ(m + γ)/dkgγ. Hence, there is no equilibrium if x > λ/d − ahμ(m + γ)/dkgγ.

We define the function h₂ on [0, λ/d − ahμ(m + γ)/dkgγ] by

()

We have h₂(0) = −gλ(m + ρ + γ)/h(m + γ) < 0,

, and h₂(λ/d − ahμ(m + γ)/dkgγ) = h₁(λ/d − ahμ(m + γ)/dkgγ).

Let us introduce the reproduction number for humoral immunity as follows:

()

which 1/h denotes the average life expectancy of antibodies and v₁ is the number of free viruses at E₁. For the biological significance, R₁ represents the average number of the antibodies activated by virus.

If R₁ < 1, we have x₁ > λ/d − ahμ(m + γ)/dkgγ and

()

Therefore, there is no equilibrium when R₁ < 1.

If R₁ > 1, then x₁ < λ/d − ahμ(m + γ)/dkgγ and

()

In this case, (32) has one root x₂ ∈ (0, λ/d − ahμ(m + γ)/dkgγ). Consequently, when R₁ > 1, there exists an equilibrium E₂(x₂, l₂, y₂, v₂, w₂) satisfying x₂ ∈ (0, λ/d − ahμ(m + γ)/dkgγ), l₂ = (λ − dx₂)/(m + γ), y₂ = γ(λ − dx₂)/a(m + γ), v₂ = h/g, and w₂ = kγg(λ − dx₂)/aqh(m + γ) − μ/q. When R₁ = 1, E₁ = E₂.

We summarize the above discussions in the following theorem.

Theorem 2.

(i)
If R₀ ≤ 1, then system (1) has one infection-free equilibrium of the form E₀(x₀, 0,0, 0,0), where x₀ = λ/d.
(ii)
If R₀ > 1, then system (1) has an infection equilibrium without humoral immunity of the form E₁(x₁, l₁, y₁, v₁, 0), where x₁ ∈ (0, λ/d), l₁ = (λ − dx₁)/(m + γ), y₁ = γ(λ − dx₁)/a(m + γ), and v₁ = kγ(λ − dx₁)/aμ(m + γ).
(iii)
If R₁ > 1, then system (1) has an infection equilibrium with humoral immunity of the form E₂(x₂, l₂, y₂, v₂, w₂), where x₂ ∈ (0, λ/d − ahμ(m + γ)/dkgγ), l₂ = (λ − dx₂)/(m + γ), y₂ = γ(λ − dx₂)/a(m + γ), v₂ = h/g, and w₂ = kγg(λ − dx₁)/aqh(m + γ) − μ/q.

3. Global Stability of Equilibria

In this section, we focus on the global stability of equilibria.

Theorem 3. If R₀ ≤ 1, then the infection-free equilibrium E₀ is globally asymptotically stable and it becomes unstable if R₀ > 1.

Proof. The proof of the first part of this theorem is based on the construction of a suitable Lyapunov functional that satisfies the conditions given in [51, Lemma 4.6]. Hence, we define a Lyapunov functional as follows:

()

where Φ(x) = x − 1 − ln(x) for x > 0. It is not hard to show that the functional L₀ is nonnegative. In fact, the function Φ has a global minimum at x = 1. Consequently, Φ(x) ≥ 0 for all x > 0.

Calculating the fractional derivative of L₀(t) along solutions of system (1) and using the results in [52], we get

()

Using λ = dx₀, we obtain

()

Hence if R₀ ≤ 1, then D^αL₀(t) ≤ 0. In addition, the equality holds if and only if x = x₀, l = 0, y = 0, w = 0, and (R₀ − 1)v = 0. If R₀ < 1, then v = 0. If R₀ = 1, from (1), we get f(x₀, v)v = 0 which implies that v = 0. Consequently, the largest invariant set of

is the singleton {E₀}. Therefore, by the LaSalle’s invariance principle [51], E₀ is globally asymptotically stable.

The proof of the instability of E₀ is based on the computation of the Jacobean matrix of system (1) and the results presented in [53–55]. The Jacobean matrix of (1) at any equilibrium E(x, l, y, v, w) is given by

()

We recall that E is locally asymptotically stable if the all eigenvalues ξ_i of (40) satisfy the following condition [53–55]:

()

From (40), the characteristic equation at E₀ is given as follows:

()

where

()

Obviously, (42) has the roots ξ₁ = −d and ξ₂ = −h. If R₀ > 1, we have g₀(0) = aμ(m + ρ + γ)(1 − R₀) < 0 and lim_ξ→+∞⁡g₀(ξ) = +∞. Then, there exists ξ^∗ > 0 satisfying g₀(ξ^∗) = 0. In addition, we have |arg(ξ^∗)| = 0 < απ/2. Consequently, when R₀ > 1, E₀ is unstable.

Theorem 4.

(i)
The infection equilibrium without humoral immunity E₁ is globally asymptotically stable if R₀ > 1, R₁ ≤ 1, and
()
(ii)
When R₁ > 1, E₁ is unstable.

Proof. Define a Lyapunov functional as follows:

()

Calculating the fractional derivative of L₁(t), we get

()

Using λ = dx₁ + (m + γ)l₁, f(x₁, v₁)v₁ = (m + ρ + γ)l₁, γl₁ = ay₁, ky₁ = μv₁, and 1 − f(x_i, v_i)/f(x, v_i) = ((α₀ + α₂v_i)/(α₀ + α₁x_i + α₂v_i + α₃x_iv_i))(1 − x_i/x)∀ i ∈ {1,2}, we obtain

()

Hence,

()

Using the arithmetic-geometric inequality, we have

()

Since R₁ ≤ 1, we have D^αL₁(t) ≤ 0 if dx₁ ≥ ρl₁. It is easy to see that this condition is equivalent to (44). Furthermore, D^αL₁(t) = 0 if and only if x = x₁, l = l₁, y = y₁, v = v₁, and (R₁ − 1)w = 0. We discuss two cases: If R₁ < 1, then w = 0. If R₁ = 1, from (1), we get D^αv₁ = 0 = ky₁ − μv₁ − qv₁w, and then w = 0. Hence, the largest invariant set of

is the singleton {E₁}. By the LaSalle’s invariance principle, E₁ is globally asymptotically stable.

At E₁, the characteristic equation of (40) is given as follows:

()

where

()

We can easily see that (50) has the root ξ₁ = gv₁ − h. Then, when R₁ > 1, we have ξ₁ > 0. In this case, E₁ is unstable.

Theorem 5. The infection equilibrium with humoral immunity E₂ is globally asymptotically stable if R₁ > 1 and

()

Proof. Consider the following Lyapunov functional:

()

Computing the fractional derivative of L₂(t) and using λ = dx₂ + (m + γ)l₂, f(x₂, v₂)v₂ = (m + ρ + γ)l₂, γl₂ = ay₂, ky₂ = (μ + qw₂)v₂, and v₂ = h/g, we get

()

From (49), we have D^αL₂(t) ≤ 0 when dx₂ ≥ ρl₂. This condition is equivalent to (52). In addition, D^αL₂(t) = 0 if x = x₂, l = l₂, y = y₂, and v = v₂. Further, D^αv₂ = 0 = ky₂ − μv₂ − qv₂w; then w = w₂. Consequently, the largest invariant set of

is the singleton {E₂}. By the LaSalle’s invariance principle, E₂ is globally asymptotically stable.

It is important to note that when ρ is sufficiently small or γ is sufficiently large, the two conditions (44) and (52) are satisfied. Then, we have the following corollary.

Corollary 6. Assume that R₀ > 1. When ρ is sufficiently small or γ is sufficiently large, then we have the following:

(i)
The infection equilibrium without humoral immunity E₁ is globally asymptotically stable if R₁ ≤ 1.
(ii)
The infection equilibrium with humoral immunity E₂ is globally asymptotically stable if R₁ > 1.

4. Numerical Simulations

In this section, we validate our theoretical results to HIV infection. Firstly, we take the parameter values as shown in Table 1.

Table 1. Parameter values of system (1).

parameters	values	parameters	values	parameters	values
λ	10	a	0.27	h	0.2
d	0.0139	γ	0.01	g	0.0001
β	0.00024	k	800	α₀	1
ρ	0.01	μ	3	α₁	0.1
m	0.0347	q	0.01	α₂	0.01
		α₃	0.00001

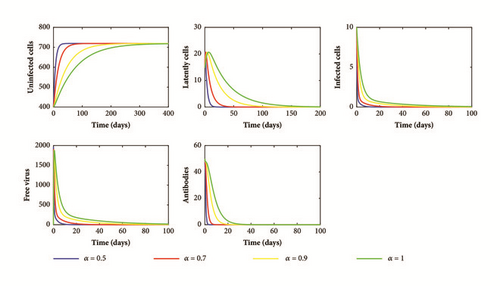
By calculation, we have R₀ = 0.4274 ≤ 1. Then system (1) has an infection-free equilibrium E₀(719.4245,0, 0,0, 0). By Theorem 3, the solution of (1) converges to E₀ (see Figure 1). Consequently, the virus is cleared and the infection dies out.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Stability of the infection-free equilibrium E₀.

Now, we choose β = 0.0012 and we keep the other parameter values. Hence, we obtain R₀ = 2.137, R₁ = 0.8334, and

()

Consequently, condition (44) is satisfied. Therefore, the infection equilibrium without humoral immunity E₁(176.6853,168.7712,6.2508,1666.9,0) is globally asymptotically stable. Figure 2 demonstrates this result. In this case, the infection becomes chronic.

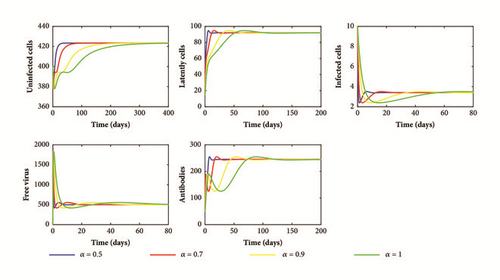
Next, we take g = 0.0004 and do not change the other parameter values. In this case, we have R₁ = 3.3338, ρβh = 0.0000024, and d(m + ρ + γ)(α₀g + α₂h) + ρλ(α₁g + α₃h) = 0.000006. Hence, condition (52) is satisfied. Consequently, system (1) has an infection equilibrium with humoral immunity E₂(423.4261,92.0442,3.4090,500,245.4473) which is globally asymptotically stable. Figure 3 illustrates this result. We can observe that the activation of the humoral immune response increases the healthy cells and decreases the productive infected cells and viral load to a lower levels but it is not able to eradicate the infection.

5. Conclusion

In the present paper, we have studied the dynamics of a viral infection model by taking into account the memory effect represented by the Caputo fractional derivative and the humoral immunity. We have proved that the solutions of the model are nonnegative and bounded which assure the well-posedness. We have shown that the proposed model has three infection equilibriums, namely, the infection-free equilibrium E₀, the infection equilibrium without humoral immunity E₁, and the infection equilibrium with humoral immunity E₂. By constructing suitable Lyapunov functionals, the global stability of these equilibria is fully determined by two threshold parameters R₀ and R₁. More precisely, when R₀ ≤ 1, E₀ is globally asymptotically stable, whereas if R₀ > 1, it becomes unstable and another equilibrium point appears, that is, E₁, which is globally asymptotically stable whenever R₁ ≤ 1 and condition (44) is satisfied. In the case that R₁ > 1, E₁ becomes unstable and there exists another equilibrium point E₂ which is globally asymptotically stable when condition (52) is satisfied. In addition, we remarked that when ρ is sufficiently small or γ is sufficiently large, conditions (44) and (52) are verified, and then the global stability of E₁ and E₂ is characterized only by R₀ and R₁.

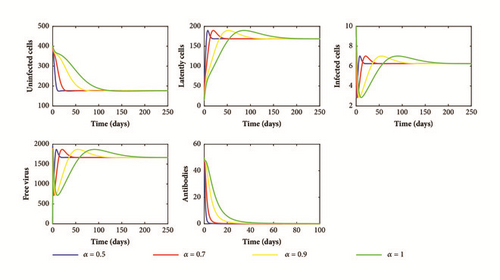
From our theoretical and numerical results, we deduce that the order of the fractional derivative α has no effect on the dynamics of the model. However, when the value of α decreases (long memory), the solutions of our model converge rapidly to the steady states (see Figures 1–3). This behavior can be explained by the memory term 1/Γ(1 − α)(t − u) ^α included in the fractional derivative which represents the time needed for the interaction between cells and viral particles and the time needed for the activation of humoral immune response. In fact, the knowledge about the infection and the activation of the humoral immune response in an early stage can help us to control the infection.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Hattaf K., Yousfi N., and Tridane A., Global stability analysis of a generalized virus dynamics model with the immune response, Canadian Applied Mathematics Quarterly. (2012) 20, no. 4, 499–518, MR3134709.
Google Scholar
2 Maziane M., Hattaf K., and Yousfi N., Global stability for a class of HIV infection models with cure of infected cells in eclipse stage and CTL immune response, International Journal of Dynamics and Control. (2016) https://doi.org/10.1007/s40435-016-0268-4.
10.1007/s40435-016-0268-4
PubMed Google Scholar
3 Wang X., Tao Y., and Song X., Global stability of a virus dynamics model with Beddington-DeAngelis incidence rate and CTL immune response, Nonlinear Dynamics. (2011) 66, no. 4, 825–830, https://doi.org/10.1007/s11071-011-9954-0, MR2859606.
10.1007/s11071-011-9954-0
Web of Science® Google Scholar
4 Lv C., Huang L., and Yuan Z., Global stability for an HIV-1 infection model with Beddington-DeAngelis incidence rate and CTL immune response, Communications in Nonlinear Science and Numerical Simulation. (2014) 19, no. 1, 121–127, https://doi.org/10.1016/j.cnsns.2013.06.025, MR3142453.
10.1016/j.cnsns.2013.06.025
Web of Science® Google Scholar
5 Nowak M. A. and Bangham C. R. M., Population dynamics of immune responses to persistent viruses, Science. (1996) 272, no. 5258, 74–79, 2-s2.0-0029985351, https://doi.org/10.1126/science.272.5258.74.
10.1126/science.272.5258.74
CAS PubMed Web of Science® Google Scholar
6 Murase A., Sasaki T., and Kajiwara T., Stability analysis of pathogen-immune interaction dynamics, Journal of Mathematical Biology. (2005) 51, no. 3, 247–267, https://doi.org/10.1007/s00285-005-0321-y, MR2206233, Zbl1086.92029, 2-s2.0-24344443729.
10.1007/s00285-005-0321-y
PubMed Web of Science® Google Scholar
7 Obaid M. A. and Elaiw A. M., Stability of Virus Infection Models with Antibodies and Chronically Infected Cells, Abstract and Applied Analysis. (2014) 2014, 12, 650371, https://doi.org/10.1155/2014/650371, MR3193532.
10.1155/2014/650371
Google Scholar
8 Obaid M. A., Dynamical behaviors of a nonlinear virus infection model with latently infected cells and immune response, Journal of Computational Analysis and Applications. (2016) 21, no. 1, 182–193, MR3469734, 2-s2.0-85014566922.
Google Scholar
9 Huo H. F., Tang Y. L., and Feng L. X., A Virus Dynamics Model with Saturation Infection and Humoral Immunity, Int. Journal of Math. Analysis. (2012) 6, no. 40.
Google Scholar
10 Elaiw A. M., Global stability analysis of humoral immunity virus dynamics model including latently infected cells, Journal of Biological Dynamics. (2015) 9, no. 1, 215–228, https://doi.org/10.1080/17513758.2015.1056846, MR3420650, 2-s2.0-84944723507, 26145479.
10.1080/17513758.2015.1056846
CAS PubMed Web of Science® Google Scholar
11 Elaiw A. M. and AlShamrani N. H., Global properties of nonlinear humoral immunity viral infection models, International Journal of Biomathematics. (2015) 8, no. 5, 1550058, 53, https://doi.org/10.1142/S1793524515500588, MR3383483.
10.1142/S1793524515500588
Web of Science® Google Scholar
12 Velasco-Herna′ndez J. X., Garci′a J. A., and Kirschner D. E., Remarks on modeling host-viral dynamics and treatment, Mathematical Approaches for Emerging and Reemerging Infectious Diseases, An Introduction to Models, Methods, and Theory. (2002) 125, 287–308.
Google Scholar
13 Perelson A. S., Modelling viral and immune system dynamics, Nature Reviews Immunology. (2002) 2, no. 1, 28–36, 2-s2.0-0036371443, https://doi.org/10.1038/nri700.
10.1038/nri700
CAS PubMed Web of Science® Google Scholar
14 Magin R. L., Fractional calculus models of complex dynamics in biological tissues, Computers & Mathematics with Applications. (2010) 59, no. 5, 1586–1593, 2-s2.0-76449091415, https://doi.org/10.1016/j.camwa.2009.08.039, Zbl1189.92007.
10.1016/j.camwa.2009.08.039
Web of Science® Google Scholar
15 Stanislavsky A. A., Memory effects and macroscopic manifestation of randomness, Physical Review E: Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics. (2000) 61, no. 5, 4752–4759, 2-s2.0-0034180313.
10.1103/PhysRevE.61.4752
CAS PubMed Web of Science® Google Scholar
16 Saeedian M., Khalighi M., Azimi-Tafreshi N., Jafari G. R., and Ausloos M., Memory effects on epidemic evolution: The susceptible-infected-recovered epidemic model, Physical Review E: Statistical, Nonlinear, and Soft Matter Physics. (2017) 95, no. 2, 2-s2.0-85014414578, https://doi.org/10.1103/PhysRevE.95.022409, 022409.
10.1103/PhysRevE.95.022409
CAS PubMed Web of Science® Google Scholar
17 Rossikhin Y. A. and Shitikova M. V., Applications of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids, Applied Mechanics Reviews. (1997) 50, no. 1, 15–67, https://doi.org/10.1115/1.3101682, 2-s2.0-0030867045.
10.1115/1.3101682
Google Scholar
18 Marks R. J. and Hall M. W., Differintegral Interpolation from a Bandlimited Signal′s Samples, IEEE Transactions on Signal Processing. (1981) 29, no. 4, 872–877, 2-s2.0-0019606817, https://doi.org/10.1109/TASSP.1981.1163636, Zbl0525.65005.
10.1109/TASSP.1981.1163636
Web of Science® Google Scholar
19 Jia G. L. and Ming Y. X., Study on the viscoelasticity of cancellous bone based on higher-order fractional models, Proceedings of the 2nd International Conference on Bioinformatics and Biomedical Engineering (ICBBE ′08), May 2008, Shanghai, China, 1733–1736, https://doi.org/10.1109/ICBBE.2008.761, 2-s2.0-50949100699.
10.1109/ICBBE.2008.761
Google Scholar
20 Magin R., Fractional calculus in bioengineering, Cretical reviews in biomedical engineering. (2004) 32, 13–77.
Google Scholar
21 Scalas E., Gorenflo R., and Mainardi F., Fractional calculus and continuous-time finance, Physica A: Statistical Mechanics and its Applications. (2000) 284, no. 1–4, 376–384, https://doi.org/10.1016/s0378-4371(00)00255-7, MR1773804, 2-s2.0-0034275979.
10.1016/S0378-4371(00)00255-7
Web of Science® Google Scholar
22 Capponetto R., Dongola G., Fortuna L., and Petras I., Fractional order systems: Modelling and control applications, World Scientific Series in Nonlinear Science, Series A. (2010) 72.
Google Scholar
23 Djordjević V. D., Jarić J., Fabry B., Fredberg J. J., and Stamenović D., Fractional derivatives embody essential features of cell rheological behavior, Annals of Biomedical Engineering. (2003) 31, no. 6, 692–699, 2-s2.0-0037596447, https://doi.org/10.1114/1.1574026.
10.1114/1.1574026
PubMed Web of Science® Google Scholar
24 Cole K. S., Electric conductance of biological systems, Cold Spring Harbor Symposium on Quantitative Biology. (1933) 1, 107–116, https://doi.org/10.1101/SQB.1933.001.01.014.
10.1101/SQB.1933.001.01.014
Google Scholar
25 Rihan F. A., Sheek-Hussein M., Tridane A., and Yafia R., Dynamics of hepatitis C virus infection: mathematical modeling and parameter estimation, Mathematical Modelling of Natural Phenomena. (2017) 12, no. 5, 33–47, https://doi.org/10.1051/mmnp/201712503, MR3716909, 2-s2.0-85031317032.
10.1051/mmnp/201712503
CAS Web of Science® Google Scholar
26 Khodabakhshi N., Vaezpour S. M., and Baleanu D., On Dynamics Of a Fractional-order Model Of HCV Infection, Journal of Mathematical Analysis. (2017) 8, no. 1, 16–27, MR3636733.
Web of Science® Google Scholar
27 Zhou X. and Sun Q., Stability analysis of a fractional-order HBV infection model, International Journal of Advances in Applied Mathematics and Mechanics. (2014) 2, no. 2, 1–6, MR3339946.
Google Scholar
28 S. M. S. and A. M. Y., On a fractional-order model for HBV infection with cure of infected cells, Journal of the Egyptian Mathematical Society. (2017) 25, no. 4, 445–451, https://doi.org/10.1016/j.joems.2017.06.003, MR3732356.
10.1016/j.joems.2017.06.003
Google Scholar
29 Ding Y. and Ye H., A fractional-order differential equation model of HIV infection of CD4+ T-cells, Mathematical and Computer Modelling. (2009) 50, no. 3-4, 386–392, 2-s2.0-67549148317, https://doi.org/10.1016/j.mcm.2009.04.019, ZBL1185.34005.
10.1016/j.mcm.2009.04.019
Web of Science® Google Scholar
30 Pinto C. M. and Carvalho A. R., The role of synaptic transmission in a HIV model with memory, Applied Mathematics and Computation. (2017) 292, 76–95, https://doi.org/10.1016/j.amc.2016.07.031, MR3542541.
10.1016/j.amc.2016.07.031
Web of Science® Google Scholar
31 Boukhouima A., Hattaf K., and Yousfi N., Dynamics of a Fractional Order HIV Infection Model with Specific Functional Response and Cure Rate, International Journal of Differential Equations. (2017) 2017, 8, 8372140, https://doi.org/10.1155/2017/8372140, MR3696023.
10.1155/2017/8372140
Google Scholar
32 Deans J. A. and Cohen S., Immunology of malaria, Annual Review of Microbiology. (1983) 37, 25–49, https://doi.org/10.1146/annurev.mi.37.100183.000325, 2-s2.0-0020653624.
10.1146/annurev.mi.37.100183.000325
CAS PubMed Web of Science® Google Scholar
33 Podlubny I., Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of their Solution and Some of their Applications, 1998, 198, Academic press.
Google Scholar
34 Hattaf K. and Yousfi N., A class of delayed viral infection models with general incidence rate and adaptive immune response, International Journal of Dynamics and Control. (2016) 4, no. 3, 254–265, MR3536136, https://doi.org/10.1007/s40435-015-0158-1, 2-s2.0-84983027265.
10.1007/s40435-015-0158-1
Google Scholar
35 Riad D., Hattaf K., and Yousfi N., Dynamics of Capital-labour Model with Hattaf-Yousfi Functional Response, British Journal of Mathematics & Computer Science. (2016) 18, no. 5, 1–7, https://doi.org/10.9734/BJMCS/2016/28640.
10.9734/BJMCS/2016/28640
Google Scholar
36 Mahrouf M., Hattaf K., and Yousfi N., Dynamics of a stochastic viral infection model with immune response, Mathematical Modelling of Natural Phenomena. (2017) 12, no. 5, 15–32, https://doi.org/10.1051/mmnp/201712502, MR3716908, 2-s2.0-85031499566.
10.1051/mmnp/201712502
Web of Science® Google Scholar
37 Hattaf K., Yousfi N., and Tridane A., Stability analysis of a virus dynamics model with general incidence rate and two delays, Applied Mathematics and Computation. (2013) 221, 514–521, MR3091948, https://doi.org/10.1016/j.amc.2013.07.005, 2-s2.0-84881093515.
10.1016/j.amc.2013.07.005
Web of Science® Google Scholar
38 Crowley P. and Martin E., Functional responses and interference within and between year classes of a dragonfly population, Journal of the North American Benthological Society. (1989) 8, 211–221, https://doi.org/10.2307/1467324.
10.2307/1467324
Web of Science® Google Scholar
39 Xu S., Global stability of the virus dynamics model with Crowley-Martin functional response, Electronic Journal of Qualitative Theory of Differential Equations. (2012) No. 9, 10, https://doi.org/10.14232/ejqtde.2012.1.9, MR2878794.
10.14232/ejqtde.2012.1.9
Web of Science® Google Scholar
40 Beddington J. R., Mutual interference between parasites or predat ors and its effect on searching efficiency, Journal of Animal Ecology. (1975) 44, 331–340, https://doi.org/10.2307/3866.
10.2307/3866
Web of Science® Google Scholar
41 DeAngelis D. L., Goldstein R. A., and ONeill R. V., A model for trophic interaction, Ecology. (1975) 881–892.
10.2307/1936298
Web of Science® Google Scholar
42 Rong L., Gilchrist M. A., Feng Z., and Perelson A. S., Modeling within-host HIV-1 dynamics and the evolution of drug resistance: trade-offs between viral enzyme function and drug susceptibility, Journal of Theoretical Biology. (2007) 247, no. 4, 804–818, https://doi.org/10.1016/j.jtbi.2007.04.014, MR2479625.
10.1016/j.jtbi.2007.04.014
CAS PubMed Web of Science® Google Scholar
43 Hu Z., Pang W., Liao F., and Ma W., Analysis of a cd4+ t cell viral infection model with a class of saturated infection rate, Discrete and Continuous Dynamical Systems - Series B. (2014) 19, no. 3, 735–745, 2-s2.0-84897475585, https://doi.org/10.3934/dcdsb.2014.19.735.
10.3934/dcdsb.2014.19.735
Web of Science® Google Scholar
44 Maziane M., Lotfi E. M., Hattaf K., and Yousfi N., Dynamics of a Class of HIV Infection Models with Cure of Infected Cells in Eclipse Stage, Acta Biotheoretica. (2015) 63, no. 4, 363–380, 2-s2.0-84945479658, https://doi.org/10.1007/s10441-015-9263-y.
10.1007/s10441-015-9263-y
PubMed Web of Science® Google Scholar
45 Hale J. K. and Verduyn Lunel S. M., Introduction to Functional-Differential Equations, 1993, Springer, Berlin, Germany, https://doi.org/10.1007/978-1-4612-4342-7, MR1243878, Zbl0787.34002.
10.1007/978-1-4612-4342-7
Google Scholar
46 Hale J. K., Sufficient conditions for stability and instability of autonomous functional-differential equations, Journal of Differential Equations. (1965) 1, 452–482, https://doi.org/10.1016/0022-0396(65)90005-7, MR0183938, Zbl0135.30301, 2-s2.0-0001186673.
10.1016/0022-0396(65)90005-7
Web of Science® Google Scholar
47 Burton T. A., Stability and Periodic sSolutions of Ordinary and Functional Differential Equations, 1985, Academic Press, Orlando, Fla, USA, MR837654, Zbl0635.34001.
Google Scholar
48 Ogundare B. S., Stability and boundedness properties of solutions to certain fifth order nonlinear differential equations, Matematicki Vesnik. (2009) 61, no. 4, 257–268, MR2578506.
Google Scholar
49 Tunç C., A study of the stability and boundedness of the solutions of nonlinear differential equations of the fifth order, Indian Journal of Pure and Applied Mathematics. (2002) 33, no. 4, 519–529, MR1902691.
Web of Science® Google Scholar
50 Tunç C., New results on the stability and boundedness of nonlinear differential equations of fifth order with multiple deviating arguments, Bulletin of the Malaysian Mathematical Sciences Society. (2013) 36, no. 3, 671–682, MR3071757.
Web of Science® Google Scholar
51 Huo J., Zhao H., and Zhu L., The effect of vaccines on backward bifurcation in a fractional order HIV model, Nonlinear Analysis: Real World Applications. (2015) 26, 289–305, https://doi.org/10.1016/j.nonrwa.2015.05.014, MR3384337.
10.1016/j.nonrwa.2015.05.014
Web of Science® Google Scholar
52 Vargas-De-Leon C., Volterra-type Lyapunov functions for fractional-order epidemic systems, Communications in Nonlinear Science and Numerical Simulation. (2015) 24, no. 1–3, 75–85, https://doi.org/10.1016/j.cnsns.2014.12.013, MR3313546.
10.1016/j.cnsns.2014.12.013
Web of Science® Google Scholar
53 Matignon D., Stability results for fractional differential equations with applications to control processing, Computational Eng. in Sys. Appl, 1996, 2, Lille, France.
Google Scholar
54 Ahmed E., El-Sayed A. M. A., and El-Saka H. A. A., On some Routh-Hurwitz conditions for fractional order differential equations and their applications in Lorenz, Rössler, Chua and Chen systems, Physics Letters A. (2006) 358, no. 1, 1–4, 2-s2.0-33746648126, https://doi.org/10.1016/j.physleta.2006.04.087, ZBL1142.30303.
10.1016/j.physleta.2006.04.087
CAS Web of Science® Google Scholar
55 Ahmed E., El-Sayed A. M. A., and El-Saka H. A. A., Equilibrium points, stability and numerical solutions of fractional-order predator-prey and rabies models, Journal of Mathematical Analysis and Applications. (2007) 325, no. 1, 542–553, https://doi.org/10.1016/j.jmaa.2006.01.087, MR2273544, 2-s2.0-33750295344.
10.1016/j.jmaa.2006.01.087
Web of Science® Google Scholar

Citing Literature

All articles

A Fractional Order Model for Viral Infection with Cure of Infected Cells and Humoral Immunity

Abstract

1. Introduction

2. Basic Properties and Equilibria

3. Global Stability of Equilibria

4. Numerical Simulations

5. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Fractional Order Model for Viral Infection with Cure of Infected Cells and Humoral Immunity

Abstract

1. Introduction

2. Basic Properties and Equilibria

3. Global Stability of Equilibria

4. Numerical Simulations

5. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information