Journal of Gravity
Volume 2017, Issue 1 9151485
Corrigendum
Open Access

Corrigendum to “Clusters of Galaxies in a Weyl Geometric Approach to Gravity”

Erhard Scholz, 

Corresponding Author

Erhard Scholz

Faculty of Mathematics & Natural Sciences and Interdisciplinary Centre for History and Philosophy of Science, University of Wuppertal, 42119 Wuppertal, Germany uni-wuppertal.de

Search for more papers by this author
First published: 15 October 2017
https://doi.org/10.1155/2017/9151485
Citations: 1

In the article titled “Clusters of Galaxies in a Weyl Geometric Approach to Gravity” [1], there was an error in equation (47) that led to a wrong relation between the acceleration due to the scale connection (aφ) and the acceleration arising from the scalar field energy density (asf). The correction of (47) has consequences for the model. It makes a new run of the data evaluation based on the corrected dynamical equations necessary. The new results are given in updated Tables 3 and 4 and Figures 1–6. The overall picture of the empirical test does not change, although now three rather than two galaxy clusters agree with the model only in the 2σ range. To facilitate controlling the correction, a detailed derivation of the corrected equation (47) is given in Appendix.

Table 3. Empirical values (M500, M200) and model values (Mtot) for total mass at r500,  r200.
Cluster r500 Mtot(r500) M500 r200 Mtot(r200) M200
Coma 1278
2300
A85 1216
1900
A400 712
1093
IIIZw54 731
1350
A1367 893
1529
MKW4 580
857
ZwCl215 1098
2093
A1650 1087
2150
A1795 1118
2136
MKW8 715
1279
A2029 1275
2286
A2052 875
1250
MKW3S 905
1450
A2065 1008
2450
A2142 1449
2364
A2147 1064
1450
A2199 957
1621
A2255 1072
2271
A2589 848
1471
  • Model values Mtot(rN00) and empirical values MN00 in 1014 M⊙, rN00 (empirical) in kpc (N = 1,2).
Table 4. Model values for halo and baryonic masses at r200.
Cluster Mt Msf Msf2 Mph1 Mgas M∗ f∗ ft
Coma 11.15 6.44 1.73 4.71 1.77 0.276 0.16 6.3
A85 8.03 4.52 1.01 3.51 1.54 0.140 0.09 5.2
A400 2.27 1.36 0.45 0.91 0.26 0.084 0.32 8.7
IIIZw54 2.77 1.65 0.54 1.11 0.25 0.080 0.32 10.9
A1367 3.77 2.21 0.65 1.56 0.42 0.089 0.21 8.9
MKW4 0.99 0.58 0.18 0.40 0.09 0.022 0.25 10.9
ZwCl215 8.00 4.55 1.11 3.45 1.19 0.137 0.12 6.7
A1650 8.15 4.69 1.24 3.45 1.10 0.162 0.15 7.4
A1795 8.04 4.59 1.14 3.45 1.15 0.14 0.12 7.0
MKW8 2.12 1.24 0.36 0.88 0.20 0.039 0.20 10.8
A2029 12.83 7.15 1.47 5.68 2.83 0.203 0.07 4.5
A2052 2.58 1.50 0.43 1.07 0.31 0.059 0.19 8.3
MKW3S 3.35 1.95 0.55 1.40 0.39 0.072 0.18 8.5
A2065 10.28 5.80 1.32 4.48 1.48 0.142 0.10 6.9
A2142 12.55 6.95 1.35 5.60 2.59 0.159 0.06 4.8
A2147 4.83 2.77 0.71 2.06 0.87 0.118 0.14 5.5
A2199 4.36 2.52 0.68 1.84 0.55 0.088 0.16 8.0
A2255 10.35 5.84 1.33 4.51 1.76 0.166 0.09 5.9
A2589 3.99 2.33 0.68 1.65 0.52 0.105 0.20 7.7
  • Mass values in 1014 M⊙,  f∗ = M∗/Mgas,  ft = (Mt/Mgas)(r200); for r200 see Table 2.
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Halo components of Coma cluster: transparent matter halo Mt = Msf + Mph1, total scalar field (SF) halo Msf, halo of freely falling galaxies Msf2, and net phantom energy Mph1 (in barycentric rest system). Empirical data (violet dot and bar): baryonic masses M∗ 500 + Mgas 500 (dot) and M500 (with error intervals) at r500 = 1280 kpc.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Comparison of the contribution of the scalar field halo of the galaxies Msf2 with the baryonic mass for the Coma cluster (empirical data for Mbar 500 violet dot).
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Contribution of the baryonic mass Mbar, of the scalar field, and the phantom energies Msf,  Mph1 to the transparent mass Mt and to the total mass Mtot = Mt + Mbar of the Coma cluster in the WST model. Model errors indicated at r500, r200 (black). Empirical data for Mbar (violet dot) and for the empirically determined total mass M500 with error bars (violet) from [2]. Additional empirical data at r200 (yellowish) from [3].
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Halo models for clusters 2–9 in Table 1: total mass Mtot (black line) with model error bars at r500,  r200, transparent matter halo Mt constituted by scalar field halo Msf2 and net phantom halo (in barycentric rest system of cluster) Mph1, and baryonic mass (gas and stars) Mbar. Empirical data for the total mass with error intervals at r500 (violet) from [2]. Additional empirical data at r200 (yellow) from [3].
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Halo models for clusters 10–19 in Table 1. For description, see Figure 4.
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Comparison of dark/transparent/phantom mass halos for Coma in NFW, WST, and TeVeS models and free parameters of halos for NFW and TeVeS (μ2 with neutrino core) adapted to mass data (black error bars) at r500 = 1280 kpc and r200 = 2300 kpc. Red error bar at r200 expresses variability of the NFW halo at this distance due to adapting it to the given error interval of mass data at r500.

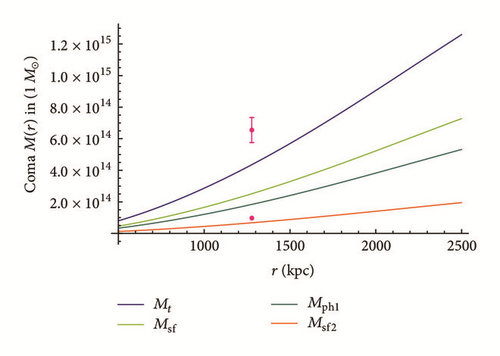
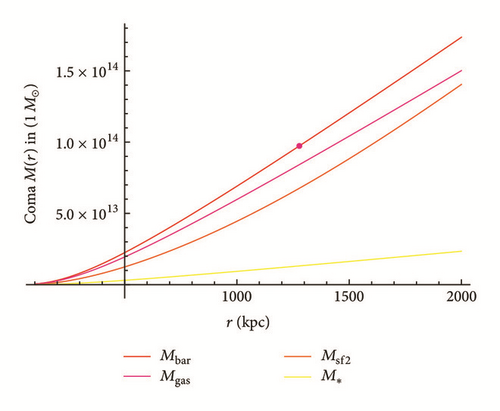
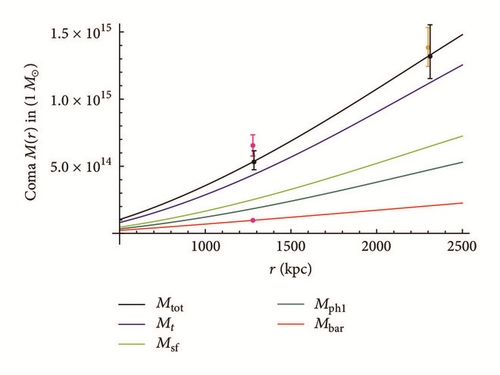
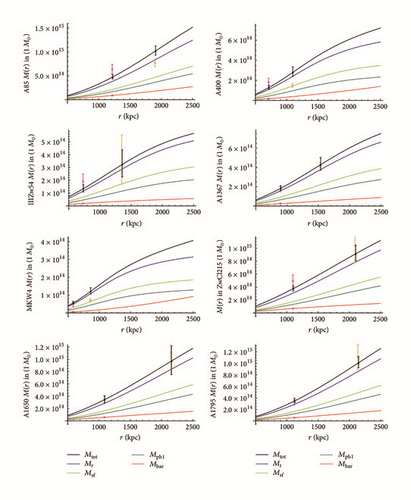
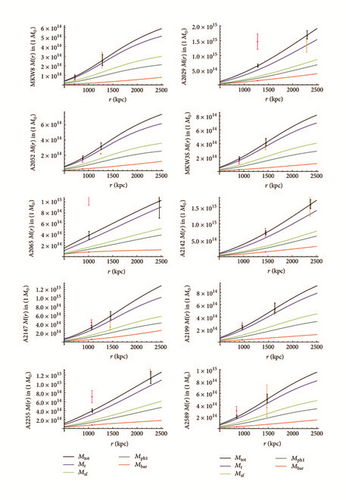
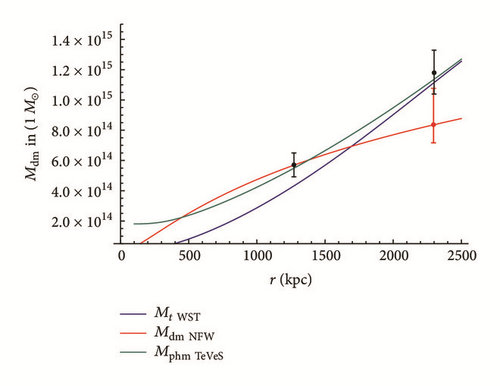
Minor Corrections. “15” should be changed to “14” in the following two sections. In the abstract, the number should be corrected in the phrase “the total mass for 15 of the outlier reduced ensemble of 17 clusters seems to be predicted correctly (in the sense of overlapping 1σ error intervals).” In paragraph 6 of Introduction, it should be corrected in the sentence “For 15 of the 17 main reference clusters the empirical and the theoretical values for the total mass agree in the sense of overlapping 1σ error intervals.” Equations (28), (57), and (58) should read as follows.

Major Corrections, Section  2. Equation (47) should read as follows:
The paragraph following equation (47), including the old equation (48), has to be cancelled. The correction of (47) entails the following modifications in the equations of Section 2:
In the comment below equation (59) “three quarters” and “one quarter” should be replaced with “one-half” and the inline formula below equation (62) should be replaced with aadd = aφ + asf = 2aφ.
Major Corrections, Sections  3–5. The modifications of the equations in Section 2 lead to the following changes in Section 3:
This makes a new run of the data evaluation necessary, now based on the corrected dynamical equations. The new results are given in updated Tables 3 and 4 and Figures 2–6. In the evaluation on p. 16, right column, first two sentences of the first paragraph should be replaced with the following:
  •  

    For 5 clusters A85, A2255, and A2589 and the outliers A2029 and A2065, the error intervals of empirical data and model data do not overlap. For the first three of them (A85, A2255, and A2589) the model predictions are consistent with the empirical data within doubled error intervals (2σ range).

In page 20, right column (Section 5), 20, at the middle of the second paragraph “15 clusters” should be replaced with “14 clusters,” and “Two clusters  …” should be substituted by “Three clusters  …” at the beginning of the last phrase.

Appendix

Energy Component of the Scalar Field

In scalar field (Einstein) gauge Dνϕ = ∂νϕ − φνϕ≐−ϕφν≐ϕ∂νω≐ϕDνω, and Dνϕ2 = 2ϕDνϕ≐2ϕ2∂νω. Similarly
()
Moreover,
()
leads to
()
Thus
()
Following (35) and (36) of the main article and using ξ−1ϕo≐H (H = 6ao, the Hubble parameter at present), the energy momentum of the scalar field,
()
becomes
()
In the static case the first two terms of vanish and the total energy component of the scalar field turns into
()
Assuming conditions under which the terms of cosmological orders of magnitude and those of order |∇ω|2 can be neglected, we arrive at
()
like in the corrected equation (47). In the central symmetric case (44) implies . In spherical coordinates and
()
Because of the approximation (47) is justified.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.