Nonnegative Periodic Solutions of a Three-Term Recurrence Relation Depending on Two Real Parameters
Abstract
Simple dynamic systems representing time varying states of interconnected neurons may exhibit extremely complex behaviors when bifurcation parameters are switched from one set of values to another. In this paper, motivated by simulation results, we examine the steady states of one such system with bang-bang control and two real parameters. We found that nonnegative and negative periodic states are of special interests since these states are solutions of linear nonhomogeneous three-term recurrence relations. Although the standard approach to analyse such recurrence relations is the method of finding the general solutions by means of variation of parameters, we find novel alternate geometric methods that offer the tracking of solution trajectories in the plane. By means of this geometric approach, we are then able, without much tedious computation, to completely characterize the nonnegative and negative periodic solutions in terms of the bifurcation parameters.
1. Introduction
When the real parameters ρ and μ are switched among different real values, it is expected (and verified by simulations) that complex dynamic behaviors will be more than abundant. Some of these behaviors can be explained (see [1–3]) but some not (at least to the best of our knowledge). Similar models of piecewise constant dynamic systems which exhibit similar behaviors with parameters can be found in many recent investigations; see for examples [4–10] and the references therein.
Yet, for other values of μ and ρ, simulations show complex periodic behaviors beyond our present comprehension, except when the periodic solutions are also “nonnegative” (or “negative”). Such exceptional results, when examined more closely, can be explained.
In this paper, we will devote ourselves to explaining the behaviors of these nonnegative (or negative) and periodic solutions of (7).
- (i)
R≔(−∞, ∞) is the entire set of real numbers.
- (ii)
Z≔{…, −1,0, 1, …} is the set of integers
- (iii)
Z+≔{1,2, 3, …} is the set of positive integers.
- (iv)
N≔{0,1, 2, …} is the set of nonnegative integers.
- (v)
Q≔{±m/n∣m ∈ N, n ∈ Z+} is the set of rational numbers.
Proposition 1. Let be a solution of (7) defined by (φ0, φ1) = (α, β) and be the “positive” orbit of φ. Then ω is a period of φ if and only if (xω, yω) = (α, β). Furthermore, if limk→∞|xk| = ∞, then φ is aperiodic and if limk→∞xkyk < 0, then φ is neither a nonnegative nor a negative solution.
The statements of Proposition 1 can be verified directly from the definitions, as well as the invariant properties of (7), and, thus, the proof is omitted here.
2. Some Basic Results of (7)
Periods and the prime periods of sequences are defined as usual. Furthermore, let be a nonnegative solution of (7). Note that for some distinct m, n ∈ N, if (φm, φm+1) = (φn, φn+1), then |m − n| is a period of φ and the least one ω among the periods is the least or prime period of φ (we also say that φ is ω-periodic). A constant solution of (7) is 1-periodic. We first find the necessary and sufficient conditions for φ to be a constant solution.
Proposition 2. Let be a solution of (7) with (φ0, φ1) = (α, β).
- (i)
Suppose ρ ≠ −2. Then φ is a constant solution if and only if α = β = μ/(2 + ρ).
- (ii)
Suppose ρ = −2. Then φ is a constant solution if and only if μ = 0 and α = β.
Proof. Suppose ρ ≠ −2. If φ is a constant solution of (7), then α = β = φ2 and
The proof is complete.
Corollary 3. Let be a solution of (7) with φ0 = φ1 = γ. Let γ = μ/(2 + ρ) where ρ ≠ −2. Then φ is 1-periodic. φ is a nonnegative solution if and only if γ ≥ 0; and φ is a negative solution if and only if γ < 0.
The results can be obtained from Proposition 2 directly and, hence, we omit the proof.
In view of Proposition 2, it is easy to see that the orbit of a constant solution is just the set containing the only point (μ/(2 + ρ), μ/(2 + ρ)).
Proposition 4. Let be a solution of (5) with (φ0, φ1) = (α, β). Then φ is 2-periodic if and only if ρ = 2, α + β = μ/2, and α ≠ β.
Proof. Suppose φ is 2-periodic. Then φ2 = α as well as φ3 = β and by (5), φ2 = μ − ρβ − α = α and φ3 = μ − ρα − β = β which lead us to 2α + ρβ = μ and ρα + 2β = μ, respectively. Accordingly, we have (2 + ρ)(α + β) = 2μ and (2 − ρ)(α − β) = 0. Note that since φ is 2-periodic, we can be sure that α ≠ β. Hence, if ρ ≠ 2, then α − β = 0 which is a contradiction; if ρ = 2, then α + β = μ/2 and α ≠ β. The converse may be checked by direct substitution into (5) and this completes the proof.
Corollary 5. Let be a solution of (7) with ρ = 2 and (φ0, φ1) = (α, β). Suppose α + β = μ/2. Then φ is periodic with period 2. φ is nonnegative if and only if α, β, μ ≥ 0; and φ is negative if and only if α, β, μ < 0.
Proof. Suppose α + β = μ/2. First of all, if α = β = μ/4, then, by Proposition 2, φ is 1-periodic; otherwise, by Proposition 4, φ is 2-periodic. Hence, φ is periodic with period 2. If φ is a nonnegative solution, then α, β ≥ 0 which implies μ ≥ 0. Furthermore, since φ is periodic with period 2, we can see that φk ≥ 0 for all k ∈ Z. If α, β, μ ≥ 0, then α + β = μ/2 is satisfied and φ is a nonnegative solution. The case where φ is a negative solution can be handled similarly and this completes the proof.
In this paper, since we are interested in the periodicity of the solutions of (4) which are also nonnegative (or negative), the following results will be useful.
Proposition 6. Let be a nonnull solution of (7). If μ ≥ 0 and ρ ≥ 0, then φ cannot be a nonpositive solution; if μ ≤ 0 and ρ ≤ 0, then φ cannot be a nonnegative solution.
Proof. Suppose μ ≥ 0 and ρ ≥ 0. If φ is nonpositive, then 0 ≥ φ2 = −ρφ1 − φ0 + μ ≥ 0 and 0 ≥ φ3 = −ρφ2 − φ1 + μ ≥ 0. Hence φ2 = φ3 = 0, which implies φ is null, contrary to our assumption.
Suppose μ ≤ 0 and ρ ≤ 0. If φ is nonnegative, then 0 ≤ φ2 = −ρφ1 − φ0 + μ ≤ 0 and 0 ≤ φ3 = −ρφ2 − φ1 + μ ≤ 0 so that φ2 = φ3 = 0. A contradiction is arrived and this completes the proof.
Proof. Suppose that is a solution of (5) with (φ0, φ1) = (α, β). By (5), we have φ2 = μ − ρβ − α. Let ψ = −φ such that (ψ0, ψ1) = (−α, −β). Accordingly, ψ2 = −φ2 and we see that
Next, we discuss nonconstant solutions of (5) (although 2-periodic solutions are discussed in Proposition 4, we may include them in the following discussions). The behavior of solution φ of (7) with least period 1 (or 2) was quite easy to analyze directly, yet it is difficult to conduct similar analyses for φ with larger least period (or φ is aperiodic) by similar manner. Hence, we will investigate the behavior of φ from a new perspective.
3. The Orbits of Solutions of (7)
- (1)
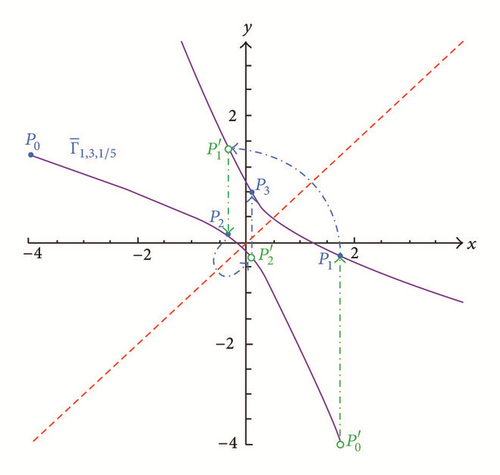
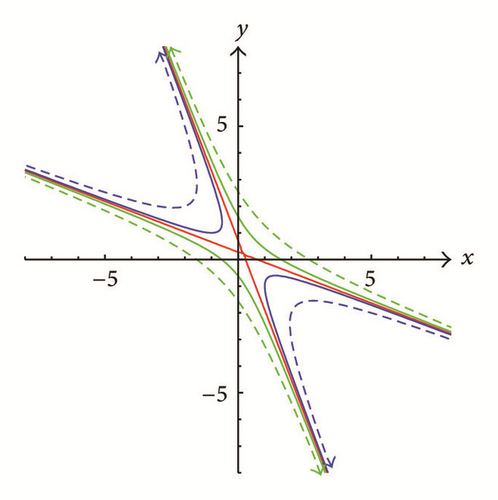
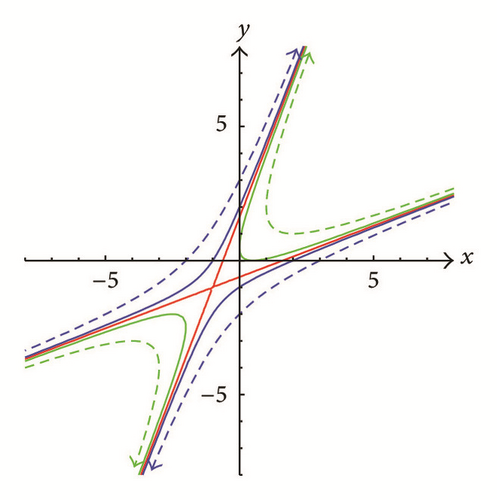
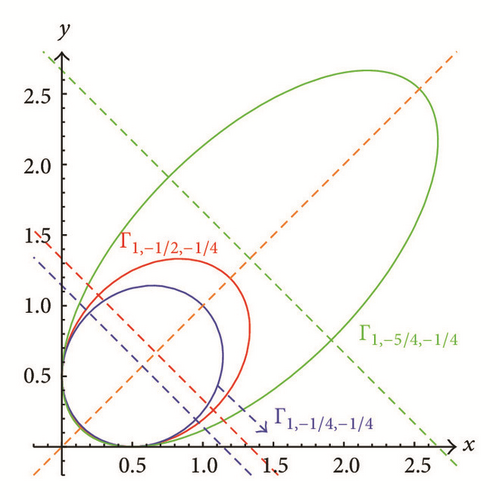
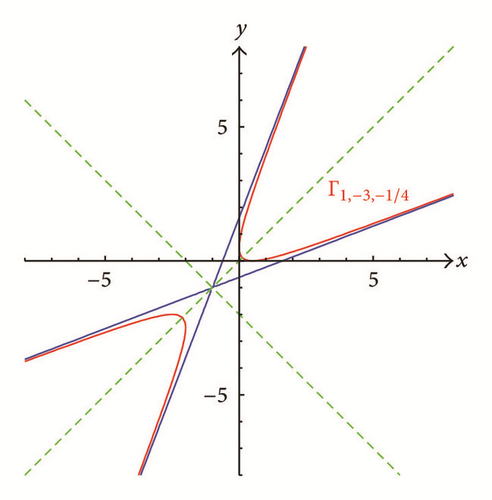
If |ρ| > 2, then Γμ,ρ,f is a hyperbola (see the green and red curves in Figures 3 and 4) when f ≠ −μ2/(2 + ρ) or a degenerate hyperbola consisting of two intersecting lines when f = −μ2/(2 + ρ) (see the blue lines in Figures 3 and 4).
- (2)
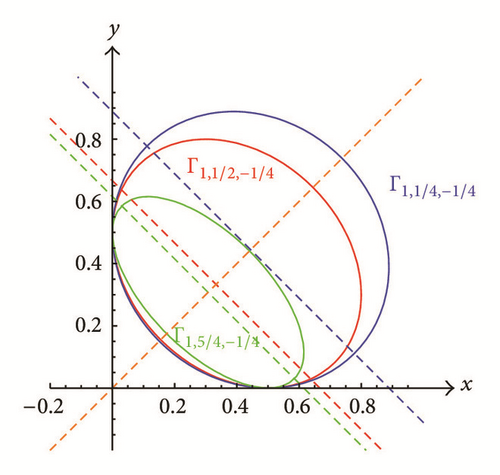
If |ρ| < 2, then Γμ,ρ,f is an ellipse (see Figure 5) when f ≠ −μ2/(2 + ρ) or a degenerate point ellipse when f = −μ2/(2 + ρ).
- (3)
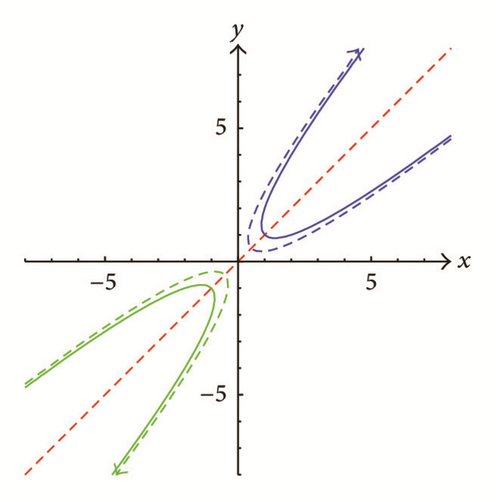
If |ρ| = 2, then Γμ,ρ,f is a parabola when ρ = −2 or a degenerate parabola consisting of a single or two distinct parallel lines when ρ = 2 (see the green and blue lines in Figure 6).
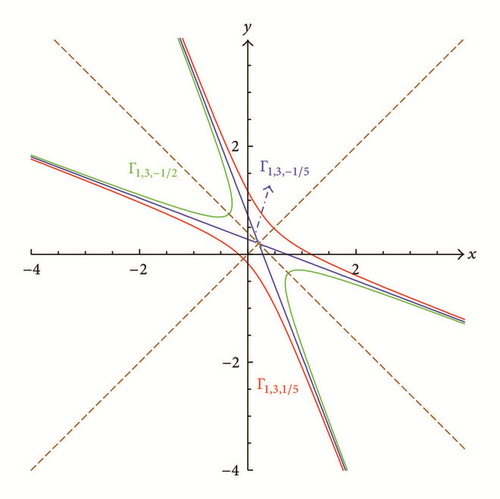
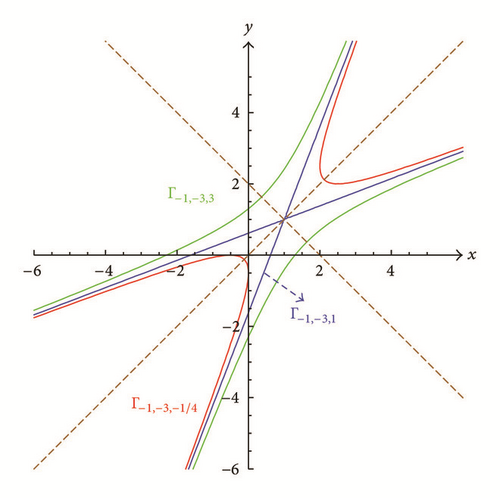
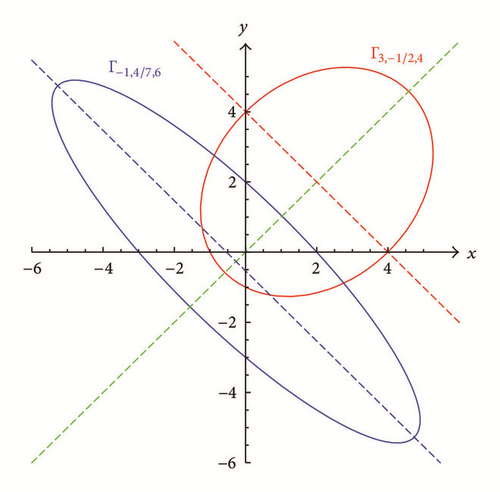
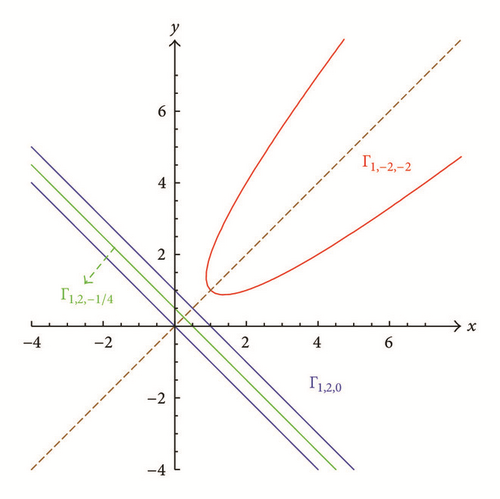
Unless indicated by the adjective “degenerate,” a conic section is meant to be nondegenerate. The conic sections Γμ,ρ,f are symmetric with respect to the x = y line. This property is a simple consequence of the fact that Γρ,f(x, y) is a symmetric function in x and y. Hence, the x = y line is one of the principal axes of the conic sections.
The conic sections will be of great help in the analysis of solutions of (4). The most significant result is the following.
Theorem 8. Let be a solution of (5). If f = Γμ,ρ(φm, φm+1) for some m ∈ Z, then Furthermore, if (α, β) ∈ Γμ,ρ,f, where f = Γμ,ρ(α, β), then
Proof. Without loss of generality, we let m = 0 and (φ0, φ1) = (α, β). Let f = Γμ,ρ(α, β). Then (α, β) ∈ Γμ,ρ,f. By (21), we see that
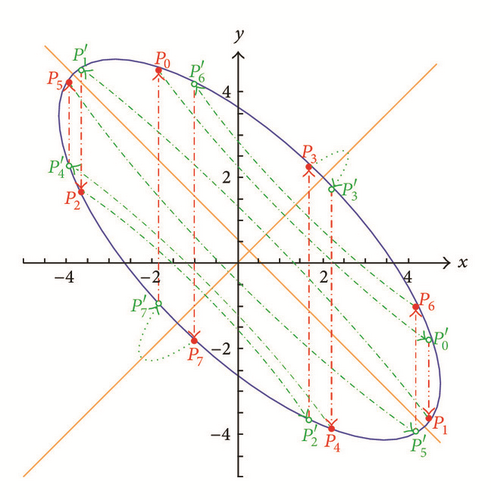
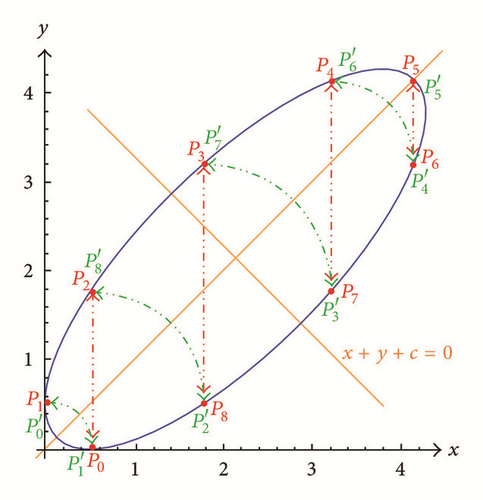
Let be a solution of (5). Then φ is uniquely determined by two consecutive terms φm and φm+1. Although we can calculate the next term φm+2 directly, the conic sections allow us to easily “track” the movements of the points from (φm, φm+1) to (φm+1, φm+2). Indeed, by Theorem 8, we see that , where f = Γμ,ρ(φm, φm+1). Then by means of this conic section, we may plot the corresponding orbit as follows.
- (1)
Plot Γμ,ρ,f where f = Γμ,ρ(α, β) on the plane.
- (2)
Take k = 0 and start at the point Pk = (xk, yk) = (α, β).
- (3)
Let be the point on Γμ,ρ,f which is symmetric to Pk with respect to the x = y line.
- (4)
Draw a vertical line Lk through
- (5)
The line Lk and the conic section Γμ,ρ,f can intersect at and possibly at another point If , then let ; otherwise, take
- (6)
If Pk+1 = P0, then stop; otherwise, let Pk = Pk+1 and go to step (3).
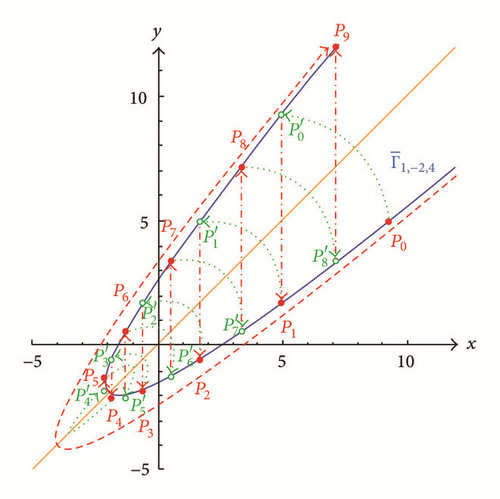
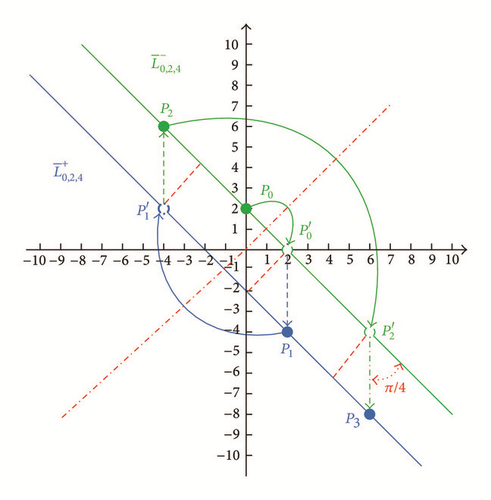
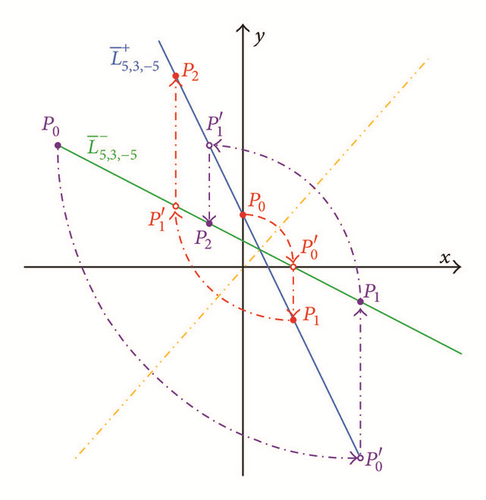
Note that by the Principal Axes Theorem, the level curve Γμ,ρ,f is defined by setting Γμ,ρ = f, which is a polynomial of degree 2. The conic section has one principal on the x = y line which implies any vertical line through meets Γμ,ρ,f at least once and at most twice through two points or If , then is on the ρx + 2y = μ line and this can be verified directly by (7). In view of the Tracking Procedure, we can generate each Pk = (xk, yk) as (φk, φk+1) by initializing P0 = (x0, y0) = (φ0, φ1) and it is not difficult to see that the above algorithm can yield the “positive” orbit ; on the other hand, the “negative” orbit of can be plotted by the “positive” orbit which is generated by the Tracking Procedure with input (φ1, φ0). In Figures 7 and 8, we illustrate the orbits of Pk on ellipses; Figures 9 and 10 depict the orbits on a parabola and a degenerate parabola correspondingly; and in Figures 11 and 12, we show the orbits on a degenerate hyperbola and a hyperbola, respectively.
As we have shown previously, the f-level curve Γμ,ρ,f of Γμ,ρ is a conic section and it can be classified into hyperbola, ellipse, or parabola (or the degenerate curves). Let be a solution of (7) defined by (φ0, φ1) = (α, β). By means of the Tracking Procedure, we can easily analyze the asymptotic behavior of φk when k → ∞. In the sequel, we will discuss the sequence which is generated by the Tracking Procedure with input (x0, y0) = (α, β) depending on |ρ| > 2, |ρ| = 2, and |ρ| < 2.
Theorem 9. Suppose |ρ| > 2 and let (α, β) ∈ R2 such that f = Γμ,ρ(α, β). Let be generated by the Tracking Procedure with input (x0, y0) = (α, β). Then Γμ,ρ,f is a hyperbola (or a degenerate one made up of two lines and ) and we have the following.
- (i)
Suppose Γμ,ρ,f is a degenerate hyperbola. If , then for all m ∈ N; if , then for all n ∈ N.
- (ii)
Suppose Γμ,ρ,f is a hyperbola. If ρ ≥ 0, then (xm, xm+1) and (xm+1, xm+2) are sitting on different branches for all m ∈ N; if ρ < 0, then (xn, xn+1) and (xn+1, xn+2) lie on the same branch for all n ∈ N.
Proof. Note that x0 = α and x1 = y0 = β. By Theorem 8 and (7), we see that y1 = μ − ρy0 − x0 = μ − ρβ − α = γ. Suppose or In the former case, and by (31), as well as (32), which implies ; in the latter case, by similar arguments, we may see that Note that if , then (α, β) = (μ/(2 + ρ), μ/(2 + ρ)) and by the Tracking Procedure, (x1, y1) = (μ/(2 + ρ), μ/(2 + ρ)) which implies (xi, yi) = (μ/(2 + ρ), μ/(2 + ρ)) for all i ∈ N. Suppose Then Γμ,ρ,f is a hyperbola and (α, β) is on one branch of Γμ,ρ,f. By the Tracking Procedure, we may see that if ρ ≥ 0, then P1 “jumps” to another branch (see Figure 3), while if ρ < 0, then P1 will stay on the same branch (see Figure 4). By induction, we may see that (ii) holds. This completes our proof.
In view of Theorem 9, we may follow the movements of (xk, yk) generated by the Tracking Procedure when |ρ| > 2. This enables us to see the asymptotic behavior of (xk, yk) when k → ∞ in Theorem 10. Before introducing Theorem 10, we denote the distance between two points P1 and P2 on R2 by |P1 − P2| and the distance from a point P to the line L by d(P, L).
Theorem 10. Suppose |ρ| > 2 and let (α, β) ∈ R2 such that f = Γμ,ρ(α, β). Let be generated by the Tracking Procedure with (x0, y0) = (α, β). Then Γμ,ρ,f is a hyperbola (or a degenerate one made up of two lines and ) and we have the following.
- (i)
Suppose If (α, β) = (μ/(2 + ρ), μ/(2 + ρ)), then (xk, yk) = (α, β) for all k ∈ N; if and (α, β) ≠ (μ/(2 + ρ), μ/(2 + ρ)), then
(33) -
and if and (α, β) ≠ (μ/(2 + ρ), μ/(2 + ρ)), then
(34) - (ii)
If ρ > 2 and Γμ,ρ,f is a hyperbola, then ; and if ρ < −2 and Γμ,ρ,f is a hyperbola, then
Proof. For the sake of convenience, we let Pc = (μ/(2 + ρ), μ/(2 + ρ)) and Pk = (xk, yk) so that P0 = (α, β) and f = Γμ,ρ(α, β). Let y1 = γ = μ − ρβ − α. By Proposition 2, if P0 = Pc, then φ is a constant solution of (7) which implies Now, we suppose P0 ≠ Pc. Since |ρ| > 2, Γμ,ρ,f is a hyperbola (or a degenerate one). Hence, we discuss the two cases where P0 is on a degenerate hyperbola or a hyperbola.
Suppose and P0 ≠ Pc. Then by Theorem 9, and are on the same line. In view of (24) and (25), we let m+ = ρ + δ, m− = ρ − δ, Δ+ = μ + δ/(2 + ρ), and Δ+ = μ − δ/(2 + ρ). For the sake of convenience, we also let
Suppose We first consider the case where ρ > 2. Then κ < 1 and by (24)
The proof is complete.
Corollary 11. Suppose |ρ| > 2 and let (α, β) ∈ R2 such that f = Γμ,ρ(α, β). Let be generated by the Tracking Procedure with input (x0, y0) = (α, β). Then Γμ,ρ,f is a hyperbola (or a degenerate one made up of two lines and ). Suppose (α, β) ≠ (μ/(2 + ρ), μ/(2 + ρ)). If , where ρ > 2, then xkxk+1 < 0 and |xk| → ∞ when k → ∞; if , where ρ < −2, then xkxk+1 > 0 and |xk| → ∞ when k → ∞.
The argument of Corollary 11 can be verified directly from Theorem 10 based on the facts that the slope of is characterized by −ρ + δ < 0 and the slope of is characterized by −ρ − δ > 0, where ρ > 2 and ρ < −2, respectively, and, thus, the proof is omitted.
In Theorem 10, we showed the asymptotic behaviors of generated by the Tracking Procedure. We illustrate the movements of when k → ∞ in Figures 13, 14, and 15 where the arrows indicate the moving directions of Pk as k → ∞.
Next, we consider the asymptotic behaviors of with ρ = 2 or ρ = −2.
Theorem 12. Suppose ρ = 2 and let (α, β) ∈ R2 such that f = Γμ,2(α, β). Let be generated by the Tracking Procedure with input (x0, y0) = (α, β). Then f ≥ −μ2/4 and Γμ,ρ,f is a degenerate parabola made up of and . If f = −μ2/4, then and (xk, yk) = (xk+2, yk+2) for all k ∈ N; otherwise, (xk, yk) as well as (xk+1, yk+1) are not on the same line. Furthermore, if f > −μ2/4, then and xkyk < 0 when k → ∞.
Proof. For the sake of convenience, we let Pc = (μ/(2 + ρ), μ/(2 + ρ)) and Pk = (xk, yk). First of all, we see that
Next, we consider the case where ρ = −2.
Theorem 13. Suppose ρ = −2 and let (α, β) ∈ R2 such that f = Γμ,−2(α, β). Let be generated by the Tracking Procedure with input (x0, y0) = (α, β). Then we have the following.
- (i)
Suppose μ = 0. Then f ≥ 0 and Γ0,−2,f is a degenerate parabola made up of two parallel lines and If f = 0, then and α = β such that (xk, yk) = (α, α) for all k ∈ N; otherwise, (xk, yk) and (xk+1, yk+1) are on the same line and d((xk, yk), P0) → ∞ when k → ∞.
- (ii)
Suppose μ ≠ 0. Then Γμ,−2,f is a parabola and when k → ∞.
Proof. Suppose μ = 0. By (20), Γ0,−2(x, y) = x2 − 2xy + y2 = (x − y)2 and, thus, f = Γ0,−2(α, β) = (α − β)2 ≥ 0. Accordingly, Γ0,−2,f is a degenerate parabola which is made up of two parallel lines and as defined in (24) and (25), respectively. More precisely, if α = β, then f = 0 which leads to ; if α ≠ β, then f > 0 which implies and are two distinct parallel lines. By the Tracking Procedure, if α = β, then (xk, yk) = (α, α) for all k ∈ N; if α ≠ β, then (xk, yk) and (xk+1, yk+1) are on the same line. Furthermore, if α ≠ β, then we have and by the Tracking Procedure again, d((xk, yk), (α, β)) = kΔtan(π/4) = kΔ, where k ∈ N. Accordingly, d((xk, yk), P0) → ∞ when k → ∞. Next, suppose μ ≠ 0. Then Γμ,−2,f is parabola. By (7), for k ∈ N, we have yk = xk+1 such that xk+2 − xk+1 = μ + xk+1 − xk and thus
Corollary 14. Suppose ρ = −2 and let (α, β) ∈ R2 such that f = Γμ,−2(α, β). Let be generated by the Tracking Procedure with input (x0, y0) = (α, β). Then we have the following.
- (i)
Suppose μ = 0. Then f ≥ 0 and Γ0,−2,f is a degenerate parabola with two parallel lines, and If α = β, then f = 0 such that and xk = α for all k ∈ N; otherwise, f > 0 such that as well as are two distinct parallel lines and
(47) - (ii)
Suppose μ ≠ 0. Then Γμ,−2,f is a parabola. If μ > 0, then Γμ,−2,f is concave upward and xk → ∞ when k → ∞; otherwise, Γμ,−2,f is concave downward and xk → −∞ when k → ∞.
The results stated in Corollary 14 can be derived directly from Theorem 13 by observing the asymptotic behavior of the points (xk, yk).
Theorem 15. Suppose |ρ| < 2 and (α, β) ≠ (μ/(2 + ρ), μ/(2 + ρ)) such that f = Γμ,ρ(α, β). Let be generated by the Tracking Procedure with input (α, β) = (x(θ0), y(θ0)). For any m ∈ N,
Proof. In view of (49), we first consider the case where ϑ = π/4. By (49), it follows that
By Theorem 15, we can find the necessary and sufficient condition for a solution φ of (7) with |ρ| < 2 to be a periodic sequence.
Corollary 16. Suppose |ρ| < 2 and (α, β) ≠ (μ/(2 + ρ), μ/(2 + ρ)) such that f = Γμ,ρ(α, β). Let be generated by the Tracking Procedure with input (x0, y0) = (α, β). Then is periodic if and only if
Proof. Note that if ρ ≠ −2 and (α, β) = (μ/(2 + ρ), μ/(2 + ρ)), then by the Tracking Procedure and Proposition 1, (x1, y1) = (α, β) which implies (xk, yk) = (α, β) for all k ∈ N. Suppose |ρ| < 2 and (α, β) ≠ (μ/(2 + ρ), μ/(2 + ρ)). By (49), we have
In view of Corollary 16, we have found the necessary and sufficient condition for , which is generated by the Tracking Procedure with input (x0, y0) ≠ (μ/(2 + ρ), μ/(2 + ρ)) such that f = Γμ,ρ(x0, y0) and |ρ| < 2, to be periodic. Let ρ = −1, 0, or 1; for instance, by (58), we take (m/n) = 1/3, 1/2, or 2/3, correspondingly, so that is 6-, 4-, or 3-periodic, respectively. For another example, by (58) again, if (m/n) = 2/5 or 4/5, then is 5-periodic where or , respectively.
For the analysis of nonnegative or negative solutions of (7) with |ρ| < 2, we need one more result.
Theorem 17. Let r ∉ Q. Suppose ϕk ≡ 2πkr mod 2π where k ∈ N. Then {ϕk∣k ∈ N} is dense in [0,2π].
Recall that by the Principal Axes Theorem, and are the principal axes of Γμ,ρ,f, where ρ ≠ −2 and f = Γμ,ρ(α, β), (α, β) ∈ R2. For −2 < ρ < 0 and (α, β) ∈ R2 such that f = Γμ,ρ(α, β), one property of which is generated by the Tracking Procedure with input (x0, y0) = (α, β) ≠ (μ/(2 + ρ), μ/(2 + ρ)) is revealed as follows.
Corollary 18. Suppose −2 < ρ < 0 and (α, β) ≠ (μ/(2 + ρ), μ/(2 + ρ)) such that f = Γμ,ρ(α, β). Let be generated by the Tracking Procedure with input (x0, y0) = (α, β). The set {(xm, ym)∣m ∈ N} cannot lie entirely in one of the half planes divided by
Proof. Since −2 < ρ < 0 and (α, β) ≠ (μ/(2 + ρ), μ/(2 + ρ)), Γμ,ρ,f is an ellipse. By Corollary 16 and Propositions 2 and 4, if π−1arccos(−ρ/2) ∈ Q, then φ is ω-periodic, where ω ≥ 3; otherwise, φ is aperiodic. Suppose π−1arccos(−ρ/2) ∈ Q. Then is ω-periodic, where ω ≥ 3 such that (xω, yω) = (α, β). First of all, by the Tracking Procedure, we see that (xk, yk) moves on Γμ,ρ,f in a clockwise manner. Secondly, Γμ,ρ,f is symmetric with respect to x = y. Hence, without loss of generality, we suppose Π(α, β) ≥ 0. Since (xk, yk) move on Γμ,ρ,f in a clockwise manner; by the Tracking Procedure, we can be sure that for some i ∈ {0,1, 2, …, ω − 1}, H(Π⊥(xi, yi))H(Π⊥(α, β)) < 0. Note that if H(Π⊥(α, β)) = 0, then we may investigate the orbit or so that H(Π⊥(β, μ − ρβ − α)) ≠ 0 or H(Π⊥(μ − ρα − β, α)) ≠ 0, respectively. Suppose π−1arccos(−ρ/2) ∉ Q. Without loss of generality, we suppose Π⊥(α, β) < 0 and (s, t) ∈ Γμ,ρ,f such that Π⊥(s, t) > 0. Then by Theorem 17, there is a subsequence such that as required and this completes the proof.
The previous discussions about the asymptotic behaviors of the solution of (7) help us to understand the periodicity of φ. To further analyze the positivity of solutions of (7), we require one specific solution with μ ≠ 0, ρ < 2, and We note that f = Γμ,ρ(μ/2,0) = −μ2/4. Also, some properties of ρμχ are useful for the ensuing analysis and they are as follows.
Proposition 19. For μ, ρ ∈ R, the lines y = 0 and x = 0 intercept with at (μ/2,0) and (0, μ/2), respectively. Furthermore, if ρ < 2 and μ ≠ 0, then is a nondegenerate conic section and the lines y = 0 and x = 0 are tangents of at the points (μ/2,0) and (0, μ/2), respectively.
Proof. First of all, we show that meets the y = 0 line at (μ/2,0). To this end, note that
We illustrate Proposition 19 by several plots of , namely, ellipses with 0 < ρ < 2 plotted in Figure 16, ellipses with −2 < ρ < 0 plotted in Figure 17, and hyperbola with ρ < −2 plotted in Figure 18.
In the following section, we establish the relation between the nonnegative (or negative) solution of (7) and a special solution in the geometric setting.
4. A Special Positive Orbit
- (1)
φ is a nonnegative solution if and only if (α, β) ∈ Φμ,ρ;
- (2)
φ is a negative solution if and only if (α, β) ∈ Ωμ,ρ.
Now, it is our objective to find Φμ,ρ and Ωμ,ρ and in several special cases where ρ < 2 and μ > 0, we will show that Φμ,ρ and Ωμ,ρ can be expressed as the intersections of certain half planes in R2.
Proposition 20. Let and be solutions of (7) with (φ0, φ1) = (α, β) and (c0, c1) = (0,0). Let and be solutions of (7) with μ = 0, with (a0, a1) = (0,1), and with (b0, b1) = (1,0). Then we have
Proof. For the sake of convenience, we suppose k ∈ N. First of all, if (a0, b0, c0) = (0,1, 0) and (a1, b1, c1) = (1,0, 0), then (φ0, φ1) = (α, β) which implies (63) is true when k ≤ 1. Next, we show that (63) holds for k ≥ 2. To this end, by (7), it follows that
Theorem 21. Given ρ, μ ∈ R, where ρ < 2 and μ > 0, then we have
Proof. First of all, we consider the case where k ≥ 0 and we show that hμ,ρ,k(x, y) = rlμ,ρ,k(x, y), where r = μ(ρ − 2)/2 < 0. To this end, we show the following results,
Corollary 22. Let be a solution of (7) with (φm, φm+1) = (σ, τ), for some m ∈ Z. If , then there is some n ∈ Z such that φn = 0.
Proof. By the definitions of in (75), if , then (σ, τ) is on the tangent line at , for some j ∈ Z. By (75) again, without loss of generality, we may further suppose that , for some i ∈ N. For the sake of convenience, we let δ = μ − ρτ − σ and such that Since , by (74), we have
In this section, we introduced the definitions of Φμ,ρ (or Ωμ,ρ) so that the necessary and sufficient conditions for a solution φ of (7) to be nonnegative (or negative) can be obtained, respectively. Also, in Theorem 21, we discussed the specific solution of (7) with and the intersection of the closed half planes generated by the tangent lines at , for all k ∈ Z. For the case where ρ < 2 and μ > 0, we will show that some Φμ,ρ can be expressed explicitly in terms of in the sequel. Note that by Proposition 7 and Theorem 8, some Φμ,ρ and Ωμ,ρ with ρ < 2 and μ < 0 can be derived from the results of the cases where ρ < 2 and μ > 0. Hence, with all the results derived in the previous discussions together, we are ready to discuss the necessary and sufficient conditions for φ to be nonnegative (or negative).
5. Nonnegative and Negative Solutions when |ρ| > 2
Theorem 23. Let be a solution of (7) with ρ > 2. Suppose (φm, φm+1) ≠ (μ/(2 + ρ), μ/(2 + ρ)), for some m ∈ Z. Then φ is neither a nonnegative solution nor a negative solution.
Proof. Without loss of generality, we let m = 0. Let (φ0, φ1) = (α, β) such that f = Γμ,ρ(α, β). Let and be generated by the Tracking Procedure with inputs (x0, y0) = (α, β) and (s0, t0) = (β, α), respectively. Then Γμ,ρ,f is a hyperbola (or a degenerate one made up of two lines and ) such that For the sake of convenience, we let Pc = (μ/(2 + ρ), μ/(2 + ρ)). If (α, β) = Pc, then, by Proposition 2, (xk, yk) = (sk, tk) = Pc, for all k ∈ N. Suppose (α, β) ≠ Pc. By the previous discussions, we first consider the case where If , then and by Corollary 11, it is found that xkxk+1 = φkφk+1 < 0 when k → ∞; if , then we take and we see that so that sksk+1 < 0 when k → ∞ as required. Next, suppose Γμ,ρ,f is a hyperbola. Then by Corollary 11 again, xkxk+1 = φkφk+1 < 0 when k → ∞. Accordingly, if (α, β) ≠ Pc, then φ is neither a nonnegative nor a negative solution and this completes the proof.
Next, we consider the case where ρ < −2 and μ ∈ R. This case is a little more complicated than the one described in Theorem 23, and we give the result of μ = 0 first.
Theorem 24. Let be a solution of (7) with ρ < −2 and μ = 0. Suppose (φm, φm+1) = (α, β), for some m ∈ Z such that f = Γμ,ρ(α, β). Then φ is a nonnegative solution if and only if (α, β) ∈ Θ0,ρ; and φ is a negative solution if and only if (α, β) ∈ Υ0,ρ.
Proof. Note that in view of (82), Θ0,ρ is symmetric with respect to the x = y line and Θ0,ρ∖{(0,0)} and Υ0,ρ are symmetric with respect to the x + y = 0 line. Let and be generated by the Tracking Procedure with inputs (x0, y0) = (α, β) and (s0, t0) = (β, α), respectively. Here, Γ0,ρ,f, where f = Γ0,ρ(α, β), is a hyperbola (or a degenerate one made up of two lines and ). Note that Θ0,ρ is a cone with two rays and such that u, v ≥ 0, where (u, v) ∈ Θ0,ρ. First of all, we show that Φ0,ρ = Θ0,ρ. To this end, we investigate (xk, yk) and (sk, yk) directly, and by Theorem 10, it is found that (xk, yk), (sk, tk) ≥ 0 for all k ∈ N if and only if (x0, y0) ∈ Θ0,ρ. Accordingly, we have Φ0,ρ = Θ0,ρ and the argument about Υ0,ρ can be handled similarly. Note that both Θ0,ρ and Θ0,ρ are symmetric with respect to the x = y line. Hence, the cases where k ∈ Z∖N can be handled by the invariances of translation and reflection. The proof is complete.
Next, we discuss the case where ρ < −2 and μ ≠ 0.
Theorem 25. Let be a solution of (7) with ρ < −2 and μ ≠ 0. Suppose (φm, φm+1) = (α, β) for some m ∈ Z such that f = Γμ,ρ(α, β).
- (i)
Suppose μ > 0. Then φ is a nonnegative solution if and only if which is the intersection of the closed half planes defined in (75). Furthermore, φ is a negative solution if and only if (α, β) ∈ Υμ,ρ.
- (ii)
Suppose μ < 0. φ is a nonnegative solution if and only if (α, β) ∈ Θμ,ρ; and φ is a negative solution if and only if , where is the intersection of the closed half planes defined in (75).
Proof. Without loss of generality, we let m = 0 and Pc = (μ/(2 + ρ), μ/(2 + ρ)). Since f = Γμ,ρ(α, β), Γμ,ρ,f is a hyperbola (or a degenerate one, two lines and ). Let and be generated by the Tracking Procedure with inputs (x0, y0) = (α, β) and (s0, t0) = (β, α), respectively. Suppose μ > 0. Then μ/(2 + ρ) < 0. By Theorem 21, it follows that as desired. Next, by Corollary 11, if (α, β) ∈ Υμ,ρ, then xk, sk < 0, for all k ∈ N. Conversely, if xk, sk < 0 for all k ∈ N, then, by Theorem 10 and Corollary 11, (α, β) ∈ Υμ,ρ. Now, we consider the case where μ < 0. From the previous discussions, Proposition 7 and Theorem 8, we can be sure that Φμ,ρ = Θμ,ρ. Next, we claim that , where is given by (75). From the previous discussions and Corollary 22, we can be sure that φ is a positive solution if and only if Thus, from Proposition 7 and Theorem 8, it follows that and this completes the proof.
Corollary 26. Let be a solution of (7) with |ρ| > 2. φ is a nonnegative and periodic solution if and only if μ ≥ 0 and (φm, φm+1) = (μ/(2 + ρ), μ/(2 + ρ)) for some m ∈ Z; φ is a negative and periodic solution if and only if μ < 0 and (φn, φn+1) = (μ/(2 + ρ), μ/(2 + ρ)) for some n ∈ Z.
From Proposition 2, Theorem 10, Corollary 11, and Theorems 23, 24, and 25, we can easily see that the statement of Corollary 26 holds.
This section shows that both Φμ,ρ and Ωμ,ρ are nonempty and if φ is not a constant solution of (7) with |μ| > 2, then φ is not periodic. Next, we will discuss Φμ,ρ and Ωμ,ρ where |ρ| = 2.
6. Nonnegative and Negative Solutions when |ρ| = 2
Let be a solution of (7) with ρ = |2| and (φ0, φ1) = (α, β). Let f = Γμ,ρ(α, β). Recall that is on the conic section Γμ,ρ,f which is a parabola or degenerate parabola that is made up of either one line or two distinct parallel lines. In this section, we now discuss the nonnegative and negative solutions of (7) by investigating ρ = 2 and ρ = −2.
Theorem 27. Let be a solution of (7) with ρ = 2. Suppose (φm, φm+1) = (α, β) for some m ∈ Z.
- (i)
Suppose μ ≥ 0. Then φ cannot be a negative solution; furthermore, φ is a nonnegative solution if and only if
(83) - (ii)
Suppose μ < 0. Then φ cannot be a nonnegative solution; furthermore, φ is a negative solution if and only if
(84)
Proof. From the previous discussions, Γμ,2,f, where f = Γμ,2(α, β) ≥ −μ2/4, is a degenerate parabola made up of two lines, and defined by (24) and (25), respectively. Moreover, if f = −μ2/4, then ; otherwise, and are two distinct parallel lines. We first consider the case where μ ≥ 0. By Theorem 12 and the Tracking Procedure, if α, β ≥ 0 such that f = Γμ,2(α, β) = −μ2/4, then φ is periodic with period 2 and φ2 ≥ 0 which implies φ is a nonnegative solution. Conversely, if φ is a nonnegative solution, then α, β ≥ 0 and by Theorem 12, f = −μ2/4 which implies Accordingly, we see that
Theorem 28. Let be a solution of (7) with ρ = −2. Suppose (φm, φm+1) = (α, β) for some m ∈ Z.
- (i)
Suppose μ = 0. Then φ is a nonnegative solution if and only if α, β ≥ 0 and which is the x = y line; furthermore, φ is negative solution if and only if and α, β < 0.
- (ii)
Suppose μ > 0. Then φ cannot be a negative solution; furthermore, φ is a nonnegative solution if and only if which is the intersection of the closed half planes defined by (75).
- (iii)
Suppose μ < 0. Then φ cannot be a nonnegative solution; furthermore, φ is a negative solution if and only if
(87) -
where is the intersection of the closed half planes defined by (75).
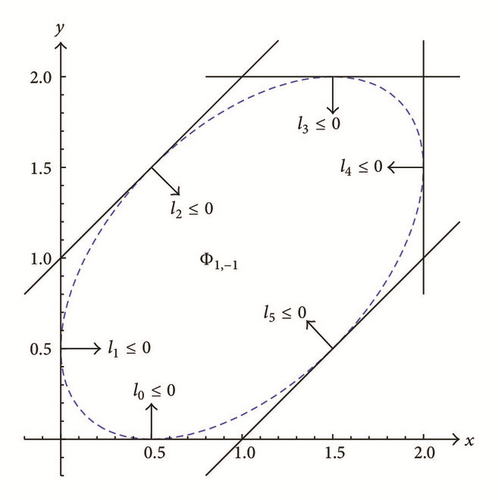
Proof. Recall that is the line x = y which is one principal axis of Γμ,ρ,f, where f = Γμ,ρ(α, β). Suppose μ = 0. By Theorem 13, if , then φ is neither a nonnegative nor a nonpositive solution. If , then φ is 1-periodic and we see that (i) holds by direct verification. Suppose μ > 0. Then by Theorem 21, we can be sure that as required and is depicted in Figure 19. For the case of (iii), from Proposition 7 and Theorem 8, it follows that (87) is true and this completes the proof.
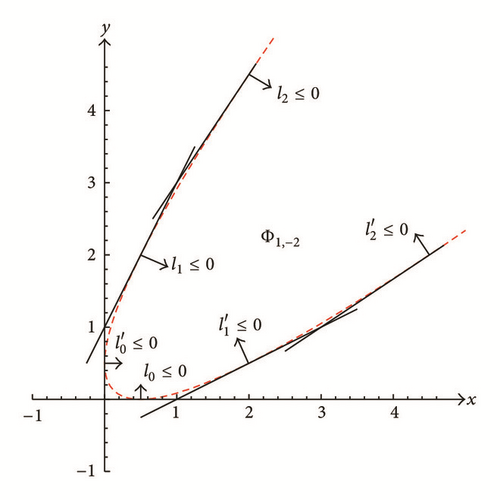
In view of Theorem 28. we have shown that which is the intersection of the half planes defined by the tangent lines at all the points of on the parabola Figure 19 illustrates Φ1,−2 where the red-dashed curve is the parabola Γ1,−2,−1/4. The discussions of the cases where |ρ| ≥ 2 are done and move forward to analyze the last cases where |ρ| < 2.
7. Nonnegative and Negative Solutions when |ρ| < 2
In the previous discussions, we have analyzed the cases where |ρ| ≥ 2 and derived the necessary and sufficient conditions for a solution φ to be nonnegative (or negative). Let be a solution of (7). From our analyses of the case where |ρ| ≥ 2, the periodicity of φ has no significant role in the analysis (albeit φ may be periodic with least period ω ≤ 2); yet the periodicity of φ is of great importance when discussing the case where |ρ| < 2. In Corollary 16, we illustrated the necessary and sufficient conditions for φ to be a periodic solution of (7) with |ρ| < 2 and we will discuss the case where μ = 0, μ > 0, and μ < 0 in the sequel.
Theorem 29. Let be a solution of (7) with |ρ| < 2 and μ = 0. Then φ cannot be a negative solution; furthermore, φ is a nonnegative solution if and only if φ is the null solution.
Proof. Let (φ0, φ1) = (α, β) such that f = Γ0,ρ(α, β). Let be generated by the Tracking Procedure with input (x0, y0) = (α, β). Suppose (α, β) = (0,0). From the previous discussions, f = Γ0,ρ(0,0) = 0 which implies Γ0,ρ,0 is a point ellipse. On the other hand, by Proposition 2, (φ0, φ1) = (0,0) which leads to φk = 0, for all k ∈ N and, thus, φ is a nonnegative solution with least period 1. Now, we suppose (α, β) ≠ (0,0). Then Γ0,ρ,f is an ellipse and we show that φ is neither a nonnegative nor a negative solution. To this end, we consider 0 ≤ ρ < 2 and −2 < ρ < 0. Suppose 0 ≤ ρ < 2. By Proposition 6, φ cannot be a nonpositive solution which implies φ is not negative. If φ is a nonnegative solution, then by Proposition 7, −φ is a nonpositive solution which is a contradiction. The case where −2 < ρ < 0 can be handled similarly and this completes the proof.
Next, we consider the corresponding results when |ρ| < 2 and μ ≠ 0.
Theorem 30. Let be a solution of (7) with |ρ| < 2 and μ ≠ 0. Suppose π−1arccos(−ρ/2) ∉ Q and let (φm, φm+1) = (α, β) for some m ∈ Z.
- (i)
Suppose μ > 0. Then φ cannot be a negative solution; furthermore, φ is a nonnegative solution if and only if
(88) -
which is the interior of the ellipse
- (ii)
Suppose μ < 0. Then φ cannot be a nonnegative solution; furthermore, φ is a negative solution if and only if , where
(89)
Proof. Without loss of generality, we let m = 0. Also, for the sake of convenience, let Pc = (μ/(2 + ρ), μ/(2 + ρ)) and r = π−1arccos(−ρ/2). Also, let be generated by the Tracking Procedure with input (x0, y0) = (α, β). Then we consider two cases where μ > 0 and μ < 0. Here, if (α, β) = Pc, then, by the previous discussions, is a point ellipse so that (xk, yk) = Pc, for all k ∈ N. Note that is tangent to lines x = 0 and y = 0 at (0, μ/2) and (μ/2,0), respectively. Suppose μ > 0. We first show that φ cannot be a nonpositive solution. If ρ ≥ 0, then, by Proposition 6, φ is not a nonpositive solution. If φ is nonpositive with ρ < 0, then, by the previous discussions, (α, β) ≠ Pc and by Corollary 18, there is some m ∈ N such that xm ≥ 0 or ym ≥ 0. Furthermore, if α = β = 0, then, by (7), φ2 = μ > 0. Accordingly, φ is not a nonpositive solution when μ > 0.
Now, we show
The proof is complete.
Theorems 30 and 17 and Proposition 7 help us to analyze the necessary and sufficient conditions for an aperiodic solution φ of (7) to be nonnegative (or negative). For the case when φ is periodic, we have to resort to the help of the specific solution ρμχ of (7).
Theorem 31. Let be a solution of (7) with |ρ| < 2 and μ ≠ 0. Suppose π−1arccos(−ρ/2) ∈ Q and (φm, φm+1) = (α, β), for some m ∈ Z. Then φ is periodic and we have the following.
- (i)
Suppose μ > 0. Then φ cannot be a negative solution; furthermore, φ is a nonnegative solution if and only if which is the intersection of the closed half planes defined by (75).
- (ii)
Suppose μ < 0. Then φ cannot be a nonnegative solution; furthermore, φ is a negative solution if and only if
(91) -
where is the intersection of the closed half planes defined by (75).
Proof. Without loss of generality, we let m = 0. Also, let be generated by the Tracking Procedure with input (x0, y0) = (α, β). Suppose μ > 0. From the previous discussions, if (α, β) = (μ/(2 + ρ), μ/(2 + ρ)), then φ is a nonnegative solution with least period 1. If (α, β) ≠ (μ/(2 + ρ), μ/(2 + ρ)), then, by Corollary 16, φ is periodic and Γμ,ρ,f is an ellipse, where f = Γμ,ρ(α, β). Also, by Theorem 21, we can be sure that as desired. Next, we show that φ is not a nonpositive solution. First of all, by Proposition 6, φ is not nonpositive when ρ ≥ 0. Secondly, suppose φ is a nonpositive solution of (7) with ρ < 0. Then by Corollary 18, there is some m ∈ N such that xm or ym ≥ 0. If xm = ym = 0, then, by (7), xm+1 = μ > 0 which is a contradiction. Accordingly, φ is not a nonpositive solution.
Suppose μ < 0. By Corollary 22, Proposition 7, and Theorem 8, it follows that (91) holds. Also, if φ is a nonnegative solution of (7) with μ < 0, then, by Proposition 7, −φ is a solution of (7) with −μ > 0 which is not possible and this completes the proof.
Corollary 32. Let be a solution of (7) with |ρ| < 2 and μ > 0. Suppose r = π−1arccos(−ρ/2) = (n/m) ∈ Q such that 0 < r < 1 and r is irreducible. Then Φμ,ρ is a closed polygon with ω sides which is circumscribed around the ellipse and ω is either 2n or n depending on whether m is even or odd, respectively.
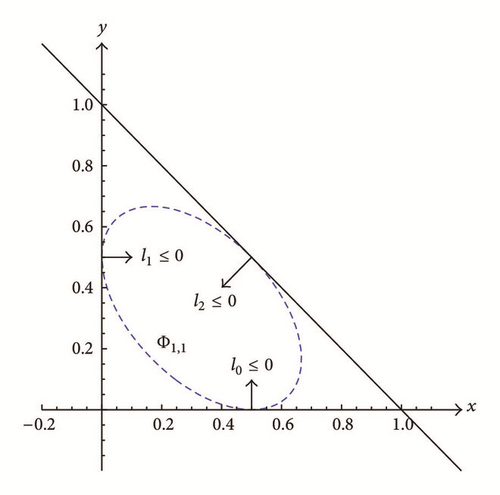
Proof. In view of Theorem 21, which is defined by the tangent lines of Furthermore, all the lines are tangent to at the points which are generated by a specific solution ρμχ of (7) with Since π−1arccos(−ρ/2) ∈ Q, by Corollary 16, ρμχ is ω-periodic where ω is dependent on n and the parity of m. Note that ω > 2. Accordingly, we see that Φμ,ρ is defined by ω distinct lines. To see Φμ,ρ is a closed polygon with ω sides which is circumscribed around , it is sufficient to show that Φμ,ρ is closed. If ρ = 0, then ρμχ is 4-periodic such that
Corollary 32 gives an explicit description of Φμ,ρ, where |ρ| < 0, and two examples for the cases (ρ, μ) = (1,1) and (ρ, μ) = (−1,1) are in Figures 20 and 21 respectively.
8. Conclusions
In the previous sections, we have analyzed the nonnegative (or negative) solution of (7) by investigating the pairs (φm, φm+1) for all m ∈ Z which are on a conic section (or degenerate one). Specifically, the orbit is the collection of (φm, φm+1) for all m ∈ Z which is a subset of a conic section and by the Tracking Procedure, (φn+1, φn+2) is uniquely determined by giving (φn, φn+1). By means of this geometric method, many qualitative properties of (7) can be obtained. In particular, we obtain the necessary and sufficient conditions for φ to be a nonnegative (or negative) solution.
- (1)
Suppose |ρ| > 2. φ is a nonnegative and periodic solution if and only if ρμ ≥ 0, and for some i ∈ Z, (φi, φi+1) = (μ/(2 + ρ), μ/(2 + ρ)). Furthermore, such φ must satisfy φj = μ/(2 + ρ) for all j ∈ Z (and hence is 1-periodic).
- (2)
Suppose |ρ| < 2. φ is a nonnegative and periodic solution if and only if μ > 0
(94) -
(where m/n is irreducible and 0 < m < n) and for some i ∈ Z, which, by Corollary 32, is a closed ω-side polygon where ω is either n or 2n depending on whether m is even or odd, respectively. Furthermore, such φ must either satisfy (φj, φj+1) = (μ/(2 + ρ), μ/(2 + ρ)) for all j ∈ Z (and hence is 1-periodic) or φ is ω-periodic.
- (3)
Suppose |ρ| = 2. If ρ = 2, then φ is a nonnegative and periodic solution if and only if μ ≥ 0, and for some m ∈ Z, φm, φm+1 ≥ 0 and (φm, φm+1) is on the x + y = μ/4 line; if ρ = −2, then φ is a nonnegative and periodic solution if and only if μ = 0, and for some n ∈ Z, φn, φn+1 ≥ 0, and (φn, φn+1) lie on the x = y line. Furthermore, such φ is either 1-periodic if φm = φm+1 (and 2-periodic if φm ≠ φm+1) when ρ = 2 or 1-periodic when ρ = −2.
- (1)
Suppose |ρ| > 2. φ is a negative and periodic solution if and only if ρμ < 0 and for some i ∈ Z, (φi, φi+1) = (μ/(2 + ρ), μ/(2 + ρ)). Furthermore, such φ must satisfy φj = μ/(2 + ρ) for all j ∈ Z (and hence is 1-periodic).
- (2)
Suppose |ρ| < 2. φ is a negative and periodic solution if and only if μ < 0
(95) -
(where m/n is irreducible and 0 < m < n) and for some i ∈ Z, , where by Corollary 32, is a closed ω-side polygon and ω is either n or 2n depending on whether m is even or odd, respectively. Furthermore, such φ must either satisfy (φj, φj+1) = (μ/(2 + ρ), μ/(2 + ρ)) for all j ∈ Z (i.e., φ is 1-periodic) or φ is ω-periodic.
- (3)
Suppose |ρ| = 2. If ρ = 2, then φ is a negative and periodic solution if and only if μ < 0, and for some m ∈ Z, φm, φm+1 < 0 and (φm, φm+1) is on the x + y = μ/4 line; if ρ = −2, then φ is a negative and periodic solution if and only if μ = 0, and for some n ∈ Z, φn, φn+1 < 0 and (φn, φn+1) lie on the x = y line. Furthermore, such φ is either 1-periodic if φm = φm+1 (and 2-periodic if φm ≠ φm+1) when ρ = 2 or 1-periodic when ρ = −2.
With the help of the Tracking Procedure, the behaviors of the solution φ of (7) can be visualized (instead of investigating each term of φ by the method of general solutions). By means of our geometric method, we may save lots of calculation and most properties of φ which may be obtained by the general solutions are also available from our geometric discoveries.
In [1–3], we conducted complete analyses on the periodic solutions (7) with μ = 1 and ρ ∈ {−1,0, 1}. By means of breaking a solution ψ into two subsequences, the companion sequence and the error sequence, we successfully show that both the companion sequence and error sequence are periodic so that ψ is periodic. Note that for ρ = −1, 0, and 1, we have arccos(−ρ/2) = π/3, π/2, and 2π/3, respectively.
The nice thing here is that by means of our geometric method, not only can we track the orbit of a solution φ on R2 easily but also we may obtain the conditions for φ to be nonnegative (or negative) quickly (especially for the case where |ρ| < 2 and φ is periodic). By [1–3], we have observed the importance of nonnegative solutions of (7) with ρ = 0, 1, and −1, respectively. However, we also realize the difficulties of analyzing the solution ζ of (7) with ρ ∉ {−1,0, 1} since the breaking of ζ into companion and error sequences is not applicable for all the solutions anymore.
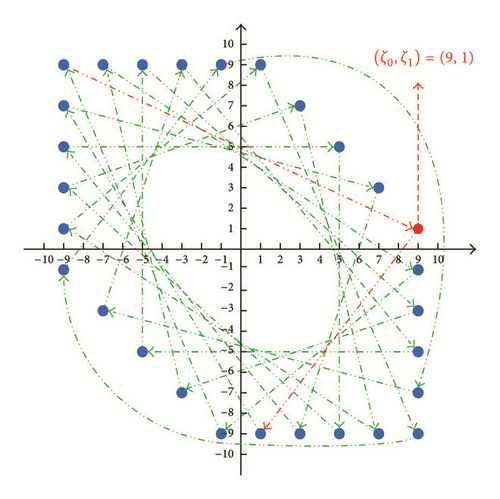
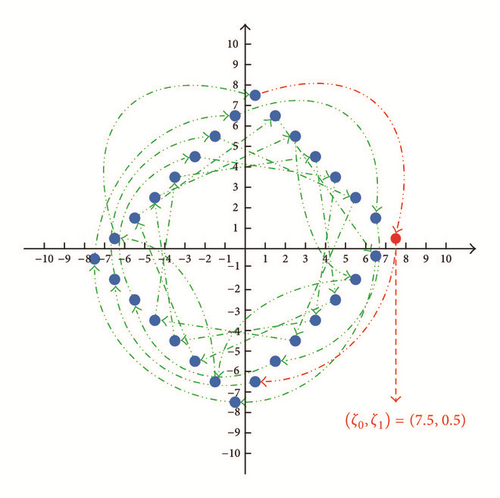
Finally, in this paper we have only touched upon one class of steady state solutions of our original neural network. Much work has to be done before the dynamic behaviors of its solutions can be fully understood. Our contributions here, however, are that elementary geometric methods can be used to explain some of the complex phenomena obtained from simulations (see, e.g., Figures 1 and 2) and these methods are also expected to be applied in other piecewise smooth dynamic systems.
Conflicts of Interest
The authors declare that there are no conflicts of interest whatsoever regarding the publication of this paper.
Acknowledgments
The third author is partially supported by the Ministry of Science and Technology, R.O.C. under Grant MOST 104-2221-E-007-061-MY3 which also complies with the declaration of conflicts of interest stated above.




