Volume 2017, Issue 1 6954902

Research Article

Open Access

Regional Frequency Analysis of Extremes Precipitation Using L-Moments and Partial L-Moments

Said Arab Khan,

Said Arab Khan

Department of Statistics, Quaid-i-Azam University, Islamabad, Pakistan qau.edu.pk

Government Degree College, Lahore, Swabi, Khyber Pakhtunkhwa, Pakistan gdcbhadarwah.com

Search for more papers by this author

Ijaz Hussain,

Corresponding Author

Ijaz Hussain

[email protected]

orcid.org/0000-0002-1586-1503

Department of Statistics, Quaid-i-Azam University, Islamabad, Pakistan qau.edu.pk

Search for more papers by this author

Tajammal Hussain,

Tajammal Hussain

orcid.org/0000-0003-2314-2223

Department of Statistics, COMSATS Institute of Information Technology, Lahore, Pakistan comsats.edu.pk

Search for more papers by this author

Muhammad Faisal,

Muhammad Faisal

Faculty of Health Studies, University of Bradford, Bradford, UK bradford.ac.uk

Bradford Institute for Health Research, Bradford Teaching Hospitals NHS Foundation Trust, Bradford, UK bradfordresearch.nhs.uk

Search for more papers by this author

Yousaf Shad Muhammad,

Yousaf Shad Muhammad

orcid.org/0000-0002-3541-6220

Department of Statistics, Quaid-i-Azam University, Islamabad, Pakistan qau.edu.pk

Search for more papers by this author

Alaa Mohamd Shoukry,

Alaa Mohamd Shoukry

Arriyadh Community College, King Saud University, Riyadh, Saudi Arabia ksu.edu.sa

Workers University, Cairo, Egypt

Search for more papers by this author

Said Arab Khan,

Said Arab Khan

Department of Statistics, Quaid-i-Azam University, Islamabad, Pakistan qau.edu.pk

Government Degree College, Lahore, Swabi, Khyber Pakhtunkhwa, Pakistan gdcbhadarwah.com

Search for more papers by this author

Ijaz Hussain,

Corresponding Author

Ijaz Hussain

[email protected]

orcid.org/0000-0002-1586-1503

Department of Statistics, Quaid-i-Azam University, Islamabad, Pakistan qau.edu.pk

Search for more papers by this author

Tajammal Hussain,

Tajammal Hussain

orcid.org/0000-0003-2314-2223

Department of Statistics, COMSATS Institute of Information Technology, Lahore, Pakistan comsats.edu.pk

Search for more papers by this author

Muhammad Faisal,

Muhammad Faisal

Faculty of Health Studies, University of Bradford, Bradford, UK bradford.ac.uk

Bradford Institute for Health Research, Bradford Teaching Hospitals NHS Foundation Trust, Bradford, UK bradfordresearch.nhs.uk

Search for more papers by this author

Yousaf Shad Muhammad,

Yousaf Shad Muhammad

orcid.org/0000-0002-3541-6220

Department of Statistics, Quaid-i-Azam University, Islamabad, Pakistan qau.edu.pk

Search for more papers by this author

Alaa Mohamd Shoukry,

Alaa Mohamd Shoukry

Arriyadh Community College, King Saud University, Riyadh, Saudi Arabia ksu.edu.sa

Workers University, Cairo, Egypt

Search for more papers by this author

First published: 07 March 2017

https://doi.org/10.1155/2017/6954902

Citations: 15

Academic Editor: Mouleong Tan

Share a link

Email
Wechat
Bluesky

Abstract

Extremes precipitation may cause a series of social, environmental, and ecological problems. Estimation of frequency of extreme precipitations and its magnitude is vital for making decisions about hydraulic structures such as dams, spillways, and dikes. In this study, we focus on regional frequency analysis of extreme precipitation based on monthly precipitation records (1999–2012) at 17 stations of Northern areas and Khyber Pakhtunkhwa, Pakistan. We develop regional frequency methods based on L-moment and partial L-moments (L- and PL-moments). The L- and PL-moments are derived for generalized extreme value (GEV), generalized logistic (GLO), generalized normal (GNO), and generalized Pareto (GPA) distributions. The Z-statistics and L- and PL-moments ratio diagrams of GNO, GEV, and GPA distributions were identified to represent the statistical properties of extreme precipitation in Northern areas and Khyber Pakhtunkhwa, Pakistan. We also perform a Monte Carlo simulation study to examine the sampling properties of L- and PL-moments. The results show that PL-moments perform better than L-moments for estimating large return period events.

1. Introduction

Hydraulic and hydrologic designs are key steps in planning of any water project. Any problem pitched at designing stage will result in the failure of design irrespective of the fact how correctly the other steps are taken. Hydrologists deal with water-related issues, problems of quantity, quality, and availability, in the society that known as hydrologic events. Stochastic methods are often used to understand sources of uncertainties in physical processes that give rise to observed hydrologic events, as precipitation and stream flow estimates depend on the past or future events. Several statistical methods offered to minimize and summarize the uncertainties of observed data and frequency analysis is one of them. It determines that how often a particular event will occur by estimating the quantile Q_T for return period of T, where Q is the magnitude of the event that occurs at a given time and location.

Dalrymple [1] proposed regional frequency analysis (RFA) method for pooling various data samples. It is index-flood procedure in hydrology. Hosking et al. [2] studied the properties of probability-weighted moments (PWMs) method based on RFA method. This method is first used by Greis and Wood [3] and Wallis [4]. Cunnane [5] reviewed twelve methods of RFA and related regional PWMs algorithm.

Initially, PWMs are considered as an alternative parameter estimation method; however, it was difficult to interpret directly as measures of the shape and scale parameters of distribution. RFA can forecast the flood flow using empirical formula and unit-hydrograph procedure Subramanya [6], and it can also estimate the quantiles of extreme precipitation.

Hosking and Wallis [7] showed that RFA method based on L-moments is used to detect homogeneous regions, to select suitable regional frequency distribution, and to predict extreme precipitation quantiles at region of interest.

Whilst L-moment methodology is effective in estimating parameters, it may not valid for predicting high return period events. Wang [8] suggested that relatively small floods might create disturbance in the analysis. To overcome such situation, a censored sample can be used as by Cunnane [9].

Wang [8] proposed partial probability-weighted moments (PPWMs) for fitting the probability distribution function to the censored sample. Partial L-moments (PL-moments) are variants of the L-moments and similar to PPWMs. PL-moments method has used in fitting generalized extreme value (GEV) distribution for censored flood samples (see Wang [8, 10, 11] and Bhattarai [12]). Bhattarai [12] found that censoring flood samples are nearly thirty percent of basic L-moments.

Shabri et al. [13] used Trim L-moments (TL-moments) for the RFA and compared its performance with L-moments. Saf [14] determined hydrologically homogeneous region and regional flood frequency estimates by using index-flood technique along with L-moments for the West Mediterranean River, Turkey. L-moments method is also used to assign a suitable regional distribution for the individual subregions and to assess their homogeneity; see Abolverdi and Khalili [15]. Hussain and Pasha [16] suggested the regional flood frequency analysis based on L-moments. They used discordancy measure for data screening and used the four-parameter Kappa distribution with 500 simulations for the heterogeneity analysis. Zakaria et al. [17] used the PL-moments technique and found another link for the homogeneity analysis. Shahzadi et al. [18] showed that the generalized normal (GNO) distribution is suitable for the regional quantile estimation at maximum return period and the GEV distribution for the overall regions at low return period based on relative RMSE and relative absolute bias. Most commonly used statistical distributions for high climate modeling are as follows: the logistic distribution with three parameters, lognormal distribution with three parameters, Log Pearson type III, GEV, and generalized Pareto (GPA) (Coles [19]; Katz et al. [20]; Abida and Ellouze [21]; Feng et al. [22]; Yang et al. [23]; Villarini et al. [24]; Zakaria et al. [17]; She et al. [25]). Moreover, GEV and GPA distributions are suitable if data contains extremes values. Over the years, the GNO, GEV, generalized logistic (GLO), and GPA distributions have been widely employed in the extreme value estimation of annual flood peaks. In this study, we aim to develop RFA method based on L- and PL-moments approach. Our proposed method can be used at all levels of regional analysis such as identification of homogeneous regions, identification, and also testing of the suitable probability regional frequency distribution based on Z-statistic and the L- and PL-moment ratio diagram and estimation of the flood quantile at site of interest. We use 17 sites of Northern areas and Khyber Pakhtunkhwa as a case study to perform the analysis.

We explain the methodology of the L-moments and PL-moments in Section 2.2. Section 2.3 shows the application of the RFA where we choose the appropriate distribution for the regional analysis. Section 3.3 provides the estimation of quantile for both, the small and large return period. The results of our simulations study will be presented in Section 4.

2. Material and Methods

2.1. Study Area and Data Sources

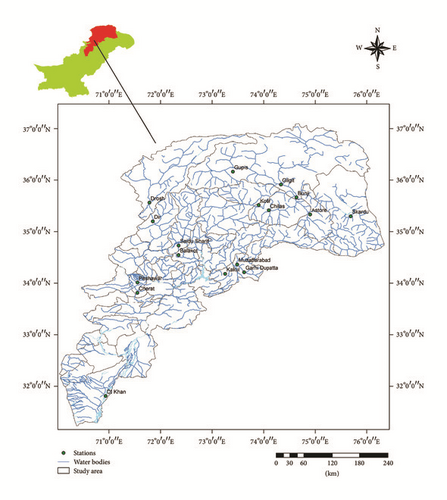
The data was collected for this study from Karachi Data Processing Center through Pakistan Meteorological (PMD) Islamabad. Monthly precipitation data has been recorded from 1999 to 2012. There are 17 meteorological stations of Northern areas and Khyber Pakhtunkhwa, Pakistan. These stations are full precipitation regions that affect areas in Pakistan, where water is essential for hydropower and flood plains. Figure 1 shows the location of the study area and geographic distribution of precipitation stations. There is no missing value in this data set.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Locations of Northern areas and Khyber Pakhtunkhwa and the meteorological stations (x axis indicates Longitude [E]; y axis indicates Latitude [N]).

2.2. Statistical Methods

2.2.1. The L-Moments

Conventional moments method may be used for estimating the parameters of probability distribution. However, this approach has some serious drawbacks. Ratio of moment estimators is biased and often assumption of being normally distributed is violated, Wallis et al. [26]. Furthermore, it is sensitive to outliers, Pearson [27]. Therefore, it is unreliable for skewed distributions.

Hosking [28] proposed L-moments approach to overcome the above problems. The L-moments may precisely describe the statistical properties of hydrological information, and it can write as a linear function of the PWMs. The PWMs of order r were properly described by Greenwood et al. [29] as

(1)

where r, s, and p are the real numbers and F(x) is the cumulative distribution function of x. A functional case is

(2)

Therefore,

(3)

where F = F(x) is the cumulative distribution function of a random variable x and r is a nonnegative integer of the real number that is r = 0,1, 2,3, …. Therefore the first four L-moments, which are the linear combinations of the PWMs, are

(4)

The L-moments have no units of measurement, which are called the L-moments ratios. The L-moments ratios, proposed by Hosking [28], are computed as

(5)

where τ represents the L-coefficient of variation (L-Cv), τ₃ represents the L-coefficient of skewness (L-Cs), and τ₄ represents the L-coefficient of kurtosis (L-Ck).

The arranged sample is given as x₍₁₎ ≤ x₍₂₎ ≤ x₍₃₎ ⋯ ≤x_(n). Wang [8] stated that the statistic

(6)

is an unbiased estimator of β_r.

(7)

where l₁, l₂, l₃, and l₄ are the first four L-moments of the sample. And similarly

(8)

are the sample L-moments ratios.

2.2.2. The Partial L-Moments

Wang [8, 10, 11] introduced a concept of partial probability-weighted moments (PPWMs) that will estimate the higher quantiles of flood flows. Data can be censored to the right tail or left tail.

Initially, PPWMs were to take out the smaller values from the process of distribution fitting because such values have slight influence on the frequency analysis and are nuisance to the fitting process.

The left tail PPWMs are defined by Wang [8, 11] as

(9)

where F₀ = F(x₀) which is the lower limit of the censored observations and x₀ is the censoring threshold value.

The PPWMs elongated form described by Wang [10] are to be given a censored sample as

(10)

If the value of F₀ is starting from the zero, then the result of PPWMs will be the same as the usual PWMs. As x₍₁₎ ≤ x₍₂₎ ≤ x₍₃₎ ⋯ ≤x_(n) is the arranged sample, Wang [10] describes the unbiased estimator of

(11)

where

(12)

The censoring level, F₀, is the prior selection of the number of censored sample data. The procedure that determines the number of sample data points are to be censored:

(13)

where n₀ and n are the lengths of sample which are to be censored and uncensored, respectively. Similarly, x₀ is the highest value of the censored sample. The first four PL-moments for the PPWMs are

(14)

Similarly, the PL-moments ratios can be written as

(15)

where

, and

denote the partial L-coefficient of variation (PL-Cv), partial L-coefficient of skewness (PL-Cs), and partial L-coefficient of kurtosis (PL-Ck), respectively. Therefore, the first four sample PL-moments can be computed as

(16)

And the first four sample PL-moments ratios can be computed as

(17)

where

, and

represent the sample partial L-moments ratios of the PL-Cv, PL-Cs, and PL-Ck, respectively. The derivation is L-moment and PL-moments are given in Appendix. In the present study, different level of censoring threshold is selected.

2.3. Regional Frequency Analysis

Hosking and Wallis [7, 30] identified the following four steps to explain the procedure of the RFA:

(1)
Data screening
(2)
Designing of the homogeneous region
(3)
Selection of an appropriate probability distribution
(4)
Parameters estimation of the appropriate probability distribution

2.3.1. Data Screening

We screened data anomalies before applying any statistical analysis.

2.3.2. Discordance Test

Hosking and Wallis [7] suggested a discordancy measure (D_i) test that recognizes the locations where sample L-moments are marked contrarily from the most other locations. Locations with the large flaws in the data will be flagged as discordant.

The discordancy test for a region containing N locations, for site i, is proposed by Hosking and Wallis [7] as follows:

(18)

where u_i is the vector containing the three sample L-moments ratios for the site i expressed as

(19)

is the average vector of u_i for the overall region that is

(20)

and S is the covariance matrix for the sample that can be expressed as

(21)

Broadly speaking, a location or a site is considered to be discordant from the whole region or group if the value of D_i is larger than the critical value.

2.3.3. Heterogeneity Test

The homogeneity measure (H_j) identifies homogenous regions, Hosking and Wallis [7]. It is also useful to tag the locations if they are plausible to handle as a homogeneous region. It estimates the amount of heterogeneity in the overall region. The heterogeneity test (H_j) is computed as

(22)

where μ_vj and σ_vj are representing the mean and standard deviation of the simulated V_j values. Also,

(23)

Here,

, and

are region average L-moments or PL-moments ratios. We assessed the heterogeneity of a region as suggested by Hosking and Wallis [7]:

Region is acceptably homogeneous if H < 1.
Region is possibly heterogeneous if 1 ≤ H < 2.
Region is definitely heterogeneous if H ≥ 2.

2.4. Selection of the Appropriate Probability Distribution

Hosking and Wallis [7] proposed two approaches to select the distribution that fitted best the data: the L-moment ratios diagram and the Z-test. The L-moment ratios diagram is using the unbiased estimators, Hosking [28], Stedinger et al. [31], Vogel and Fennessey [32], and Hosking [33]. The L-moments ratio diagram is a plot of the computed values L-Cs and the observed values L-Ck of the distribution function. The curves indicate the hypothetical connections between L-Cs and L-Ck of the candidate distribution. The L-moment ratio diagrams have been proposed for discriminating between the candidate probability distributions in describing the regional information (Hosking [28]; Stedinger et al. [31]; Hosking and Wallis [7]). The L-moments ratio diagrams have been used as a component of probability distribution process for regional information (Schaefer [34]; Pearson [35]; Vogel and Fennessey [32], Vogel et al. [36]; Chow and Watt [37]; ÖnÖz and Bayazit [38]; Vogel and Wilson [39]; Peel et al. [40]).

Hosking and Wallis [7] suggested a measure to see how well the L-Cs and L-Ck of the fitted probability distribution match the regional average L-Cs and L-Ck of the observed information.

The measure goodness of fit for every single selected probability distribution is computed as follows:

(24)

where

represents the value of the L-Ck of the fitted distribution,

represents the weighted regional average L-Ck, and σ₄ represents standard deviation of the

, which is obtained from the simulation of the Kappa probability distribution.

If the computed value of Z^Dis is equal to zero, the probability distribution will be the most suitable fit. If the computed value of Z-statistic is less than 1.64 at 90% confidence level (i.e., |Z^Dis| ≤ 1.64), it will indicate that the distribution qualifies the goodness of fit criteria. If there are more than one distribution that qualify the criteria, the most suitable distribution has the minimum |Z^Dis| value.

3. Estimation

The sites’ information and statistic by using L-moments for the present study are presented in Table 1. In Table 1, mean represents the first sample L/PL-moments and t, t₃, and t₄ are the sample L/PL-moments ratios of the L-Cv/PL-Cv, L-Cs/PL-Cs, and L-Ck/PL-Ck, respectively. The lower level censoring threshold is selected from 10 to 23%. Table 2 expresses the feasible threshold values according to the percentile technique along with Average Annual Occurrence Number (AAON). Jiang et al. [41] and Yuguo [42] suggested that the optimal threshold can be obtained if the values of AAON lie between 1 and 2. Table 2 shows that 90th percentile observations are suitable for the optimum threshold selection of most of areas in the present study. We have 168 values in each station; according to the above table, Astore station has 3.2 threshold values due to which 16 values are being censored in 168. According to censored level, 10.2% censored level was selected. Similarly, 10.5% was selected for Balakot and Muzaffarabad. According to this process, maximum threshold level 22.3% was selected for Gupis. By using the above process for each station, 17 different censoring levels were selected. So we decide that the range from 10 to 23% of censoring level should be kept for selecting threshold values.

Table 1. Statistics of annual extreme monthly precipitation for study region based on L-moments and PL-moments.

Sites	L-moments				PL-moments
Sites	Mean	t	t₃	t₄	Mean	t	t₃	t₄
Astore	37.624	0.518	0.366	0.193	41.752	0.467	0.377	0.183
Balakot	120.450	0.478	0.322	0.192	133.259	0.428	0.335	0.198
Bunji	14.297	0.609	0.456	0.259	16.339	0.553	0.450	0.257
Chilas	15.091	0.585	0.392	0.194	17.603	0.516	0.375	0.200
Cherat	49.038	0.580	0.375	0.162	55.289	0.526	0.355	0.161
DI khan	28.885	0.689	0.516	0.262	32.351	0.651	0.487	0.250
Dir	105.694	0.432	0.216	0.098	116.741	0.378	0.222	0.097
Drosh	45.284	0.525	0.317	0.136	50.316	0.474	0.307	0.137
Garhi Dupatta	111.352	0.454	0.227	0.111	123.374	0.398	0.229	0.120
Gilgit	12.677	0.591	0.412	0.228	14.290	0.539	0.399	0.239
Gupis	23.446	0.678	0.529	0.331	30.299	0.583	0.506	0.350
Kakul	99.431	0.453	0.247	0.102	110.068	0.399	0.254	0.093
Kotli	95.070	0.542	0.332	0.136	106.903	0.487	0.314	0.138
Muzaffarabad	118.439	0.459	0.284	0.182	131.122	0.405	0.301	0.194
Peshawar	46.216	0.572	0.398	0.216	51.761	0.520	0.392	0.222
Saidu Sharif	85.667	0.455	0.265	0.181	94.978	0.399	0.283	0.200
Skardu	20.438	0.616	0.4564	0.238	22.885	0.570	0.444	0.231

Table 2. Precipitation threshold selection in GPA distribution for 17 stations.

Station	80th	90th	95th	97.5th	99th
Astore
Threshold	9.8	3.2	0.2	0	0
AAON	2.43	1.21	0.64	0.43	0.43
Balakot
Threshold	32.5	14.8	5.1	3	0
AAON	2.43	1.29	0.57	0.29	0.14
Muzaffarabad
Threshold	30.4	11.8	5	1	0
AAON	2.5	1.21	0.57	0.29	0.21
Garhi Dupatta
Threshold	28.8	10	3.8	0	0
AAON	2.43	1.21	0.57	0.29	0.29
Dir
Threshold	31	20	5	0.05	0
AAON	2.43	1.21	0.57	0.29	0.21
Kakul
Threshold	28.9	13.4	2.1	0.5	0
AAON	1.64	1.29	0.57	0.29	0.21
Kotli
Threshold	13	6	0.05	0	0
AAON	2.43	1.35	0.57	0.36	0.36
Saidu Sharif
Threshold	25.6	8.3	2	0	0
AAON	2.43	1.21	0.57	0.36	0.36
cherat
Threshold	5	0.05	0	0	0
AAON	2.43	1.43	0.93	0.93	0.93
Peshawar
Threshold	6	0.05	0	0	0
AAON	2.43	1.29	0.57	0.57	0.57
Drosh
Threshold	7.6	1.5	0.2	0.05	0
AAON	2.43	1.21	0.57	0.5	0.21
D I Khan
Threshold	0.3	0	0	0	0
AAON	2.57	1.29	1.29	1.29	1.29
Gupis
Threshold	0	0	0	0	0
AAON	2.71	2.71	2.71	2.71	2.71
Skardu
Threshold	2	0.3	0	0	0
AAON	2.43	0.71	0.71	0.71	0.71
Chilas
Threshold	1	0.5	0	0	0
AAON	1.71	1.07	1.07	1.07	1.07
Bunji
Threshold	1.3	0	0	0	0
AAON	1.5	1.5	1.5	1.5	1.5
Gilgit
Threshold	1.2	0.05	0	0	0
AAON	2.43	1.35	0.71	0.71	0.71

3.1. Regional Frequency Analysis

The following four steps are considered as prerequisite for frequency analysis, Hosking and Wallis [7, 30]:

(1)
Data screening
(2)
Designing of the homogeneous region
(3)
Selection of an appropriate probability distribution
(4)
Parameters estimation of the appropriate probability distribution

3.1.1. Data Screening

In this study, we use secondary data after carefully examining all locations for abnormalities and missing observations. Therefore, we use 14 years of data for RFA that were obtained from seventeen locations.

3.1.2. Discordance Test

Table 3 shows D_i result of (18) for 17 locations of this study region. It can be observed from the results of L/PL-moments in Table 3 that the value of D-statistic varies from 0.07 to 2.44. If D_i is greater than 3, the location is considered to be discordant from the rest of the regional data, Hosking and Wallis [7]. In this study region, no location is diagnosed as discordant (D_i ≥ 3). Therefore, we use all data for the development of the RFA based on L-moments and PL-moments.

Table 3. Discordance test result based on L-moments and PL-moments.

Name of site	L-moments (D_i)	PL-moments (D_i)
Astore	2.05	2.44
Balakot	1.42	0.85
Bunji	0.55	0.60
Chilas	0.29	0.07
Cherat	0.79	0.64
DI khan	1.29	1.90
Dir	0.82	0.86
Drosh	0.51	0.43
Garhi Dupatta	1.43	1.33
Gilgit	0.26	0.59
Gupis	2.37	2.31
Kakul	0.82	1.22
Kotli	0.77	0.59
Muzaffarabad	0.99	0.85
Peshawar	0.07	0.08
Saidu Sharif	1.91	1.57
Skardu	0.67	0.65

3.1.3. Regional Heterogeneity Measure

The next step is the formation of the homogeneous region, which is conventionally tougher and needs the higher number of subjective judgments. The homogeneity conditions are defined as the locations that have the same frequency distributions.

For the present study area, realization of the Kappa probability distribution is used to conduct the heterogeneity test based on the L-moments and PL-moments.

Number of simulations are 10,000 for computing the heterogeneity. We computed the regional average L-moments ratios, the regional PL-moments ratios, and the corresponding parameter values of the fitted Kappa probability distribution (see Table 4). Table 4 shows the results of the heterogeneity measure using L-moments and PL-moments methods. It can be observed from Table 4 that the different values for the H-statistic are −0.41, −1.60, and −2.89 based on L-moments and −0.06, −1.8, and −3.17 based on PL-moments. Therefore, we concluded that, by comparing these results and the heterogeneity conditions, study region is acceptably homogeneous for L-moments and PL-moments. No further subdivisions of the present study are necessary.

Table 4. Heterogeneity measures for the study region based on L-moments and PL-moments.

Heterogeneity measures	L-moment	PL-moment
Heterogeneity measure H₁
Observed standard deviation of group L-Cv	0.078	0.077
Simulated mean of standard deviation of group L-Cv	0.084	0.077
Simulated standard deviation of standard deviation of group L-Cv	0.015	0.014
Value of the heterogeneity measure H₁	−0.410	−0.060

Heterogeneity measure H₂
Observed average of L-Cv/L-skewness distance	0.105	0.139
Simulated mean of average L-Cv/L-skewness distance	0.141	0.139
Simulated standard deviation of average L-Cv/L-skewness distance	0.023	0.022
Value of the heterogeneity measure H₂	−1.600	−1.800

Heterogeneity measure H₃
Observed average of L-skewness/L-kurtosis distance	0.094	0.088
Simulated mean of average L-skewness/L-kurtosis distance	0.175	0.176
Simulated standard deviation of average L-skewness/L-kurtosis distance	0.028	0.028
Value of the heterogeneity measure H₃	−2.890	−3.170

3.2. Fitting Appropriate Probability Distribution

After homogeneity analysis of the study area, a suitable probability distribution is required for the RFA. The objective is not only to recognize a suitable probability distribution for RFA but also to observe a probability distribution that will provide robust quantile estimate for each location and for the regional growth cure. List of candidate probability distributions for RFA is GLO, GEV, GPA, and GNO.

We plotted L-moments and PL-moments diagrams for preliminary evaluation of the probability distribution for the study area.

Figure 2 illustrates an analogy of the observed and hypothetical relationships of the probability distribution. Figure 2 shows that GLO distribution is not a suitable candidate for the L-moments and PL-moments.

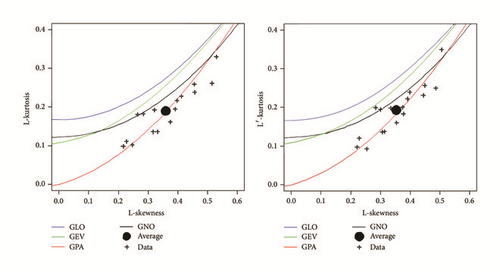
Interestingly, both analyses of the L-moments and the PL-moments diagram show that the sample average values are appropriately distinguished by the hypothetical L-moments and PL-moments for GPA and GNO distributions.

However, it is hard to find a suitable probability distribution that fits most of the regional observed data. Table 5 shows the goodness of fit test results for candidate probability distributions.

Table 5. Z-test result for the goodness of fit.

Method	GLO	GEV	GNO	GPA
L-moments	1.96	1.38	0.61	−0.42
PL-moments	1.77	1.19	0.43	−0.61

Table 5 shows that GLO distribution failed the goodness of fit test for both L-moments and for PL-moments methods as the calculated value of the Z-test for the GLO distribution is larger than the critical value of 1.64 (at 90% confidence level).

It has been observed that the computed values of |Z^Dis| are less than 1.64 (at 90% confidence level), namely, GEV, GNO, and GPA distributions. However, GEV, GNO, and GPA distributions are suitable for regional distribution based on L-moments and PL-moments methods and for obtaining the future estimates of the quantile.

Further, it can be noted that GPA distribution is suitable for L-moments method (lowest critical |Z^Dis| value). Similarly, GNO distribution is suitable for PL-moments method (lowest critical value). Table 6 shows the estimates of the regional parameters for L-moments and PL-moments for the suitable probability distribution.

Table 6. Regional parameters for the three candidate distributions for L-moments and PL-moments.

Method	Distribution	Parameters
Method	Distribution	ξ	α	K
L-moments	GEV	0.4660	0.5644	−0.2751
	GNO	0.6671	0.7565	−0.7594
	GPA	−0.0551	0.9944	−0.0575

PL-moments	GEV	0.5220	0.5116	−0.2686
	GNO	0.7046	0.6837	−0.7487
	GPA	0.0478	0.9073	−0.0472

3.3. Estimation of the Quantiles

The regional quantile estimates , with varying nonexceedance probability F for the GNO, GEV, and GPA distributions, are presented in Table 7 based on L-moments and PL-moments. Quantile function is normally represented as for fitted regional frequency distribution. The quantile estimate at location i is established by joining the estimate of μ_i and q(·).

Table 7. Regional quantile estimates with nonexceedance probability F.

Method	Distribution	F
Method	Distribution	0.1000	0.5000	0.8000	0.9000	0.9500	0.9800	0.9900	0.9975	0.99875	0.9990
L-moments	GEV	0.0454	0.6836	1.5139	2.2247	3.0591	4.4161	5.6871	9.0748	11.3165	12.1338
	GNO	0.0473	0.6671	1.5585	2.3072	3.1448	4.4098	5.4997	8.0676	9.5666	10.0823
	GPA	0.0500	0.6481	1.6217	2.3931	3.1958	4.3073	5.1878	7.0578	8.0502	8.3782

PL-moments	GEV	0.1397	0.7190	1.4670	2.1034	2.8469	4.0497	5.1703	8.1363	10.086	10.7950
	GNO	0.1412	0.7046	1.5062	2.1752	2.9203	4.0410	5.0032	7.2608	8.5739	9.0249
	GPA	0.1436	0.6871	1.5649	2.2547	2.9674	3.9460	4.7149	6.3304	7.1786	7.4577

Mathematical form of the quantile estimate with nonexceedance probability F is

(25)

The regional growth curves for the GEV, GNO, and GPA distributions are shown in Figure 3.

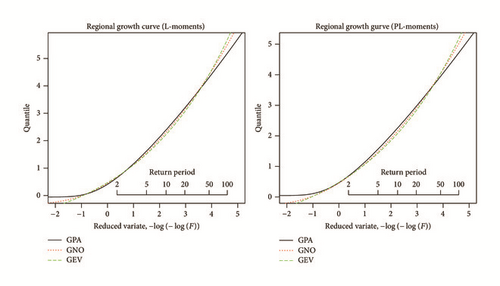
Figure 3 shows the regional growth curves of each candidate distribution for L-moments and PL-moments. GEV, GNO, and GPA distributions are approximately identical up until 100-year return period (F = 0.99) for both L-moments and PL-moments. However, afterward the growth curves of the GPA distribution lie below the GEV and GNO distributions.

Therefore, it is necessary to assess the performance of regional quantile estimates.

4. Accuracy of the Estimated Quantiles and the Regional Growth Curve

A Monte Carlo simulation is designed to assess accuracy of the regional quantile estimates that are obtained by the RFA. We use logical L-moments algorithm that has been reported by Hosking and Wallis [7] in Section 6.4. This algorithm takes samples from a region that has comparable characteristics as of the actual region, such as having the same record length, same number of locations, and the regional L-moments ratios. The area used for simulation should report the plausible heterogeneity in the area and intersite dependency if exist (Hosking and Wallis [7]). In the repeated sampling procedure, the quantile estimates are computed for the different nonexceedance probabilities. Suppose that, at mth repetition and location i, quantile estimate can be written as

for the nonexceedance probability F. The relative error for this estimator is

(26)

The bias and the RMSE of the above quantity over all M repetition are

(27)

Also, for the estimated quantile, the regional average bias and the relative RMSE are

(28)

We use empirical quantities of quantile distribution for the assessment analysis that can be computed by taking the ratio of estimated to true values,

for the quantile, and

for the regional growth curves. Therefore, 90% of the regional growth curve lie in between the interval:

(29)

Inverting the expression for q_i(F), we have

(30)

The 90% confidence interval limits show the measure of variation between the estimated and the true quantiles. These limits provide the expected magnitude of errors in the estimated quantiles and the regional growth curves.

We computed L-moments ratios to find the most suitable distribution and the precision of original growth curves. The correlation between the study region sites varies from −0.05 to 0.86 with an average of 0.40. Therefore, we use algorithm from Table 6.1 of Hosking and Wallis [7].

We held out the analysis for recurrence of different years. We run 10,000 simulations with sample size of 30, 60, and 90 in each case. The whole process is repeated for GEV, GNO, and GPA distributions. From these repetitions, we computed several performance measures, such as the regional average relative bias, regional average RMSE, regional average relative RMSE, and the error bounds for the estimated regional growth curves for the selected nonexceedance probability F. Overall results for the suitable probability distribution for both methods are presented in Tables 8, 9, and 10 for sample size of 30, 60, and 90, respectively.

Table 8. Accuracy measure of the estimated growth curves of the region for sample size of 30.

Method	Distribution	F	0.1	0.5	0.8	0.9	0.95	0.98	0.99	0.995	0.998	0.999
L-moments	GEV	B^R(F)	−0.5400	−19.7674	−19.5328	−19.3602	−19.1579	−18.8659	−18.6376	−18.4097	−18.1165	−17.9056
		R(F)	0.0900	0.0695	0.0963	0.1952	0.3334	0.6038	0.9057	1.3261	2.1337	3.0048
		R^R(F)	1.9873	0.1019	0.0635	0.0876	0.1090	0.1369	0.1595	0.1839	0.2191	0.2478
		LBE^∗	−2.0937	0.8829	0.9296	0.8842	0.8411	0.7862	0.7460	0.7065	0.6557	0.6177
		UBE^∗	1.8714	1.1949	1.1208	1.1580	1.1884	1.2244	1.2516	1.2818	1.3285	1.3683

L-moments	GNO	B^R(F)	0.8124	−19.6279	−19.3846	−19.2837	−19.1816	−19.0506	−18.9573	−18.8699	−18.7636	−18.6899
		R(F)	0.0986	0.0696	0.0917	0.2051	0.3520	0.6027	0.8421	1.1312	1.6008	2.0312
		R^R(F)	2.0766	0.1045	0.0587	0.0889	0.1120	0.1368	0.1533	0.1686	0.1878	0.2016
		LBE^∗	−2.1331	0.8683	0.9271	0.8780	0.8379	0.7958	0.7691	0.7453	0.7172	0.6978
		UBE^∗	1.6569	1.1974	1.1077	1.1569	1.1954	1.2355	1.2615	1.2851	1.3149	1.3369

L-moments	GPA	B^R(F)	3.8654	−19.4351	−19.3564	−19.3226	−19.2616	−19.1706	−19.1060	−19.0506	−18.9966	−18.9727
		R(F)	0.1242	0.0669	0.0998	0.2136	0.3552	0.5968	0.8313	1.1188	1.5941	2.0368
		R^R(F)	2.4785	0.1033	0.0614	0.0892	0.1111	0.1386	0.1602	0.1833	0.2162	0.2431
		LBE^∗	−2.5192	0.8591	0.9215	0.8817	0.8444	0.7979	0.7646	0.7327	0.6919	0.6623
		UBE^∗	1.4272	1.1911	1.1115	1.1588	1.1976	1.2459	1.2841	1.3257	1.3859	1.4367

PL-moments	GEV	B^R(F)	−0.2662	−19.7059	−19.4770	−19.3340	−19.1600	−18.8996	−18.6909	−18.4797	−18.2052	−18.0066
		R(F)	0.5379	0.0687	0.0947	0.2023	0.3467	0.6171	0.9087	1.3058	2.0551	2.854
		R^R(F)	3.8117	0.0948	0.0649	0.0960	0.1210	0.1508	0.1736	0.1977	0.2324	0.2609
		LBE^∗	−7.7814	0.8892	0.9252	0.8725	0.8259	0.7697	0.7296	0.6911	0.6417	0.6050
		UBE^∗	4.5516	1.1827	1.1207	1.1716	1.2117	1.2554	1.2881	1.3211	1.3693	1.4104

PL-moments	GNO	B^R(F)	3.5142	−19.5922	−19.3485	−19.2704	−19.1894	−19.0806	−19.0003	−18.9235	−18.8284	−18.7617
		R(F)	0.6203	0.0689	0.0939	0.2141	0.3644	0.6143	0.8483	1.1272	1.5747	1.9809
		R^R(F)	4.3522	0.0971	0.0626	0.0980	0.1238	0.1504	0.1675	0.1831	0.2024	0.2162
		LBE^∗	−10.618	0.8772	0.9204	0.8655	0.8233	0.7800	0.7530	0.7290	0.7012	0.6822
		UBE^∗	4.6353	1.1849	1.1122	1.1734	1.2189	1.2653	1.2949	1.3218	1.3546	1.3780

PL-moments	GPA	B^R(F)	12.123	−19.4300	−19.3238	−19.3113	−19.2716	−19.2046	−19.1555	−19.1141	−19.0768	−19.0649
		R(F)	0.8513	0.0666	0.1041	0.2250	0.3684	0.6021	0.8215	1.0853	1.5144	1.9094
		R^R(F)	5.8811	0.0962	0.0669	0.0996	0.1233	0.1509	0.1720	0.1941	0.2258	0.2518
		LBE^∗	−17.507	0.8698	0.9130	0.8680	0.8299	0.7846	0.7524	0.7220	0.6831	0.6552
		UBE^∗	4.7307	1.1791	1.1189	1.1774	1.2215	1.2739	1.314	1.3567	1.4195	1.4722

Table 9. Accuracy measure of the estimated growth curves of the region for sample size of 60.

Method	Distribution	F	0.1	0.5	0.8	0.9	0.95	0.98	0.99	0.995	0.998	0.999
L-moments	GEV	B^R(F)	−1.3271	−19.4230	−19.3551	−19.3241	−19.2649	−19.1612	−19.0736	−18.9839	−18.8690	−18.7888
		R(F)	0.0846	0.0624	0.0851	0.1873	0.3250	0.5841	0.8652	1.2505	1.9839	2.7721
		R^R(F)	1.9155	0.0833	0.0612	0.0855	0.1024	0.1213	0.1360	0.1523	0.1770	0.1983
		LBE^∗	−1.9593	0.8756	0.9254	0.8851	0.8491	0.8074	0.7796	0.7501	0.7118	0.6834
		UBE^∗	1.6242	1.1675	1.1015	1.1472	1.1879	1.2309	1.2678	1.3038	1.3659	1.4141

L-moments	GNO	B^R(F)	0.8417	−19.3335	−19.2795	−19.2984	−19.2999	−19.2879	−19.2742	−19.2593	−19.2399	−19.2264
		R(F)	0.0968	0.0634	0.0858	0.2000	0.3439	0.5850	0.8123	1.0845	1.5235	1.9239
		R^R(F)	2.1055	0.0881	0.0582	0.0861	0.1050	0.1235	0.1354	0.1463	0.1599	0.1699
		LBE^∗	−2.2887	0.8647	0.9244	0.8794	0.8466	0.8141	0.7957	0.7798	0.7597	0.7443
		UBE^∗	1.5863	1.1714	1.096	1.1511	1.1934	1.2405	1.2666	1.2939	1.3253	1.3505

L-moments	GPA	B^R(F)	4.6371	−19.2512	−19.2631	−19.3160	−19.3417	−19.3606	−19.3745	−19.3933	−19.4306	−19.4708
		R(F)	0.1280	0.0624	0.0950	0.2094	0.3468	0.5740	0.7903	1.0536	1.4878	1.8928
		R^R(F)	2.6442	0.0915	0.0614	0.0882	0.1064	0.1270	0.1429	0.1599	0.1849	0.2059
		LBE^∗	−3.8088	0.8628	0.9186	0.8815	0.8510	0.8167	0.7924	0.7703	0.7422	0.7178
		UBE^∗	1.4699	1.1721	1.1020	1.1534	1.1925	1.2454	1.2791	1.3236	1.3869	1.4405

PL-moments	GEV	B^R(F)	−1.6968	−19.3984	−19.3601	−19.3623	−19.3319	−19.2576	−19.1861	−19.1081	−19.0026	−18.9255
		R(F)	0.5431	0.0596	0.0888	0.1978	0.3366	0.5844	0.8417	1.1838	1.8179	2.4868
		R^R(F)	3.8656	0.0783	0.0634	0.095	0.1166	0.1387	0.1541	0.1700	0.1928	0.2120
		LBE^∗	−9.2921	0.8907	0.9201	0.8750	0.8403	0.7984	0.7714	0.7434	0.7043	0.6783
		UBE^∗	5.3553	1.1521	1.1099	1.1664	1.2098	1.2572	1.2869	1.3216	1.3697	1.4105

PL-moments	GNO	B^R(F)	2.3785	−19.3306	−19.2979	−19.3417	−19.3628	−19.3678	−19.3617	−19.3509	−19.3331	−19.3185
		R(F)	0.6278	0.0601	0.0911	0.2100	0.3523	0.5804	0.788	1.0303	1.4113	1.7516
		R^R(F)	4.3743	0.0812	0.0623	0.0965	0.1186	0.1391	0.1513	0.1618	0.1742	0.1830
		LBE^∗	−12.083	0.8856	0.9188	0.8709	0.8389	0.8061	0.7870	0.7706	0.7517	0.7380
		UBE^∗	5.2707	1.1561	1.1059	1.1704	1.2152	1.2613	1.2898	1.3138	1.3361	1.356

PL-moments	GPA	B^R(F)	11.187	−19.2590	−19.2910	−19.3681	−19.4084	−19.4322	−19.4404	−19.4463	−19.4560	−19.4673
		R(F)	0.8596	0.0597	0.1009	0.2229	0.3581	0.5615	0.7391	0.9418	1.2558	1.5341
		R^R(F)	5.8310	0.0840	0.0660	0.0991	0.1195	0.1391	0.1522	0.1650	0.1828	0.1971
		LBE^∗	−18.977	0.8800	0.9127	0.8699	0.8413	0.8098	0.7912	0.7682	0.7447	0.7255
		UBE^∗	5.1281	1.1551	1.1117	1.1769	1.2173	1.2615	1.2887	1.3227	1.3609	1.3899

Table 10. Accuracy measure of the estimated growth curves of the region for sample size of 90.

Method	Distribution	F	0.1	0.5	0.8	0.9	0.95	0.98	0.99	0.995	0.998	0.999
L-moments	GEV	B^R(F)	−0.0117	−19.4226	−19.3109	−19.2926	−19.2542	−19.1809	−19.1151	−19.0448	−18.9497	−18.8790
		R(F)	0.0787	0.0556	0.0823	0.1850	0.3151	0.5459	0.7840	1.0989	1.6793	2.2883
		R^R(F)	1.7329	0.0814	0.0544	0.0832	0.1031	0.1238	0.1381	0.1525	0.1727	0.1892
		LBE^∗	−1.9303	0.8935	0.9287	0.8885	0.8587	0.8246	0.8006	0.7772	0.7463	0.7229
		UBE^∗	1.5717	1.1499	1.0973	1.1461	1.1804	1.2156	1.2393	1.2635	1.2966	1.3242

L-moments	GNO	B^R(F)	1.5851	−19.3606	−19.2517	−19.2695	−19.2747	−19.2678	−19.2569	−19.2437	−19.2245	−19.2098
		R(F)	0.0917	0.0567	0.0846	0.1967	0.3305	0.5446	0.7392	0.9660	1.3223	1.6400
		R^R(F)	1.9328	0.0850	0.0543	0.0853	0.1052	0.1237	0.1347	0.1442	0.1554	0.1632
		LBE^∗	−2.3268	0.8848	0.9261	0.8844	0.8568	0.8301	0.8139	0.8000	0.7833	0.7722
		UBE^∗	1.5168	1.1542	1.0942	1.1489	1.1851	1.2197	1.2401	1.2575	1.2779	1.2925

L-moments	GPA	B^R(F)	4.9081	−19.2995	−19.2417	−19.2865	−19.3078	−19.3175	−19.3195	−19.3209	−19.3256	−19.3330
		R(F)	0.1234	0.0571	0.0935	0.2081	0.3365	0.5322	0.7054	0.9053	1.2180	1.4975
		R^R(F)	2.4688	0.0882	0.0576	0.0870	0.1054	0.1239	0.1364	0.1489	0.1660	0.1798
		LBE^∗	−4.5353	0.8783	0.9210	0.8838	0.8594	0.8326	0.8141	0.7961	0.7731	0.7557
		UBE^∗	1.4833	1.1574	1.0996	1.1532	1.1870	1.2223	1.2467	1.2711	1.3044	1.3312

PL-moments	GEV	B^R(F)	−0.0877	−19.4145	−19.3060	−19.3062	−19.2847	−19.2278	−19.1698	−19.1038	−19.0100	−18.9374
		R(F)	0.5458	0.0565	0.0855	0.1963	0.3338	0.5712	0.8090	1.1156	1.6650	2.2276
		R^R(F)	3.9079	0.0784	0.0585	0.0934	0.1172	0.1406	0.1558	0.1703	0.1897	0.2050
		LBE^∗	−10.190	0.8983	0.9236	0.8765	0.8431	0.8067	0.7818	0.7579	0.7271	0.7041
		UBE^∗	5.8730	1.1448	1.1036	1.1652	1.2081	1.2504	1.2771	1.3026	1.3364	1.3623

PL-moments	GNO	B^R(F)	3.8414	−19.3665	−19.2536	−19.2859	−19.3044	−19.3102	−19.3057	−19.2966	−19.2804	−19.2665
		R(F)	0.6308	0.0578	0.0896	0.2088	0.3488	0.5690	0.7659	0.9926	1.3434	1.6524
		R^R(F)	4.4651	0.0819	0.0596	0.0961	0.1193	0.1405	0.1526	0.1628	0.1744	0.1822
		LBE^∗	−13.011	0.8910	0.9192	0.8716	0.8411	0.8122	0.7949	0.7801	0.7634	0.7519
		UBE^∗	5.6756	1.1491	1.1030	1.1693	1.2128	1.2539	1.2775	1.2974	1.3197	1.3347

PL-moments	GPA	B^R(F)	12.6398	−19.3142	−19.2484	−19.3077	−19.3404	−19.3589	−19.3637	−19.3655	−19.3680	−19.3720
		R(F)	0.8641	0.0588	0.0999	0.2220	0.3558	0.5535	0.7227	0.9125	1.2009	1.4521
		R^R(F)	6.0116	0.0855	0.0640	0.0985	0.1199	0.1400	0.1529	0.1651	0.1812	0.1937
		LBE^∗	−19.889	0.8842	0.9130	0.8700	0.8435	0.8156	0.7970	0.7789	0.7566	0.7399
		UBE^∗	5.3743	1.1528	1.1103	1.1755	1.2158	1.2552	1.2807	1.3055	1.3385	1.3636

Figures 4, 5, and 6 show estimated regional growth curves for sample sizes 30, 60, and 90, respectively, and also GEV, GNO, and GPA distributions with the 90% error bounds.

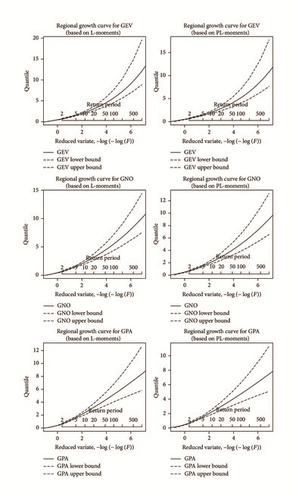
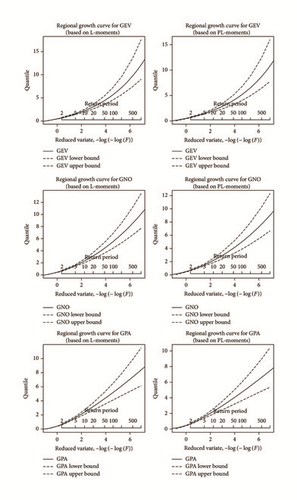
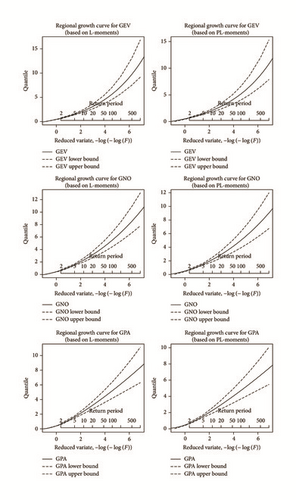
Tables 8, 9, and 10 show that increase in the sample size such as 30 to 90 improved the performance particularly in the prediction of the large nonexceedance probability F. L-moments method provides similar performance for the GNO and GPA distributions in terms of relative bias that is presented in Tables 8, 9, and 10. We found that the GPA distribution produced the lowest relative bias compared to GEV and GNO distribution for the PL-moment for the various values of the nonexceedance probability F. However, the GPA distribution performs better in terms of RMSE than the GEV and GNO distribution for both methods (L-moments and PL-moments). Furthermore, RMSE is lowest for PL-moments compared to L-moments. In addition, the error bounds for the GPA distribution of regional quantiles are narrow compared to GEV and GNO distributions. It shows that the estimation of censored sample improves the prediction of extreme precipitation explicitly at large nonexceedance probability F.

5. Discussion and Conclusion

This study provides a comprehensive evaluation of the L-moments and the PL-moments. First, revisiting RFA on L-moments by Hosking and Wallis [7], we aimed to develop similar connections of regional homogeneity for PL-moments. The L-moments and the PL-moments for candidate probability distributions (GLO, GEV, GNO, and GPA) are also developed for presenting the corresponding L-ratio and PL-ratio diagrams with the goodness of fit test results. The regional growth curves for the selected distribution have been shown in Figures 4, 5, and 6. At the lower tail, GEV, GPA, and GNO distributions are approximately the same, but, at the upper tail, there is variation between the regional quantiles. The regional homogeneity analysis starts by assuming 17 locations of Northern areas and Khyber Pakhtunkhwa, Pakistan, as one homogeneous region, based on L-moments and PL-moments at censoring level ranging from 10 to 23%. This assumption is statistically accepted after applying the heterogeneity and discordancy tests. The Z-statistic provides appropriate distribution for modeling the monthly extreme precipitation in Northern areas and Khyber Pakhtunkhwa, Pakistan. We found that GPA distribution is suitable for the L-moments and GNO distribution for the PL-moments.

Finally, Monte Carlo simulation used for performance evaluation by commonly used error functions. Several accuracy measures such as relative bias, RMSE, relative RMSE, and error function bounds for the regional quantiles are computed with 10,000 runs of Monte Carlo simulations. We found that GPA distribution produced robust quantile estimates for both return periods and methods (L-moments and PL-moments). Our results support the finding of previous study (e.g., Cunnane [9]; Bhattarai [12]) for censored sample analysis where PL-moments method outperformed the L-moments method for the estimation of large return periods events.

Ethical Approval

The manuscript is prepared in accordance with the ethical standards of the responsible committee on human experimentation and with the latest (2008) version of Helsinki Declaration of 1975.

Conflicts of Interest

The manuscript is prepared by using secondary data and authors declared that there are no conflicts of interest.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at King Saud University for funding this work through Research Group no. RG-1437-027.

Appendix

The partial L-moments (PL-moments) for generalized logistic (GLO), generalized Pareto (GPA), generalized normal (GNO), and generalized extreme value (GEV) distributions were derived based on the formula defined by Wang (Water Resour Res 32:1767Ö 1771, 1996 (In references lines from 442 to 444 mentioned that in study)). The summary of the derived distributions and parameters estimation for these distributions is as follows.

PL-moments for the GEV Distribution [10] are as follows.

The CDF and quantile function of the GEV are given by

(A.1)

and quantile function

(A.2)

Wang [10] developed the partial probability-weighted moments (PWMs) of the GEV as

(A.3)

where

(A.4)

The first four PL-moments of the GEV are defined as

(A.5)

In previous equation, P(·, ·) is an Incomplete Gamma function:

(A.6)

Then the first four PL-moments are computed to develop the PL-moment ratios (PL-Cv, PL-Cs, and PL-Ck) for the GEV distribution.

The PL-moments for the GLO Distribution are as follows.

The CDF and quantile function of the GLO are given by

(A.7)

and quantile function

(A.8)

The partial PWMs of the GLO are developed as follows:

(A.9)

where

is an Incomplete Beta function

(A.10)

The first four PL-moments of the GLO are defined as

(A.11)

Then the first four PL-moments are computed to develop the PL-moment ratios (PL-Cv, PL-Cs, and PL-Ck) for the GLO distribution.

The PL-moments for the GPA Distribution are as follows.

The CDF and quantile function of the GPA are given by

(A.12)

and quantile function

(A.13)

The partial PWMs of the GPA are developed as follows:

(A.14)

The first four PL-moments of the GPA are defined as

(A.15)

where

(A.16)

Then the first four PL-moments are computed to develop the PL-moment ratios (PL-Cv, PL-Cs, and PL-Ck) for the GPA distribution.

References

1 Dalrymple T., Flood-frequency analyses, Water Supply Paper, 1960, no. 1543-A, U.S.Geological Survey, Reston, Va, USA.
Google Scholar
2 Hosking J. R. M., Wallis J. R., and Wood E. F., An appraisal of the regional flood frequency procedure in the UK flood studies report, Hydrological Sciences Journal. (1985) 30, no. 1, 85–109, https://doi.org/10.1080/02626668509490973, 2-s2.0-0022025328.
10.1080/02626668509490973
Web of Science® Google Scholar
3 Greis N. P. and Wood E. F., Regional flood frequency estimation and network design, Water Resources Research. (1981) 17, no. 4, 1167–1177, https://doi.org/10.1029/wr017i004p01167, 2-s2.0-0019727509.
10.1029/WR017i004p01167
Web of Science® Google Scholar
4 Wallis J. R., S. Rinaldi, Hydrologic problems associated with oilshale devel opment, Environmental Systems and Management, 1982, 85–102.
Web of Science® Google Scholar
5 Cunnane C., Methods and merits of regional flood frequency analysis, Journal of Hydrology. (1988) 100, no. 1–3, 269–290, https://doi.org/10.1016/0022-1694(88)90188-6, 2-s2.0-0024165507.
10.1016/0022-1694(88)90188-6
Web of Science® Google Scholar
6 Subramanya K., Engineering Hydrology, 2007, 2nd edition, McGraw-Hill, Singapore.
Google Scholar
7 Hosking J. R. and Wallis J. R., Regional Frequency Analysis: An Approach Based on L-Moments, 1997, Cambridge University Press, New York, NY, USA, https://doi.org/10.1017/cbo9780511529443.
10.1017/CBO9780511529443
Google Scholar
8 Wang Q. J., Estimation of the GEV distribution from censored samples by method of partial probability weighted moments, Journal of Hydrology. (1990) 120, no. 1–4, 103–114, https://doi.org/10.1016/0022-1694(90)90144-m, 2-s2.0-0025573376.
10.1016/0022-1694(90)90144-M
Web of Science® Google Scholar
9 Cunnane C., Statistical distributions for flood frequency analysis, World Meteorological Organization Operational Hydrology Report, 1987, no. 33.
Google Scholar
10 Wang Q. J., Using partial probability weighted moments to fit the extreme value distributions to censored samples, Water Resources Research. (1996) 32, no. 6, 1767–1771, https://doi.org/10.1029/96WR00352, 2-s2.0-0029663972.
10.1029/96WR00352
Web of Science® Google Scholar
11 Wang Q. J., Unbiased estimation of probability weighted moments and partial probability weighted moments from systematic and historical flood information and their application to estimating the GEV distribution, Journal of Hydrology. (1990) 120, no. 1-4, 115–124, https://doi.org/10.1016/0022-1694(90)90145-N, 2-s2.0-0025573377.
10.1016/0022-1694(90)90145-N
Web of Science® Google Scholar
12 Bhattarai K. P., Partial L-moments for the analysis of censored flood samples, Hydrological Sciences Journal. (2004) 49, no. 5, 855–868, 2-s2.0-4944263960.
10.1623/hysj.49.5.855.55138
Web of Science® Google Scholar
13 Shabri A. B., Daud Z. M., and Ariff N. M., Regional analysis of annual maximum rainfall using TL-moments method, Theoretical and Applied Climatology. (2011) 104, no. 3-4, 561–570, https://doi.org/10.1007/s00704-011-0437-5, 2-s2.0-79957445183.
10.1007/s00704-011-0437-5
Web of Science® Google Scholar
14 Saf B., Regional flood frequency analysis using L-moments for the West Mediterranean region of Turkey, Water Resources Management. (2009) 23, no. 3, 531–551, https://doi.org/10.1007/s11269-008-9287-z, 2-s2.0-58549116494.
10.1007/s11269-008-9287-z
Web of Science® Google Scholar
15 Abolverdi J. and Khalili D., Development of regional rainfall annual maxima for Southwestern Iran by L-moments, Water Resources Management. (2010) 24, no. 11, 2501–2526, https://doi.org/10.1007/s11269-009-9565-4, 2-s2.0-77955768130.
10.1007/s11269-009-9565-4
Web of Science® Google Scholar
16 Hussain Z. and Pasha G. R., Regional flood frequency analysis of the seven sites of Punjab, Pakistan, using L-moments, Water Resources Management. (2009) 23, no. 10, 1917–1933, https://doi.org/10.1007/s11269-008-9360-7, 2-s2.0-67650381958.
10.1007/s11269-008-9360-7
Web of Science® Google Scholar
17 Zakaria Z. A., Shabri A., and Ahmad U. N., Regional Frequency Analysis of Extreme Rainfalls in the West Coast of Peninsular Malaysia using Partial L-Moments, Water Resources Management. (2012) 26, no. 15, 4417–4433, https://doi.org/10.1007/s11269-012-0152-8, 2-s2.0-84868213242.
10.1007/s11269-012-0152-8
Web of Science® Google Scholar
18 Shahzadi A., Akhter A. S., and Saf B., Regional frequency analysis of annual maximum rainfall in monsoon region of pakistan using L-moments, Pakistan Journal of Statistics and Operation Research. (2013) 9, no. 1, 111–136, https://doi.org/10.18187/pjsor.v9i1.461, 2-s2.0-84877137882.
10.18187/pjsor.v9i1.461
Google Scholar
19 Coles S., An Introduction to Statistical Modeling of Extreme Values, 2001, Springer-Verlag, London, England, Springer Series in Statistics, https://doi.org/10.1007/978-1-4471-3675-0, MR1932132.
10.1007/978-1-4471-3675-0
Google Scholar
20 Katz R. W., Parlange M. B., and Naveau P., Statistics of extremes in hydrology, Advances in Water Resources. (2002) 25, no. 8–12, 1287–1304, https://doi.org/10.1016/s0309-1708(02)00056-8, 2-s2.0-0036704796.
10.1016/S0309-1708(02)00056-8
Web of Science® Google Scholar
21 Abida H. and Ellouze M., Probability distribution of flood flows in Tunisia, Hydrology and Earth System Sciences. (2008) 12, no. 3, 703–714, https://doi.org/10.5194/hess-12-703-2008, 2-s2.0-43749111995.
10.5194/hess-12-703-2008
Web of Science® Google Scholar
22 Feng S., Nadarajah S., and Hu Q., Modeling annual extreme precipitation in China using the generalized extreme value distribution, Journal of the Meteorological Society of Japan. (2007) 85, no. 5, 599–613, https://doi.org/10.2151/jmsj.85.599, 2-s2.0-38049031712.
10.2151/jmsj.85.599
Web of Science® Google Scholar
23 Yang T., Shao Q., Hao Z.-C., Chen X., Zhang Z., Xu C.-Y., and Sun L., Regional frequency analysis and spatio-temporal pattern characterization of rainfall extremes in the Pearl River Basin, China, Journal of Hydrology. (2010) 380, no. 3-4, 386–405, https://doi.org/10.1016/j.jhydrol.2009.11.013, 2-s2.0-72249094311.
10.1016/j.jhydrol.2009.11.013
Web of Science® Google Scholar
24 Villarini G., Smith J. A., Baeck M. L., Vitolo R., Stephenson D. B., and Krajewski W. F., On the frequency of heavy rainfall for the Midwest of the United States, Journal of Hydrology. (2011) 400, no. 1-2, 103–120, https://doi.org/10.1016/j.jhydrol.2011.01.027, 2-s2.0-79952470530.
10.1016/j.jhydrol.2011.01.027
Web of Science® Google Scholar
25 She D., Xia J., Song J., Du H., Chen J., and Wan L., Spatio-temporal variation and statistical characteristic of extreme dry spell in Yellow River Basin, China, Theoretical and Applied Climatology. (2013) 112, no. 1-2, 201–213, https://doi.org/10.1007/s00704-012-0731-x, 2-s2.0-84875380136.
10.1007/s00704-012-0731-x
Web of Science® Google Scholar
26 Wallis J. R., Matalas N. C., and Slack J. R., Just a moment!, Water Resources Research. (1974) 10, no. 2, 211–219, https://doi.org/10.1029/WR010i002p00211, 2-s2.0-0016046857.
10.1029/WR010i002p00211
Google Scholar
27 Pearson C. P., New Zealand regional flood frequency analysis using L-moments, Journal of Hydrology. (1991) 30, no. 2, 53–64, 2-s2.0-0026360913.
Google Scholar
28 Hosking J. R., L-moments: analysis and estimation of distributions using linear combinations of order statistics, Journal of the Royal Statistical Society. Series B. Methodological. (1990) 52, no. 1, 105–124, MR1049304.
10.1111/j.2517-6161.1990.tb01775.x
Web of Science® Google Scholar
29 Greenwood J. A., Landwehr J. M., Matalas N. C., and Wallis J. R., Probability weighted moments: definition and relation to parameters of several distributions expressable in inverse form, Water Resources Research. (1979) 15, no. 5, 1049–1054, https://doi.org/10.1029/wr015i005p01049, 2-s2.0-0018713386.
10.1029/WR015i005p01049
Web of Science® Google Scholar
30 Hosking J. R. M. and Wallis J. R., Some statistics useful in regional frequency analysis, Water Resources Research. (1993) 29, no. 2, 271–281, https://doi.org/10.1029/92WR01980, 2-s2.0-0027341450.
10.1029/92WR01980
Web of Science® Google Scholar
31 Stedinger J. R., Vogel R. M., and Foufoula-Georgiou E., D. R. Maidment, Frequency analysis of extreme events, Hand Book of Hydrology, 1993, McGraw-Hill, New York, NY, USA.
Google Scholar
32 Vogel R. M. and Fennessey N. M., L-moment diagrams should replace product moment diagrams, Water Resources Research. (1993) 29, no. 6, 1745–1752, https://doi.org/10.1029/93wr00341, 2-s2.0-0027796194.
10.1029/93WR00341
Web of Science® Google Scholar
33 Hosking J. R. M., N. Balakrishnan, The use of L-moments in the analysis of censored data, Recent Advances in Life-Testing and Reliability, 1995, CRC Press, Boca Raton, Fla, USA, 545–564.
Google Scholar
34 Schaefer M. G., Regional analyses of precipitation annual maxima in Washington State, Water Resources Research. (1990) 26, no. 1, 119–131, https://doi.org/10.1029/WR026i001p00119, 2-s2.0-0025223964.
10.1029/WR026i001p00119
Web of Science® Google Scholar
35 Pearson C., Application of l-moments to maximum river ows, The New Zealand Statistician. (1993) 28, no. 1, 2–10.
Google Scholar
36 Vogel R. M., Thomas W. O., and McMahon T. A., Flood-flow frequency model selection in southwestern united states, Journal of Water Resources Planning and Management. (1993) 119, no. 3, 353–366, https://doi.org/10.1061/(ASCE)0733-9496(1993)119:3(353), 2-s2.0-0027596099.
10.1061/(ASCE)0733-9496(1993)119:3(353)
Web of Science® Google Scholar
37 Chow K. C. A. and Watt W. E., Practical use of the L-moments, Stochastic and Statistical Methods in Hydrology and Environmental Engineering. (1994) 1, no. 3, 55–69.
Google Scholar
38 ÖnÖz B. and Bayazit M., Best-fit distributions of largest available flood samples, Journal of Hydrology. (1995) 167, no. 1-4, 195–208, https://doi.org/10.1016/0022-1694(94)02633-M, 2-s2.0-0028974857.
10.1016/0022-1694(94)02633-M
Web of Science® Google Scholar
39 Vogel R. M. and Wilson I., Probability distribution of annual maximum, mean, and minimum streamflows in the United States, Journal of Hydrologic Engineering. (1996) 1, no. 2, 69–76, https://doi.org/10.1061/(ASCE)1084-0699(1996)1:2(69), 2-s2.0-0030126025.
10.1061/(ASCE)1084-0699(1996)1:2(69)
Web of Science® Google Scholar
40 Peel M. C., Wang Q. J., Vogel R. M., and McMahon T. A., The utility of L-moment ratio diagrams for selecting a regional probability distribution, Hydrological Sciences Journal. (2001) 46, no. 1, 147–155, https://doi.org/10.1080/02626660109492806, 2-s2.0-0035248477.
10.1080/02626660109492806
Web of Science® Google Scholar
41 Jiang Z., Ding Y., Zhu L., and Zhang J., Extreme precipitation experimentation over eastern china based on generalized pareto distribution, Plateau Meteorology. (2009) 28, no. 3, 573–580.
Google Scholar
42 Yuguo S. B. Y. J. D., Research on extreme value distribution of short-duration heavy precipitation in the Sichuan basin, Journal of the Meteorological Sciences. (2012) 4, article 007.
Google Scholar

Citing Literature

All articles

Regional Frequency Analysis of Extremes Precipitation Using L-Moments and Partial L-Moments

Abstract

1. Introduction

2. Material and Methods

2.1. Study Area and Data Sources

2.2. Statistical Methods

2.2.1. The L-Moments

2.2.2. The Partial L-Moments

2.3. Regional Frequency Analysis

2.3.1. Data Screening

2.3.2. Discordance Test

2.3.3. Heterogeneity Test

2.4. Selection of the Appropriate Probability Distribution

3. Estimation

3.1. Regional Frequency Analysis

3.1.1. Data Screening

3.1.2. Discordance Test

3.1.3. Regional Heterogeneity Measure

3.2. Fitting Appropriate Probability Distribution

3.3. Estimation of the Quantiles

4. Accuracy of the Estimated Quantiles and the Regional Growth Curve

5. Discussion and Conclusion

Ethical Approval

Conflicts of Interest

Acknowledgments

Appendix

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Regional Frequency Analysis of Extremes Precipitation Using L-Moments and Partial L-Moments

Abstract

1. Introduction

2. Material and Methods

2.1. Study Area and Data Sources

2.2. Statistical Methods

2.2.1. The L-Moments

2.2.2. The Partial L-Moments

2.3. Regional Frequency Analysis

2.3.1. Data Screening

2.3.2. Discordance Test

2.3.3. Heterogeneity Test

2.4. Selection of the Appropriate Probability Distribution

3. Estimation

3.1. Regional Frequency Analysis

3.1.1. Data Screening

3.1.2. Discordance Test

3.1.3. Regional Heterogeneity Measure

3.2. Fitting Appropriate Probability Distribution

3.3. Estimation of the Quantiles

4. Accuracy of the Estimated Quantiles and the Regional Growth Curve

5. Discussion and Conclusion

Ethical Approval

Conflicts of Interest

Acknowledgments

Appendix

References

Citing Literature

Figures

References

Related

Information