Integrating wind generation, photovoltaic power, and battery storage to form hybrid power systems has been recognized to be promising in renewable energy development. However, considering the system complexity and uncertainty of renewable energies, such as wind and solar types, it is difficult to obtain practical solutions for these systems. In this paper, optimal sizing for a wind/PV/battery system is realized by trade-offs between technical and economic factors. Firstly, the fuzzy c-means clustering algorithm was modified with self-adapted parameters to extract useful information from historical data. Furthermore, the Markov model is combined to determine the chronological system states of natural resources and load. Finally, a power balance strategy is introduced to guide the optimization process with the genetic algorithm to establish the optimal configuration with minimized cost while guaranteeing reliability and environmental factors. A case of island hybrid power system is analyzed, and the simulation results are compared with the general FCM method and chronological method to validate the effectiveness of the mentioned method.

1. Introduction

Hybrid power systems (HPS) [1, 2], especially those dependent on renewable energy generations (REGs), such as solar photovoltaic (PV), together with wind turbine generations (WTGs), have been regarded as the most promising configurations for remote areas power supply, since it is neither economical nor practical for delivering power over long distances. Although these clean energies provide significant contributions and opportunities, the unpredictable nature [3] of these resources has posed serious challenges to power systems [4, 5]. In the context of remote HPS, the greatest obstacle is to maintain power balance, because the adjustable capacity depends merely on REGs and batteries [6]. Hence, the dynamic characteristic of the wind speed and solar irradiance, together with the power management of batteries, should be investigated to obtain practical configurations for HPS.

In previous literature, various methods have been introduced for sizing optimization of HPS. The stochastic nature of the REGs has been investigated with several probabilistic and chronological methods. The autoregressive moving average (ARMA) is utilized to model the uncertainties of wind generation, photovoltaic (PV) power, and load in [3, 7, 8]. However, methods for parameters estimation of ARMA are always somewhat cumbersome. Reference [9] put forward an efficient approach for sizing optimization in a stand-alone HPS with Hybrid Big Bang-Big Crunch algorithm. Reference [10] analyzed the different results obtained by four heuristic algorithms; nevertheless the uncertainties of renewable energies have not been considered detailedly. Reference [11] suggested a method for technical and economic optimization in an isolated PV system; the solar radiation classification and power supply reliability calculation are performed hourly. However, only the cluster corresponding to the minimum solar radiation is selected, which may not be suitable in the context of HPS. The other investigations are based on gross chronological data [12, 13] where the computation time is always too unbearable. In [14], the traditional fuzzy c-means (FCM) is adopted, which divides the data of wind speed, solar radiation, and load evenly. Thus the inherent characteristics of the data are handled in a somewhat arbitrary way.

This proposed methodology will be complementary to the previous studies and take a step further. First of all, time series analysis [15] was used to describe the characteristic of hourly wind and solar and load data with FCM, the function of which is to group the elements of data sets that have analogous characteristics. Considering that FCM is sensitive to the initialization number of clusters [16], a parameters self-adaptive method is introduced to optimize the initial state. Furthermore, the Markov model [17] is combined to obtain the system scenarios of HPS. Then the correlation and time dependency of data sets are maintained with the time-dependent clusters of the renewable generations and load power consumption. The optimal sizes for WTGs, PV, DG, and batteries are determined with the genetic algorithm (GA), in which a power balance strategy is designed to ensure that the capitalized and operational costs are minimized and the reliability requirements, CO₂ emission, and batteries constraints are preserved at the same time.

The remaining parts of the article can be demonstrated in the following manner. The models of the components in HPS and the technique of FCM with self-adapted clustering number are introduced in Section 2. Section 3 presents the objective function and constraints for optimal sizing method in HPS. Section 4 utilizes a case of stand-alone hybrid system located in Hainan, China, to verify the advantage of the proposed methodology, where the comparison between the self-adapted FCM model and the traditional model with chronological data is analyzed. In Section 5, conclusions are summarized and the relationship between reliability and cost is discussed.

2. Models of the Components in HPS

2.1. The Components in HPS

2.1.1. WTGs Generation System

The output power of each WTG [10, 18] is obtained by (1), and the power curve of IEC 61400-12 standard is displayed in Figure 1.

()

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Power curve of IEC 61400-12 standard.

The parameters a and b are calculated by

()

where v denotes the rated wind speed, v_ci and v_co are, respectively, the cut-in wind speed and cut-off wind speed. p_r means the rated power of WTGs.

The overall wind power

can be derived with (3), and the total wind energy

can be obtained with (4):

()

where N_W is the number of wind turbines and Δt is the time step.

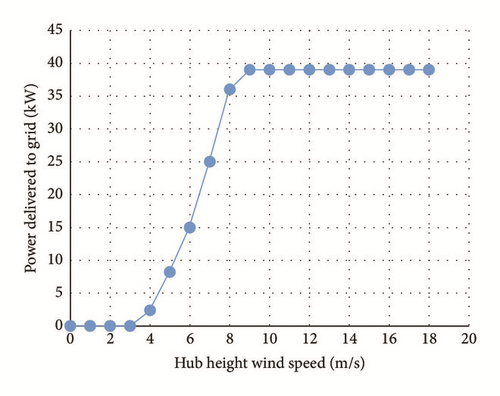
2.1.2. PV System

For each PV panel, the output power can be obtained [10] with

()

where p_PV(t) denotes the PV module power at time t. P_pvr means the rated power, G means the solar irradiance, and R_Ref means the referenced solar irradiance, in 1000 W/m². T_Ref means the referenced temperature on the surface of panels, which can be set to be equal to 25°C. α_T means the temperature-coefficients of PV panels, and it can be set to be equal to −3.7 × 10⁻³. The temperature T_c of each cell is deduced with

()

where T_air is the atmospheric temperature. R means the solar irradiance and T_stc means the standard operation cell temperature and set to be 25°C.

The overall wind power

can be obtained with (7), and the total wind energy

can be calculated with (8):

()

where the number of PV panels is given with N_PV.

2.1.3. Battery Bank and the Power Balance Strategy

To accommodate the stochastic behavior of PV and wind resources, battery banks are widely utilized for hybrid power systems. The power balance strategy is mainly based on the flexibility of batteries and diesel generations. The diesel generator in [14] is the only adjustable power generation without consideration of storage devices. Thus the power balance strategy is limited to only one pattern, namely, the diesel generators run to make up for the power shortage of renewable energies. To maximize the utilization of REG and minimization of diesel generation, a power balance strategy is illustrated in Figure 2.

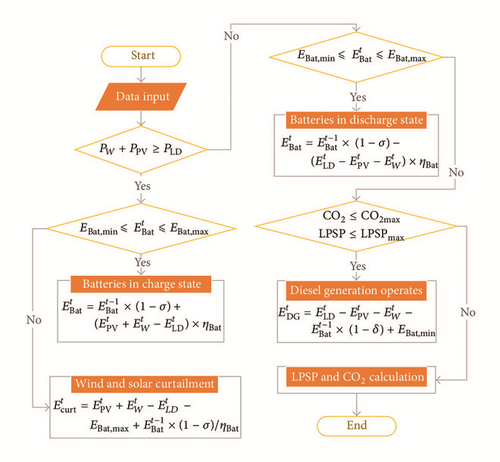
2.2. FCM with Self-Adaptive Cluster Number

In this section, FCM clustering is modified to identify the operation state of HPS. The calculation complexity can be significantly optimized considering the number of states will be much less than the 8760 h in the chronological methods. Traditional FCM clustering algorithm can only deal with a prescribed data set with clustering number given in advance, which is not flexible in the context of large data sets. A new validity function [19] is introduced to construct the proportion of compactness and divergence; thus the cluster number can be obtained according to the given data set.

2.2.1. FCM Clustering for HPS

The FCM clustering algorithm established by Dunn and then further improved by Bezdek has been used extensively.

The given data set is divided into c clusters relating to some given criterions to optimize an objective function. The problem can be formulated as

()

An effective partition of a given data set should be divergent and compacted. The degree of compactness and divergence are evaluated with a clustering validity function. Hence, a new validity function is adopted in

()

where m is the fuzzy weighting index and greater than 1 and c means the clustering number. n is the subscript index of the data set X, in which x_j (j = 1,2, …, n) is each pattern. x_j (j = 1,2, …, n) is the clustering prototype. ∥·∥ means the statistical distance of the very data set. The central vector of the overall data is given with

2.2.2. Clustering Procedure

Then, the FCM algorithm with self-adapted clustering number is outlined with the proposed validity function L(c). The clustering procedure is illustrated in Figure 3.

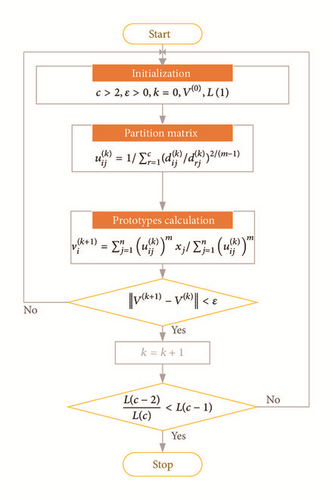
The partition matrix U(0) is set as an initial condition; merely two local values of L(c) are required to be compared since the solution is locally minimized of the object function, which validates the effectiveness of Step 4 in Figure 3.

In [14], the cluster number for WTGs is selected by evenly dividing the range between the cut-in and cut-off wind speed. The selection of cluster number of PV and load is the same. However, the inner uncertain nature of the wind resource may be disregarded by this means, and the accuracy of this method may be reduced significantly.

In this paper, the cluster numbers for WTGs, PV, and load are obtained via the method proposed in Section 3.1. More specifically, the wind speed v, solar irradiance, and load power can be divided into C_WT, C_PV, and C_LD clusters coherently. The cluster centers P_Wc, P_PVc, and P_LDc are the representative in this cluster, namely, the representative state of wind speed, solar radiation, and load.

2.2.3. The Markov Stochastic Process

In the analysis of a stochastic process, the Markov chain is an effective method to relate the probability of a state with the frequency of the corresponding event. The operation states are P_WT(c_WT), P_PV(c_PV), and P_LD(c_LD), where c_WT, c_PV, and c_LD are the state indices obtained by the proposed method in Section 3.1. Take a wind farm with four Markov states as an example, shown in Figure 4. The state transfer probability and failure rate among different states are given with λ and μ, respectively.

If p_c, c = 1,2, …, C, are probabilistic for C states (C is the cluster number), then they should satisfy

()

The diagonal elements T_c,c are equal to the negative-sum of each off-diagonal element at column c of transition probability matrix φ, and the elements in other positions correspond, respectively, to φ.

()

where n_i,j denotes the transition number from state i to j, and N_i means the number of states i. Rate of departure (RD) is the modulus of the diagonal elements; the frequency (F_i) and duration for state i (D_i) can be formulated as

()

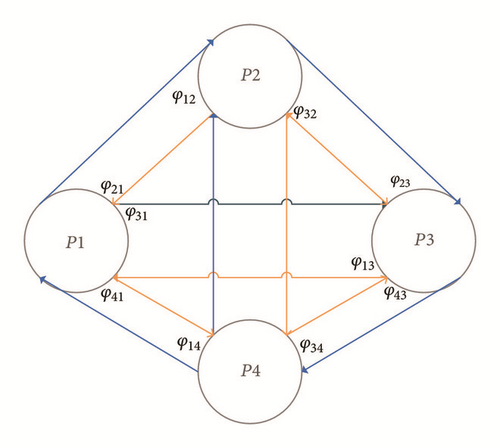
The system states of HPS are mainly determined by the combination of WT and PV states, which also determine the state of DG and batteries.

3. Sizing Optimization

3.1. Objective Functions

In the proposed optimal sizing methodology of HPS, the main goal is to determine the amounts of each kind of DG. For a given system load, the objective can be set for the overall cost optimization.

()

where subscript i denotes the type of generations, namely, WT, PV, DG, and batteries, and j contains the cost of the unit, installation, and fuel consumption of the HPS.

The fuel consumption of the DGs using fossil fuel is given with

()

Then the cost model of a diesel generator is

()

For the DGs using renewable energy resources like WG and PV, the operation cost can be ignored. For the DGs using fossil fuel, the operation cost should be accumulated in the studied period. The combustion of fossil fuel will contribute to the emission of CO₂ and gaseous pollutants. The ramping characteristics of diesel generation are neglected in the article since the time resolution is set to be one hour.

In (17), the fuel consumption cost C_d can be obtained.

()

By means of FCM clustering, it can be reduced to

()

where P_d can be obtained with the proposed power balance strategy.

3.2. Constraints

On the basis of normal operation in the stand-alone HPS, in order to associate the reliability factor and environmental factors, the main constraints of the proposed methodology are as follows.

3.2.1. Power Balance in the Given Time Resolution

The foundation of the sizing optimization problem is the power balance. The power balance strategy in this paper is illustrated in Figure 2 (power balance strategy of HPS). The power balance equation is

()

where N_x.i.t means output power of each kind of DG in the given time interval t, the length of which is associated with the length of the planning period and is set to be 1 h in this paper.

3.2.2. The Minimum and Maximum Scale of the DGs

()

where the subscripts max and min mean the maximum and minimum restraints for DG scales, respectively.

3.2.3. Battery Constraints

At time t, the value of charge level for each battery bank should satisfy

()

The battery banks capacity (S_Bat) sets the maximum value of charge level (E_Bat,max) and the depth of discharge (DOD) determines the minimum value of charge level for the batteries (E_Bat,min).

()

3.2.4. Reliability Index

LPSP (loss of power supply probability) is selected for its simplicity, which can be derived from the division of total time of power unbalance and the studied period with

()

The subscript “max” signifies the maximum limits.

3.2.5. Environmental Factors

The CO₂ emission of the DGs using fossil fuel can be obtained with (24), when considering it in the total period, and should be constrained by a maximum

()

In this article, d, e, and f of a 30-kW diesel generator are set to be 0.028144, 0.001728, and 0.0000017.

3.3. Using Genetic Algorithm to Get Optimal Solution

The genetic algorithm (GA) is chosen to solve the sizing problem considering its ability to obtain a globally optimal solution for optimization problems. It is inspired by the process of biological evolution, namely, crossover, mutation, and selection. The population of individual solutions is repeatedly modified with a “fitness” function, typically related to the objective function.

In this article, the optimization problem (14)~(25) is handled with GA, where the variables N_WT, N_PV, N_DG, and N_BAT are linked to form the gene strings in the state variable (chromosome), and (14) is set to be the fitness function.

4. Results

4.1. Case Introduction

The data from an island in Hainan province of China are used to analyze the proposed problem. There are abundant wind and solar resources in this island.

4.2. Simulation Results and Analysis

The monthly average wind speed, solar irradiation, temperature, and load power profile consumption are shown in Figures 5–8.

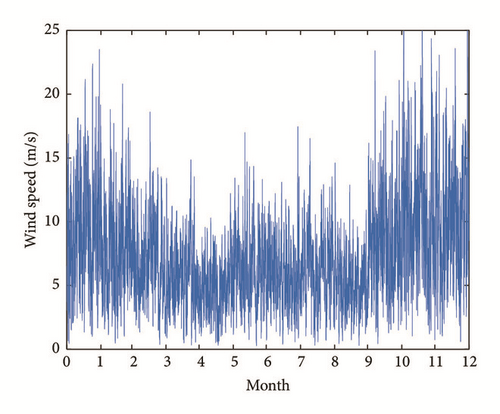
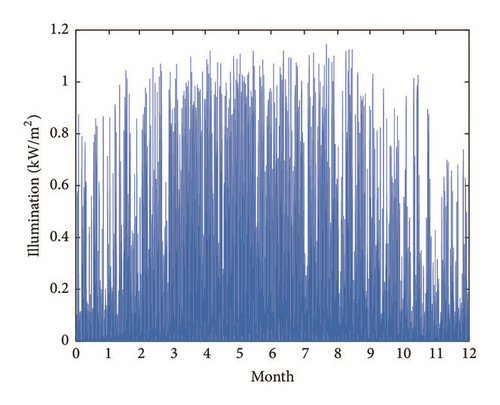
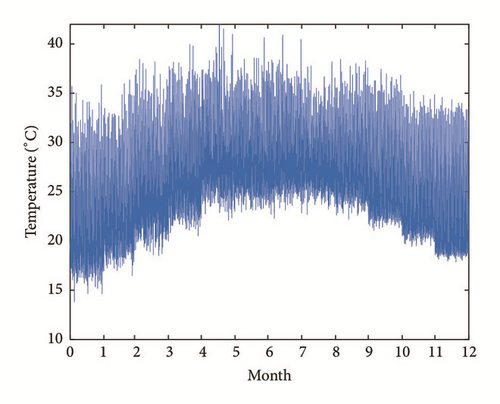
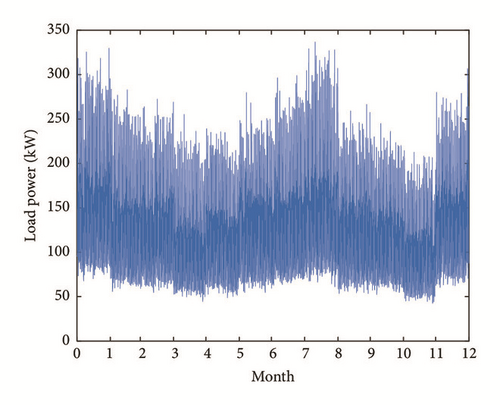
Firstly, the wind speed v, illumination G, and temperature T are imported to the HPS model to obtain the power output of WTGs (P_W) and PV (P_PV). Then the cluster numbers for WT, PV, and load are obtained via the method proposed in Section 2.1. The cluster centers Vc, Gc, and Lc are, respectively, the representative states for wind speed, solar irradiance, and load, illustrated in Tables 1–3.

Table 1. Markov model of WT/35 kW.

State (c1)	Pw/kW	ps	RD	F/(oc⋅h⁻¹)	D (h)
1	0.20	0.08	0.47	0.03	2.15
2	3.90	0.09	0.65	0.05	1.53
3	7.48	0.15	0.52	0.08	1.92
4	10.99	0.08	0.82	0.07	1.22
5	14.56	0.08	0.59	0.05	1.69
6	18.08	0.09	0.62	0.12	1.61
7	21.86	0.09	0.85	0.08	1.18
8	25.89	0.06	0.72	0.06	1.39
9	30.19	0.09	0.84	0.08	1.20
10	34.87	0.19	0.76	0.07	1.32

Table 2. Markov model of PV/200 W.

State (c1)	P_PV/W	ps	RD	F/(oc⋅h⁻¹)	D (h)
1	1.37	0.61	0.37	0.22	2.71
2	83.14	0.10	0.62	0.06	1.63
3	37.23	0.13	0.44	0.06	2.29
4	134.05	0.09	0.59	0.05	1.69
5	188.58	0.07	0.26	0.02	3.82

Table 3. Markov model of load.

State (c1)	P_PV/W	ps	RD	F/(oc⋅h⁻¹)	D (h)
1	135.66	0.16	0.67	0.11	1.49
2	83.78	0.18	0.56	0.10	1.77
3	156.19	0.17	0.74	0.13	1.34
4	217.17	0.07	0.82	0.05	1.23
5	182.49	0.10	0.63	0.07	1.60
6	63.81	0.17	0.22	0.04	4.46
7	111.11	0.13	0.51	0.06	1.96
8	268.08	0.03	0.28	0.01	3.61

According to the simulation results from self-adaptive FCM, the optimal cluster numbers for wind WT, PV, and LD are 10, 5, and 8. Namely, each WT has 10 states, each PV has 5 states, and the overall load has 8 states. There are 80 possible states for the renewable energy generations as a whole. It can be noted here that the scenario of HPS has been significantly simplified.

The operation scenario considered here is greatly simplified to be the aggregation of clustering states. The outputs of DGs and batteries are also determined by these states, according to the power balance strategy demonstrated before.

For a new state, the probability is the multiplication of state probabilities for every individual WTG, PV, and LD. The frequency F and duration time D for a new scenario can be obtained likewise.

Then the results from chronology-based, traditional FCM based, and the self-adapted clustering number based GAs are compared; results are illustrated in Table 4. GA is capable of realizing global optimization but cannot guarantee it. The chronological-based method requires 8760 iterative loops, and the traditional FCM based method needs 920 (=23 ∗ 4 ∗ 10) iterative loops, and the proposed method needs 400 (=10 ∗ 5 ∗ 8) iterative loops.

Table 4. Performance comparison.

Method	N_w	N_PV	N_d	N_bat	Cost/M$	CO₂/kg	Time/s
Proposed method	15	126	62	864	2,03M	556,000	27.5
Basic FCM	10	96	56	956	2.20M	542,000	27.8
Chronology-based	13	104	64	886	2.06M	560,000	126

It should be noted that the wind energy is superfluous in the winter nights. The output power of PV panels is redundant in the summer daytimes.

It can be found that chronology-based method is the most time-consuming due to complicate loops. With regard to the overall cost, the proposed method still has advantages. Figure 9 shows the iteration performance for the mentioned algorithms.

The proposed self-adapted FCM clustering model is superior to traditional method in two aspects:

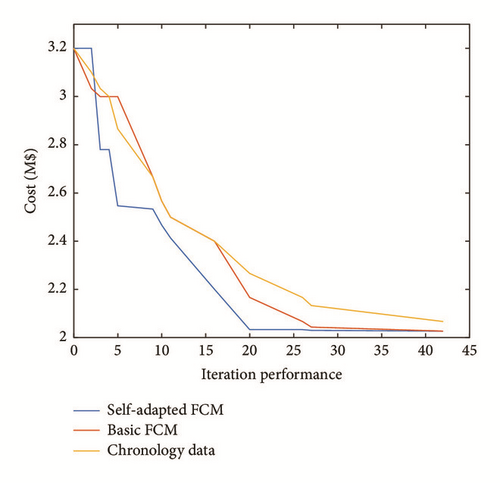
(1)
Compared to chronological-based methods, with the reduction of investigated data set, the number of system scenarios of HPS can be significantly reduced, and the computation burden and CPU time can be significantly reduced, shown in Table 4.
(2)
Compared to the traditional FCM based method, the clustering numbers of data sets are inherently obtained and optimized, which increases the probability to obtain a global optimum solution. While the traditional method simply makes the partition by uniform division, the scenarios selection is somewhat arbitrary and disregards the inner stochastic characteristic of the data sets. Thus the basic FCM based method finally obtains a locally optimized solution.

In the proposed method, the benefits of the renewable energies are thought to be the reduction of CO₂ and the improvement of LOSP, which has been set as constraint to the very problem. Considering the impacts of different reliability index on the investment cost, let be 30000 kg/y. The overall investment cost grows higher as the reliability request (LPSP_max) increases, as shown in Figure 10. The impact of CO₂ is similar to the LPSP index.

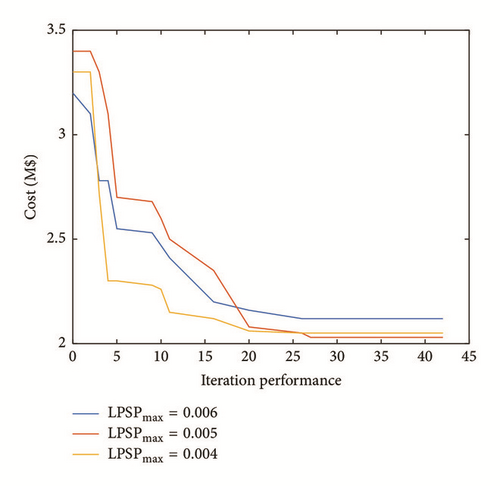
Actually, the benefits of the reduction of CO₂ and the improvement of LOSP are negatively related to the cost optimization procedure. We have modified the discussion on this issue in our revised manuscript.

5. Conclusion

In this paper, a novel method utilizing the self-adapted FCM clustering combined with the Markov model and GA is proposed to determine the best mix of HPS. A power balance strategy is also designed to guide the optimization process. The self-adapted FCM clustering can handle the stochastic characteristics of REGs, and the Markov model can significantly reduce the operational scenarios of REGs. The proposed method has comparable competitive overall cost, and it can be concluded that the benefits of the reduction of CO₂ and the improvement of LOSP are negatively related to the cost optimization procedure.

The future work will include the following:

(1)
Improving the clustering model to further study the correlation among renewable resources
(2)
Adding the local and global control strategy to the power balance analysis process
(3)
Extending the proposed method to the operation plan stage of the HPS.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

References

1 Wai R.-J., Cheng S., Lin Y.-F., and Chen Y.-C., Installed capacity selection of hybrid energy generation system via improved particle-swarm-optimisation, IET Generation, Transmission and Distribution. (2014) 8, no. 4, 742–752, 2-s2.0-84897440060, https://doi.org/10.1049/iet-gtd.2012.0092.
10.1049/iet-gtd.2013.0092
Web of Science® Google Scholar
2 McGowan J. G. and Manwell J. F., Hybrid wind/pv/diesel system experiences, Renewable Energy. (1999) 16, no. 1-4, 928–933, 2-s2.0-0032917438, https://doi.org/10.1016/S0960-1481(98)00319-X.
10.1016/S0960-1481(98)00319-X
Web of Science® Google Scholar
3 Arabali A., Ghofrani M., Etezadi-Amoli M., and Fadali M. S., Stochastic performance assessment and sizing for a hybrid power system of Solar/Wind/Energy Storage, IEEE Transactions on Sustainable Energy. (2014) 5, no. 2, 363–371, https://doi.org/10.1109/tste.2013.2288083, 2-s2.0-84898018359.
10.1109/TSTE.2013.2288083
Web of Science® Google Scholar
4 Barton R. R., Presenting a more complete characterization of uncertainty: Can it be done, Proceedings of the in Proceedings of the Simulation Society research workshop (INFORMS ′07 ), 2007, 26–60.
Google Scholar
5 Ela E. and O′Malley M., Studying the variability and uncertainty impacts of variable generation at multiple timescales, IEEE Transactions on Power Systems. (2012) 27, no. 3, 1324–1333, 2-s2.0-84864288818, https://doi.org/10.1109/TPWRS.2012.2185816.
10.1109/TPWRS.2012.2185816
Web of Science® Google Scholar
6 Keane A., Ochoa L. F., Borges C. L. T., Ault G. W., Alarcon-Rodriguez A. D., Currie R. A. F., Pilo F., Dent C., and Harrison G. P., State-of-the-art techniques and challenges ahead for distributed generation planning and optimization, IEEE Transactions on Power Systems. (2013) 28, no. 2, 1493–1502, 2-s2.0-84885021397, https://doi.org/10.1109/TPWRS.2012.2214406.
10.1109/TPWRS.2012.2214406
Web of Science® Google Scholar
7 Mohamed Abd El Motaleb A., Kazim Bekdache S., and Barrios L. A., Optimal sizing for a hybrid power system with wind/energy storage based in stochastic environment, Renewable and Sustainable Energy Reviews. (2016) 59, 1149–1158, 2-s2.0-84955617357, https://doi.org/10.1016/j.rser.2015.12.267.
10.1016/j.rser.2015.12.267
Web of Science® Google Scholar
8 Koutroulis E., Kolokotsa D., Potirakis A., and Kalaitzakis K., Methodology for optimal sizing of stand-alone photovoltaic/wind-generator systems using genetic algorithms, Solar Energy. (2006) 80, no. 9, 1072–1088, https://doi.org/10.1016/j.solener.2005.11.002, 2-s2.0-33746776198.
10.1016/j.solener.2005.11.002
Web of Science® Google Scholar
9 Ahmadi S. and Abdi S., Application of the Hybrid Big Bang-Big Crunch algorithm for optimal sizing of a stand-alone hybrid PV/wind/battery system, Solar Energy. (2016) 134, 366–374, 2-s2.0-84968820407, https://doi.org/10.1016/j.solener.2016.05.019.
10.1016/j.solener.2016.05.019
Web of Science® Google Scholar
10 Maleki A. and Pourfayaz F., Optimal sizing of autonomous hybrid photovoltaic/wind/battery power system with LPSP technology by using evolutionary algorithms, Solar Energy. (2015) 115, 471–483, 2-s2.0-84925451621, https://doi.org/10.1016/j.solener.2015.03.004.
10.1016/j.solener.2015.03.004
Web of Science® Google Scholar
11 Benmouiza K., Tadj M., and Cheknane A., Classification of hourly solar radiation using fuzzy c-means algorithm for optimal stand-alone PV system sizing, International Journal of Electrical Power and Energy Systems. (2016) 82, 233–241, 2-s2.0-84961613745, https://doi.org/10.1016/j.ijepes.2016.03.019.
10.1016/j.ijepes.2016.03.019
Web of Science® Google Scholar
12 Mosadeghy M., Yan R., and Saha T. K., A time-dependent approach to evaluate capacity value of wind and solar PV generation, IEEE Transactions on Sustainable Energy. (2016) 7, no. 1, 129–138, 2-s2.0-84958113816, https://doi.org/10.1109/TSTE.2015.2478518.
10.1109/TSTE.2015.2478518
Web of Science® Google Scholar
13 Xu L., Ruan X., Mao C., Zhang B., and Luo Y., An improved optimal sizing method for wind-solar-battery hybrid power system, IEEE Transactions on Sustainable Energy. (2013) 4, no. 3, 774–785, https://doi.org/10.1109/tste.2012.2228509, 2-s2.0-84880312673.
10.1109/TSTE.2012.2228509
Web of Science® Google Scholar
14 Hong Y.-Y. and Lian R.-C., Optimal sizing of hybrid wind/PV/diesel generation in a stand-alone power system using markov-based genetic algorithm, IEEE Transactions on Power Delivery. (2012) 27, no. 2, 640–647, 2-s2.0-84859783921, https://doi.org/10.1109/TPWRD.2011.2177102.
10.1109/TPWRD.2011.2177102
CAS Web of Science® Google Scholar
15 Gopiya Naik S. N., Khatod D. K., and Sharma M. P., Analytical approach for optimal siting and sizing of distributed generation in radial distribution networks, IET Generation, Transmission and Distribution. (2015) 9, no. 3, 209–220, 2-s2.0-84923200620, https://doi.org/10.1049/iet-gtd.2014.0603.
10.1049/iet-gtd.2014.0603
Web of Science® Google Scholar
16 Yejun X., Fitzwilliam College, Proceedings of the 10th International Conference on Computer Science & Education (ICCSE′ 15), 2015, Cambridge, UK, Fitzwilliam College, Cambridge University, 22–24.
Google Scholar
17 Dobakhshari A. S. and Fotuhi-Firuzabad M., A reliability model of large wind farms for power system adequacy studies, IEEE Transactions on Energy Conversion. (2009) 24, no. 3, 792–801, 2-s2.0-70049107322, https://doi.org/10.1109/TEC.2009.2025332.
10.1109/TEC.2009.2025332
Web of Science® Google Scholar
18 Chen L., Chen H., Shu Z., Zhang G., Xia T., and Ren L., Comparison of inductive and resistive SFCL to robustness improvement of a VSC-HVDC system with wind plants against DC fault, IEEE Transactions on Applied Superconductivity. (2016) 26, no. 7, 1–8, https://doi.org/10.1109/tasc.2016.2595622, 2-s2.0-84982300236.
10.1109/tasc.2016.2595622
CAS Web of Science® Google Scholar
19 Li Y. and Yu F., A new validity function for fuzzy clustering, 1, Proceedings of the International Conference on Computational Intelligence and Natural Computing (CINC ′09), June 2009, IEEE, 462–465, https://doi.org/10.1109/cinc.2009.100, 2-s2.0-70350527258.
10.1109/cinc.2009.100
Google Scholar

Citing Literature

All articles

Optimal Sizing for Wind/PV/Battery System Using Fuzzy c-Means Clustering with Self-Adapted Cluster Number

Abstract

1. Introduction