By tangential curvature of the stacking line of the profiles guide vanes can be designed, which have on both ends an obtuse angle between suction side and sidewall. This configuration, according to literature, is capable of reducing secondary loss. This type of vanes develops considerable radial components of the blade force and effects a displacement of the meridional flow towards both sidewalls. In this paper we work with a finite-volume-code for computations of the three-dimensional Reynolds averaged Navier-Stokes equations for an axial turbine stage with radial and two types of tangentially curved guide vanes. With computational results, mathematical formulations are developed for a new flow model of deflection of such blades that are formally compatible with the assumption of a rotation-symmetrical flow and with the existing throughflow codes, in order to predict the deflection angle over the blade height for the tangential leaned and curved blades.

1. Introduction

The classic design method for the blading of axial turbines, applied for many decades, stipulates that the profiles constituting the blade body are stacked in radial direction. Such stacked profiles can be different forms in the case of twisted blades. When such blading profiles are arranged with the profile centers of inertia on a radial line, the stacking line, bending stress by centrifugal force is avoided in rotor blades. The normal of the surface elements of blades designed accordingly is directed essentially to be tangential-axial, so that the pressure forces of the blades have no or quite small radial components; these are usually neglected in the aerodynamic calculation. Consequently only the radial pressure gradient and the centrifugal force resulting from the circumferential component of the flow velocity are acting in radial direction on the fluid particles passing through the turbine stage. Minor additional radial forces may result from streamline curvature and inclination. They enter as important parts into the equation of radial equilibrium, which is one of the basic equations for the fluid-dynamic design of axial turbomachines.

The classic blade design results in difficulties, particularly in the case of long blades as in the LP-part of condensing steam-turbines (e.g., [1]), because the large radial pressure gradient in the gap between stator and rotor causes a considerable variation of the degree of reaction over the blade length (e.g., 0% at the hub and 80% at the tip), which complicates blade design and reduces efficiency.

Consequently the idea was born by Deich et al. [2], to produce additional blade forces in radial inward direction by circumferential inclination of the stator blades in order to counteract the centrifugal forces and so to reduce the radial pressure gradient. The idea proved successful and caused extensive research on different blade forms with nonradial surface elements (e.g., [3–6]).

It was found in addition that a blade inclination in the sidewall area, which produces an obtuse angle between blade suction side and sidewall, can reduce secondary loss, while an acute angle will increase it. A pure inclination of the stacking line in circumferential direction (lean) will therefore create a positive effect on secondary loss at one end of the blade and a negative effect at the other end. Such inclined blade has been discussed by several authors; see, for example, Deich et al. [2, 7–9]; Han et al. [10, 11]; Harrison [12]; Hourmouziadis and Hübner [13]; Suslov and Filippov [14]; Wang et al. [15], an experiment research, and Deich et al. [2, 7–9]; Hourmouziadis and Hübner [13]; Pioske and Gallus [16]; Smith Jr. and Yeh [5]; Suslov and Filippov [14], a numerical research, as well as the references therein.

In order to realize the loss reducing obtuse angle between suction side and sidewall on both ends of the blade a curvature (bow) of the stacking line of the profiles is necessary. For stator blades this can be realized without mechanical trouble. This design appears favourable especially for short blades, as in height pressure (HP) and middle pressure (MP), part of steam-turbines, since there secondary loss together with clearance loss amounts to 20–40% of the total aerodynamic loss, while a reduction of the radial pressure gradient, not realizable with this type of blade, is not important. The research work of the flow in axial turbine stages with curved stator blades is therefore an important research topic for actual turbomachinery and aeroengines. And some results of the curvature blades can be found in Deich et al. [7–9]; Filippov and Wang [17, 18]; Wanjin et al. [11]; Harrison [12]; Hourmouziadis and Hübner [13]; Jiang et al. [19]; Vogt and Zippel [20]; Wang and Zheng [21]; Wolf and Romanov [22], an experiment research, and Filippov et al. [18, 23]; Hourmouziadis and Hübner [13]; Jiang et al. [19]; Pioske and Gallus [16]; Suslov and Filippov [14]; Wang and Zheng [21], a numerical research, where the curvature form of such researches is however mostly a simple curvature (circle) form.

Experimental researches and numerical computations are available as tools to obtain a detailed knowledge of the 3D-flow field and to understand the effect of geometric modifications. Simulation offers the opportunity of a very detailed insight in the complete flow field which is hardly accessible by experimental means. In addition it is ideally suitable for systematic research of geometry variations, as necessary in the present case. However, the quality of simulation results will be influenced by numerical iteration procedure, turbulence model, mesh-structure, wall-flow model, and so forth in a way that is difficult to control. It is therefore highly recommendable to validate the results of simulation with the aid of experimental data, as has been possible in the present case.

The object of the present paper is the numerical simulation of the flow in an axial turbine stage equipped with several variations of tangentially curved stator blades by using a finite-volume-code for the 3D Reynolds averaged Navier-Stokes equations. The research work is centered on

(i)
effects of blade curvature on the flow in the stator,
(ii)
effects of the stator blade curvature on the flow in the rotor (which remained unchanged in geometry),
(iii)
effects of the blade curvature on stage characteristic,
(iv)
new modeling of the radial blade force and the deflection angle over the blade height for the tangential leaned and curved blades that are formally compatible with the assumption of a rotation-symmetrical flow and with the existing throughflow codes.

Definition of Curved Blade. The research is restricted to stator blades curved of both ends as follows. The stacking line of the profiles is curved in circumferential direction as, for example, in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Definition of guide vanes curved on both ends by its stacking line in S₃-plane.

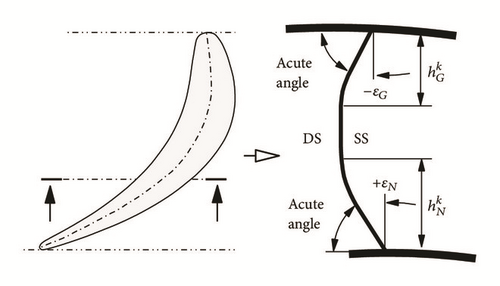
The curvature is defined by the angle ε between the stacking line and the sidewall at the blade end and by the extension h^k of the nonradial part of the stacking line. These values can be different at both ends of the blade.

(i) Positive Tangential Blade Curvature. If an acute angle between the pressure side DS and the sidewall is realized, the curvature is defined as positive.

(ii) Negative Tangential Blade Curvature. A blade with negative curvature shows acute angles between suction side SS and sidewall.

2. Computational Methods

The applied numerical procedure solves the 3D-time-dependent Reynolds averaged Navier-Stokes equations with the finite volume method and comprises different turbulence models. Some validations showed a very good quality of the results. For turbomachinery as well as aeroengine applications the program contains a procedure for circumferential averaging of flow parameters in planes between blade rows, for example, between stators and rotor, in order to make a steady-state calculation feasible in both blade rows. A suitable averaging plane was provided in the grid design. The calculation used the Baldwin-Lomax turbulence model [24] and a three-level full multigrid method for convergence acceleration. Our simulation results showed a difference of mass flow in the inlet and outlet plane of less than about 0.02%. Details on the computational methods of this code are available in some literatures, for example, [25–30].

2.1. Governing Equations

The applied numeric procedure regards the so-called Reynolds averaged Navier-Stokes (RANS) equations as the physical basic model. Their hyperbolic system of conservation equations applied for mass, impulse, and energy depends on velocity, pressure, and enthalpy. They can be mostly written as a recapitulatory form

()

Thereby

denotes the conservative variables,

the matrices of the fluxes, and Q the source terms column-vector.

is actually combined from the matrices of the frictionless flux (Euler)

and the dissipative flux (Navier-Stokes)

. It can be rewritten as the following compact form further into the following general conservative form [25, 27, 29, 30]:

()

where

denote the density, the velocity vector, the total energy, the total enthalpy, the 3 × 3 unit matrix tensor, the viscous shear stress tensor, the external force vector, the column-vector of characteristic variables, and the source term, whereby the velocity vector has components u, v, w. According to the character of flow we can differentiate in each case according to the hyperbolic, parabolic, and elliptical type of equation. The time-dependent Navier-Stokes equation possesses a hyperbolic-parabolic character within the temporal-spatial ranges, because the steady Navier-Stokes equations are a mixed type in the spatial domain. From it we obtain the elliptical-parabolic type which describes subsonic flows and the hyperbolic-parabolic type supersonic flows. For the flows with high Reynolds numbers the system of the conservative equations causes convection obtained in most flow domains.

2.2. Method of the Spatial Discretization

The spatial fluxes of the applied basic equations of (1) and (2) are actually discretized using the finite volume scheme. The finite volumes scheme has been usually spread using numeric technology in particular for flow problems, because the integral form of the conservative equations can be interpreted by direct discretization for a volume cell of the grids with the structured as well as unstructured grids very flexibly and easily [25, 27, 29, 30].

Under the condition that the temporal derivatives are exchangeable with the spatial integrations (i.e., the integrands are constantly differentiable in t), the integral forms can be normally deduced from the above differential expression (1). For this reason the following integral form of the conservative equations is given by

()

therefore it is formulated for any volume V with the control surface S = ∂V. The discretization in the spatial is realized with an approximation of the volume V by elementary cells, which contain, respectively, an element ΔS of control surface S. Then the above integral equation (3) can be discretized and rewritten as follows:

()

whereby

denotes the flux where they are combined, respectively, from frictionless

and dissipative

fluxes.

2.2.1. Numerical Fluxes

The frictionless flux

and the dissipative flux

are discretized, for example, in each case by the upwind scheme and an application of Gauss theorems. The treatment of the two fluxes will be not implemented here; their detailed description is represented in [25, 27, 29–35]. The physical fluxes are mainly discretized in the approximation of the central scheme as follows:

()

This treatment for the numeric flux does not lead actually to a stable scheme, because it does not give sufficient numeric dissipation. Therefore one needs an artificial dissipation term, in order to eliminate odd-even oscillations because of the central discretization (high frequency oscillations) and in order to capture shocks without oscillation. The usual formulation prosecutes the type of the dissipation from Jameson et al. [31]; it is actually formulated as sum of conservative variable derivation, respectively, in second order with nonlinear coefficients for shock capturing and in linear fourth order for the background oscillations. In this way the numeric flux (5) transferred into the form [25, 27, 29, 30]

()

where d_i+(1/2) is the artificial dissipation. This term from Jameson et al. is defined as follows in one-dimensional form [31]:

()

The scalar coefficients ϵ are defined in the following way

()

and connected with the variables of pressure and temperature

()

The pressure quantities are only used for liquids.

For the Navier-Stokes equation, the friction-affected dissipation is normally not sufficient in the solution and therefore is the above term of the artificial dissipation necessarily by the numeric solution of the Navier-Stokes equation. The unexpected difficulty with this approximation hence comes from the fact that the solution and the convergence can be strongly dependent on the coefficients [25, 27]. This approximation will be used with either explicit or implicitly temporal integration.

2.3. Turbulence Model

Since there is still no universal and general turbulence model, the turbulence model will govern the results simulated [24, 25, 27]. In this study, Baldwin-Lomax turbulence model, which is suitable for the wider class of interference model to achieve enough accurate and reliable results for a turbomachinery, is chosen for the fully turbulence condition. The added blended wall function implemented in the Baldwin-Lomax turbulence model leads to the boundary layer at the solid walls with further refinement by y⁺ value with y⁺ ≈ 1.

3. Computational Conditions

As a starting point data from an experimental research of a single stage air turbine with different types of curved guide vanes were made available to us by the department for power, nuclear turbine construction, and aircraft engines of State St. Petersburg Technical University (Russia). They comprised stage characteristics as well as detailed flow measurements with aerodynamic probes. Comparison of these data with the results of numerical simulation of the same geometries, reported in [36], showed good agreement and served as validation of the simulation technique chosen. A number of stator configurations with different types of bow was derived from the geometry of the experimental turbine and investigated numerically.

3.1. Single Stage Experimental Air Turbine

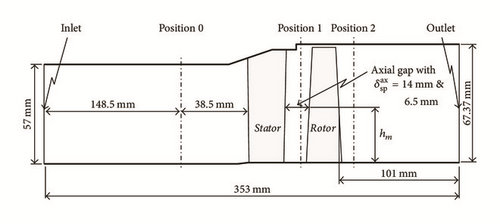
Figure 2 shows the meridional section of the turbine, the test results of which have been used for the validation of the numerical simulation procedure. For the measuring planes positions 0, 1, and 2 data of probe measurements were available. The extension of the meridional section in Figure 2 shows, too, the field of the numerical calculation.

3.2. Geometrical Data of the Researched Blades

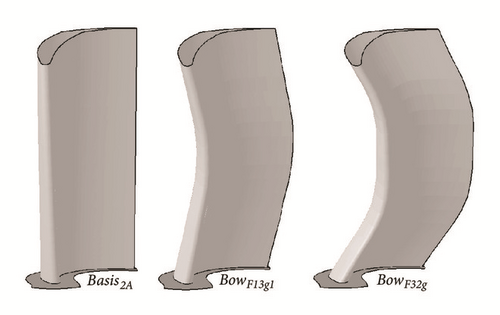
The experimental investigations were made for a radial guide vane Basis_2A and a curved guide vane Bow_2B, both combined with the same rotor. Characteristic data of the center-line profiles are given in Table 1. For the numerical research 8 different stator blade rows have been calculated with a systematic variation of curvature by tangential displacement of the unchanged profiles of the radial stator Basis_2A. Results are given here for the basis blading and the two most characteristic bow stators. Data describing the curvature are shown in Table 2; the parameters describing the curvature are ε and the relative extension according to Figure 1. Figure 3 shows a 3D representation of the three guide vanes.

Table 1. Geometrical data of the center line profiles.

Notation	Unit	Basis_2A	Bow_2B	Rotor
Blade height	[mm]	65.6	65.6	66.87
Middle diameters	[mm]	363.98	363.98	364.24
Blade chord	[mm]	31.159	32.101	20.26
Max. camber	[mm]	7.047	5.254	6.063
Stagger-angle	[deg.]	43.00	36.00	57.20
Inlet angle	[deg.]	80.00	90.00	42.00
Outlet angle	[deg.]	15.37	13.95	21.33
Rel. pitch	[—]	0.4898	0.4745	0.7433
Blade number	[—]	74	74	76
δ_sp	[mm]	—	—	0.5

Table 2. Geometrical data of the investigated guide vanes.

Notation	Abbreviation	ε_N	ε_G
Unit	[—]	[deg.]	[deg.]	[—]	[—]
1	Basis_2A	0.0	0.0	—	—
2	Bow_F13g1	+13.2	−12.2	0.453	0.438
3	Bow_F32g	+32.0	−29.0	0.409	0.374

3.3. Computational Mesh

The calculation mesh for the numerical simulation is identical in form as well as in cell number for all investigated blading. Table 3 gives the cell numbers in three coordinate directions (i circumferential, j radial, and k axial direction). The entire computation area was divided into three zones in order to realize a rather orthogonal mesh. Near the blade profiles an O-mesh was used, for the inlet channel an H-mesh, and for the outlet area of the stator an I-mesh with H-mesh extension in order to adapt the wake of the blade. In the outlet channel of the rotor only an H-mesh was applied. A total of 973191 nodes resulted for the complete calculation area.

Table 3. The mesh distributions of the turbine stage.

Notation	H-mesh	O-mesh	I + H/H-mesh
	(Inlet)	(Blade)	(Outlet)
	[i × j × k]	[i × j × k]	[i × j × k]
le	33 × 57 × 33	33 × 57 × 217	33 × 57 × 49
la	41 × 57 × 17	41 × 57 × 177	41 × 57 × 25

Figure 4 shows the grid configuration for the applied guide vanes and rotor blades. The interfaces of the two domains for stator and rotor are the only overlapped region and there is only one accepted virtual translating direction along the interfaces; that is, it is unacceptable to translate across the interfaces. Considering the complex geometry of this system, for accuracy of the prediction, the regions near interfaces and boundary layers of the stator and rotor, finer structured mesh was employed in the present numerical computation; on the other side, regions far from stator and rotor are meshed with coarser structured mesh.

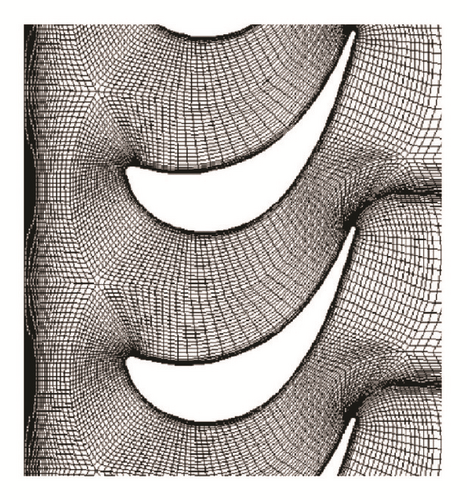
This mesh configuration considers the calculation and comparison of turbulence model and combines it with the near wall modified function with low Reynolds numbers in order to effectively offset the interference that occurs in the internal flow field to improve the near wall computational grid’s deficiencies.

Therefore, the distance of the first cell layer from the blade surface was 0.001 mm; the added blended wall function implemented in the turbulence model leads to the boundary layer at the solid walls with further refinement by y⁺ value; this gave a value of the dimensionless wall-distance y⁺ ≈ 1.

The computation of entire mesh used a three-level full multigrid method for convergence acceleration. Our simulation results for such a mesh configuration showed a difference of mass flow in the inlet and outlet plane of less than about 0.02%. This validation showed a very good quality of the applied mesh configuration.

3.4. Operating Conditions of the Turbine Stage

The numerical calculation of the flow in the turbine stage was realized for its optimum operating point deduced from the experimental data, all relevant data for inlet and outlet are summarized in Table 4. The total-static pressure ratio .

Table 4. The aerodynamic data in the optimal operation point.

Notation	Unit	Value
	[Pa]	142857
	[Pa]	140812.5
	[Pa]	100000
	[K]	323.1
	[K]	321.772
Tu	[%]	1 ⋯ 2%
h/S_Bi	[—]	2.1^le
	[m/s]	51.657
	[m/s]	0.0
	[m/s]	0.0
	[kg/s]	4.93
n	[rpm]	7190
R	[J/(kgK)]	287.14
ρ	[kg/m³]	1.53

The applied 3D calculations of total stage efficiency with axial gap 6.5 mm were performed for two different ranges of the run number ν.

(i) Run Number ν in the Range 0.3 to 0.6. In this range of the run number, the pressure ratio Π = 0.7 remained constant, so the enthalpy change remained also constant. But the rotational speed was changed for different operating points. The applied data are shown in Table 5.

Table 5. The operating points of rotating speed as a variable in the range of run number ν between 0.3 and 0.6.

ν [—]	0.314	0.366	0.455	0.484	0.539	0.550	0.563	0.578
n [rpm]	4113	4790	5955	6326	7046	7190	7366	7567

(ii) Run Number ν in the Range 0.6 to 0.9. In this range of the run number, the rotational speed was no longer changed, but the reduced rotational speed was maintained at a constant value 4000. However, on the contrary, the pressure ratio was changed by various static pressures on entry. This data is shown in Table 6. Therefore, the enthalpy or the mass flow is also changed.

Table 6. The operating points of total pressure at the inlet as a variable in the range of run number ν between 0.3 and 0.6.

ν [—]	0.600	0.612	0.672	0.704	0.778	0.800
[Pa]	134543	132957	126460	123753	118911	117797

4. Results and Discuss

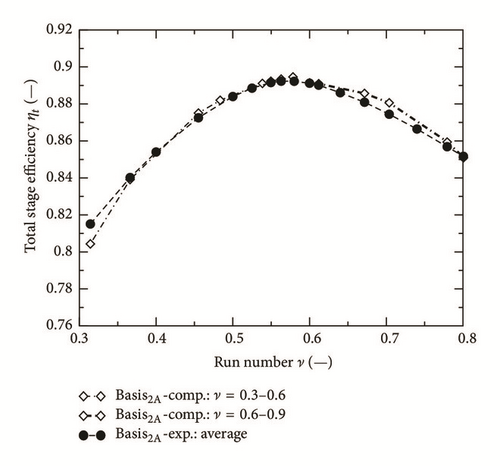
4.1. Validation of Numerical Results

For the operating points in both Tables 5 and 6, the turbine stage was computed with a real axial gap 6.5 mm, the results are shown in Figure 5. It shows that the stage efficiency is a function of the run number ν. The run number ν has been divided into two ranges for the computations of the stage efficiency. In the range of the run number between 0.3 and 0.6, the stage efficiency of the radial blade Basis2A agrees very well with the experimental data. However, the computations of this radial blade in the range between 0.6 and 0.9 also show a pretty good consistency outside the range between 0.65 and 0.85 since in this range only a deviation of about 0.3 occurs. The accuracy of presented numerical results can therefore be validated by this comparison result clearly.

4.2. Effect on the Meridional Streamlines

The form of meridional streamlines is essentially determined by the radial blade forces acting on the flow, mainly the centrifugal force and the radial pressure gradient ∂p/∂r. In the familiar stage design according to the free vortex law (approximately it is realized in the Basis_2A-stage), these are balanced so that no radial displacement of streamlines occurs, as in Figure 6.

The type of bow applied in two guide vanes presented here will create additional radial blade forces acting towards the hub and the casing in the sidewall regions. The balance of radial forces and the radial flow displacement will vary to extent in the circumferential direction too and then a 3D-flow field will be formed really. A simplified presentation is shown in Figure 6; a circumferential averaged flow over the pitch is calculated and applied to the calculation of meridional streamlines in this figure; a similar result would be achieved by a 2D-calculation of the flow field.

By the comparison with both curved guide vanes of the meridional flow in Figure 6, it shows that the radial displacement of streamlines towards the guide vane ends has the same effect of bow. The bow-effect for the vane Bow_F32g, whose inclination (bow) angles ε have more than double the value of the vane Bow_F13g1, is more distinct. The radial deflection tapers off in the gap between stator and rotor and is concentrated in the outlet part of guide vanes, where the radial blade force has its full effect. Consequently, the deflection of streamlines towards the sidewall will cause a deceleration of the axial flow velocity in the middle part of guide vanes, which can be seen under the increased distance of streamlines compared with the radial guide vane Basis_2A; such an effect for the velocity distribution over the blade height is important.

4.3. Radial Blade Forces Produced by Blade Curvature

4.3.1. Treatment and Modeling of the Radial Blade Force

Blading designed according to standard principles with radial stacking line produces blade forces acting essentially in circumferential and axial directions, and the radial component remains very small. In addition, the inclined and curved guide vanes develop the radial blade force, which can attain the same magnitude as the circumferential and axial components and therefore enter into the radial equilibrium as important terms, which influences the flow field.

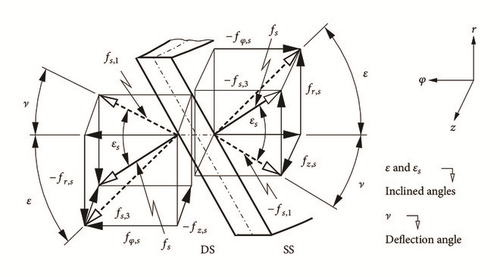
A schematic representation of three-dimensional blade force and an element angle of inclined or curved guide vane are represented as a definition of balance direction in Figure 7 at the blade trailing edge. It shows that on the flow the reaction blade forces of guide vane are exerted on the pressure side and the suction side , respectively. They act on the blade surface perpendicularly and have different values on both sides.

The local blade force

is defined by the inclined surface element of the blade and its axial and radial length elements Δz_z and Δh_r can be calculated from the local static pressure p_s at the blade surface in the following form:

()

where ε is the inclination angle against the radial direction and the deflection angle ν against the axial direction of the surface element. In addition, the element length along the blade contour Δz_E and the element height along the inclined blade height Δh_E can be computed by the forms Δz_E = Δz_z/cos v and Δh_E = Δh_r/cos ε, respectively.

The local blade force

in Figure 7 can be divided into two components of blade force

in the S₁-plane (blade to blade) and

in the S₃-plane. The blade force in the S₁-plane arises from the blade force

with the inclined angle ε_s in the following form:

()

thereby the inclined angle ε_s is determined over the tangent through the radial blade force

and the blade force in the S₁ plane

()

Both blade forces in the S₁ and S₃-planes can be further divided into three coordinate directions,

, and

describing the blade forces in circumferential, radial, and axial directions, respectively. By the blade force in the S₁-plane, the circumferential blade force can be also indicated in the form

()

with this definition the radial blade force in the S₃-plane arises

()

The local radial blade force

can be therefore obtained by the following new general form:

()

4.3.2. Distribution of the Resultant Radial Blade Force

The distribution of the radial blade force over the entire blade height must be described in detail for the effect of the blade curvature. The total radial blade force

of a profile section with the elementary height dh results from the integration over all surface elements on this profile

()

where the indices i, j are the ith and jth surface element of the blade on the pressure (DS) and suction (SS) sides, respectively. The total radial blade force is the sum of the pressure side part and the suction side part; it is always directed from the pressure side to the suction side. The distribution of the total radial blade force per length-element of the blade is shown in Figure 8 for the radial guide vane (assuming no radial blade force) and both curved guide vanes. From Figure 8 we find the following phenomena:

(i)
The region for the radial blade force is about equal to the region of blade zones for bow (ca. 40% of blade height on both ends).
(ii)
The radial blade force is increasing in the inclination (curved) angle ε as well as on the same blade in direction of the increasing bow as from blade to blade with increased bow.
(iii)
The radial blade force tapers off in the proximity of sidewall, even if the inclination (curved) angle increases there. This is probably due to reduced aerodynamic loading of profiles there.

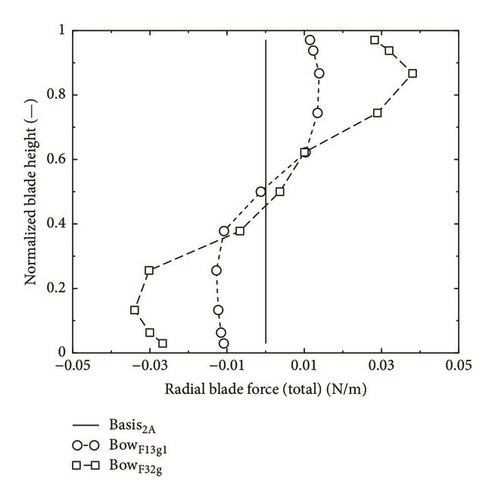
The distributions and magnitude of the radial blade force correspond directly with the deflection of meridional streamlines in Figure 6, introducing the radial blade force in the equation of radial equilibrium; their form can be calculated quantitatively.

4.4. Effect of the Blade Curvature on the Static Pressure Distribution at the Profiles

The aerodynamic blade forces and their components result from the static pressure on the profile and the geometric orientation of its surface elements. The pressure distribution itself is, also, of great importance for the flow over the profile, especially the boundary layer and its development. Boundary layer thickness, transition, and eventually separation depend to a great deal on the pressure distribution. It is of great interest therefore how the inclination and curvature of a blade influence the pressure distribution.

4.4.1. Aerodynamic Load of the Blade Profiles

If the static pressure distribution over a profile is presented over the axial chord, as in Figure 9, the area circumscribed by the pressure side and the suction side curve is directly proportional to the circumferential (or working) total force of the blade profile; the difference between the two curves at an axial station describes the local aerodynamic loading and the form, especially of the suction side curve, is important for the boundary layer development and hence for the profile loss.

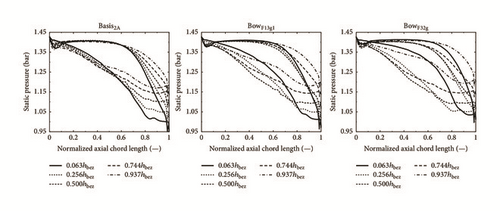
Figure 9 shows the static pressure distributions over the profile sections at different height positions for the three guide vanes treated here. Two curves are near the sidewalls (0.063 and 0.937 normalized blade height), two are in the middle of the bow zones (0.256 and 0.744), and one is in the middle of the blades (0.5). It is obvious that, because of the radial pressure gradient between stator and rotor, the outlet pressure increases with increasing blade height, as visible in Figure 9 for all three stators. Noteworthy is the decrease in aerodynamic loading (circumscribed area) towards the sidewall with increasing bow, especially in the hub area. Finally remarkable and quite unexpected is the fact that the pressure distributions of the profiles close to the sidewalls of the curved vanes are distinctly deformed, so that the aerodynamic loading is not only reduced, but also displaced towards the trailing edge and acceleration on the suction side is delayed. This effect seems, too, to be proportional to the degree of curvature.

4.4.2. Pressure Distribution on the Suction Side

The variation of the pressure distribution, especially on the suction side, by the blade curvature is shown in Figure 9 for several distinct profile sections. It can also be demonstrated in a continuous way by a graph of the pressure distribution on the suction side over the blade height as shown in Figure 10 for the three vanes. The isobaric lines of the radial basis vane extend essentially in radial direction over the blade height; the peaks near the trailing edge are a result of a slight overspeed on the profile. In direct proximity of the sidewalls they bow a little downstream. This somewhat more distinct effect near the casing is probably due to the conical contour.

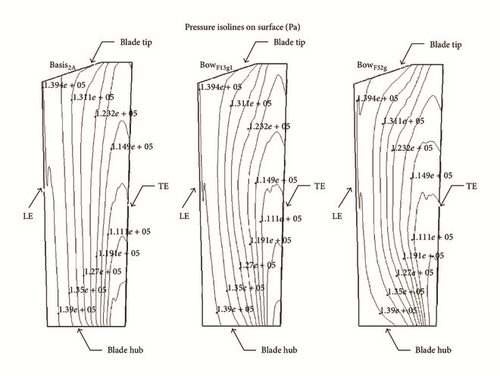
Blade curvature now effects a clear displacement of the isobars in downstream direction near both sidewalls, more pronounced by stronger blade curvature, and resulting from the downstream movement of the blade loading described in Section 4.4.1. While the local inclination of the blade produces for the bulk of the flow an additional force directed towards the sidewalls, as shown before, it creates, somewhat unexpected, near the suction surface of the blade a component of the pressure gradient, which is directed towards the middle of the blade. As is well-known the low energy fluid of the secondary flow accumulates in the corner between suction side and sidewall. This static pressure component directed towards the center of the blade might be able to transport part of the low energy fluid out of the suction corner and might be assisted by the obtuse angle between sidewall and suction side resulting from the blade inclination. Here is a reason for the repeatedly observed reduction of secondary loss by bowing of blades.

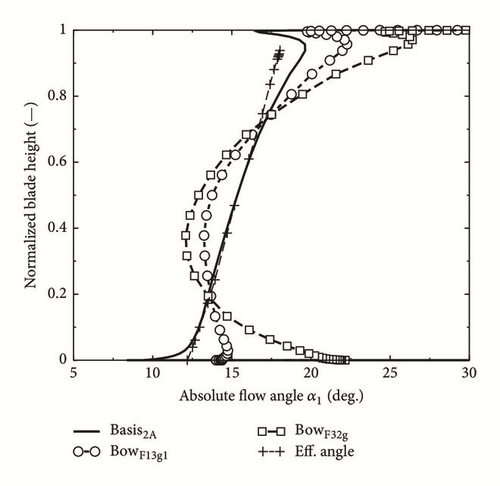
4.5. Effect of the Curvature on the Vane Outlet Angle

Since the inclination of the blade changes the aerodynamic loading as well as the circumferential component of the blade force the turning of the flow (e.g., [37]), that is, the outlet angle of the vane, will be influenced, too (e.g., [38]). Figure 11 shows the distribution of the flow outlet angle, averaged over one pitch, over the blade height. The angle of the radial blade is equal to the value according to the sine-rule (effective angle) over most of the blade height. The curved blades exhibit clear underturning over 20% of the blade length at both ends, intensified by higher blade inclination, which is certainly due to the reduced blade loading in these areas. Not so obvious is the explanation for the overturning by 2 to 4 deg. in the middle zone. Probably it can be attributed to the deceleration of the axial flow velocity in this area because of the deflection of the flow towards the sidewalls.

4.6. Effect of the Blade Curvature on the Loss Coefficient of the Vanes

As explained initially the advantage gained by use of partly or completely inclined vanes is the reduction of the radial pressure gradient and hence the gradient of the degree of reaction especially for long blades. The interest in real bow vanes in turbines accrues mainly from the possibility of reducing the flow losses. Therefore the research of the influence of vane curvature on aerodynamic loss is of central importance. The vane loss coefficient was defined according to Traupel [39] as

()

The isentropic enthalpy drop

of the stator is

()

The loss coefficient at a sufficient number of stations along the streamtubes of constant % blade height was determined from the results of the 3D-simulation with circumferentially averaged values of the parameters and is presented for the three different vane types in Figure 12, whereby p_0,s is a function of the radius in (18) and all parameters are used in this connection along the streamlines over blade height in each case for stator and rotor. The curves are not simple to interpret, but it is obvious that the vane with moderate bow has lower losses near both sidewalls and a certain increase in the middle zone, compared with the radial vane. The vane with high bow exhibits a sharp reduction of the loss coefficient in direct proximity of the sidewalls, but then a considerable increase around 0.2 and 0.8 normalized blade length, while in the middle of the blade the loss is equal to that of the radial blade.

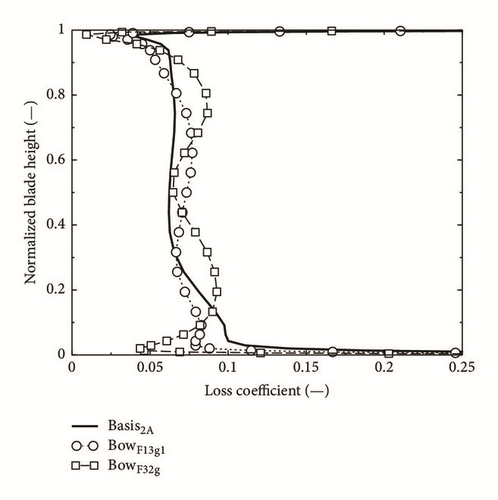
The changes of the loss distribution and magnitude will be due to a combination of influences, as different development of profile boundary layer because of different pressure distribution, oblique movement of boundary layer on inclined parts of the blade, different secondary flow, and so forth. Finally the well-known deficiencies of Navier-Stokes-solvers in calculating dissipation correctly must not be forgotten.

The integrated loss of the three stators is calculated by the presented curves of the illustrations according to

()

and their differences according to

()

The values are presented in Table 7. Such results are identical to Figure 6 for the effects of the radial displacement of the meridional streamlines for radial and curved blades. It turns out that a moderate bow effects a reduction in total loss, while the high bow vane exhibits higher loss than the radial vane.

Table 7. Integrated loss coefficient of all investigated vanes.

Notation		[%]
Basis_2A	0.0767	—
Bow_F13g1	0.0744	−2.943
Bow_F32g	0.0782	+2.005

5. Effects of the Vane Curvature on the Rotor Flow

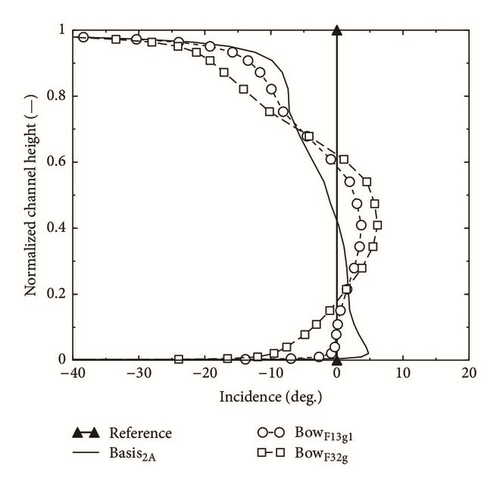
Any modification of the stator of a turbine stage, which changes the flow field at its outlet, will directly influence the flow entering the rotor and therefore its aerodynamic effectivity (e.g., [40–45]). In our case the curvature of the stator vanes changes the outlet angle and the axial flow velocity; together they define in the velocity triangle the relative inlet flow angle for the rotor. The difference between aerodynamic inlet angle and the geometric inlet angle of the rotor blade, the incidence angle, is of central importance for the aerodynamic action of the rotor blade profiles. High positive inlet angles cause an aerodynamic overload of the profile and high loss. Negative incidence angle may result in adverse profile pressure distribution and increased loss, too.

Figure 13, showing the rotor incidence angles for the three cases, makes it clear that the basis stage, which had been conceived for the experiments at the department for power, nuclear turbine construction, and aircraft engines of State St. Petersburg Technical University, had already not been designed in an optimum way, since in the top half of the rotor blade a considerable negative incidence prevails. The loss distribution, presented in Figure 14, shows however that this design seemed not to have a negative consequence. The influence of the vane bow on rotor incidence in Figure 13 results directly from the variation of the vane outlet angle α₁. Therefore its values move towards negative in the two sidewall areas and towards positive on the middle of the blade. Interesting, though not quite easy to explain, is the reaction of the rotor loss coefficient on the bow of the stators. The remarkable reduction of the loss coefficient in the lower half of the blade is not directly attributable to the variation of the incidence. Probably it results from a reduction of profile loss as well as secondary loss and would require a detailed study of the loss characteristics of the rotor profiles in function of the incidence. Values of the integrated loss coefficient of the rotor for the three cases in question are given in Table 8.

Table 8. Integrated loss coefficient of the rotor for the calculated blading.

Notation		[%]
Basis_2A	0.0814	—
Bow_F13g1	0.0771	−5.346
Bow_F32g	0.0728	−10.531

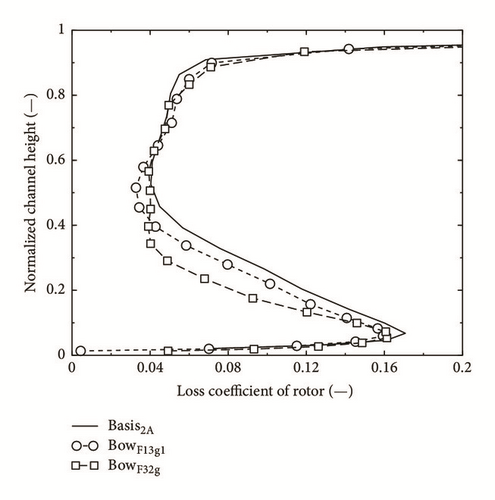
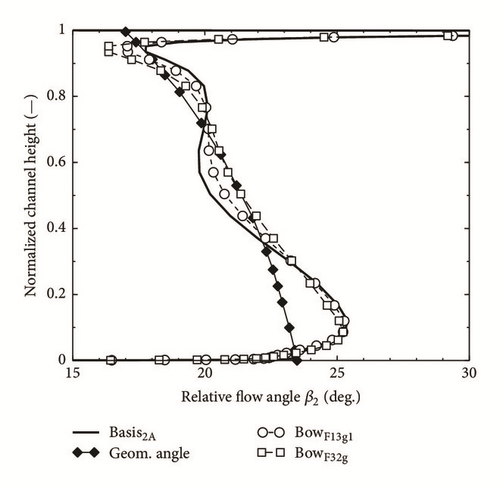
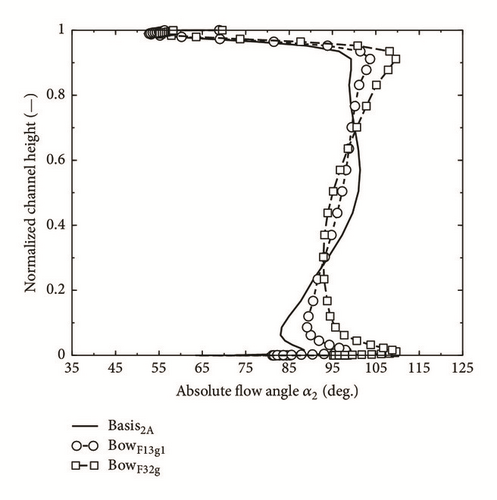
As could be expected from Figure 14 they show a distinct reduction of loss for the cases with bow vanes. Finally the rotor outlet angle β₂ is presented in Figure 15. Since the outlet angle of turbine blade profiles is within a certain range independent of the inflow angle, it could be expected that the β₂-distribution is little influenced by the bow of the vanes. It shows the familiar underturn near the wall and the overturn directly at the wall, both due to secondary flow, in a pronounced way near the hub and less clear near the tip, where directly at the wall the clearance flow predominates. The influence of the vane bow is small. The absolute flow angle α₂ behind the rotor is defined not only by β₂, but via the velocity triangle by the axial velocity, too. This is, as we have seen, influenced considerably by the curvature of the vanes and this influence is still sensible behind the rotor. Therefore, as Figure 16 shows, the flow angle α₂ can be changed by 10 deg. and more through the vane bow, even if β₂ differs by one or two deg. only for the different cases.

6. 2D-Modeling of the Flow Deflection

In preliminary design and optimization of turbines (e.g., [46]) the two-dimensional flow calculation (throughflow method) assuming rotation-symmetric flow is still widely in use and of high practical importance, since the blades cannot be introduced directly into the calculation models for flow deflection and loss, representing the chosen blading, has to be used. For radial blading the familiar sine-rule is quite appropriate to describe the exit flow angle α₁ of the cascade in a simple form

()

where a₁ is the exit channel width and t the blade pitch. We denote the exit angle and so calculated the effective angle.

6.1. Correction Function for the Exit Flow Angle of Curved Blade

Tangential curvature will change the exit flow angle of a blade over the blade height in a way mainly influenced by the local tangential inclination angle ε. In a general way a correction function for the effective flow angle α₁ can be defined, which renders the exit flow angle

of the curved blade

()

This function will depend on the local inclination ε and the effective flow angle α₁ and varies over the blade height.

6.1.1. Correction Function Based on Experimental Data

Experimental investigations were made at the department for power, nuclear turbine construction, and aircraft engines of State St. Petersburg Technical University for the guide vane Bow_2B (not treated here in detail), which is inclined in the lower half and curved towards radial near the casing. The relevant data in our definition are ε_N = +13.2^°, ε_G = 0^°, and

. Because of the moderate curvature a rather simple correction function is proposed

()

From the experimental data a value for k = 0.435 is deducted. A validation is given in Section 6.2.

6.1.2. Correction Function for Vanes with High Curvature

The numerically investigated vanes with high curvature on both ends produce high underturning in the sidewall zones, which cannot be described by a correction approximately proportional to ε as in (23). A nonlinear version for the correction parameter k has been devised, which makes use of several additional parameters

()

where α₁ is again the sine-rule flow angle along the blade height,

the effective flow angle at the extreme blade end (hub or tip). and α_k an assumed maximum value of the exit flow angle of the curved blade at its end.

The value

depends on the geometry of the hub profile cascade and is invariable (e.g., 13^° for the vane Basis_2A and the curved vanes deduced from it). The two coefficients α_k and k_k have to be chosen suitably for the different curvatures. The exponent n will take care of the nonlinear character of the angle distribution; a value n = 3 seems appropriate. From the results of experimental investigations of turbine stages with curved vanes it seems that an optimal angle of tangential inclination of approximately 20^° exists. We assume therefore that the value of α_k can be chosen up to a maximum of 20^° only; similarly the coefficient k_k should not be assumed higher than 1.2. If (24) is inserted in (23) we receive a new general formulation for the exit flow angle of curved vanes

()

6.2. Validation of the Correction Function

Since the numerically investigated vanes have been developed by tangential displacement of the unvaried profiles of the radial basis stator their effective exit flow angle distribution is identical with that of the stator Basis_2A. The geometry and hence the effective flow angle distribution of the stator Bow_2B, for which experimental data are available, are quite different. The exit flow angle distribution of the two curved stators Bow_2B and Bow_F32g has been calculated with the correction function described above. The values of the geometrical and empirical coefficients that have been used are shown in Table 9. Further validations of other blade types from the numerical simulation are carried out in this investigation, respectively (not treated here in detail).

Table 9. Values of the empirical coefficients in (25) for the curvature blading (a = general).

Notation	Bow_2B	Bow_F32g	K
n	3	3	k
	13	13	k
	20	15.35	a
	1.195	1.085	a

Figure 17 shows the results for the vane Bow_2B, which comprises inclination mainly in the lower half. The resulting exit flow angle differs sensibly in this region from the sine-rule value; the corrected angle according to (25) and the coefficients in Table 9 agree well with the experimental and the values of the 3D-computation. Because of the moderate degree of inclination the correction in the simplified form of (23) with a constant value of k = 0.435 would render good results.

Figure 18 shows results for the vane Bow_F32g with considerable curvature on both ends. The corrected angles according to (25) with the coefficients in Table 9 represent the results of the 3D-simulation very well in both sidewall regions. Since the correction model cannot take care of the redistribution of the aerodynamic blade load into the middle of the blade the reduction of the flow angle in that region will not be correctly described (see Figure 11). The validation of this correlation is tested at present likewise for the throughflow calculation by the TU St. Petersburg as well as industry in St. Petersburg.

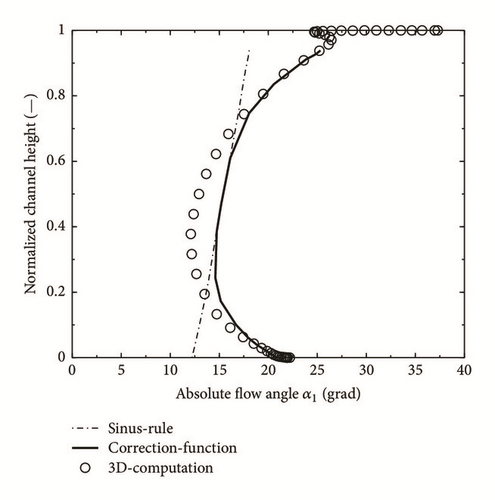
Because the sine-rule is valid for two-dimensional cascade flow, the exit flow angle distribution will show some deviations from these values in the sidewall zones of radial blades, too. Secondary flow will cause underturning when approaching the sidewall and overturning in its direct proximity; radial clearance will cause considerable underturning. These deviations from the sine-rule values can be calculated by specific flow models, described, for example, in [47], and then introduced in our correction procedure instead of the effective flow angle α₁ for improved modeling. In Figure 17 these influences are visible to some extent. A distinct tangential curvature, however, will render flow angle modifications, which surpass the secondary flow influence considerably, as is clearly visible in Figure 18.

7. Conclusions

Results of numerical 3D flow simulations of an axial turbine stage with radial and two different curved guide vanes are presented. The curved guide vanes are developed by tangential displacement of the profiles of the radial vane. The simulation procedure was validated with the aid of experimental data, not presented here.

The guide vanes with curvature on both ends form an obtuse angle between suction side and sidewall. They generate radial pressure forces, which displace the fluid flow towards the sidewalls. The axial velocity is increased there as well as the exit flow angle. The pressure distribution of the blade profiles is deformed, so that the aerodynamic loading is shifted backwards. This produces a radial component of the pressure gradient on the suction side directed towards the middle of the blade. This phenomenon probably promotes a displacement of the secondary flow and a reduction of the secondary loss. All effects are intensified by increased blade inclination and extended area of the curvature.

The modification of vane exit angle and axial velocity distribution will cause changes of the incidence to the rotor up to 10^° and more, so that adaption of the rotor geometry, when applying curved stators, seems necessary.

In order to render the flow calculation of curved stators feasible by the widespread 2D-methods (through flow method) a radial force model and an exit angle model for curved stators were developed. It departs from the familiar sine-rule and comprises a correction function, which depends mainly on the local inclination angle ε of the vane. General coefficients permit the adaption to different blade curvatures. Further research by numerical simulation, finally validated by experiments, which is extended to other profile types, profile modifications in the inclined zone, other types of curvature, and so forth, will probably lead to optimum forms of bow vanes with reduced secondary loss and increased efficiency.

Symbols

a:: Exit channel width
c:: Flow velocity in abs. system
:: Vector of the force
h_s:: Specific enthalpy
h:: Blade and channel height
Δh_s:: Change of the isentropic spe. enthalpy
i:: Incidence
k:: Coefficient
:: Mass flow rate
n:: Speed in normal direction
p:: Pressure
r:: Radius
R:: Gas constant
S:: Blade chord length
T:: Temperature
Tu:: Turbulence degree
α:: Flow angle in the abs. system
β:: Flow angle in the rel. system
Δ:: Difference
δ:: Curving angles of meridian streamlines
δ_sp:: Gap width of tip clearance
ε:: Curvature angle of blade stacking line
ζ:: Loss coefficient
κ:: Specific heat ratio
ν:: Angle of the meridional stream surface
ρ:: Flow density
Π:: Pressure ratio of turbine stage.

Indices

0,1, 2:: Exp. measured positions
aus:: Outlet of the stage
ax:: Axial
bez:: Normalized
Bi:: Bitangent
DS:: Pressure side
ein:: Inlet of the stage mesh
eff:: Effective according to sine-rule
G:: At the casing
int:: Integration
is:: Isentropic
k:: Curvature zone and coefficient
la:: Rotor
le:: Stator
m:: Meridional comp. and middle value
N:: At the hub
r:: Radial component
rech:: Computation
s:: Static
sp:: Gap losses or gap
SS:: Suction side
t:: Total
z:: z-axial component
φ:: Circumference component.

Conflicts of Interest

The author declares that they have no conflicts of interest.

Acknowledgments

This study described here was supported by the Ministry of Science and Technology and the National Science Council (MOST104-2221-E-035-052; MOST103-2632-E-035-001-MY3; MOST103-2221-E-035-064; NSC102-2221-E-035-029; NSC101-2221-E-035-010) and was completed due to the support of Professor W. Riess and Professor J. Seume of the Institute for Turbomachinery and Fluid Dynamics of Leibniz University of Hannover. The author is very grateful for this aid and wants to thank their continuously encouragement and cooperation as well as their helpful discussions to this work for the writing. The basic blade data and experimental results were completed and available due to the support of Professor Lapschin of the Department for Power, Nuclear Turbine Construction and Aircraft Engines of State St. Petersburg Technical University.

References

1 MacDonald J. A., Increasing Steam Turbine Power Generation Efficiency, June 2003 issue of Energy-Tech magazine (2003).
Google Scholar
2 Deich M. E., Gubarev A. V., Filippov G. A., and Wang Z. Q., A new method of profiling the guide vane cascades of stages with small ratios of diameter to length, Thermal Engineering. (1962) no. 8 (in Russian), 42–46, Associated Electrical Industries, Research Laboratory, Manchester, Translation No. 3277.
Google Scholar
3 Leyzerovich A. S., Steam Turbine for Modern Fossil-Fuel Power Plants, 2008, Taylor & Francis, UK.
Google Scholar
4 Deckers M. and Pfitzinger E. W., The exploitation of advanced blading technologies for the design of highly efficient steam turbines, Proceedings of the 6th International Charles Parsons Turbine Conference, 2003, Dublin, Ireland.
Google Scholar
5 Smith Jr. L. H. and Yeh H., Sweep and Dihedral Effects in Axial-Flow Turbomachinery. Trans. of the ASME, Journal of Basic Engineering. (1963) 85, 401–406.
10.1115/1.3656623
Google Scholar
6 Watanabe E. Y., Tanaka Y., Nakano T. et al., Development of New High Efficiency Steam Turbine, Mitsubishi Heavy Industries Technical Review. (2003) 40, no. 4, 1–6.
Google Scholar
7 Deich M. E. and Trojanovskij B. M., Investigation and Design of Axial Turbine Stages (Untersuchung und Berechnung Axialer Turbinenstufen), 1973, VEB Verlag Technik, Berlin, Germany.
Google Scholar
8 Deich M. E., Troyanovskii B. M., and Filippov G. A., An effective way of improving the efficiency of turbine stages, Thermal Engineering. (1990) 37, no. 10, 520–523, 2-s2.0-0025497025.
Google Scholar
9 Deich M. E., G. A. Filippov, Gas Dynamics of Turbine Blade Rows, Edited by G.A. Filippov, 1996, Energoatomizdat, Moscow.
Google Scholar
10 Han W., Wang Z., and Xu W., An experimental investigation into the influence of blade leaning on the losses downstream of annular cascades with a small diameter-height ratio, Proceedings of the International Gas Turbine and Aeroengine Congress and Exposition (GT ′88), June 1988, 1–9, ASME Paper, 88-GT-19 (1988)https://doi.org/10.1115/88-GT-19, 2-s2.0-84939142923.
10.1115/88?GT?19
Google Scholar
11 Wanjin H., Zhongqi W., Chunqing T., Hong S., and Mochun Z., Effects of leaning and curving of blades with high turning angles on the aerodynamic characteristics of turbine rectangular cascades, Journal of Turbomachinery. (1994) 116, no. 3, 417–424, https://doi.org/10.1115/1.2929428, 2-s2.0-0027974665.
10.1115/1.2929428
Web of Science® Google Scholar
12 Harrison S., Influence of blade lean on turbine losses, Journal of Turbomachinery. (1992) 114, no. 1, 184–190, 2-s2.0-0026736960, https://doi.org/10.1115/1.2927982.
10.1115/1.2927982
Web of Science® Google Scholar
13 Hourmouziadis J. and Hübner N., 3-D Design of Turbine Airfoils, ASME Paper 85-GT-188, 1985, pp. 1-7.
Google Scholar
14 Suslov D. I. and Filippov G. A., An approximate method for calculating and profiling cascades of curved vanes, Thermal Engineering. (1995) 42, no. 3, 259–264.
Google Scholar
15 Wang Z., Xu W., Han W., and Jie B., An experimental investigation into the reasons of reducing secondary flow losses by using leaned blades in rectangular turbine cascades with incidence angle, Proceedings of the ASME 1988 International Gas Turbine and Aeroengine Congress and Exposition (GT ′88), June 1988, https://doi.org/10.1115/88-GT-4, 2-s2.0-84939205857.
10.1115/88?GT?4
Google Scholar
16 Pioske C. and Gallus H. E., Dreidimensionale Turbinenbeschaufelung, MTZ Motortechnische Zeitschrift. 1 358–362, Band 58, Heft 6 (1997).
Google Scholar
17 Filippov G. A. and Wang Z. Q., Die Berechnung der rotationssymmetrischen Strömung für die letzte Stufe der turbomaschinen, Publikation des Moskauer Energetisches Institut (MEI). (1963) no. 47.
Google Scholar
18 Filippov G. A. and Wang Z. Q., The effect of flow twisting on the characteristics of guide rows, Thermal Engineering (Teploenergetika). (1964) no. 5, 69–73.
Google Scholar
19 Jiang H. D., Lu Y. L., Zhou F. Z., and Wang S. J., Study of a subsonic combind-leaning turbine guide vane with tip endwall contouring, Journal of Aerospace Power. (1993) 8, no. 1, 41–44.
Google Scholar
20 Vogt H.-F. and Zippel M., Sekundärströmungen in turbinengittern mit geraden und gekrümmten schaufeln: visualisierung im ebenen wasserkanal, Forschung im Ingenieurwesen/Engineering Research. (1996) 62, no. 9, 247–253, https://doi.org/10.1007/BF02601431, 2-s2.0-0013331990.
10.1007/BF02601431
Google Scholar
21 Wang Z. and Zheng Y., Research status and development of the bowed-twisted blade for turbomachines, Engineering Science. (2000) 2, 40–48.
Google Scholar
22 Wolf R. and Romanov K., Steam Turbines: Siemens Reactive Blading - Designed for Highest Efficiency and Minimal Performance Degradation, 2014, Russia Power 2014 (March 2003), pp. 1-19.
Google Scholar
23 Filippov G., Gribin V., Tischenko A., Gavrilov I., and Tischenko V., Experimental studies of polydispersed wet steam flows in a turbine blade cascade, Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy. (2014) 228, no. 2, 168–177, 2-s2.0-84899078718, https://doi.org/10.1177/0957650913518768.
10.1177/0957650913518768
Web of Science® Google Scholar
24 Baldwin B. and Lomax H., Thin layer approximation and algebraic model for separated turbulent flow, Proceedings of the 16th Aerospace Sciences Meeting, 1978, 78-0257, AIAA.
10.2514/6.1978-257
Google Scholar
25 Hirsch Ch., Numerical Computational of Internal and External Flows, Fundamentals of Computational Fluid Dynamics, 2007, 2nd edition, Butterworth-Heinemann.
Google Scholar
26 Hirsch Ch. et al., An Integrated CFD System for 3D Turbomachinery Applications, ADARD-CP-510, 1992.
Google Scholar
27 Hirsch Ch., CFD Methodology and Validation for Turbomachinery Flows. AGARD Lecture Series on ′Turbomachinery Design Using CFD′, 1994, pp. 4.1-4.17, May to June.
Google Scholar
28 Kang S. and Hirsch C., Numerical simulation of three-dimensional viscous flow in a linear compressor cascade with tip clearance, Journal of Turbomachinery. (1996) 118, no. 3, 492–502, 2-s2.0-0030465082, https://doi.org/10.1115/1.2836694.
10.1115/1.2836694
Web of Science® Google Scholar
29 Kröner D., Numerical Schemes for Conservation Laws, 1997, Wiley, Teubner.
Google Scholar
30 Slooff J. W. and Schmidt W., Computational Aerodynamics Based on the Euler Equations, AGARD-AG-325, 1994.
Google Scholar
31 Jameson A., Schmidt W., and Turkel E., Numerical simulation of the euler equations by finite volume methods using runge-kutta time stepping schemes, Proceedings of the AIAA 5th Computational Fluid Dynamics Conference, AIAA Paper 81-1259 (1981).
Google Scholar
32 Shieh T.-H. and Li M.-R., Numeric treatment of contact discontinuity with multi-gases, Journal of Computational and Applied Mathematics. (2009) 230, no. 2, 656–673, https://doi.org/10.1016/j.cam.2009.01.014, MR2532357, Zbl1166.76034, 2-s2.0-62649100864.
10.1016/j.cam.2009.01.014
Web of Science® Google Scholar
33 Shieh T.-H., Liou T.-M., Li M.-R., Liu C.-H., and Wu W.-J., Analysis on numerical results for stage separation with different exhaust holes, International Communications in Heat and Mass Transfer. (2009) 36, no. 4, 342–345, 2-s2.0-62649128380, https://doi.org/10.1016/j.icheatmasstransfer.2009.01.011.
10.1016/j.icheatmasstransfer.2009.01.011
Web of Science® Google Scholar
34 Shieh T.-H., Li M.-R., Li Y.-T., and Chen M.-C., A comparative study of flux limiters using new numerical methods in unsteady supersonic flows, Numerical Heat Transfer, Part B: Fundamentals. (2015) 67, no. 2, 135–160, 2-s2.0-84908701518, https://doi.org/10.1080/10407790.2014.949578.
10.1080/10407790.2014.949578
Web of Science® Google Scholar
35 Shieh T.-H. and Chen M.-C., Study of high-order-accurate limiters for time-dependent contact discontinuity and shock capturing, Numerical Heat Transfer, Part B: Fundamentals. (2016) 70, no. 1, 56–79, 2-s2.0-84976571698, https://doi.org/10.1080/10407790.2015.1052296.
10.1080/10407790.2015.1052296
CAS Web of Science® Google Scholar
36 Shieh T. H., Untersuchung von Axialturbinen-Beschaufelungen mit dreidimensionalen Gestaltungselementen [Ph.D. dissertation], 2003, Universität Hannover.
Google Scholar
37 Wang D., Ding H., and Zhong J., The influence of tailboard on the exit flow fields of compressor cascade with curved blade, Proceedings of the China Engineering Thermal Physics Society (HMA′00), 2000, 344–348.
Google Scholar
38 Jujii H., Kimura T., and Segawa K., A high-efficiency steam turbine utilizing optimized reaction blades—an application to the kwangyang combined-cycle power plant of K-power of Republic of Korea, Hitachi Review. (2007) 56, no. 4, 104–108, 2-s2.0-36048941328.
Google Scholar
39 Traupel W., Thermische Turbomaschinen, 2000, 1, Springer-Verlag, Berlin, Germany.
Google Scholar
40 Feng Z.-M., Gu H.-B., Zhang J.-D., and Lu Y., Different three-dimensional blades aerodynamic performance research comparison, Information Technology Journal. (2013) 12, no. 11, 2219–2224, 2-s2.0-84880886741, https://doi.org/10.3923/itj.2013.2219.2224.
10.3923/itj.2013.2219.2224
Google Scholar
41 Feng Z. M., Gu H. B., and Zhang J. D., Curved rotor blade cascades aerodynamic performance at off-design incidence in axial steam turbine, International Journal of Digital Content Technology and its Applications. (2013) 7, no. 7, 1086–1093.
10.4156/jdcta.vol7.issue7.129
Google Scholar
42 Murugan M., Ghoshal A., Xu F., Hsu M., Bazilevs Y., Bravo L., and Kerner K., Articulating turbine rotor blade concept for improved off-design performance of gas turbine engines, 1, Proceedings of ASME 2016 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, 2016, Paper No. SMASIS2016-9045, pp. V001T04A004https://doi.org/10.1115/SMASIS2016-9045.
10.1115/SMASIS2016?9045
Google Scholar
43 Segawa K. et al., Development of a highly loaded rotor blade for steam turbines (2nd report, performance verification), JSME International Journal, Series B. (2002) 45, no. 4, https://doi.org/10.1299/jsmeb.45.881, 2-s2.0-0036879131.
10.1299/jsmeb.45.881
Google Scholar
44 Segawa K. et al., A high performance optimized reaction blade for high pressure steam turbines, Proceedings of ASME Power Conference, March 2004, 307–314, https://doi.org/10.1115/POWER2004-52110, 2-s2.0-2942527109.
10.1115/POWER2004?52110
Google Scholar
45 Mischo B., Axial Turbine Rotor Aero-thermal Blade Tip Performance Improvement through Flow Control [Ph.D. dissertation], 2008, TU Kaiserslautern.
Google Scholar
46 Lampart P. and HirT L., Complex multidisciplinary optimization of turbine blading systems, Archives of Mechanics. (2012) 64, no. 2, 153–175, 2-s2.0-84862279243, Zbl1291.76274.
Web of Science® Google Scholar
47 Petrovic M., Berechnung der Meridianströmung in mehrstufigen Axialturbinen bei Nenn- und Teillastbetrieb [Ph.D. dissertation], 1995, Universität Hannover, VDI Fortschritt-Berichte, Netherlands.
Google Scholar

All articles

Aerothermodynamic Effects and Modeling of the Tangential Curvature of Guide Vanes in an Axial Turbine Stage

Abstract

1. Introduction

2. Computational Methods

2.1. Governing Equations

2.2. Method of the Spatial Discretization

2.2.1. Numerical Fluxes

2.3. Turbulence Model

3. Computational Conditions

3.1. Single Stage Experimental Air Turbine

3.2. Geometrical Data of the Researched Blades

3.3. Computational Mesh

3.4. Operating Conditions of the Turbine Stage

4. Results and Discuss

4.1. Validation of Numerical Results

4.2. Effect on the Meridional Streamlines

4.3. Radial Blade Forces Produced by Blade Curvature

4.3.1. Treatment and Modeling of the Radial Blade Force

4.3.2. Distribution of the Resultant Radial Blade Force

4.4. Effect of the Blade Curvature on the Static Pressure Distribution at the Profiles

4.4.1. Aerodynamic Load of the Blade Profiles

4.4.2. Pressure Distribution on the Suction Side

4.5. Effect of the Curvature on the Vane Outlet Angle

4.6. Effect of the Blade Curvature on the Loss Coefficient of the Vanes

5. Effects of the Vane Curvature on the Rotor Flow

6. 2D-Modeling of the Flow Deflection

6.1. Correction Function for the Exit Flow Angle of Curved Blade

6.1.1. Correction Function Based on Experimental Data

6.1.2. Correction Function for Vanes with High Curvature

6.2. Validation of the Correction Function

7. Conclusions

Symbols

Indices

Conflicts of Interest

Acknowledgments

References

Figures

References

Related

Information