This study deals with the influence of radial body forces on FGM and non-FGM pressure vessels. It contains an extended overview of pressure vessels made from both kinds of material. Furthermore, full mathematical development of stress-strain field for both kinds of cylindrical vessels while being influenced by body forces has been performed. In addition, a new power law model for FGM materials was suggested and discussed. Finally, tables of composed plastic-elastic states are discussed.

1. Introduction

Pressure vessels have many engineering applications in many aspects of life, like energy, electronics, mechanics, and biomedical engineering as described by the author and others [1–3]. In continuation to the author previous essay [1], a unique group of pressure vessels made from special materials will be discussed here. These pressure vessels are often called FGM pressure vessels. FGM is a well-known shortcut to functionally graded materials, from which many structures and constructions including pressure vessels are made. These materials are heterogeneous (nonhomogenous) while its materials constituent’s composition is varying continuously gradually in the microscopic phase. These materials have been proved to have special thermomechanical properties. However, their applications are numerous, especially, for military and aerospace applications industry, thermal loading, heat resistance, and so forth. Recent researchers and studies on this field are well described by Kalali and Hadidi-Moud [2], Ansari Sadrabadi and Rahimi [3], and Sadeghian and Ekhteraei Toussi [4]. In more detail, Kalali and Hadidi-Moud have developed an analytical method for predicting elastic-plastic stress distribution in cylindrical and spherical pressure vessels made from a ceramic/metal functionally graded material, while the vessel was subjected to plane-stress conditions and von Mises yield criterion was considered. Also, small strains have been assumed and Hencky’s stress-strain relation was used to obtain the governing differential equations for the plastic region. Other study in this field was presented last year by Ansari Sadrabadi and Rahimi. They examined thick-walled cylindrical vessels made from functionally graded material under internal pressure with the presence of a temperature gradient, while material parameters have been modeled using power functions. They have shown that material distribution parameters and temperature gradient play an important role in FGM elastoplastic behavior. It should be noted that calculation of loading effect has been determined in the first yield point. Another study that was mentioned above has been done by Sadeghian and Ekhteraei Toussi in 2012. Their study includes an axisymmetric thermal elastoplastic stress analysis of FGM cylindrical vessels based on Tresca’s yield criterion and small deformation theory. The investigation of temperature distribution effect upon the evolution and growth of the plastic zone was their study uniqueness. They proved that the interface line between elastic and plastic regions may take shape in different radii while being dependent on the thermomechanical composition properties of the FG material.

Moreover, other structures of beam and spherical shapes have been examined by Eraslan and Akis [5], Nemat-Alla et al. [6], Akis [7], Kanlıkama et al. [8], and Chandel et al. [9], respectively. For instance, Eraslan and Akis have developed plane strain analytical solutions to functionally graded elastic and elastic-plastic pressurized tube under small deformation. Also, plastic behavior and Tresca’s yield criterion were considered. They also assumed radial change of tube material elasticity modulus based on a two-parameter model in a general parabolic form. Field equations exact solutions for elastic and plastic deformations have been obtained together with elastoplastic response which was proved to be affected by the radial variation of the modulus of elasticity. Moreover, nonhomogeneous solution was found to be sensitive to the choice of material parameters. In continuation to the latter study, Kanlıkama et al. [8] have investigated coupled thermoelastic phenomenon determining the stress-strain relations in thick-walled pressurized vessel and a reactor pressure vessel exposed to an inner moderator pressure and thermal loads. Good agreement was found between reactor and classical pressure vessels solutions. Furthermore, Chandel et al. [9] have presented recently a general analysis of thermal stresses and strains in a thin rotating circular FGM disk. For more information on their study, see [9].

In general, physical behavior of non-FGM thick-walled pressure vessels has been investigated in the last decade by several researchers, like Sinclair and Helms [10] who have performed a fundamental review study of elastic hoop stress formulas in cylindrical and spherical pressure vessels. Other researchers like Zhao et al. [11] have proposed a technique for elastic-plastic analysis of a thick-walled elastic-plastic cylinder under internal pressure. Their calculation was based on two parametric functions including piecewise linearization of the stress-strain curve. They have found that the required strain energy value of deformation is found to be dependent on initial or final geometry choice where boundary conditions are satisfied. Moreover, it was found that, in case of low work-hardening solid, the difference is significant and cannot be ignored. Finally, the researchers have shown that the new formulation is appropriate for elastic-plastic fracture calculations. Another research that would be mentioned concerns nonlinear kinematic hardening behavior of pressure cylinder and was studied by Nayebi [12]. He dealt with Bree’s cylinder which was used to simulate different material properties under constant mechanical and cyclic thermal gradient loadings. Nayebi reconsidered Bree’s theory by using nonlinear kinematic hardening material model. Two-dimensional model including Poisson’s effect was also assumed. After comparison with Bree’s model, it was found that Bree’s one-dimensional model is relatively conservative and the bidimensional diagram did not correspond to the complete model. However, calculation of stress-strain field in cylinder or other shapes using finite element method (FEM) is discussed broadly by Szabó et al. [13]. Briefly described, they developed FEM solution for small-strain elastic-plastic stress problems by using p-version elements.

When dealing with plastic behavior of non-FGM pressure vessels, one cannot ignore the autofrettage phenomenon. Autofrettage is a process that is intended mainly to enhance pressure vessels fatigue life and to reduce the vessel weight. The method works by creating plastic expansion (yielding) of the inner wall thickness by overloading the vessel inner diameter or just a portion of it. As a result, compressive residual stresses are being created in the inner diameter (ID) region while in response residual tensile hoop stresses are being created in the outer diameter as was explained in detail by Gibson [14]. The idea of thick wall prestressing is aimed at having a beneficial distribution of tensile hoop stress and compressive stress on the outer diameter (OD) when the pressure is released, while Gibson has investigated autofrettage phenomenon with the appropriate processes. As mentioned in his study, two methods of autofrettage exist: hydraulic and swage. He has made a comparison between both methods using FE model of hydraulic autofrettage. He has found good agreement between the obtained solutions and existing analytical and numerical models. According to Gibson, bilinear material representation is preferred to be used for modeling over other materials since radial position is dependent on the nonlinear material behavior. In the second step, he has developed full model of swage autofrettage. One year later, Lee et al. [15] have published their own study on autofrettage process analysis of a compound cylinder based on the elastic-perfectly plastic material behavior and strain hardening stress-strain curve. They showed that compound cylinder resistance ability is higher than a one layer cylinder while both kinds of cylinders have the same size. Additionally, they found that shrink fit is a relatively efficient way to extend compressive residual stress. Moreover, they found that Bauschinger effect has significant impact on compressive residual stress of the strain-hardening model, such that the stress is smaller than elastic-perfectly plastic case. According to the last studies, an obvious question should be asked: what are the limits of autofrettage process or what is the optimum autofrettage process under a given pressure? An answer was given by Wahi et al. [16]. They performed a research about the influence of optimum autofrettage on the pressure limits of thick-walled cylinder. The tradeoff that researchers have dealt with was between strength-weight ratio increase and fatigue life extending. Their main target is to solve this apparent contradiction by using optimal autofrettage procedure while they have found the required autofrettage pressure for given various levels of allowable pressure. Consequently, three distinguished cases of thick-walled cylinders design have been created. It should be mentioned that, according to their study, the optimal autofrettage is achieved only if both minimum equivalent stress and maximum fatigue life conditions are fulfilled. During the years 2012–2014, various fresh studies have been published on the subject while only few researches among them will be pointed out here. For instance, Hu and Puttagunta [17] have presented numerical investigation study of thick-walled cylinder under overloading internal pressure involved in autofrettage process while the Bauschinger effect was considered inside the elastoplastic material. Moreover, they have found the optimal autofrettage pressure and the maximum reduction percentage of the von Mises stress under the elastic-limit working pressure. In addition, comparison between Bauschinger and the non-Bauschinger effect model has been made by the authors [17]. One year later, fresh study which includes most of the latter subjects together with new approaches has been presented by Trojnacki and Krasinski [18]. They have developed analytic expressions for calculating the autofrettage pressure based on both Tresca and von Mises yield criteria including the Bauschinger effect. The results have been compared with FEM and other analytical models whereas experimental data and analytical model were dealing with multilinear kinematic hardening. The authors have concluded that the autofrettage technique is the preferred technology to use over other technologies discussed. Thorough mathematical analysis of pressure vessel during autofrettage process which also concerns the optimum operation conditions has been published in 2013 by R. Zhu and G. Zhu [19]. Moreover, autofrettage compounded tube had been modeled according to Huang’s model which considers the Bauschinger effect as was introduced by Bhatnagar [20]. He has found that compounded tube advantages include maximum pressure, fatigue life, and manufacturing economy. In 2014, short review on autofrettage process in cylindrical pressure vessels was presented by Gupta and Vora [21]. During the past year of 2015, new studies and approaches have come out. For example, a new process to create autofrettage by applying thermal stresses on the cylinder wall has been performed by Kamal and Dixit [22]. Last fresh study on the autofrettage subject that would be mentioned here has been performed by Kumar and Moulick [23]. They made comparative stress analysis based on FEM for both elliptical and cylindrical pressure vessel with and without autofrettage. For more information relating to autofrettage process in FGM vessels one should read [2–4]. Buckling of FGM and non-FGM materials is summarized by Patil et al. [24]. Specifically, post buckling of FGM plate and shells has been investigated by Shen [25]. In 2006, Kadoli and Ganesan [26] have made analysis research of linear thermal buckling and free vibration of FG cylindrical shells with clamped-clamped BC based on temperature-dependent material properties. Two years later, Shariyat [27] has presented a study about dynamic thermal buckling due to temperature heat shock on FGM cylindrical shells, while a combination of axial compression and external pressure was applied. During his research he has found that buckling behavior is dependent on the volume fraction index and the differences between the thermal stresses in the outer and the inner surfaces. Moreover, he has revealed that temperature gradient and initial material imperfections effects are relatively small on the buckling phenomenon of a shell subjected to a pure external pressure. In 2009, Huang and Han [28] have performed nonlinear buckling and postbuckling examinations for axially compressed FG cylindrical shells by using the Ritz energy method and the nonlinear large deflection theory. One year later, Sofiyev [29] has presented buckling analysis of the simply supported truncated conical shell made of FGM. One of his main findings on this area relates to cylindrical shell stress-strain analysis including buckling analysis based on parametric examination. During the current year of 2015, another study has been published by Zhao and Liew [30, 31] on the subject of buckling response of FG ceramic-metal cylindrical shell panels while axial compression and thermal load are applied. Their model is based on the first-order shear deformation shell theory and element-free kp-Ritz method. One year later, Huang et al. [32] published their research on Buckling of FGM cylindrical shells subjected to pure bending load. Their findings under the appropriate assumptions indicate that the materials inhomogeneity is significant for buckling of FGM cylindrical shells.

In the current essay, stress-strain relations mathematical development of FGM and non-FGM cylindrical vessels behavior in the presence of physical phenomena like magnetic, gravitation, rotational, and electrical charge will be performed. Firstly, general model including body forces of FGM and non-FGM will be introduced for elastic phase. Next step, general model of the plastic phase based on von Mises criterion will be brought up. Additionally, a new power law model was suggested and discussed with the relevant literature studies. Moreover, the elastoplastic states conditions of the FGM and non-FGM vessels will be introduced here are as follows:

(i)
FGM: elastic-plastic.
(ii)
FGM: plastic-elastic.
(iii)
FGM: plastic-elastic-plastic.
(iv)
FGM: elastic-plastic-elastic.
(v)
Non-FGM: elastic-plastic.
(vi)
Non-FGM: plastic-elastic.
(vii)
Non-FGM: plastic-elastic-plastic.

However, the case of elastic-plastic-elastic in non-FGM pressure vessels will not be discussed, since it is not physically valid due to vessels material homogenously structure which results in inability to create elastic state interface. The developed model in this essay demonstrates a body rotating around itself while another body with the same length applies magnetic, gravity, and electrical forces. In other words, possible application or model for this study could be expressed by hollow rotating cylinder affected by gravity, magnetic, and electrical fields caused by inner rotating cylinder. Notice that content of this chapter is based on the author’s previous knowledge and publications [1, 33].

2. General Elastic Stress-Strain Relations with Thermal and Body Forces Influence of Non-FGM Pressure Vessels

General polar equations of element equilibrium including radial and tangential forces as shown in Figure 1 are as follows [1]:

()

where σ_r and σ_θ denote the radial and tangential stresses acting normal to the sides of the element in steady state (t → ∞) as shown in Figure 1, respectively. Body forces acting in the radial and tangential directions are represented by F_r and F_θ as shown in Figure 1, respectively. Assuming symmetrical deformation about z-axis, one can infer that τ_rθ = 0 and thus equilibrium exists only in the

direction, as follows:

()

Now, according to Hooke’s law including thermal effects, strains behave like

()

where u is the displacement in the radial direction. E, G, and υ represent Young’s modulus, shear modulus, and Poisson’s ratio, respectively. Solving algebraically relations (3) for the stress field yields the following relations:

()

Substituting the above relations (4) into equilibrium (2) results in the following radial displacement equation:

()

The homogenous and the particular solution parts of (5) are expressed by

()

Thus the complete solution is

()

Accordingly, the stress field (4) will be written as

()

Now, in order to find coefficients a₁ and a₂, the following BC will be used:

()

Consequently,

()

Subtracting first and second expressions (11) from each other leads to the following equation which is dependent on the parameter a₂ only:

()

From here, a₂ will be defined as

()

Substituting a₂ into (11) leads to the following expression for a₁ constant:

()

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Stress element in polar coordinate system using [1].

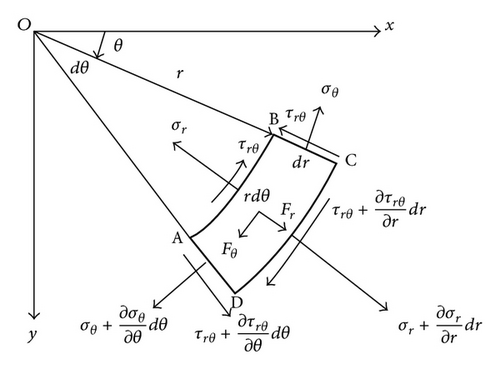
In the next section, the elastic stress-strain relations of FGM pressure vessels including the body forces effect will be developed.

3. General Elastic Stress-Strain Relations with Thermal and Body Forces Influence of FGM Pressure Vessels

Here, elastic stress-strain relations will be developed using Sadeghian and Ekhteraei Toussi [4] and Eraslan and Akis [5] models. Accordingly, the total general stress-strain relationships under axisymmetric assumption are as follows:

()

α(r) and E(r) are being dependent on r coordinate and represent the elastic modulus and heat expansion coefficients, respectively. Applying simple algebraic manipulations on ((15a) and (15b)) leads to

()

The differential equation of displacement (also called Navier equation) is derived by substitution of ((16a) and (16b)) into (2) by the form

()

Equation (17) is a nonlinear differential equation with variable coefficients. The next step is to define the appropriate form of α(r) and E(r) such that simplified solution of (17) will be obtained. Dividing (17) by E((1 − υ)/(1 + υ)(1 − 2υ)) leads to the following equilibrium form:

()

Analysis of (18) will be done here using the following coefficients examination. The guideline of this analysis will be based on the requirement to have one nonlinear differential equation dependent on the radial direction. Thereby, it is obtained that

()

while both h(r) and g(r) functions are dependent on r where h(r) ≠ g(r). This leads to conclusion about the shape of the elastic modulus E:

()

Φ(r) is general function dependent on r coordinate. Literature and author suggestions for Φ and E function forms are presented in Table 1.

Table 1. Elasticity modulus functions suggestions.

Suggestions/properties	Φ	E
Sadeghian and Ekhteraei Toussi [4]	(n/r)r_o

Eraslan and Akis [5]

Author’s suggestion

Eraslan and Akis model for modulus of elasticity as shown in Table 1 is an improved model of Horgan and Chan [34]; a decade later, it has also been used by Sadeghian and Ekhteraei Toussi [4]. The idea of using power law model in order to represent elasticity modulus quality is derived due to nonlinearity of the material behavior. In order to enhance the model flexibility, it has been expanded to be dependent on two parameters (m, n) instead of one. Moreover, by setting n parameter to be zero (n = 0), all of the model suggestions above are satisfied (E = E₀) and homogenous solution is being obtained. In this current essay, new model of elasticity modulus is being suggested by the author and developed based on modulus of elasticity general form (20) inspiration. This model is based on power function and embedded with the properties of the two former models. Here, it will be assumed that elasticity modulus should have the following form:

()

Moreover, we will assume that all other properties like heat expansion coefficient, yielding stress, heat conduction, density function, electric constant, and vacuum permeability behave according to the following power law approximation along the radial distance, normalized by the outer radius:

()

α₀, k₀,

, ρ₀, ε₁, and μ₁ represent the reference data for the physical properties mentioned above. n_i, i = 1,2, 3,4, 5, and m_j, j = 1,2, 3,4, 5, represent the power law constants and the internal function constants, respectively, while c represents the speed of light coefficient in vacuum. It should be noted that Nemat-Alla et al. [6] and Çallıoğlu et al. [35] have also used similar power law model for the yielding stress during their study. In addition, Wang et al.’s [36] analytical study deals with FGM vessel consisting of a finite length hollow cylinder and two closed ends subjected to thermomechanical loadings based on power law model. Moreover, Nejad and Rahimi [37] have used power law model for the density distribution. However, vacuum permeability behaves according to the power law model based on Bhangale and Ganesan study [38]. One step before solving (18) is to define the temperature function. The thermal equation will be brought up in the following form, based on Nowacki [39]:

()

T represent the temperature and k is the heat conduction coefficient. Now, considering the thermal coefficient value possibilities, there are two main solutions:

k is variable [3]:
()
k is constant [6]:
()

Note that (24a) has no dependency on the constants k₀ and m₂. According to the appropriate boundary conditions,

()

It should be remarked that Sadeghian and Ekhteraei Toussi BC includes the thermal convection effect with the appropriate factors. In this essay, this effect will not be discussed despite the fact that it can be easily obtained by redetermination the constants T_i and T_o. In addition, the body force F_r will be defined by the following expression:

()

where ω and ρ₁ represent the angular velocity and the vessel material density, respectively. Additionally, G, ρ₁, and ρ₂ are the gravitational constant, vessel material density, and the another body mass density, respectively. Also, Q, ρ, ε₀, v, I, and μ₀ represent the total charge, charge density per unit length, electric permittivity, charge velocity, electrical current, and the vacuum permeability constant, respectively. Substituting relations (21)–(26) into equilibrium (18) including simple algebraic manipulation gives

()

where

()

The total solution of (27) is a combination of two parts, homogenous and particular solution, according to the following expression:

()

The homogenous solution takes the following form:

()

whereas the following constants are obtained as a result of quadratic equation solution due to substitution of (30) into (27) homogenous part:

()

A₁ and A₂ will be calculated continuously according to the total displacement boundary conditions.

Next step is to handle the particular solution part. Firstly, the particular solution type will be written as follows (after multiplying both sides of the equilibrium (82) by r²):

()

where

()

while f_i ≠ z_1,2 for each value of i since otherwise B_i is undefined (singularity). Therefore the total solution takes the form

()

It should be noted that, for the particular case m = 1, solution (29) coincided with Sadeghian and Ekhteraei Toussi solution [4]. Now, radial and tangential strains will be found together with the appropriate stresses by using (15a) and (15b) and (16a) and (16b), respectively:

()

However,

()

Final step before ending this section will be determining the constants A₁ and A₂ through the presuming of the following boundary conditions:

()

Applying BC (39) on (37a) leads to a two-variable system of linear equations. Solving the linear system using Cramer’s rule yields the following relations for the constants A₁ and A₂:

()

However,

()

It should be noted that elastic-plastic response of metal-ceramic composites has been investigated by Vena et al. [40]. However, more information on FGM temperature variations can be found in [37, 38, 41–43].

In similar way to (32) development, the particular solution of the non-FGM vessels case will be developed. Initially, substituting relations (24b) and (26) back into (5) and (7) results in the next relation:

()

where ρ₁, ε₀, and μ₀ are constants. After applying algebraic manipulations, equilibrium (42) turns to be in the form

()

However,

()

where the particular solution of the non-FGM displacement case is in the following form:

()

In similar way to (32) power coefficients development procedure, the following coefficients are obtained:

()

However,

()

Analyzing expression (47) compared to (34) leads to conclusion that for n = 0 both relations coincided. In addition, for n = n₁ = n₂ = n₃ = 0 FGM and non-FGM cylinder cases both coincided. Different discussion on different permutations of power law properties should be done (like n = 0 with n₁ ≠ n₂ ≠ n₃ ≠ 0 or n ≠ n₃ ≠ 0 with n₁ = n₂ = 0). Moreover, a singularity for the case β₁ = 1 (also β = −1) does exist. Therefore this special case will be solved separately by using the following form:

()

After applying integration over the radial direction on (48) as shown broadly in Ugural and Fenster book [44], the particular solution for the obtained differential equation is

()

Accordingly, the full particular solution for the FGM case using (45)–(49) is

()

while the constants are redefined by

()

Thereby, the final displacement solution takes the form

()

Substituting (48) back into (13)-(14) yields the values for the constants a₁ and a₂ by

()

The strain relations for the elastic non-FGM case will be found by using (48) as follows:

()

Therefore stress relations (9) will be found using expressions (53) by

()

From here, the discussion will pass to concern the plastic behavior of FGM pressure vessels due to thermal and body forces effects.

4. General Elastic-Plastic Stress-Strain Relations with Thermal and Body Forces Influence of FGM Pressure Vessels

Assume that tangential stress is greater than radial stress (σ_θ > σ_r > σ_z) according to the following form:

()

For honesty, note that other criteria for solution also exist [2, 14]. Substituting (56) into (2) using relations (22) leads to the following expressions for σ_r and σ_θ:

()

while c₁ constant will be calculated continuously. The total displacement is calculated by using relations (15a) and (15b) according to

()

while assuming that ε_r,plastic + ε_θ,plastic = 0. Equation (59) will be rewritten using expressions (57) and (58) including relations (21)-(22) and (24a) as follows:

()

Firstly, equilibrium (60) will be represented as follows:

()

while J coefficients are determined using relations (23) according to

()

The solution of differential equation (61) is composed of two parts, homogenous and particular solution, by

()

However, homogenous and particular solutions will be achieved simultaneously. By multiplying both sides of (61) with r (r ≠ 0) including the rearrangement of equilibrium left side, the following differential equation is obtained:

()

However, the final solution for the displacement will be obtained by simple integration over the radial direction r:

()

while S₉ is constant. From here, plastic strains will be defined by the following relations:

()

while,

()

Initial observation on expressions (68) for S_i constants leads to conclusion that these constants have singularity at

. For these specific cases, one should insert each case into (64) with the appropriate integration over the radial direction, while obtained displacement results are presented in Table 2.

Table 2. Plastic-elastic states inside pressure vessels cylinder.

n_i	u	Limitations
n = n₃ + 2

n = n₄ + 4

n = n₄ + 1

n = 2 − n₅

n = 2

n₁ = n₂ − 2

n₁ = −2

Unlike homogenous cylinder pressure, the plastic region in FGM pressure vessels (inhomogeneous material) can be created anywhere along the thickness defined by its first yielding [4]. Hence, in order to determine the value of c₁ constant like other constants, BC will be applied through distinction between four main cases as shown in Table 3. In order to make it simple, Figure 2 illustrates the possible states of FGM pressure vessels. FGM materials properties in this essay are as follows:

(i)
FGM qualities are variable and are dependent on the power n and radius r.
(ii)
Stresses are also temperature dependent.
(iii)
Body forces are not neglected.

These three assumptions are the main reason for the nonfeasibility of Lame’s plane strain criterion σ_r + σ_θ = constant, since it is no longer valid for each of the assumptions separately or combined (see App. 1 as brought up by Nayebi [12]). This comprehension is also true for non-FGM vessels while being dependent on temperature. In these cases, where the elastic and plastic states are both mixed together, the plastic state field relations will be found initially. Afterwards, the elastic stress-strain relations will be calculated while being dependent on the plastic constant due to interface conditions. However, stress-strain expressions are affected not only by the edge conditions (BC) but also due to the function shape. In other words, equilibrium (2) together with elastic (see (16a) and (16b)) and plastic (56) relations has crucial impact on the final analytical solution shape. For the plastic-elastic state, c₁ will be found by applying BC (39) on the radial pressure (57) as follows:

()

Similarly, in case of elastic-plastic, c₁ will be determined by

()

All other parameters would be calculated according to the elastic-plastic regions appropriate conditions including interface zone as shown in Table 3. From here, the discussion will pass directly to the elastic-plastic stress-strain field definition of non-FGM pressure vessels.

Table 3. Plastic-elastic states inside non-FGM pressure vessels cylinder.

Case/conditions	B.C.	Representative equations	Constants to define
Plastic-elastic	Plastic region: Elastic region: Interface zone: u^Plastic(r = r_p) = u^Elastic(r = r_p)	Plastic region: (56) Elastic region: ((16a) and (16b))	A₁, A₂ in (30) c₃ in (57)-(58) S₁₀ in (64)–(66) r_p

Elastic-plastic	Plastic region: Elastic region: Interface zone: Same as plastic-elastic	Same as plastic-elastic	Same as plastic-elastic

Plastic-elastic-plastic	Plastic region 1: Elastic region: no BC Interface zone 1: u^Plastic(r = r_p1) = u^Elastic(r = r_p1) Plastic region 2: Interface zone 2: u^Plastic(r = r_p2) = u^Elastic(r = r_p2)	Same as plastic-elastic	A₁, A₂ in (30) c₃ in (57)-(58) S₁₀ in (64)–(66) r_p1, r_p2, while c₃ and S₁₀ are duplicated for two plastic cases Consequently, there are 8 variables

Elastic-plastic-elastic	Elastic region 1: Plastic region: No BC Interface zone 1: Same as plastic-elastic-plastic Elastic region 2: Interface zone 2: Same as plastic-elastic-plastic	Same as plastic-elastic	A₁, A₂ in (30) c₃ in (57)-(58) S₁₀ in (64)–(66) r_p1, r_p2, while A₁, A₂ are duplicated for two elastic cases Consequently, there are 8 variables

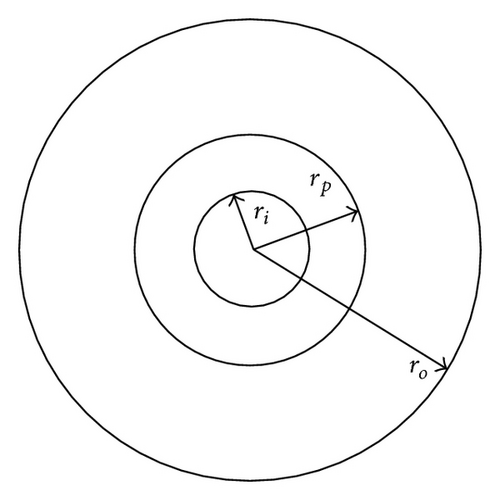
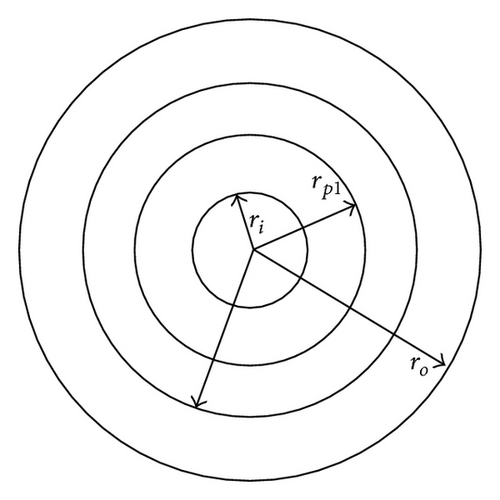
5. General Elastic-Plastic Stress-Strain Relations with Thermal and Body Forces Influence of Non-FGM Pressure Vessels

Assuming that the tangential stress is greater than the radial stress (σ_θ > σ_r > σ_z) according to von Mises yield criterion,

()

while

is constant. Substituting (71) into (2) leads to the following relations for σ_r and σ_θ:

()

while V₁ is constant and will be calculated continuously. The total displacement is calculated by using relations (72)-(73) according to

()

while assuming that ε_r,plastic + ε_θ,plastic = 0 and E, α are constants. Equation (74) will be written using expressions (54a) and (54b):

()

First step before solving equilibrium (75) is to use the following representation:

()

while U coefficients are determined by

()

Differential equation (76) solution is composed of two parts, homogenous and particular solution, according to

()

while homogenous and particular solutions will be derived in one step. Multiplying both sides of (77) by r (r ≠ 0) including the rearrangement of equilibrium left side yields

()

while the final solution for the displacement will be obtained by simple integration over the radial direction r, by the form

()

while U₆ is constant. From here, plastic strains will be defined by the following relations:

()

The plastic region in non-FGM pressure vessels (inhomogeneous material) may be created in the bore or at the outer cylinder regions (not in the middle) defined by its first and secondary yielding states [14]. Hence, in order to determine the value of V₁ constant like other constants, BC will be applied through distinguishing between four main cases as shown in Table 4. To make it simple, Figure 3 illustrates the possible plastic states of non-FGM pressure vessels not including the elastic-plastic-elastic state (Figure 2(b)). Non-FGM main assumptions are as follows:

(i)
Material properties are constants (E, α).
(ii)
Stresses are temperature dependent.
(iii)
Body forces are not neglected.

The second assumption for temperature distribution is the main reason for the nonfeasibility of Lame’s plane strain criterion σ_r + σ_θ = constant, since it is no longer valid for each of the assumptions separately or combined (see App. 1 as brought up by Gibson [14]). In these cases, where elastic and plastic states are both mixed together, in order to find stress and strain relations, the plastic state field relations will be found initially. Afterwards, the elastic stress-strain relations will be calculated while being dependent on the plastic constant due to interface conditions. However, it is required to mention that in case of non-FGM materials while body forces and temperature effects are both neglected elastic stresses and strains will be calculated initially and plastic stress strains constants will be dependent on that due to interface zone conditions. For the plastic-elastic case, V₁ will be determined by applying BC (39) for the radial pressure (72) as follows:

()

Similarly, in case of elastic-plastic state, V₁ will be determined by

()

All other parameters would be determined by the appropriate conditions for the elastic-plastic regions including interface zone as shown in Table 4. Note that plastic-elastic-plastic state is created by applying primary yielding pressure in the inner (bore) and/or at the outer cylinder regions while pressures may be different. During the act of pressure an intermediate elastic region which has not been transformed into the plastic state might exist. Boundaries of the elastic state region should be evaluated using primary yield radius (r_p1, r_p2, r_p) according to Table 4. In the meantime, unloading compressive stresses are developed upon specifically highly enough values, and secondary yielding state may occur, termed by the secondary yield radius, r_s, r_s1, and r_s2, as shown in Figure 3. In order to decide whether secondary yield stage is developed one should check the difference σ_θ − σ_r where r_s < r_p for plastic-elastic case whereas the ratio of comparison is reversed in elastic-plastic case (r_s > r_p). For detailed explanation see Gibson [14] (section 11.2.3 in App. A2). Final remark for this section deals with general stresses and strains calculation in z direction. Evaluation of the longitudinal stresses and strains is based on the following constitutive relation:

()

Finally, one should subtract expression −υε_z from the strains expressions in the radial and tangential directions, according to

()

Table 4. Plastic-elastic states inside non-FGM pressure vessels cylinder.

Case/conditions	B.C.	Representative equations	Constants to define
Plastic-elastic	Plastic region: Elastic region: Interface zone: u^Plastic(r = r_p) = u^Elastic(r = r_p)	Plastic region: (71) Elastic region: (4)	a₁, a₂ in (9) V₁ in (72)-(73) U₆ in (80) r_p

Elastic-plastic	Plastic region: Elastic region: Interface zone: Same as plastic-elastic	Same as plastic-elastic	Same as plastic-elastic

Plastic-elastic-plastic	Plastic region 1: Elastic region: no BC Interface zone 1: u^Plastic(r = r_p1) = u^Elastic(r = r_p1) Plastic region 2: Interface zone 2: u^Plastic(r = r_p2) = u^Elastic(r = r_p2)	Same as plastic-elastic	a₁, a₂ in (9) V₁ in (72)-(73) U₆ in (80) r_p1, r_p2, while V₁ and U₆ are duplicated for two plastic cases Consequently, there are 8 variables.

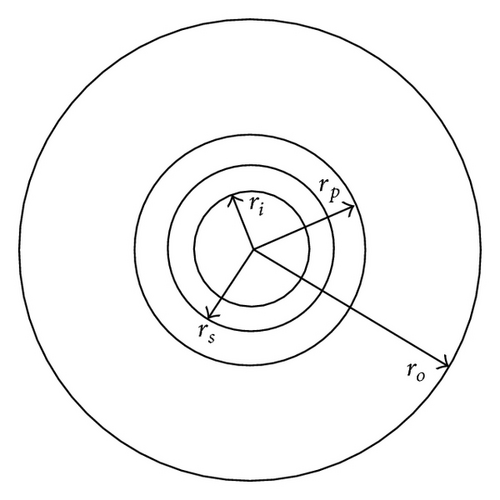
6. Summary and Future Topics

During this study, stress-strain relations of FGM and non-FGM cylindrical vessels behavior in the presence of physical phenomena like magnetic, gravitation, rotational, and electrical charge were developed. In addition, a new power law model for FGM materials was suggested and discussed.

In the next stage, development of plastic phase mathematical model was performed based on von Mises criterion. The elastoplastic states conditions of the FGM and non-FGM vessels that were developed are as follows:

(i)
FGM: elastic-plastic.
(ii)
FGM: plastic-elastic.
(iii)
FGM: plastic-elastic-plastic.
(iv)
FGM: elastic-plastic-elastic.
(v)
Non-FGM: elastic-plastic.
(vi)
Non-FGM: plastic-elastic.
(vii)
Non-FGM: plastic-elastic-plastic.

However, the case elastic-plastic-elastic in non-FGM pressure vessels was not being discussed since it is not physically valid due to vessels material homogeneity.

In the future, thorough examination including numerical and experimental aspects of the developed elastic-plastic states of FGM and non-FGM materials influenced by body force effect should be performed.

Competing Interests

The author declares that he has no competing interests.

References

1 Nagler J., Parametric examination including brief survey of composite and homogenous closed ended cylindrical pressure vessels, WSEAS Transactions on Applied and Theoretical Mechanics. (2014) 9, 136–160, 2-s2.0-84900791637.
Google Scholar
2 Kalali A. T. and Hadidi-Moud S., A semi-analytical approach to elastic-plastic stress analysis of FGM pressure vessels, Journal of Solid Mechanics. (2013) 5, no. 1, 63–73, 2-s2.0-84890406976.
Google Scholar
3 Ansari Sadrabadi S. and Rahimi G. H., Yield onset of thermo-mechanical loading of FGM thick walled cylindrical pressure vessels, World Academy of Science, Engineering and Technology. (2014) 8, no. 7, 1321–1325.
Google Scholar
4 Sadeghian M. and Ekhteraei Toussi H., Elasto-plastic axisymmetric thermal stress analysis of functionally graded cylindrical vessel, International Journal of Basic Applied Silences. (2012) 2, no. 10, 10246–10257.
Google Scholar
5 Eraslan A. N. and Akis T., Elastoplastic response of a long functionally graded tube subjected to internal pressure, Turkish Journal of Engineering and Environmental Sciences. (2005) 29, no. 6, 361–368, 2-s2.0-30644464317.
Google Scholar
6 Nemat-Alla M., Ahmed K. I. E., and Hassab-Allah I., Elastic-plastic analysis of two-dimensional functionally graded materials under thermal loading, International Journal of Solids and Structures. (2009) 46, no. 14-15, 2774–2786, https://doi.org/10.1016/j.ijsolstr.2009.03.008, ZBL1167.74343, 2-s2.0-65549120137.
10.1016/j.ijsolstr.2009.03.008
CAS Web of Science® Google Scholar
7 Akis T., Elastoplastic analysis of functionally graded spherical pressure vessels, Computational Materials Science. (2009) 46, no. 2, 545–554, https://doi.org/10.1016/j.commatsci.2009.04.017, 2-s2.0-67651091549.
10.1016/j.commatsci.2009.04.017
CAS Web of Science® Google Scholar
8 Kanlıkama B., Abuşoğlu A., and Güzelbey İ. H., Coupled thermoelastic analysis of thick-walled pressurized cylinders, International Journal of Energy and Power Engineering. (2013) 2, no. 2, 60–68.
10.11648/j.ijepe.20130202.15
Google Scholar
9 Chandel N., Manthena V. R., and Lamba N. K., Thermoelastic behavior of a thin circular functionally graded material (FGM) disk subjected to thermal loads, International Journal on Recent and Innovation Trends in Computing and Communication. (2015) 3, no. 2, 72–74.
Google Scholar
10 Sinclair G. B. and Helms J. E., A review of simple formulae for elastic hoop stresses in cylindrical and spherical pressure vessels: What can be used when, International Journal of Pressure Vessels and Piping. (2015) 128, 1–7, https://doi.org/10.1016/j.ijpvp.2015.01.006, 2-s2.0-84924286602.
10.1016/j.ijpvp.2015.01.006
Web of Science® Google Scholar
11 Zhao W., Seshadri R., and Dubey R. N., On thick-walled cylinder under internal pressure, Journal of Pressure Vessel Technology. (2003) 125, no. 3, 267–273, https://doi.org/10.1115/1.1593082, 2-s2.0-0041426738.
10.1115/1.1593082
Web of Science® Google Scholar
12 Nayebi A., Analysis of bree′s cylinder with nonlinear kinematic hardening behavior, Iranian Journal of Science and Technology, Transaction B: Engineering. (2010) 34, no. 5, 487–498, 2-s2.0-78751555028.
Web of Science® Google Scholar
13 Szabó B. A., Actis R. L., and Holzer S. M., Solution of elastic-plastic stress analysis problems by the P-version of the finite element method, Modeling, Mesh Generation, and Adaptive Numerical Methods for Partial Differential Equations, 1995, 75, Springer, New York, NY, USA, 395–416, The IMA Volumes in Mathematics and its Applications, https://doi.org/10.1007/978-1-4612-4248-2_19.
10.1007/978-1-4612-4248-2_19
Google Scholar
14 Gibson M. C., Determination of residual stress distributions in autofrettaged thick-walled cylinders [Ph.D. thesis], 2008, Cranfield University, Cranfield, UK.
Google Scholar
15 Lee E.-Y., Lee Y.-S., Yang Q.-M., Kim J.-H., Cha K.-U., and Hong S.-K., Autofrettage process analysis of a compound cylinder based on the elastic-perfectly plastic and strain hardening stress-strain curve, Journal of Mechanical Science and Technology. (2010) 23, no. 12, 3153–3160, https://doi.org/10.1007/s12206-009-1009-9, 2-s2.0-74749105758.
10.1007/s12206-009-1009-9
Web of Science® Google Scholar
16 Wahi N., Ayob A., and Elbasheer M. K., Effect of optimum autofrettage on pressure limits of thick-walled cylinder, International Journal of Environmental Science and Development. (2011) 2, no. 4, 329–333, https://doi.org/10.7763/ijesd.2011.v2.146.
10.7763/IJESD.2011.V2.146
Google Scholar
17 Hu Z. and Puttagunta S., Computer modeling of internal pressure autofrettage process of a thick-walled cylinder with the Bauschinger effect, American Transactions on Engineering and Applied Science. (2012) 1, no. 2, 143–161.
Google Scholar
18 Trojnacki A. and Krasinski M., New concepts in verification of analytical solutions for autofrettaged high-pressure vessels, Proceedings of the 9th International Conference on Fracture and Strength of Solids, June 2013, Jeju, Republic of Korea, 1–11.
Google Scholar
19 Zhu R. and Zhu G., On autofrettage of cylinders by limiting circumferential residual stress based on mises yield criterion, Journal of Theoretical and Applied Mechanics. (2013) 51, no. 3, 697–710, 2-s2.0-84914100981.
Web of Science® Google Scholar
20 Bhatnagar R. M., Modelling, validation and design of autofrettage and compound cylinder, European Journal of Mechanics—A/Solids. (2013) 39, 17–25, https://doi.org/10.1016/j.euromechsol.2012.09.013, 2-s2.0-84871772861.
10.1016/j.euromechsol.2012.09.013
Web of Science® Google Scholar
21 Gupta S. R. and Vora C. P., A Review paper on pressure vessel design and analysis, International Journal of Engineering Research and Technology. (2014) 3, no. 3, 295–300.
CAS Google Scholar
22 Kamal S. M. and Dixit U. S., Feasibility study of thermal autofrettage process, Advances in Material Forming and Joining, 2015, Springer, 81–107, Topics in Mining, Metallurgy and Materials Engineering, https://doi.org/10.1007/978-81-322-2355-9_5.
10.1007/978-81-322-2355-9_5
Google Scholar
23 Kumar M. and Moulick S. K., Comparative stress analysis of elliptical and cylindrical pressure vessel with and without autofrettage consideration using finite element method, International Journal of Advanced Engineering Research and Studies. (2015) 4, no. 2, 189–195.
Google Scholar
24 Patil A., Kolhe A., Sayeed A., and Shaikh A. W., Review of buckling in various structures like plate and shells, International Journal of Research in Engineering and Technology. (2014) 3, no. 4, 396–402, https://doi.org/10.15623/ijret.2014.0304072.
10.15623/ijret.2014.0304072
Google Scholar
25 Shen H. S., Post buckling analysis of axially-loaded FG cylindrical shells in thermal environments, Composites Science and Technology. (2002) 62, 977–987.
10.1016/S0266-3538(02)00029-5
Web of Science® Google Scholar
26 Kadoli R. and Ganesan N., Buckling and free vibration analysis of functionally graded cylindrical shells subjected to a temperature-specified boundary condition, Journal of Sound and Vibration. (2006) 289, no. 3, 450–480, https://doi.org/10.1016/j.jsv.2005.02.034, 2-s2.0-27744473911.
10.1016/j.jsv.2005.02.034
Web of Science® Google Scholar
27 Shariyat M., Dynamic thermal buckling of suddenly heated temperature-dependent FGM cylindrical shells, under combined axial compression and external pressure, International Journal of Solids and Structures. (2008) 45, no. 9, 2598–2612, https://doi.org/10.1016/j.ijsolstr.2007.12.015, ZBL1169.74438, 2-s2.0-40649106662.
10.1016/j.ijsolstr.2007.12.015
CAS Web of Science® Google Scholar
28 Huang H. and Han Q., Nonlinear elastic buckling and post-buckling of axially compressed functionally graded cylindrical shells, International Journal of Mechanical Sciences. (2009) 51, no. 7, 500–507, https://doi.org/10.1016/j.ijmecsci.2009.05.002, 2-s2.0-67650744254.
10.1016/j.ijmecsci.2009.05.002
Web of Science® Google Scholar
29 Sofiyev A. H., The buckling of FGM truncated conical shells subjected to axial compressive load and resting on Winkler-Pasternak foundations, International Journal of Pressure Vessels and Piping. (2010) 87, no. 12, 753–761, https://doi.org/10.1016/j.ijpvp.2010.08.012, 2-s2.0-78649842445.
10.1016/j.ijpvp.2010.08.012
Web of Science® Google Scholar
30 Zhao X. and Liew K. M., A mesh-free method for analysis of the thermal and mechanical buckling of functionally graded cylindrical shell panels, Computational Mechanics. (2010) 45, no. 4, 297–310, https://doi.org/10.1007/s00466-009-0446-8, ZBL05674232, 2-s2.0-79955522533.
10.1007/s00466-009-0446-8
Web of Science® Google Scholar
31 Zhao X. and Liew K. M., An element-free analysis of mechanical and thermal buckling of functionally graded conical shell panels, International Journal for Numerical Methods in Engineering. (2011) 86, no. 3, 269–285, https://doi.org/10.1002/nme.3059, ZBL1235.74378, 2-s2.0-79952773842.
10.1002/nme.3059
Web of Science® Google Scholar
32 Huang H., Han Q., and Wei D., Buckling of FGM cylindrical shells subjected to pure bending load, Composite Structures. (2011) 93, no. 11, 2945–2952, https://doi.org/10.1016/j.compstruct.2011.05.009, 2-s2.0-80052388236.
10.1016/j.compstruct.2011.05.009
Web of Science® Google Scholar
33 Nagler J., On Homogeneous and Composite Cylindrical Pressure Vessels, 2016, LAP Lambert Academic.
Google Scholar
34 Horgan C. O. and Chan A. M., Pressurized hollow cylinder or disk problem for functionally graded isotropic linearly elastic materials, Journal of Elasticity. (1999) 55, no. 1, 43–59, https://doi.org/10.1023/A:1007625401963, ZBL0965.74012, 2-s2.0-0033281093.
10.1023/A:1007625401963
Web of Science® Google Scholar
35 Çallıoğlu H., Sayer M., and Demir E., Elastic-plastic stress analysis of rotating functionally graded discs, Thin-Walled Structures. (2015) 94, 38–44, https://doi.org/10.1016/j.tws.2015.03.016.
10.1016/j.tws.2015.03.016
Web of Science® Google Scholar
36 Wang Z. W., Zhang Q., Xia L. Z., Wu J. T., and Liu P. Q., Stress analysis and parameter optimization of an FGM pressure vessel subjected to thermo-mechanical loadings, Procedia Engineering. (2015) 130, 374–389, https://doi.org/10.1016/j.proeng.2015.12.230.
10.1016/j.proeng.2015.12.230
Google Scholar
37 Nejad M. Z. and Rahimi G. H., Deformations and stresses in rotating FGM pressurized thick hollow cylinder under thermal load, Scientific Research and Essay. (2009) 4, no. 3, 131–140.
Google Scholar
38 Bhangale R. K. and Ganesan N., Static analysis of simply supported functionally graded and layered magneto-electro-elastic plates, International Journal of Solids and Structures. (2006) 43, no. 10, 3230–3253, https://doi.org/10.1016/j.ijsolstr.2005.05.030, ZBL1120.74597, 2-s2.0-33645146765.
10.1016/j.ijsolstr.2005.05.030
CAS Web of Science® Google Scholar
39 Nowacki W., Thermoelasticity, 1962, Pergamon Press, Oxford, UK.
Google Scholar
40 Vena P., Gastaldi D., and Contro R., Determination of the effective elastic-plastic response of metal-ceramic composites, International Journal of Plasticity. (2008) 24, no. 3, 483–508, https://doi.org/10.1016/j.ijplas.2007.07.001, ZBL1145.74035, 2-s2.0-37049027483.
10.1016/j.ijplas.2007.07.001
CAS Web of Science® Google Scholar
41 Nayebi A., Tirmomenin A., and Damadam M., Elasto-plastic analysis of a functionally graded rotating disk under cyclic thermo-mechanical loadings considering continuum damage mechanics, International Journal of Applied Mechanics. (2015) 7, no. 2, 1550026, https://doi.org/10.1142/s175882511550026x, 2-s2.0-84928521958.
10.1142/S175882511550026X
Web of Science® Google Scholar
42 Ozturk A. and Gulgec M., Elastic-plastic stress analysis in a long functionally graded solid cylinder with fixed ends subjected to uniform heat generation, International Journal of Engineering Science. (2011) 49, no. 10, 1047–1061, https://doi.org/10.1016/j.ijengsci.2011.06.001, 2-s2.0-80051784518.
10.1016/j.ijengsci.2011.06.001
Web of Science® Google Scholar
43 Nayebi A. and Ansari Sadrabadi S., FGM elastoplastic analysis under thermomechanical loading, International Journal of Pressure Vessels and Piping. (2013) 111-112, 12–20, https://doi.org/10.1016/j.ijpvp.2013.04.028, 2-s2.0-84887607182.
10.1016/j.ijpvp.2013.04.028
Web of Science® Google Scholar
44 Ugural A. C. and Fenster S. K., Advanced Strength and Applied Elasticity, 2011, 5th edition, Prentice Hall.
Google Scholar

Citing Literature

All articles

Radial Body Forces Influence on FGM and Non-FGM Cylindrical Pressure Vessels

Abstract

1. Introduction

2. General Elastic Stress-Strain Relations with Thermal and Body Forces Influence of Non-FGM Pressure Vessels

3. General Elastic Stress-Strain Relations with Thermal and Body Forces Influence of FGM Pressure Vessels

4. General Elastic-Plastic Stress-Strain Relations with Thermal and Body Forces Influence of FGM Pressure Vessels

5. General Elastic-Plastic Stress-Strain Relations with Thermal and Body Forces Influence of Non-FGM Pressure Vessels

6. Summary and Future Topics

Competing Interests

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Radial Body Forces Influence on FGM and Non-FGM Cylindrical Pressure Vessels

Abstract

1. Introduction

2. General Elastic Stress-Strain Relations with Thermal and Body Forces Influence of Non-FGM Pressure Vessels

3. General Elastic Stress-Strain Relations with Thermal and Body Forces Influence of FGM Pressure Vessels

4. General Elastic-Plastic Stress-Strain Relations with Thermal and Body Forces Influence of FGM Pressure Vessels

5. General Elastic-Plastic Stress-Strain Relations with Thermal and Body Forces Influence of Non-FGM Pressure Vessels

6. Summary and Future Topics

Competing Interests

References

Citing Literature

Figures

References

Related

Information