The Investigation of EM Scattering from the Time-Varying Overturning Wave Crest Model by the IEM

1. Introduction

A considerable amount of research has recently focused on sea spikes, which are a matter of great importance. Sea spikes have been found to cause false target detections and are typically characterized by horizontal polarization (HH) signals that exceed vertical polarization (VV) signals by as much as 10 dB or more [1, 2]. Breaking waves are believed to be responsible for strong sea spikes [3] and occur in areas of the overturning wave crest where nonlinear sea surfaces are generated. Therefore, knowledge of the EM scattering characteristics of the overturning wave crest model is critical for analyzing sea spikes and represents a special area of interest in the detection of sea spike generation.

LONGTANK waves [4] have been widely used in studies of breaking waves [5]. Holliday [6] studied the backscattering of LONGTANK waves at incident angles of θ_i = 40^°, 60^°, 85^° and found that strong sea spikes are generated at the incident wave frequency of 10 GHz. Yang et al. [3] employed MLFMA with higher-order hierarchical Legendre basis functions to conduct a preliminary study on the scattering of 3D breaking water wave crests at LGA and analyzed the VV and HH polarized scattering of profiles of LONGTANK breaking waves. Guan et al. [7] also introduced an algebraic fractal model-Paretian Poisson process to sea spike modeling and target detection. In this work, an improved 3D time-varying overturning wave crest model is described and investigated. This model is based on the 2D time-varying overturning wave crest model in [8], which, in turn, is based on the sea wave of the virtual reality scene in computer graphics; the influences of wind speed on the size and height of the overturning wave were considered in the model.

Numerical techniques have been widely used in recent research on sea surface scattering. However, these techniques involve long computational time and large memory requirements; thus, numerical techniques have become research bottlenecks, especially when considering high-frequency 3D scattering problems. Although several integral equation-based techniques [9, 10] are proposed to improve the efficiency of the classic numerical techniques, it is still difficult to deal with the high-frequency 3D scattering problems. High-frequency techniques, such as geometric optics (GO) and physical optics (PO) [11–13], are fast but they present relatively low accuracy. Therefore, IEM [14] is preliminarily employed to address the EM scattering problems of the improved time-varying overturning wave crest model. IEM was developed by Fung based on an approximate solution of a pair of integral equations for tangential surface fields and was later improved by several groups [15–17]. In this paper, an improved time-varying overturning wave crest model was generated and meshed into a large number of triangles. According to the direction of the incident wave, a triangle which is lighted can be determined, after which the scattered far field is calculated. The total far-field is the sum of the scattered far-fields of all lighted triangles. According to the simulation results, the phenomenon of backscattering RCS of HH polarization exceeding that of VV polarization is observed. Therefore, this phenomenon demonstrated that the overturning wave crest is a reason of the sea spikes. In addition, the backscattering RCS of HH polarization exceeding that of VV polarization by as much as 10 dB or more is more likely to occur for the upwind incidence, which is because the multiple scattering is more obvious when the incident wave is along with the upwind direction compared with the downwind direction.

The remainder of this paper is organized as follows. Section 2 presents the improved time-varying overturning wave crest model and the theoretical IEM formulas used to calculate the EM scattering of this model. The backscattering RCS of HH and VV polarization at different time points is discussed in Section 3. Concluding remarks are addressed and further investigations are proposed in Section 4.

2. Theoretical Analysis

The improved time-varying overturning wave crest was modeled according to [8], where the influences of wind speed on the size and height of overturning wave crest model were considered during modeling. The overturning wave crest model in [8] is a 2D model; the 3D model was obtained by stretching the traditional 2D overturning wave crest model in the y-axis. IEM was then used to calculate the backscattering of the 3D model.

2.1. Improved Time-Varying Overturning Wave Crest Model

The construction of the 2D time-varying overturning wave crest model will be described in detail at first. As is known, the Beaufort wind scale is always used to describe the sea condition, which includes the wind speed and the wave height. The sea condition for the different Beaufort wind scales and the relationship between the Beaufort wind scale and wind speed have been presented in [8].

Furthermore, the relationship between the wave height and the wind speed can be obtained by the Gaussian function fitting method and can be approximately written as [18]

$$ ()

where S = H/L,  α = u^2/3 − 12.6549,  β = u^2/3 − 6.4463,  H is the height of the sea wave and u is the wind speed, and L is the length of sea wave.

For the 2D time-varying overturning wave crest model, the length and height of the wave crest are varying with the time stepping. Therefore, the time factor was included to control the profile of the overturning wave crest model; the 2D time-varying overturning wave crest model can be expressed as

$$ ()

where $$, the period of overturning wave crest is T = 2s,  $$, z_max = max{z^′}, and  k can be obtained from Table 1. s is an arithmetic progress between 0 and 1, and each term of s contributes to the calculation of the location of the sampling point of the overturning wave crest. For the ith sampling point, s₁ and s₂ are calculated according to s(i) and k₁, k₂. The dimensional information can be achieved by s₁ and s₂ according to (2). k₁~k₇ vary with the parameter t and are employed to calculate the location of the sampling point.

Table 1. Computational parameters.

k	Overturning		After overturning
	s > 0.5	s ≤ 0.5	s > 0.5	s ≤ 0.5
k1	2	0.7	2	0.5
k2	(1 − t0.85)/4	0.25	0	0.25
k3	t0.85/4	0	−t/4	(t + 1) 0.7/2
k4	4	0	4	40
k5	t1.5	t1.5	1	1
k6	16	4	16	4
k7	(t + 4)/5	(t + 4)/5	−t	−t

The 3D model was obtained by stretching the 2D overturning wave crest model in the y-axis, as illustrated in Figure 1; here, the −x direction is the downwind direction and the +x direction is the upwind direction.

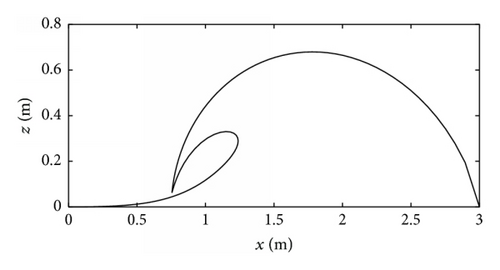
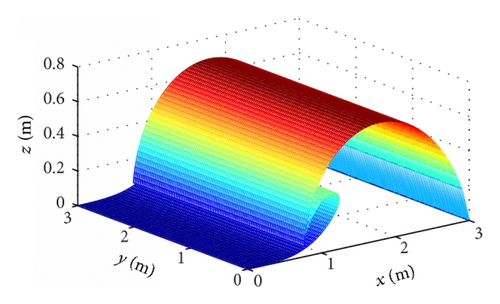
2.2. The IEM for the EM Scattering of Improved Time-Varying Overturning Wave Crest Model

For the EM scattering of the 3D time-varying overturning wave crest, the multiple scattering plays a major role in the scattering results because of the steep part of the model. However, the traditional Kirchhoff method is difficult to deal with this problem, because the multiple scattering is not considered. Therefore, IEM is utilized to study the EM scattering of improved time-varying overturning wave crest model.

Considered an incident plane wave, it can be expressed as

$$ ()

In the IEM, the governing equations for the tangential surface fields on a dielectric surface can be written as the sum of the standard Kirchhoff surface field and a complementary surface field, which can be written as [19]

$$ ()

where $$ is the unit normal vector of the surface.

$$, $$, $$ are the local coordinate vectors and can be obtained by

$$ ()

According to [18], the standard Kirchhoff surface field and the complementary surface field can be written as

$$ ()

where R_⊥, R_∥ are the Fresnel reflection coefficients which can be expressed as

$$ ()

where G is Green’s function and ε_r, μ_r are the ratios of the permittivity and permeability of medium 2 to medium 1.

For the IEM, a complementary surface field was added to the Kirchhoff surface field to improve the resulting accuracy. However, the Kirchhoff surface field is widely used to determine the EM scattering of rough surfaces and is valid when the surface roughness is large and the surface slope is small, while if the surface slope is large, the related multiple scattering will be significant and the Kirchhoff surface field becomes invalid. Moreover, the complementary surface field part represents the scattering from the other facets. Therefore, the IEM obviously has wider applications than the Kirchhoff method.

The improved time-varying overturning wave crest model should be meshed into a large number of triangles to determine EM scattering by the IEM; the EM scattering process is divided into three steps.

(1) Shelter Determination. Whether or not a triangle is lighted is easily determined, if given the direction of incident plane wave.

When the direction of incident wave is given, if a triangle can be lighted by the incident wave, it should meet two necessary conditions: At first, the triangular facet should not be sheltered by itself—$$; secondly, the triangular facet should not be sheltered by any other facets, where $$ is the vector of the incident plane wave and $$ is the normal vector of the triangle.

Figure 2 shows how to determine whether a triangle is sheltered by the others. As shown in Figure 2, S is the center of facet 1. PS is a ray whose direction is the direction of incident wave, and PS passes through point S. If ray PS has an intersection Q with facet 2, facet 2 is sheltered by facet 1; otherwise facet 2 is not sheltered by triangle facet 1.

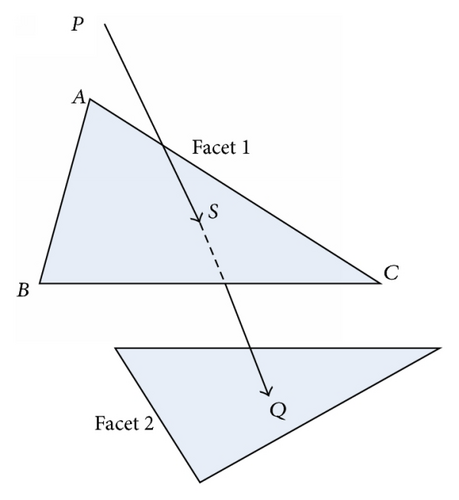
In addition, it should be noted that the determination of the lighted triangles is time-consuming. Therefore, oct-tree [20], which is an accelerated technique, is utilized to further decrease the computational time and improve the efficiency.

(2) Tangential Surface Field Calculation. When a triangle is lighted, the tangential surface fields are calculated according to (4)–(7). The integral area of the complementary surface field is indicated by the other lighted triangles.

(3) Scattered Far-Field Calculation. Scattered far-fields can be obtained from the tangential surface fields using the Stratton-Chu integral:

$$ ()

where $$, $$ is the unit vector in the scattered direction, $$ is the unit vector normal to interface inside the medium in which scattering is considered, η_s is the intrinsic impendence of the medium in which E^s is calculated, k_s is the wave number of the medium in which E^s is calculated, R₀ is the range from the center of the illuminated area to the point of observation, and E, H are the total electric and magnetic field on the interface. In the end, the total scattered far-fields are the sum of scattered far-fields from all the lighted triangles.

3. Numerical Simulations and Discussions

The validity of the IEM results for EM scattering of the 3D overturning wave crest model was compared with that of the finite element method (FEM), which was performed on FEKO. FEM is a numerical technique, and FEKO is an EM simulation software program that is widely used for EM computation. The 3D overturning wave crest model is shown in Figure 1(b). The size is 3 m × 3 m, and the wind speed is u = 5 m/s. The frequency of incident plane wave is given by f = 1 GHz, the incident angle θ_i varies from 0^° to 80^°, the azimuthal angle is ϕ = 0^°, and the relative permittivity of sea water is ε_r = (73.6087,54.5816), which is obtained from the Debye model [21]. HH polarization is considered. The simulation result is presented in Figure 3.

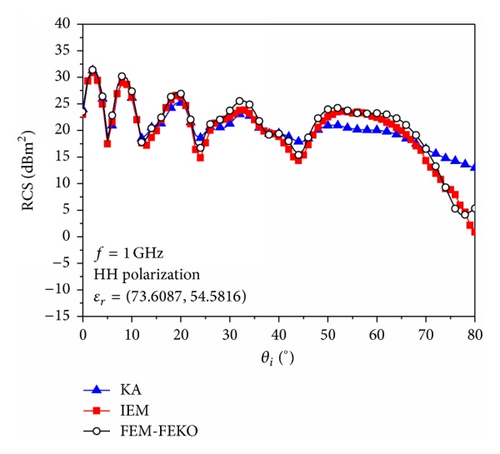
Figure 3 shows that the KA method is valid for incident angles of 0^°~ 40^°; a considerable difference may be observed between the KA method and FEM at incident angles larger than 40^°. The simulation results of IEM are consistent with those of FEM based on FEKO at incident angles of  0^°~80^°. This result indicates that the scattered Kirchhoff field is dominant at incident angles smaller than 40^°, whereas the complementary scattered field dominates with increasing incident angle. Therefore, compared with the KA method, a much wider region of validity may be achieved by IEM.

Profiles of the 16 overturning wave crest models in the xoz-plane are shown in Figure 4; here, the wind speed was u = 10 m/s, and S = 1/7. The length of the 3D overturning wave crest model in the y-axis was set to 3 m. Figure 4 shows that the height and length of the overturning wave crest model increased with time during the generation process. This observation is consistent with that observed in real situations. The heights of the first and the 16th overturning wave crest models were 1.3796 m and 2.1474 m, respectively, and the lengths of the first and the 16th overturning wave crest models were 9.657 m and 15.0316 m, respectively.

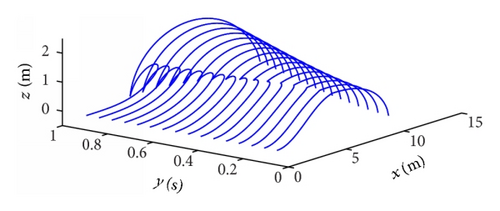
Figures 5 and 6 show the simulation results of the backscattering of 16 overturning wave crest models at 16 time sampling points as shown in Figure 4 with ϕ = 0^° and ϕ = 180^°, respectively; here, the time sampling interval was Δt = 0.9/15 (s). These 16 overturning wave crest models represent the generation process of the overturning wave crest.

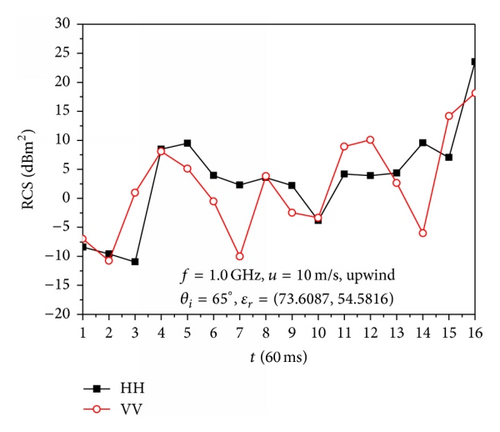
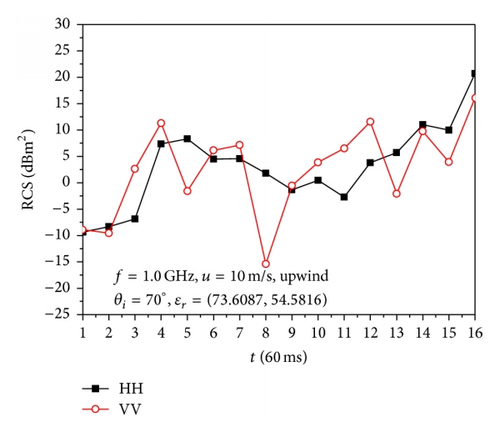
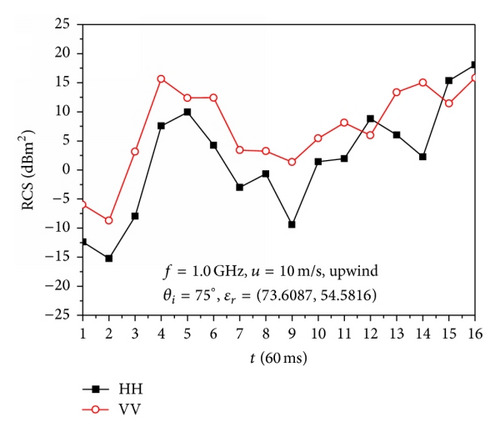
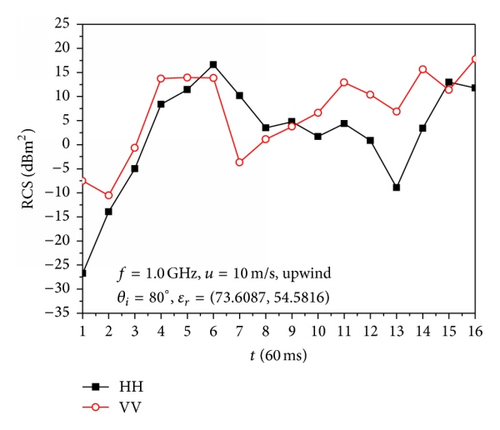
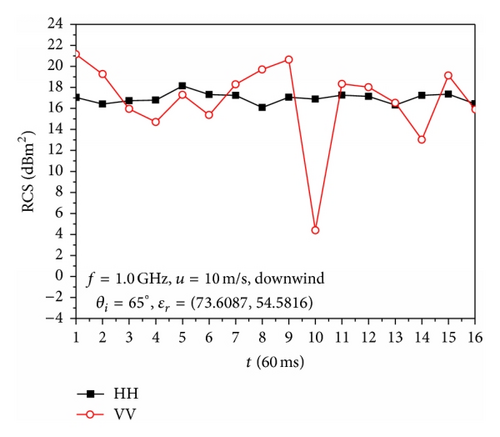
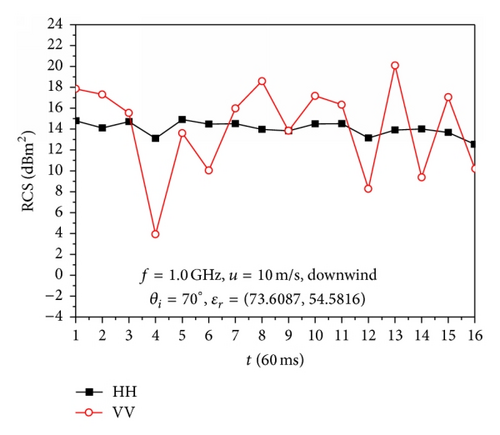
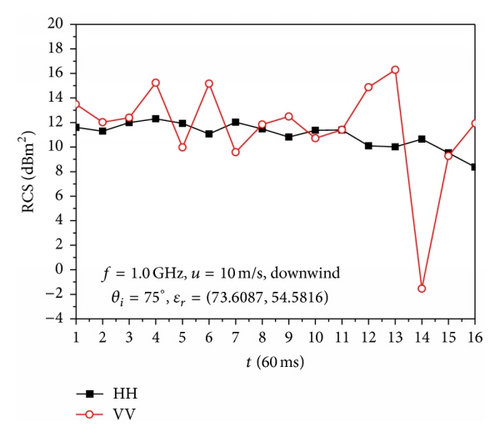
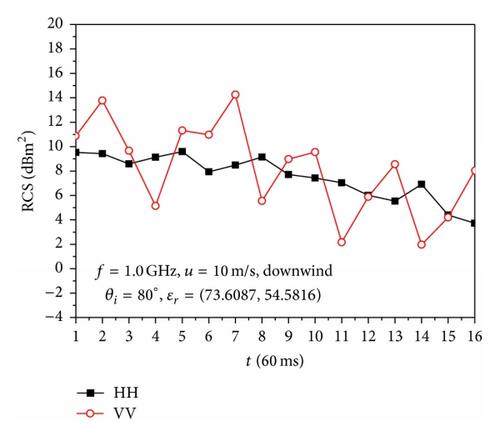
Figure 5 shows that the backscattering RCS of HH polarization and VV polarization varies quickly with the time for upwind incidence. At t = Δt~4Δt, the related overturning wave crest models are at the very beginning of the generation of overturning wave crest, and steep profiles are not initially observed and the sea spike phenomenon is not serious. The profiles became steeper in the overturning wave crest models at t = 5Δt~16Δt; therefore the sea spike phenomenon is observed and the strong sea spike phenomenon occurred in some models at the calculated incident angles.

Figure 6 shows that the phenomenon of backscattering RCS of HH polarization larger than that of VV polarization occurs in some time samples; this observation is related to the instantaneous profile of the overturning wave crest model as well as the incident angle. The RCS of VV polarization has more dramatic changes than that of HH polarization with the direction of incident wave along with the downwind direction. The backscattering RCS of VV polarization has a sharp decrease for incident angles of 65^°,  70^°, and 75^° during the generation of overturning wave crests, at which sea spikes are easier to take place.

Figure 7 illustrates the difference value of the backscattering RCS between HH polarization and VV polarization for the 16 overturning wave crest models with different incident angles, where the blue lines represent that the difference value of the backscattering RCS between HH polarization and VV polarization is equal to 10 dBm². The computational parameters are the same as those in Figures 5 and 6.

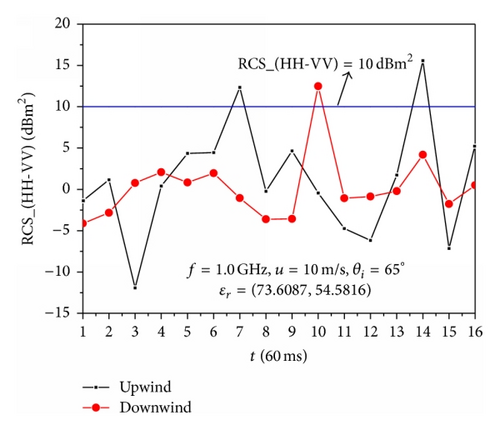
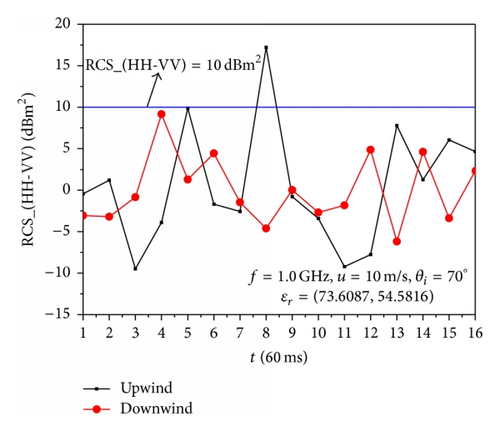
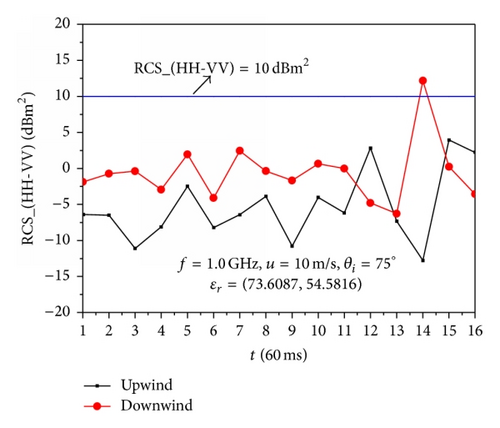
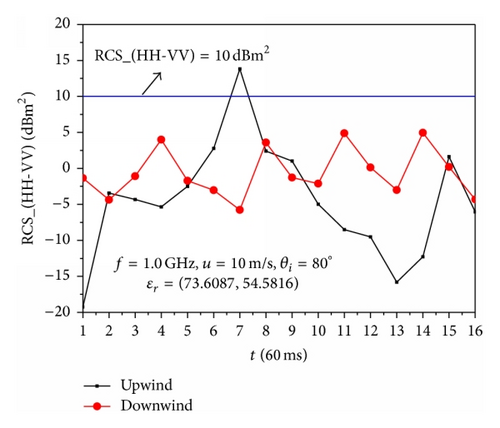
As presented in Figure 7, the phenomenon of the RCS of HH polarization larger than that of VV polarization is observed for the upwind and downwind incidence. However, it can be seen that the strong sea spikes which are characterized as HH polarization RCS exceeding VV polarization RCS by as much as 10 dBm² or more are more likely to be observed for the upwind incidence. This is because the overturning part of the wave is lighted when the incident wave is along with the upwind direction, and the multiple scattering is obvious, which is the main reason of the phenomenon of the RCS of HH polarization larger than that of VV polarization. Therefore, the overturning wave crest is one of the reasons of the sea spikes, and the sea spikes are more likely to occur for the upwind incidence.

4. Conclusions

In this paper, an improved time-varying overturning wave crest model was described in detail. In this model, the influence of wind speed on the size and height of overturning wave was considered. The element of time was also discussed to control the overturning wave crest model profile. The corresponding 3D overturning wave crest model was then obtained by stretching the 2D overturning wave crest model in the y-axis.

Based on the geometrical features of the 3D overturning wave crest model, we employed the IEM to investigate the backscattering RCS of 16 3D overturning wave crest models and reveal the process of overturning wave crest generation. Simulation results show that the sea spike phenomenon occurs in some time samples, and this result is attributed to the instantaneous profile of the overturning wave crest model as well as the incident angle. The overturning wave crest is one of the reasons of the sea spikes, and the sea spikes are more likely to occur for the upwind incidence.

Competing Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.