We define and study several properties of what we call Maximal Strichartz Family of Gaussian Distributions. This is a subfamily of the family of Gaussian Distributions that arises naturally in the context of the Linear Schrödinger Equation and Harmonic Analysis, as the set of maximizers of certain norms introduced by Strichartz. From a statistical perspective, this family carries with itself some extrastructure with respect to the general family of Gaussian Distributions. In this paper, we analyse this extrastructure in several ways. We first compute the Fisher Information Matrix of the family, then introduce some measures of statistical dispersion, and, finally, introduce a Partial Stochastic Order on the family. Moreover, we indicate how these tools can be used to distinguish between distributions which belong to the family and distributions which do not. We show also that all our results are in accordance with the dispersive PDE nature of the family.

1. Introduction

The most important multivariate distribution is the Multivariate Normal (MVN) Distribution. To fix the notation, we give here its definition.

Definition 1. One says that a random variable X is distributed as a Multivariate Normal Distribution if its probability density function (pdf)

(1)

takes the form

(2)

where μ≔E[X] ∈ Rⁿ is the mean value vector and

is the n × n positive definite symmetric Variance-Covariance Matrix.

Its importance derives mainly (but not only) from the Multivariate Central Limit Theorem which has the following statement.

Theorem 2. Suppose that X = (x₁, …, x_n) ^T is a random vector with Variance-Covariance Matrix Σ. Assume also that for every i = 1, …, n. If X₁, X₂, X₃, … is a sequence of i.i.d. random variables distributed as X, then

(3)

where →^d represents the convergence in distribution.

Due to its importance, several authors have tried to give characterizations of this family of distributions. See, for example, [1, 2] for an extended discussion on multivariate distributions and their properties. Here, we concentrate on characterizing the MVN through variational principles, such as the maximization of certain functionals. A well-known characterization of the Gaussian Distribution is through the maximization of the Differential Entropy, under the constraint of fixed variance Σ. We focus on the case of when the support of the pdf is the whole Euclidean Space Rⁿ.

Theorem 3. Let X be a random variable whose pdf is f_X. The Differential Entropy h(X) is defined by the following functional:

(4)

The Multivariate Normal Distribution has the largest Differential Entropy h(X) amongst all the random variables X with equal variance Σ. Moreover, the maximal value of the Differential Entropy h(X) is h(MVN(Σ)) = (1/2)log⁡[(2πe)ⁿ|Σ|].

We refer to Appendix for a proof of this well-known theorem. This characterization is, in some sense, not completely satisfactory because it is given just with the restriction of fixed variance. A more general characterization of the Gaussian Distribution has been given in a setting which, at first sight, seems very far, and it is the one of Harmonic Analysis and Partial Differential Equations. We first introduce the so-called admissible exponents.

Definition 4. Fix n ≥ 1. One calls a set of exponents (q, r) admissible if 2 ≤ q, r ≤ +∞ and

(5)

Remark 5. These exponents are characteristic quantities of certain norms, the Strichartz Norms, naturally arising in the context of Dispersive Equations and can vary from equation to equation. We refer to [3] for more details.

Here is the precise characterization of the Multivariate Normal Distribution, through Strichartz Estimates.

Theorem 6 (see [4]–[7].)Suppose n = 1 or n = 2. Then, for every (q, r) and admissible and for every such that , we have

(6)

where S_h(n, q, r) = S_h(n, r) is the Sharp Homogeneous Strichartz Constant, defined by

(7)

and given by

(8)

Moreover, inequality (6) becomes an equality if and only if

is the pdf of a Multivariate Normal Distribution.

For several other important results on Strichartz Estimates, we refer to [8–11] and the references therein.

Remark 7. This characterization does not need the restriction of fixed variance as the one achieved using the Differential Entropy Functional and so it is, in some sense, more “general.” The result is conjectured to be true for any dimension n ≥ 1. See, for example, [7], where the optimal constant has been computed in any dimension n ≥ 1, under the hypothesis that the maximizers are Gaussians also in dimension n ≥ 3.

We refer to [7] for the relation of this result with harmonic analysis and restriction theorems.

Strichartz Estimates are a fundamental tool in the problem of global well-posedness of PDEs and measure a particular type of dispersion (see, e.g., [3–5, 7, 12, 13]). Strichartz Estimates bring with themselves some interesting statistical features and this is what we want to analyse in the present paper.

The symmetries of the functional in (6) give rise to a family of distributions that we call Maximal Strichartz Family of Gaussian Distributions:

(9)

(10)

We refer to Section 2 for its precise construction. This is a subfamily of the family of Gaussian Distributions and, among the other things, it has the feature that the Mean Vector μ and the Variance-Covariance Matrix Σ depend on common parameters. Therefore, from a statistical perspective, this family carries with itself some extrastructure with respect to the general family of Gaussian Distributions. This extrastructure becomes evident from the form of the Fisher Information Metric of the family.

Theorem 8. Consider p(t, x), a probability distribution function belonging to the Maximal Strichartz Family of Gaussian Distributions , defined in (9). The vector of parameters θ, indexing , is given by

(11)

Then, the Fisher Information Matrix of p(t, x) is given

(i)
in the spherical case (R^TR = σ²Id) by
(12)
(ii)
in the elliptical case (; see Section 3 for the precise definition) by
(13)

Remark 9. Technically, the only possible case inside the Maximal Strichartz Family of Gaussian Distributions is when R^TR = Id_n×n, since R ∈ SO(n) (the spherical case, with σ² = 1). The form of the Fisher Information Matrix, in that case, is simplified to a lower dimension. Nevertheless, the computation performed in the way we did gives the possibility to compute a distance (in some sense centred at the Maximal Strichartz Family of Gaussian Distributions) between members of the Maximal Strichartz Family of Gaussian Distributions and other Gaussian Distributions, for which the orthogonal matrix condition R^TR = Id_n×n is not necessarily satisfied. In particular, it can distinguish between Gaussians evolving through the PDE flow (see Section 2) and Gaussians which do not.

Remark 10. We believe that using the flow of a Partial Differential Equation is a natural way to produce probability density functions, in particular, in this case, since the flow of the PDE, that we are using, preserves the probability constraint. See Section 2.2 for more details on this comment.

As we said, Strichartz Estimates are a way to measure the dispersion caused by the flow of the PDE to which they are related. In statistics, dispersion explains how stretched or squeezed is a distribution. A measure of statistical dispersion is a nonnegative real number which is small for data which are very concentrated and increases as the data become more spread-out. Common examples of measures of statistical dispersion are the variance, the standard deviation, the range, and many others. Here, we connect the two closely related concepts (dispersion in statistics and PDEs) by introducing some measures of statistical dispersion like the Index of Dispersion in Definition 38 (see Section 4) which reflect the dispersive PDE nature of the Maximal Strichartz Family of Gaussian Distributions.

Definition 11. Consider the norms ‖·‖_a and ‖·‖_b on the space of Variance-Covariance Matrices Σ and ‖·‖_c on the space of mean values μ. One defines the following Index of Dispersion:

(14)

with t ≠ 0 and where μ(t) is as follows:

(15)

while Σ(t) is given by

(16)

One calls

the abc-Dispersion Index of the Maximal Family of Gaussians and one calls

(17)

a-Static Dispersion Index of the Maximal Family of Gaussians.

We compute this Index of Dispersion for our family of distributions and show that it is consistent with PDE results. We refer to Definition 38 for more details.

Another important concept in probability and statistics is the one of Stochastic Order. A Stochastic Order is a way to consistently put a set of random variables in a sequence. Most of the Stochastic Orders are partial orders, in the sense that an order between the random variables exists, but not all the random variables can be put in the same sequence. Many different Stochastic Orders exist and have different applications. For more details on Stochastic Orders, we refer to [14]. Here, we use our Index of Dispersion to define a Stochastic Order on the Maximal Strichartz Family of Gaussian Distributions and see how there are natural ways of partially ranking the distributions of the family (see Section 5), in agreement with the flow of the PDE.

Definition 12. Consider two random variables X₁ and X₂ such that , for any θ₁ and θ₂. One says that the two random variables are ordered according to their Dispersion Index if and only if the following condition is satisfied:

(18)

Remark 13. In this definition the index can vary according to the context and the choices of the norms in the definition of the index.

An important tool which will be fundamental in our analysis is what we call 1/α-Characteristic Function (see Section 2 and [7, 15]). We conclude the paper with an appendix in which, among the other things, we use the concept of 1/α-Characteristic Function to define generalized types of Momenta that exist also for the Multivariate Cauchy Distributions.

2. Construction of the Maximal Strichartz Family of Gaussian Distributions

This section is devoted to the construction of the Maximal Strichartz Family of Gaussian Distributions; see Figure 1. This is basically done through PDE methods. The program is the following.

(1)
We define 1/α-Characteristic Functions.
(2)
We prove that if u₀ generates a probability distribution p₀(x), then u(t, x) = e^itΔu₀ (see below its precise definition) still defines a probability distribution p_t(x) = |u(t, x)|².
(3)
By means of 1/α-Characteristic Functions, we give the explicit expression of u(t, x) the generator of the family.
(4)
We use symmetries and invariances to build the complete family .

Description unavailable — **Figure 1**
Open in figure viewer PowerPoint

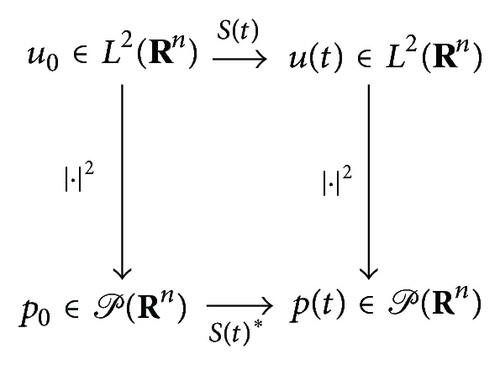
2.1. The 1/α-Characteristic Functions

Following the program, we first need to introduce the tool of 1/α-Characteristic Functions to characterize . It is basically the Fourier Transform, but, differently from the Characteristic Function, the average is not taken with the pdf, but with a power of the pdf.

Definition 14. Consider u : Rⁿ → C to be a Schwartz function, namely, a function belonging to the space

(19)

with α and β being multi-indices, endowed with the following norm:

(20)

Moreover, suppose that

(21)

namely, |u|^α defines a continuous probability distribution function. Then, one defines

(22)

One calls

the 1/α-Characteristic Function of u. Moreover, one defines the Inverse 1/α-Characteristic Function by

(23)

We refer to the note [15] for examples and properties of 1/α-Characteristic Functions and to Appendix for a simple straightforward application of this tool. In particular, we notice that .

Remark 15. If u is complex valued (not just real valued) and, for example, α = n ∈ N, then there are n-distinct complex roots of |u|². In our discussion, this will not create to us any problem, because our process starts with u and produces |u|². We want to remark that the map |u|^α ↦ u is a multivalued function. For this reason, we cannot reconstruct uniquely a generator, given the family that it generates. See formula (39) below and [15] for more details.

Remark 16. We could define 1/α-Characteristic Functions for more general functions u : X → F with X a locally compact abelian group and F a general field. We do not pursue this direction here and we will leave it for a future work. We notice that can be considered also as a 1/α-Expected Value:

(24)

2.2. Conservation of Mass and Flow on the Space of Probability Measures

In this subsection, we show that if defines a probability distribution, then also defines a probability distribution. This is mainly a consequence of the property of e^itΔ of being a unitary operator.

Theorem 17. Consider , the set of all probability distributions on Rⁿ and u : (0, ∞) × Rⁿ → C a solution to (27). Then u induces a flow in the space of probability distributions.

Proof. Consider u₀ : Rⁿ → C such that ; so is a probability distribution on Rⁿ. Consider u(t, x), the solution of (27) with initial datum u₀. Then

(25)

and hence

(26)

Therefore, for every t ∈ R, p(t, x)≔|u(t, x)|² is a probability distribution.

Remark 18. This situation is in striking contrast with respect to the heat equation, where if you start with a probability distribution as initial datum, instantaneously the constraint of being a probability measure is broken.

2.3. Fundamental Solution for the Linear Schrödinger Equation Using 1/α-Characteristic Functions

In this subsection, we solve the Linear Schrödinger Equation

(27)

with initial datum

. This will produce a natural generator u(t, x) of a family of probability distributions, due to Theorem 17.

We first notice that the initial datum becomes a probability density function, if and only if multiplied by a constant. But, since the equation is linear, we can do everything without that constant and then include it at the end.

Remark 19. These computations are well known, but we perform them in detail here, in order to clarify what we will compute in the context of 1/α-Characteristic Functions.

Since

, then also

and

. So, we can apply the 1/2-Characteristic Function to both sides of (27) and get

(28)

whose solution is

(29)

We now need to compute the 1/α-Characteristic Function of the initial datum and then the Inverse 1/2-Characteristic Function of

to get the explicit form of the solution. We have

(30)

by using contour integrals. We notice that, with a simple change of variables, we have

(31)

Hence

(32)

With this, we can conclude

(33)

Now, we make the change of variables

to get

(34)

Hence, we obtain

(35)

Now, we have to find a constant c > 0 such that, for every t ∈ R, the function p(t, x) = c²|u(t, x)|² is a probability density function. The condition to be satisfied is the following:

(36)

which implies c = (π/2)^−n/4. Therefore, the function

(37)

induces the probability density function:

(38)

(39)

is going to be the generator of the family of distributions

Remark 20. This procedure works because the Gaussian Distribution is, up to constants, a fixed point of the 1/α-Characteristic Function. Indeed, if u is Gaussian, then for some normalizing constant c > 0. Moreover, the Schrödinger flow preserves Gaussian Distributions; namely, if your initial datum is Gaussian, then the solution is Gaussian for any future and past times.

2.4. Strichartz Estimates and Their Symmetries

In this subsection, we deduce the Strichartz Estimates for the Schrödinger equation in the case of probability distributions and discuss their symmetries. For clarity, we repeat here the definition of admissible exponents and the Strichartz Estimate.

Definition 21. Fix n ≥ 1. One calls a set of exponents (q, r) admissible if 2 ≤ q, r ≤ +∞ and

(40)

Theorem 22 (see [4]–[7].)For dimension n = 1 or n = 2 (and for any n ≥ 1, supposing that Gaussians are maximizers) and (q, r) admissible pair, the Sharp Homogeneous Strichartz Constant S_h(n, q, r) = S_h(n, r) defined by

(41)

is given by

(42)

Moreover, if one defines S_h(n)≔S_h(n, 2 + 4/n, 2 + 4/n) by

(43)

then, for every n ≥ 1 (always supposing that Gaussians are maximizers), one has that

(44)

S_h(n) is a decreasing function of n and

(45)

For any n ≥ 1 and

admissible pair, the Sharp Dual Homogeneous Strichartz Constant S_d(q, r, n) = S_d(n, r) is defined by

(46)

One has that S_h(n, r) = S_d(n, r).

This is the version of the theorem on Strichartz Estimates without the restriction , as proved in [7]. From this, we can very easily deduce Theorem 6.

Proof of Theorem 6. Just substitute the condition in all the statements.

As explained for example in [12], Strichartz Estimates are invariant by the following set of symmetries.

Lemma 23 (see [12].)Let be the group of transformations generated by

(i)
space-time translations: u(t, x) ↦ u(t + t₀, x + x₀), with t₀ ∈ R, x₀ ∈ Rⁿ;
(ii)
parabolic dilations: u(t, x) ↦ u(λ²t, λx), with λ > 0;
(iii)
change of scale: u(t, x) ↦ μu(t, x), with μ > 0;
(iv)
space rotations: u(t, x) ↦ u(t, Rx), with R ∈ SO(n);
(v)
phase shifts: u(t, x) ↦ e^iθu(t, x), with θ ∈ R;
(vi)
Galilean transformations:
(47)
with v ∈ Rⁿ.

Then, if u solves (27) and

, v = g∘u solves (27) also. Moreover, the constants S_h(n, q, r), S_d(n, q, r), and

are left unchanged by the action of

The only point here is that not all these symmetries leave the set of probability distributions invariant. Therefore, we need to reduce the set of symmetries in our treatment and, in particular, we need to combine the scaling and the parabolic dilations in order to have all the family inside the space of probability distributions .

Lemma 24. Consider u_μ,λ = μu(λ²t, λx) such that maximizes (6); then μ = λ^n/2.

Proof. Consider

(48)

so μ = λ^n/2.

Remark 25. We notice that some of the symmetries can be seen just at the level of the generator of the family u but not by the family of probability distributions p_t(x). For example, the phase shifts u(t, x) ↦ e^iθu(t, x), with θ ∈ R, give rise to the same probability distribution function because and, partially, the Galilean transformations , with v ∈ Rⁿ, reduces to a space translation with x₀ = vt, since . In some sense, the parameter θ can be seen as a latent variable.

Therefore, we have the complete set of probability distributions induced by the generator u(t, x).

Theorem 26. Consider p_t(x) = |u(t, x)|² a probability distribution function generated by u(t, x) (see Section 2.3). Let be the group of transformations generated by

(i)
inertial-space translations and time translations: p(t, x) ↦ p(t + t₀, x + x₀ + vt), with t₀ ∈ R, x₀ ∈ Rⁿ and v ∈ Rⁿ;
(ii)
scaling-parabolic dilations: u(t, x) ↦ λⁿu(λ²t, λx), with λ > 0;
(iii)
space rotations: u(t, x) ↦ u(t, Rx), with R ∈ SO(n);

Then, if u solves (27) and

, v = g∘u solves (27) also, q_t(x) = |v(t, x)|² is still a probability distribution for every

, and the constant S_h(n, q, r) is left unchanged by the action of

This theorem produces the following definition.

Definition 27. One calls Maximal Strichartz Family of Gaussian Distributions the following family of distributions:

(49)

Remark 28. Let p(t, x) be the pdf defined in (39). Then, choose with R = Id, x₀ = v₀ = 0, and λ = 0. This implies that . For this reason, we call p(t, x) the Family Generator of . We notice also that, in the definition of the family and with respect to Theorem 26, we used as scale parameter λ^1/2 instead of λ. This is done without loss of generality, since λ > 0.

Right away we can compute the Variance-Covariance Matrix and Mean Vector of the family.

Corollary 29. Suppose X is a random variable with pdf . Then its Expected Value is

(50)

and its Variance is

(51)

Proof. The proof is a direct computation.

Remark 30. We see here that, differently from the general family of Gaussian distributions, here the Mean Vector and the Variance-Covariance Matrix are related by a parameter, which represents the time flow.

3. The Fisher Information Metric of the Maximal Strichartz Family

Information geometry is a branch of mathematics that applies the techniques of differential geometry to the field of statistics and probability theory. This is done by interpreting probability distributions of a statistical model as the points of a Riemannian Manifold, forming in this way a statistical manifold. The Fisher Information Metric provides a natural Riemannian Metric for this manifold, but it is not the only possible one. With this tool, we can define and compute meaningful distances between probability distributions, in both the discrete and the continuous cases. Crucial is then the set of parameters on which a certain family of distributions is indexed and the geometrical structure of the parameter set is also crucial. We refer to [16] for a general reference on information geometry. The first one to introduce the notion of distance between two probability distributions has been Rao in [17], who used the Fisher Information Matrix as a Riemannian Metric on the space of parameters.

In this section, we restrict our attention to the Fisher Information Metric of the Maximal Strichartz Family of Gaussian Distributions and provide details on the additional structure that the family has with respect to the hyperbolic model of the general Family of Gaussian Distributions. See, for example, [18–20].

3.1. The Fisher Information Metric for the Multivariate Gaussian Distribution

First, we give the general definition of the Fisher Information Metric.

Definition 31. Consider a statistical manifold , with coordinates given by θ = (θ₁, θ₂, …, θ_n) and with probability density function p(x; θ). Here, x is a specific observation of the discrete or continuous random variables X. The probability is normalized, so that ∫_Xp(x, θ)dx = 1 for every . The Fisher Information Metric I_ij is defined by the following formula:

(52)

Remark 32. The integral is performed over all values x that the random variable X can take. Again, the variable θ is understood as a coordinate on the statistical manifold , intended as a Riemannian Manifold. Under certain regularity conditions (any that allows integration by parts), I_ij can be rewritten as

(53)

Now, to compute explicitly the Fisher Information Matrix of the family , we use the following theorem that you can find in [21].

Theorem 33. The Fisher Information Matrix for an n-variate Gaussian Distribution can be computed in the following way. Let

(54)

be the vector of Expected Values and let Σ(θ) be the Variance-Covariance Matrix. Then, the typical element

, of the Fisher Information Matrix for

(55)

where (·)^T denotes the transpose of a vector, tr⁡(·) denotes the trace of a square matrix, and

(56)

Now, we have just to compute the Fisher Information Matrix entry by entry, following the theorem. We recall here that we are considering the following family of Gaussian Distributions:

(57)

and that, in particular, we have that the Expected Value of a random variable X with distribution belonging to the family

is given by

(58)

while the Variance-Covariance Matrix is given by

(59)

Remark 34. We remark again that μ and Σ depend on some common parameters, like the time t.

3.2. Proof of Theorem 8: The Spherical Multivariate Gaussian Distribution

Here, we consider the case in which R^TR = σ²Id_n×n, namely, the case where the Variance-Covariance Matrix is given by Σ≔(1/4)(λ² + 16t²)σ²Id_n×n. In this case, the vector of parameters θ is given by

(60)

with x₀ and v₀ being n × 1, while λ, σ², and t are scalars. In order to fix the notation, we call (θ₁, …, θ_n) ^T≔(x₀, …, x_n),

, θ_2n+1 = λ, θ_2n+2 = σ², and θ_2n+3 = t. Now, we want to compute all the coefficients of I_ij. We use the symmetry of the information matrix I_ij, so I_ij = I_ji. The relevant coefficients are

(i)
i = 1, …, n, j = 1, …, n
(61)
(ii)
i = 1, …, n, j = n + 1, …, 2n
(62)
(iii)
i = 1, …, n, j = 2n + 1
(63)
because μ does not depend on λ and Σ does not depend on x₀;
(iv)
i = 1, …, n, j = 2n + 2
(64)
because μ does not depend on σ² and Σ does not depend on x₀;
(v)
i = 1, …, n, j = 2n + 3
(65)
(vi)
i = n + 1, …, 2n, j = n + 1, …, 2n
(66)
(vii)
i = n + 1, …, 2n, j = 2n + 1
(67)
because μ does not on λ and Σ does not depend on v₀;
(viii)
i = n + 1, …, 2n, j = 2n + 2
(68)
because μ does not depend on σ² and Σ does not depend on v₀;
(ix)
i = n + 1, …, 2n, j = 2n + 3
(69)
(x)
i = 2n + 1, j = 2n + 1
(70)
(xi)
i = 2n + 1, j = 2n + 2
(71)
(xii)
i = 2n + 1, j = 2n + 3
(72)
(xiii)
i = 2n + 2, j = 2n + 2
(73)
(xiv)
i = 2n + 2, j = 2n + 3
(74)
(xv)
i = 2n + 3, j = 2n + 3
(75)

In conclusion, we have

(76)

3.3. Proof of Theorem 8: The Elliptical Multivariate Gaussian Distribution

We define

(77)

We define also

(78)

Using this notations, we are going to compute the matrix I_ij. The relevant coefficients are

(i)
i = 1, …, n, j = 1, …, n
(79)
(ii)
i = 1, …, n, j = n + 1, …, 2n
(80)
(iii)
i = 1, …, n, j = 2n + 1
(81)
because μ does not depend on λ and Σ does not depend on x₀;
(iv)
i = 1, …, n, j = 2n + 2
(82)
because μ does not depend on σ² and Σ does not depend on x₀;
(v)
i = 1, …, n, j = 2n + 3
(83)
(vi)
i = n + 1, …, 2n, j = n + 1, …, 2n
(84)
(vii)
i = n + 1, …, 2n, j = 2n + 1
(85)
because μ does not depend on λ and Σ does not depend on v₀;
(viii)
i = n + 1, …, 2n, j = 2n + 2
(86)
because μ does not depend on σ² and Σ does not depend on v₀;
(ix)
i = n + 1, …, 2n, j = 2n + 3
(87)
(x)
i = 2n + 1, j = 2n + 1
(88)
(xi)
i = 2n + 1, j = 2n + 2
(89)
(xii)
i = 2n + 1, j = 2n + 3
(90)
(xiii)
i = 2n + 2, j = 2n + 2
(91)
(xiv)
i = 2n + 2, j = 2n + 3
(92)
(xv)
i = 2n + 3, j = 2n + 3
(93)

In conclusion, we have

(94)

This concludes the proof of Theorem 8.

3.4. The General Multivariate Gaussian Distribution

As pointed out in [18, 19], for general Multivariate Normal Distributions, the explicit form of the Fisher distance has not been computed in closed form yet even in the simple case where the parameters are t = 0, λ = 0, and v₀ = 0. From a technical point of view, as pointed out in [18, 19], the main difficulty arises from the fact that the sectional curvatures of the Riemannian Manifold induced by and endowed with the Fisher Information Metric are not all constant. We remark again here that the distance induced by our Fisher Information Matrix is centred at the Maximal Strichartz Family of Gaussian Distributions, to enlighten the difference between members of the Maximal Strichartz Family of Gaussian Distributions and other Gaussian Distributions, for which R^TR = Id_n×n is not necessarily satisfied. In particular, our metric distinguishes between Gaussians evolving through the PDE flow (see Section 2) and Gaussians who do not.

Remark 35. We say that two parameters α and β are orthogonal if the elements of the corresponding rows and columns of the Fisher Information Matrix are zero. Orthogonal parameters are easy to deal with in the sense that their maximum likelihood estimates are independent and can be calculated separately. In particular, for our family the parameters x₀ and v₀ are both orthogonal to both the parameters λ and σ². Some partial results, for example, when either mean or variance is kept constant, can be deduced. See, for example, [18–20].

Remark 36. The Fisher Information Metric is not the only possible choice to compute distances between pdfs of the family of Gaussian Distributions. For example, in [20], the authors parametrize the family of normal distribution as the symmetric space SL(n + 1)/SO(n + 1) endowed with the following metric:

(95)

Moreover, the authors in [20] computed the Riemann Curvature Tensor of the metric and, in any dimension, the distance between two normal distributions with the same mean and different variance and also the distance between two normal distributions with the same variance and different mean.

Remark 37. If we consider just the submanifold given by the restriction to the coordinates i = 1, …, n and i = 2n + 2 on the ellipse λ² + 16t² = 4, we recover the hyperbolic distance:

(96)

The geometry, however, does not seem the one of a product space, at least considering the fact that mixed entries are not zero, in our parametrization.

4. Overdispersion, Equidispersion, and Underdispersion for the Family

As we said, Strichartz Estimates are a way to measure the dispersion caused by the flow of the PDE to which they are related. In statistics, dispersion explains how a distribution is spread-out. In this section, we connect the two closely related concepts (dispersion in statistics and PDEs) by introducing some measures of statistical dispersion like the Index of Dispersion in Definition 38 (see Section 4) which reflect the dispersive PDE nature of the Maximal Strichartz Family of Gaussian Distributions. We compute this Index of Dispersion for our family of distributions and show that it is consistent with PDE results.

Definition 38. Consider the norms ‖·‖_a and ‖·‖_b on the space of Variance-Covariance Matrices Σ and ‖·‖_c on the space of mean values μ. One defines the following Index of Dispersion:

(97)

with t ≠ 0 and where μ(t) is as follows:

(98)

while Σ(t) is given by

(99)

One calls

the abc-Dispersion Index of the Maximal Family of Gaussians and one calls

(100)

a-Static Dispersion Index of the Maximal Family of Gaussians. Moreover, one says that the distribution is

(i)
abc-overdispersed, if ;
(ii)
abc-equidispersed, if ;
(iii)
abc-underdispersed, if .

Analogously, one says that the distribution is

(i)
a-overdispersed, if ;
(ii)
a-equidispersed, if ;
(iii)
a-underdispersed, if .

Here, we discuss some particular cases and compute the dispersion indexes and for certain specific norms ‖·‖_a, ‖·‖_b and ‖·‖_c.

(i) In the case t = 0, the a-Static Dispersion Index of the Maximal Family of Gaussians that we choose is given by the variance of the distribution. We choose ‖Σ‖_a = det⁡(Σ) and so we get

(101)

Now, in the spherical case R^TR = σ²Id, one gets

(102)

So, the distribution is

(i)
a-overdispersed, if (1/4)λ²σ² < 1;
(ii)
a-equidispersed, if (1/4)λ²σ² = 1;
(iii)
a-underdispersed, if (1/4)λ²σ² > 1.

Therefore, with ‖Σ‖_a = det⁡(Σ), the type of dispersion does not depend on the dimension n.

Remark 39. In the strictly Strichartz case σ² = 1, we have that the dispersion is measured just by the scaling factor λ.

Choosing instead ‖Σ‖_a = tr⁡(Σ) as a-Static Dispersion Index of the Maximal Family of Gaussians, we have some small differences:

(103)

Now, in the spherical case R^TR = σ²Id, we get

(104)

So, the distribution is

(i)
a-overdispersed, if n(1/4)λ²σ² < 1;
(ii)
a-equidispersed, if n(1/4)λ²σ² = 1;
(iii)
a-underdispersed, if n(1/4)λ²σ² > 1.

So with ‖Σ‖_a = tr⁡(Σ) the type of dispersion does depend on the dimension n.

(ii) In the case t ∈ R, when t is different from zero, we can express Σ as a function of μ. In fact we have

(105)

and so

(106)

For example, if now we choose x₀ = 0 and μ = v₀ = (1,0, …, 0) ^T we get

(107)

so for ‖Σ‖_a = ‖Σ‖_b = det⁡(Σ) and

we get, in the spherical case R^TR = σ²Id,

(108)

So the distribution is

(i)
abc-overdispersed, if ;
(ii)
abc-equidispersed, if ;
(iii)
abc-underdispersed, if .

Remark 40. In particular, from this, we notice that if at t = 0 the distribution is a-equidispersed, an instant after the distribution is abc-overdispersed, in fact

(109)

This is in agreement with the dispersive properties of the family

and legitimates, in some sense, our choice of Indexes of Dispersion. Moreover, if

(110)

is actually different from

, namely, σ² = 1, we can argue that the Gaussian Distribution that we are analysing does not come from the Maximal Strichartz Family of Gaussian Distributions.

Remark 41. This index is different from the Fisher Index which is basically the variance to mean ratio

(111)

and it is the natural one for count data. The index

is then more appropriate for families of distributions related to the Poisson distribution and that are dimensionless. In fact, in our case and in contrast with the Poisson case, we scale the Variance-Covariance Matrix as the square of the Expected Value: Σ≃μ².

Remark 42. The characterization of the Gaussian Distribution given by Theorems 6 and 22 can be used also to give a measure of dispersion with respect to the Maximal Family of Gaussian Distributions, considering the Strichartz Norm:

(112)

By Theorem 6, one has that

. When the index is close to one, the distribution is close, in some sense, to the family

, while, when the index is close to zero, the distribution is very far from

. This index clearly does not distinguish between distributions in the family

. It would be very interesting to see if the closeness to one of the Indexes of Dispersion

computed on a general distribution implies a proximity to the Maximal Family of Gaussian Distributions from the distribution point of view also and not just from the point of view of the dispersion.

5. Partial Stochastic Ordering on

Using the concept of Index of Dispersion, we can give a Partial Stochastic Order to the family . For a more complete treatment on Stochastic Orders, we refer to [14]. We start the analysis of this section with the definition of Mean-Preserving Spread.

Definition 43. A Mean-Preserving Spread (MPS) is a map from to itself

(113)

where p(x; θ₁) and p(x; θ₂) are, respectively, the pdf of the random variables X₁ and X₂ with the property of leaving the Expected Value unchanged:

(114)

for any θ₁ and θ₂ in the space of parameters.

The concept of a Mean-Preserving Spread provides a partial ordering of probability distributions according to their level of dispersion. We then give the following definition.

Definition 44. Consider two random variables X₁ and X₂ such that , for any θ₁ and θ₂. One says that the two random variables are ordered according to their Dispersion Index if and only if the following condition is satisfied:

(115)

Now, we give some examples of ordering according to the Indexes of Dispersion that we discussed previously.

(i) In case t = 0, we choose ‖Σ‖_a = det⁡(Σ) and so we get

(116)

Now, in the spherical case R^TR = σ²Id, one gets

(117)

Using this index, we have the following partial ordering:

(118)

This order does not depend on the dimension n. By choosing instead ‖Σ‖_a = tr⁡(Σ), we obtain

(119)

Now, again in the spherical case R^TR = σ²Id, one gets

(120)

which is the same ordering as before. This order does not depend on the dimension n again and this seems to suggest that even if the value of the Dispersion Index might depend on the choice of the norms, the Partial Order is less sensible to it.

Remark 45. In the strictly Strichartz case σ² = 1, we have that the Stochastic Order is given just by the scaling factor λ.

(ii) In the case when t is different from zero, we have

(121)

If now we choose x₀ = 0 and μ = v₀ = (1,0, …, 0) ^T, we get

(122)

so, for ‖Σ‖_a = ‖Σ‖_b = det⁡(Σ) and

, we get, in the spherical case R^TR = σ²Id, the following Partial Order:

(123)

Remark 46. Again, in the strictly Strichartz case σ² = 1, we have that the Stochastic Order is given just by the scaling factor λ.

Remark 47. In the case of the the a-Static Dispersion Index of the Maximal Family of Gaussians , the role of σ² and λ² seems interchangeable. This suggests a dimensional reduction in the parameter space, but, when t ≠ 0, σ² and the parameter λ decouple and start to play a slightly different role. This suggests again a way to distinguish between Gaussian Distributions which come from the family and Gaussians which do not and so to distinguish between Gaussians which are solutions of the Linear Schrödinger Equation and Gaussians which are not.

Remark 48. Using the definition of Entropy, we deduce that, for Gaussian Distributions, h(X) = (1/2)log⁡(2πe) ⁿdet⁡(Σ). We see that, for our family , the Entropy increases, every time we increase λ, σ², and t, but not when we increase x₀ and v₀. In particular, the fact that the Entropy increases with t is in accordance with the Second Principle of Thermodynamics.

Remark 49. It seems that the construction of similar indexes can be performed in more general situations. In particular, we think that an index similar to can be computed in every situation in which a family of distributions has the Variance-Covariance Matrix and the Expected Value which depend on common parameters.

6. Conclusions

In this paper, we have constructed and studied the Maximal Strichartz Family of Gaussian Distributions. This subfamily of the family of Gaussian Distributions arises naturally in the context of Partial Differential Equations and Harmonic Analysis, as the set of maximizers of certain functionals introduced by Strichartz [4] in the context of the Schrödinger Equation. We analysed the Fisher Information Matrix of the family and we showed that this matrix possesses an extrastructure with respect to the general family of Gaussian Distributions. We studied the spherical and elliptical case and computed explicitly the Fisher Information Metric in both cases. We interpreted the Fisher Information Metric as a distance which can distinguish between Gaussians which maximize the Strichartz Norm and Gaussians which do not and also as a distance between Gaussians which are solutions of the Linear Schrödinger Equation and Gaussians which are not. After this, we introduced some measures of statistical dispersion that we called abc-Dispersion Index of the Maximal Family of Gaussian Distributions and a-Static Dispersion Index of the Maximal Family of Gaussian Distributions. We showed that these Indexes of Dispersion are consistent with the dispersive nature of the Schrödinger Equation and can be used again to distinguish between Gaussians belonging to the family and other Gaussians. Moreover, we showed that our Indexes of Dispersion induce a Partial Stochastic Order on the Maximal Strichartz Family of Gaussian Distributions, which is in accordance with the flow of the PDE.

Competing Interests

The author declares that he has no competing interests.

Acknowledgments

The author wants to thank their family and Victoria Ban for their constant support. They thank Professor Maung Min-Oo for useful discussions on the Fisher Information Metric. The author thanks also their Supervisor Professor Narayanaswamy Balakrishnan for his constant help and guidance and for an inspiring talk on dispersion indexes.

Appendix

In this Appendix, we give the proof of Theorem 3 (for completeness) and we will use the concept of 1/α-Characteristic Function to define a generalized type of Moments that exist also for the Multivariate Cauchy Distribution.

A. Proof of Theorem 3

The proof is very simple and can be found in several places (see, e.g., a nice treatment in [22]). We report here, for completeness, the computation in the case n = 1. We consider the variational derivative of h(X) with the constrain of f being a probability distribution and with the constraint of having a fixed variance σ². This gives rise to the following Euler Lagrange Equation with two Lagrangian multipliers λ₀ and λ₂:

(A.1)

where v(x) is some function with Expected Value μ. The two Lagrangian multipliers appear because of the two constraints. One constraint is related to the normalization condition

(A.2)

and the other is related to the requirement of fixed variance:

(A.3)

Now, we take the variational derivative of the functional

. To be at a critical point, we need to impose that this variational derivative is zero. Therefore, we get

(A.4)

Since this must hold for any variation g(x), the term in brackets must be zero, and so, solving for v(x) yields

(A.5)

Now, we use the constraint of the problem and solve for λ₀ and λ₂. From ∫_R v(x)dx = 1, we get the condition

(A.6)

and from σ² = ∫_R v(x)(x − μ) ²dx, we get

(A.7)

Solving for λ₀ and λ₂ we get λ₀ = (1/2)log⁡(2πσ²) − 1 and λ₂ = 1/2σ² which altogether give the Gaussian Distribution:

(A.8)

B. On the 1/α-Momenta of Order k and the Cauchy Distribution

In this subsection, we discuss another application of the concept of 1/α-Characteristic Functions. In particular, we build 1/α-Momenta in a similar way of what happens for the usual characteristic function and usual Momenta. We apply this tool to the case of the Cauchy Distribution and see that, in certain cases, in contrast to the well-known case of α = 1, we can build some finite generalized Momenta. We refer to [15] for a more detailed discussion on 1/α-Characteristic Functions.

Definition 50. Consider the 1/α-Characteristic Function of u:

(B.1)

Then, if

is k times that is continuously differentiable on R, one defines the 1/α-Moment of order k by the formula

(B.2)

Proof. This is a direct and simple computation.

Remark 51. Here, we do not consider the possibility of different roots of the unity that can appear in the computation of the 1/α-Characteristic Function. We refer, for the precise theory, to [15].

From now on, we concentrate only on the case of the Multivariate Cauchy Distribution.

Definition 52. One says that a random variable X is distributed as a Multivariate Cauchy Distribution if and only if its pdf f(x; μ, Σ, n) takes the form

(B.3)

Now, we want to determine for which α > 0 and k, n = 1,2, … the 1/α-Momenta of order k exist and are finite. In other words, we want to find for which values of n, k, and α, we have that |E^1/α[X^k]| < +∞. Therefore, we compute

(B.4)

where the constant C may vary from step to step. So, we have that the 1/α-Momenta of order k exist and are finite, when

(B.5)

namely, if and only if the order of the momentum k satisfies the following condition:

(B.6)

In the case n = k = 1, we need 0 < α < 1 and, in general, we need 0 < α < (n + 1)/(n + k) in order to have that the 1/α-Moment of order k, E^1/α[X^k] is well defined.

References

1 Muirhead R. J., Aspects of Multivariate Statistical Theory, 1982, John Wiley & Sons, New York, NY, USA, MR652932.
10.1002/9780470316559
Google Scholar
2 Kotz S., Balakrishnan N., and Johnson N. L., Continuous Multivariate Distributions, Vol. 1: Models and Applications, 2000, 2nd edition, Wiley, New York, NY, USA.
10.1002/0471722065
Web of Science® Google Scholar
3 Tao T., Nonlinear Dispersive Equations: Local and Global Analysis, 2006, BMS Regional Conference Series in Mathematics, No. 106.
10.1090/cbms/106
Google Scholar
4 Strichartz R. S., Restrictions of Fourier transforms to quadratic surfaces and decay of solutions of wave equations, Duke Mathematical Journal. (1977) 44, no. 3, 705–714, https://doi.org/10.1215/S0012-7094-77-04430-1, MR0512086.
10.1215/S0012-7094-77-04430-1
Web of Science® Google Scholar
5 Keel M. and Tao T., Endpoint Strichartz estimates, American Journal of Mathematics. (1998) 120, no. 5, 955–980, https://doi.org/10.1353/ajm.1998.0039, MR1646048, 2-s2.0-0001138601.
10.1353/ajm.1998.0039
Web of Science® Google Scholar
6 Christ M. and Quilodrán R., Gaussians rarely extremize adjoint Fourier restriction inequalities for paraboloids, Proceedings of the American Mathematical Society. (2014) 142, no. 3, 887–896, https://doi.org/10.1090/s0002-9939-2013-11827-7, MR3148523, 2-s2.0-84891895903.
10.1090/S0002-9939-2013-11827-7
Web of Science® Google Scholar
7 Selvitella A., Remarks on the sharp constant for the Schrodinger Strichartz estimate and applications, Electronic Journal of Differential Equations. (2015) 2015, no. 270, 1–19.
Google Scholar
8 Bennett J., Bez N., Jeavons C., and Pattakos N., On sharp bilinear Strichartz estimates of Ozawa-Tsutsumi type, Journal of the Mathematical Society of Japan. In Press. http://mathsoc.jp/publication/JMSJ/pdf/JMSJ7238.pdf.
Google Scholar
9 Hundertmark D. and Zharnitsky V., On sharp Strichartz inequalities in low dimensions, International Mathematics Research Notices. (2006) 2006, 18, 34080, https://doi.org/10.1155/imrn/2006/34080, MR2219206, 2-s2.0-33646388645.
10.1155/imrn/2006/34080
Web of Science® Google Scholar
10 Jiang J. and Shao S., On characterization of the sharp Strichartz inequality for the Schrödinger equation, Analysis & PDE. (2016) 9, no. 2, 353–361, https://doi.org/10.2140/apde.2016.9.353.
10.2140/apde.2016.9.353
Web of Science® Google Scholar
11 Klainerman S. and Machedon M., Remark on Strichartz-type inequalities, International Mathematics Research Notices. (1996) no. 5, 201–220, https://doi.org/10.1155/S1073792896000153, MR1383755.
10.1155/S1073792896000153
Google Scholar
12 Foschi D., Maximizers for the Strichartz inequality, Journal of the European Mathematical Society. (2007) 9, no. 4, 739–774, https://doi.org/10.4171/jems/95, MR2341830.
10.4171/jems/95
Web of Science® Google Scholar
13 Kunze M., On the existence of a maximizer for the Strichartz inequality, Communications in Mathematical Physics. (2003) 243, no. 1, 137–162, https://doi.org/10.1007/s00220-003-0959-5, MR2020224, ZBL1060.35133, 2-s2.0-0344552007.
10.1007/s00220-003-0959-5
Web of Science® Google Scholar
14 Lehmann E. L., Ordered families of distributions, The Annals of Mathematical Statistics. (1955) 26, 399–419, https://doi.org/10.1214/aoms/1177728487, MR0071684.
10.1214/aoms/1177728487
Web of Science® Google Scholar
15 Selvitella A., On 1/α-characteristic functions and applications to asymptotic statistical inference, Communications in Statistics—Theory and Methods. (2016) https://doi.org/10.1080/03610926.2015.1030427.
10.1080/03610926.2015.1030427
Web of Science® Google Scholar
16 Amari S. and Nagaoka H., Methods of Information Geometry, 2000, 191, American Mathematical Society, Providence, RI, USA, Translations of Mathematical Monographs.
Google Scholar
17 Rao C. R., Information and the accuracy attainable in the estimation of statistical parameters, Bulletin of the Calcutta Mathematical Society. (1945) 37, 81–91, MR0015748.
Google Scholar
18 Costa S. I. R., Santos S. A., and Strapasson J. E., Fisher information distance: a geometrical reading, Discrete Applied Mathematics. (2015) 197, 59–69, https://doi.org/10.1016/j.dam.2014.10.004, MR3398961, 2-s2.0-84941949691.
10.1016/j.dam.2014.10.004
Web of Science® Google Scholar
19 Costa S. I. R., Santos S. A., and Strapasson J. E., Fisher information matrix and hyperbolic geometry, Proceedings of the IEEE Information Theory Workshop (ITW ′05), August-September 2005, IEEE, 34–36, https://doi.org/10.1109/ITW.2005.1531851.
10.1109/ITW.2005.1531851
Google Scholar
20 Lovrić M., Min-Oo M., and Ruh E. A., Multivariate normal distributions parametrized as a Riemannian symmetric space, Journal of Multivariate Analysis. (2000) 74, no. 1, 36–48, https://doi.org/10.1006/jmva.1999.1853, MR1790612, 2-s2.0-0347117629.
10.1006/jmva.1999.1853
Web of Science® Google Scholar
21 Mardia K. V. and Marshall R. J., Maximum likelihood estimation of models for residual covariance in spatial regression, Biometrika. (1984) 71, no. 1, 135–146, https://doi.org/10.1093/biomet/71.1.135, MR738334, 2-s2.0-0001196683.
10.1093/biomet/71.1.135
Web of Science® Google Scholar
22 Conrad K., Probability Distributions and Maximum Entropy, http://www.math.uconn.edu/~kconrad/blurbs/analysis/entropypost.pdf.
Google Scholar

All articles

The Maximal Strichartz Family of Gaussian Distributions: Fisher Information, Index of Dispersion, and Stochastic Ordering

Abstract

1. Introduction

2. Construction of the Maximal Strichartz Family of Gaussian Distributions

2.1. The 1/α-Characteristic Functions

2.2. Conservation of Mass and Flow on the Space of Probability Measures

2.3. Fundamental Solution for the Linear Schrödinger Equation Using 1/α-Characteristic Functions

2.4. Strichartz Estimates and Their Symmetries

3. The Fisher Information Metric of the Maximal Strichartz Family

3.1. The Fisher Information Metric for the Multivariate Gaussian Distribution

3.2. Proof of Theorem 8: The Spherical Multivariate Gaussian Distribution

3.3. Proof of Theorem 8: The Elliptical Multivariate Gaussian Distribution

3.4. The General Multivariate Gaussian Distribution

4. Overdispersion, Equidispersion, and Underdispersion for the Family

5. Partial Stochastic Ordering on

6. Conclusions

Competing Interests

Acknowledgments

Appendix

A. Proof of Theorem 3

B. On the 1/α-Momenta of Order k and the Cauchy Distribution

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

The Maximal Strichartz Family of Gaussian Distributions: Fisher Information, Index of Dispersion, and Stochastic Ordering

Abstract

1. Introduction

2. Construction of the Maximal Strichartz Family of Gaussian Distributions

2.1. The 1/α-Characteristic Functions

2.2. Conservation of Mass and Flow on the Space of Probability Measures

2.3. Fundamental Solution for the Linear Schrödinger Equation Using 1/α-Characteristic Functions

2.4. Strichartz Estimates and Their Symmetries

3. The Fisher Information Metric of the Maximal Strichartz Family

3.1. The Fisher Information Metric for the Multivariate Gaussian Distribution

3.2. Proof of Theorem 8: The Spherical Multivariate Gaussian Distribution

3.3. Proof of Theorem 8: The Elliptical Multivariate Gaussian Distribution

3.4. The General Multivariate Gaussian Distribution

4. Overdispersion, Equidispersion, and Underdispersion for the Family

5. Partial Stochastic Ordering on

6. Conclusions

Competing Interests

Acknowledgments

Appendix

A. Proof of Theorem 3

B. On the 1/α-Momenta of Order k and the Cauchy Distribution

References

Figures

References

Related

Information