This study proposes a memetic approach for optimally determining the parameter values of single-diode-equivalent solar cell model. The memetic algorithm, which combines metaheuristic and gradient-based techniques, has the merit of good performance in both global and local searches. First, 10 single algorithms were considered including genetic algorithm, simulated annealing, particle swarm optimization, harmony search, differential evolution, cuckoo search, least squares method, and pattern search; then their final solutions were used as initial vectors for generalized reduced gradient technique. From this memetic approach, we could further improve the accuracy of the estimated solar cell parameters when compared with single algorithm approaches.

1. Introduction

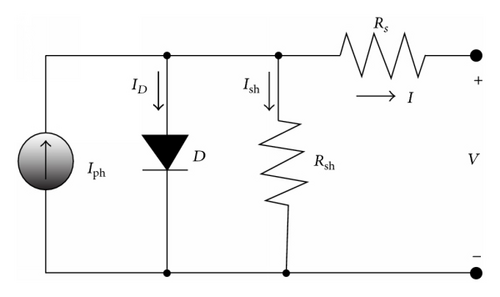
Determining the parameter values of photovoltaic (PV) cell models is very important when designing solar cells and estimating their performance. The key parameters that represent the behavior of solar cells include generated photocurrent, saturation current, series resistance, shunt resistance, and ideality factor [1]. Estimating these parameters accurately is essential for precise modeling and accurate performance evaluation of solar cells.

Several models have been proposed to describe the behavior of solar cells using current-voltage (I-V) relationship [2–4]. The I-V curve of a solar cell has nonlinear characteristics determined by the solar cell parameters. These models generally consist of analytical equations based on a physical description that formulate PV-generated current with the technical characteristics and the environmental variables including the operating voltage, the ambient temperature, and the irradiance [5]. Among numerous modeling approaches, the single-diode model (SDM) is the most widely utilized solar cell model in the literature. A general SDM includes five parameters: photocurrent, saturation current, diode ideality constant, series resistance, and shunt resistance.

So far various computational intelligence methods, such as genetic algorithm, particle swarm optimization, simulated annealing, and harmony search, have been proposed for optimal estimation of solar cell parameters. Many studies have aimed to overcome the shortcomings of the conventional deterministic algorithms and to investigate the efficiency and applicability of the algorithms. Hybrid methods combining two or more metaheuristic algorithms also have been applied to explore the capability of stochastic artificial intelligence algorithms in estimating solar cell parameters. These algorithms could find relevant parameter values by minimizing the root mean square error (RMSE) as the objective function in the optimization process.

Up to now, metaheuristic algorithms have shown a higher level of applicability in estimating solar cell parameters with fine performance. Nonetheless, we also presume that a memetic approach, which combines the well-developed evolutionary frameworks with gradient-based local search algorithm, can provide an opportunity for better solutions. Through this memetic combination, it can be seen that the accuracy represented by RMSE can be further improved because metaheuristic algorithm can be reinforced by calculus-based method in terms of local search performance and calculus-based method can be reinforced by metaheuristic algorithm in terms of global search performance.

This paper is organized as follows. Optimization formulation of the problem to determine the solar cell parameters is described in Section 2. In Section 3, a memetic implementation, which integrates gradient-based local search into the evolutionary frameworks for better determining the parameters, is described. Then, simulation results of the proposed approach are provided in Section 4, followed by conclusions in Section 5.

2. Optimization Formulation of Photovoltaic Model

Solar cells are made of various semiconductor materials. The working mechanism of solar cells is essentially based on the PV effect, which is the generation of a potential difference at the P-N junction in regard to visible or other radiations. When a solar cell is exposed to light source, the semiconductor materials capture photons, and then charged carriers are generated. Potential difference and current in the external circuit guide to the separation of carriers in the internal electric field created by the junction and collection at the electrodes. The photogenerated charge carriers can be accordingly captured in the form of an electric current, that is, I_ph. Eliminating this effect, a solar cell behaves like a traditional diode that does not rely on any light parameters. The Shockley diode equation is utilized to represent the current flowing through the diode (I_D) [5] as follows:

()

where I_SD denotes diode saturation current (normal diode current), V_d denotes electrical potential difference between both ends of the diode, n denotes ideality factor, and V_t denotes thermal voltage. Here, the thermal voltage can be represented as follows:

()

where k denotes Boltzmann constant (1.380650 × 10⁻²³ J/K), T denotes ambient temperature (306 K in this study), and q denotes electron charge (1.602176 × 10⁻¹⁹ C).

SDM, which can be visually described in Figure 1, follows the superposition principle [6–8]. Thus, the terminal current I is equal to I_ph subtracting the currents diverting through the diode and resistance as follows:

()

where I_sh denotes shunt current, V denotes operating voltage, R_s denotes series resistance, and R_sh denotes shunt resistance.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Single-diode-equivalent circuit model of solar cell.

Figure 1 can be transformed into an optimization problem with respect to RMSE once measured data of I-V relationship is given, as follows:

()

This optimization problem has five decision variables of cell-generated photocurrent I_ph, diode saturation current I_SD, diode ideality factor n, series resistance R_s, and shunt resistance R_sh. The measured I-V data is given in Table 1 [5] where the first column represents measured voltage data and the second column represents measured current data, which originally came from a commercial (RTC France) 57 mm diameter silicon solar cell performing at the standard irradiance level (1 sun (1000 W/m²) at 306°K) [9]. Also, the I-V data is graphically shown in Figure 2.

Table 1. Measured I-V data and computation results.

V	I	Algorithm
V	I	SA	GA2	PS	NLS1	PSO	LS	NLS2	HS	RADE	CS
−0.2057	0.7640	0.7662	0.7662	0.7645	0.7641	0.7641	0.7637	0.7645	0.7640	0.7641	0.7641
−0.1291	0.7620	0.7644	0.7644	0.7633	0.7627	0.7627	0.7624	0.7629	0.7626	0.7627	0.7627
−0.0588	0.7605	0.7628	0.7628	0.7622	0.7614	0.7614	0.7612	0.7615	0.7613	0.7614	0.7614
0.0057	0.7605	0.7613	0.7612	0.7612	0.7602	0.7602	0.7601	0.7602	0.7601	0.7602	0.7602
0.0646	0.7600	0.7599	0.7598	0.7603	0.7591	0.7591	0.7592	0.7590	0.7590	0.7591	0.7591
0.1185	0.7590	0.7586	0.7585	0.7595	0.7581	0.7581	0.7583	0.7579	0.7580	0.7580	0.7581
0.1678	0.7570	0.7574	0.7573	0.7586	0.7571	0.7571	0.7574	0.7569	0.7570	0.7571	0.7571
0.2132	0.7570	0.7563	0.7561	0.7577	0.7562	0.7562	0.7565	0.7559	0.7561	0.7561	0.7562
0.2545	0.7555	0.7550	0.7547	0.7566	0.7551	0.7551	0.7556	0.7547	0.7550	0.7551	0.7551
0.2924	0.7540	0.7532	0.7529	0.7550	0.7537	0.7537	0.7542	0.7532	0.7536	0.7537	0.7537
0.3269	0.7505	0.7506	0.7500	0.7522	0.7515	0.7515	0.7520	0.7507	0.7513	0.7514	0.7514
0.3585	0.7465	0.7460	0.7452	0.7472	0.7475	0.7475	0.7480	0.7463	0.7473	0.7473	0.7473
0.3873	0.7385	0.7379	0.7368	0.7386	0.7403	0.7403	0.7407	0.7387	0.7401	0.7401	0.7401
0.4137	0.7280	0.7240	0.7227	0.7238	0.7278	0.7278	0.7278	0.7253	0.7274	0.7272	0.7273
0.4373	0.7065	0.7020	0.7008	0.7011	0.7077	0.7077	0.7072	0.7040	0.7069	0.7067	0.7067
0.4590	0.6755	0.6683	0.6677	0.6668	0.6766	0.6766	0.6751	0.6713	0.6751	0.6748	0.6748
0.4784	0.6320	0.6213	0.6220	0.6199	0.6329	0.6328	0.6299	0.6256	0.6303	0.6300	0.6300
0.4960	0.5730	0.5595	0.5622	0.5590	0.5751	0.5751	0.5703	0.5657	0.5710	0.5708	0.5708
0.5119	0.4990	0.4838	0.4886	0.4848	0.5042	0.5042	0.4969	0.4924	0.4981	0.4979	0.4979
0.5265	0.4130	0.3937	0.4007	0.3970	0.4199	0.4199	0.4098	0.4057	0.4114	0.4114	0.4114
0.5398	0.3165	0.2928	0.3011	0.2985	0.3257	0.3257	0.3122	0.3092	0.3144	0.3145	0.3145
0.5521	0.2120	0.1818	0.1902	0.1899	0.2225	0.2225	0.2054	0.2038	0.2082	0.2084	0.2084
0.5633	0.1035	0.0654	0.0721	0.0754	0.1149	0.1148	0.0939	0.0941	0.0974	0.0976	0.0978
0.5736	−0.0100	−0.0529	−0.0504	−0.0422	0.0063	0.0062	−0.0186	−0.0163	−0.0144	−0.0142	−0.0140
0.5833	−0.1230	−0.1782	−0.1819	−0.1673	−0.1080	−0.1081	−0.1371	−0.1323	−0.1319	−0.1319	−0.1316
0.5900	−0.2100	−0.2680	−0.2785	−0.2583	−0.1891	−0.1893	−0.2212	−0.2145	−0.2153	−0.2155	−0.2151

RMSE		0.02165	0.02158	0.01741	0.00719	0.00715	0.00477	0.00474	0.00280	0.00278	0.00269

3. Memetic Implementation

Memetic computing is a branch in computer science which considers complicate structures as the combination of heterogeneous operators, named memes, whose evolutionary interactions contribute to intelligent structures for problem solving [10, 11]. For recent decades, memetic algorithms have been widely applied in the large-scale complex optimization problems.

The problem of balance between global and local search, that is, balance between computational intelligence and gradient-based search algorithm, has been explored under a multiobjective optimization setting in [12, 13]. In [14], a memetic algorithm was presented to analyze the evolutionary artificial neural network for training of a medical application. For a large-scale combinatorial optimization problem, a parallel memetic algorithm with selective local search was proposed in [15]. In [16–18], memetic algorithms were applied to solve scheduling and planning problems such as vehicle routing and path planning. A fast adaptive memetic algorithm for a design of controller of engineering drives was presented in [19], and a compact memetic differential algorithm has been developed for a robot control in [20]. In [21], a differential evolution-based hybrid algorithm was provided to solve the optimization problem in flow-dynamic design. In [22] a novel memetic algorithm scheme was proposed by combining metaheuristic algorithm and gradient-based technique to find better solutions for an economic load dispatch problem with valve-point loading.

In order to explore the opportunity of better solution in determining solar cell parameters using the memetic combination proposed in this study, various metaheuristic algorithms, such as genetic algorithm, simulated annealing, particle swarm optimization, harmony search, and cuckoo search, as well as mathematical approaches, such as least squares method and pattern search, have been performed, which have shown the good level of performances among all the existing relevant approaches in literature.

Once good parameter values for the PV cell model are obtained using the above-mentioned various algorithms, the values can be further polished using gradient-based techniques. In this study, we adopted generalized reduced gradient (GRG) method as the gradient-based local search technique.

The GRG algorithm was first developed by Abadie and Carpentier [23] as an extension of the reduced gradient method to solve a general constrained nonlinear programming problem, which can be stated as follows [24]:

()

where x = (x₁, x₂, …, x_n) is a vector of n variables, f(x) is the objective function, h_i(x) is the ith equality constraint, and g_j(x) is the jth inequality constraint (q < n). S is the whole search space and F is the feasible search space. The a_k and b_k denote the lower and upper bounds of the variable x_k, respectively. It is assumed that all problem functions f(x), h_i(x), and g_j(x) are twice continuously differentiable.

GRG transforms inequality constraints into equality constraints by introducing slack variables. Hence all the constraints are of equality form and can be represented as follows:

()

where x contains both original variables and slacks. Variables are divided into dependent variables x_D and independent ones x_I (or basic and nonbasic variables, resp.):

()

The names of basic and nonbasic variables are from linear programming. Similarly, the gradient of the objective function, bounds, and the Jacobian matrix may be partitioned as follows:

()

Let x⁰ be an initial feasible solution, which satisfies equality constraints and bound constraints. Note that basic variables must be selected so that J_D(x⁰) is nonsingular.

The reduced gradient vector is determined as follows:

()

The search directions for the independent and the dependent variables are given by

()

A line search is performed to find the step length α as the solution to the following problem:

()

The optimal solution α^∗ to the problem gives the next solution:

()

A more detailed description of the GRG method can be found in [25].

4. Computational Results

For this PV parameter optimization problem, various metaheuristic and mathematical algorithms have so far proposed their solutions, as summarized in Table 2. As seen in Table 2, the obtained solution vector of PV model parameters from simulated annealing (SA) [26] made RMSE of 0.02165, which is the worst one among various solution vectors if outlier from genetic algorithm 1 (GA1) is not considered; genetic algorithm 2 (GA2) [27] produced RMSE of 0.02158, which is slightly better than SA; pattern search (PS) [28] produced RMSE of 0.01741; nonlinear least squares 1 (NLS1) [9] produced RMSE of 0.00719; particle swarm optimization (PSO) [4] produced RMSE of 0.00715; least squares (LS) method [29] produced RMSE of 0.00477; nonlinear least squares 2 (NLS2) [1] produced RMSE of 0.00474; harmony search (HS) [30] produced RMSE of 0.00280; repaired adaptive differential evolution (RADE) [31] produced RMSE of 0.00278; and cuckoo search (CS) [5] produced RMSE of 0.00269 which is the best one among algorithms. Ye et al. [4] proposed GA1, but it does not appear to be good because its RMSE is huge (132,590). Although there are two nonlinear least squares (NLS1 and NLS2) and two genetic algorithms (GA1 and GA2), they are different in terms of algorithm structure and algorithm parameter values.

Table 2. Optimal parameter values from various algorithms.

Parameter	Algorithm
Parameter	SA	GA2	PS	NLS1	PSO	LS	NLS2	HS	RADE	CS	GA1
I_ph	0.7620	0.7619	0.7617	0.7608	0.7608	0.7607	0.7609	0.7607	0.7608	0.7608	0.7756
I_SD	4.8 × 10⁻⁷	8.1 × 10⁻⁷	10.0 × 10⁻⁷	3.2 × 10⁻⁷	3.2 × 10⁻⁷	3.3 × 10⁻⁷	4.0 × 10⁻⁷	3.0 × 10⁻⁷	3.2 × 10⁻⁷	3.2 × 10⁻⁷	5.6 × 10⁻⁷
R_s	0.0345	0.0299	0.0313	0.0364	0.0364	0.0364	0.0364	0.0366	0.0364	0.0364	0.0697
R_sh	43.103	42.373	64.103	53.763	53.796	60.241	49.505	53.595	53.7185	53.7185	10.084
n	1.5172	1.5751	1.6000	1.4837	1.4838	1.4816	1.5039	1.4754	1.4812	1.4812	0.8053
RMSE	0.02165	0.02158	0.01741	0.00719	0.00715	0.00477	0.00474	0.00280	0.00278	0.00269	132590

The search range of decision variable is I_ph = [0,1], I_SD = [0,1e − 6], R_s = [0,0.5], R_sh = [0,100], and n = [1,2] [30], and several metaheuristic algorithms such as HS, RADE, and CS provided a number of function evaluations (HS = 5,000; RADE = 10,000; and CS = 5,000) while PSO provided time taken (242 seconds) and SA and GA2 did not mention any.

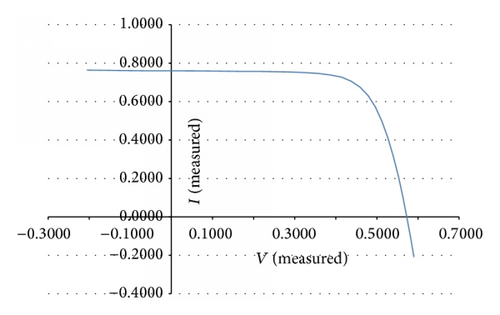
Table 1 shows corresponding currents calculated by various algorithms, and Figure 3 shows the errors between calculated and measured currents from various algorithms. As observed in the figure, the magnitude of the errors abruptly increases after around 0.4 V. Presumably this is because representing rapid change is more difficult than representing monotonic change. The measured current abruptly drops after around 0.4 V as seen in Figure 2.

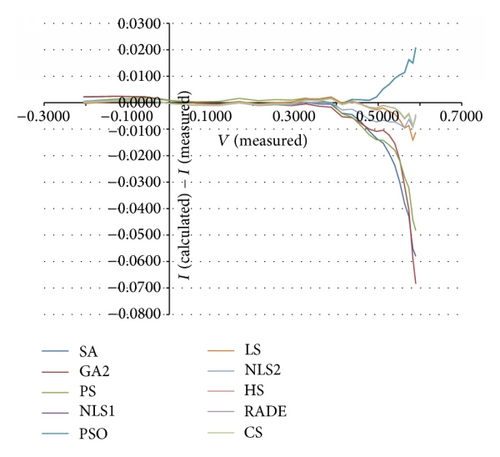
The above-enumerated algorithms found good PV parameter values with small RMSE. However, is it possible to further improve the solution quality? The memetic algorithm, which combines metaheuristic and gradient-based algorithms, may answer to this question because the memetic algorithm can complement the weakness of metaheuristic algorithm by using gradient-based algorithm. Thus, we can obtain even better solutions if we introduce gradient-based algorithm to the metaheuristic algorithm.

The gradient-based algorithm (GRG in this study) by itself cannot find good solution unless it starts with good and feasible initial vector. Otherwise, it will get stuck in a local optimum or will diverge instead of converging.

For this PV parameter optimization problem also, finding good solutions using gradient-based algorithm requires proper feasible initial vector, which is not very easy and tedious task. Thus, the result vectors from metaheuristic or other mathematical algorithms can be used as the proper initial vectors for the gradient-based algorithm.

The results from the memetic approach were tabulated in Table 3. As seen in the table, some initial vectors could be further improved while others could not because of getting stuck in local optimal (LO). SA + GRG could improve RMSE from 0.02165 to 0.00209; GA2 + GRG could improve RMSE from 0.02158 to 0.00432; PS + GRG could improve RMSE from 0.01741 to 0.00261; however, NLS1 + GRG, PSO + GRG, LS + GRG, NLS2 + GRG, HS + GRG, RADE + GRG, and CS + GRG could not improve RMSE any further because they already reached local optima where there is no room to escape using the local search technique. Here, the computation time of GRG part is less than one second, so it does not become a burden.

Table 3. Optimal parameter values from memetic algorithms.

Parameter	Algorithm
Parameter	SA + GRG	GA2 + GRG	PS + GRG	NLS1 + GRG	PSO + GRG	LS + GRG	NLS2 + GRG	HS + GRG	RADE + GRG	CS + GRG
I_ph	0.7620	0.7619	0.7617	LO	LO	LO	LO	LO	LO	LO
I_SD	4.5 × 10⁻⁷	7.6 × 10⁻⁷	9.5 × 10⁻⁷
R_s	0.0345	0.0301	0.0313
R_sh	43.103	42.373	64.103
n	1.5172	1.5749	1.6000
RMSE	0.00209	0.00432	0.00261

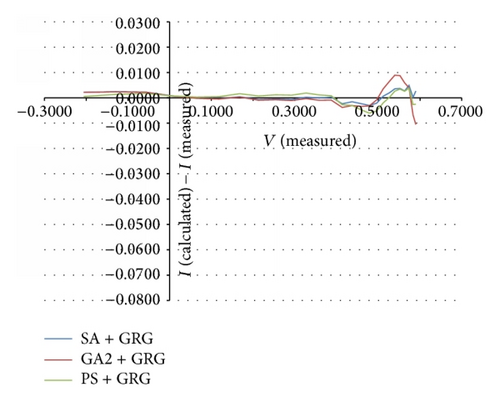
Figure 4 shows the errors between calculated and measured currents from various memetic approaches. As observed in the figure, the magnitude of the errors is less than single algorithm approach. While CS found the best RMSE of 0.00269 in single algorithm approach, PS + GRG could find the better RMSE of 0.00261, and SA + GRG could find even better RMSE of 0.00209.

While the above approach used the constant ambient temperature (306°K or 32.85°C), the sensitivity of the ambient temperature was also tested under various operation (weather) conditions between −5°C and 40°C. SA + GRG produced the computation results as shown in Table 4. As seen in the table, I_ph and R_s are fluctuating, I_SD is increasing, n is decreasing, and R_sh is almost constant.

Table 4. Sensitivity analysis of ambient temperature.

Celsius (°C)	Kelvin (°K)	RMSE	I_ph	I_SD	R_s	R_sh	n
−5	268.15	0.01438	0.7776	1.72E − 07	0.0397	43.1035	1.6201
0	273.15	0.01658	0.7509	2.37E − 07	0.0293	43.1034	1.6310
5	278.15	0.00520	0.7666	2.05E − 07	0.0400	43.1033	1.5808
10	283.15	0.01107	0.7756	2.78E − 07	0.0400	43.1033	1.5837
15	288.15	0.01454	0.7802	2.93E − 07	0.0403	43.1032	1.5610
20	293.15	0.01952	0.7620	2.30E − 07	0.0345	43.1034	1.5172
25	298.15	0.00391	0.7620	3.10E − 07	0.0345	43.1034	1.5172
30	303.15	0.00203	0.7620	3.96E − 07	0.0345	43.1034	1.5172
35	308.15	0.01491	0.7620	4.80E − 07	0.0345	43.1034	1.5172
40	313.15	0.00236	0.7626	6.27E − 07	0.0331	43.1034	1.5171

5. Conclusions

In this study, a memetic approach has proposed for optimally determining the parameter values of single-diode-equivalent solar cell model. The memetic approach considered various metaheuristic and mathematical algorithms and combined them with GRG technique. The results validated the performance of the memetic approach, which further improved the quality of solutions originally obtained by various algorithms.

The proposed memetic approach in this work can be also further applied to more complicated and realistic PV models with various module types [32] in the future. And theoretically the balance between global search and local search can be a good future research topic because too much exploited solutions do not appear to be good initial vectors for local search algorithms. In addition, parameter-setting-free technique [33, 34] can be also incorporated in metaheuristic approach in order to eliminate tedious algorithm parameter setting task.

Nomenclature

I:: Observed terminal current
I_D:: Diode current
I_ph:: Cell-generated photocurrent
I_SD:: Diode saturation current
I_sh:: Shunt current
k:: Boltzmann constant (1.380650 × 10⁻²³ J/K)
n:: Diode ideality factor
q:: Electron charge (1.602176 × 10⁻¹⁹ C)
R_s:: Series resistance
R_sh:: Shunt resistance
T:: Ambient temperature (306 K in this study)
V:: Observed operation voltage
V_d:: Electrical potential difference between both ends of the diode
V_t:: Thermal voltage.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgment

This research was supported by the Gachon University research fund of 2015 (GCU-2015-0030).

References

1 Chegaar M., Ouennoughi Z., and Hoffmann A., A new method for evaluating illuminated solar cell parameters, Solid-State Electronics. (2001) 45, no. 2, 293–296, https://doi.org/10.1016/S0038-1101(00)00277-X, 2-s2.0-0035246832.
10.1016/S0038-1101(00)00277-X
CAS Web of Science® Google Scholar
2 Chegaar M., Ouennoughi Z., Guechi F., and Langueur H., Determination of solar cells parameters under illuminated conditions, Journal of Electron Devices. (2003) 2, 17–21.
Google Scholar
3 Xiao W., Lind M. G. J., Dunford W. G., and Capel A., Real-time identification of optimal operating points in photovoltaic power systems, IEEE Transactions on Industrial Electronics. (2006) 53, no. 4, 1017–1026, https://doi.org/10.1109/TIE.2006.878355, 2-s2.0-33747622794.
10.1109/TIE.2006.878355
Web of Science® Google Scholar
4 Ye M., Wang X., and Xu Y., Parameter extraction of solar cells using particle swarm optimization, Journal of Applied Physics. (2009) 105, no. 9, 094502, https://doi.org/10.1063/1.3122082, 2-s2.0-67249113030.
10.1063/1.3122082
CAS Web of Science® Google Scholar
5 Ma J., Ting T. O., Man K. L., Zhang N., Guan S.-U., and Wong P. W. H., Parameter estimation of photovoltaic models via cuckoo search, Journal of Applied Mathematics. (2013) 2013, 8, 362619, https://doi.org/10.1155/2013/362619, 2-s2.0-84883165354.
10.1155/2013/362619
Google Scholar
6 Lo Brano V., Orioli A., Ciulla G., and Di Gangi A., An improved five-parameter model for photovoltaic modules, Solar Energy Materials and Solar Cells. (2010) 94, no. 8, 1358–1370, https://doi.org/10.1016/j.solmat.2010.04.003, 2-s2.0-77953131709.
10.1016/j.solmat.2010.04.003
CAS Web of Science® Google Scholar
7 De Soto W., Klein S. A., and Beckman W. A., Improvement and validation of a model for photovoltaic array performance, Solar Energy. (2006) 80, no. 1, 78–88, https://doi.org/10.1016/j.solener.2005.06.010, 2-s2.0-29144478675.
10.1016/j.solener.2005.06.010
CAS Web of Science® Google Scholar
8 Villalva M. G., Gazoli J. R., and Filho E. R., Comprehensive approach to modeling and simulation of photovoltaic arrays, IEEE Transactions on Power Electronics. (2009) 24, no. 5, 1198–1208, https://doi.org/10.1109/TPEL.2009.2013862, 2-s2.0-67349141404.
10.1109/TPEL.2009.2013862
Web of Science® Google Scholar
9 Easwarakhanthan T., Bottin J., Bouhouch I., and Boutrit C., Nonlinear minimization algorithm for determining the solar cell parameters with microcomputers, International Journal of Solar Energy. (1986) 4, no. 1, 1–12, https://doi.org/10.1080/01425918608909835.
10.1080/01425918608909835
CAS Google Scholar
10 Iacca G., Neri F., Mininno E., Ong Y.-S., and Lim M.-H., Ockham′s razor in memetic computing: three stage optimal memetic exploration, Information Sciences. (2012) 188, 17–43, https://doi.org/10.1016/j.ins.2011.11.025, MR2873662, 2-s2.0-84855440057.
10.1016/j.ins.2011.11.025
Web of Science® Google Scholar
11 Caraffini F., Neri F., Iacca G., and Mol A., Parallel memetic structures, Information Sciences. (2013) 227, 60–82, https://doi.org/10.1016/j.ins.2012.11.017, MR3015749, 2-s2.0-84872342797.
10.1016/j.ins.2012.11.017
Web of Science® Google Scholar
12 Ishibuchi H., Yoshida T., and Murata T., Balance between genetic search and local search in memetic algorithms for multiobjective permutation flowshop scheduling, IEEE Transactions on Evolutionary Computation. (2003) 7, no. 2, 204–223, https://doi.org/10.1109/tevc.2003.810752, 2-s2.0-0038273913.
10.1109/TEVC.2003.810752
Web of Science® Google Scholar
13 Tan K. C., Chiam S. C., Mamun A. A., and Goh C. K., Balancing exploration and exploitation with adaptive variation for evolutionary multi-objective optimization, European Journal of Operational Research. (2009) 197, no. 2, 701–713, https://doi.org/10.1016/j.ejor.2008.07.025, 2-s2.0-60649107309.
10.1016/j.ejor.2008.07.025
Web of Science® Google Scholar
14 Abbass H. A., An evolutionary artificial neural networks approach for breast cancer diagnosis, Artificial Intelligence in Medicine. (2002) 25, no. 3, 265–281, https://doi.org/10.1016/s0933-3657(02)00028-3, 2-s2.0-0036275180.
10.1016/S0933-3657(02)00028-3
PubMed Web of Science® Google Scholar
15 Tang J., Lim M. H., and Ong Y. S., Diversity-adaptive parallel memetic algorithm for solving large scale combinatorial optimization problems, Soft Computing. (2007) 11, no. 9, 873–888, https://doi.org/10.1007/s00500-006-0139-6, 2-s2.0-34247380230.
10.1007/s00500-006-0139-6
Web of Science® Google Scholar
16 Hasan S. M. K., Sarker R., Essam D., and Cornforth D., Memetic algorithms for solving job-shop scheduling problems, Memetic Computing. (2009) 1, no. 1, 69–83, https://doi.org/10.1007/s12293-008-0004-5, 2-s2.0-65149102896.
10.1007/s12293-008-0004-5
Google Scholar
17 Lim K. K., Ong Y.-S., Lim M. H., Chen X., and Agarwal A., Hybrid ant colony algorithms for path planning in sparse graphs, Soft Computing. (2008) 12, no. 10, 981–994, https://doi.org/10.1007/s00500-007-0264-x, 2-s2.0-44349184898.
10.1007/s00500-007-0264-x
Web of Science® Google Scholar
18 Tan K. C., Cheong C. Y., and Goh C. K., Solving multiobjective vehicle routing problem with stochastic demand via evolutionary computation, European Journal of Operational Research. (2006) 177, no. 2, 813–839, https://doi.org/10.1016/j.ejor.2005.12.029, 2-s2.0-33750485322.
10.1016/j.ejor.2005.12.029
Web of Science® Google Scholar
19 Caponio A., Cascella G. L., Neri F., Salvatore N., and Sumner M., A fast adaptive memetic algorithm for online and offline control design of PMSM drives, IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics. (2007) 37, no. 1, 28–41, https://doi.org/10.1109/TSMCB.2006.883271, 2-s2.0-33847648902.
10.1109/TSMCB.2006.883271
PubMed Google Scholar
20 Neri F. and Mininno E., Memetic compact differential evolution for cartesian robot control, IEEE Computational Intelligence Magazine. (2010) 5, no. 2, 54–65, https://doi.org/10.1109/mci.2010.936305, 2-s2.0-77951285978.
10.1109/MCI.2010.936305
Web of Science® Google Scholar
21 Geem Z. W., Parameter estimation for the nonlinear muskingum model using the BFGS technique, Journal of Irrigation and Drainage Engineering. (2006) 132, no. 5, 474–478, https://doi.org/10.1061/(asce)0733-9437(2006)132:5(474), 2-s2.0-33748792293.
10.1061/(ASCE)0733-9437(2006)132:5(474)
Web of Science® Google Scholar
22 Kim J., Kim C. S., and Geem Z. W., A memetic approach for improving minimum cost of economic load dispatch problems, Mathematical Problems in Engineering. (2014) 2014, 11, 906028, https://doi.org/10.1155/2014/906028, 2-s2.0-84896978869.
10.1155/2014/906028
Web of Science® Google Scholar
23 Abadie J. and Carpentier J., Generalization of the wolfe reduced gradient method to the case of nonlinear constraints, Optimization, 1969, Academic Press, 37–47.
Google Scholar
24 Yeniay O., A comparative study on optimization methods for the constrained nonlinear programming problems, Mathematical Problems in Engineering. (2005) 2005, no. 2, 165–173, https://doi.org/10.1155/mpe.2005.165, MR2184261, 2-s2.0-27444438797.
10.1155/MPE.2005.165
Google Scholar
25 Lasdon L. S., Waren A. D., Jain A., and Ratner M., Design and testing of a generalized reduced gradient code for nonlinear programming, ACM Transactions on Mathematical Software. (1978) 4, no. 1, 34–50, https://doi.org/10.1145/355769.355773, 2-s2.0-0017949075.
10.1145/355769.355773
Google Scholar
26 El-Naggar K. M., AlRashidi M. R., AlHajri M. F., and Al-Othman A. K., Simulated Annealing algorithm for photovoltaic parameters identification, Solar Energy. (2012) 86, no. 1, 266–274, https://doi.org/10.1016/j.solener.2011.09.032, 2-s2.0-84855190625.
10.1016/j.solener.2011.09.032
Web of Science® Google Scholar
27 Jervase J. A., Bourdoucen H., and Al-Lawati A., Solar cell parameter extraction using genetic algorithms, Measurement Science and Technology. (2001) 12, no. 11, 1922–1925, https://doi.org/10.1088/0957-0233/12/11/322, 2-s2.0-0035504875.
10.1088/0957-0233/12/11/322
CAS Web of Science® Google Scholar
28 AlRashidi M. R., AlHajri M. F., El-Naggar K. M., and Al-Othman A. K., A new estimation approach for determining the I-V characteristics of solar cells, Solar Energy. (2011) 85, no. 7, 1543–1550, https://doi.org/10.1016/j.solener.2011.04.013, 2-s2.0-79956069243.
10.1016/j.solener.2011.04.013
Web of Science® Google Scholar
29 Bouzidi K., Chegaar M., and Nehaoua N., New methods to extract the parameters of solar cells from their illuminated I-V curve, Proceedings of the 4th International Conference on Computer Integrated Manufacturing, 2007, Sétif, Algeria.
Google Scholar
30 Askarzadeh A. and Rezazadeh A., Parameter identification for solar cell models using harmony search-based algorithms, Solar Energy. (2012) 86, no. 11, 3241–3249, https://doi.org/10.1016/j.solener.2012.08.018, 2-s2.0-84866534835.
10.1016/j.solener.2012.08.018
Web of Science® Google Scholar
31 Gong W. and Cai Z., Parameter extraction of solar cell models using repaired adaptive differential evolution, Solar Energy. (2013) 94, 209–220, https://doi.org/10.1016/j.solener.2013.05.007, 2-s2.0-84879327406.
10.1016/j.solener.2013.05.007
Web of Science® Google Scholar
32 Siddiqui M. U. and Abido M., Parameter estimation for five- and seven-parameter photovoltaicelectrical models using evolutionary algorithms, Applied Soft Computing Journal. (2013) 13, no. 12, 4608–4621, https://doi.org/10.1016/j.asoc.2013.07.005, 2-s2.0-84886725793.
10.1016/j.asoc.2013.07.005
Web of Science® Google Scholar
33 Geem Z. W., Economic dispatch using parameter-setting-free harmony search, Journal of Applied Mathematics. (2013) 2013, 5, 427936, https://doi.org/10.1155/2013/427936, MR3056205.
10.1155/2013/427936
Google Scholar
34 Geem Z. W., Parameter estimation of the nonlinear muskingum model using parameter-setting-free harmony search, Journal of Hydrologic Engineering. (2011) 16, no. 8, 684–688, https://doi.org/10.1061/(ASCE)HE.1943-5584.0000352, 2-s2.0-79961076102.
10.1061/(ASCE)HE.1943-5584.0000352
Web of Science® Google Scholar

Citing Literature

All articles

Parameter Optimization of Single-Diode Model of Photovoltaic Cell Using Memetic Algorithm

Abstract

1. Introduction

2. Optimization Formulation of Photovoltaic Model

3. Memetic Implementation

4. Computational Results

5. Conclusions

Nomenclature

Conflict of Interests

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Parameter Optimization of Single-Diode Model of Photovoltaic Cell Using Memetic Algorithm

Abstract

1. Introduction

2. Optimization Formulation of Photovoltaic Model

3. Memetic Implementation

4. Computational Results

5. Conclusions

Nomenclature

Conflict of Interests

Acknowledgment

References

Citing Literature

Figures

References

Related

Information