Volume 2015, Issue 1 837053

Research Article

Open Access

Study on Index of Stochastic Linear Continuous-Time Systems

Yan Li

College of Electrical Engineering and Automation, Shandong University of Science and Technology, Qingdao, Shandong 266590, China sdust.edu.cn

Search for more papers by this author

Tianliang Zhang,

Tianliang Zhang

orcid.org/0000-0002-6937-7418

College of Information and Control Engineering, China University of Petroleum (East China), Qingdao, Shandong 266590, China cup.edu.cn

Search for more papers by this author

Xikui Liu,

Corresponding Author

Xikui Liu

[email protected]

College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao, Shandong 266590, China sdust.edu.cn

Search for more papers by this author

Xiushan Jiang,

Xiushan Jiang

College of Information and Control Engineering, China University of Petroleum (East China), Qingdao, Shandong 266590, China cup.edu.cn

Search for more papers by this author

Yan Li,

Yan Li

College of Electrical Engineering and Automation, Shandong University of Science and Technology, Qingdao, Shandong 266590, China sdust.edu.cn

Search for more papers by this author

Tianliang Zhang,

Tianliang Zhang

orcid.org/0000-0002-6937-7418

College of Information and Control Engineering, China University of Petroleum (East China), Qingdao, Shandong 266590, China cup.edu.cn

Search for more papers by this author

Xikui Liu,

Corresponding Author

Xikui Liu

[email protected]

College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao, Shandong 266590, China sdust.edu.cn

Search for more papers by this author

Xiushan Jiang,

Xiushan Jiang

College of Information and Control Engineering, China University of Petroleum (East China), Qingdao, Shandong 266590, China cup.edu.cn

Search for more papers by this author

First published: 19 October 2015

https://doi.org/10.1155/2015/837053

Citations: 1

Academic Editor: Ruihua Liu

Share a link

Email
Wechat
Bluesky

Abstract

This paper studies the index problem. We obtain a necessary and sufficient condition of index larger than γ > 0. A generalized differential equation is introduced and it is proved that its solvability and the feasibility of the index are equivalent. We extend the deterministic cases to the stochastic models. Our results can be used to fault detection filter analysis. Finally, the effectiveness of the proposed results is illustrated by an example.

1. Introduction

It is well known that many control and filtering problems have been discussed based on a certain performance index of a system, such as norm, norm, and index; see [1–9]. norm is the measure of the worst-case disturbance inputs on the controlled outputs [1–4]. The index is a measure of the minimum sensitivity of system outputs to system inputs. norm and index with specific application to fault detection filter have been carried out in [10–17]. To ensure robustness, index should be maximized and norm should be minimized. Using performance can make certain that the residual signal is maximally sensitive to faults and highly robust to disturbance inputs; see [16, 17].

In [12], index was defined as the minimum nonzero singular value in zero frequency. In [10], the authors extended the results of [12] to all frequency range. By means of LMIs, a necessary and sufficient condition was given for the infinite frequency range. The case for finite frequency range was concluded through frequency weighting. In recent decades, a great deal of attention has been attracted to index in time domain. A fault residual generator was designed to maximize the fault sensitivity in the finite time domain [16–20]. Based on index, results on optimal fault detection can be found in [17, 18] and the references. The lower bound of index for linear time-varying systems was proposed in [19, 20]. A sliding mode observer was designed for sensor fault diagnosis of nonlinear time-delay systems; see [21]. In [22], a fault-tolerant controller was projected to compensate nonlinear faults by using a fuzzy adaptive fault observer.

Although there is much work on the index problem, to the best of our knowledge, very little work was concerned with the index in stochastic systems. In this paper, the index for stochastic linear continuous-time systems is discussed. The definition of the index is extended to the stochastic case. We present a necessary and sufficient condition of the index. A generalized differential equation is introduced and it is proved that its solvability and the feasibility of the index are equivalent. Comparing our results with the bounded real lemma [2, 9], it shows that the index is not completely dual to norm. The index discussed in this paper is only for tall or square systems. The reason for this is that index is zero for wide systems. But bounded real lemma for is applicable to any systems. Finally, the effectiveness of the given methods is illustrated by numerical example.

The outline of the paper is organized as follows. In Section 2, some efficient criteria are given for the index of stochastic linear systems in finite horizon. Section 3 contains an example provided to show the efficiency of the proposed results. Finally, we conclude this paper in Section 4.

Notations. R is the field of real numbers. R^m×n is the vector space of all m × n matrices with entries in R. is the set of all real symmetric matrices R^n×n. A^′ is the transpose of matrix A. A⁻¹ is the inverse of A. Given positive semidefinite (positive definite) matrix A, we denote it by A ≥ 0 (A > 0). E is the mathematical expectation. I is identity matrix. 0_n is n × n zero matrix. is the space of nonanticipative stochastic process y(t) ∈ R^p with respect to increasing σ-algebras (t ≥ 0) satisfying , where . A square (wide or tall) system denotes a system when the number of inputs equals (is more than or less than) the outputs number.

2. Finite Horizon Stochastic Index

In this section, we will discuss the index problem of stochastic linear continuous-time systems. We give a necessary and sufficient condition of the index larger than γ > 0 in finite horizon.

Consider the following stochastic linear time-varying system

(1)

In the above, ω(t) is the one-dimensional standard Wiener process defined on the complete probability space

, with the natural filter

generated by ω(t) up to time t. Consider x(t) ∈ Rⁿ,

, and z(t) ∈ R^l are the system state, control input, and regulated output, respectively. A(t), B(t), A₀(t), B₀(t), C(t), and D(t) are coefficients with appropriate dimensions. For any 0 < T < ∞ and

, there exists unique solution

of (1).

The finite horizon stochastic index of system (1) can be stated as follows.

Definition 1. For stochastic system (1), given 0 < T < ∞, its index in [0, T] is defined as

(2)

where

Remark 2. If v is fault signal and z is the residual, then the index describes the smallest fault sensitivity of system (1). In this paper, we suppose that system (1) is tall or square because the index is zero for wide system.

Given γ > 0 and 0 < T < ∞, let

(3)

We will study the following optimal problem:

(4)

Remark 3. It can be shown that is equivalent to the following inequality

(5)

, v(t) ≠ 0.

Remark 4. When T = ∞, (2) corresponds to the infinite horizon case.

Lemma 5. Suppose is continuously differentiable, T > 0. Then, for every x₀ ∈ Rⁿ, ,

(6)

where

(7)

Proof. Let x₀ ∈ Rⁿ, , and x(t) = x(t; v, x₀) denote the corresponding solution of (1). Applying Ito’s formula to x(t)^′P(t)x(t) and taking expectations, we have that, for any T > 0,

(8)

where

(9)

(10)

which ends the proof.

Below, we prove the following theorem which is necessary in this paper.

Theorem 6. For (1) and some given γ > 0, if the following differential Riccati equation

(11)

admits solution P_T(t) on [0, T], then

Proof. By Lemma 5, for every , v ≠ 0, x₀ = 0, we conclude that

(12)

By using completion of squares argument and the first equality in (11), we have

(13)

where

From H^γ(P_T(t)) > 0, , to show , we define the operator : with its realization:

(14)

Then exists, which is determined by

(15)

where

We assume that H^γ(P_T(t)) ≥ ϵI, ϵ > 0, so there exists constant C₀ > 0, such that

(16)

That is,

Now, we consider the following equation:

(17)

where F(t) ∈ C[0, T] and this equation has unique solution

, t ∈ [0, T].

It is easy to see that (17) satisfies the following equation:

(18)

Lemma 7. Suppose F(t) ∈ C[0, T] and is the solution of (18). Then if , one obtains

(19)

where x_F(t) = x(t, F(t)x_F(t) + v(t), x₀) is the solution of

(20)

with x_F(0) = x₀ and

(21)

As v = 0, then

(22)

Proof. In terms of Lemma 5 with and F(t)x_F(t) + v(t) for v(t),

(23)

This means that (19) holds. Let v = 0 in (19); we obtain (22).

Now we are in a position to prove that is invertible for t ∈ [0, T].

Lemma 8. For system (1), if for some given γ > 0, F(t) ∈ C[0, T], T > 0, and satisfies (18). Then,

(24)

Proof. Let us first prove that . Suppose this is false; then there exists t^∗ ∈ [0, T), u ∈ R^l, ‖u‖ = 1 such that for some η > 0. Then, for sufficiently small δ > 0,

(25)

Define

(26)

Using Lemma 7 with this v(t) and x₀ = 0, we can derive that x_F(t) = 0 for t ∈ [0, t^∗] and

(27)

Since x_F(t) is continuous and x_F(t^∗) = 0, (27) is negative. Moreover, the condition

implies

. As a result, this is a contradiction. If t^∗ = T, we can replace [t^∗, t^∗ + δ] by [T − δ, T] and use a similar proof.

Next, let for any ρ > 0 and λ = (γ² + ρ²) ^1/2. Replacing γ with λ in (18), we obtain the corresponding solution . Applying the previous step, we can deduce that . For any t₀ ∈ [0, T), set , t ∈ [0, T − t₀]. Let be the solution of (18) with γ replaced by λ and F replaced by on [0, T − t₀]. Then, , t ∈ [0, T − t₀]. By (22), for any t₀ ∈ [0, T), x₀ ∈ Rⁿ,

(28)

and so

. By continuity,

for all t ∈ [0, T]. As this holds for arbitrary

, it follows that

. This completes the proof.

Remark 9. When t = T, (24) becomes . If system (1) is time-invariant, then

(29)

Remark 10. By the equality A(I − BA) ⁻¹ = (I − AB) ⁻¹A, we have that C^′[I − D(D^′D − γ²I) ⁻¹D^′]C = C^′(I − γ⁻²DD^′) ⁻¹C. If system (1) is time-invariant and square, by (29),

(30)

Now, we present the following theorem which is important in this paper.

Theorem 11. Suppose system (1) is time-invariant and square and satisfies for given γ ≤ 0. Then (11) has a unique solution P_T(t) ≤ 0 on [0, T] for every T > 0. Moreover, is minimized by the feedback control:

(31)

where

satisfies

(32)

and the optimal cost is

(33)

Proof. We prove that implies the existence of solution P_T(t) of (11) on [0, T]. Using a contradiction argument, we suppose that (11) does not admit a solution. By the standard theory of differential equations, there exists unique solution P_T(t) backward in time on maximal interval [T₀, T] (T₀ ≥ 0), and as t → T₀, P_T(t) becomes unbounded.

Let 0 < δ < T − T₀, , , , by completing the squares; then

(34)

Obviously,

(35)

where v^∗(t) = −R(t) ⁻¹Q(t)x(t).

Furthermore, we can see that

(36)

From Remark 10,

(37)

where

. Considering (35), we get

(38)

which implies that

(39)

By linearity, the solution of (1) with initial state

satisfies

(40)

Suppose Φ(t) is the solution of

(41)

and we have

(42)

Take ,

(43)

and it is easy to show that

(44)

It follows that

(45)

It is obvious that there exists constant C₀ > 0 such that

(46)

So, there is constant C₁ > 0 such that

(47)

In addition,

(48)

From (45), we have

(49)

In view of (35) and (39), it yields

(50)

So, P_T(T₀ + δ) can not become unbounded as δ → 0, which means that (11) has unique solution P_T(t) on [0, T].

Setting F(t) = F_T(t), t ∈ [0, T], in (17), from (31), we obtain

(51)

Hence P_T(t) satisfies (17), or equivalently (18). So

(52)

By (31),

(53)

and, in terms of Lemma 7,

(54)

But by Lemma 8,

(55)

Hence, v^∗(t) = F_T(t)x(t) minimizes

and

According to Theorems 6 and 11, we get the following theorem.

Theorem 12. If system (1) is time-invariant and square, for given γ > 0, the following are equivalent:

(i)
Consider .
(ii)
The following equation
(56)

has unique solution P_T(t) ≤ 0 on [0, T]. Moreover,

Remark 13. For given γ > 0, if we replace B, C, D, and v(t) with , , , and , respectively, and z(t) with z_δ(t) in (1), we deduce the corresponding index and

(57)

When

, then

. Using Theorem 12 to the modified data, it is easy to see that the following equation

(58)

has unique solution P_δ,T(t) ≤ 0 on [0, T]. Moreover,

Now, we are to show what happens as T increases.

Theorem 14. If system (1) is time-invariant and square, for some γ > 0. Then P_T(t) in (56) decreases as T increases for every t ∈ [0, T].

Proof. Suppose , t ∈ [0, T], and x₀ ∈ Rⁿ. Let be optimal for x₀ on [0, T − t], and set

(59)

By the time invariance of P_T(t), P_T−t(0) = P_T(t). Then,

(60)

This means that P_T(t) decreases as T increases for every t ∈ [0, T].

3. A Numerical Example

Below, we give a numerical example to illustrate the rightness of Theorems 12 and 14.

Example 1. In system (1), we consider a two-dimensional linear stochastic system with the following parameters:

(61)

Set γ = 0.5, T = 2,3; by solving (56), we can obtain the solutions of

(62)

for which their trajectories are shown in Figure 1. If we set t = 1, then it yields

(63)

It is easy to see that P₂(1) > P₃(1), which verifies the rightness of Theorem 14.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The trajectories of P₂(t) and P₃(t).

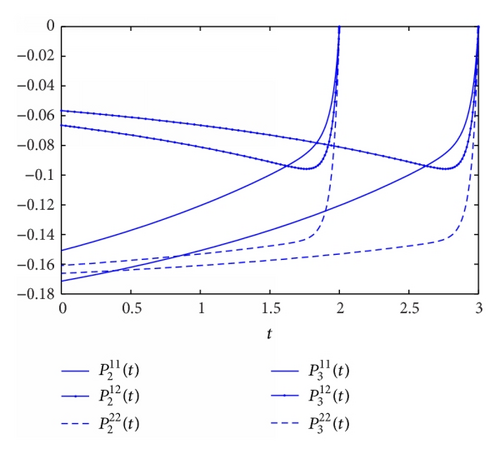
4. Conclusion

In this paper, we have solved the index problem where both stochastic and deterministic perturbations are present. Necessary and sufficient condition for the lower bound of index is given by means of the solvability of a generalized differential equation. The proposed results are not completely dual to norm, and the effectiveness of the given methods is illustrated by numerical example.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

This work is supported by National Natural Science Foundation of China (Grants nos. 61174078, 61170054, and 61402265) and the Research Fund for the Taishan Scholar Project of Shandong Province of China.

References

1 Zhou K., Doyle J. C., and Clover K., Robust and Optimal Control, 1996, Prentice Hall, Upper Saddle River, NJ, USA.
Google Scholar
2 Chen B.-S. and Zhang W., Stochastic control with state-dependent noise, IEEE Transactions on Automatic Control. (2004) 49, no. 1, 45–57, https://doi.org/10.1109/tac.2003.821400, 2-s2.0-0742269301.
10.1109/TAC.2003.821400
Web of Science® Google Scholar
3 Zhang W. H. and Chen B.-S., State feedback control for a class of nonlinear stochastic systems, SIAM Journal on Control and Optimization. (2006) 44, no. 6, 1973–1991, https://doi.org/10.1137/s0363012903423727, 2-s2.0-33645831442.
10.1137/S0363012903423727
Web of Science® Google Scholar
4 Zhang W., Zhang H., and Chen B.-S., Generalized Lyapunov equation approach to state-dependent stochastic stabilization/detectability criterion, IEEE Transactions on Automatic Control. (2008) 53, no. 7, 1630–1642, https://doi.org/10.1109/tac.2008.929368, 2-s2.0-52249113750.
10.1109/TAC.2008.929368
Web of Science® Google Scholar
5 Zhu Q. X., Asymptotic stability in the pth moment for stochastic differential equations with Lévy noise, Journal of Mathematical Analysis and Applications. (2014) 416, no. 1, 126–142, https://doi.org/10.1016/j.jmaa.2014.02.016, MR3182752, 2-s2.0-84897051235.
10.1016/j.jmaa.2014.02.016
Web of Science® Google Scholar
6 Zhu Q. and Cao J., Stability of Markovian jump neural networks with impulse control and time varying delays, Nonlinear Analysis: Real World Applications. (2012) 13, no. 5, 2259–2270, https://doi.org/10.1016/j.nonrwa.2012.01.021, 2-s2.0-84859111285.
10.1016/j.nonrwa.2012.01.021
Web of Science® Google Scholar
7 Zhu Q. X., Cao J. D., and Rakkiyappan R., Exponential input-to-state stability of stochastic Cohen-Grossberg neural networks with mixed delays, Nonlinear Dynamics. (2015) 79, no. 2, 1085–1098.
10.1007/s11071-014-1725-2
Web of Science® Google Scholar
8 Zhu Q. X. and Cao J. D., Mean-square exponential input-to-state stability of stochastic delayed neural networks, Neurocomputing. (2014) 131, 157–163, https://doi.org/10.1016/j.neucom.2013.10.029, 2-s2.0-84894040421.
10.1016/j.neucom.2013.10.029
Web of Science® Google Scholar
9 Hinrichsen D. and Pritchard A. J., Stochastic , SIAM Journal on Control and Optimization. (1998) 36, no. 5, 1504–1538, https://doi.org/10.1137/s0363012996301336, 2-s2.0-0032166437.
10.1137/S0363012996301336
Web of Science® Google Scholar
10 Liu J., Wang J. L., and Yang G.-H., An LMI approach to minimum sensitivity analysis with application to fault detection, Automatica. (2005) 41, no. 11, 1995–2004, https://doi.org/10.1016/j.automatica.2005.06.005, 2-s2.0-24944462280.
10.1016/j.automatica.2005.06.005
Web of Science® Google Scholar
11 Wang J. L., Yang G. H., and Liu J., An LMI approach to index and mixed fault detection observer design, Automatica. (2007) 43, 1656–1665.
10.1016/j.automatica.2007.02.019
Web of Science® Google Scholar
12 Chen J. and Pattor R. J., Robust Model-Based Fault Diagnosis for Dynamic Systems, 1999, Kluwer Academic Publishers, Boston, Mass, USA.
10.1007/978-1-4615-5149-2
Google Scholar
13 Hwang I., Kim S., Kim Y., and Seah C. E., A survey of fault detection, isolation, and reconfiguration methods, IEEE Transactions on Control Systems Technology. (2010) 18, no. 3, 636–653, https://doi.org/10.1109/TCST.2009.2026285, 2-s2.0-77951880498.
10.1109/TCST.2009.2026285
Web of Science® Google Scholar
14 Yin S., Ding S. X., Haghani A., Hao H., and Zhang P., A comparison study of basic data-driven fault diagnosis and process monitoring methods on the benchmark Tennessee Eastman process, Journal of Process Control. (2012) 22, no. 9, 1567–1581, https://doi.org/10.1016/j.jprocont.2012.06.009, 2-s2.0-84866069902.
10.1016/j.jprocont.2012.06.009
CAS Web of Science® Google Scholar
15 Wang D., Shi P., and Wang W., Robust fault detection for continuous-time switched delay systems: an linear matrix inequality approach, IET Control Theory and Applications. (2010) 4, no. 1, 100–108, https://doi.org/10.1049/iet-cta.2008.0517, 2-s2.0-75649113788.
10.1049/iet-cta.2008.0517
Web of Science® Google Scholar
16 Yin S., Luo H., and Ding S. X., Real-time implementation of fault-tolerant control systems with performance optimization, IEEE Transactions on Industrial Electronics. (2014) 61, no. 5, 2402–2411, https://doi.org/10.1109/tie.2013.2273477, 2-s2.0-84885571740.
10.1109/TIE.2013.2273477
Web of Science® Google Scholar
17 Iftikha K., Khan P. Q., and Abid M., Optimal fault detection filter design for switched linear systems, Nonlinear Analysis. (2015) 15, 132–144.
Google Scholar
18 Zhong M., Ding S. X., and Ding E. L., Optimal fault detection for linear discrete time-varying systems, Automatica. (2010) 46, no. 8, 1395–1400, https://doi.org/10.1016/j.automatica.2010.05.022, 2-s2.0-77955428671.
10.1016/j.automatica.2010.05.022
Web of Science® Google Scholar
19 Li X. B. and Liu H. H. T., Characterization of index for linear time-varying systems, Automatica. (2013) 49, no. 3, 1449–1457, https://doi.org/10.1016/j.automatica.2013.02.001.
10.1016/j.automatica.2013.02.001
Web of Science® Google Scholar
20 Li X. and Liu H. H. T., Minimum system sensitivity study of linear discrete time systems for fault detection, Mathematical Problems in Engineering. (2013) 2013, 13, 276987, https://doi.org/10.1155/2013/276987, 2-s2.0-84875545322.
10.1155/2013/276987
Web of Science® Google Scholar
21 Chen M., Jiang C.-S., and Wu Q.-X., Sensor fault diagnosis for a class of time delay uncertain nonlinear systems using neural network, International Journal of Automation and Computing. (2008) 5, no. 4, 401–405, https://doi.org/10.1007/s11633-008-0401-8, 2-s2.0-54249096923.
10.1007/s11633-008-0401-8
Google Scholar
22 Zhang K., Jiang B., and Shi P., A new approach to observer-based fault-tolerant controller design for Takagi-Sugeno fuzzy systems with state delay, Circuits, Systems, and Signal Processing. (2009) 28, no. 5, 679–697, https://doi.org/10.1007/s00034-009-9109-4, ZBL1173.94476, 2-s2.0-70349272305.
10.1007/s00034-009-9109-4
Web of Science® Google Scholar

Citing Literature

All articles

Study on Index of Stochastic Linear Continuous-Time Systems

Abstract

1. Introduction

2. Finite Horizon Stochastic Index

3. A Numerical Example

4. Conclusion

Conflict of Interests

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Study on Index of Stochastic Linear Continuous-Time Systems

Abstract

1. Introduction

2. Finite Horizon Stochastic Index

3. A Numerical Example

4. Conclusion

Conflict of Interests

Acknowledgments

References

Citing Literature

Figures

References

Related

Information