The linearized Euler equations (LEEs) solver for aeroacoustic problems has been developed on block-structured Cartesian mesh to address complex geometry. Taking advantage of the benefits of Cartesian mesh, we employ high-order schemes for spatial derivatives and for time integration. On the other hand, the difficulty of accommodating curved wall boundaries is addressed by the immersed boundary method. The resulting LEEs solver is robust to complex geometry and numerically efficient in a parallel environment. The accuracy and effectiveness of the present solver are validated by one-dimensional and three-dimensional test cases. Acoustic scattering around a sphere and noise propagation from the JT15D nacelle are computed. The results show good agreement with analytical, computational, and experimental results. Finally, noise propagation around fuselage-wing-nacelle configurations is computed as a practical example. The results show that the sound pressure level below the over-the-wing nacelle (OWN) configuration is much lower than that of the conventional DLR-F6 aircraft configuration due to the shielding effect of the OWN configuration.

1. Introduction

To satisfy the severe requirements of environmentally friendly aircraft, the applications of significant technological advances to conventional aircraft are needed. Presently, some of the most urgent targets are noise, emission, and fuel consumption. Green aviation, which seeks to meet the demands of the noise regulations of the next generation, has been proposed and intensively studied worldwide [1–9]. The continual reduction of noise has been steadily advanced for about 40 years mainly due to improvements in engine performance [4]. Examples of these advances are an increase of the bypass ratio, the use of geared fan machinery, and the improvement of liners and vanes. However, airport noise regulations are becoming increasingly stringent. Aircraft of the next generation must meet these regulations with sufficient margin for future, tougher limits.

The noise generated from aircraft is classified into two main groups, airframe noise and engine noise. Airframe noise is mainly turbulent noise generated from high-lift devices and landing gears. Engine noise is the sum of fan and jet noises. During takeoff, fan and jet noises are dominant because the engine is at full throttle. On the other hand, the airframe and fan noises are dominant during landing. Under both conditions, fan noise is one of the dominant factors of community noise generated from aircraft. To realize a dramatic reduction of engine noise, shielding the fan noise from the engine nacelle by the fuselage or wings is one of the reasonable approaches that have been applied [10–12]. Various unique aircrafts have been proposed and evaluated from this point of view using computational and experimental approaches. To design such unconventional aircraft, it is imperative that noise propagation be reliably analyzed to estimate the shielding effect accurately.

A common computational approach used to analyze noise propagation is based on the linearized Euler equations (LEEs), which is one of the accurate methods available for capturing the propagation of sound [13]. LEEs can address noise propagation from known noncompact sound sources in a nonuniform mean flow field. The method can also address scattering, diffraction, and reflection by objects. LEEs are often solved on body-fitted structured and unstructured meshes [14–17]. From a practical point of view, these meshes have some drawbacks in the computation of realistic complex geometries. Body-fitted structured mesh is fit to the object and is able to adapt to detailed components precisely; however, the computational cost of mesh generation around an entire aircraft or more complex geometry is quite high. Unstructured mesh is applicable to complex geometry; however, it generally achieves low-order accuracy in space. In addition, high-order unstructured methods incur considerable computational cost. Due to these reasons, a simple Cartesian mesh is the focus of the present research. Generation of Cartesian mesh is based on the simple division of the computational domain, and, thus, it can easily accommodate complex geometries. Furthermore, a high-order scheme is easily employed by the extension of stencils. Rapid computation is achieved owing to the simple computational structure of the Cartesian mesh. However, the main problem associated with Cartesian mesh is numerical error caused by the staircase wall boundary. In this research, a block-structured Cartesian mesh method, denoted as the building-cube method (BCM) [18–22], and the immersed boundary method (IBM) are applied to solve the abovementioned problem. Using the BCM, an appropriate mesh resolution can be locally assigned over the entire computational domain. IBM helps to maintain a practical minimum mesh size and to achieve highly accurate wall boundary conditions.

The purpose of this research is to develop the LEEs solver to compute noise propagation around complex geometry easily and robustly. To achieve this purpose, the BCM is employed in conjunction with IBM. First, a one-dimensional wave propagation problem is evaluated. Second, acoustic scattering around a sphere is computed. Third, noise propagation from the JT15D nacelle is computed and compared with results obtained from other sources. At last, noise propagation around fuselage-wing-nacelle configurations is computed, and the noise shielding effect of the over-the-wing nacelle (OWN) configuration is estimated as a realistic computation around complex geometry.

2. Computational Method

2.1. Linearized Euler Equations

In the Euler equations, the physical quantities Q are divided into a mean flow field vector Q₀ and fluctuation vector Q^′. By linearization of the Euler equations around Q₀ = Q − Q^′, the time evolution equations of Q^′ are obtained in (1). These are the LEEs. In the LEEs, the sound source term S is added to incorporate a realistic sound source. For computation of the LEEs, S and the mean flow field vector Q₀ are introduced. The time evolution of Q^′ is then computed. The governing equations are nondimensionalized by the mean flow density ρ₀, speed of sound c, and reference length D:

(1)

Here, γ = 1.4 is the specific heat ratio. δ_ij is the Kronecker delta. In the computations with mean flow field, ∂Q₀/∂x, ∂Q₀/∂y, and ∂Q₀/∂z are neglected to avoid the instability waves caused by the shear mean flow field. The effect of neglecting the terms about the gradient of the mean flow field is discussed in [23].

2.2. Computational Mesh of the BCM

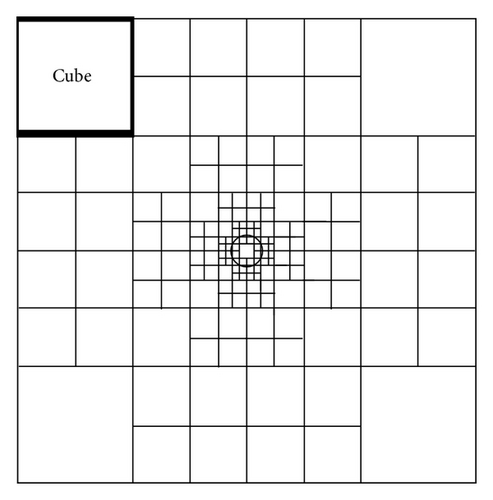
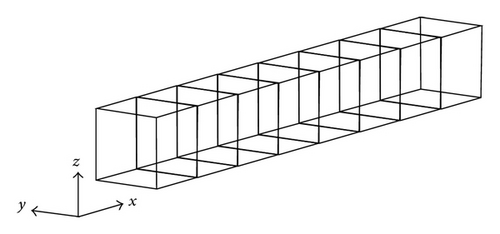
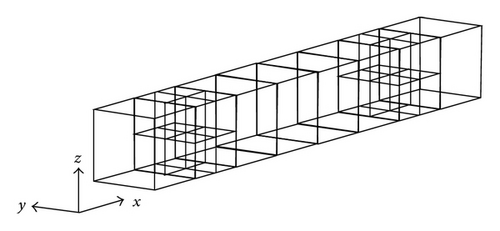
The computational mesh of BCM is generated by the following procedures in two dimensions [24]. The computational domain is divided into an aggregation of square areas (cubic areas in three dimensions), where each area is denoted as a “cube,” as shown in Figure 1(a). Each cube is then divided by an equispaced Cartesian mesh, as shown in Figure 1(b). Cells located outside the wall boundary are defined as fluid cells. On the other hand, cells located inside the wall boundary are defined as wall cells. In this method, all cubes have the same number of cells so that the computational effort required for all cubes is essentially equivalent in parallel computation, and excellent parallel efficiency is achieved. Each cube has three overlap cells, as shown by the hatched cells in Figure 1(b) for data exchange. When a cube is locally refined, the cube selected for refinement is divided into four cubes (eight cubes in three dimensions), and each cube is subdivided by prescribed cells. After the refinement, the size of the cube is smoothed so that the sizes of adjacent cubes are restricted to the same, double, or half that size. The sizes of adjacent cubes are checked for all cubes. If the size of an adjacent cube is larger than double the size of a focusing cube, the adjacent cube is divided into four cubes (eight cubes in three dimensions), and each cube is subdivided by prescribed cells.

Details are in the caption following the image — **Figure 1 (a) Computational domain and cube boundary**
Open in figure viewer PowerPoint

Computational mesh of the building-cube method (BCM) in two dimensions.

2.3. Computational Algorithm of the LEEs Solver

Figure 2 shows the computational algorithm of the LEEs solver. At the beginning, mesh information, object shape, initial conditions, and the mean flow field are given. The mean flow field is computed by the compressible Euler solver in this research. The details of the compressible Euler solver are provided in [25]. The computational scheme of inviscid flux is changed from that of the reference to the simple low-dissipative advection upstream splitting (SLAU) [26] scheme.

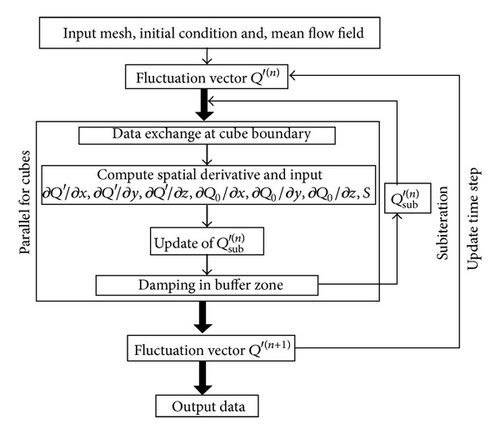
The spatial derivative of the LEEs solver is computed by the dispersion relation preserving (DRP) scheme [27]. Through the use of the overlap cells, a fourth-order DRP scheme using seven-point stencils can be implemented over the entire area of the computational domain. Time integration is computed by a six-stage fourth-order Runge-Kutta scheme [28]. In the time integral, six subiterations constitute one time step. In addition, artificial selective damping [27] of the seven-point stencils is applied at each iteration to eliminate the nonphysical oscillation. The above computations, including boundary treatments, are parallelized for all cubes using Open Multi-Processing (OpenMP).

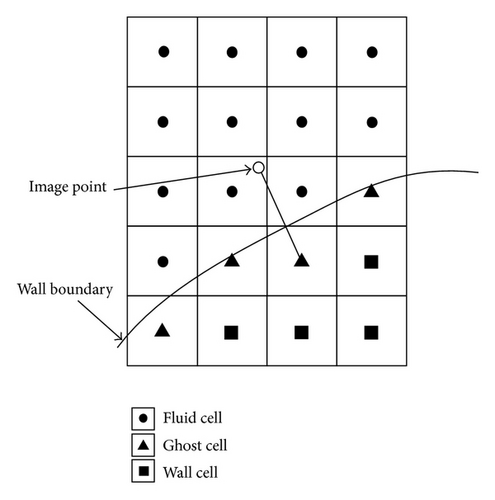
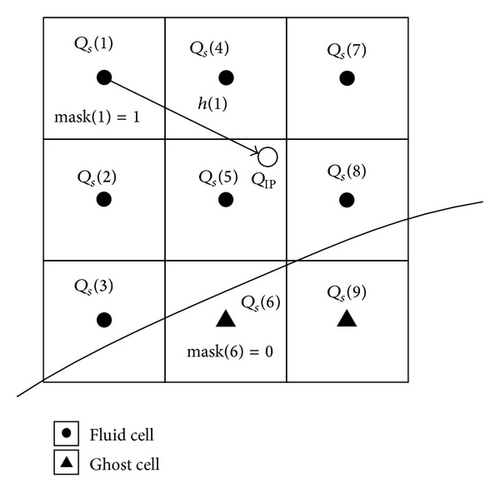
2.4. Wall Boundary

For computation by Cartesian mesh, it is important to apply mesh to wall boundaries realistically because real surfaces have curvature. Therefore, various IBMs have been proposed for diverse implementations. In the present solver, an IBM that employs a ghost cell (GC) approach using an image point (IP) [29] is applied. Wall cells adjacent to fluid cells are defined as GCs. The IP is defined from the GC in the direction normal to the closest wall boundary, as shown in Figure 3(a). In this process, surface stereo lithography (STL) data is used to determine the intersection point of the normal vector with the wall boundary. The physical quantities of the IP are interpolated by the inverse distance weighting method of (2) using 3 × 3 × 3 = 27 stencils, as illustrated in Figure 3(b):

(2)

Here, Q_IP is the physical quantities of the IP, Q_s isthe physical quantities of stencils, w is the weight function based on the distance h between the IP and stencils, and mask is a value that reflects whether the stencil is a fluid cell or wall cell. Fluid cells have mask = 1, and wall cells have mask = 0.

The physical quantities of a GC are computed by the following equations so that the slip condition is satisfied using the physical quantities of the IP:

(3)

Here, d_IP is the distance from the IP to the wall surface; d_GC is the distance from the GC to the wall surface; n is the unit normal vector of the wall surface; and V_IP, p_IP, and ρ_IP are the velocity vector, pressure, and density at the IP and V_GC, p_GC, and ρ_GC are those at the GC, respectively. In this study, d_GC + d_IP = 1.75Δx to avoid the instability caused by the wall boundary condition. The spatial derivative at the fluid cell adjacent to the GC is conducted using the second-order central difference based on the physical quantities of the GC.

2.5. Cube Boundary

At the boundaries between cubes with different sizes, the three overlap cells are hanging nodes. Therefore, data exchange with interpolation is needed. In the solver, Lagrange interpolation [30] is employed for data exchange at the boundary, as given by

(4)

Here, Q_o represents the physical quantities of an overlap cell; Q_s represents the physical quantities of stencils; w_j, w_k, and w_l are computed weight functions based on the distance between an overlap cell and stencils; and x_o, y_o, and z_o are the coordinates of an overlap cell.

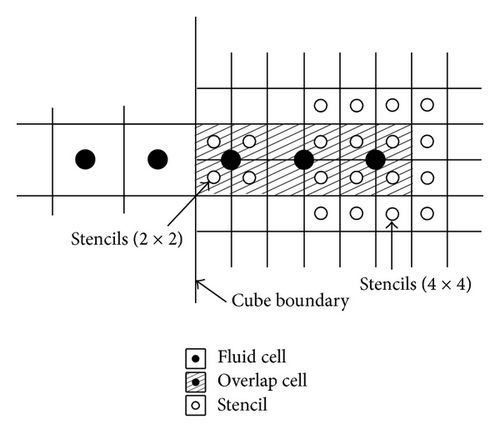
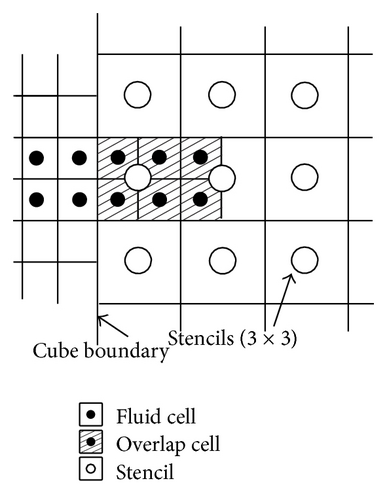
Figure 4(a) illustrates the stencils used for data exchange from smaller to larger cubes in two dimensions. In this figure, black points are the fluid cells of a larger cube. The shaded fluid cells of the larger cube are the overlap cells. The white circles are stencils of the smaller cube and are used for the interpolation. Interpolation to three overlap cells per one row is needed. The stencils of the overlap cell that is closest to the boundary are 2 × 2 × 2 = 8 points and those of the other two cells are 4 × 4 × 4 = 64 points so that the location of stencils is symmetrical. For interpolation from larger to smaller cubes, as shown in Figure 4(b), stencils of 3 × 3 × 3 = 27 points are used for four rows in three dimensions, which achieves third-order accuracy.

2.6. Outer Boundary

In LEEs computation, outgoing waves should be damped so that the inner sound field is not disturbed by reflected waves. To this end, the buffer zone boundary condition [31] is implemented in the present solver. To damp the outgoing waves gradually, the magnitude of the damping coefficients varies as a quadratic function of the coordinates toward the outer boundary. Equations (5) provide the damping equation in the buffer zone. The fluctuation vector is damped in each direction individually:

(5)

Here, Q^′(n) is the fluctuation vector at each iteration and with respect to each direction;

, and

are the damped fluctuation vectors; σ(x), σ(y), and σ(z) are the damping coefficients in the buffer zone; Δx, Δy, and Δz are the mesh spaces; L_b,x, L_b,y, and L_b,z are the widths of the buffer zone; and x_b, y_b, and z_b are the distances from the inner end of buffer zone. Figure 5 shows the buffer zone (illustrated as the hatched area) and an expanded view of the bottom left corner in a two-dimensional case.

3. Evaluation of the Order of Accuracy

The order of accuracy of the present computational method is evaluated by the one-dimensional wave propagation problem. The IBM and Lagrange interpolation are employed in their three-dimensional forms. Equations (6) are the one-dimensional wave equations. The initial pressure distribution is given by

(6)

(7)

The root mean square error (RMSE) between the analytical solution and the computed solution is computed by

(8)

The RMSE is computed for two meshes. Figure 6 illustrates the computational cubes with and without cube refinement. The size of the computational domain is 16D × 4D × 4D. The periodic boundary condition is set at the end of the x-directional boundaries. The RMSE is also computed in the case where a wall boundary exists. When the wall boundary exists, the wave reflects at the end of the x-directional boundaries.

The RMSE and the order of accuracy are listed in Table 1. The order of accuracy of each mesh is computed using the RMSE of one mesh and that of a coarser mesh. Case 1 employs no wall boundary and is conducted without cube refinement. Therefore, the prescribed order of accuracy is as shown. In Case 2, the order of accuracy is slightly reduced because the spatial derivative at the fluid cell adjacent to the GC is conducted using the second-order central difference. The order of accuracy of Case 3 is approximately two because the accuracy of the cube boundary is dominated by the interpolation from a larger to smaller cube. Case 4 provides a slightly smaller order of accuracy than that of Case 3 because of the existence of the wall boundary. These results indicate that the general order of accuracy of the present computational method is approximately two.

Table 1. Root mean square error and the order of accuracy.

	Wall	Cube refinement	Number of cells in one cube	Root mean square error	Order of accuracy
Case 1	Without	Without	36 × 36 × 36	1.063 × 10⁻⁵	—
			48 × 48 × 48	3.422 × 10⁻⁶	3.941
			72 × 72 × 72	6.887 × 10⁻⁷	3.954

Case 2	With	Without	36 × 36 × 36	1.269 × 10⁻⁵	—
			48 × 48 × 48	4.145 × 10⁻⁶	3.890
			72 × 72 × 72	8.326 × 10⁻⁷	3.959

Case 3	Without	With	36 × 36 × 36	1.200 × 10⁻⁴	—
			48 × 48 × 48	6.574 × 10⁻⁵	2.093
			72 × 72 × 72	2.890 × 10⁻⁵	2.027

Case 4	With	With	36 × 36 × 36	1.258 × 10⁻⁴	—
			48 × 48 × 48	7.086 × 10⁻⁵	1.995
			72 × 72 × 72	3.156 × 10⁻⁵	1.995

4. Acoustic Scattering around a Sphere

Acoustic scattering around a sphere [32] is computed under various mesh conditions in this section. The magnitude of error relative to an analytical solution and the computational time are compared. A sphere is located at the origin of a three-dimensional domain. The reference length D is the diameter of the sphere. A monopole Gaussian sound source S is given by the following equation as a function of time t:

(9)

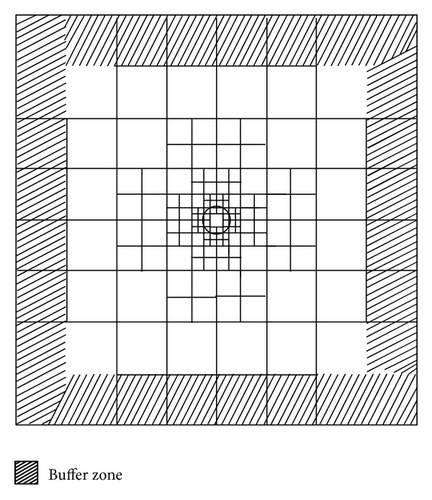
The influence of three important parameters on the error is investigated: the minimum cell size around the sphere, points per wavelength (PPW) in the computational domain, and the size of the buffer zone. The minimum cell size around the sphere has an effect on the error generated from the wall boundary. A small cell size not only suppresses the error but also restricts the time step size and results in greater computational time. The PPW is an important factor for acoustic simulations because insufficient PPW introduces dissipation and dispersion errors in wave propagation. The size of the buffer domain is important for setting the outer boundary condition. If the width of the buffer zone is short, the reflected wave is generated at the outer boundary, and the reflected wave disturbs the inner sound field.

Figure 7 shows computational domains of the Coarse, BCM_Middle2, and BCM_Fine3 meshes listed in Table 2. The gray lines indicate the cube boundaries. Table 2 summarizes the mesh information of all the cases used for the parametric study. Coarse mesh forms the base mesh of the other meshes employed. The size of the computational domain is 16D × 8D × 8D, referring to [33] where 128 cubes of a size 1D × 1D × 1D constitute the domain, as shown in Figure 7(a). The number of cells in one cube is 48 × 48 × 48 and the PPW is eight. In the Uniform_Middle and Uniform_Fine meshes, the domain size and the number of cubes are the same as those of the Coarse mesh. The number of cells in one cube is 72 × 72 × 72 in the Uniform_Middle mesh and 96 × 96 × 96 in the Uniform_Fine mesh; thus, the PPW is 12 and 16, respectively. In the BCM_Middle1 mesh, the eight cubes in the Coarse mesh surrounding the sphere are subdivided into half size cubes. Similarly, the eight cubes surrounding the sphere are subdivided from the BCM_Middle1 mesh in the BCM_Fine1 mesh. The number of cubes is 184 in the BCM_Middle1 mesh and 240 in the BCM_Fine1 mesh, and the maximum PPW is 16 and 32, respectively. In the BCM_Middle2 mesh shown in Figure 7(b) and BCM_Fine2 meshes, the buffer zone is expanded to add 112 cubes to the BCM_Middle1 and BCM_Fine1 meshes. In the BCM_Middle3 and BCM_Fine3 (shown in Figure 7(c)) meshes, eight cubes located at 2 ≤ x ≤ 6, −2 ≤ y ≤ 2, and −2 ≤ z ≤ 2, and eight cubes located at −6 ≤ x ≤ −2, −2 ≤ y ≤ 2, and −2 ≤ z ≤ 2 are subdivided from the BCM_Middle2 and BCM_Fine2 meshes to increase the PPW of the computational domain. The inner end of the buffer zone is set at x = [−7D, 7D], y = [−3D, 3D], and z = [−3D, 3D] in all meshes to compare the sizes of the buffer zones.

Table 2. Mesh information for acoustic scattering around a sphere of diameter D.

	Minimum cell size	Number of cubes	Number of cells in one cube	PPW	Width of buffer zone [x, y, z]
Coarse	0.0415D	128	48 × 48 × 48	8	1D, 1D, 1D
Uniform_Middle	0.0277D	128	72 × 72 × 72	12	1D, 1D, 1D
BCM_Middle1	0.0208D	184	48 × 48 × 48	8, 16	1D, 1D, 1D
BCM_Middle2	0.0208D	296	48 × 48 × 48	4, 8, 16	9D, 5D, 5D
BCM_Middle3	0.0208D	408	48 × 48 × 48	4, 8, 16	9D, 5D, 5D
Uniform_Fine	0.0208D	128	96 × 96 × 96	16	1D, 1D, 1D
BCM_Fine1	0.0104D	240	48 × 48 × 48	8, 16, 32	1D, 1D, 1D
BCM_Fine2	0.0104D	352	48 × 48 × 48	4, 8, 16, 32	9D, 5D, 5D
BCM_Fine3	0.0104D	464	48 × 48 × 48	4, 8, 16, 32	9D, 5D, 5D

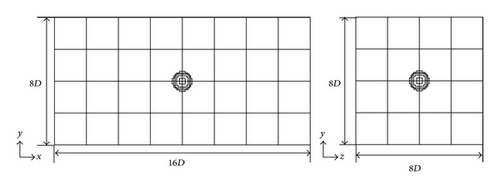
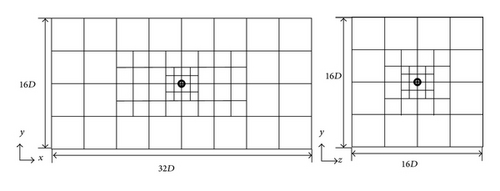
Figure 8 shows the instantaneous pressure distribution around the sphere computed using the Coarse mesh. In this figure, the buffer zone is not drawn. Waves generated from the sound source are scattered by the sphere, and interference fringes appear. The computation is executed in nondimensional time T = 15, and a periodic steady state is observed after T = 11. Figure 9 shows the pressure distribution near the inner end of the buffer zone and the time history of the pressure near the sphere for all meshes. The pressure distribution is sampled at −6D ≤ x ≤ −4D on the x-axis. The time history of the pressure is sampled at (−2D, 0, 0) and 14 ≤ T ≤ 15.

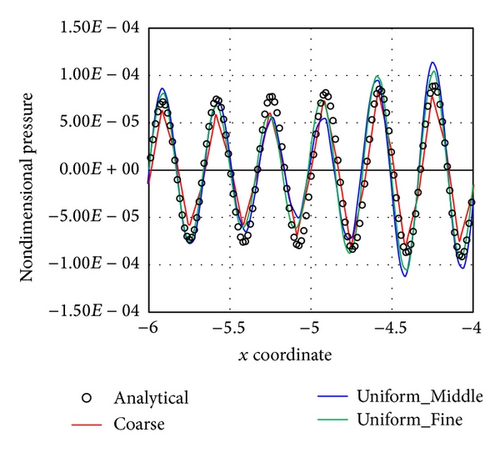
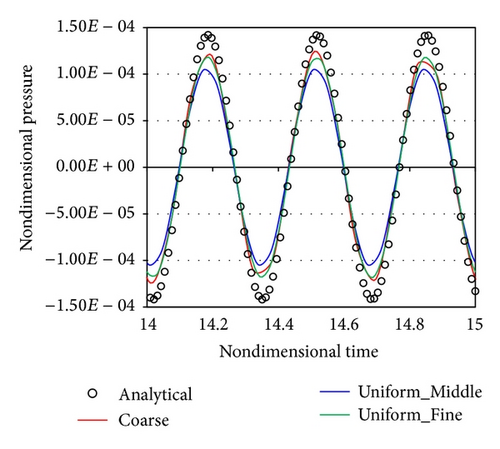
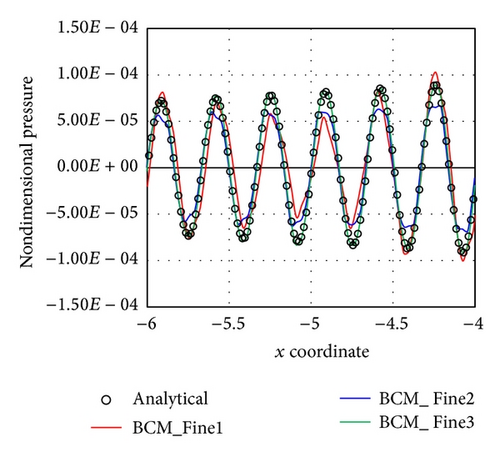
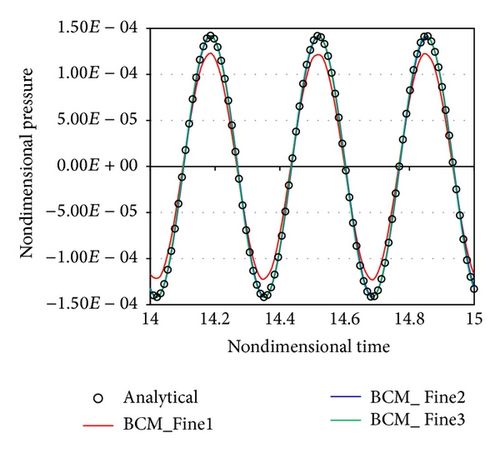
In Figures 9(a) and 9(b), the uniform meshes are compared. The pressure distributions do not follow the decreasing trend of the analytical solution in Figure 9(a). Reflection occurs at the outer boundary because of the insufficient width of the buffer zone. Additionally, the Uniform_Middle and Uniform_Fine meshes show a higher pressure amplitude compared with the pressure distribution of the Coarse mesh. It is assumed that the sound wave is damped at the Coarse mesh because of the insufficient PPW. The time histories of the uniform meshes provide lower amplitudes than the analytical solution.

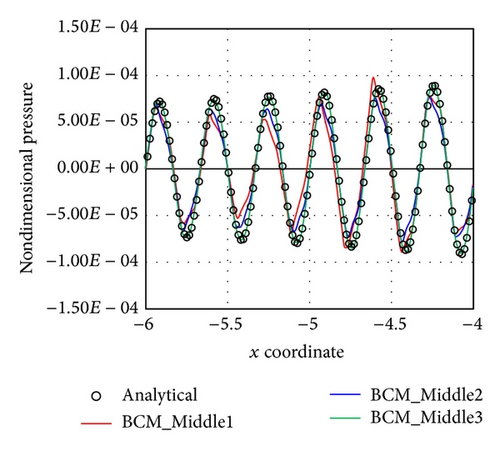
In Figures 9(c) and 9(d), the BCM_Middle meshes are compared. The BCM_Middle2 and BCM_Middle3 meshes follow the analytical solution in Figure 9(c). These meshes have a buffer zone of width 9D in the x direction, and outgoing waves are damped appropriately. However, the BCM_Middle2 mesh provides a lower amplitude. This is owing to the insufficient PPW at the sampling points. On the other hand, phase error is not observed in the BCM_Middle2 mesh. In Figure 9(d), the amplitude of the pressure converges to the analytical solution for the BCM_Middle2 mesh. Only the BCM_Middle1 mesh provides a lower amplitude. This amplitude is the same as that of the uniform meshes. Therefore, it is confirmed that the amplitude of the inner sound field is diminished when using a buffer zone of short width.

In Figures 9(e) and 9(f), the BCM_Fine meshes are compared. The pressure distributions and the time histories of the BCM_Fine meshes exhibit similar tendencies as those of the BCM_Middle meshes.

To compare the magnitude of errors more quantitatively, the root mean square pressure, P_rms, of the scattered sound is computed and the normalized RMSE (NRMSE) and the normalized maximum error (MME) between the analytical solution and the solutions of each mesh are compared, as given by

(10)

The number of sampling points N are set clockwise at a radius r = 2 D from the origin. The points (−2D, 0, 0) and (2D, 0, 0) correspond to 0 deg. and 180 deg. The errors are summarized in Table 3. As shown in the table, the refined meshes provide lower errors than the coarser mesh, and the meshes that utilize a large buffer zone also provide lower errors. The minimum cell size around the sphere also affects the errors. The smallest errors are provided by the BCM_Fine3 mesh. A comparison of the uniform and BCM meshes indicates that the BCM_Middle3 and BCM_Fine3 meshes, which use cubes of different sizes at the appropriate locations, provide lower errors than Uniform_Middle meshes that utilize a similar number of mesh points. Moreover, the errors of the BCM_Fine3 mesh are about one-half the errors of the Uniform_Fine mesh, which has twice the number of mesh points as the BCM_Fine3 mesh. These results indicate the effectiveness of the BCM arrangement.

Table 3. Comparison of errors relative to an analytical solution and respective computational times for the meshes listed in Table 2.

	Total number of cells	Normalized root mean square error [%]	Normalized maximum error [%]	Computational time [ μsec/timestep/cell]	Real time [sec.] (128 CPUs)
Coarse	14,155,776	11.97	23.82	0.08454	302
Uniform_Middle	47,775,744	5.02	11.31	0.08631	1,388
BCM_Middle1	20,348,928	3.62	14.86	0.10891	1,088
BCM_Middle2	32,735,232	3.07	7.14	0.11027	1,710
BCM_Middle3	45,121,536	2.89	7.34	0.09665	2,172
Uniform_Fine	113,246,208	3.57	10.93	0.07329	4,240
BCM_Fine1	26,542,080	6.14	22.24	0.08851	2,654
BCM_Fine2	38,928,384	3.04	7.00	0.08777	3,358
BCM_Fine3	51,314,688	1.62	5.00	0.09019	4,794

The computational wall-clock times for a single time step per cell and the total wall-clock time required to reach a nondimensional time T = 15 are also listed in Table 3. All meshes were computed using 128 CPUs of an SGI AltixUV1000 computer. Regarding the wall-clock time per one time step per cell, the computational times of the uniform and BCM meshes are comparable. However, the total wall-clock times of the BCM meshes are slightly longer than those of the uniform meshes. The BCM meshes employ a larger number of cubes than the number of CPUs used in the evaluation. The mismatch between the numbers of cubes and CPUs can degrade the load balance. Computations using an equivalent number of CPUs and cubes are more effective for BCM meshes.

5. Noise Propagation from the JT15D Nacelle

Noise propagation from the JT15D [34] nacelle is computed and the far-field sound pressure level (SPL) is compared with data derived from experiment and the computational results of others. The JT15D is a small Pratt and Whitney turbofan engine with a bellmouth inlet. The sound source is introduced via a discrete frequency spinning mode. The spinning mode input [35] is a typical sound source generated by the fan or rotor-stator intersections in the engine. The sound source of a single spinning mode (m, n) is defined by

(11)

Here, J_m and Y_m are the mth order Bessel functions of the first and second kind, respectively, k is the angular frequency, k_a is the axial wavenumber, k_r is the radial wavenumber, and θ is the phase. The nth solution k_r of the following equation is determined by the hard-wall boundary condition of the duct:

(12)

Here, r_outer and r_inner are the bypass duct inner wall radius and the inner hub radius, respectively. The axial wave number k_a is computed from

(13)

where M_j is the Mach number at the fan face. The selection of plus or minus signs in the parentheses is determined by the propagation direction of the sound wave, where plus (+) represents the positive propagation direction along the axial coordinate, and vice versa. The constant c₁ satisfies the following relation:

(14)

Parameters are set from experimental data: (m, n) = (−13,0), r_outer = 0.2667 m, and r_inner = 0.0998 m. The reference length D = 0.6223 mis the length from the fan face to the leading edge of the nacelle. The blade passing frequency (BPF) is set to 3,150 Hz, which is derived from the fan rotating speed of 6,750 rpm. The experiments were conducted in the static condition, and the fan face axial Mach number is 0.175. The present computation is also conducted in the static condition. In the present computation, the axial flow velocity of the ghost cell at the fan face boundary is directly modified to this Mach number. The pressure and the density are the same values as those of the adjacent fluid cells. The SPL is measured at a radius of 49D. The integration method of Ffowcs-Williams and Hawkings (FW-H) [36] is employed to estimate the far-field pressure from the near-field pressure.

Figure 10 shows the computational domain and Table 4 lists the mesh information. The computations of the compressible Euler solver and the LEEs solver are conducted using the same mesh. The PPW in Table 4 is the PPW reduced by the Doppler effect of the fan face axial Mach number. The computational domain is set at −1D ≤ x ≤ 7D, −8D ≤ y ≤ 8D, and −8D ≤ z ≤ 8D. The fan face is at x = 0.5D. The inner end of the buffer zone is set at x = [0,4D], y = [−4D, 4D], and z = [−4D, 4D]. The FW-H surfaces are located at the cube boundaries between the smallest size cubes and the larger size cubes.

Table 4. Mesh information for the JT15D nacelle.

JT15D	Minimum cell size	Number of cubes	Number of cells in one cube	Total number of cells	PPW
Case 1	0.0166D	1,544	30 × 30 × 30	41,688,000	8.7
Case 2	0.0125D	1,544	40 × 40 × 40	98,816,000	11.6

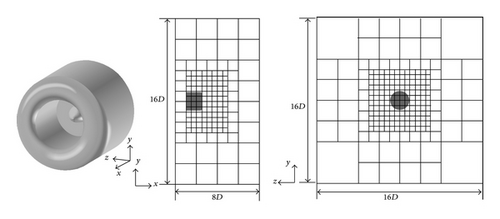
Figure 11 shows the Mach number distribution around the JT15D nacelle. In Figure 11, the acceleration region near the internal wall of the nacelle lip and the stagnation at the spike are shown. Because the experiments and computations were conducted under the static condition, the mean flow field exists only near the nacelle.

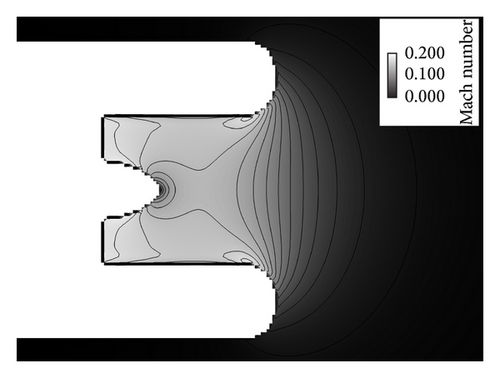
Figure 12 shows the instantaneous pressure distributions at the planes defined at z = 0 and x = 1.7D. In the figure, only the distributions of the smallest sized cubes are drawn. The fan noise is diffracted at the inlet of the nacelle and propagates along the radial direction. The 13 peaks and valleys of the swirling fan noise at the x = 1.7D plane are clearly captured, which is equivalent to the number of spinning modes. The time history of the pressure is sampled at the established points on the FW-H surface, and the periodic steady state is observed after T = 8.

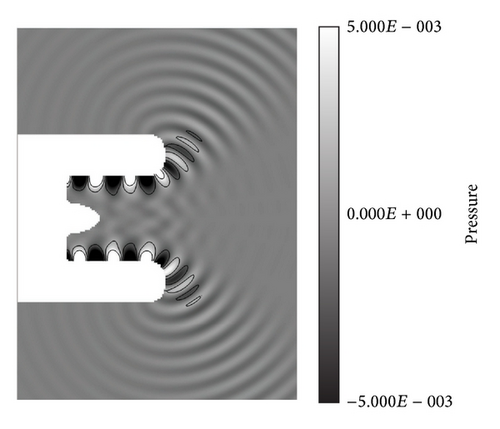
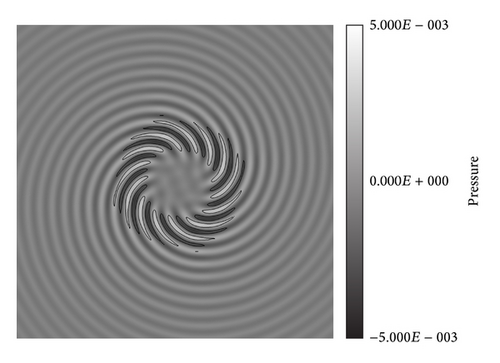
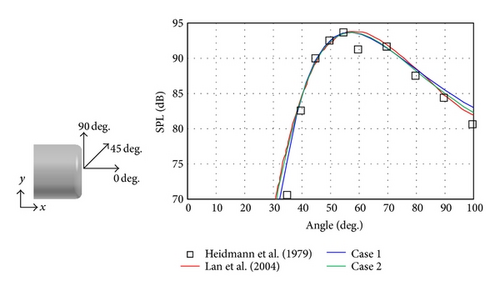
Figure 13 shows a comparison of the predicted SPL with the experimental results conducted by Heidmann et al. [37] and the computational results computed by Lan et al. [34]. The horizontal axis in the figure is the angle from the +x-axial direction. In the figure, the predicted SPL using the present solver shows good agreement with the computational result of Lan et al. (within 1 dB). Compared with the experimental data, a difference of about 3 dB is found at 60 deg. However, this discrepancy is also shown between the experimental data and the result of Lan et al. The SPL peak, obtained near 55 deg., is equivalent to that obtained by Lan et al. and that obtained experimentally.

6. Noise Propagation around a Fuselage-Wing-Nacelle Configuration

The noise propagation around a fuselage-wing-nacelle configuration is computed as a realistic example. The focus of the example was that of the OWN configuration [38], where the engine nacelle is mounted over the main wing, which serves as one of the configurations designed to achieve substantial airport noise reduction. The main feature of this configuration is that the main wing serves as a shield between the ground and the noise generated by the engine. To investigate the effect of the OWN configuration, the propagation of fan noise of both the conventional DLR-F6 aircraft configuration [39] and the OWN configuration is computed and the SPL below the aircraft for both configurations is compared. These configurations have complex geometry with large curvatures near the wing-body and the nacelle-pylon junctions. In the OWN configuration, the nacelle is moved 1.1D in the +x direction and 0.6D in the +y direction relative to its location in the DLR-F6 configuration. Here, the reference length D = 4.9 m is the longitudinal length of the nacelle. The cross-sectional geometry of the pylon is used without any changes and has a sweepback angle of 40 deg. A mean flow field of Mach number 0.3 with zero angle of attack is computed using the compressible Euler solver. The sound source is introduced via a discrete frequency spinning mode. As an example of a modern turbofan engine, the CFM56-7B engine is considered. The bypass ratio is 5.5, the fan diameter is 1.54 m, the number of blades is 24, the maximum rotational rate is 5,382 rpm, and the fundamental BPF is 2,152.8 Hz. The BPF is used as the input frequency of the spinning mode. The spinning mode (m, n) is set to (−24, 0). The SPL is measured at a radius of 10D using the FW-H method.

Figure 14 shows the computational domain of each configuration. The black dot shows the origin of coordinate system. The computations of the compressible Euler and LEEs solvers are conducted using an equivalent mesh. The size of the computational domains is 4D × 2D × 2D. The symmetric boundary condition is set at the −z boundary. The computational domains are set to ensure that sufficient computational domains surround the nacelle. It is assumed that the geometry out of the computational domain has little influence on the noise directivity below the aircraft. The minimum size cubes are located within the domain wherein the reflection and diffraction by the aircraft must be resolved. The inner end of the buffer zone is set at x = [−0.75D, 1.75D], y = [−0.5D, 0.5D], and z = 1.75D in the DLR-F6 calculation and at x = [0D, 2.75D], y = [−0.25D, 0.75D], and z = 1.75D in the OWN calculation. FW-H surfaces are located at the inner end of the buffer zone and the symmetrical plane. The size of the buffer zones of the DLR-F6 calculation is 0.75D in the −x and +x directions, 0.5D in the −y and +y directions, and 0.25D in the +z direction. The size of the buffer zones of the OWN calculation is 0.5D in the −x direction, 0.75D in the +x direction, 0.25D in the −y direction, 0.75D in +y direction, and 0.25D in the +z direction. Table 5 lists the mesh information of the computations. The PPW in Table 5 is the PPW reduced by the Doppler effect of the mean flow field Mach number.

Table 5. Mesh information for calculations of noise propagation around the fuselage-wing-nacelle configurations.

	Minimum cell size	Number of cubes	Number of cells in one cube	Total number of cells	PPW
DLR-F6	0.0025D	3,474	50 × 50 × 50	434,250,000	9.0
OWN	0.0025D	3,425	50 × 50 × 50	428,125,000	9.0

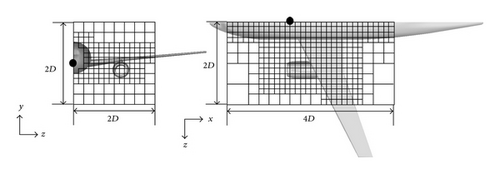
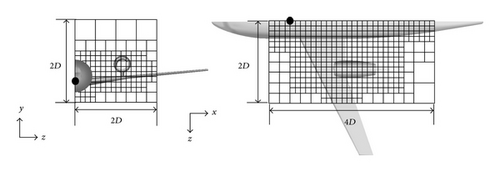
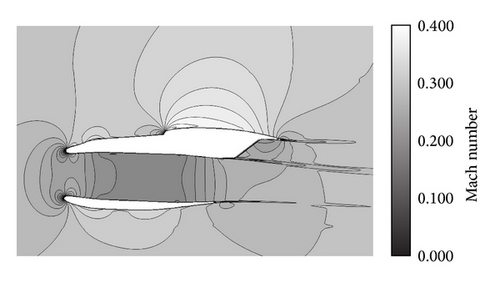
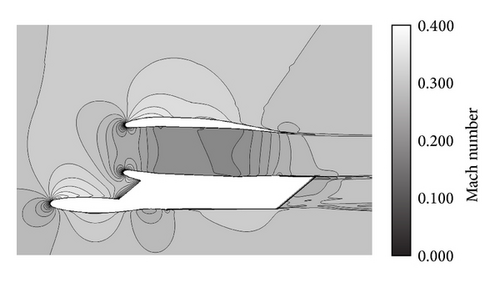
Figure 15 shows the Mach number distributions at the nacelle center for the two configurations. In Figure 15, the acceleration region over the wing and the stagnation at the inlet of the nacelle are shown. A Mach number greater than 0.3 is shown in the acceleration region. Figure 16 shows the SPL distributions on the aircraft surface for the two configurations. Noise from the nacelle propagates in the radial direction and the noise is shielded by the main wing in the OWN configuration. On the other hand, noise from the inlet reaches the fuselage and generates a high SPL in the OWN configuration compared to the DLR-F6 configuration.

To check the propriety of the computations, the SPL distribution computed for the OWN configuration on the suction side of the main wing is compared with data captured during flight and the computations of others [40]. The flight data of a twin-engine business jet aircraft was acquired at a flight Mach number of 0.3 at an altitude of 1,500 m. This aircraft has the aft fuselage nacelle configuration that the inlet of the engine nacelle is located over the main wing. Therefore, qualitative comparisons can be conducted. The SPL on the suction side of the main wing was measured using Kulite microphones. The computation of Xu et al. was conducted using the discrete frequency spinning mode (20, 0) without a mean flow field. The computed SPL is normalized so that the peak SPL is equal to that of the flight data. Figure 17 shows the SPL versus the angle from the inlet axis. The computed SPL agrees with the flight data from 50 to 70 deg. within 3 dB. The peak SPL is at 63 deg. This is similar to the peak given by the flight data, which has a peak at 60 deg. The discrepancy at an angle of 40 deg. is caused by the different clearances between the engine and the main wing, where the clearance of the aircraft employed in the experiment is smaller than that of the present computation.

Figure 18 shows the estimated SPL distribution at a radius of 10D based on the center of the front face of nacelle. Based on International Civil Aviation Organization rules, aircraft noise is determined by the noise levels at the side and the bottom locations relative to the fuselage. Therefore, the SPL distribution below the aircraft is estimated. From Figure 18, the SPL of the OWN configuration is lower than that of the DLR-F6 configuration by about 10 dB over the range of 40 deg. to 70 deg. This represents significant noise reduction relative to conventional aircraft design. Using the proposed method, it would be possible to optimize the position of the nacelle to obtain maximum noise shielding performance.

7. Conclusion

The linearized Euler equationssolver on block-structured Cartesian mesh of the building-cube method (BCM) coupled with the immersed boundary method (IBM) has been developed to compute noise propagation around complex geometry. The accuracy and effectiveness of the solver for practical problems were validated by application to one-dimensional and three-dimensional noise propagation problems and the application of fan noise propagation around fuselage-wing-nacelle configurations.

For the one-dimensional noise propagation problem, the IBM slightly decreased the order of accuracy of the system because the second-order central difference is employed at fluid cells adjacent to ghost cells. However, a fourth order of accuracy is nearly retained even when employing the IBM. Interpolation between cubes of different sizes causes degradation to a second order of accuracy.

For the problem of acoustic scattering around a sphere, the error was suppressed by mesh refinement near the sphere and by expansion of the buffer zone. The results computed on the BCM meshes provided quantitative agreement with the analytical solution. A normalized root mean square error of 1.62% and a normalized maximum error of 5% for the results computed by the BCM_Fine3 mesh were about one-half of the errors computed by the Uniform_Fine mesh, which has twice as many mesh points as the BCM_Fine3 mesh. The computational time required for the BCM mesh was slightly longer than that required for the uniform mesh because of the mismatch between the number of CPUs and cubes.

The estimated sound pressure level (SPL) from the JT15D nacelle provided good agreement with experimental data and with other computational results. The present solver demonstrated accurate computations for a curved object like an axisymmetric nacelle.

Noise propagation around two fuselage-wing-nacelle configurations was computed as a realistic example to verify the capability of the present solver and to estimate the noise shielding effect of the OWN configuration. The aircraft configuration has complicated geometries, especially near the wing-body and the nacelle-pylon junctions, and the present solver demonstrated a robust treatment of these geometries. For the OWN configuration, the noise from the nacelle inlet was shielded effectively by the main wing because the noise diffracted strongly in the radial direction. The computed SPL at the suction side of the main wing agrees with data obtained during flight. The SPL distribution of the OWN configuration below the aircraft was lower by about 10 dB than that of the conventional DLR-F6 configuration.

Through application to simple test cases and realistic cases, the effectiveness of the solver was confirmed. Using the present solver, noise propagation around next-generation unconventional aircraft can be estimated, and the method is expected to contribute to the future of aircraft design.

Nomenclature

i, j, k, l:: Cell index coordinates
x, y, z:: Coordinates in the computational domain
Δx, Δy, Δz:: Mesh spacing
Q:: Physical quantities vector
Q^′:: Fluctuation vector
u₁, u₂, u₃:: Velocity fluctuation of x, y, and z direction
Q₀:: Mean flow field vector
u₁₀, u₂₀, u₃₀:: Mean velocity of x, y, and z direction
S:: Sound source vector
γ:: Specific heat ratio
δ:: Kronecker delta
n:: Unit normal vector
V_IP:: Velocity vector at the image point
V_GC:: Velocity vector at the ghost cell
d_IP:: Distance from the image point to the wall surface
d_GC:: Distance from the ghost cell to the wall surface
Q_o:: Physical quantities at an overlap cell
Q_s:: Physical quantities at a surrounding cell
x_o, y_o, z_o:: x, y, z coordinates of an overlap cell
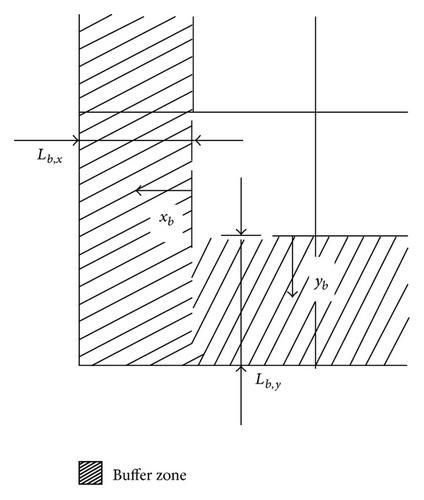
σ:: Damping coefficient in the buffer zone
x_b, y_b, z_b:: Distance from the inner end of the buffer zone
L_b,x, L_b,y, L_b,z:: Width of the buffer zone
D:: Reference length
:: Initial pressure
:: Computed pressure
:: Analytical solution of the pressure
T:: Nondimensional time
P_rms:: Root mean square pressure
c:: Speed of sound
(m, n):: Input spinning mode
J_m, Y_m:: mth order Bessel functions of the first and second kind.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

This work was supported by JSPS KAKENHI Grant nos. 21226018 and 25·9225. The computation in this research was conducted using an SGI AltixUV1000 of the Institute of Fluid Science, Tohoku University. The Ffowcs-Williams and Hawkings code used in this research was provided by the Aviation Program Group of Japan Aerospace Exploration Agency (JAXA).

References

1 Kwak D.-Y., Hirotani T., Noguchi M., and Ito T., Experimental research for aerodynamic interference by upper mounted engine exhaust jet on sst configurations, Proceedings of the 27th Congress of the International Council of the Aeronautical Sciences 2010 (ICAS ′10), September 2010, Nice, France, 1211–1219, 2-s2.0-84878446027.
Google Scholar
2 Ishikawa H., Tanaka K., Makino Y., and Yamamoto K., Sonic-boom prediction using euler CFD codes with structured/unstrucutured overset method, Proceedings of the 27th Congress of the International Council of the Aeronautical Sciences (ICAS ′10), September 2010, 744–751, 2-s2.0-84878488238.
Google Scholar
3 Murakami A., Silent supersonic technology demonstration program, Proceedings of the 25th Congress of International Council of the Aeronautical Sciences, September 2006, Hamburg, Germany.
Google Scholar
4 Envia E., Emerging community noise reduction approaches, Proceedings of the 3rd AIAA Atmospheric Space Environments Conference, June 2011, AIAA Paper 2011-3532, 2-s2.0-84883474510.
Google Scholar
5 Russell T., Casey B., and Erik O., Hybrid wing body aircraft system noise assessment with propulsion airframe aeroacoustic experiments, Proceedings of the 16th AIAA/CEAS Aeroacoustic Conference, June 2010, Stockholm, Sweden, AIAA Paper 2010-3913.
Google Scholar
6 Felder J. L., Kim H. D., and Brown G. V., Turboelectric distributed propulsion engine cycle analysis for hybrid-wing-body aircraft, Proceedings of the 47th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, January 2009, AIAA paper 2009-11322-s2.0-78549281466.
Google Scholar
7 Redonnet S., Desquesnes G., Manoha E., and Parzani C., Numerical study of acoustic installation effects with a computational aeroacoustics method, AIAA Journal. (2010) 48, no. 5, 929–937, https://doi.org/10.2514/1.42153, 2-s2.0-77952523408.
10.2514/1.42153
Web of Science® Google Scholar
8 Hepperle M., Environmental friendly transport aircraft, New Results in Numerical and Experimental Fluid Mechanics IV, 2004, 87, Springer, Notes on Numerical Fluid Mechanics and Multidisciplinary Design.
10.1007/978-3-540-39604-8_4
Google Scholar
9 Nagy A. B., Aeroacoustics research in Europe: the CEAS-ASC report on 2010 highlights, Journal of Sound and Vibration. (2011) 330, no. 21, 4955–4980, https://doi.org/10.1016/j.jsv.2011.05.015, 2-s2.0-79960555759.
10.1016/j.jsv.2011.05.015
Web of Science® Google Scholar
10 Powell S., Sóbester A., and Joseph P., Performance and noise trade-offs on a civil airliner with over-the-wing engines, Proceedings of the 49th AIAA Aerospace Sciences Meeting, 2011, Orlando, Fla, USA, AIAA paper 2011-0266, https://doi.org/10.2514/6.2011-266.
10.2514/6.2011-266
Google Scholar
11 Fukata S., Hayama K., Sylvand G., Alestra S., and Axuma T., Study of jet noise source modeling and shielding effect for future aircraft, Inter-Noise 2011, 2011.
Google Scholar
12 Czech M., Thomas R., and Elkoby R., Propulsion airframe aeroacoustic integration effects for a hybrid wing body aircraft configuraion, Proceedings of the 16th AIAA/CEAS Aeroacoustics Conference, June 2010, Stockholm, Sweden, AIAA Paper 2010-3912.
Google Scholar
13 Huang X., Chen X., Ma Z., and Zhang X., Efficient computation of spinning modal radiation through an engine bypass duct, AIAA Journal. (2008) 46, no. 6, 1413–1423, https://doi.org/10.2514/1.31136, 2-s2.0-45849112128.
10.2514/1.31136
Web of Science® Google Scholar
14 Chiba K., Imamura T., Amemiya K., and Yamamoto K., Design optimization of shielding effect for aircraft engine noise, Journal of Environment and Engineering. (2007) 2, no. 3, 567–577, https://doi.org/10.1299/jee.2.567.
10.1299/jee.2.567
Google Scholar
15 Kamatsuchi T., Computational aeroacoustic analysis around an airfoil using linearized Euler equations, Journal of Japan Society of Fluid Mechanics. (2004) 23, 285–294.
Google Scholar
16 Chen X., Huang X., and Zhang X., Sound radiation from a bypass duct with bifurcations, AIAA Journal. (2009) 47, no. 2, 429–436, https://doi.org/10.2514/1.39710, 2-s2.0-60049097741.
10.2514/1.39710
Web of Science® Google Scholar
17 Bauer M., Dierke J., and Ewert R., Application of a discontinuous Galerkin method to discretize acoustic perturbation equations, AIAA Journal. (2011) 49, no. 5, 898–908, https://doi.org/10.2514/1.J050333, 2-s2.0-79955394577.
10.2514/1.J050333
Web of Science® Google Scholar
18 Onda H., Sakai R., Sasaki D., and Nakahashi K., Unsteady flow and aerodynamic noise analysis around JAXA landing gear model by building-cube method, Proceedings of the 49th AIAA Aerospace Sciences Meeting, 2011, AIAA Paper 2011-1081.
Google Scholar
19 Sasaki D., Onda H., Deguchi A., Sakai R., and Nakahashi K., Landing gear aerodynamic noise prediction using building-cube method, Proceedings of the 29th AIAA Applied Aerodynamics Conference, June 2011, AIAA Paper 2011-33662-s2.0-84880643255.
Google Scholar
20 Deguchi A., Sasaki D., Nakahashi K., Murayama M., Yamamoto K., and Yokokawa Y., Aeroacoustic simulation of JAXA landing gear by building-cube method and non-compact Curle′s equation, Proceedings of the 50th AIAA Aerospace Sciences Meeting, 2012, AIAA Paper 2012-0388.
Google Scholar
21 Nakahashi K. and Kim L.-S., C. Groth and D. W. Zinggm, High-density mesh flow computations by building-cube method, Computational Fluid Dynamics 2004, 2006, Springer, Berlin, Germany, 121–126, https://doi.org/10.1007/3-540-31801-1_13.
10.1007/3-540-31801-1_13
Google Scholar
22 Nakahashi K., S. Armfield, R. Morgan, and K. Srinivas, Building-cube method for flow problems with broadband characteristic length, Computational Fluid Dynamics 2002, 2003, Springer, 77–81.
10.1007/978-3-642-59334-5_7
Web of Science® Google Scholar
23 Bogey C., Bailly C., and Juvé D., Computation of flow noise using source terms in linearized Euler′s equations, AIAA Journal. (2002) 40, no. 2, 235–243, https://doi.org/10.2514/2.1665, 2-s2.0-0036472045.
10.2514/2.1665
Web of Science® Google Scholar
24 Ishida T., Takahashi S., and Nakahashi K., Efficient and robust Cartesian mesh generation for building-cube method, Journal of Computational Science and Technology. (2011) 2, 33–45.
Google Scholar
25 Nakahashi K., Immersed boundary method for compressible Euler equations in the building-cube method, Proceedings of the 20th AIAA Computational Fluid Dynamics Conference, 2011, AIAA Paper 2011-3386.
Google Scholar
26 Shima E. and Kitamura K., On new simple low-dissipation scheme of AUSM-family for all speeds, Proceedings of the 47th AIAA Aerospace Sciences Meeting, January 2009, AIAA Paper 2009-136, 2-s2.0-78549277746.
Google Scholar
27 Tam C. K. W., Recent advances in computational aeroacoustics, Fluid Dynamics Research. (2006) 38, 591–615.
10.1016/j.fluiddyn.2006.03.006
Web of Science® Google Scholar
28 Allampalli V., Hixon R., Nallasamy M., and Sawyer S. D., High-accuracy large-step explicit Runge-Kutta (HALE-RK) schemes for computational aeroacoustics, Journal of Computational Physics. (2009) 228, no. 10, 3837–3850, https://doi.org/10.1016/j.jcp.2009.02.015, ZBL1171.76039, 2-s2.0-62849095275.
10.1016/j.jcp.2009.02.015
Web of Science® Google Scholar
29 Mittal R., Dong H., Bozkurttas M., Najjar F. M., Vargas A., and von Loebbecke A., A versatile sharp interface immersed boundary method for incompressible flows with complex boundaries, Journal of Computational Physics. (2008) 227, no. 10, 4825–4852, https://doi.org/10.1016/j.jcp.2008.01.028, MR2414837, 2-s2.0-41249094535.
10.1016/j.jcp.2008.01.028
CAS PubMed Web of Science® Google Scholar
30 Ishida T., Kawai S., and Nakahashi K., A high-resolution method for flow simulations on block-structured Cartesian meshes, Proceedings of the 6th International Conference on Computational Fluid Dynamics (ICCFD6 ′10), July 2010, Saint Petersburg, Russia.
Google Scholar
31 Wasistho B., Geurts B. J., and Kuerten J. G. M., Simulation techniques for spatially evolving instabilities in compressible flow over a flat plate, Computers and Fluids. (1997) 26, no. 7, 713–739, https://doi.org/10.1016/s0045-7930(97)00021-2, 2-s2.0-0031225139.
10.1016/S0045-7930(97)00021-2
Web of Science® Google Scholar
32 Tam C. K. W. and Hardin J. C., Second Computational Aeroacoustics (CAA) Workshop on Benchmark Problems, 1997, NASA Conference Publication 3352.
Google Scholar
33 Seo J. H. and Mittal R., A high-order immersed boundary method for acoustic wave scattering and low-Mach number flow-induced sound in complex geometries, Journal of Computational Physics. (2011) 230, no. 4, 1000–1019, https://doi.org/10.1016/j.jcp.2010.10.017, MR2753346, ZBL05867071, 2-s2.0-78650559755.
10.1016/j.jcp.2010.10.017
PubMed Web of Science® Google Scholar
34 Lan J. H., Guo Y., and Breard C., Validation of acoustic propagation code with JT15D static and flight test data, Proceedings of the 10th AIAA/CEAS Aeroacoustic Conference, May 2004, AIAA paper 2004-2986.
Google Scholar
35 Tyler J. M. and Sofrin T. G., Axial flow compressor noise studies, SAE Transactions. (1962) 70, 309–332, https://doi.org/10.4271/620532, 2-s2.0-84877189790.
10.4271/620532
Google Scholar
36 Lyrintzis A. S., Surface integral methods in computational aeroacoustics—from the (CFD) near-field to the (Acoustic) far-field, International Journal of Aeroacoustics. (2003) 2, no. 2, 95–128, https://doi.org/10.1260/147547203322775498.
10.1260/147547203322775498
Google Scholar
37 Heidmann M. F., Saule A. V., and McArdle J. G., Analysis of radiation patterns of interaction tones generated by inlet rods in the JT15D engine, Proceedings of the 5th AIAA Aeroacoustics Conference, 1979, AIAA paper 79-0581.
Google Scholar
38 Sasaki D. and Nakahashi K., Aerodynamic optimization of an over-the-wing-nacelle-mount configuration, Modelling and Simulation in Engineering. (2011) 2011, 13, 293078, https://doi.org/10.1155/2011/293078, 2-s2.0-79959257825.
10.1155/2011/293078
Google Scholar
39 Laflin K. R., Klausmeyer S. M., Zickuhr T., Vassberg J. C., Wahls R. A., Morrison J. H., Brodersen O. P., Rakowitz M. E., Tinoco E. N., and Godard J.-L., Data summary from second AIAA computational fluid dynamics drag prediction workshop, Journal of Aircraft. (2005) 42, no. 5, 1165–1178, https://doi.org/10.2514/1.10771, 2-s2.0-27144462823.
10.2514/1.10771
Web of Science® Google Scholar
40 Xu J., Stanescu D., Hussaini M. Y., and Farassat F., Computation of engine noise propagation and scattering off an aircraft, Proceedings of the 41th AIAA Aerospace Sciences Meeting, January 2003, Reno, Nev, USA, AIAA Paper 2003-0542.
Google Scholar

Citing Literature

All articles

Cartesian Mesh Linearized Euler Equations Solver for Aeroacoustic Problems around Full Aircraft

Abstract

1. Introduction