An Extensive Photometric Investigation of the W UMa System DK Cyg
Abstract
DK Cyg (P = 0.4707) is a contact binary system that undergoes complete eclipses. All the published photoelectric data have been collected and utilized to reexamine and update the period behavior of the system. A significant period increase with rate of 12.590 × 10−11 days/cycle was calculated. New period and ephemeris have been calculated for the system. A long term photometric solution study was performed and a light curve elements were calculated. We investigated the evolutionary status of the system using theoretical evolutionary models.
1. Introduction
The eclipsing binary DK Cyg (BD +330 4304, 10.37–10.93 mv) is a well known contact binary system with a period of about 0.4707 days. It was discovered as variable star earlier by Guthnick and Prager [1], so their epoch of intensive observations is very long. The earliest photographic light curve classified the system as a W Ursae Majoris type. Rucinski and Lu [2] carried out the first spectroscopic observations and estimated the mass ratio as q = 0.325 and classified the system as an A-subtype contact system with spectral type of A8V. Visual light curves were published by Piotrowski [3] and Tsesevitch [4] from Klepikova’s observations.
First photoelectric observations for the system were carried out by Hinderer [5], while Binnendijk [6] observed the system photoelectrically in B- and V-bands and derived least squares orbital solution. The system DK Cyg was classified in the General Catalogue of Variable Stars as A7V [7], while Binnendijk [6] adopted it as A2. Mochnacki and Doughty [8] showed that the color index of the system judged its spectral type and found that the spectral type of the system is more likely to be about F0 to F2. Because the system DK Cyg is a summer object in the Northern hemisphere with 11.5-hour period and short durations of night, it is bound to remain ill-observed [9]. Only four complete light curves by Binnendijk [6], Paparo et al. [10], Awadalla [9], and Baran et al. [11] are published. Photoelectric observations and new times of minima have been carried out by many authors: Borkovits et al. [12], Sarounová and Wolf [13], Drozdz and Ogloza [14], Hübscher et al. [15], Dogru et al. [16], Hubscher et al. [17], Hubscher et al. [18], Erkan et al. [19], Diethelm [20], Dogru et al. [21], Simmons [22], Diethelm [23], and Diethelm [24].
In the present paper we are going to perform comprehensive photometric study for the system DK Cyg. The structures of the paper are as follows: Section 2 deals with the period change, Section 3 is devoted to the light curve modeling, and Section 4 presents the discussion and conclusion reached.
2. Period Change
Although the period variation of contact binary systems of the W UMa-type is a controversial issue of binary star astrophysics, the cause of the variations (long as well as short term) is still a mystery for a discussion of possible physical mechanisms [25]. Magnetic activity cycle is one of the main mechanisms that caused a period variation together with the mass exchange between the components of each system. Kaszas et al. [26] stated that the long term period variation may be interpreted by a perturbation of the third companion or surface activity of the system components.
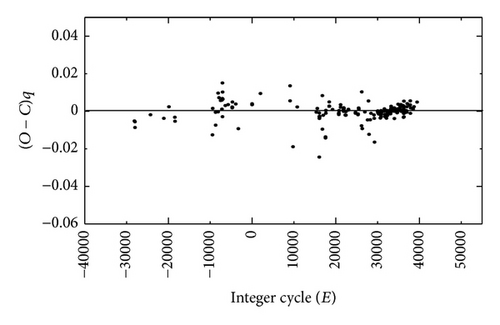
Observations by Binnendijk [6] showed a change of the secondary minimum depth and a new linear light element was derived. Period study by Paparo et al. [10] showed that the orbital period of the system DK Cyg increases and the first parabolic light elements were calculated, which confirmed the light curve variability. Kiss et al. [25] updated the linear ephemeris of DK Cyg, while Awadalla [9] recalculated a new quadratic element for the system and confirmed the light curve variability suggested by Paparo et al. [10]. Wolf et al. [27] used a set of 101 published times of minimum covering the interval between 1926 and 2000 in order to update the quadratic element calculated by Awadalla [9]. They showed that the period increases by the rate 11.5 × 10−11 days/cycle. Borkovits et al. [28] follow the period behavior of the system using set of published minima from HJD 2424760 to HJD 2453302.
| HJD | Method | E | (O − C) | (O − C)q | References | HJD | Method | E | (O − C) | (O − C)q | References |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2434179.4690 | Vis | −8116 | 0.00970 | 0.00971 | 1 | 2451749.4450 | pe | 29212 | 0.04885 | −0.00370 | 3 |
| 2447758.4352 | Pe | 20733 | 0.02423 | −0.00099 | 2 | 2451777.6740 | ccd | 29272 | 0.03642 | −0.01636 | 5 |
| 2447790.4437 | Pe | 20801 | 0.02577 | 0.00037 | 2 | 2452163.6590 | ccd | 30092 | 0.05517 | −0.00074 | 5 |
| 2447963.6620 | Pe | 21169 | 0.02995 | 0.00354 | 3 | 2452245.5592 | ccd | 30266 | 0.05521 | −0.00137 | 5 |
| 2447963.8960 | Pe | 21169.5 | 0.02860 | 0.00220 | 3 | 2452253.5613 | ccd | 30283 | 0.05557 | −0.00108 | 5 |
| 2448265.1380 | Pe | 21809.5 | 0.02865 | 0.00046 | 4 | 2452441.8384 | ccd | 30683 | 0.05645 | −0.00176 | 5 |
| 2448265.1382 | Pe | 21809.5 | 0.02885 | 0.00066 | 4 | 2452512.4415 | pe | 30833 | 0.05597 | −0.00284 | 7 |
| 2448272.1987 | Pe | 21824.5 | 0.02899 | 0.00076 | 4 | 2452525.6231 | ccd | 30861 | 0.05824 | −0.00069 | 5 |
| 2448297.6160 | Pe | 21878.5 | 0.02900 | 0.00062 | 3 | 2452526.5644 | ccd | 30863 | 0.05816 | −0.00078 | 5 |
| 2448302.7930 | Pe | 21889.5 | 0.02841 | −0.00001 | 3 | 2452811.8062 | ccd | 31469 | 0.06148 | 0.00013 | 5 |
| 2448308.2078 | Pe | 21901 | 0.03027 | 0.00182 | 4 | 2453223.4286 | ccd | 32343.5 | 0.06500 | −0.00006 | 8 |
| 2448308.2079 | Pe | 21901 | 0.03037 | 0.00192 | 4 | 2453228.3681 | ccd | 32354 | 0.06225 | −0.00274 | 8 |
| 2448336.4491 | Pe | 21961 | 0.03013 | 0.00152 | 4 | 2453246.4950 | ccd | 32392.5 | 0.06756 | 0.00242 | 8 |
| 2449988.5840 | ccd | 25471 | 0.04120 | 0.00182 | 5 | 2453247.4346 | ccd | 32394.5 | 0.06578 | 0.00063 | 8 |
| 2450003.6456 | ccd | 25503 | 0.04070 | 0.00122 | 5 | 2453285.3260 | ccd | 32475 | 0.06659 | 0.00110 | 8 |
| 2450313.8240 | ccd | 26162 | 0.03403 | −0.00765 | 5 | 2453286.2657 | ccd | 32477 | 0.06491 | −0.00059 | 8 |
| 2450341.6130 | ccd | 26221 | 0.05229 | 0.01041 | 5 | 2453302.2672 | ccd | 32511 | 0.06293 | −0.00271 | 8 |
| 2450397.6060 | ccd | 26340 | 0.03311 | −0.00917 | 5 | 2454799.5505 | ccd | 35692 | 0.07959 | 0.00004 | 9 |
| 2450692.7400 | ccd | 26967 | 0.04414 | −0.00030 | 5 | 2455043.8381 | ccd | 36211 | 0.07882 | −0.00310 | 10 |
| 2451000.0990 | pe | 27620 | 0.04221 | −0.00452 | 5 | 2455062.6680 | ccd | 36251 | 0.08107 | −0.00105 | 11 |
| 2451095.6600 | ccd | 27823 | 0.05303 | 0.00557 | 5 | 2455088.5544 | ccd | 36306 | 0.07953 | −0.00285 | 10 |
| 2451160.5980 | ccd | 27961 | 0.03573 | −0.01222 | 5 | 2455810.6029 | ccd | 37840 | 0.08870 | −0.00096 | 12 |
| 2451379.4820 | pe | 28426 | 0.04863 | −0.00101 | 3 |
| JD | Period | Quadratic term | References |
|---|---|---|---|
| 2437999.5838 | 0.470690550 | Binnendijk [6] | |
| 2437999.5828 | 0.470690660 | 5.390 × 10−10 | Paparo et al. [10] |
| 2437999.5825 | 0.470690730 | 5.760 × 10−11 | Awadalla [9] |
| 2451000.0999 | 0.470692900 | Kiss et al. [25] | |
| 2437999.5825 | 0.470690640 | 5.750 × 10−11 | Wolf et al. [27] |
| 2451000.1031 | 0.470693909 | 5.862 × 10−11 | Borkovits et al. [28] |
| 2437999.5961 | 0.470692060 | Present work | |
| 2437999.5803 | 0.470690640 | 6.284 × 10−11 | Present work |

3. Light Curve Modeling
Light curve modeling for the system DK Cyg by Mochnacki and Doughty [8] using Binnendijk [6] observations in V-band showed nonmatching between the theoretical curve and the observations. The photometric mass ratio calculated from their accepted model was qph = 0.33 ± 0.02, while the spectroscopic value estimated using radial velocity study by Rucinski and Lu [2] is qsp = 0.325 ± 0.04. Baran et al. [11] estimated an alternating model of spectroscopic and photometric data based on iterative solutions. Their model shows a better fit by introducing a cool spot on the surface of the more luminous component and adopted the third light as free parameter in the computations. On the other hand Rucinski and Lu [2] stated that they did not find any evidence for the existence of a third component in the system during their spectroscopic study. They refer the probability for the presence of a third star in the system to the (O − C) diagram [29], which shows sinusoidal variation. This evidence is weak because only one cycle is covered up to date.
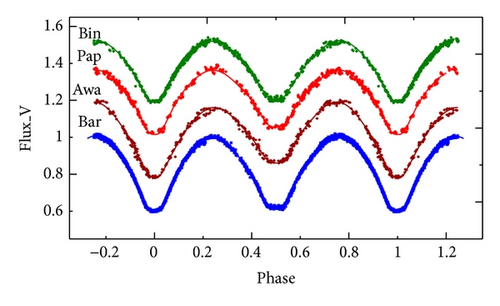
In the present work we used complete light curves published by Binnendijk [6], Paparo et al. [10], Awadalla [9], and Baran et al. [11] in V-band through a long term photometric solution study in order to estimate the physical parameters of the system and to follow its evolutionary status. The collected light curves showed a flat-bottom minima and O’Connell effect. Observations by Paparo et al. [10] and Awadalla [9] displayed some scattering specially at the two maxima of their light curves. Also the observed light curve by Awadalla [9] shows sudden increase in the light level at secondary minimum with respect to the other collected curves.
Photometric analysis for the studied light curves of the system DK Cyg was carried out using Mode 3 (overcontact) of WDint56a Package [43] based on the 2009 version of Wilson and Devinney (W-D) code with Kurucz model atmospheres [44–46]. The observed light curves were analyzed using all individual observations. Appropriate gravity darkening and bolometric albedo exponents were assumed for the convective envelope. We adopted g1 = g2 = 0.32 [47] and A1 = A2 = 0.5 [48]. Bolometric limb darkening values are adopted using the table of van Hamme [49]. Temperature of the primary star was adopted according to Baran et al. [11] model (T1 = 7500°K).
The adjustable parameters are the mean temperature of the secondary component T2, orbital inclination i, and the potential of the two components Ω = Ω1 = Ω2, while the spectroscopic mass ratio (qsp = 0.306) by Baran et al. [11] was fixed for all calculated models together with the primary star’s temperature (T1).
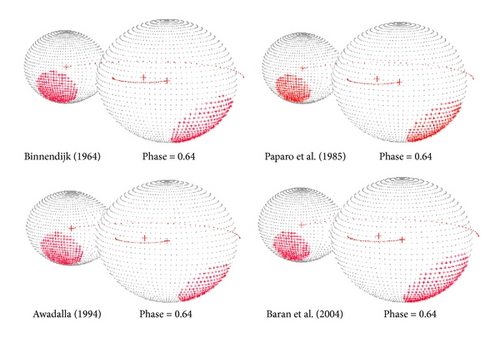
We started modeling using as initial values the parameters of Baran et al. [11] solution based on cool spot on the luminous components and a third light as a free parameter. The used parameters show disagreement between the theoretical and observed light curves, except for Baran et al. observations. Regarding the conclusion of Rucinski and Lu [2], which stated a weak evidence of presence of a third component, we tried to construct a spotted model without the third light. We constructed a model including two spots; the first one is a cool spot located on surface of the more massive component, while the other is a hot spot located on the surface of the other component. The accepted model reveals good agreement between theoretical and observed light curves for all collected data. Table 3 lists the calculated parameters for the four light curves, while Figure 3 represented the theoretical light curves according to the accepted solution together with the reflected points in V-band. The ∑(O − C) 2 values in Table 3 are indicative of comparisons in future studies, since the number of observations and the accuracy are not the same in the four light curves. Absolute physical parameters for each component of the system DK Cyg were calculated based on the results of the radial velocity data of Baran et al. [11] and our new photometric solution for each light curve. The calculated parameters are listed in Table 3. The results show that the primary component is more massive and hotter than the secondary component. A three-dimensional geometrical structure for the system DK Cyg is displayed in Figure 4 using the software Package Binary Maker 3.03 [50] based on the calculated parameters resulting from our models.
| Parameter | Binnendijk [6] | Paparo et al. [10] | Awadalla [9] | Baran et al. [11] |
|---|---|---|---|---|
| A | 5500 | 5500 | 5500 | 5500 |
| i (°) | 80.59 ± 0.12 | 80.22 ± 0.21 | 80.83 ± 0.27 | 79.97 ± 0.06 |
| g1 = g2 | 0.32 | 0.32 | 0.32 | 0.32 |
| A1 = A2 | 0.5 | 0.5 | 0.5 | 0.5 |
| q (M2/M1) | 0.306* | 0.306* | 0.306* | 0.306* |
| Ω1 = Ω2 | 2.4064 ± 0.002 | 2.4077 ± 0.005 | 2.3325 ± 0.004 | 2.3886 ± 0.001 |
| Ωin | 2.4794 | 2.4794 | 2.4794 | 2.4794 |
| Ωout | 2.2888 | 2.2888 | 2.2888 | 2.2888 |
| T1 (°K) | 7500* | 7500* | 7500* | 7500* |
| T2 (°K) | 6767 ± 4 | 6726 ± 7 | 6726 ± 9 | 6759 ± 2 |
| r1 pole | 0.4696 ± 0.0007 | 0.4694 ± 0.0013 | 0.4861 ± 0.0014 | 0.4735 ± 0.0003 |
| r1 side | 0.5091 ± 0.0010 | 0.5087 ± 0.0018 | 0.5328 ± 0.0021 | 0.5145 ± 0.0004 |
| r1 back | 0.5400 ± 0.0013 | 0.5395 ± 0.0024 | 0.5716 ± 0.0029 | 0.5471 ± 0.0005 |
| r2 pole | 0.2792 ± 0.0008 | 0.2789 ± 0.0014 | 0.2980 ± 0.0017 | 0.2835 ± 0.0003 |
| r2 side | 0.2932 ± 0.0010 | 0.2929 ± 0.0017 | 0.3166 ± 0.0022 | 0.2985 ± 0.0004 |
| r2 back | 0.3414 ± 0.0019 | 0.3407 ± 0.0034 | 0.3982 ± 0.0068 | 0.3522 ± 0.0008 |
| Spot A of star 1 | ||||
| Colatitude | 130* | 130* | 130* | 130* |
| Longitude | 180* | 180* | 180* | 180* |
| Spot radius | 33.61 ± 0.230 | 30.74 ± 0.437 | 27.23 ± 1.14 | 35.014 ± 0.09 |
| Temp. factor | 0.796 ± 0.003 | 0.840 ± 0.007 | 0.924 ± 0.01 | 0.819 ± 0.001 |
| Spot A of star 2 | ||||
| Colatitude | 120* | 120* | 120* | 120* |
| Longitude | 290* | 290* | 290* | 290* |
| Spot radius | 32.99 ± 3.60 | 29.42 ± 1.34 | 33.08 ± 1.24 | 29.44 ± 1.20 |
| Temp. factor | 1.01 ± 0.01 | 1.01 ± 0.01 | 1.17 ± 0.01 | 1.02 ± 0.002 |
| ∑(O − C)2 | 0.0229 | 0.02909 | 0.02458 | 0.0453 |
- *Not adjusted.
4. Discussion and Conclusion
Studying of the period behavior of the system DK Cyg based on all available published times of minima, covering 86 yr of observations including 195 times of light minima, shows a continuous period increase with the rate dP/dE = 12.590 × 10−11 days/cycle or 9.763 × 10−8 days/year or 0.84 seconds/century. New linear and quadratic elements were calculated using all available published data and yield a new period of P = 0.47069203 days. A long term photometric study was performed using published observations by Binnendijk [6], Paparo et al. [10], Awadalla [9], and Baran et al. [11]. More systematic and continuous photometric observations for the system DK Cyg are needed to confirm a continuous change in the period and follow its light curve variation.
One of the difficulties for W UMa binaries is to use stellar models of single stars to investigate the evolutionary status of these systems. However, using these theoretical models may give approximate view about the evolutionary status of the system.
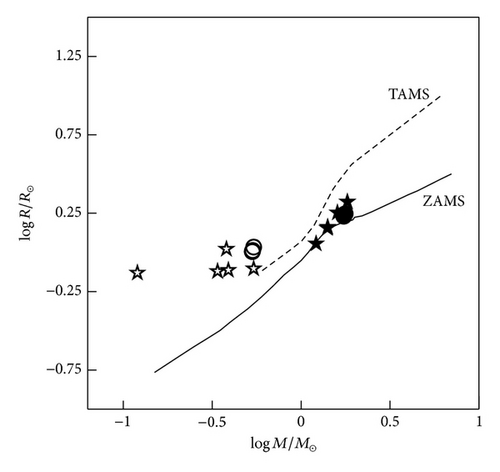
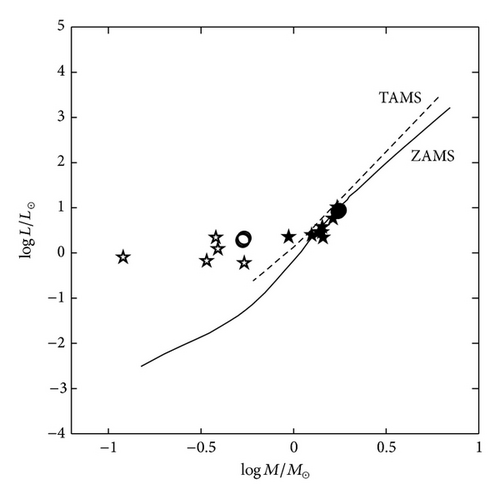
We used the physical parameters listed in Table 4 to investigate the current evolutionary status of DK Cyg. In Figures 5 and 6, we plotted the components of DK Cygon on the mass-luminosity (M-L) and mass-radius (M-R) relations along with the evolutionary tracks computed by Girardi et al. [51] for both zero age main sequence stars (ZAMS) and terminal age main sequence stars (TAMS) with metallicity z = 0.019. As it is clear from the figures, the primary component of the system is located nearly on the ZAMS for both the M-L and M-R relations. The secondary component is above the TAMS track for M-L and the M-R relations. For the sake of comparison, we plotted sample of A-type contact binaries listed in Table 5. The components of DK Cyg have the same behavior of the selected A-type systems.
| Parameter | Binnendijk [6] | Paparo et al. [10] | Awadalla [9] | Baran et al. [11] |
|---|---|---|---|---|
| M1⊙ | 1.7363 ± 0.0709 | 1.7358 ± 0.0709 | 1.7679 ± 0.0722 | 1.7438 ± 0.0712 |
| M2⊙ | 0.5313 ± 0.0217 | 0.5312 ± 0.0217 | 0.5410 ± 0.0221 | 0.5336 ± 0.0218 |
| R1⊙ | 1.7037 ± 0.0696 | 1.7029 ± 0.0695 | 1.7635 ± 0.0720 | 1.7178 ± 0.0701 |
| R2⊙ | 1.0129 ± 0.0414 | 1.0118 ± 0.0413 | 1.0811 ± 0.0441 | 1.0285 ± 0.0420 |
| T1⊙ | 1.2980 ± 0.0530 | 1.2980 ± 0.0530 | 1.2980 ± 0.0530 | 1.2980 ± 0.053 |
| T2⊙ | 1.1712 ± 0.0478 | 1.1641 ± 0.0475 | 1.1641 ± 0.0475 | 1.1698 ± 0.0478 |
| M1_bol | 2.4617 ± 0.1005 | 2.4627 ± 0.1005 | 2.3868 ± 0.0974 | 2.4438 ± 0.1000 |
| M2_bol | 4.0375 ± 0.1648 | 4.0662 ± 0.1660 | 3.9224 ± 0.1601 | 4.0094 ± 0.1637 |
| L1⊙ | 8.2285 ± 0.3359 | 8.2208 ± 0.3356 | 8.8163 ± 0.3600 | 8.3653 ± 0.3415 |
| L2⊙ | 1.9276 ± 0.0787 | 1.8772 ± 0.0766 | 2.1431 ± 0.0875 | 1.9780 ± 0.0808 |
- Note: subscripts 1 and 2 mean primary and secondary component, respectively.
| Star name | Parameters | References | |||||
|---|---|---|---|---|---|---|---|
| M1(M⊙) | M2(M⊙) | R1(R⊙) | R2(R⊙) | L1(L⊙) | L2(L⊙) | ||
| YY CrB | 1.404 | 0.339 | 1.427 | 0.757 | 2.58 | 6.68 | 1 |
| AW UMa | 1.6 | 0.121 | 1.786 | 0.739 | 7.47 | 0.804 | 2 |
| EQ Tau | 1.214 | 0.541 | 1.136 | 0.787 | 1.31 | 0.6 | 3 |
| RR Cen | 1.82 | 0.38 | 2.1 | 1.05 | 8.89 | 2.2 | 4 |
| V566 Oph | 1.41 | 0.34 | 1.45 | 0.77 | 4.46 | 1.23 | 5 |
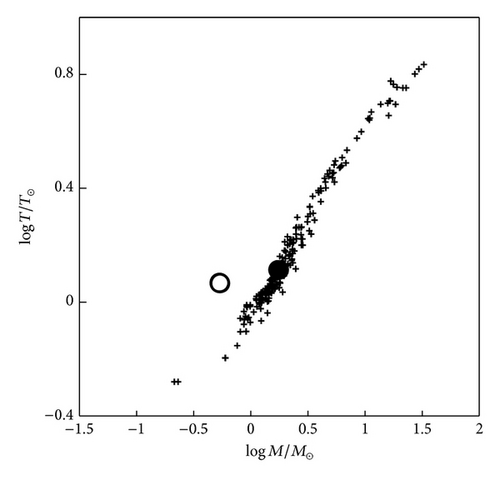
The mass-effective temperature relation (M-Teff) for intermediate and low mass stars [37] is displayed in Figure 7. The location of our mass and radius on the diagram revealed a good fit for the primary and poor fit for the secondary components. This gave the same behavior of the system on the mass-luminosity and mass-radius relations.
Conflict of Interests
The authors declare that they have no conflict of interests regarding the publication of this paper.
Acknowledgments
This research has made use of NASA’s ADS and the available on-line material of the IBVS. The authors sincerely thank Dr. Bob Nelson, who allowed them to use his windows interface code WDwint56a, for his helpful discussions and advice.




