Volume 2015, Issue 1 548905

Research Article

Open Access

Numerical Approximation of Nonlinear Klein-Gordon Equation Using an Element-Free Approach

Dong-mei Huang,

Dong-mei Huang

College of Information Technology, Shanghai Ocean University, Shanghai 201306, China shou.edu.cn

Search for more papers by this author

Guo-liang Zou,

Guo-liang Zou

College of Information Technology, Shanghai Ocean University, Shanghai 201306, China shou.edu.cn

Search for more papers by this author

L. W. Zhang,

Corresponding Author

L. W. Zhang

[email protected]

College of Information Technology, Shanghai Ocean University, Shanghai 201306, China shou.edu.cn

Search for more papers by this author

Dong-mei Huang,

Dong-mei Huang

College of Information Technology, Shanghai Ocean University, Shanghai 201306, China shou.edu.cn

Search for more papers by this author

Guo-liang Zou,

Guo-liang Zou

College of Information Technology, Shanghai Ocean University, Shanghai 201306, China shou.edu.cn

Search for more papers by this author

L. W. Zhang,

Corresponding Author

L. W. Zhang

[email protected]

College of Information Technology, Shanghai Ocean University, Shanghai 201306, China shou.edu.cn

Search for more papers by this author

First published: 11 October 2015

https://doi.org/10.1155/2015/548905

Citations: 6

Academic Editor: Kim M. Liew

Share a link

Email
Wechat
Bluesky

Abstract

Numerical approximation of nonlinear Klein-Gordon (KG) equation with quadratic and cubic nonlinearity is performed using the element-free improved moving least squares Ritz (IMLS-Ritz) method. A regular arrangement of nodes is employed in this study for the numerical integration to compute the system equation. A functional formulation for the KG equation is established and discretized by the Ritz minimization procedure. Newmark’s integration scheme combined with an iterative technique is applied to the resulting nonlinear system equations. The effectiveness and efficiency of the IMLS-Ritz method for the KG equation have been testified through convergence analyses and comparison study between the present results and the exact solutions.

1. Introduction

The Klein-Gordon (KG) equation is essentially a relativistic version of the Schrödinger equation. It has wide applications in many scientific fields, such as quantum mechanics, solid state physics, and nonlinear optics [1]. Similar to the Schrödinger equation, the KG equation is considered as one of the important equations in mathematical physics, as well as kinds of solitons studies, especially in the investigation of solitons interactions for a collisionless plasma and the recurrence of initial states [2, 3].

As a kind of essential nonlinear PDEs, the KG type equations have received considerable attention in deriving both analytical and numerical solutions by using different types of methods, such as the Adomian decomposition method [3, 4], the sine-cosine ansatz and the tanh methods [2, 5, 6], the auxiliary equation method, the Weierstrass elliptic function method, the elliptic equation rational expansion method, and the extended F-function method [7–9]. In the process, various numerical schemes have also been developed based on different theories, such as the homotopy method [10], the cubic B-spline collocation method on a uniform mesh [11], and the approximation with thin plate splines (TPS) radial basis functions (RBF) based collocation approach [12].

To seek for an effective and efficient numerical technique, the meshless method has been successfully developed to solve partial differential equations that used to describe many physical and engineering problems. The advantages of these meshless methods are as follows: (i) solutions can be obtained with only a minimum of meshing or no meshing at all [13–18]; (ii) a set of scattered nodes is used instead of meshing the entire domain of the problem. Several meshless methods have been proposed and can be chosen as an alternative to search for approximate solutions of the KG equations [19, 20]. Based on different approximation functions, various meshless methods were proposed, such as the element-free Galerkin (EFG) method [21], the moving least squares differential quadrature method [22], the radial point interpolation method [23], the smooth particle hydrodynamics methods [24], the radial basis function [25], the element-free kp-Ritz method [26–30], the meshless local Petrov-Galerkin method [31], the reproducing kernel particle method [32], and the local Krigging method [33].

In this study, by combining the IMLS approximation and the Ritz procedure, the element-free IMLS-Ritz method for numerical solution of the nonlinear KG equation is presented. The cubic spline weight function and linear basis are employed in this study. A regular arrangement of nodes is employed for numerical integration to compute the system equation. A functional formulation for the KG equation is established and discretized by the Ritz procedure. The essential boundary conditions are imposed by the penalty method. Newmark’s integration scheme is employed to solve the nonlinear system equations. The applicability of the IMLS-Ritz method is examined on a few selected example problems. The accuracy of the presented method is also investigated by comparing the obtained numerical results with the existing analytical solutions.

2. Theoretical Formulation

2.1. Equivalent Functional of the One-Dimensional Nonlinear KG Equation

We consider the following KG equation including the nonlinear term as

()

subject to the initial condition

()

and the boundary conditions

()

where Ω = [a, b] ⊂ R, u(x, t) denotes the wave displacement at position x and time t, u₀, g₁(t), and g₂(t) are known functions, and α, β, and γ are real numbers (γ ≠ 0). The function u is to be determined when functions f, g₁, and g₂ are given; k = 2 for the case of quadratic nonlinearity and k = 3 for a cubic nonlinearity.

An equivalent functional is defined in the weighted integral form based on (1) with the initial condition in the following form:

()

Using integration by parts and the divergence theorem, (4) yields the following expression:

()

where the weight w is set to be u in this numerical study.

2.2. Improved Moving Least Squares Shape Functions

The IMLS approximation was proposed for construction of the shape functions in the element-free method. In one-dimensional IMLS approximation, for all f(x), g(x) ∈ span(p), we define

()

where (f, g) is an inner product and span(p) is the Hilbert space.

In span(p), for the set of points {x_i} and weight functions {w_i}, if functions p₁(x), p₂(x), …, p_m(x) satisfy the conditions

()

we furnish the function set p₁(x), p₂(x), …, p_m(x) as a weighted orthogonal function set with a weight function {w_i} about points {x_i}. If p₁(x), p₂(x), …, p_m(x) are polynomials, the function set p₁(x), p₂(x), …, p_m(x) is called a weighted orthogonal polynomials set with a weight function {w_i} about points {x_i}.

Consider an equation system from MLS approximation:

()

where A is the moment matrix. Then, (8) can be expressed as

()

If the basis function set p_i(x) ∈ span(p), i = 1,2, …, m, is a weighted orthogonal function set about points {x_i}, that is, if

()

then (8) becomes

()

Subsequently, coefficients a_i(x) can be determined accordingly:

()

that is,

()

where

()

From (8) and (12), the expression of approximation function u^h(x) is

()

where

is the shape function and

()

The abovementioned formulation details an IMLS approximation in which coefficients a_i(x) are obtained directly. It is, therefore, avoiding forming an ill-conditioned or singular equation system.

From (16), we have

()

which represents the shape function of the IMLS approximation corresponding to node I. From (17), the partial derivatives of

lead to

()

The weighted orthogonal basis function set p = (p_i) is formed by using the Schmidt method as

()

Moreover, using the Schmidt method, the weighted orthogonal basis function set p = (p_i) can be formed from the monomial basis function. For example, for the monomial basis function

()

the weighted orthogonal basis function set can be generated by

()

When the weighted orthogonal basis functions in (20) and (21) are used, there exist fewer coefficients in the trial function.

3. The Ritz Minimization Procedure and Discretion Implementation

In the present work, the penalty method is used to modify the constructed functional in implementing the specified Dirichlet boundary conditions for a domain Ω bounded by Γ. We use a penalty parameter λ to penalize the difference between the displacement of the IMLS approximation and the prescribed displacement on the essential boundary. The penalty function can be expressed as

()

where λ is the penalty parameter and

is the specified function on the Dirichlet boundary Γ₁. Normally, λ is chosen as 10³ ~ 10⁷ which is case dependent.

The resulting functional enforcing the Dirichlet boundary conditions for the KG equation is

()

Substituting (5) and (22) into the functional of (23), we have the modified functional

()

The approximation of the field function can be obtained from (15) as follows:

()

where

()

Substituting (25) into (24) and applying the Ritz minimization procedure to the maximum energy function Π^∗

()

that yields the following matrix form:

()

where

()

To solve the above nonlinear system, time discretization of (28) is forming with Newmark’s integration scheme. According to the fundamental assumptions of Newmark’s integration

()

we have

()

where δ ≥ 0.5 and α ≥ 0.25(0.5 + δ) ² are redefined as parameters here to influence the accuracy and stability of the integration.

The dynamic form of (28) at t + Δt can be written as

()

Substituting (31) into (32), we have the full discretized equation

()

By solving the above iteration equations, we can obtain numerical solutions to the one-dimensional nonlinear Klein-Gordon equation.

4. Numerical Results and Discussion

Three selected examples are included with their numerical solutions obtained by the presented method for the nonlinear KG equation. The problems are solved using regular node arrangements. The convergence study is carried out for the results of the KG equation. The accuracy and efficiency of the IMLS-Ritz method are compared with available analytical solutions by evaluating the L₂-norm and L_∞ errors defined as

()

where u_exact and u_numerical present the exact solution and numerical approximation, respectively.

4.1. Example 1

Consider the KG equation (1) with quadratic nonlinearity (k = 2), by taking the parameters α = −1, β = 0, γ = 1, and f(x, t) = −xcost + x²cos²t.

The exact solution of the equation is given as [1]

()

The corresponding initial conditions and Dirichlet boundary function can be extracted from the analytical solution directly as

()

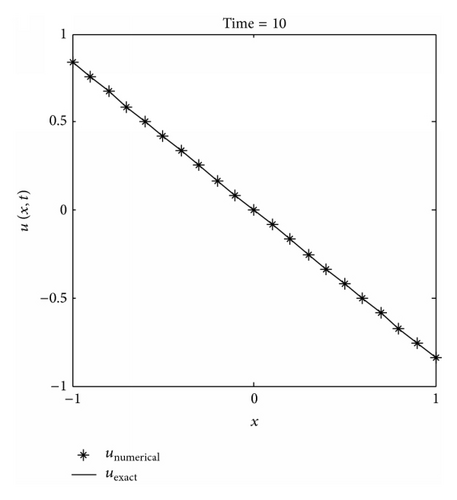
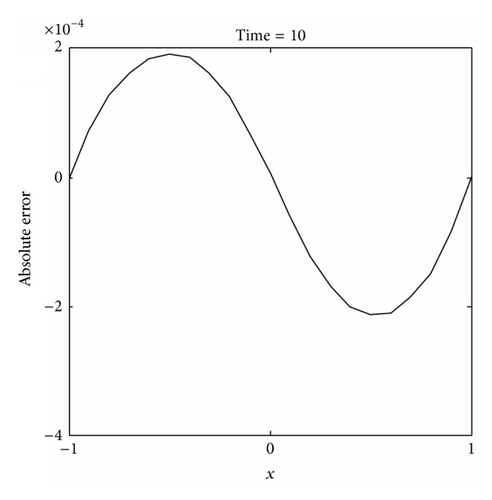
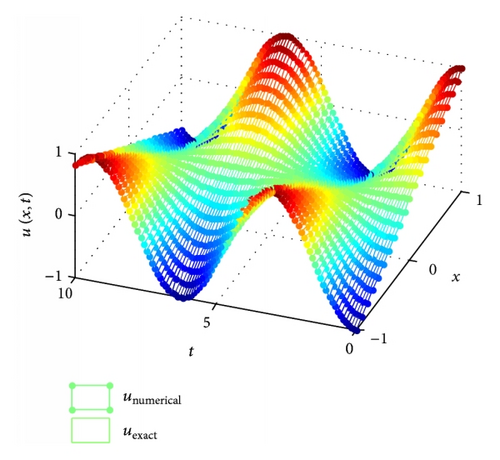
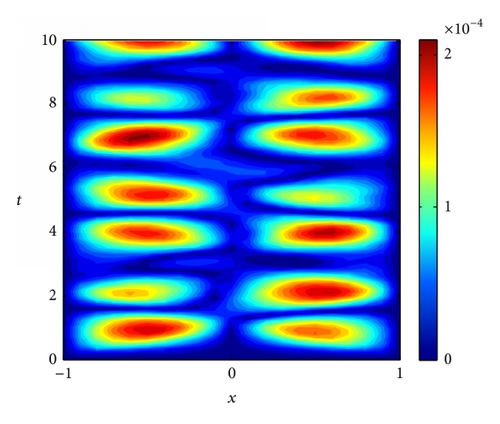
In the present example, the numerical solutions are obtained as the penalty factor α = 10³ and d_max = 3. We examine the convergence of the element-free IMLS-Ritz method by varying the number of nodes (N) from 11 to 201. The L₂-norm and L_∞ errors of u(x, t) with CPU times are computed at t = 10 with Δt = 0.1 and tabulated in Table 1. We found that both L₂-norm and L_∞ errors arise as N increases. This may be due to that once convergent result has been obtained, in this case on N = 11, the additional arranged nodes will cause errors being accumulated. Based on this observation, the following analysis will be performed using N = 11 for accuracy consideration. We also investigated the influence of d_max on the accuracy of the IMLS-Ritz method. As illustrated in Table 2, by varying d_max from 2 to 3, accurate results can be furnished when d_max = 2. Furthermore, the predicted results are compared with the available exact solutions at t = 10 and illustrated in Figure 1. It is apparent that a close agreement is obtained from the illustrated results. The computed results of u(x, t) for a time history are also predicted between t = 0 s and t = 10 s (Δt = 0.1) (see Figure 2(a)). The corresponding absolute error contour is plotted in Figure 2(b). From the presented results, we can conclude that the approximate solutions generated by the IMLS-Ritz method agree well with the analytical results.

Table 1. Values of L₂-norm errors and L_∞-norm errors and CPU time as functions of the number of nodes (N) for the solutions of Example 1 (t = 10, Δt = 0.1, and d_max⁡ = 3).

N	L₂-norm error	L_∞ error	CPU time (s)
11	4.7172 × 10⁻⁴	2.0891 × 10⁻⁴	1.5224
21	6.6446 × 10⁻⁴	2.1335 × 10⁻⁴	1.7486
51	1.0503 × 10⁻³	2.1488 × 10⁻⁴	5.2065
101	1.5343 × 10⁻³	2.1500 × 10⁻⁴	10.3477
201	2.1912 × 10⁻³	2.1504 × 10⁻⁴	19.8889
251	2.3485 × 10⁻³	2.1505 × 10⁻⁴	25.6620

Table 2. Values of L₂-norm errors and L_∞-norm errors and CPU time as functions of the d_max⁡ for the solution of Example 1 (N = 11, t = 10, and Δt = 0.1).

d_max⁡	L₂-norm error	L_∞ error	CPU time (s)
2	6.7304 × 10⁻⁴	2.1170 × 10⁻⁴	1.7510
2.2	6.9125 × 10⁻⁴	2.1913 × 10⁻⁴	1.7888
2.4	7.1843 × 10⁻⁴	2.2411 × 10⁻⁴	1.8604
2.6	6.5686 × 10⁻⁴	2.2234 × 10⁻⁴	1.7744
2.8	6.4655 × 10⁻⁴	2.1186 × 10⁻⁴	1.7812
3	6.6445 × 10⁻⁴	2.1335 × 10⁻⁴	1.7949

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

IMLS-Ritz and exact solutions of u(x, t) at N = 21, Δt = 0.1 (Example 1). (a) Solutions of u(x, t); (b) absolute error.

4.2. Example 2

In the present numerical example, we consider KG in (1) with a quadratic nonlinearity (k = 2), by taking the parameters α = −1, β = 0, γ = 1, and f(x, t) = 6xt(x² − t²) + x⁶t⁶. The initial conditions are described by

()

The exact solution of the equation is given as [1]

()

The corresponding Dirichlet boundary function can be extracted from the analytical solution directly as

()

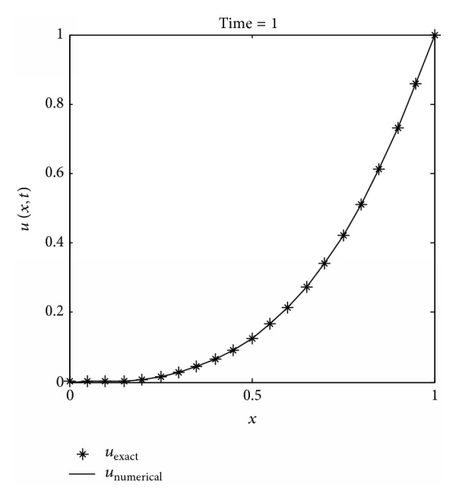
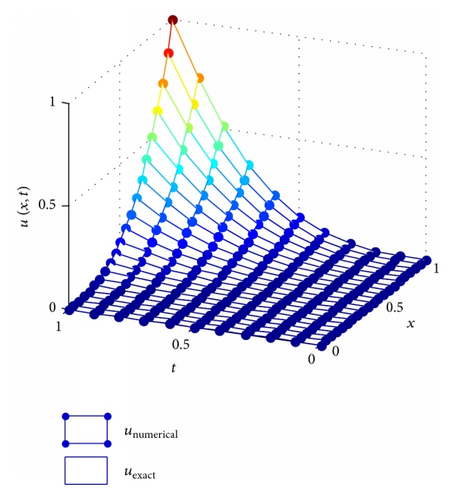
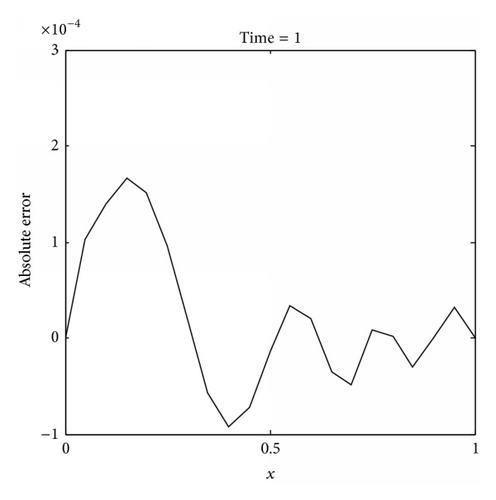
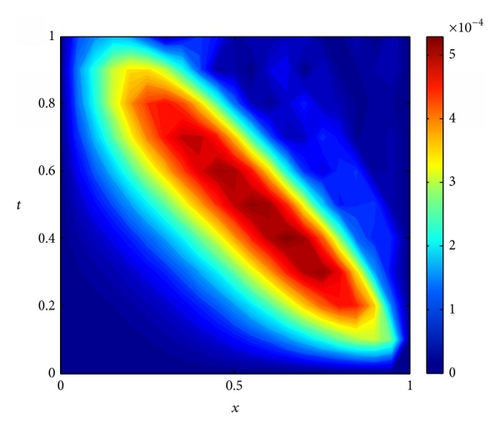
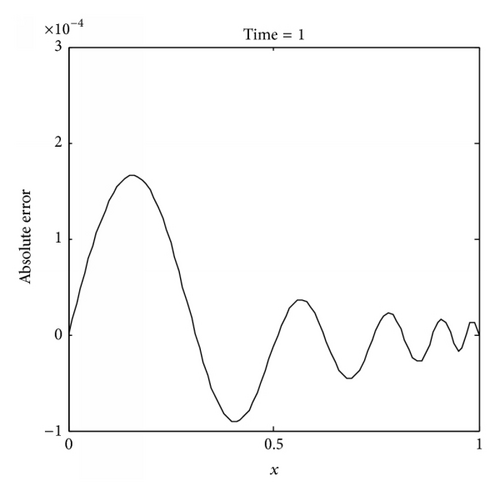
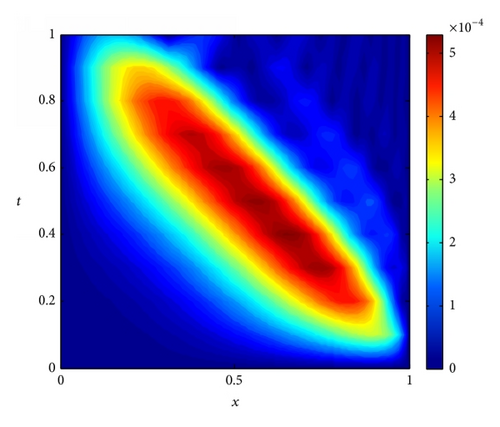
In this analysis, numerical solutions are predicted and compared with the analytical solutions at t = 1, Δt = 0.01, d_max = 2.2, and the penalty factor λ = 10³. Table 3 presents the convergence patterns of the IMLS-Ritz results by varying N from 6 to 101. A similar convergence trend is observed in Example 1; that is, convergent results can be obtained from N = 6 to 21; then, the errors are accumulated as N increases. Table 4 illustrates the values of L₂-norm and L_∞ errors as d_max varying from 2 to 3.5. A growing trend of L₂-norm and L_∞ errors is observed from Table 4, and the CPU time rises oscillatory as d_max increases. As presented in Figure 3, the comparison study shows that the IMLS-Ritz method provides very similar solutions to the exact results. In Figure 4, the absolute errors of u(x, t) at a selected time point (t = 1) and the absolute error contour on a time period (0 ≤ t ≤ 1) are exhibited at N = 21. Figure 5 is plotted at N = 101 for comparison with Figure 4. Although the increase in number of nodes has been identified to be unaided in enhancing the accuracy of the approximation, it influences the smoothness of the solutions indeed.

Table 3. Values of L₂-norm errors and L_∞-norm errors and CPU time as functions of the number of nodes (N) for the solutions of Example 2 (t = 1, Δt = 0.1, and d_max⁡ = 2.2).

N	L₂-norm error	L_∞ error	CPU time (s)
6	2.1937 × 10⁻²	1.7231 × 10⁻²	0.1081
21	3.3745 × 10⁻⁴	2.0891 × 10⁻⁴	0.2683
26	3.7023 × 10⁻⁴	1.6600 × 10⁻⁴	0.3275
51	5.1750 × 10⁻⁴	1.6589 × 10⁻⁴	0.6268
101	7.2991 × 10⁻⁴	1.6588 × 10⁻⁴	1.1983

Table 4. Values of L₂-norm errors and L_∞-norm errors and CPU time as functions of the d_max⁡ for the solution of Example 2 (N = 11, t = 1, and Δt = 0.1).

d_max⁡	L₂-norm error	L_∞ error	CPU time (s)
2	3.3081 × 10⁻⁴	2.1170 × 10⁻⁴	0.2637
2.2	3.3746 × 10⁻⁴	1.6616 × 10⁻⁴	0.2644
2.4	3.4597 × 10⁻⁴	1.6866 × 10⁻⁴	0.2754
2.6	3.7193 × 10⁻⁴	1.7459 × 10⁻⁴	0.2690
2.8	3.8596 × 10⁻⁴	1.8276 × 10⁻⁴	0.2686
3	3.8960 × 10⁻⁴	1.9179 × 10⁻⁴	0.2650
3.2	4.2300 × 10⁻⁴	1.999 × 10⁻⁴	0.2644
3.5	4.9035 × 10⁻⁴	2.3717 × 10⁻⁴	0.2819

4.3. Example 3

Consider the nonlinear Klein-Gordon equation (1) with a cubic nonlinearity (k = 3), by taking parameters as α = −2.5, β = 1, γ = 1.5, and f(x, t) = 0. The initial conditions are given by

()

where

and

and c = 0.05.

The exact solution of the equation is given as [4]

()

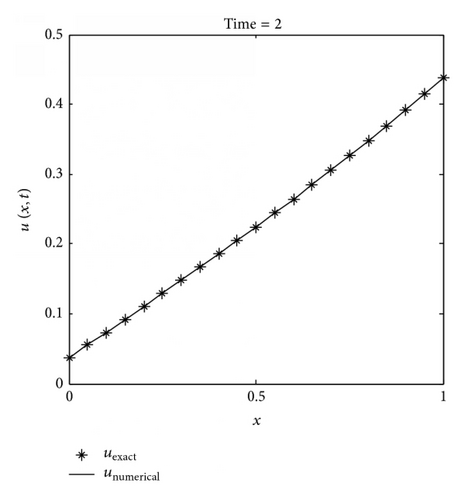
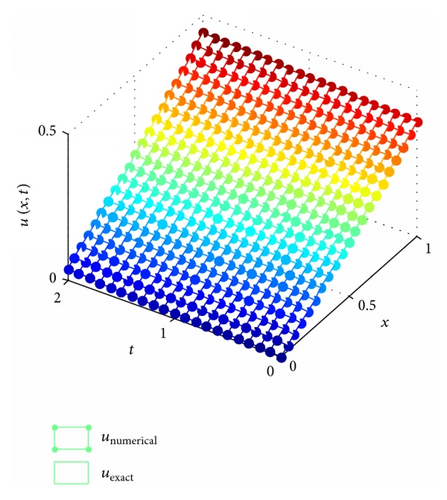
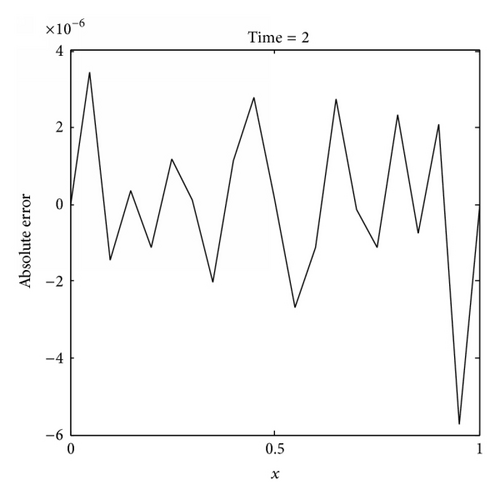
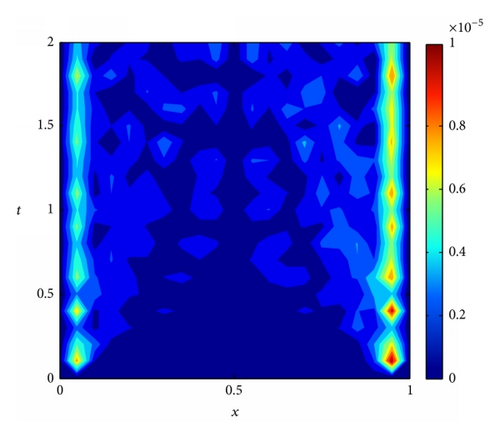
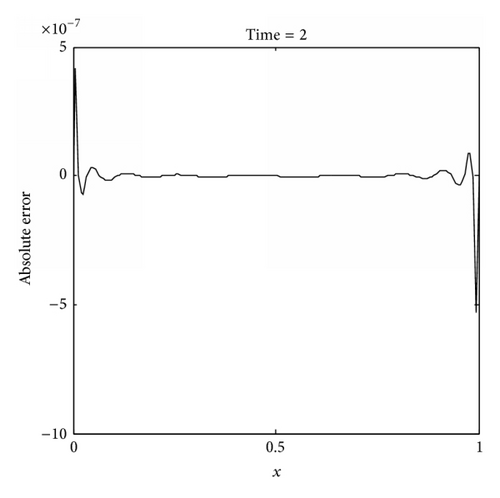
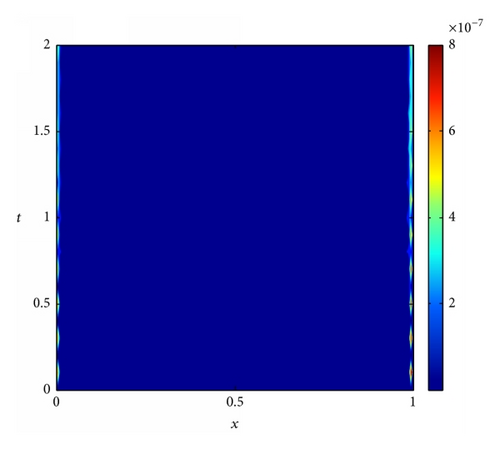
The IMLS-Ritz computation is carried out by setting Δt = 0.1, the penalty factor λ = 10³, and d_max = 2.5. The L₂-norm and L_∞ errors of u are computed with the number of nodes varied from 13 to 201. The results are tabulated in Table 5. It is apparent that both L₂-norm and L_∞ errors decrease as N increases, indicating that convergent results are obtained by the IMLS-Ritz method. From Table 6, the results of numerical analysis suggested that satisfied accuracy can be achieved when d_max = 2. In Figure 6, the numerical and analytical solutions are plotted on a time point (t = 2) and a time period (0 ≤ t ≤ 2). From the comparison results, we can conclude that the IMLS-Ritz method provides very similar solutions to the exact results. In Figures 7 and 8, the absolute errors of u(x, t) at a selected time point (t = 2) and the absolute error contour on a time period (0 ≤ t ≤ 1) are depicted at N = 21 and N = 201, respectively. As expected, more accurate results can be obtained as N increases in this example. From the results presented in both tables and figures, it is evident that the IMLS-Ritz values almost coincide with the exact solutions.

Table 5. Values of L₂-norm errors and L_∞-norm errors and CPU time as functions of the number of nodes (N) for the solutions of Example 3 (t = 2, Δt = 0.1, and d_max⁡ = 2.5).

N	L₂-norm error	L_∞ error	CPU time (s)
13	1.9791 × 10⁻⁵	1.3049 × 10⁻⁵	447.3713
21	9.5355 × 10⁻⁶	5.7505 × 10⁻⁶	559.7717
51	2.8692 × 10⁻⁶	1.7171 × 10⁻⁶	600.6953
101	1.8512 × 10⁻⁶	1.3635 × 10⁻⁶	650.4551
126	1.4819 × 10⁻⁶	1.0907 × 10⁻⁶	687.4458
201	7.8596 × 10⁻⁷	5.3053 × 10⁻⁷	721.8184

Table 6. Values of L₂-norm errors and L_∞-norm errors and CPU time as functions of the d_max⁡ for the solution of Example 3 (N = 11, t = 10, and Δt = 0.1).

d_max⁡	L₂-norm error	L_∞ error	CPU time (s)
2	5.5466 × 10⁻⁶	3.4260 × 10⁻⁶	793.1491
2.2	1.8244 × 10⁻⁵	1.0416 × 10⁻⁵	826.7344
2.4	3.2447 × 10⁻⁵	1.8490 × 10⁻⁵	891.1543
2.6	4.5397 × 10⁻⁵	2.5715 × 10⁻⁵	945.6493
2.8	4.4504 × 10⁻⁵	2.6234 × 10⁻⁵	975.9027
3	2.7963 × 10⁻⁵	1.6959 × 10⁻⁵	1027.5762
3.2	3.2756 × 10⁻⁵	1.6014 × 10⁻⁵	1070.3232

5. Conclusion

In this paper, an element-free IMLS-Ritz method and its numerical implementation on three examples of nonlinear KG equation have been presented. The effectiveness and efficiency of the IMLS-Ritz method for KG equation have been testified through convergence and comparison studies. From the numerical results, it is concluded that the agreement of the IMLS-Ritz solutions with the exact results is excellent. Due to difficulties of constructing analytical solutions for many nonlinear PDEs, the element-free IMLS-Ritz method will have great advantages for solving them through simple implementation with high accuracy.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

The work described in this paper was partly supported by the National Natural Science Foundation of China (Grant no. 61272098 and Grant no. 11402142), Open Research Fund Program for State Key Laboratory of Estuarine and Coastal Research (SKLEC201207), and Open Research Fund Program for Shandong Province Key Laboratory of Marine Ecology Environment and Disaster Prevention (2012011).

References

1 Wazwaz A.-M., The modified decomposition method for analytic treatment of differential equations, Applied Mathematics and Computation. (2006) 173, no. 1, 165–176, https://doi.org/10.1016/j.amc.2005.02.048, MR2203379, 2-s2.0-32144452761.
10.1016/j.amc.2005.02.048
Web of Science® Google Scholar
2 Wazwaz A.-M., Compactons, solitons and periodic solutions for some forms of nonlinear Klein-Gordon equations, Chaos, Solitons & Fractals. (2006) 28, no. 4, 1005–1013, 2-s2.0-27744509855, MR2212787, https://doi.org/10.1016/j.chaos.2005.08.145.
10.1016/j.chaos.2005.08.145
Web of Science® Google Scholar
3 El-Sayed S. M., The decomposition method for studying the Klein-Gordon equation, Chaos, Solitons and Fractals. (2003) 18, no. 5, 1025–1030, https://doi.org/10.1016/S0960-0779(02)00647-1, MR1988710, 2-s2.0-0038577058.
10.1016/S0960-0779(02)00647-1
Web of Science® Google Scholar
4 Kaya D. and El-Sayed S. M., A numerical solution of the Klein-Gordon equation and convergence of the decomposition method, Applied Mathematics and Computation. (2004) 156, no. 2, 341–353, 2-s2.0-3943090453, https://doi.org/10.1016/j.amc.2003.07.014, MR2087512.
10.1016/j.amc.2003.07.014
Web of Science® Google Scholar
5 Wazwaz A.-M., New travelling wave solutions to the Boussinesq and the Klein-Gordon equations, Communications in Nonlinear Science and Numerical Simulation. (2008) 13, no. 5, 889–901, MR2372135, https://doi.org/10.1016/j.cnsns.2006.08.005, 2-s2.0-36248992919.
10.1016/j.cnsns.2006.08.005
Web of Science® Google Scholar
6 Wazwaz A.-M., The tanh and the sine-cosine methods for compact and noncompact solutions of the nonlinear Klein-Gordon equation, Applied Mathematics and Computation. (2005) 167, no. 2, 1179–1195, https://doi.org/10.1016/j.amc.2004.08.006, MR2169760, 2-s2.0-25144449613.
10.1016/j.amc.2004.08.006
Web of Science® Google Scholar
7 Sirendaoreji, A new auxiliary equation and exact travelling wave solutions of nonlinear equations, Physics Letters A: General, Atomic and Solid State Physics. (2006) 356, no. 2, 124–130, https://doi.org/10.1016/j.physleta.2006.03.034, 2-s2.0-33745235497.
10.1016/j.physleta.2006.03.034
CAS Google Scholar
8 Sirendaoreji A., Auxiliary equation method and new solutions of Klein-Gordon equations, Chaos, Solitons & Fractals. (2007) 31, no. 4, 943–950, https://doi.org/10.1016/j.chaos.2005.10.048, MR2262187, 2-s2.0-33747332288.
10.1016/j.chaos.2005.10.048
Web of Science® Google Scholar
9 Sirendaoreji, Exact travelling wave solutions for four forms of nonlinear Klein-Gordon equations, Physics Letters: A. (2007) 363, no. 5-6, 440–447, MR2287822, https://doi.org/10.1016/j.physleta.2006.11.049, 2-s2.0-33847035933.
10.1016/j.physleta.2006.11.049
CAS Web of Science® Google Scholar
10 Kumar D., Singh J., and Kumar S., Numerical computation of Klein-Gordon equations arising in quantum field theory by using homotopy analysis transform method, Alexandria Engineering Journal. (2014) 53, no. 2, 469–474, https://doi.org/10.1016/j.aej.2014.02.001, 2-s2.0-84901303175.
10.1016/j.aej.2014.02.001
Google Scholar
11 Rashidinia J., Ghasemi M., and Jalilian R., Numerical solution of the nonlinear Klein-Gordon equation, Journal of Computational and Applied Mathematics. (2010) 233, no. 8, 1866–1878, https://doi.org/10.1016/j.cam.2009.09.023, MR2564022, 2-s2.0-70549087999.
10.1016/j.cam.2009.09.023
Web of Science® Google Scholar
12 Dehghan M. and Shokri A., Numerical solution of the nonlinear Klein-Gordon equation using radial basis functions, Journal of Computational and Applied Mathematics. (2009) 230, no. 2, 400–410, https://doi.org/10.1016/j.cam.2008.12.011, MR2532333, 2-s2.0-67349194320.
10.1016/j.cam.2008.12.011
Web of Science® Google Scholar
13 Liew K. M., Ng T. Y., Zhao X., and Reddy J. N., Harmonic reproducing kernel particle method for free vibration analysis of rotating cylindrical shells, Computer Methods in Applied Mechanics and Engineering. (2002) 191, no. 37-38, 4141–4157, 2-s2.0-0037119508, https://doi.org/10.1016/S0045-7825(02)00358-4.
10.1016/S0045-7825(02)00358-4
Web of Science® Google Scholar
14 Liew K. M., Chen X. L., and Reddy J. N., Mesh-free radial basis function method for buckling analysis of non-uniformly loaded arbitrarily shaped shear deformable plates, Computer Methods in Applied Mechanics and Engineering. (2004) 193, no. 3–5, 205–224, https://doi.org/10.1016/j.cma.2003.10.002, 2-s2.0-0347300455.
10.1016/j.cma.2003.10.002
Web of Science® Google Scholar
15 Liew K. M., Cheng Y., and Kitipornchai S., Boundary element-free method (BEFM) and its application to two-dimensional elasticity problems, International Journal for Numerical Methods in Engineering. (2006) 65, no. 8, 1310–1332, https://doi.org/10.1002/nme.1489, 2-s2.0-32444439975.
10.1002/nme.1489
Web of Science® Google Scholar
16 Sun F. X., Liu C., and Cheng Y. M., An improved interpolating element-free Galerkin method based on nonsingular weight functions, Mathematical Problems in Engineering. (2014) 2014, 13, 323945, https://doi.org/10.1155/2014/323945, MR3179005, 2-s2.0-84896996038.
10.1155/2014/323945
Web of Science® Google Scholar
17 Zhao N. and Ren H., The interpolating element-free Galerkin method for 2D transient heat conduction problems, Mathematical Problems in Engineering. (2014) 2014, 9, 712834, https://doi.org/10.1155/2014/712834, MR3176877, 2-s2.0-84896923026.
10.1155/2014/712834
Web of Science® Google Scholar
18 Wei Q. and Cheng R., The improved moving least-square Ritz method for the one-dimensional sine-Gordon equation, Mathematical Problems in Engineering. (2014) 2014, 10, 383219, 2-s2.0-84896950197, MR3176856, https://doi.org/10.1155/2014/383219.
10.1155/2014/383219
Web of Science® Google Scholar
19 Shao W. and Wu X., The numerical solution of the nonlinear Klein-GORdon and sine-GORdon equations using the Chebyshev tau meshless method, Computer Physics Communications. (2014) 185, no. 5, 1399–1409, MR3176174, https://doi.org/10.1016/j.cpc.2014.02.002, 2-s2.0-84900237421.
10.1016/j.cpc.2014.02.002
CAS Web of Science® Google Scholar
20 Hussain A., Haq S., and Uddin M., Numerical solution of Klein-GORdon and sine-GORdon equations by meshless method of lines, Engineering Analysis with Boundary Elements. (2013) 37, no. 11, 1351–1366, 2-s2.0-84882245957, MR3110528, https://doi.org/10.1016/j.enganabound.2013.07.001.
10.1016/j.enganabound.2013.07.001
Web of Science® Google Scholar
21 Belytschko T., Lu Y. Y., and Gu L., Element-free Galerkin methods, International Journal for Numerical Methods in Engineering. (1994) 37, no. 2, 229–256, https://doi.org/10.1002/nme.1620370205, MR1256818, 2-s2.0-0028259955.
10.1002/nme.1620370205
Web of Science® Google Scholar
22 Liew K. M., Huang Y. Q., and Reddy J. N., Moving least squares differential quadrature method and its application to the analysis of shear deformable plates, International Journal for Numerical Methods in Engineering. (2003) 56, no. 15, 2331–2351, https://doi.org/10.1002/nme.646, 2-s2.0-0013116104.
10.1002/nme.646
Web of Science® Google Scholar
23 Liew K. M. and Chen X. L., Buckling of rectangular Mindlin plates subjected to partial in-plane edge loads using the radial point interpolation method, International Journal of Solids and Structures. (2004) 41, no. 5-6, 1677–1695, 2-s2.0-0742270392, https://doi.org/10.1016/j.ijsolstr.2003.10.022.
10.1016/j.ijsolstr.2003.10.022
Web of Science® Google Scholar
24 Monaghan J. J., An introduction to SPH, Computer Physics Communications. (1988) 48, no. 1, 89–96, https://doi.org/10.1016/0010-4655(88)90026-4, 2-s2.0-0023165466.
10.1016/0010-4655(88)90026-4
CAS Web of Science® Google Scholar
25 Chen W., New RBF collocation methods and kernel RBF with applications, Meshfree Methods for Partial Differential Equations, 2000, 1, Springer, 75–86.
Google Scholar
26 Liew K. M., Zhao X., and Ng T. Y., The element-free kp-Ritz method for vibration of laminated rotating cylindrical panels, International Journal of Structural Stability and Dynamics. (2002) 2, 523–558.
10.1142/S0219455402000701
Google Scholar
27 Zhao X. and Liew K. M., Geometrically nonlinear analysis of functionally graded plates using the element-free kp-Ritz method, Computer Methods in Applied Mechanics and Engineering. (2009) 198, no. 33–36, 2796–2811, https://doi.org/10.1016/j.cma.2009.04.005, 2-s2.0-65849226845.
10.1016/j.cma.2009.04.005
Web of Science® Google Scholar
28 Zhang L. W., Lei Z. X., Liew K. M., and Yu J. L., Static and dynamic of carbon nanotube reinforced functionally graded cylindrical panels, Composite Structures. (2014) 111, no. 1, 205–212, https://doi.org/10.1016/j.compstruct.2013.12.035, 2-s2.0-84896035313.
10.1016/j.compstruct.2013.12.035
Web of Science® Google Scholar
29 Zhang L. W., Deng Y. J., and Liew K. M., An improved element-free Galerkin method for numerical modeling of the biological population problems, Engineering Analysis with Boundary Elements. (2014) 40, 181–188, https://doi.org/10.1016/j.enganabound.2013.12.008, MR3161279, 2-s2.0-84892962543.
10.1016/j.enganabound.2013.12.008
Web of Science® Google Scholar
30 Zhang L. W., Lei Z. X., Liew K. M., and Yu J. L., Large deflection geometrically nonlinear analysis of carbon nanotube-reinforced functionally graded cylindrical panels, Computer Methods in Applied Mechanics and Engineering. (2014) 273, 1–18, https://doi.org/10.1016/j.cma.2014.01.024, 2-s2.0-84894233262.
10.1016/j.cma.2014.01.024
Web of Science® Google Scholar
31 Atluri S. N. and Zhu T., A new meshless local Petrov-Galerkin (MLPG) approach in computational mechanics, Computational Mechanics. (1998) 22, no. 2, 117–127, MR1649420, https://doi.org/10.1007/s004660050346.
10.1007/s004660050346
Web of Science® Google Scholar
32 Liu W. K., Jun S., and Zhang Y. F., Reproducing kernel particle methods, International Journal for Numerical Methods in Fluids. (1995) 20, no. 8-9, 1081–1106, https://doi.org/10.1002/fld.1650200824, MR1333917, 2-s2.0-0029102512.
10.1002/fld.1650200824
Web of Science® Google Scholar
33 Zhang L. W., Zhu P., and Liew K. M., Thermal buckling of functionally graded plates using a local Kriging meshless method, Composite Structures. (2014) 108, no. 1, 472–492, 2-s2.0-84896054111, https://doi.org/10.1016/j.compstruct.2013.09.043.
10.1016/j.compstruct.2013.09.043
Web of Science® Google Scholar

Citing Literature

All articles

Numerical Approximation of Nonlinear Klein-Gordon Equation Using an Element-Free Approach

Abstract

1. Introduction

2. Theoretical Formulation

2.1. Equivalent Functional of the One-Dimensional Nonlinear KG Equation

2.2. Improved Moving Least Squares Shape Functions

3. The Ritz Minimization Procedure and Discretion Implementation