Volume 2015, Issue 1 428525

Research Article

Open Access

An Empirical Method of Estimating Soil Thermal Inertia

Corresponding Author

Jing Tian

[email protected]

orcid.org/0000-0002-7442-352X

Key Laboratory of Water Cycle and Related Land Surface Processes, Institute of Geographical Sciences and Natural Resources Research (IGSNRR), Chinese Academy of Sciences (CAS), A11 Datun Road, Beijing 100101, China cas.cn

Search for more papers by this author

Hongbo Su,

Hongbo Su

Search for more papers by this author

Honglin He,

Honglin He

Synthesis Center of Chinese Ecosystem Research Network, IGSNRR, CAS, A11 Datun Road, Beijing 100101, China cas.cn

Search for more papers by this author

Xiaomin Sun,

Xiaomin Sun

Synthesis Center of Chinese Ecosystem Research Network, IGSNRR, CAS, A11 Datun Road, Beijing 100101, China cas.cn

Search for more papers by this author

Jing Tian,

Corresponding Author

Jing Tian

[email protected]

orcid.org/0000-0002-7442-352X

Search for more papers by this author

Hongbo Su,

Hongbo Su

Search for more papers by this author

Honglin He,

Honglin He

Synthesis Center of Chinese Ecosystem Research Network, IGSNRR, CAS, A11 Datun Road, Beijing 100101, China cas.cn

Search for more papers by this author

Xiaomin Sun,

Xiaomin Sun

Synthesis Center of Chinese Ecosystem Research Network, IGSNRR, CAS, A11 Datun Road, Beijing 100101, China cas.cn

Search for more papers by this author

First published: 27 July 2015

https://doi.org/10.1155/2015/428525

Citations: 4

Academic Editor: Filomena Romano

Share a link

Email
Wechat
Bluesky

Abstract

A method of estimating soil thermal inertia (STI), which uses midday soil heat flux (G_m) and diurnal surface temperature amplitude as the inputs, is presented in the paper. G_m is achieved from an empirical relationship between net radiation (Rn) and soil heat flux (G). To validate the STI method, a method proposed by Verhoef, which requires STI and a Fourier series analysis on surface temperature, is used to estimate diurnal G. By comparing diurnal G estimates and diurnal G measurements, the STI method is evaluated indirectly. The results show that the diurnal curve of G estimates can coincide with that of G measurements for bare soil, with the correlation coefficient (R²) of 0.64, bias of 10.1 W·m⁻², and root mean squared errors (RMSE) of 40.9 W·m⁻². For the vegetated surface, R² is 0.56, bias is −11.9 W·m⁻², and RMSE is 49.2 W·m⁻². The large uncertainty in the estimation of G_m resulting from the wider variation of the empirical relationship between Rn and G and the difference between mixed surface temperature and soil surface temperature may be the two primary factors for the larger deviation of the diurnal shape and the magnitude between G estimates and G measurements for the vegetated surface.

1. Introduction

Soil thermal inertia (STI, J m⁻² K⁻¹ s^−1/2) formulated as (1) is an important surface property and is a function of specific heat capacity (c, J kg⁻¹ K⁻¹), soil bulk density (ρ, kg m⁻³), and thermal conductivity (k, W m⁻¹ K⁻¹), defined in

()

It determines the resistance of a material or surface to surface temperature variations and is used to determine surface characteristics since the 1970s, such as geological interpretation, soil moisture, and soil heat flux (G) [1–4].

It is difficult to achieve spatial distributions of STI based on (1) because it is almost impossible to estimate c, ρ, and k at a regional scale. At present, the achievement of the spatial distributions of STI is mainly dependent on remote sensing methods. The method proposed by Price [5], shown in (2), is a milestone in the estimation of STI with remote sensing method. The primary contribution of this method is that it builds the connection between STI and the remotely sensed parameters of surface albedo (a, %) and day-night surface temperature difference (T_day − T_night, K), which makes the retrieval of STI possible at a regional scale:

()

where S is the solar constant (J m⁻² s⁻¹), V (%) is the atmospheric transmittance in the visible spectrum, C₁ is the first item of the Fourier series analysis on surface temperature (T), ω is (rad s⁻¹) the frequency of diurnal variation, and φ₁ (rad) is solar declination. In this method, solar radiation absorbed by the Earth’s surface is taken as the driving force of the variation of T.

Following this method, thermal inertia has been approximated by land surface temperature differences as acquired by infrared thermometers for several decades [6]. The most widely used method is the apparent thermal inertia (ATI, K⁻¹) named by Short and Stuart [7]. ATI method is a simplification of (2) and requires only surface albedo and diurnal surface temperature amplitude (ΔT, K):

()

where C is the solar correction factor that can be calculated from latitude and solar declination. Similar to (2), the ATI method also takes solar radiation absorbed by the Earth’s surface as the driving force of the variation of T. However, ATI has been found to be of very limited use in areas with strong evapotranspiration [8] as evapotranspiration can reduce surface temperature through evaporative cooling. Additionally, there is large uncertainty when ATI is applied to vegetated surfaces because the canopy obscures the soil surface and the remote determination of soil temperature for soils under vegetation is still problematic [9]. As a result, there are still some constraints in the applications of ATI.

To reduce the effects of evapotranspiration and sensible heat flux (H) on surface temperature, Brunt [10] indicates that it is better to use surface temperature difference between sunset and sunrise (ΔT_n) than to use diurnal surface temperature when estimating STI because evapotranspiration and H are close to zero at night and have few effects on surface temperature. Equation (4) gives the function, which uses ΔT_n and the average net radiation (

, J m⁻² s⁻¹) between sunset and sunrise to estimate real thermal inertia. It is only suitable for bare soil because of the difficulty in acquiring

and ΔT_n (K) for soils under vegetation. Consider

()

where Δt_n (s) is the time between sunset and sunrise and

is the average net radiation between sunset and sunrise. Obviously,

is regarded as the driving force of the decrease of T at night. There are two limitations for this method. One is that this method can only be applied to the clear and calm nights because only in this condition are evapotranspiration and H close to zero. The other limitation is that it is difficult to get

and ΔT_n from remotely sensed data. Idso et al. [11, 12] and Menenti [13] proposed a simple model to derive remote estimates of STI with ΔT and the variation of G during the time between the maximum and minimum surface daily temperature. On the basis of this method, Minacapilli et al. [14] mapped STI from the airborne data and then used it to retrieve surface soil water content.

So far, developing STI estimation methods is still an ongoing progress. Many methods have been proposed. Xue and Cracknell [15] proposed a real thermal inertia analytical model by taking into consideration the phase information of surface temperature changes and ΔT. Murray and Verhoef [16] proposed a method to calculate STI based upon the normalized theory of soil thermal conductivity. On the basis of this method, Lu et al. [17] developed this method further by improving the Kersten function and the estimation of STI at saturation. Ma et al. [18] derived a STI method based on the heat conduction equation and an approximated energy budget equation. However, the above methods require the information on soil properties, which limit their applications of remote sensing methods to a certain degree. Using multitemporal land surface temperatures retrieved from satellite data, some other STI estimation methods were presented. Sobrino and El Kharraz [19] presented a method which uses satellite data at four moments (2:30, 7:30, 14:30, and 20:30 in local time). Cai [20] modified Sobrino’s method for MODIS (Moderate Resolution Imaging Spectroradiometer) data. Nearing et al. [21] developed a method with two daily measurements of surface temperature. The limitation of these methods is that they are restricted to the availability of satellite overpasses or field measured data [22]. Geostationary satellite data may provide a good alternative input for these methods.

According to the soil conductive heat transfer, soil heat flux is the real driving force of T [23, 24]. However, because G is difficult to acquire accurately at a regional scale by remote sensing method, G is usually replaced by S or Rn when estimating STI, as used in (3) and (4). When the alternative driving energy is close to G, the estimated STI would be close to the real STI [25]. Otherwise, the estimated STI would deviate greatly.

As is well known, G has a close relationship with Rn. Many studies have formulated the empirical function between them (f(G, Rn)) [26–28]. Equations (5) and (6) are the two typical methods widely used to estimate G for bare soil (see (5)) and for vegetated surface (see (6)) at a regional scale, respectively:

()

where VI is the vegetation index; a, b, and c are the empirical coefficients, which are mainly determined by soil properties, soil moisture, H, and LE [29, 30].

The objective of this paper is to present a STI estimation method which uses midday G (G_m) and ΔT as the inputs. Here, G_m is acquired from the empirical relationship between G and Rn. Another purpose of this paper is to investigate whether the empirical function about G, respectively, for bare soil and for vegetated surfaces can be used to estimate soil thermal inertia in combination with ΔT. Due to the large uncertainties in the estimation of STI for vegetated surface, STI method is limited in a variety of applications, such as soil moisture retrieval. If the method proposed in the paper is applicable, it will provide a feasible way to estimate STI for vegetated surface and thereby expand the applications of STI. The major difference between the method proposed in this paper and the previous methods is that the combination of G_m is used to estimate STI, which could be better than Rn or solar radiation according to the soil conductive heat transfer. The relationship between G and Rn is a simple method for acquiring G_m. For an area with relatively uniform soil properties and meteorological conditions (namely, there is a reliable relationship between G and Rn), STI could be estimated conveniently using the proposed method.

In the paper, a method of estimating soil thermal inertia, which uses G_m and ΔT as the inputs, is described in Section 2. Study site, data description, and the evaluation method are also illustrated in Section 2. Section 3 presents the results. Conclusions are given in Section 4.

2. Materials and Methods

2.1. Site Description

Measurement data used in the study are from the Yucheng (YC) Agro-Ecosystem Station, Chinese Academy of Sciences (CAS). The station is located in an irrigated agricultural field (36.8570N, 116.8360E) in the North China Plain characterized by a semihumid and monsoon climate. Mean annual precipitation, temperature, and global solar radiation at the station are 528 mm, 13.1°C, and 5225 MJ m⁻², respectively. The dominant soil type is sandy loam with an average bulk density of 1.43 (g cm⁻³), soil wilting point of 0.07 (v/v), and saturated soil moisture of 0.462 (v/v). The groundwater table varies from 1.5 to 3.5 m with an average of 2.5 m. This site is a typical representative of the agricultural area of winter wheat and summer maize production in the North China Plain. According to the traditional tillage practice, winter wheat is sown in middle October and harvested in early or mid-June of the next year, and summer maize is planted in mid- to late June and harvested at the end of September. It is almost a bare soil surface in the nongrowing season (Jan, Feb, mid- and late Oct, Nov, and Dec). In the growing season, winter wheat and summer maize are the dominant vegetation types, respectively, in the periods from March to June and from July to September.

2.2. Soil Thermal Inertia Method

Similar to the concepts of STI_n and ATI, the method of estimating STI used in this study is given in

()

where G_m (J m⁻² s⁻¹) is the midday soil heat flux. Δt (s) is the time difference between daily maximum and minimum surface temperature. The difference between (7), STI_n, and ATI is that (7) uses G_m rather than

or solar radiation absorbed by the surface as the driving force of the variation of T. Because it is easier to get midday soil heat flux from remotely sensed data, (7) can be applied to remote sensing data.

In the study, G_m is determined by the empirical function between Rn and G, like (5) and (6). The relationship between Rn and G is established on the basis of in situ measurements of Rn and G in 2003 at YC Station. Under the condition that there is only a small annual variation of surface conditions at YC Station in a few years, the relationship between Rn and G can be assumed to be almost constant; namely, the empirical coefficients of a, b, and c in (5) and (6) are constant. In this case, G_m in other years can be estimated on the basis of the established function of Rn and G. With the midday Rn (Rn_m) as the input, G_m of 2004 was estimated and used to estimate STI of 2004 in the study. Note that Rn_m, ΔT, and Δt all can be estimated from remotely sensed data, for example, MODIS. Therefore, as long as the empirical function between Rn and G is determined, STI can be estimated by (7).

2.3. Diurnal Soil Heat Flux Estimation

Because there are no data of in situ soil thermal inertia measurements, an indirect validation for the STI method was used. Firstly, diurnal G in 2004 at YC Station was estimated based on the method proposed by Verhoef [9]. By comparing diurnal G estimates with G measurements, the STI method was then evaluated indirectly.

Based on the method of Horton [4], Verhoef [25] presented a remote sensing method of estimating diurnal G for bare soil, as shown in (8). This approach requires a Fourier series analysis on surface temperature first:

()

where t (s) is the time during the 24 h cycle, M is the total number of harmonics, u is the harmonic number, and w (rad s⁻¹) is the radial frequency used in the harmonic analysis. A_bu (°C) is the overall amplitude of the nth harmonic and φ_bu (rad) is the phase shift of the nth harmonic, which are calculated from

()

where A_u (°C) and B_u (°C) are the amplitudes in the harmonic representation of soil surface temperature and can be obtained from the Fourier series analysis on T. In this way, T for each 24 h period was represented by a sum of sine and cosine terms (harmonics) according to the following equation:

()

where the overbar denotes the average of T over 24 h (°C). Other parameters have the same meanings as in (8). It can be seen from (8) that the summation of harmonic terms determines the diurnal shape of G estimates and STI determines the magnitude of G estimates.

With (8) and (10), diurnal G in 2004 is estimated based on the measurements of T and STI estimated from (7). Diurnal G measurements in 2004 are then compared with the measurements of G of 2004 at YC Station.

2.4. Data Description

At YC Station, Rn was measured by a four-component radiometer (CNR-1, Kipp & Zonen) mounted at 2 m height. Surface temperature was then back-calculated from the long wave downwelling (L_down, J m⁻² s⁻¹) and the upwelling (L_up, J m⁻² s⁻¹) radiation using the following formula:

()

where ε is the surface emissivity, taken as 0.95 for bare soil and 0.98 for vegetation surface, and σ (W m⁻² K⁻⁴) is the Stefan-Boltzmann constant.

Soil heat flux at a depth of 0.05 m was measured by a soil heat flow plate (HFP01SC, Hukseflux). Soil heat flux at the surface was estimated using the following formula:

()

where G_p (J m⁻² s⁻¹) is the plate heat flow measurement, ΔT_sD (K) is the change in mean soil temperature during the measurement period, C_s (J m⁻³ K) is the volumetric heat capacity of the soil, D (m) is the depth of the plate, and t (s) is the length of the measurement period. The standard equation given by De Vries [31] was used to estimate the volumetric heat capacity, C_s:

()

where C_w and C_m are the volumetric heat capacity of water and solid soil minerals, respectively (i.e., 4.2 and 2.0 MJ m⁻³ K⁻¹) and θ (m³ m⁻³) is the actual soil volumetric water content and was measured with a water content reflectometer (Model CS615-L, Compbell Scientific) at a depth of 20 cm. θ_∗ is the saturated soil moisture content.

Data in the rainy days were not considered in the study due to the large variation of soil moisture, which would have great effect on the determination of the empirical coefficients between Rn and G. Rainfall was monitored with a rain gauge (52203, RM Young, Inc.).

Three steps were used to perform the data quality control: (1) checking for null values for G, T_s, and Rn data for the same day, which is mainly caused by the broken electricity problem (if one null value was found, the data for the day were eliminated); (2) eliminating data on rainy and snowy days based on the rain and snow observations; (3) checking whether there were diurnal variations for G, T_s, and Rn for the same day. Only data with obvious diurnal variations for all the three parameters were kept. After this screening, 96 days and 128 days of observations for bare soil and vegetated surfaces, respectively, in 2003 were used to establish the regression function between Rn and G. In 2004, 100 days and 115 days of observations, respectively, for bare soil and for vegetated surface were used to validate the method.

The data of VI at YC Station are from the MODIS 16-day vegetation indices product (MOD13Q1) acquired from the Land Process Distributed Active Archive Center (LPDAAC) (https://lpdaac.usgs.gov/). Its spatial resolution is 250 m. A linear interpolation method is used to retrieve the Normalized Difference Vegetation Index (NDVI) of each day.

2.5. The Determination of the Coefficients of a, b, and c

In the study, the measurements of Rn and G in 2003 at YC Station in nongrowing season (Jan, Feb, mid- and late Oct, Nov, and Dec) were used to determine the empirical coefficient of c in (5), which is realized in two steps: First, c for each day is determined by the linear regression between the measurements of Rn and G, which is the slope of the regression. Then, the average of c is calculated by averaging c of each day and is used to calculate G of bare soil in 2004.

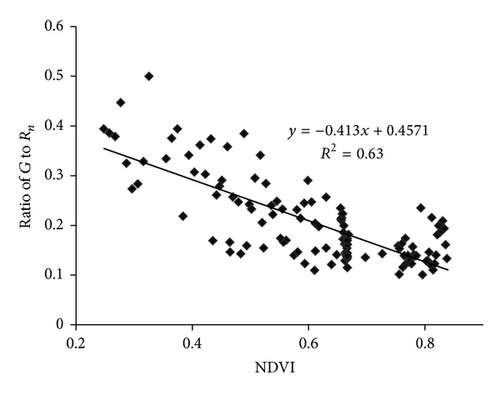
A regression function between Normalized Difference Vegetation Index (NDVI) and the ratio of G and Rn was established for the growing season using the field measurements of G and Rn in 2003, from which a and b in (6) are determined. Figure 1(a) shows the scatter plot of Rn and G in the nongrowing season. Figure 1(b) shows the scatter plot of NDVI and the ratio of G and Rn in the growing season.

Details are in the caption following the image — **Figure 1 (a) Bare soil**
Open in figure viewer PowerPoint

The linear relationship between the ratio of G to Rn and NDVI at YC Station in 2003.

Using the above methods, the regression functions between Rn and G were established, shown in (14). The coefficients of a, b, and c are −0.413, 0.457, and 0.472, respectively. They were used to estimate G_m at YC Station in 2004, with Rn_m as the input:

()

3. Results and Discussions

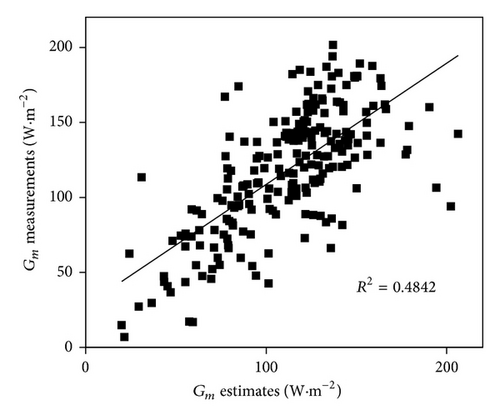
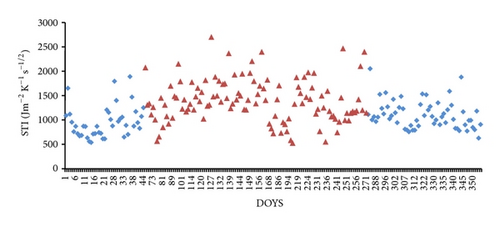
Figure 2 shows the scatter plot between G_m estimates calculated from (14) and G_m measurements at YC Station in 2004. It shows that their values are close to 1 : 1 line as a whole, with a bias of −6.5 W·m⁻² and a RMSE (root mean squared error) of 30.7 W·m⁻². Integrating G_m estimates and ΔT determined from T measurements into (7), STI was estimated. Figure 3 shows the annual variations of STI in 2004. It can be seen that STI ranges from 500 to 2500 (J m⁻² K⁻¹ s^−1/2) and higher STI was found in the growing season, with average STI of 1061.2 (J m⁻² K⁻¹ s^−1/2) in the nongrowing season and of 1370.6 (J m⁻² K⁻¹ s^−1/2) in the growing season. Rainfall and frequent irrigation may be the primary reason for the higher STI in the growing season because high soil water content can usually produce high soil thermal inertia [17].

Integrating STI obtained above into (8) and on the basis of the Fourier series analysis on the surface temperature, diurnal G in 2004 was estimated. The comparisons between diurnal G estimates and G measurements during the growing season and during the nongrowing season are given in Figure 4. The scatter plots are given in Figure 5.

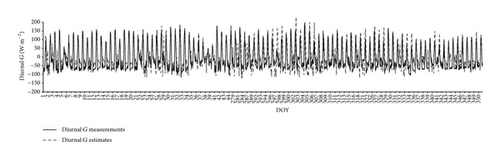
As a whole, G estimates can fit with G measurements, with correlation coefficient (R²) of 0.64 and 0.56 for the nongrowing season and the growing season, respectively. The biases and the RMSE for the nongrowing season and for the growing season are 10.1 W·m⁻², 40.9 W·m⁻² and −11.9 W·m⁻², 49.2 W·m⁻², respectively. G estimates for the bare soil are slightly better than that for the vegetated surface. The biases show that G is slightly overestimated in the nongrowing season and is underestimated in the growing season. It was also seen from Figure 4 that the discrepancies between G estimates and G measurements in the nighttime are larger than that in the daytime, which suggests that G_m estimates used in (8) deviate more greatly from the nighttime soil heat flux in comparison with the daytime soil heat flux.

As mentioned in Section 2.3, the diurnal variation of T determines the shape of the diurnal curve of G estimates by determining the summation of harmonic terms in (8) and STI determines the magnitude. Therefore, the larger errors in the STI estimates for the vegetated surface may be the main reason for the larger errors in G estimates. As described in Section 2, G_m for vegetated surface is obtained from the empirical function between NDVI and the ratio of G and Rn (see (14)). Vegetation conditions, irrigation activity, radiation conditions, and soil properties all influence the relationship between NDVI and the ratio of G and Rn. Therefore, there are wide variations in the empirical coefficients of the function, which leads to the uncertainties in the G_m estimation for the vegetated surface and thereby produces the errors in the STI estimation. Comparatively, the relationship between G and Rn for bare soil is relatively stable because soil properties play a dominant role in their relationship, which is relatively invariable in the same place. It seldom rains at YC Station and there is no irrigation activity in the nongrowing season, so soil moisture is relatively stable, which reduces the effects of the variation of soil moisture on the relationship between G and Rn.

To see the comparisons of G estimates and G measurements clearly, Figure 6 displays the 5-day results.

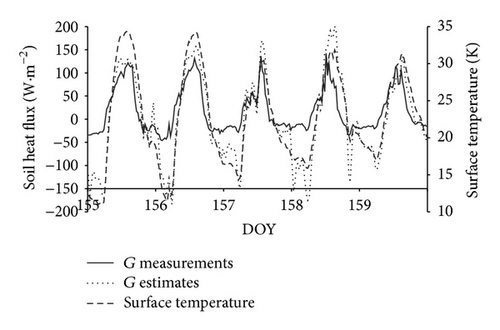
It is obvious that the diurnal curve of G estimates coincides with the diurnal shape of T, which illustrates that the diurnal variation of T determines the shape of the diurnal curve of G estimates by determining the summation of harmonic terms in (8). Compared with the in situ G, G estimates have a similar diurnal shape in the nongrowing season, while in the growing season, the fitness of the diurnal shape is worse. As mentioned above, the errors in the estimation of G_m are a primary reason for the discrepancy between G estimates and G measurements. For the vegetated surface, there is another reason. Surface temperature used to calculate diurnal G at vegetated surface is a mixed temperature which is composed of soil surface temperature and canopy temperature. However, the fact is that G only has relationship with soil temperature. For vegetated surface, soil temperature for soils under vegetation is usually not available from the conventional observation and remotely sensed data. Therefore, the difference between mixed surface temperature and soil temperature would produce the difference in the diurnal shape of G estimates and G measurements in the growing season. An underestimation of G was found during nighttime periods (G estimates are lower than G measurements at nighttime). This underestimation arises from differences between canopy and soil temperatures, where temperatures at the top of the canopy fall below those of the soil due to the effect of the sheltering of the soil surface by the canopy coverage. In the study, canopy temperature calculated from the radiative measurements by a four-component radiometer was used to compute the summation of harmonic terms in (10). Thus, the influence of canopy temperature on the radiation measurements induces a lower estimate of the summation of harmonic terms at nighttime. The same phenomenon was found in the study of Murray and Verhoef [9]. They attributed this to the differences between canopy and soil temperatures.

The above results of the comparison between diurnal G and in situ G illustrate that (8) can be used to estimate soil thermal inertia correctly. However, there are larger uncertainties in the estimation of STI at vegetated surfaces than that at bare soil due to the larger uncertainties in the estimation of G_m caused by the wider variation of the relationship between Rn and G. Using mixed surface temperature to replace soil temperature is another uncertainty in the estimation of STI for the vegetated surface.

The method can be applied to map STI with remotely sensed data. As is known, Rn can be retrieved from remotely sensed albedo, surface temperature, and some auxiliary meteorological data, such as solar radiation and air temperature. On the basis of the regression function between Rn and G in the study area, G_m can be calculated according to Rn. ΔT in (7) can also be obtained from satellite data, such as MODIS. Therefore, STI at a regional scale can be estimated. By using the regression function between Rn and G for vegetated surfaces, STI at vegetated surface can be retrieved, which provide an opportunity to overcome the difficulty in acquiring STI at vegetated surface. The method is simpler than the physically based STI methods that usually require soil properties. It is difficult to acquire soil properties by remote sensing; as a result, STI at a regional scale usually is not dependent on the physically based STI methods.

The limitation of the method presented in the paper is that the estimation of G_m depends on the empirical relationship between Rn and G. Actually, the relationship between Rn and G is not constant. It varies with soil properties, meteorological condition, and vegetation condition. Therefore, if the surface condition changes, errors will be produced in the estimation of G_m and thereby in the estimation of STI. In the application of the method, it is recommended that the regression function between Rn and G for the study area is established first, which would make G_m estimation more accurate and thereby make the STI estimation more reliable. The investigation of the accuracy of the G estimation method at a regional scale will be one of the future researches, which is expected to reduce the limitation of the empirical method of the determination of G_m. Applying the method to retrieve soil water content for both bare soil surface and vegetated surface is another implication of this research.

4. Conclusions

On the basis of the fact that soil thermal inertia (STI) can be estimated by the combinations of the driving force of the variation of surface temperature and the diurnal amplitude of surface temperature, a STI method, using midday soil heat flux (G_m) and ΔT as the inputs, is presented in the paper. G_m is achieved from an empirical method.

In the study, the measurements of net radiation and G in 2003 at the Yucheng (YC) Agro-Ecosystem Station, Chinese Academy of Sciences, were used to establish the empirical functions between Rn and G, respectively, for bare soil (nongrowing season) and for vegetated surface (growing season). According to the empirical functions, G_m of 2004 at YC Station is estimated and thereby STI of 2004 is estimated.

To validate the STI method, diurnal G of 2004 at YC Station is estimated with the method proposed by Verhoef [25], which requires STI and a Fourier series analysis on surface temperature. The comparisons of diurnal G estimates and the diurnal G measurements show that (1) G estimates agree well with G measurements, with correlation coefficient (R²) of 0.64 and 0.56 for the nongrowing season and the growing season, respectively. The biases and the root mean squared errors (RMSE) for the nongrowing season and for the growing season are 10.1 W·m⁻², 40.9 W·m⁻² and −11.9 W·m⁻², 49.2 W·m⁻², respectively. (2) The diurnal curve of G estimates coincides well with the diurnal curve of G measurements for bare soil. For the vegetated surface, the consistence between them is poorer than that for bare soil. The large uncertainties in the estimation of G_m resulting from the wider variation of the empirical relationship between Rn and G and the difference between mixed surface temperature and soil temperature may be the two primary reasons for the larger discrepancies in the diurnal shape and in the magnitude of G estimates and G measurements in the growing season. (3) The performance of G estimates in the daytime is better than that in the nighttime.

The comparison results between G estimates and in situ G illustrated that the STI method presented in the paper can be used to estimate soil thermal inertia reliably and the method can estimate STI more accurately for bare soil than for vegetated surface.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgment

This work was supported by the National Natural Science Foundation of China (41271380, 41171286).

References

1 Kahle A. B., Gillespie A. R., and Goetz A. F., Thermal inertia imaging—new geologic mapping tool, Geophysical Research Letters. (1976) 3, no. 1, 26–28, https://doi.org/10.1029/gl003i001p00026.
10.1029/GL003i001p00026
Web of Science® Google Scholar
2 Pratt D. A. and Ellyett C. D., The thermal inertia approach to mapping of soil moisture and geology, Remote Sensing of Environment. (1979) 8, no. 2, 151–168, https://doi.org/10.1016/0034-4257(79)90014-2, 2-s2.0-0018466697.
10.1016/0034-4257(79)90014-2
Web of Science® Google Scholar
3 Price J. C., The potential of remotely sensed thermal infrared data to infer surface soil-moisture and evapotranspiration, Water Resources Research. (1980) 16, no. 4, 787–795, https://doi.org/10.1029/wr016i004p00787, 2-s2.0-0019229290.
10.1029/WR016i004p00787
Web of Science® Google Scholar
4 Horton R., Wierenga P. J., and Nielsen D. R., Evaluation of methods for determining the apparent diffusivity of soil near the surface, Soil Science Society of America Journal. (1983) 47, no. 1, 25–32, https://doi.org/10.2136/sssaj1983.03615995004700010005x, 2-s2.0-0020971529.
10.2136/sssaj1983.03615995004700010005x
Web of Science® Google Scholar
5 Price J. C., Thermal inertia mapping: a new view of the earth, Journal of Geophysical Research. (1977) 82, no. 18, 2582–2590, https://doi.org/10.1029/jc082i018p02582, 2-s2.0-0017500754.
10.1029/JC082i018p02582
Web of Science® Google Scholar
6 Van Doninck J., Peters J., De Baets B., De Clercq E. M., Ducheyne E., and Verhoest N. E. C., The potential of multitemporal Aqua and Terra MODIS apparent thermal inertia as a soil moisture indicator, International Journal of Applied Earth Observation and Geoinformation. (2011) 13, no. 6, 934–941, https://doi.org/10.1016/j.jag.2011.07.003, 2-s2.0-84859333417.
10.1016/j.jag.2011.07.003
Web of Science® Google Scholar
7 Short N. and Stuart J. L., The Heat Capacity Mapping Mission (HCMM) Anthology, 1982, Scientific and Technical Information Branch, National Aeronautics & Space Administration, Washington, DC, USA.
Google Scholar
8 Price J. C., On the analysis of thermal infrared imagery: the limited utility of apparent thermal inertia, Remote Sensing of Environment. (1985) 18, no. 1, 59–73, https://doi.org/10.1016/0034-4257(85)90038-0, 2-s2.0-0022267530.
10.1016/0034-4257(85)90038-0
Web of Science® Google Scholar
9 Murray T. and Verhoef A., Moving towards a more mechanistic approach in the determination of soil heat flux from remote measurements. II. Diurnal shape of soil heat flux, Agricultural and Forest Meteorology. (2007) 147, no. 1-2, 88–97, https://doi.org/10.1016/j.agrformet.2007.06.009, 2-s2.0-34548503172.
10.1016/j.agrformet.2007.06.009
Web of Science® Google Scholar
10 Brunt D., Notes on radiation in the atmosphere, Quarterly Journal of the Royal Meteorological Society. (1932) 58, no. 247, 389–420, https://doi.org/10.1002/qj.49705824704.
10.1002/qj.49705824704
Web of Science® Google Scholar
11 Idso S. B., Jackson R. D., and Reginato R. J., Compensating for environmental variability in the thermal inertia approach to remote sensing of soil moisture, Journal of Applied Meteorology. (1976) 15, 811–817, https://doi.org/10.1175/1520-0450(1976)01560;0811:cfevit62;2.0.co;2.
10.1175/1520-0450(1976)015<0811:CFEVIT>2.0.CO;2
Google Scholar
12 Minacapilli M., Iovino M., and Blanda F., High resolution remote estimation of soil surface water content by a thermal inertia approach, Journal of Hydrology. (2009) 379, no. 3-4, 229–238, https://doi.org/10.1016/j.jhydrol.2009.09.055.
10.1016/j.jhydrol.2009.09.055
Web of Science® Google Scholar
13 Menenti M., Physical aspects and determination of evaporation in deserts applying remote sensing techniques, Report, 1984, no. 10, Institute for Land and Water Management Research (ICW), Wageningen, The Netherlands.
Google Scholar
14 Minacapilli M., Iovino M., and Blanda F., High resolution remote estimation of soil surface water content by a thermal inertia approach, Journal of Hydrology. (2009) 379, no. 3-4, 229–238, https://doi.org/10.1016/j.jhydrol.2009.09.055, 2-s2.0-70449465208.
10.1016/j.jhydrol.2009.09.055
Web of Science® Google Scholar
15 Xue Y. and Cracknell A. P., Advanced thermal inertia modelling, International Journal of Remote Sensing. (1995) 16, no. 3, 431–446, https://doi.org/10.1080/01431169508954411, 2-s2.0-0028869248.
10.1080/01431169508954411
Web of Science® Google Scholar
16 Murray T. and Verhoef A., Moving towards a more mechanistic approach in the determination of soil heat flux from remote measurements. I. A universal approach to calculate thermal inertia, Agricultural and Forest Meteorology. (2007) 147, no. 1-2, 80–87, https://doi.org/10.1016/j.agrformet.2007.07.004, 2-s2.0-34548499923.
10.1016/j.agrformet.2007.07.004
Web of Science® Google Scholar
17 Lu S., Ju Z. Q., Ren T. S., and Horton R., A general approach to estimate soil water content from thermal inertia, Agricultural and Forest Meteorology. (2009) 149, no. 10, 1693–1698, https://doi.org/10.1016/j.agrformet.2009.05.011, 2-s2.0-67949095826.
10.1016/j.agrformet.2009.05.011
Web of Science® Google Scholar
18 Ma C. F., Wang W. Z., Han X. J., and Li X., Soil moisture retrieval in the Heihe River Basin based on the real thermal inertia method, IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing. (2013) 6, no. 3, 1460–1467, https://doi.org/10.1109/jstars.2013.2252149, 2-s2.0-84880310507.
10.1109/JSTARS.2013.2252149
Web of Science® Google Scholar
19 Sobrino J. A. and El Kharraz M. H., Combining afternoon and morning NOAA satellites for thermal inertia estimation: 1. Algorithm and its testing with hydrologic atmospheric pilot experiment-sahel data, Journal of Geophysical Research: Atmospheres. (1999) 104, no. 8, 9445–9453, https://doi.org/10.1029/1998jd200109, 2-s2.0-0033608903.
10.1029/1998JD200109
Web of Science® Google Scholar
20 Cai G., MODIS data based thermal inertia and land surface temperature modeling and their applications in determination of soil moisture and heat exchange [Ph.D. dissertation], 2006, Graduate University of Chinese Academy of Sciences, Beijing, China.
Google Scholar
21 Nearing G. S., Moran M. S., Scott R. L., and Ponce-Campos G., Coupling diffusion and maximum entropy models to estimate thermal inertia, Remote Sensing of Environment. (2012) 119, 222–231, https://doi.org/10.1016/j.rse.2011.12.012, 2-s2.0-84856077978.
10.1016/j.rse.2011.12.012
Web of Science® Google Scholar
22 Di A., Xue Y., Li C., Guang J., Mei L., and Pan P., Estimation of soil thermal inertia from geostationary Meteosat Second Generation (MSG) data, Remote Sensing Letters. (2014) 5, no. 8, 763–772, https://doi.org/10.1080/2150704x.2014.967879, 2-s2.0-84907867460.
10.1080/2150704X.2014.967879
Web of Science® Google Scholar
23 Zhang R. H., Experimental Remote Sensing Modeling and Surface Foundations, 1996, Sciences Press, Beijing, China.
Google Scholar
24 Sun X. M., Zhu Z. L., Tang X. Z., Su H. B., and Zhang R. H., A new measuring technique of soil thermal inertia, Science in China, Series E: Technological Sciences. (2000) no. supplement 43, 67–69, 2-s2.0-24044519394.
Web of Science® Google Scholar
25 Verhoef A., Remote estimation of thermal inertia and soil heat flux for bare soil, Agricultural and Forest Meteorology. (2004) 123, no. 3-4, 221–236, https://doi.org/10.1016/j.agrformet.2003.11.005, 2-s2.0-2442714288.
10.1016/j.agrformet.2003.11.005
Web of Science® Google Scholar
26 Daughtry C. S. T., Kustas W. P., Moran M. S., PinterP. J.Jr., Jackson R. D., Brown P. W., Nichols W. D., and Gay L. W., Spectral estimates of net radiation and soil heat flux, Remote Sensing of Environment. (1990) 32, no. 2-3, 111–124, https://doi.org/10.1016/0034-4257(90)90012-b, 2-s2.0-0025659495.
10.1016/0034-4257(90)90012-B
Web of Science® Google Scholar
27 Kustas W. P., Daughtry C. S. T., and Van Oevelen P. J., Analytical treatment of the relationships between soil heat flux/net radiation ratio and vegetation indices, Remote Sensing of Environment. (1993) 46, no. 3, 319–330, https://doi.org/10.1016/0034-4257(93)90052-y, 2-s2.0-0027787844.
10.1016/0034-4257(93)90052-Y
Web of Science® Google Scholar
28 Ma Y. M., Su Z. B., Li Z. L., Koike T., and Menenti M., Determination of regional net radiation and soil heat flux over a heterogeneous landscape of the Tibetan Plateau, Hydrological Processes. (2002) 16, no. 15, 2963–2971, https://doi.org/10.1002/hyp.1079, 2-s2.0-0037202146.
10.1002/hyp.1079
Web of Science® Google Scholar
29 Idso S. B., Aase J. K., and Jackson R. D., Net radiation—soil heat flux relations as influenced by soil water content variations, Boundary-Layer Meteorology. (1975) 9, no. 1, 113–122, https://doi.org/10.1007/bf00232257, 2-s2.0-0001768326.
10.1007/BF00232257
Google Scholar
30 SantanelloJ. A.Jr. and Friedl M. A., Diurnal covariation in soil heat flux and net radiation, Journal of Applied Meteorology. (2003) 42, no. 6, 851–862, https://doi.org/10.1175/1520-0450(2003)042lt;0851:dcishf>2.0.co;2, 2-s2.0-0038606443.
10.1175/1520-0450(2003)042<0851:DCISHF>2.0.CO;2
Google Scholar
31 De Vries D. A., W. R. van Wijk, Thermal properties of soil, Physics of the Plant Environment, 1963, North-Holland Publisher, Amsterdam, The Netherlands, 210–235.
Google Scholar

Citing Literature

All articles

An Empirical Method of Estimating Soil Thermal Inertia

Abstract

1. Introduction

2. Materials and Methods

2.1. Site Description

2.2. Soil Thermal Inertia Method

2.3. Diurnal Soil Heat Flux Estimation

2.4. Data Description

2.5. The Determination of the Coefficients of a, b, and c

3. Results and Discussions

4. Conclusions

Conflict of Interests

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley