Volume 2015, Issue 1 349716

Research Article

Open Access

Robust Design Optimization of a 4-UPS-S Parallel Manipulator for Orientation-Regulating Control System of Solar Gather Panels

Guohua Cui,

Corresponding Author

Guohua Cui

[email protected]

College of Equipment Manufacturing, Hebei University of Engineering, Handan 056038, China hebeu.edu.cn

Search for more papers by this author

Haidong Zhou,

Haidong Zhou

College of Equipment Manufacturing, Hebei University of Engineering, Handan 056038, China hebeu.edu.cn

Search for more papers by this author

Haiqiang Zhang,

Haiqiang Zhang

College of Equipment Manufacturing, Hebei University of Engineering, Handan 056038, China hebeu.edu.cn

Search for more papers by this author

Dan Zhang,

Dan Zhang

Department of Automotive, Mechanical and Manufacturing Engineering, University of Ontario Institute of Technology, Oshawa, ON, Canada L1H 7K4, uoit.ca

Search for more papers by this author

Yanwei Zhang,

Yanwei Zhang

College of Equipment Manufacturing, Hebei University of Engineering, Handan 056038, China hebeu.edu.cn

Search for more papers by this author

Guohua Cui,

Corresponding Author

Guohua Cui

[email protected]

College of Equipment Manufacturing, Hebei University of Engineering, Handan 056038, China hebeu.edu.cn

Search for more papers by this author

Haidong Zhou,

Haidong Zhou

College of Equipment Manufacturing, Hebei University of Engineering, Handan 056038, China hebeu.edu.cn

Search for more papers by this author

Haiqiang Zhang,

Haiqiang Zhang

College of Equipment Manufacturing, Hebei University of Engineering, Handan 056038, China hebeu.edu.cn

Search for more papers by this author

Dan Zhang,

Dan Zhang

Department of Automotive, Mechanical and Manufacturing Engineering, University of Ontario Institute of Technology, Oshawa, ON, Canada L1H 7K4, uoit.ca

Search for more papers by this author

Yanwei Zhang,

Yanwei Zhang

College of Equipment Manufacturing, Hebei University of Engineering, Handan 056038, China hebeu.edu.cn

Search for more papers by this author

First published: 17 March 2015

https://doi.org/10.1155/2015/349716

Academic Editor: C. K. Kwong

Share a link

Email
Wechat
Bluesky

Abstract

This paper proposes a redundantly actuated parallel manipulator 4-UPS-S that is applicable for orientation adjustment in the gathering process of solar power. A thorough analysis involving the kinematic issues is performed. Inverse kinematic problems are solved in the close-loop. The Jacobian matrix and some performance indexes are analytically derived. The multiobjective optimization model is established, and the determinacy optimization is completed on the basis of previous research works. Six-Sigma robust analysis is performed on the basis of the determinacy optimal solution. Results show that 4-UPS-S does not satisfy the quality requirement. Therefore, it is necessary to implement Six-Sigma robust optimization, and select optimial solution of robustness to complete the nondeterminacy optimization. The research results show that the proposed methodology has a simple operation and high optimization efficiency. The methodology commodiously obtains robustness parallel manipulator that satisfies the quality requirement.

1. Introduction

Determinacy analysis and design is a traditional optimization design of system inputs, mechanical structures, material properties, manufacturing, and installation with no error or with a constant error value. Most of the above parameters in practical engineering application problems are uncertain problems with some existing errors [1–3]. In accordance with certain distributions, the actual values fluctuate up and down beside the theoretical values and are not artificially controlled. The robust analysis and design are the process of studying parameter errors as random variables. Research on the robust design optimization of the parallel manipulators is uncommon [4, 5]. Gao [6] used the robustness optimization design of the 3-RPS parallel manipulator by adopting the Box-Behken experimental design and the ANSYS Workbench that generated the initial sample points. He further used the Kriging interpolation and neural network methods to regenerate new sample points. Yu [7] analyzed and solved the parallel robot manipulator deviation used in the sheet metal assembly. He further derived a new robustness design index on the basis of the sheet metal assembly deviation model. Meng et al. [8] treated the design variables as random variables and built the robustness optimization design mathematical model with a four-bar manipulator. Kato and Muramatsu [9] proposed a method that is the Monte Carlo simulation and particle swarm optimization method to evaluate robustness of adjustable mechanisms. Abdellatif et al. [10] presented a self-contained approach for the robust dynamics identification of parallel manipulators in terms of uncertain parameters and illustrated the control accuracy by numerous experimental investigations. Rahman et al. [11] presented the robust design of suspension arm using stochastic design improvement technique based on Monte Carlo simulation. Many scholars employed different methods for robustness design optimization (e.g., blind number theory [12] and Monte Carlo simulation method [13, 14]).

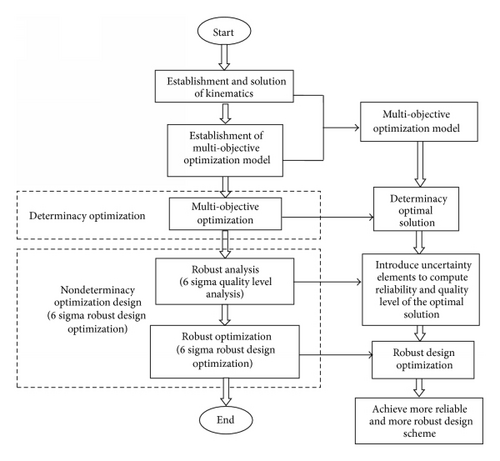
The paper is organized as follows. In Section 2, the structure of the 4-UPS-S parallel manipulator that can be applied in the solar gather panel orientation control system is described and the reference systems of the parallel manipulator are established. In Section 3, the inverse kinematics of the parallel legs and forward kinematics of serial passive legs of the manipulator are studied. Section 4 explains the performance indexes including the maximum payload capacity, maximum and minimum stiffness, and kinematic dexterity to evaluate mechanical performances. In Section 5 a determinacy optimization design is performed based on software Isight. In Section 6, Six-Sigma optimization technique for robust design optimization is analyzed. In Section 7, Six Sigma robust optimization is conducted with consideration uncertain parameters and achieves reliability and quality level. Section 8 analyzes and explains the results of the robust design optimization. Finally, Section 9 summarizes and arranges contents of this study. The robustness analysis optimization flow diagram is described in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Flow diagram of the Six Sigma robust design and optimization based on Isight.

2. Parallel Manipulator Description

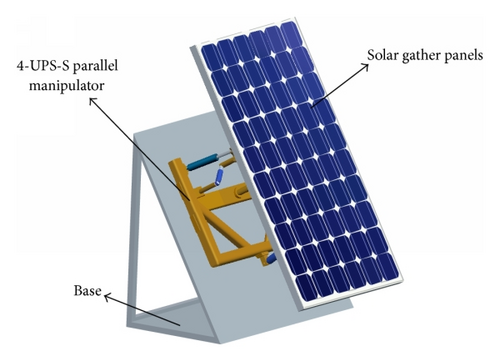
The traditional orientation-regulating control manipulators of solar gather panels generally have two degrees of freedom. These degrees of freedom regulate the azimuth and manipulator elevation to track the trajectory of the sun. However, solar equipment cannot achieve the requirement of maintaining the azimuth level with changes in the tracking process (e.g., solar water heaters). This paper adds a degree of freedom on the basis of the original two degrees of freedom. The additional degree of freedom rotates on its own to regulate the equipment level. This study further proposes a three-rotation redundant parallel manipulator (i.e., 4-UPS-S) for the orientation control system of solar gather panels. The redundant active chain of the 4-UPS-S eliminates the various singular configurations of the 3-UPS-S parallel manipulator [15].

The structural schematic of the 4-UPS-S parallel manipulator and its application as an adjusting manipulator in the solar gather panel are shown in Figure 2. The four active UPS chains contain the hinged points A_i of the bases A and B_i moving platform B (i = 1,2, 3,4). The distance between the base and moving platform is constant and equal to 500 mm. The moving platform is directly connected to the fixed base by a passive spherical joint O. Each chain consists of universal, prismatic, and spherical joints. We assign a fixed Cartesian coordinate system O-X_AY_AZ_A and the moving Cartesian system O-X_BY_BZ_B at the centered point O for analysis (Figure 2(a)). The X_A axis of the fixed coordinate system is parallel to the O_AA₁. The Z_A axis is perpendicular to the base and top. The Y_A axis is based on the right-hand rule. The X_B axis of the moving coordinate is parallel to O_BB₁. Z_B is perpendicular to the moving platform. The Y_B axis is based on the right-hand rule. The distance between the coordinate origin and moving platform is h. The circumcircle radii of points A₁, A₂, and A₃ are r_A. Point A₄ is located in the plane perpendicular to the base and parallel to O_AA₃. Point A₄ in the region to the base is calculated as h_A = 250 mm. The projection distance between points A₁ and A₄ is s. The circumcircle radii of points B₁, B₂, and B₃ are r_B. Point B₄ is located in the X_BOZ_B plane. The distance from the point to the Z_B axis line is (t · r_B). The distance to the moving platform is h_B.

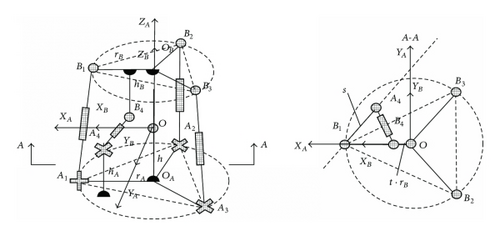
3. Kinematics Model Solution of the Parallel Manipulator

3.1. Inverse Kinematic Solution

According to coordinate transformation theory and the closed-loop vector method, we can obtain the following [16]:

()

where l_i is the vector for each prismatic actor length,

is the position vector of point with respect to the fixed system, and

is the position vector of point with respect to the moving system.

The 4-UPS-S is a redundantly actuated parallel manipulator with three orientation degrees of freedom. According to the roll-pitch-yaw rotations, the rotation matrix of the moving system with respect to the fixed system is described as follows:

()

where ψ, θ, and φ are the yaw (along the X axis), pitch (along the Y axis), and roll (along the Z axis) angles, respectively. sψ stands for sinψ, and cψ stands for cos⁡ψ.

According to the inverse kinematic solution, once we obtain the output angles ψ, θ, and φ, vector l_i is obtained by using (1). The square of the length is a function about angles ψ, θ, and φ. Consider

()

The derivative of both sides of (3) about time leads to the following:

()

namely,

()

where J = A⁻¹B is the Jacobian matrix velocity of the parallel manipulator, with

()

3.2. Passive Constraint Chain Forward Model

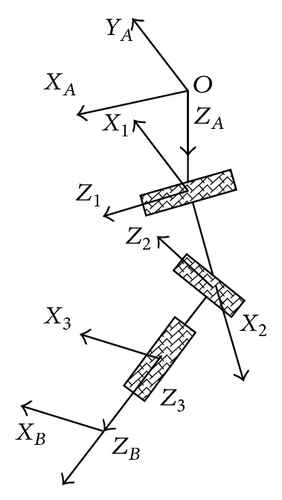
The passive constraint chain of the 4-UPS-S parallel manipulator is an open-kinematics chain with three-rotation degrees of freedom. For analysis, we separate the spherical joint into three revolute joints by adopting the Denavit-Hartenberg (D-H) method. We use three rotation angles (i.e., φ₁, φ₂, and φ₃) to describe its orientation. The coordinate system of the adjacent links is settled by using the D-H method. The overlap coordinate system origin is separated for convenience of illustration (Figure 3).

The transformation matrix between adjacent links is expressed in terms of the D-H method:

()

The θ_i, d_i, a_i, and α_i parameter values are shown in Table 1.

Table 1. D-H parameter for the passive constraint chain.

	θ_i	α_i
0	0	0
1	90^° + ϕ₁	90°
2	90^° + ϕ₂	90°
3	ϕ₃	0

The transformation matrix from the coordinate system O-X_AY_AZ_A to the coordinate system O-X_BY_BZ_B is described as follows:

()

Combining (2) and (8), we obtain the following function relationship between ϕ₁, ϕ₂, and ϕ₃ and ψ, θ, and φ:

()

By deviating both sides of (9), we generate the following:

()

where

()

where J_s is the Jacobian matrix of the middle passive chain between the input angular velocity and output angular velocity.

4. Establishment of the Parallel Manipulator Performance Indexes

4.1. Global Kinematic Dexterity

The 4-UPS-S parallel manipulator is a pure rotation manipulator. We adopt the reciprocal of the condition number of the Jacobian matrix to measure the dexterity and transmission relationship of the manipulator between the input and output. The reciprocal of the condition number of the Jacobian matrix is defined as follows:

()

where λ_max⁡(J^TJ) and λ_min⁡(J^TJ) are the maximum and minimum eigenvalues of J^TJ, respectively.

The global dexterity index is employed to describe the mean condition value of the Jacobian matrix in the entire workspace [17].

()

where W is the parallel manipulator workspace.

This paper employs the output angle to describe the orientation workspace of the parallel manipulator. According to the application requirements, the parallel manipulator workspace is expressed as follows:

()

The global dexterity index is in the range 0 ≤ kj ≤ 1. A global dexterity index closer to one corresponds to better dexterity and control precision. We generally calculate the condition number κ_J of the Jacobian matrix in different workspace positions and orientations to increase indicator operability. The mean of the reciprocal of the Jacobian matrix is calculated as a global kinematic dexterity index kj.

4.2. Global Stiffness Performance Index

The friction force of the hinges and joints is ignored for brevity. According to the virtual work principle, one obtains the following [18]:

()

where τ = χΔl is the actuator force vector applied at each actuated joint, τ_v = χ_vΔψ is the passive chain internal torque, and F is the torque applied to the moving platform. The moving platform is assumed to have no gravitational forces acting on any of the intermediate links. The gravitational forces are generally neglected in industrial applications. χ and χ_v are the equivalent stiffness of the active and passive chains, respectively.

Substituting (5) and (10) into (15) yields the following:

()

where

()

where K is the parallel manipulator’s whole stiffness matrix.

According to vector extreme calculation theory, when the moving platform deformation reaches ‖Δω‖ = Δω^TΔω = 1, the followings are generated:

()

where λ_max⁡(K^TK) and λ_min⁡(K^TK) are the maximum and minimum eigenvalues of matrix K^TK, respectively.

To evaluate the parallel manipulator stiffness performance in the entire workspace, the global stiffness performance index is similarly defined as follows:

()

where W is the parallel manipulator workspace. We can compute the stiffness index by using the mean method.

Larger global stiffness evaluation indexes kmax⁡ and kmin⁡ correspond to better parallel manipulator stiffness.

4.3. Global Maximum Payload Capability

Similar to (18), the maximum payload capability performance index is defined as follows:

()

where λ_Fmax⁡(G^TG) is the maximum eigenvalue of matrix G^TG. The relationship is G = J^T.

The global maximum payload capability performance index is written as follows:

()

where W is the parallel manipulator workspace.

A greater global maximum payload capability-evaluation index gmax⁡ corresponds to better parallel manipulator payload capability.

5. Deterministic Optimization Design Model of the Parallel Adjusting Manipulator

This study maximizes the global payload capacity and global maximum stiffness to improve the parallel adjusting manipulator of the loading ability that bears the solar equipment weight. The global kinematic dexterity and minimum stiffness are the constraint conditions. The design variables are h, s, and t (Figure 2(a)).

The deterministic optimization design model is represented as

()

where

denotes the design variables, and f₁(X) and f₂(X) are the global payload capability and global maximum stiffness index, respectively.

We employed the Simcode components to integrate MATLAB and calculate the parallel manipulator evaluation indexes. The NSGA-II optimization algorithm is adopted for the present study. The population size is 16, rate of crossover is set to 0.9, rate of mutation is set to 0.1, rate of migration is set to 0.1, and the generation number is 15. The design variables, constraint conditions, and optimization objectives are selected on the basis of the application requirement [2, 19]. We run the software platform once the parameter setting is completed.

The deterministic optimization design is a multiobjective optimization design problem. The history points of the two objective functions in the solving process are plotted in Figure 4. The two objectives increase or decrease at the same time. The Pareto optimal solution is a convenient solution for this multiobjective optimization design problem when the global stiffness and global payload capacity obtain the maximum values at the same time.

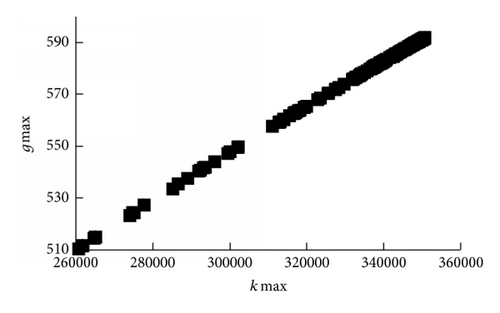
The deterministic optimization design result and initial scheme comparison is presented in Table 3. The deterministic optimization design analysis solution results show that the optimization objectives (i.e., global maximum stiffness and global payload capacity) have a considerable improvement. However, the parameters (i.e., h, s, t, and kj) are all close to the constraint boundary at the same time. If the uncertainty factor influences are considered, the deterministic optimization scheme violates the constraint conditions. Therefore, performing a robust analysis that evaluates the quality and reliability level of the deterministic optimization design scheme is necessary [20, 21].

6. Six-Sigma Robust Analysis

In this study, some uncertainty factors include the design variables h, s, and t. The radii r_A and r_B of the base and moving platform follow the same normal distribution. The optimal design point value of the deterministic optimization design is considered the mean of the random design variables. The standard deviation is presented in Table 2. σ = 1% × μ represents the 1% coefficient of variation (i.e., σ/μ = 0.01). The robust analysis of the 4-UPS-S parallel manipulator is implemented by adopting the Six-Sigma component based on Isight software.

Table 2. Six-Sigma-based robust analysis description.

Random design variables	h: μ = 200.005, σ = 1% × μ
	s: μ = 129.096, σ = 1% × μ
	t: μ = 0.799, σ = 1% × μ
Random noises	The radius r_A of the base: μ = 500 mm, σ = 1% × μ
Random noises	The radius r_B of the moving platform: μ = 400 mm, σ = 1% × μ
Quality constraints	The global kinematic dexterity: kj ≥ 0.3
Quality constraints	The global minimum stiffness: kmin⁡≥3 × 10⁴

Table 3. Six-Sigma-based robust design and optimization results.

Variables	Initial scheme	Determinacy optimization scheme			Robust optimization scheme
Variables	Initial scheme	Determinacy optimal solutions		Six-Sigma analysis	Robust optimization analysis	Quality level
Input variables
h	300	μ	200.005	Sigma level 0.676 reliability 50.099%	213.330	6.356
h	300	σ	2.00005	Sigma level 0.676 reliability 50.099%	2.13330	6.356
s	200	μ	129.096	Sigma level 7.142 reliability 100%	218.936	8.0
s	200	σ	1.29096	Sigma level 7.142 reliability 100%	2.18936	8.0
t	0.6	μ	0.799	Sigma level 0.755 reliability 54.980%	0.683	8.0
t	0.6	σ	0.00799	Sigma level 0.755 reliability 54.980%	0.00683	8.0
Output variables (performance indexes)
Global kinematic dexterity kj	0.310	μ	0.305	Sigma level 1.187 reliability 76.47%	0.305	7.809
Global kinematic dexterity kj	0.310	σ	0.007	Sigma level 1.187 reliability 76.47%	0.007	7.809
Global minimum stiffness kmin⁡	30045	μ	36880	Sigma level 4.161 reliability 99.99%	42991.7	7.563
Global minimum stiffness kmin⁡	30045	σ	1721	Sigma level 4.161 reliability 99.99%	1739	7.563
Global maximum payload capability gmax⁡	538.736	μ	591.702		574.223
Global maximum payload capability gmax⁡	538.736	σ	4.276		4.014
Global maximum stiffness kmax⁡	290141	μ	350500		329940
Global maximum stiffness kmax⁡	290141	σ	5084		4624

The Six-Sigma robust analysis results are concretely summarized in Table 3. The input variables h and t do not reach the One Sigma level. The reliability is approximately 50%, which is considered low. The global kinematic dexterity and the global minimum stiffness have a relatively high reliability. The minimum stiffness attains a reliability of 99.99% but cannot reach the Six-Sigma level. The global minimum stiffness Sigma level is 4.161. In the long term, when the 1.5σ quality shift occurs in the system, the defective products per million with a Sigma level of four will sharply increase from the short term 63 × 10⁻⁶ to 6200 × 10⁻⁶. The quality levels of h and t are low and do not achieve the One Sigma level. Therefore, performing a robust optimization for this problem is necessary in the long term.

7. Six-Sigma Robust Optimization (Uncertainty Optimization)

The essence of the Six-Sigma robust optimization is to add the mean, the variance of the response in optimization objectives, and the upper quality level limit of the random variables in the constraint conditions to satisfy the quality level, minimize the mean of the optimal objectives, and increase the robustness and reliability of the mean [22].

This paper sets the lower limit of the Sigma level of random variables and responses to 6σ. The mean of the global kinematic dexterity and global minimum stiffness is maximized, whereas the standard deviation of the global kinematic dexterity and the global minimum stiffness is minimized. The robust optimization design model is summarized as follows:

()

where μ(gmax⁡) and σ(gmax⁡) are the mean and variance of the maximum payload capability, respectively. The mean and variance are similar to the others. Sigma Level(h, s, t, kj, kmin⁡) denotes the Sigma level value of the parameters (i.e., h, s, t, kj, and kmin⁡).

When setting the optimization objectives, the scale factor of the standard deviation should be set to 0.01 to ensure that the standard deviation and mean have the same order of magnitude.

The Six-Sigma robust design optimization flow diagram is shown in Figure 5. During the procedure, the Six-Sigma component robust analysis is used to analyze the single design point robustness. The optimization design component robust optimization is employed to perform the optimization design on the basis of robustness analysis. If the quality of the single design point cannot satisfy the quality level requirements, Isight will continue to improve the optimization variables for the quality analysis of the next group; otherwise, the results will be exported, and the robust optimization is completed. The present study selects the nondominated sorting evolution strategy, namely, NSGA-II, as the optimization algorithm.

Some genetic parameters and operators are set as follows [23].

The population size: 4.
The generation number: 10.
Crossover probability: 0.9.
Crossover distribution index: 10.
Mutation distribution index: 20.
Max failed runs: 5.
Failed run penalty value: 1.0E30.
Failed run objective value: 1.0E30.

We obtain the Pareto solutions and frontier after the Six-Sigma robust optimization design. The Pareto frontier of the mean, as well as the variance of the maximum payload capacity and maximum stiffness, is illustrated in Figure 6. The relationship among the optimization objectives from the Pareto solutions is observed. According to this relationship and the practical application requirements, we select the optimal solution for the multiobjective design problems and choose the point of optimal solution (Figure 6). In view of reliability and quality level theory, we can obtain the quality level, mean, and variance of each response after the robust optimization through the post-processing functions of Isight software. And the results are listed in Table 3.

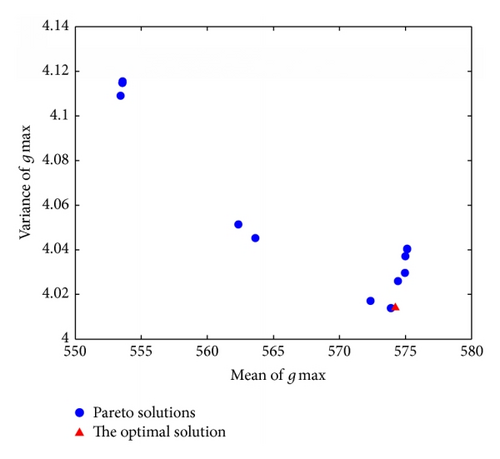
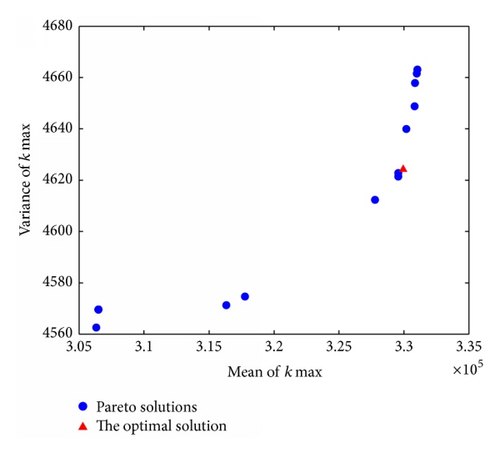
Comparing the quality level with robust optimization, that is, variable quality level of h, s, t is 0.676, 7.142, 0.755, respectively. Performance indexes quality level of kj, k_min⁡ is 1.187, 4.161, respectively. After robust optimization, the quality level of each response is greater than six.

8. Result Analysis of the Six-Sigma Robust of the Parallel Adjusting Manipulator

By taking the global kinematic dexterity index as an example, the probability distribution and Six-Sigma level were compared before and after optimization (Figure 7). We intuitively obtained the probability distribution, mean, standard deviation, and Six-Sigma level of each response (Figure 7).

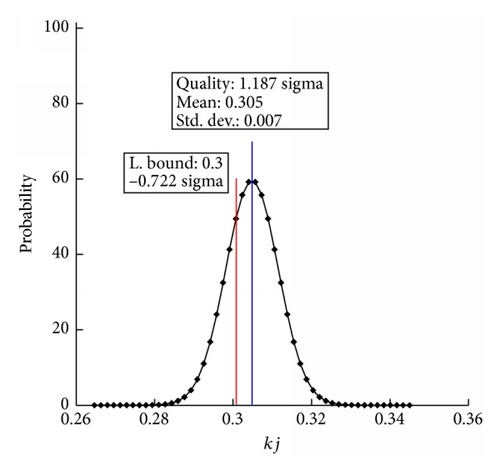
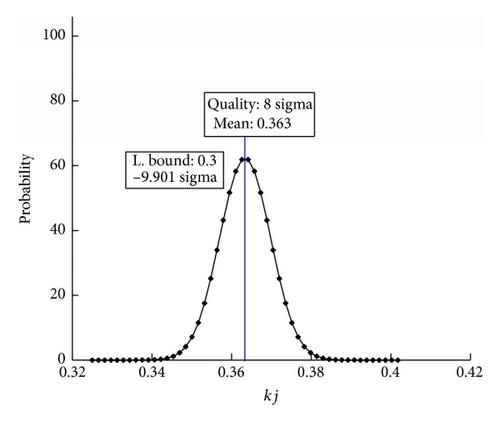
We rearranged and listed the reliability of each variable before and after optimization (Table 4) to concretely illustrate the difference between the reliability and defective quality per million before and after the robust analysis. The defective products per million are shown in Table 5.

Table 4. Comparison of the reliability before and after optimization.

	Before robust optimization	After robust optimization
h	50.099%	99.999%
s	100%	100%
t	54.980%	100%
kj	76.472%	100%
kmin⁡	99.997%	100%

Table 5. Comparison of the defective quality per million before and after optimization.

	Before robust optimization	After robust optimization
h	499002.670	2.069e − 4
s	9.213e − 7	0
t	450199.849	0
kj	235279.150	5.773e − 9
kmin⁡	31.653	3.930e − 8

The parameter variables (i.e., h and t) and quality constraints (i.e., global kinematic dexterity kj) (Tables 4 and 5) greatly improves after optimization. However, the reliability of the other parameter variables only improved slightly. By contrast, the defective quality per million improved considerably (Table 5). In the long term, the adjusting manipulator designed and manufactured with optimal design variables has fewer defective products per million than before optimization. This result is based on the assumption that the design variables, manufacturing, and installation error of the base and moving platform can be effectively controlled, thus greatly improving the resistance ability of the uncertainty factor disturbance in the whole manufacturing process. Data in Tables 4 and 5 show that the Six-Sigma robust optimization design based on Isight is effective and feasible.

9. Conclusions

The parallel adjusting manipulator applied in solar gather panels is the research objective of this paper. Determinacy optimization analysis was performed with consideration to the performance indexes. By considering the influence of the uncertainty factors implemented in the robust analysis and optimization, the following conclusions are drawn.

(1)
The parallel adjusting manipulator was designed by using multiobjective optimization design on the basis of the inverse kinematic solution. The performance indexes are established, the optimal solution is obtained, and the determinacy optimization is completed.
(2)
Robustness analysis is performed on the basis of determinacy optimization design. Some parameter variables and performance indexes are close to the constraint boundary. The Sigma level is low, and the defective quality per million is high. The implementation of the Six-Sigma robust optimization is necessary to complete the nondeterminacy optimization design.
(3)
The comparison of the manipulator before and after the robust design optimization shows that the new one has a higher Sigma level. Furthermore, the comparison shows a lower defective quality per million than before optimization. The optimization objectives are optimal. The mean and standard deviation are in their minimum. This result indicates that in the long term, the manipulator after optimization is more suitable for batch production applications than the manipulator before optimization. The robust optimization based on Isight is efficient and convenient for operation with accurate results. These results are applicable to the robust design optimization of large-scale and complex manipulators.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

This research is supported by the National Natural Science Foundation of China (Grant no. 51175143).

Supporting Information

References

1 Linda O. and Manic M., Uncertainty-robust design of interval type-2 fuzzy logic controller for delta parallel robot, IEEE Transactions on Industrial Informatics. (2011) 7, no. 4, 661–670, https://doi.org/10.1109/TII.2011.2166786, 2-s2.0-81255129699.
10.1109/TII.2011.2166786
Web of Science® Google Scholar
2 Kelaiaia R., Company O., and Zaatri A., Multiobjective optimization of a linear Delta parallel robot, Mechanism and Machine Theory. (2012) 50, 159–178, https://doi.org/10.1016/j.mechmachtheory.2011.11.004, 2-s2.0-84855998927.
10.1016/j.mechmachtheory.2011.11.004
Web of Science® Google Scholar
3 Ivezic D. D. and Petrovic T. B., Robust IMC controllers with optimal setpoints tracking and disturbance rejection for industrial boiler, Journal of Mechanical Engineering. (2010) 56, no. 9, 565–574, 2-s2.0-77957200822.
Google Scholar
4 Evgeny S., Odellia B., and Michael M., Robust optimization of system design, Procedia Computer Science. (2014) 28, 489–496.
10.1016/j.procs.2014.03.060
Google Scholar
5 Takeo K. and Masatoshi M., Robust design method for adjustable mechanisms, Journal of Mechanics Engineering and Automation. (2014) 4, 16–24.
Google Scholar
6 Gao P., The robust optimization design of minimally invasive spinal surgery guidance equipment based on the 3-RPS parallel mechanism [M.S. thesis], 2013, Hebei University of Engineering, Handan, China.
Google Scholar
7 Yu H. J., Research on Parallel Robot Based on Flexible Fixtures for Automotive Sheet Metal Assembly, 2010, Harbin Institute of Technology, Harbin, China.
Google Scholar
8 Meng X. J., Zhang C., and Shi Z. X., Optimization design for robustness of linkages, Journal of Machine Design. (2004) 24, no. 6, 31–33.
Google Scholar
9 Kato T. and Muramatsu M., Robust design method for adjustable mechanisms, Journal of Mechanics Engineering and Automation. (2011) 4, 16–24.
Google Scholar
10 Abdellatif H., Heimann B., and Kotlarski J., On the Robust Dynamics Identification of Parallel Manipualtors: Methodology and Experiments, 2008, I-Tech Education and Publishing, Vienna, Austria.
Google Scholar
11 Rahman M. M., Mohyaldeen H. M., Noor M. M., Kadirgama K., and Bakar R. A., Robust design of suspension arm based on stochastic design improvement, Proceedings of the 2nd International Conference on Mechanical and Electronics Engineering (ICMEE ′10), August 2010, V1460–V1464, https://doi.org/10.1109/icmee.2010.5558508, 2-s2.0-77957763497.
10.1109/icmee.2010.5558508
Google Scholar
12 Li H. P., Shi B. Q., and Zhang W. M., Robust optimization design of a machine based on the blind number theory, Journal of University of Science and Technology Beijing. (2006) 28, no. 12, 1178–1181, 2-s2.0-33846830066.
Google Scholar
13 Thrun S., Fox D., Burgard W., and Dellaert F., Robust Monte Carlo localization for mobile robots, Artificial Intelligence. (2001) 128, no. 1-2, 99–141, https://doi.org/10.1016/S0004-3702(01)00069-8.
10.1016/S0004-3702(01)00069-8
Web of Science® Google Scholar
14 Eric V., Robust Monte Carlo Methods for Light Transport Simulation, 1997, Stanford University, MR2697641.
Google Scholar
15 Cui G. H., Zhang D., Zhou H. D., and Zhang Y. W., Operating dexterity optimization and analysis of a 3-DOF parallel manipulator for a tunnel segment assembly system, International Journal of Mechanics and Materials in Design. (2014) https://doi.org/10.1007/s10999-014-9268-8.
10.1007/s10999-014-9268-8
Web of Science® Google Scholar
16 Cheng G., Xu P., Yang D.-H., Li H., and Liu H.-G., Analysing kinematics of a novel 3CPS parallel manipulator based on rodrigues parameters, Journal of Mechanical Engineering. (2013) 59, no. 5, 291–300, https://doi.org/10.5545/sv-jme.2012.727, 2-s2.0-84879989724.
10.5545/sv-jme.2012.727
Google Scholar
17 Gosselin C. and Angeles J., Global performance index for the kinematic optimization of robotic manipulators, Journal of Mechanisms, Transmissions, and Automation in Design. (1991) 113, no. 3, 220–226, 2-s2.0-0026223179.
10.1115/1.2912772
Google Scholar
18 Chi Z. Z., Zhang D., Xia L., and Gao Z., Multi-objective optimization of stiffness and workspace for a parallel kinematic machine, International Journal of Mechanics and Materials in Design. (2013) 9, no. 3, 281–293, https://doi.org/10.1007/s10999-013-9219-9, 2-s2.0-84881479598.
10.1007/s10999-013-9219-9
Web of Science® Google Scholar
19 Ren Z., Zhang D., and Koh C. S., Multi-objective optimization approach to reliability-based robust global optimization of electromagnetic device, The International Journal for Computation and Mathematics in Electrical and Electronic Engineering. (2014) 33, no. 1-2, 191–200, https://doi.org/10.1108/compel-11-2012-0341, MR3184028, 2-s2.0-84897487501.
10.1108/COMPEL-11-2012-0341
Web of Science® Google Scholar
20 Luo Y., Wen H., and Li H., Multidisciplinary robust optimization design of multi-functional open-air hydraulic drill, Applied Mechanics and Materials. (2011) 44-47, 1135–1140, https://doi.org/10.4028/www.scientific.net/AMM.44-47.1135, 2-s2.0-78651318879.
10.4028/www.scientific.net/AMM.44-47.1135
Google Scholar
21 Bowling A. P., Renaud J. E., Newkirk J. T., Patel N. M., and Agarwal H., Reliability-based design optimization of robotic system dynamic performance, Journal of Mechanical Design, Transactions of the ASME. (2007) 129, no. 4, 449–454, https://doi.org/10.1115/1.2437804, 2-s2.0-34248373761.
10.1115/1.2437804
Web of Science® Google Scholar
22 Csébfalvi A., A new theoretical approach for robust truss optimization with uncertain load directions, Mechanics Based Design of Structures and Machines. (2014) 42, no. 4, 442–453, https://doi.org/10.1080/15397734.2014.880064, 2-s2.0-84901439184.
10.1080/15397734.2014.880064
Web of Science® Google Scholar
23 Lee D. S., Gonzalez L. F., Periaux J., and Srinivas K., Robust design optimisation using multi-objective evolutionary algorithms, Computers and Fluids. (2008) 37, no. 5, 565–583, https://doi.org/10.1016/j.compfluid.2007.07.011, 2-s2.0-40649086425.
10.1016/j.compfluid.2007.07.011
Web of Science® Google Scholar

All articles

Robust Design Optimization of a 4-UPS-S Parallel Manipulator for Orientation-Regulating Control System of Solar Gather Panels

Abstract

1. Introduction

2. Parallel Manipulator Description