International Journal of Aerospace Engineering
Volume 2015, Issue 1 253478
Research Article
Open Access

Adaptive Integrated Guidance and Fault Tolerant Control Using Backstepping and Sliding Mode

Mohsen Fathi Jegarkandi, 

Mohsen Fathi Jegarkandi

Department of Aerospace Engineering, Sharif University of Technology, P.O. Box 11365-11155, Tehran, Iran sharif.ir

Search for more papers by this author
Asghar Ashrafifar, 

Corresponding Author

Asghar Ashrafifar

Department of Aerospace Engineering, Sharif University of Technology, P.O. Box 11365-11155, Tehran, Iran sharif.ir

Search for more papers by this author
Reza Mohsenipour, 

Reza Mohsenipour

Department of Aerospace Engineering, Sharif University of Technology, P.O. Box 11365-11155, Tehran, Iran sharif.ir

Search for more papers by this author
First published: 17 November 2015
https://doi.org/10.1155/2015/253478
Citations: 7
Academic Editor: Mahmut Reyhanoglu

Abstract

A new method of integrated guidance and control for homing missiles with actuator fault against manoeuvring targets is proposed. Model of the integrated guidance and control system in the pitch plane with actuator fault and some uncertainty is developed. A control law using combination of adaptive backstepping and sliding mode approaches is designed to achieve interception in the presence of bounded uncertainties and actuator fault. Simulation results show that new approach has better performance than adaptive backstepping and has good performance in the presence of actuator fault.

1. Introduction

The traditional way to design a missile guidance and control system is to form subsystems separately followed by integrating them. This method presents successful results and demonstrates some remarkable performance in designing several missile guidance and control systems. However, since in this method interactive relationships between the cooperating subsystems cannot be completely exploited, the overall system performance may be constrained. Therefore, a design method named as integrated guidance and control (IGC) system is provided by incorporating some control theories to enhance the performance of the whole system.

There are a variety of methods to solve IGC problem that some of them are presented in the following. In [1] an adaptive nonlinear IGC approach is proposed by adopting a backstepping scheme for missile-target engagement model with uncertainties without fault. Reference [2] has addressed IGC problem using nonlinear optimal control technique which is called θ-D method. In work [3] an integrated guidance and autopilot system is designed for homing missiles against ground fixed targets. To this intent, an integrated model in the pitch plane is formulated, and then the adaptive nonlinear control law is designed by adopting the sliding mode control approach. Also, other control theories have been employed in the design of guidance laws, including H∞ control [4], variable structure control [5], feedback linearization scheme [6], sliding mode control [7], and adaptive fuzzy sliding mode control [8].

A fault tolerant control system is capable of controlling a system with satisfactory performance even if one or several faults occur in the system. Fault tolerant control systems can be classified into two main families: passive fault tolerant controllers and active fault tolerant controllers. In a passive fault tolerant controller, deviations of the plant parameters from their actual values or deviations of the actuators from their expected position may be efficiently compensated by a fixed robust feedback controller [9]. Many control design laws described by fault tolerant control have been proposed in [10–12] for different practical systems. In [13] some fault tolerant controllers designed guidance strategy in the presence of actuator faults. Furthermore, authors of [14] have proposed a fault tolerant control for induction motors based on backstepping strategy.

In this paper, first, IGC system in the pitch plane with an actuator fault and some uncertainties is modelled. Since the actuator fault uncertainty is multiplied by input, we must use some scheme of such sliding mode. Then a control law using combination of adaptive backstepping and sliding mode is designed to achieve the interception in the presence of bounded uncertainties and actuator fault. The proposed control law is compared with control law of [1] for a free fault system. Then, the performance of designed law control is investigated for the faulty system.

The paper is organized as follows. In Section 2, missile-target engagement geometry will be derived in the pitch plane. In Section 3, actuator fault is modelled. In Section 4 control law is derived using the proposed new approach. In Section 5 control law is derived for the faulty system. Simulation results and their analysis are presented in Section 6. Finally, a conclusion is made in Section 7.

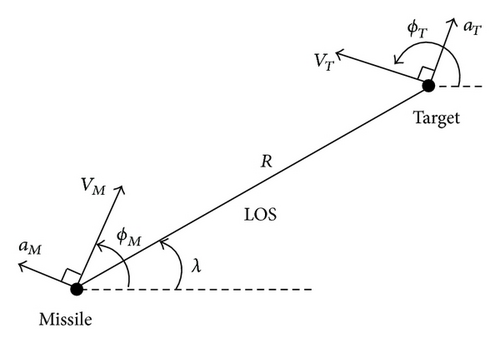
2. Engagement of Model Derivation

In this section, the integrated guidance and control model for two-dimensional point mass missile-target engagement geometry is driven in the pitch plane [1]. In order to establish a better understanding of the concept, engagement strategy is illustrated in Figure 1. Consider an inertial coordinate system fixed to the surface of a flat-earth model. The corresponding kinematic equations of motion are given as follows:
()
where R is the range along the line of sight (LOS); λ is the LOS angle; VM and VT are the speed of missile and target, respectively, that both are assumed to be constant. ϕM and ϕT are missile and target’s flight path angles, respectively. Differentiating yields
()
where , aM and aT are normal acceleration of missile and target, respectively, and aTλ is the projection of bounded target acceleration perpendicular to the line of sight.
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Two-dimensional missile-target engagement geometry.
For modelling of planar missile dynamics, proposed model in [1, 7] is used as follows:
()
Therefore
()
where θ is the pitch attitude angle and q is the missile pitch rate; δz is deflection angle for pitch control and m and Jz are the mass and moment of inertia, respectively. Also, M is the pitch moment and L is the lift forces, where
()
Therefore
()
where lα = ∂l/∂α, mx = ∂m/∂x, and Δα = −ΔL/VM in which ΔL and ΔM are bounded uncertainties. On the other hand, missile acceleration can be written as
()
By substituting (7) into (2) and defining , x2 = α, and x3 = q one can obtain
()
where
()
The above closed-loop system dynamics are actuator fault-free. In next section, closed-loop system dynamics with actuator fault is driven.

3. Modeling of Actuator Fault

A loss of effectiveness actuator fault is considered in this work. For this, the desired control input δz was disconnected and replaced by a faulty control signal that takes control over the plant. The true input of the plant can be written as [9]
()
where
()
The faulty control signal can be expressed as follows:
()
where f is a random constant that 0.3 ≤ f < 1. If f becomes less than 0.3, the actuator is saturated. Therefore, a faulty system can be written:
()
In the following sections, first, a control law using new approach is derived for a free fault system so one can be able to compare the results of the new approach with the results of [1]. Next, the given approach is applied to the faulty system.

4. Integrated Guidance and Control Design Using Combination of Sliding Control and Backstepping

System (8) is not in the standard form of common backstepping procedure because x2 appeared in the nonlinear term of cos(q + x2 − θ)a12. In order to deal with this situation, [1] has introduced an adaptive backstepping control scheme to design an IGC law that can zero LOS rate and maintain stability of the overall system.

In this paper, sliding mode control is used to improve the performance of proposed IGC in [1] and we can consider actuator fault. To this purpose, suppose that virtual controls α1(x1) and α2(x1, x2) in two backsteps are obtained such that they keep x1 around zero and guarantee x1 and to be input-to-state stable with respect to uncertainties, respectively [1]; consider
()
where k, c2, δ1,2, and the expressions of partial derivatives ∂α1/∂x1 and ∂α1/∂t can be found in [1].
Now, instead of using of backstep again for calculating u, sliding mode control is used. To this purpose, sliding surface S is selected as
()
It is obvious that if a dynamic state feedback control law is designed such that the trajectories of the closed-loop system are driven on the sliding surface and kept along it, then the guidance strategy can be achieved. Therefore, differentiation of S must be zero:
()
Then
()
With the given sliding surface, the control law is obtained as
()
where |ΔM| ≤ M.
In order to prevent chattering, one can write
()

5. Fault Tolerant Control Design

For the faulty system, sliding surface S is selected as before. Differentiation of S must be zero; then
()
Equation (20) can be rewritten as
()
where is the nominal value of f. By considering the input as
()
(21) can be expressed as follows:
()
where
()
()
By substituting (25) in (24),
()
From (26) it follows that
()
where
()
Values and can be calculated from [1] easily. By defining
()
control law is obtained as
()

6. Numerical Results and Analysis

To evaluate performance of the proposed approach, in this section, first the proposed approach is compared with the results of [1] for free fault system. This comparison is shown in Figure 2. As it can be seen, the proposed control law, with less acceleration applied to the missile, causes smaller miss distance. This shows efficiency of the proposed approach to use for faulty system:
()
The initial missile and target flight path angles, their initial velocities, and the relative motion parameters can be found in [1].
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Comparing missile acceleration and deflection angle for free fault system.

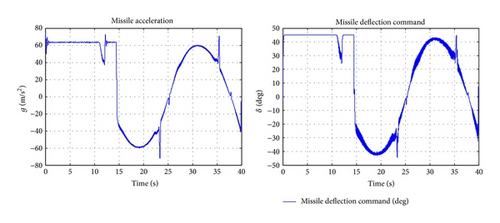
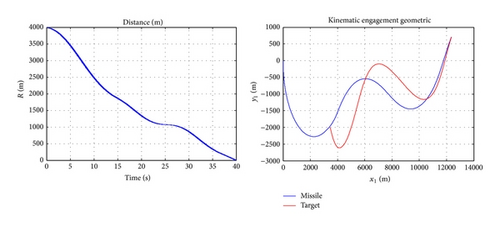
Next, performance of the proposed control law is investigated for faulty system. For this purpose, actuator effectiveness is selected between 30% and 100%; in other words 0.3 ≤ f < 1. It is assumed that the actuator commands are taken as a first-order lag system with a time constant 0.001 and limited by |δz| < 45 deg.

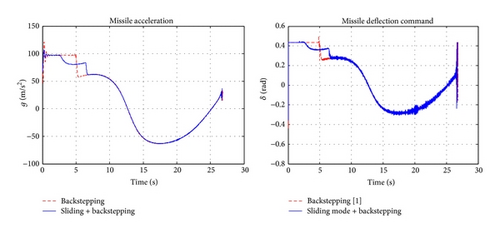
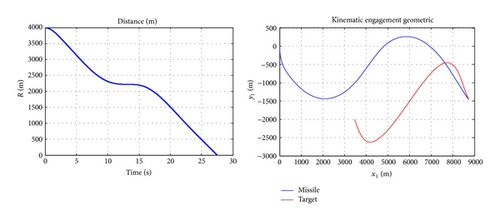
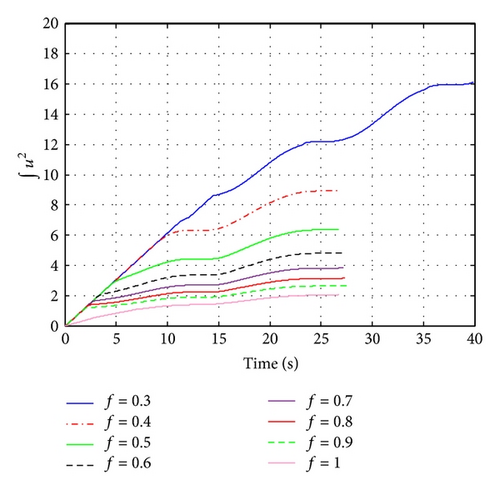
As can be seen in Figures 3–6, the controllers are robust to achieve the missile interception in the presence of the target acceleration and actuator fault. It is clear that the less efficiency of actuator increases the time to go, interception distance, and deflection angle for pitch control. Also, it increases the control effort (Figure 7).

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Missile acceleration and deflection angle for faulty system with f = 0.9.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Relative range and interception trajectory for faulty system with f = 0.9.
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Missile acceleration and deflection for faulty system with f = 0.3.
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Relative range and interception trajectory for faulty system with f = 0.3.
Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Control effort comparison.

7. Conclusion

In this paper, we introduce a new approach to design of guidance laws for two-dimensional point mass missile-target engagement in the presence of bounded uncertainties and actuator fault. In proposed approach, sliding mode control is combined with adaptive backstepping to improve the performance. Numerical results show that the new control law has better performance than adaptive backstepping and has good performance in faulty system.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.