This paper presents the numerical density derivative approach (another phase of numerical welltesting) in which each fluid’s densities around the wellbore are measured and used to generate pressure equivalent for each phase using simplified pressure-density correlation, as well as new statistical derivative methods to determine each fluid phase’s permeabilities, and the average effective permeability for the system with a new empirical model. Also density related radial flow equations for each fluid phase are derived and semilog specialised plot of density versus Horner time is used to estimate k relative to each phase. Results from 2 examples of oil and gas condensate reservoirs show that the derivatives of the fluid phase pressure-densities equivalent display the same wellbore and reservoir fingerprint as the conventional bottom-hole pressure BPR method. It also indicates that the average effective k_ave ranges between 43 and 57 mD for scenarios (a) to (d) in Example 1.0 and 404 mD for scenarios (a) to (b) in Example 2.0 using the new fluid phase empirical model for K estimation. This is within the k value used in the simulation model and likewise that estimated from the conventional BPR method. Results also discovered that in all six scenarios investigated, the heavier fluid such as water and the weighted average pressure-density equivalent of all fluid gives exact effective k as the conventional BPR method. This approach provides an estimate of the possible fluid phase permeabilities and the % of each phase contribution to flow at a given point. Hence, at several dp^′ stabilisation points, the relative k can be generated.

1. Introduction

Several sets of well and reservoir models have been generated with pressure derivatives with different boundary conditions. Likewise, several type curves, which account for different combinations of wellbore, reservoir characteristics, and boundary effects with associated flow regimes for computation of well and reservoir parameters, have been used to simplify well test interpretation. This demonstrates that the log-log plot of the pressure derivative is a powerful tool for reservoir model identification in pressure transient analysis.

However, in practice, each current method of transient data analysis has its own strengths and limitations with no single pressure and production data analysis method capable of handling all types of data and reservoir types with clear reliable results [1]. The log derivative and derivative type curve, which have remained reference flow regime’s diagnostic tools for over four decades, are the only unified approach for welltest interpretation and are applicable in a wide range of situations.

The derivative method, which is the greatest breakthrough in welltest analysis, was first introduced by Tiab in 1976 [2, 3] and developed by French mathematician Dominique Bourdet in 1983 [4]. It has remained the reference solution for identifying flow regime, boundary response, and use for diagnosing complex reservoir features till date. This approach has helped to reduce the uncertainties surrounding the interpretation of welltest data because key regions of radial flow and boundary features have been adequately diagnosed. However, due to the nonunique solution of the mathematical fluid flow equation, mostly in heterogeneous reservoir, most engineers in the industry are compelled to use analytical model and type curve solutions to match complex model, which is oftentimes not realistic. Assumptions made are ignored while pursuing a perfect match and results obtained from this approach are often misleading [5].

This marked the beginning of numerical well testing in the industry by Zheng, 2006 [5], although the approach started from the early 1990s [6–10]. Zheng made more advances in 2006, providing more solutions to the nonunique problems mostly in heterogeneous reservoirs through numerical welltesting, thereby promoting its application. More papers have been published by researchers on the subject, thereby reflecting the advancement of numerical welltesting and its application in solving various reservoir engineering practical problems.

One of the main limitations of the pressure derivative is that the measured pressure data must be constructed into derivative data, by means of numerical differentiation. Oftentimes derivative data from real field are very noisy and difficult to interpret, resulting in various smoothing techniques developed by researchers on this subject. It is practically believed that smoothing of pressure derivative data often alters the characteristics of the data. Also, it is difficult to distinguish between fluid and reservoir fingerprints in critical saturated reservoirs.

Another limitation of these derivatives is diagnosing flow regimes in complex reservoir structures such as complex faulted systems and high permeability streak with interbedded shales, which is common in deep water turbidite systems, channel-levee, lobe, and channelized deposits. Also, in situations of multiphase flow around the wellbore, the derivative data are always noisy and difficult to interpret, resulting in the application of deconvolution and various smoothing techniques to obtain a perceived representative model which often might not be. Additionally, the analytical solution for transient pressure analysis is limited to single phase flow, which in real case is never the situation. Presently there are few literatures or research on multiphase transient pressure analysis. However, the combination of the new statistical approach [11] and the density derivative approach serves as a support tool for better interpretation and estimation of reservoir properties in these conditions.

The diagnosis of flow, which appears as distinctive patterns in the pressure derivative curve, is a vital point in welltest interpretations since each flow regime reflects the geometry of the flow streamlines in the tested formation. Hence, for each flow regime identified, a set of well and/or reservoir parameters can be estimated using the region of the transient data that exhibits the characteristic pattern behaviour [11]. In the study, the pressure derivative formulation from Horne (1995) [12] and the new statistical approach by Biu and Zheng (2015) [11] would be used throughout the analysis.

The mathematical formulation for pressure derivative by Horne (1995) [12] is given as

()

Also the mathematical formulation for the new statistical derivative approach by Biu and Zheng (2015) [11] is given as follows.

Model 1. Consider the following:

()

Model 2 (the exponential function). Consider the following:

()

Model 3. Consider the following:

()

Model 4 (the time function). Consider the following:

()

Equations (1) to (5) are the derivative and statistical models used for flow regime diagnosis, behaviours, and estimation of wellbore and reservoir properties using the log-log derivative plot.

2. Theoretical Concept of the Density Derivatives

The basic concepts involved in the derivation of fluid flow equation include

(i)
conservation of mass equation,
(ii)
transport rate equation (e.g., Darcy’s law),
(iii)
equation of state.

Consider flow in a cylindrical coordinate with flow but with flow in angular and z-directions neglected as shown in Figure 1; the equations are given as follows:

()

Equation (6) represents the conservation of mass. Since the fluid is moving, the equation

()

is applied. By conserving mass in an elemental control volume as shown in Figure 1 and applying transport rate equation, the following equation is obtained:

()

Expand the equation using Taylor series:

()

Equations (6) to (9) apply to both liquid and gas. Equation (9) is known as the general diffusivity equation and for each fluid; the density or pressure term in (9) can be replaced by the correct expression in terms of density or pressure.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Schematics of basic fluid flows concept.

For small or constant compressibility liquid,

()

Substituting for pressure in the equation, the diffusivity equation in terms of density is given as

()

Equation (12) is known as the density diffusivity equation, which can also be rewritten in the form of pressure.

Over the decades, the transient test analysis has applied the general diffusivity equation in pressure term to generate several nonunique solutions using several pressure-rate data.

Invariably, as in pressure term, the density term also implored

()

For inner boundary condition,

()

For outer boundary condition,

()

Presently there are permanent downhole gauges (PDG) with density measurement tool along with pressure and temperature installed during flowing and shut-in testing conditions but the data are not interpreted or used for reservoir monitoring. For simplification and application of the density derivative in existing welltest software, the density-pressure equivalent equation is formulated.

3. Software Suitability (Pressure Equivalent)

To apply the numerical density approach in existing software, the pressure equivalent of the fluid density changes at the wellbore is generated from the relationship below.

Using the isothermal compressibility coefficient C, in terms of density,

()

3.1. For Small or Constant Compressibility Fluid Such as Oil and Water

Consider the following:

()

Integrating

()

or applying the e^x expansion series,

()

Because the term C[P₀ − P] is very small, the e^x term can be approximated as

()

Therefore (14) can be rewritten as

()

For small compressibility fluid such as oil and water, either (19) or (22) is used to generate the pressure equivalent from well fluid density obtained from reservoir simulation or PDG tool. This pressure is then analyzed in any available well test softwares.

3.2. For Compressible Fluid in Isothermal Conditions

Consider the following:

()

For real gas equation of state,

()

Differentiating with respect to pressure at constant temperature,

()

Substituting (23) into (25),

()

In terms of density,

()

This equation is applicable for real gas condition.

For compressible fluid,

()

Applying the power series for lnp,

()

Limit lnx to the 1st term only:

()

For compressible fluids such as gas, (32) is used to generate the pressure equivalent from the fluid density obtained from reservoir simulation or PDG tool at the well and then the pressure is analyzed in any available well test softwares.

Also, outside the available welltest software, the pressure derivative can be generated from the pressure equivalent obtained from the oil, gas, and water densities at the well by applying (1) formulated by Horne (1995) [12] or (2) to (4) by Biu and Zheng (2015) [11].

4. Density Weighted Average (DWA)

While (19) or (22) and (32) give the pressure equivalent for independent fluid phases such as gas, oil, and water, the weighted average method is used to obtain the density equivalent for a two- or three-phase combination. The equivalent pressure derived from the density for all three fluid components such as gas, oil, and water is given as

()

Equation (33) comprises all the fluid phases in the system and as such will be comparable to the conventional bottom-hole pressure measurement during the derivative analysis.

4.1. Empirical Model Correlation between Fluid Phases K

An empirical model integrating the fluid phase’s permeabilities for a given system is formulated to determine the average reservoir permeability. The mathematical model is given as

()

where k_o = oil phase permeability, k_g = gas phase permeability, and k_w = water phase permeability.

With the estimation of the phase’s permeabilities, it is therefore possible to estimate the possible relative permeability to each phase and the percentage contribution to flow by each phase at one point analysis; hence, at several points, the relative k can be generated.

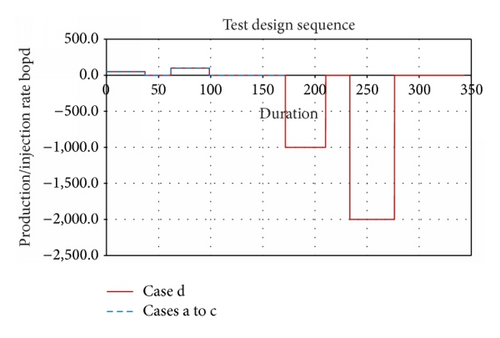
To illustrate applicability of this approach, 6 scenarios in conventional oil reservoir and gas condensate reservoir are investigated using numerical model built with a commercial simulator. Local grid refinement (LGR) is imposed around the well to capture sharp change in fluid densities as shown in Figure 2.

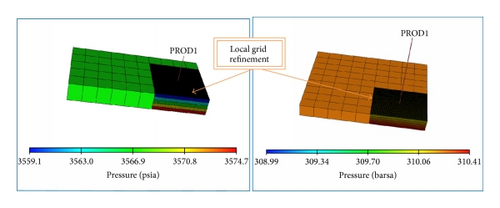
The simulation software keywords LBPR, LDENO, LDENW, LDENG AND WBHP were outputs to obtain the density and pressure change around the well and as far as the perturbation could extend.

Example 1. Table 1 presents a summary of the well and reservoir synthetic data used for the buildup and drawdown simulated scenarios with additional information given below. It is required to generate the pressure equivalent and derivative for each phase, compare their diagnostic signatures, and also determine the phases permeabilities and average reservoir permeability.

Table 1. Reservoir and fluid data for Example 1.

Parameters	Design value
Eclipse model	Black oil
Model dimension	10 × 5 × 5
Length by width, ft by ft	500 × 400
Thickness h, ft	250
Permeability Kx by Ky, mD	50.0 by 50.0
Porosity %	20
Well diameter, ft	0.60
Initial water saturation Sw_i, %	22
Permeability, K, mD	50
Gas oil contact (GOC), ft	8820
Oil water contact (OWC), ft	9000.0
Initial pressure, P_i, psia	4000.0
Formation temperature, T, oF	200.0

Assumption. (i) Oil reservoir + gas cap is completed with one well.

(ii) LGR is imposed around the well and far across to account for pressure and density changes.

Gas, oil, and water densities around the local grid refinement (wellbore) and WBHP were output using the simulator keywords. The following scenarios were evaluated.

(a)
Flowing + buildup sequence: well perforated h_p = 30 ft between oil and water layer. Net sand thickness h = 250 ft.
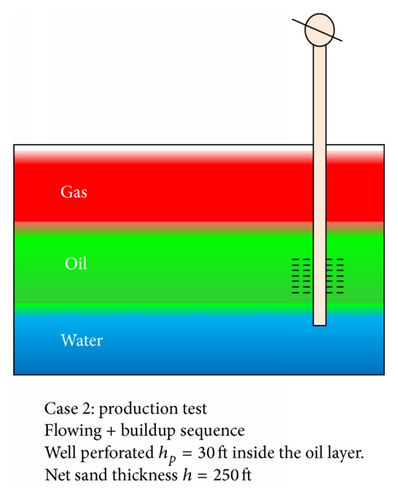
(b)
Flowing + buildup sequence: well perforated h_p = 30 ft inside the oil layer. Net sand thickness h = 250 ft.
(c)
Flowing + buildup sequence: well perforated h_p = 30 ft between gas and oil layer. Net sand thickness h = 250 ft.
(d)
Falloff test; flowing + buildup sequence: well perforated h_p = 30 ft inside the oil layer. Net sand thickness h = 250 ft.

The schematic of the 4 scenarios is depicted in Figures 3 and 4. Figure 5 shows the production, shut-in and injection sequence for the 4 scenarios in Example 1.

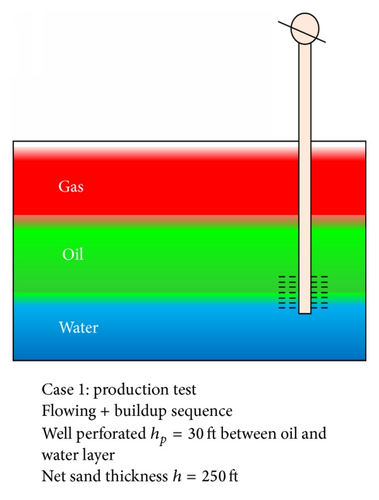
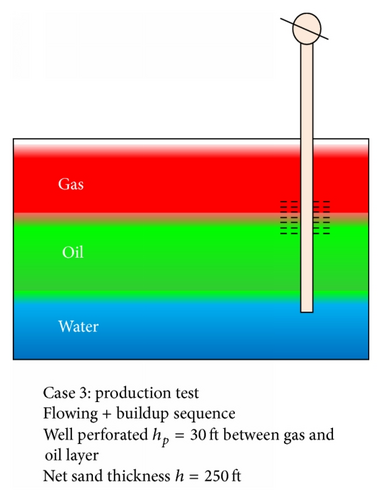
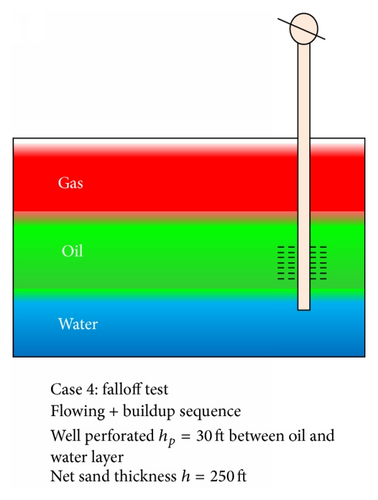
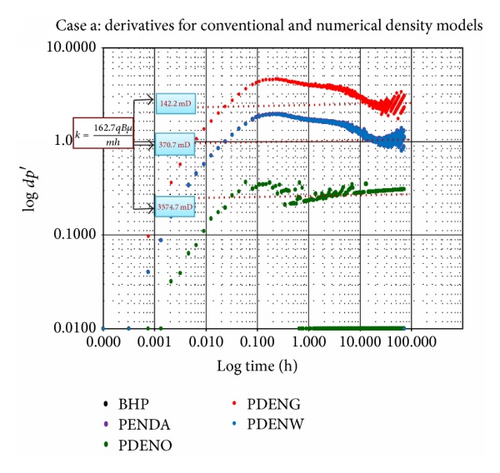
In scenario (a), the well is completed between the oil and water layer to mimic multiphase conditions at the wellbore and some distance away from the well and also see the effect on pressure distribution, fluid densities changes around the wellbore, and estimate fluid phase permeabilities k using the specialised plot and k_ave from the empirical model for three-phase conditions.

The derivative in Figure 6 shows a good radial flow but drop in derivative at late time due to constant pressure support (likely aquifer support). A continuous drop is seen from 10 hrs in the model parameters. The derivatives for all output parameters display the same well and reservoir signatures (3 flow periods, early to late time response) but with different dp^′ stabilisation. The well bottom-hole pressure (BPR → BHP) response shows good overlay with pressure equivalent of density weighted average (PDENDWA → PDENA) and pressure equivalent of water density (PDENWAT → PDENW) while pressure equivalent of gas density (PDENGAS → PDENG) and pressure equivalent of oil density (PDENOIL → PDENO) differ completely. The PDENDWA gives a better fingerprint that is less noisy.

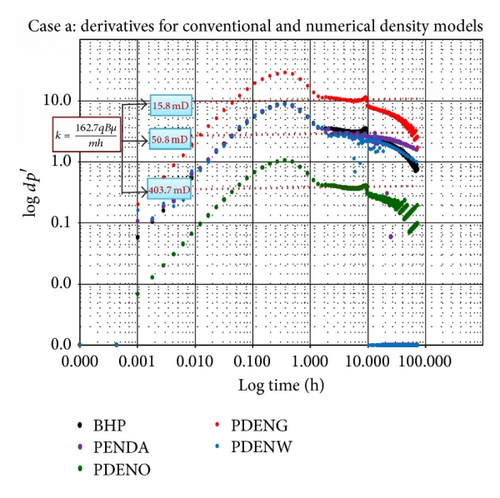
A permeability value of 50.8 mD is estimated from the bottom-hole pressure BPR where k = 162.7qBμ/mh and m is obtained from the specialised plot. This is an approximate of the input value in the simulation model. Also the simulator outputs PDENDWA and PDENWAT in the simulation give the same k value while PDENGAS and PDENOIL differ, giving 15.8 and 403.7 mD, respectively. At h = 50 ft, the best k estimate is obtained depicting h = 50 ft as the thickness contributing to flow. At h > 50 ft, k drops below the k imputed in the model.

Using (34), k_ave = 47.3 mD is obtained, which is approximately close to that of BPR, hence a good estimate of the fluid phase permeabilities. A summary of the result is shown in Tables 2 and 5.

Table 2. K estimates for new approach versus conventional approach for scenario (a).

Parameters	Numerical density k (mD)	Equivalent h (ft)
BHP	50.8
PDENA	50.8
PDENG	15.8	50
PDENO	403.7
PDENW	50.8

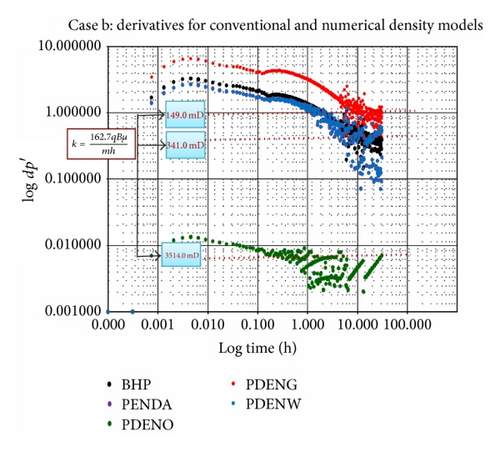
In scenario (b), the well is completed within the oil section to capture the pressure and fluid densities changes around the well. The derivative in Figure 7 shows a good radial flow but with noisy numerical artefact. It is likely that the boundary response is masked by numerical artefact. Also a continuous drop is seen after 10 hrs in the derivative.

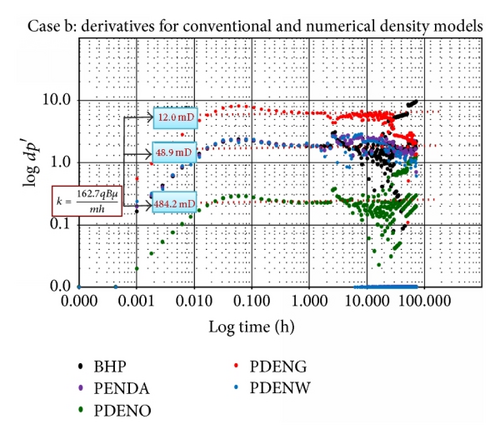
Using the estimated fluid phase permeabilities, k_ave from (34) is 47.2 mD as shown in Table 3, which is the same as scenario (a). This is in line with the uniform k used in the simulation model. Also the BPR gives a permeability value of 50.0 mD, which is the same for PDENDWA and PDENWAT but differs with PDENGAS and PDENOIL that give 12.1 and 484.4 mD, respectively. At h = 150 ft (60% of sand thickness and 83% of oil thickness), the estimated k is still within range (k = 48.9 mD). This indicates h = 50 ft or 83% of oil thickness contributing to flow.

Table 3. K estimates for new approach versus conventional approach for scenario (b).

Parameters	Numerical density k (mD)	Equivalent h (ft)
BHP	50.0
PDENA	50.0
PDENG	12.1	50
PDENO	484.2
PDENW	50.0

To test this approach in the gas column, the well was completed in between the gas and oil layer, which is considered as scenario (c) and scenario (d) with the well completed within the oil layer but with water injection after flowing and shut-in sequence. In both scenarios, the multiphase fluid distribution is triggered at the wellbore in order to capture the density changes for each phase and calculate fluid phase permeabilities. First, the well fluid densities equivalent pressures and pressures at bottom-hole for flowing and buildup test are generated.

The derivative for both scenarios declines after 3 hours probably due to fluid redistribution but is noisy (numerical artefact) in scenario (c) as shown in Figure 8. A good radial stabilisation for both the conventional method BPR and the density outputs PDENDWA, PDENWAT, PDENGAS, and PDENOIL is observed. Likewise, as obtained in scenarios (a) and (b), a good K_ave value of 57 and 52 mD from (34) is obtained for scenarios (c) and (d), respectively. This is slightly higher than k = 50 mD imputed in the simulation model.

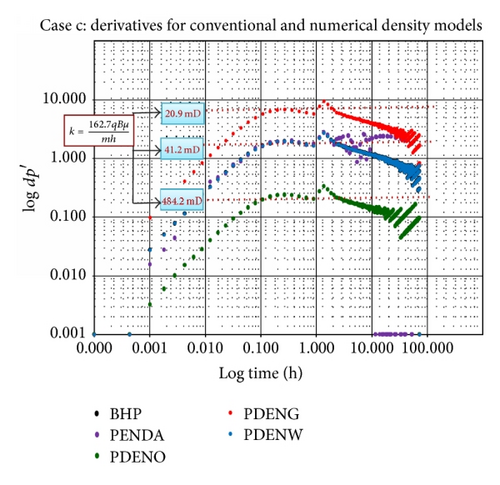
For each of the fluid phase permeabilities estimates, k value of 50 mD is obtained using the conventional BPR for scenario (c), which is in line with the uniform k in the simulation model. This is the same for the PDENDWA and PDENWAT. Also, at h = 150 ft (60% of sand thickness and 83% of oil thickness), the estimated k is still within range (k = 41.2 mD). This also indicates that h = 150 ft or 83% of oil thickness is contributing to flow. The k values for PDENGAS and PDENOIL are 20.9 and 484.2 mD, respectively. Summary of the result is shown in Table 4.

Table 4. K estimates for new approach versus conventional approach for scenario (d).

	Parameters	Numerical Density k (mD)	Equivalent h (ft)
Scenario (d)	BHP	50.0	100
	PDENA	50.0	100
	PDENG	17.5	50
	PDENO	490	250
	PDENW	50.0	100

Table 5. Comparison of K estimates between conventional and numerical density parameters.

Scenario	Numerical density method		Calculated K (mD)	Conventional k (mD)	Simulation model K (mD)	Relative K	% phase contribution to flow
Scenario	Phases	K (mD)	Calculated K (mD)	Conventional k (mD)	Simulation model K (mD)	Relative K	% phase contribution to flow
(a)	Gas	15.8				0.03	3.0
	Oil	403.7	47.3	50.8	50.0	0.86	86.0
	Water	50.8				0.11	11.0

(b)	Gas	12				0.03	2.0
	Oil	484.4	43.2	50.0	50.0	1.13	89.0
	Water	50				0.12	9.0

(c)	Gas	20.9				0.04	4.0
	Oil	484.2	57.0	50.0	50.0	0.86	87
	Water	50				0.09	9.0

(d)	Gas	17.5				0.03	3.0
	Oil	490	52.3	50.0	50.0	0.95	88.0
	Water	50				0.10	9.0

However, in scenario (d), the permeability value of 50.0 mD using the conventional BPR, which is the same for PDENDWA and PDENWAT, is only achieved if h = 100 ft (40% of sand thickness and 56% of oil thickness). PDENGAS and PDENOIL differ, giving 35.0 mD at h = 50 ft and 196.0 mD at h = 250 ft, respectively. This indicates the impact of water injection on densities and pressures changes around the well and consequently its impact on sand thickness contributing to flow. The drop in derivative curve in Figure 9 depicts the impact of the injected water.

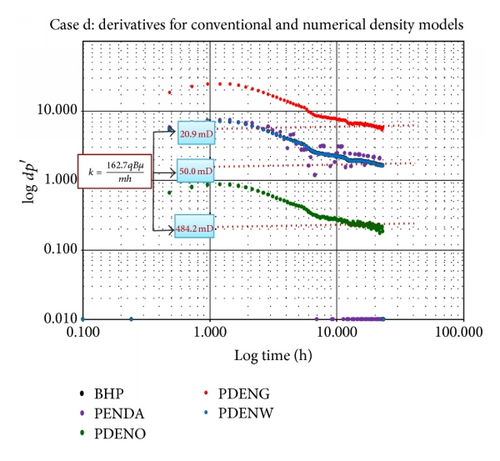
In summary, for scenarios (a) to (d), the k value of 50.0 mD is achieved if the thickness contributing to flow ranges from 50 to 150 ft. Generally, results indicate that, in all 4 scenarios investigated, the heavier fluid such as water and the weighted average pressure-density equivalent of all fluid give exact effective k as the BPR, likewise the density outputs PDENDWA and PDENWAT. Also results from Table 5 show that the empirical model from (34) with all fluid phase permeabilities gives an average effective k_ave of 47–57 mD, which is within that used in the simulation model and also the same as the estimated conventional approach. This approach provides an estimate of the possible fluid phase permeabilities and the % of each phase contribution to flow; hence, at several points, the relative k can be generated as shown in Table 5.

Example 2. To capture the influence of highly compressible fluid on estimated fluid phase permeabilities, an example on gas condensate reservoir (volatile system) was tested. Table 6 presents a summary of the well and reservoir synthetic data used for the buildup and drawdown simulated scenarios with additional information given below. It is required to generate the pressure equivalent and derivative for each fluid phase, compare their diagnostic signatures, and also determine the phases permeabilities and average reservoir permeability.

Table 6. Summary of reservoir simulations data.

Parameters	Design value
Eclipse model	Black oil
Model dimension	9 × 3 × 3
Length by width, ft by ft	1312 × 984
Thickness h, ft	150
Permeability Kx by Ky, mD	400.0 by 300.0
Porosity, %	30
Well diameter, ft	1.15
Initial water saturation Sw_i, %	60
Permeability, K, mD	400
Gas oil contact (GOC), ft	6890
Oil water contact (OWC), ft	6890
Initial pressure, P_i, psi	4495
Formation temperature, T, °C 120	200.0

Assumption. (i) Condensate reservoir is completed with one well.

(ii) LGR is imposed around the well and far across to account for pressure and density changes.

Gas, condensate, and water densities around the local grid refinement (wellbore) and WBHP were output using the simulator′s keywords. The following scenarios were evaluated.

(a)
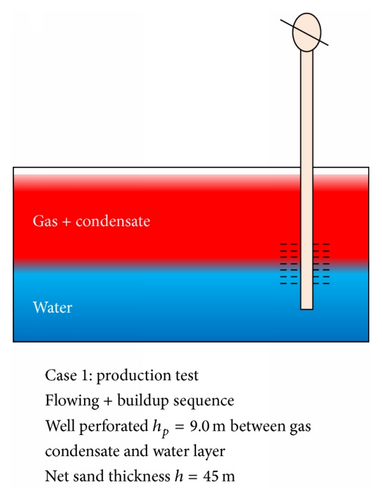
Flowing + buildup sequence: well perforated h_p = 30 ft between gas condensate and water layer. Net sand thickness h = 150 ft.
(b)
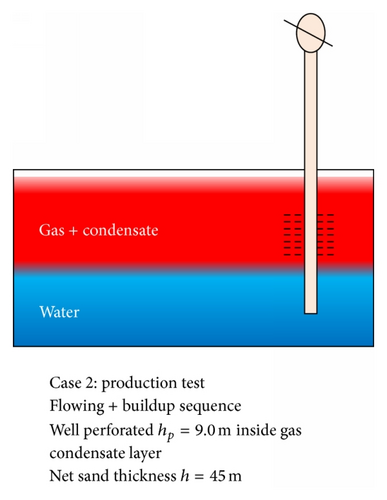
Flowing + buildup sequence: well perforated h_p = 30 ft inside gas condensate layer. Net sand thickness h = 150 ft.

Figure 10 shows the production and shut-in sequence for 2 scenarios in Example 2.

As in Example 1, the derivative in scenario (a) of Example 2 also shows good radial flow with no late time effect as seen in Figure 11. A negative half-slope fingerprint is seen at 0.3 to 3.0 hrs of buildup and a good stabilisation from 4.0 hrs in the model parameters.

The derivatives for all output parameters display the same well and reservoir fingerprint (2 flow periods, early to middle time response) but with different dp^′ stabilisation.

Permeability value of 370.7 mD was obtained from the conventional method BPR where k = 1637qT/mh is the same for the PDENDWA and PDENWAT, and m is obtained from the specialised plot. This is in line with the uniform k (kx = 400 mD and ky = 300 mD) imputed in the simulation model. However PDENGAS and PDENOIL differ, giving 35.0 mD and 3574.7 mD, respectively, if h = 148 ft.

Also the derivative in Figure 12 shows good radial flow and a negative half-slope fingerprint is seen at 0.5 to 2.0 hrs of buildup and a good stabilisation from 3.0 hrs in the model parameters. After 3 hrs of shut-in, some noisy data (numerical artefact) is seen in all the fluid phase derivatives but still good enough to identify dp^′ stabilisation.

For each of the fluid phase permeabilities, k value of 340.9 mD at h = 148 ft is obtained using BPR, which is the same for the PDENDWA and PDENWAT. PDENGAS and PDENOIL differ, giving 149.0 and 3514.1 mD at h = 148 ft, respectively.

For scenarios (a) and (b), a good k_ave value of 405.0 and 403.0 mD is obtained, respectively, from the empirical model (34) integrating all fluid phase permeabilities, which is within that used in the simulation model and the estimated conventional approach. From the 2 scenarios investigated, it has been demonstrated that the heavier fluid such as water and the weighted average pressure-density equivalent of all fluid give exact effective k as the conventional method BPR. A summary of the result is shown in Table 7.

Table 7. Summary of reservoir modelling properties imputed in eclipse model for case study 2.

	Parameters	Numerical density k (mD)	Equivalent h (ft)
Scenario (a)	BHP	371
	PDENA	371
	PDENG	142	148
	PDENO	3575
	PDENW	371

Scenario (b)	BHP	341
	PDENA	341
	PDENG	149	148
	PDENO	3514
	PDENW	341

This approach estimates the fluid phase permeabilities and the % of each phase contribution to flow at a given point; hence at several points the relative k can be generated as shown in Table 8.

Table 8. Comparison of K estimates between conventional and numerical density parameters.

Scenario	Numerical density method		Calculated K (mD)	Conventional k (mD)	Simulation model K (mD)	Relative K	% phase contribution to flow
Scenario	Phases	K (mD)	Calculated K (mD)	Conventional k (mD)	Simulation model K (mD)	Relative K	% phase contribution to flow
(a)	Gas	142.2				0.04	3.0
	Oil	3574.7	404.6	370.7	400	0.89	87.0
	Water	370.7				0.09	9.0

(b)	Gas	149				0.04	4.0
	Oil	3514.1	403.8	340.9	400	0.89	88.0
	Water	340.9				0.08	9.0

5. Density Related Radial Flow Equation Derivation for Each Fluid Phase

Radial diffusivity equation is given as

()

For oil,

()

For water phase,

()

For gas phase,

()

5.1. From Equation for Slight and Small Compressibility Such as Water and Oil

From (22),

()

Differentiating with respect to ρ,

()

From Darcy flow equation,

()

Substitute for ∂P:

()

To derive the analytical density transient equation for each phase, the following assumption/conditions are applicable.

For oil phase, from (35),

()

Initial condition is as follows:

()

BC at the wellbore is as follows:

()

BC at infirmity is as follows:

()

Using the Boltzmann transformation, consider the following.

Assuming η = ϕμcr²/kt,

()

Therefore

()

Differentiating with respect to r is equal to differentiating with respect to η; multiply by 2η/r.

From (35), the L.H.S is resolved as follows:

()

Equating (44) and (46), we have

()

This is the simplified ordinary differential equation of ρ as a function of η.

Apply boundary conditions as follows.

Initial condition is as follows:

()

Substituting (43) into (40),

()

Assume that m = η(∂ρ/∂η).

From (47),

()

Integrating from η = 0 to η,

()

Recall boundary condition

()

Recall that m = η(∂ρ/∂η).

Therefore,

()

Integrating from η = ∞ where ρ = ρ_i,

()

where

()

Assuming u = η/4, then ∂η/η = ∂u/u and u = ϕμcr²/4kt.

Hence,

()

where

()

Known as the exponential integral function defined by [13],

()

where x = ϕμcr²/4kt and

()

At large times, x will be small applying Taylor’s series and integrating

()

where γ is known as Euler’s number.

For 1/4x > 25, consider the following.

Then

()

Plotting ρ_w(t) versus ln(t) will yield a straight line at longer time and the slope of the line is given as

()

Therefore,

()

5.2. For Water Phase

The radial density equation is given as

()

Plotting ρ_w(t) versus ln(t) will yield a straight line at longer time and the slope of the line is given as

()

where

()

5.3. For Gas Phase

From equation for compressible fluid such as gas, consider the following.

From (32),

()

From the fundamental,

()

At standard condition,

()

where

()

Substitute into the equation, where

()

From the diffusivity equation for gas,

()

Initial condition is as follows:

()

BC at the wellbore is as follows:

()

BC at infirmity is as follows:

()

where R, P_sc, and T_sc are known as temperature, pressure, and gas constant at standard condition.

Therefore, integrating from η = ∞ where ρ = ρ_i,

()

where

()

Assume that u = (η/4) (∂η/η) = ∂u/u and u = ϕμcr²/4kt.

Hence

()

where

Known as the exponential integral function defined by [13],

()

where x = ϕμcr²/4kt and

At large times, x will be small applying Taylor’s series and integrating

()

where γ is known as Euler’s number.

For 1/4x > 25, consider the following.

Then,

()

Plotting

or m(ρ_w) versus ln(t) will yield a straight line at longer time and the slope of the line is given as follows:

()

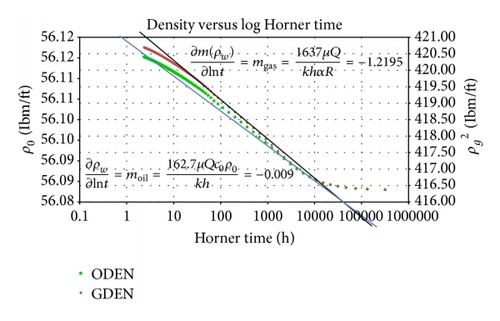
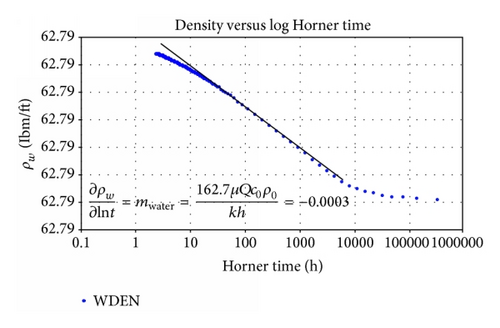
Example 3. Data from Example 1(a) was used for this case and the semilog plot of density for each phase (oil, water, and gas) is plotted against log of Horner time.

^∗∗Q used for k calculation is the average rate for all flowing periods.

From Figures 13 and 14, the calculated slopes of the radial flow for oil and water phases are given as

()

The estimated phase permeabilities are

()

Also, for the gas phase, consider the following.

The calculated slope from the semilog plot shown in Figure 13 is given as

()

And estimated gas permeability is

()

Using the empirical model for all three phases, the average estimated permeability is as follows:

()

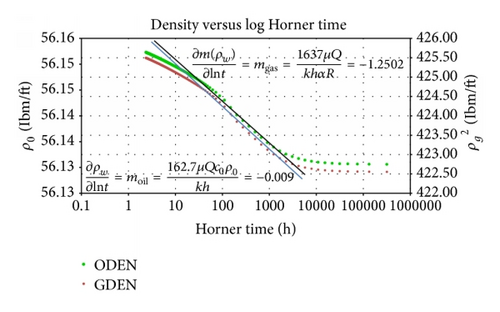
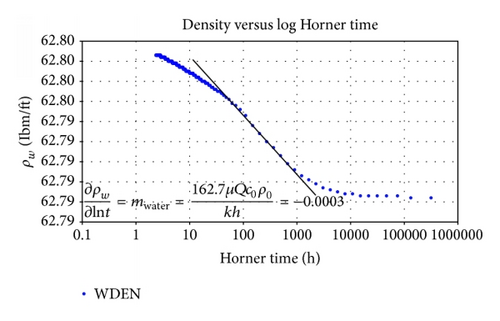
Example 4. Data from Example 1(c) was used for this case and the semilog plot of density for each phase (oil, water, and gas) is plotted against log of Horner time.

From Figures 15 and 16, the calculated slopes of the radial flow for oil and water phases are given as

()

The estimated phase permeabilities are

()

Also, for the gas phase, consider the following.

The calculated slope from the semilog plot shown in Figure 15 is given as

()

And estimated gas permeability is

()

Using the empirical model for all three phases, the average estimated permeability is as follows:

()

6. Conclusion

The following inferences were drawn from the six scenarios reviewed:

(i)
Results from the three-phase fluid empirical model developed for average effective k_ave estimation range between 47 and 57 mD for Example 1 and give 404 mD for Example 2, which is within that used in the simulation model and also estimated from BPR.
(ii)
The BPR, PDENDWA, and PDENWAT give the same stabilisation and the same k estimates making it suitable for interpretation of pressure transient analysis.
(iii)
It has been demonstrated in all 6 scenarios investigated that the heavier fluid such as water and the weighted average pressure-density equivalent of all fluid give exact effective k as the conventional method.
(iv)
For oil reservoir system (scenarios (a) to (d)), k = 50.0 mD is achieved if the thickness contributing to flow ranges from 50 to 150 ft while, for gas condensate reservoir (scenarios (a) to (b)), k ranges between 340 and 371 mD which is achieved if the net sand thickness h = 148 ft is contributing to flow.
(v)
This approach also provides an estimate of the possible fluid phase permeabilities and the % of each phase contribution to flow at a given point; hence, at several dp^′ stabilisation points, the relative k can be generated.
(vi)
The derivatives for all output parameters display the same wellbore and reservoir fingerprint as the BPR method.
(vii)
Generally, where output parameters (BPR, PDENOIL, PDENGAS, PDENWAT, and PDENDW) depict different fingerprint, the density derivative will serve as support to distinguish between reservoir and nonreservoir response.

Nomenclature

P:: Pressure, psi
T:: Temperature, oF
r:: Radius, ft
k:: Permeability, mD
Ø:: Porosity fraction
µ:: Viscosity, cp
t:: Time, hrs
q:: Production rate, bbl/day
B:: Formation volume factor, rb/Stb
Ct:: Total compressibility, psi⁻¹
rw:: Wellbore radius, ft
Δp:: Change in pressure, psia
h:: Formation thickness, ft
A:: Drainage area acres
Pwf:: Bottom-hole flowing pressure, psi
P_i:: Initial pressure, psi
Z:: Difference between two point/time series
i:: Subscript of an observed variable
c:: Subscript of a calculated variable
STEYX:: SSE of data point
n:: Number of data points
Cov:: Covariance of data point
δ:: Standard deviation
tp:: Cumulative production time
Cs:: Wellbore storage constant
:: Mean of data point.

Abbreviations

LBPR:: Local grid bottom-hole pressure
LDENO:: Local grid oil density
LDENW:: Local grid water density
LDENG:: Local grid gas density
WBHP:: Well bottom-hole pressure
BPR:: Well bottom-hole pressure
PDENOIL:: Pressure equivalent of LDENO
PDENGAS:: Pressure equivalent of LDENG
PDENWAT:: Pressure equivalent of LDENW
PDENDWA:: Pressure equivalent of density weighted average (LDENO, LDENG, and LDENW).

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

References

1 Jalali J., Mohaghegh S. D., and Gaskari R., Identifying infill locations and underperformer wells in mature fields using monthly production rate data, Carthage Field, Cotton Valley Formation, Texas, Proceedings of the SPE Eastern Regional Meeting, October 2006, Canton, Ohio, USA, SPE Paper 104550, 104550.
Google Scholar
2 Tiab D. and Kumar A., Application of PD function to interference analysis, Proceedings of the 51st Annual Fall Meeting of the Society of Petroleum Engineers of AIME, 1976, New Orleans, La, USA, Paper SPE 6053.
Google Scholar
3 Tiab D. and Kumar A., Detection and location of two parallel sealing fault around a well, Proceedings of the 51st Annual Fall Meeting of the Society of Petroleum Engineers of AIME, 1976, New Orleans, La, USA, SPE Paper 6056.
Google Scholar
4 Bourdet D., Whittle T. M., Douglas A. A., and Pirard Y. M., A new set of type curves simplifies well test analysis, World Oil. (1983) 196, no. 6, 95–106, 2-s2.0-0020750902.
Web of Science® Google Scholar
5 Zheng S. Y., Fighting against non-unique solution problems in heterogeneous reservoirs through numerical well testing, Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, September 2006, Adelaide, Australia, SPE 100951.
Google Scholar
6 Horne R. N. and Temeng K. O., Recognition and location of pinch-out boundaries by pressure transient analysis, SPE, 1981, no. 9905, Society of Petroleum Engineers.
Google Scholar
7 Ayestaran L. C., Nurmi R. D., Shehab G. A. K., and Elsi W. S., Welltest design and interpretation improved by integrated well testing and geological efforts, SPE, 1989, no. 17945.
Google Scholar
8 Massonnat G. J. and Bandiziol D., Interdependence between geology and well test interpretation, SPE, 1991, no. 22740.
Google Scholar
9 Du K. F. and Stewart G., Reservoir description from well test interpretation, North Sea Oil and Gas Reservoir—III, 1994, Norwegian Institute of Technology (NTH), 339–356.
10.1007/978-94-011-0896-6_31
Google Scholar
10 Zheng S. Y., Well testing and characterisation of meandering fluvial channel reservoirs [Ph.D. thesis], 1997, Heriot-Watt University.
Google Scholar
11 Biu V. T. and Zheng S. Y., A new approach in pressure transient analysis part I: improved diagnosis of flow regimes in oil and gas wells, Proceedings of the 3rd EAGE/AAPG Workshop on Tight Reservoirs in the Middle East, 2015, Abu Dhabi, United Arab Emirates.
Google Scholar
12 Horne R. N., Modern Welltest Analysis, 1995, Petroway, Palo Alto, Calif, USA.
Google Scholar
13 Matthews C. S. and Russell D. G., Pressure Buildup and Flow Tests in Wells, 1967, 1, SPE, Richardson, Tex, USA, Monograph Series.
10.2118/9780895202000
Google Scholar

All articles

A New Approach in Pressure Transient Analysis: Using Numerical Density Derivatives to Improve Diagnosis of Flow Regimes and Estimation of Reservoir Properties for Multiple Phase Flow

Abstract

1. Introduction

2. Theoretical Concept of the Density Derivatives

3. Software Suitability (Pressure Equivalent)

3.1. For Small or Constant Compressibility Fluid Such as Oil and Water

3.2. For Compressible Fluid in Isothermal Conditions

4. Density Weighted Average (DWA)

4.1. Empirical Model Correlation between Fluid Phases K

5. Density Related Radial Flow Equation Derivation for Each Fluid Phase

5.1. From Equation for Slight and Small Compressibility Such as Water and Oil

5.2. For Water Phase

5.3. For Gas Phase

6. Conclusion

Nomenclature

Abbreviations

Conflict of Interests

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley