We report on the inverse problem for the truncated Fourier series representation of f(x) ∈ BV(−L, L) in a form with a quadratic degeneracy, revealing the existence of the Gibbs-Wilbraham phenomenon. A new distribution-theoretic proof is proposed for this phenomenon. The paper studies moreover the iterative numerical solvability and solution of this inverse problem near discontinuities of f(x).

1. Introduction

This paper reinvestigates the Fourier series [1, 2] representation

()

of a piecewise continuous 2L –periodic signal f(x) ∈ BV(−L, L), with

()

The Gibbs phenomenon (see, e.g., [3]) is a statement of the fact that the infinite series g(x) tends to overshoot the positive corner of a discontinuity of f(x) by ~9% of the jump size and to undershoot the negative corner by the same amount. An overshoot/undershoot effect that is accompanied with spurious oscillations “ringing” near the discontinuity (as described in the appendix) when the series in (1) is truncated at m = N. However, according to a theorem by Fejer [1], the infinite series g(x) of a BV(−L, L) function converges to f(x) at each point x of continuity of f(x).

This shortcoming in the infinite Fourier series representation of piecewise continuous f(x) was first observed by H. Wilbraham in 1848 and then analyzed in detail [4] by J. W. Gibbs in 1898. The main reasons of the Gibbs-Wilbraham effect are that (i) not all frequencies (only integer ones) are employed in (1), (ii) a_m and b_m happen to decay slowly with increasing m, and (iii) the global nature of the approximation of f(x): the expansion coefficients are obtained, via (2), by integration over the entire period, including the points of discontinuity.

What is unpleasant though, with all of this, is that the Gibbs-Wilbraham effect is generic and is present for any periodic signal f(x) ∈ BV(−L, L) with isolated discontinuities. The presence of this effect can in fact lead to quite negative consequences when single infinite Fourier series, multiple infinite Fourier series, or even infinite wavelet series are employed to approximate signals of various dimensions, in many fields such as radio engineering and signal transmission.

The Gibbs-Wilbraham effect can nevertheless have both positive and negative consequences in different applications. The negative consequences call for Gibbs effect reduction, and this can in principle be achieved with the use [4] of a variety of filters. This effect can also be reduced theoretically and for all purposes. In addition to classical mathematical filters, recently (in 2011) Rim and Yun [5] defined a kind of spectral series to filter off completely the Gibbs effect near a discontinuity. The construction of this series is based on the method of adding the Fourier coefficients of a Heaviside function to the given Fourier partial sums.

This paper is organized as follows. After this introduction, we propose in Section 2 a new distribution-theoretic proof for the Gibbs-Wilbraham effect. In Section 3, we advance the inverse problem of the truncated Fourier series and the new stereographic truncated Fourier series and its relation to resolution of the undershoot/overshoot pair associated to the Gibbs-Wilbraham effect. Here we illustrate how solving the inverse problem for the truncated representation (1) contains a quadratic degeneracy that indicates the existence of the Gibbs phenomenon. Section 4 deals with the numerical iterative solution of the previous inverse problem and its convergence, with a proof and demonstration that stereographic projection does not affect such a numerical solution and its posedness.

2. Distribution-Theoretic Proof for the Gibbs-Wilbraham Effect

Let f(x) ∈ BV(−L, L) be a 2L –periodic piecewise continuously differentiable function on (−L, L), and let x_s be a point in (−L, L) at which f(x) has a discontinuity of the first kind. Consider

and

, and

, to assume, without loss of generality, that

and define the discontinuity jump by

()

Moreover,

()

Theorem 1. Let a 2L –periodic f(x) ∈ BV(−L, L) be discontinuous at x_s. The Fourier series representation g(x) of f(x) converges over (−L, L), as N → ∞ so as,

()

where ρ = u(0), an uncertainty.

Proof. According to distribution theory [6] when g(x) coincides a.e. with f(x) over (−L, L), it may always be differentiated; namely,

()

with δ as Dirac’s delta. Cancellation of this differentiation is performed by sweeping the x-axis during a compensating integration from −L to L. Indeed, integration of (6) first from −L to x leads to

()

and since g(−L) = f_c(−L), then

()

with u as Heaviside’s unit step function.

By a theorem of Fejer [1], g(x) should converge to f_c(x) when N → ∞, ∀x ≠ x_s on (−L, L). Hence the term Δ_su(x − x_s) in (8) can have a compact support only on an infinitesimal interval σ = lim_N→∞⁡σ_N = 0 to the right of x_s, that is, ending at . Hence

()

Furthermore, despite the fact that

, which is an uncertainty to be denoted by ρ. Consequently, relation (9) is representable as

()

Next complete the sweeping by integrating (6) from x to L; namely,

()

Here again since g(L) = f_c(L), then the left-hand side of (11) becomes −g(x) + f_c(x). The right-hand side requires standardization by means of the substitution τ = −ν, leading to dτ = −dν, [x, L] becoming [−x, −L] and

()

It is obvious then that (11) is reducible to

()

Repeated application of the same arguments employed in the derivation of (9)-(10) to (13) allows for writing it as

()

and subsequently in the form

()

Taking into consideration that

and

in (10) and (15), respectively, then combining these equations with Dirichlet’s theorem [1] leads to the required result.

It should be pointed out that in the previous proof relations (10) and (15) say nothing specifically about the behavior of g(x) at and , respectively, while asserting the existence of a spiky behavior of g(x) individually at then at . Moreover, the uncertainty ρ had been resolved in the past (by Wilbraham; see also the Appendix) computationally to satisfy ρ = 0.09 and long before the advance of the theory of distributions (generalized functions) by S. L. Sobolev in 1936. The number 0.09 for ρ remains until now, however, a mysterious theoretical puzzle that calls for a rigorous distribution-theoretic justification.

Clearly, in the neighborhood of x_s, g(x) can only be a rudimentary approximation to f(x), even when N → ∞, with an added spike pair

()

. Relation (16) represents the Gibbs-Wilbraham effect which, due to the fact that

, is not practically computable. This effect degenerates, however, when N is finite, to an undershoot-overshoot pair

on an interval

, splitted by Δ_s at x_s. In this case, it is always possible to compute

()

Furthermore, since

, then these computations with (17) over

can reveal only a feature

, associated with the Gibbs-Wilbraham effect Q_s(x) but not the effect itself.

3. The Inverse Problem for Truncated Fourier Series

Substitution of any value of x ∈ [−L, L] in (1) yields a number c = g(x), which may differ [2] from f(x) by

if x is in the neighborhood of a discontinuity of f(x). Obviously c satisfies, the nonlinear in x, trigonometric series equation

()

which is, however, linear in the data

Definition 2 (the inverse problem for the truncated Fourier series representation). Given a number c = g(x) satisfying (18), what is the corresponding x?

This inverse problem happens to be a discretized version of the similar deconvolution problem [4] of x from a given number q in a singular first kind integral equation of the form

()

in which γ represents the data. It is well known, additionally (see, e.g., [7, 8]) that this deconvolution problem can be computationally ill-posed if an arbitrarily small deviation of the γ data may cause an arbitrarily large deviation in the solution x. This situation may further prevail when the operator

does not continuously depend on γ.

Moreover, the inverse problem of the previous definition has a unique solution that satisfies (19) and is expected to accept a double root when the horizontal line h(x) = c > f(x) intersects with a sharp peak (overshoot) of a truncated g(x). We shall call this feature a duplicated (quadratic) degeneracy of the solution for this inverse problem.

The existence of the Fourier series truncation peak (and the corresponding two roots for x) is not directly evident from the structure of G(γ, x, m), and despite its linearity in the data .

3.1. The Tangent Half-Angle Stereographic Projection

The tangent half-angle substitution (the Euler-Weirstrass substitution [9]) tan⁡(θ/2) is widely used in integral calculus for finding antiderivatives of rational expressions of circular function pairs (cos⁡θ, sin⁡θ). Geometrically the construction goes like this: draw the unit circle, and let P be the point (−1,0). A line through P (except the vertical line) passes through a point (cos⁡θ, sin⁡θ) on the circle and crosses the y-axis at some point y = t. Obviously t determines the slope of this line. Furthermore, each of the lines (except the vertical line) intersects the unit circle in exactly two points, one of which is P. This determines a function from points on the unit circle to points on a straight line. The circular functions determine therefore a map from points (cos⁡θ, sin⁡θ) on the unit circle to slopes t. In fact this is a stereographic projection [9] that expresses these pairs in terms of one variable: tan⁡(θ/2) = t.

Numerical algorithms employing these trigonometric pairs like Fourier series (1) could in principle be influenced by such a projection. In this context, the tangent half-range transformation relates the angle θ_m = m(π/L)x to the slope t_m = tan⁡(θ_m/2) of a line intersecting the unit circle centered around (0,0).

Indeed as θ_m varies, the point (cos⁡θ_m, sin⁡θ_m) winds repeatedly around the unit circle centered at (0,0). The point

()

goes only once around the circle as t_m goes from −∞ to ∞ and never reaches the point (−1,0), which is approached as a limit when t_m → ±∞.

Clearly the stereographic projection t_m = tan⁡(θ_m/2) is defined on the entire unit circle except at the projection point P : (−1,0). Where it is defined, this mapping is smooth and bijective [9]. It is conformal, meaning that it preserves angles. it is however not isometric; that is, it does not preserve distances as

()

The rest of this section illustrates how stereographic projection of Fourier series reveals a quadratic degeneracy that indicates the existence of the Gibbs-Wilbraham effect. It also addresses the question of solving the inverse problem for the truncated Fourier series representations. The impact of stereographic projection on the ill-posedness of the numerical solution of this inverse problem is moreover a main question that has been addressed in this paper.

Our analysis starts however by illustrating how the tangent half-angle stereographic projection can provide a new insight into the behavior of truncated Fourier series near a discontinuity of f(x).

Lemma 3. The solution x of the inverse problem for the truncated Fourier series representation satisfies

()

Proof. By studying solvability for x of (18) Let t_m = tan⁡m(π/2L)x, and then , and . Further consideration of these facts in (18) leads to the tangent half-angle stereographically transformed, , form

()

The harmonic trinomial in the left-hand side of (23) has two harmonic zeros, , for each x; namely,

()

It is worth noting at this point that these

zeros should, by no means, be confused with the possible roots of the x variable. Substitution then of (24) in (23) leads to

()

which is the same as

()

The quadratic degeneracy of the harmonic zeros of t_m can disappear only when σ_m = 0, for all m. And this happens to be equivalent with

()

Obviously, satisfaction of (27) by (26) reduces it to the equation

()

which is the same as

()

It is interesting to remark that condition (27) is entirely different from

()

which can be derived from the Parseval identity [1] (completeness relation)

()

Hence a possible nondegenerate solution for x of the nonlinear equation (29) is, on one hand, fundamentally incorrect, because it involves a violation of (30) and Parseval’s identity. On the other hand, a consistent solution x, in the sense of satisfaction of (31), is intrinsically degenerate because of its emergence, as a must, from the nonlinear equation (26), which rewrites as

()

Equation (32) is easily transformable to the required result (23); here the proof completes.

3.2. The Stereographic Fourier Series

To further analyze the variability of stereographically projected Fourier series, we make the substitution

()

in G(γ, x, m) to rewrite it as

()

The tangent half-angle (stereographic) transformation t_m = tan⁡(θ_m/2) or θ_m = 2tan⁻¹⁡t_m is conceived as

()

and subsequently

()

It is clear then that this stereographic projection effectively leads to insertion of an additional bracket into the composition of G as a function of x. This paves the way to the definition

()

Proposition 4. The following:

()

always holds.

Proof. Since N is finite, then the proof of implies the correctness of this proposition. So let us differentiate G(x) = G[θ_m(x)] with respect to x by applying the chain rule; namely,

()

which is the same as

()

Take then the

transformation of the previous relation to arrive, after some algebra, at

()

Invoke then

()

to differentiate it with respect to x as

()

which is the required result.

Let us rewrite (1) in the form

()

then try to differentiate it term-by-term as

()

where G^∗(γ, x, m) is the harmonic conjugate of G(γ, x, m). The trigonometric series

is called the trigonometric series conjugate (see, e.g., [10]) to g(x).

In addition to the fact that the convergence of g^∗(x) can sometimes become worse than convergence of g(x) (see, e.g., [10]) the presence of the m(π/L) factor in (d/dx)g(x) can aggravate the convergence problem of (45) when the coefficients a_m and b_m do not decay fast enough.

Next we may stereographically transform (∂/∂x)g(x), using the notation

, where

()

Similarly, for the stereographic Fourier series representation

()

in which

()

we may approximate (44) by

()

Differentiate then (49) term-by-term as

()

Note here that

()

is the harmonic conjugate of H(γ, x, m) and that

()

This rather interesting fact leads to a remark that follows.

Remark 5. Away from points of discontinuity of f(x), the stereographically transformed differentiated Fourier series , which defines , is the same as the derivative , which defines H^∗(γ, x, m), of the stereographic Fourier series . Moreover, even at points of discontinuity of .

Theorem 6 (see [1].)Let f(x) be (i) continuous on [−L, L] such that (ii) f(−L) = f(L), and let (iii) f^′(x) be piecewise continuous over [−L, L]; then the corresponding Fourier series g(x) of (1) or (47) is differentiable at each point where (iv) f^′′(x) exists.

The previous remark can incidentally have useful applications when differentiating certain slowly converging Fourier series, as illustrated by the following example.

Example 7. Consider the 2π-periodic odd signal f(x), defined over one period, by f(x) = x. Its Fourier series is known to be

()

that is, with a_m = 0, ∀m, b_m = 2((−1) ^m+1/m), and m(π/L) = m.

Differentiating term-by-term, we obtain

()

which is not uniformly convergent because f(x) is not only discontinuous at x = ±π but f(−π) ≠ f(π) and f^′′(±π) does not exist. In particular, at x = 0, the sum of the series

oscillates between 0 and 1, that is, divergent. It is also well known, nevertheless, that the series

is C − 1 summable [1, 2] to 1/2 and that turns out to yield the right answer g^′(0) = f^′(0) = 1. Moreover, at x = π, the sum of the series

, that is, divergent.

Alternatively, by means of (47)

()

and by means of (46)

()

Here, at x = π, the sum of the series

is also divergent.

Note in general that, for even signals, that is, when b_m = 0, ∀m, it follows from (22) that

()

Moreover, for odd signals, that is, when a_m = 0, ∀m, the situation is not of the same clarity.

Indeed, according to (22),

()

which is an uncertainty. Luckily however this uncertainty is not an essential one and can straightforwardly be resolved by resorting to the stereographic form (23) of (22), which yields the correct result

()

Also when b_m = 0, ∀m,

()

and this is resolvable in a similar fashion.

Both G(γ, x, m), of (2), and H(γ, x, m), of (22), equivalent forms are nonlinear trigonometric functions of the x solution. However, while G(γ, x, m) is linear in , thestereographic H(γ, x, m) is nonlinear in this γ. This can raise a question on a possibility for at singular points of f(x). A question that will be answered negatively in the next section. Furthermore, since the data is discrete, then the operators and do not depend continuously on γ, and this is the main reason for ill-posedness of the present inverse problem.

In conclusion, the quadratic degeneracy of the solution of the present inverse problem, explicit when using H(γ, x, m), is a nonlinear indicator of the existence of the peak pertaining to the Gibbs phenomenon. However, the numerical ill-posedness, associated with the relative values of a trial iterative variable in the γ set, happens to remarkably remain invariant under the tangent half-angle stereographic projection.

Following the same arguments of Wilbraham, we may cancel the artificially induced differentiation by integrating (50) to represent the stereographic Fourier series

in integral form as

()

4. Numerics of Solving the Inverse Problem

The solution of the present inverse problem is in fact a problem of finding the roots of (44) when g(x) is truncated at m = N. For that reason, we shall focus on such roots in the neighborhood of a step-like discontinuity of f(x) at x = x^o, say, where f(x^o − ε) < f(x^o + ε), 0 < ε ≪ 1. The associated with the Gibbs phenomenon overshoot of or over f(x^o + ε) and undershoot of this g(x) below f(x^o − ε). The intersection of a horizontal line h(x) = c ≥ f(x^o + ε), corresponding to φ(x) = 0, can be at two points α₁ and α₂ on both sides of the peak location α₀, representing two distinct roots of φ(x) = 0. It can also be at one point α₀, corresponding to the maximum of the truncated g(x); that is, a double root of φ(x) = 0.

Obviously,

, where

and

are possible points of inflection, defined by

()

The existence of both

and

or at least one of them, namely,

, is however not mandatory. Moreover, for the α₁, α₀, and α₂ points we expect to have

()

Equation (44) can be solved for x : φ(x) = 0 by a Newton-Raphson (see, e.g., [11, 12]) iterative process

()

which is repeated until a sufficiently accurate value is reached. This process, for each series truncation number N, rewrites as

()

or in the stereographic form

()

which is the same as

()

and is started off with some rather free initial value x₀. Obviously here t_m = tan⁡m(π/2L)x.

The sequence {x_n} will usually converge, provided that x₀ is close enough to the unknown zero α and that

()

4.1. Computation of the Peak Location α₀

Being a maximization problem for φ(x) = 0, the determination of α₀ by the Newton-Raphson process [11] becomes

()

in stereographic form.

Straightforwardly, this process can be expressed as

()

or in the stereographic form

()

which is the same as

()

It is remarkable how this algorithm is distinctively independent of c.

Proposition 8. The ill-posedness of the inverse problem of the truncated Fourier series is invariant under stereographic projection.

Proof. The tangent half-angle stereographic projection, though not isometric (distance preserving), is nevertheless variability preserving. Indeed, the main ingredients of this inverse problem are, namely, , c, and x₀, with . Under this projection θ_m(x₀) transforms to t_m(x₀) = tan⁡⁡[θ_m(x₀)/2], and G[θ_m(x₀)] transforms to H[t_m(x₀)]. But according to Proposition 4, . Hence the variation of G(γ, x₀, m) with x₀ in the Fourier series inverse problem and the variation of H(γ, x₀, m) with x₀ in the stereographic form are identical.

Equivalently, this makes the ill-posedness of this inverse problem invariant under stereographic projection.

Expected manifestations of the correctness of this proposition are as follows: (i) the results of computations by the (71) and (73) algorithms for α₀ with the same x₀ must be identical and (ii) the results of computations by the (65) and (67) algorithms for α₁ (or α₂) with the same x₀ and c must also be identical.

4.2. Convergence Analysis

Let us focus first on the convergence of the iterative process (65) or (67). In many situations where term-by-term differentiability does not hold, the Newton-Raphson method can always be replaced by some quasi-Newton method [12, 13], where φ^′(x_n) or ψ^′(x_n) in (65) or (67) is replaced by a suitable approximation. For example, in the chord method φ^′(x_n) is replaced by φ^′(x₀) for all iterations.

If ϵ_n = α − x_n, ϵ_n+1 = α − x_n+1 and β_n is some point between x_n and α, it can be easily proved (see [11] or [12]) that

()

Taking absolute value of both sides gives

()

implying quadratic convergence; that is, ϵ_n is squared (the number of correct digits roughly doubles) at each step. The same arguments apply of course to the ψ(x) = 0 equation.

In actual fact for a distinct α the convergence of {x_n} in (65)–(67) is at least quadratic in the neighborhood of this α. The process may face a difficulty when

diverges. This is however a special but not a general problem, and (75) always holds if the following conditions are satisfied:

(i)
φ^′(x) ≠ 0, ∀x ∈ I, where I = [α − η, α + η] for some η ≥ |(α − x₀)|.
(ii)
φ^′′(x) is finite ∀x ∈ I.
(iii)
x₀ is sufficiently close to α.

The term sufficiently close in this context means the following:

(a)
Taylor approximation is accurate enough such that we can ignore higher order terms.
(b)
(1/2)|φ^′′(x_n)/φ^′(x_n)| < K|φ^′′(α)/φ^′(α)| for some K < ∞.
(c)
K|φ^′′(α)/φ^′(α)|ϵ_n < 1 for .

Consequently, (75) can be expressed in the following way:

()

where

()

The initial point x₀ has to be chosen such that conditions (i) through (iii) are satisfied, where the third condition requires that M|ϵ₀| < 1. Moreover, with increasing N the distance |α₁ − α₂| is known to decrease in a way making the satisfaction of these conditions very difficult and actually impossible as N → ∞. Here it should be underlined that the iterative method (65)–(67) may fail to converge to the α root in the following situations:

(i)
If a point like α₀ is included in I, the method will terminate due to division by zero.
(ii)
When the initial estimate x₀ is poor, the pertaining wrong I can contribute to nonconvergence of the algorithm.

As for convergence of the Newton-Raphson process towards α₀, let ε_n = α₀ − x_n, ε_n+1 = α₀ − x_n+1, and θ_n is some point between x_n and α₀, to arrive at

()

The convergence of {x_n} in (71)–(73) is at least quadratic in the neighborhood of this α₀. The process may face a difficulty, however, when

or ψ^′′(x_n) diverges. Moreover (79) always holds if the following conditions are satisfied:

(i)
φ^′′(x) ≠ 0, ∀x ∈ I, where I = [α₀ − η, α₀ + η] for some η ≥ |(α₀ − x₀)|.
(ii)
φ^′′′(x) is finite ∀x ∈ I.
(iii)
x₀ is sufficiently close to α₀.

Sufficient closeness in this context means that

(a)
Taylor approximation is accurate enough such that we can ignore higher order terms;
(b)
(1/2)|φ^′′′(x_n)/φ^′′(x_n)| < K|φ^′′′(α₀)/φ^′′(α₀)| for some K < ∞;
(c)
K|φ^′′′(α₀)/φ^′′(α₀)|ε_n < 1 for .

Consequently,

()

where

()

4.3. Applications

The standard iterative algorithms, (71) or (73), for finding the location of overshoots in of the Gibbs effect employ the fact that the first derivative of a peak, in g(x) or , respectively, has a downward-going-zero-crossing at the peak maximum. But the presence of many neighboring smaller peaks in the ringing close to the overshoot will cause many undesirable zero-crossings to be invoked if the initial trial root x₀ is not correctly chosen. This fact makes the numerical problem of peak finding in the Gibbs effect of pathological difficulty. A difficulty that aggravates with the increase in the number N of truncated terms in the employed Fourier series. Indeed, with the increase of N the number of undesirable zero-crossings increases in the neighborhood of α₀, as illustrated in Section 1. This can increasingly lead to oscillatory and even unstable values in sequence {x_n}, the more the distance |x₀ − α₀| contains unwanted zero-crossings.

These problems have been resolved in the two examples that follow, which simultaneously illustrate the applicability of Proposition 8.

Example 9. Consider the 2π-periodic odd signal f(x), of Example A.1, defined over one period, by

()

which has, for each truncation number N, the truncated Fourier series approximations

()

This signal has a jump discontinuity at x = 0 of magnitude 2. We shall focus our computations on the Gibbs phenomenon overshoot near this discontinuity.

Here is a printout list of results for the parameters of the posing inverse problem, via computations by both the direct and stereographic algorithms.

It is remarkable how results by both algorithms are practically identical and share the same following features that are observed by results of the direct algorithm, discussed below.

Case I (N = 40). The computations of α₀ for the previous example, using (71), with x₀ = 0.02 lead to x₁ = 0.039 109; this varies quickly with n (only beyond the 4th decimal) to stabilize towards x₃ = x₄ = x₅ = ⋯ = 0.039 299 = α₀. Here using (1) gives g(α₀) = g(0.039 299) = 1.179 030, which is quite close to the theoretically expected value, by (A.7), of ~1.18.

Then using (65) for c = 1.09 and x₀ = 0.000381 leads to x₁ = 0.021 697; this varies quickly with n (only beyond the 3-d decimal) to stabilize quickly towards x₅ = x₆ = x₇ = ⋯ = 0.028 368 = α₁. Also using (65) for c = 1.09 and x₀ = 0.04 leads to x₁ = 0.067 699; this varies quickly with n (beyond the 2nd decimal) to stabilize quickly towards x₅ = x₆ = x₇ = ⋯ = 0.052 873 = α₂.

For both α₁ and α₂, using (1) yields g(α₁) = g(0.028368) = g(α₂) = g(0.052873) = 1.09 = c, as expected.

Case II (N = 100). Computations of α₀, using (71), with x₀ = 0.02 lead to x₁ = 0.014 221; this varies quickly with n (only beyond the 4th decimal) to stabilize towards x₃ = x₄ = x₅ = ⋯ = 0.015 708 = α₀. Here using (1) gives g(α₀) = g(0.015708) = 1.178 990. This result appears to be slightly excessive, perhaps due to increased rounding off errors with increasing N to 100.

Then using (65) for c = 1.09 and x₀ = 0.015 237 leads after a negative value to x₂ = 0.014 462; this varies with n (beyond the 2nd decimal) to stabilize quickly towards x₇ = x₈ = x₉ = ⋯ = 0.011 3348 = α₁. The used value of x₀ is apparently not appropriate, and this illustrates the generic ill-posedness of this inverse problem.

The pertaining computations of α₂, with x₀ = 0.017000, lead to x₁ = 0.020 434; this varies with n (beyond the 3-d decimal) to stabilize quickly towards x₄ = x₅ = x₆ = ⋯ = 0.021 149 = α₂.

For both α₁ and α₂, using (1), yields g(α₁) = g(0.0113348) = g(α₂) = g(0.021149) = 1.09 = c, as expected.

Case III (N = 150). The computations of α₀, using (71), with x₀ = 0.005 lead to x₁ = 0.010 595; this varies insignificantly with n (only beyond the 4th decimal) to stabilize towards x₃ = x₄ = x₅ = ⋯ = 0.010 472 = α₀. Here using (1) gives g(α₀) = g(0.010472) = 1.178 980, which does not significantly differ from g(α₀) when N = 100.

Then using (65) for c = 1.09 and x₀ = 0.010 158 leads after a negative value to x₂ = 0.009 643; and this varies (beyond the 3-d decimal) to stabilize quickly towards x₇ = x₈ = x₉ = ⋯ = 0.007 565 = α₁.

The pertaining computations of α₂, with x₀ = 0.010 800, lead to x₁ = 0.025 998; this varies (beyond the 2nd decimal) to stabilize towards x₁₄ = x₁₅ = x₁₆ = x₁₇ = x₁₈ = ⋯ = 0.014 099 = α₂.

For both α₁ and α₂, using (1) yields g(α₁) = g(007 565) = g(α₂) = g(0.014 099) = 1.09 = c.

During the previous computations, summarized in Table 1, it has been observed that varying x₀ in the present Newton-Raphson process, for all N, can lead to strong oscillations and even completely unstable values for α₀, α₁, and α₂ of the Fourier series inverse problem, which though ill-posed is practically regularizible. Apart from this drawback, the (71) with (65) iterative algorithms (i) converge quickly to the theoretically expected values and are (ii) of demonstrated stability of the iterations, for properly chosen x₀ (which act as effective regularizing parameters). Moreover, computations by the stereographic algorithm, invoking (73) and (67), share the same magnitude and convergence rates with results by the direct algorithm. Finally, it is demonstrated that the present signal exhibits an overshoot, when N = 150, of ~9% of a jump discontinuity, of magnitude 2, that is, located at a distance of ~0.0105.

To illustrate robustness of both numerical algorithms and their possible effective regularizibility we shall study also the numerical inverse problem for the Fourier series representation of an arbitrary (nonsymmetric) periodic signal.

Table 1. Results of computations for Example 9.

N	α₁	α₀	α₂
40	0.028 368	0.039 299	0.052 873
100	0.011 335	0.015 705	0.021 149
150	0.007 565	0.010 472	0.014 099

Example 10. Consider the 2π-periodic signal f(x), defined over one period, by

()

It has, for each truncation number N, the truncated Fourier series approximations

()

This signal has, like the signal of Example 9, a jump discontinuity at x = 0 of magnitude 2. For the sake of comparison, we shall also focus our computations on the Gibbs phenomenon overshoot part of near this discontinuity.

It should be noted here that the results by both algorithms, summarized in Table 2, are also identical, a feature indicating that the degree of ill-posedness of the posing inverse problem is not affected, as predicted by Proposition 8, by the tangent half-angle stereographic projection.

Table 2. Results of computations for Example 10.

N	α₁	α₀	α₂
40	0.0564765	0.0781391	0.105155
100	0.0226546	0.0313516	0.0422024
150	0.0151124	0.0209153	0.028156

Case I (N = 40). The computations of α₀ for this example, using (71) and (73), with x₀ = 0.03 lead to an identical sequence {x_n} that converges by both algorithms after the x₄ iteration to 0.078 139 with .

Case II (N = 100). The computations of α₀, with x₀ = 0.01, lead to an identical sequence {x_n} that converges by both algorithms after the x₅ iteration to 0.031 351 with .

Case III (N = 150). The computations of α₀, with x₀ = 0.007, lead also to an identical sequence {x_n} that converges by both algorithms after the x₅ iteration to 0.020 915 with .

Therefore the present signal exhibits an overshoot when N = 150, of ~9% of a jump discontinuity of magnitude 2, that is, located at a distance of ~0.020 9.

Comparison of the computed Gibbs overshoot parameters of the two considered signals with jump discontinuities at the same x = 0 of the same magnitude illustrates that the relative size of the overshoot depends essentially exclusively on the magnitude of the stimulating jump discontinuity. For instance, based on the present numerical results, one can suggest here that nonsymmetric signals have equal overshoots with symmetric signals. Their respective α₀’s are however different. Indeed the nonsymmetric signal has a significantly larger α₀ (0.020 9) than the α₀ (0.0105) of the symmetric signal.

A further analysis has also been performed of Example 10 with N = 100,200,300, to compute the corresponding α₀ with α₁, α₂ that correspond simultaneously to c = 1.08,1.10,1.12 as illustrated in Figure 1. Results of these computations are summarized in Table 3 and then used for the partial plots, of Figure 2, that interpolate α₁, α₂ (for c = 1.08,1.10,1.12) with α₀, for each N = 100,200,300. In this table x_∗ stands for the first convergence step of the {x_n} sequence of Newton Raphson iterations.

Table 3. Summary of computations of all overshoot parameters in Example 10.

α₀ results
N	x₀	x_∗	α₀	g(α₀)
100	0.030	x₃	0.031 3516	1.178 87
200	0.015	x₃	0.015 6919	1.178 92
300	0.008	x₃	0.010 4648	1.178 94

α₁ results
N	x₀	x_∗	α₁	c

	0.025	x₄	0.022 2027	1.08
100	0.025	x₃	0.023 1344	1.10
	0.025	x₃	0.024 2027	1.12

	0.010	x₃	0.011 1117	1.08
200	0.010	x₃	0.011 5779	1.10
	0.010	x₄	0.012 1123	1.12

	0.008	x₃	0.007 410 08	1.08
300	0.008	x₃	0.007 720 95	1.10
	0.008	x₂	0.008 077 32	1.12

α₂ results
N	x₀	x_∗	α₂	c

100	0.35	x₄	0.042 9439	1.08
	0.35	x₄	0.041 4445	1.10
	0.35	x₄	0.039 8513	1.12

200	0.018	x₃	0.021 4960	1.08
	0.018	x₃	0.020 7456	1.10
	0.018	x₃	0.019 9483	1.12

300	0.012	x₃	0.014 3360	1.08
	0.012	x₃	0.013 8356	1.10
	0.012	x₄	0.013 3039	1.12

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Plots of g(x) near a discontinuity of f(x) in Example 10.

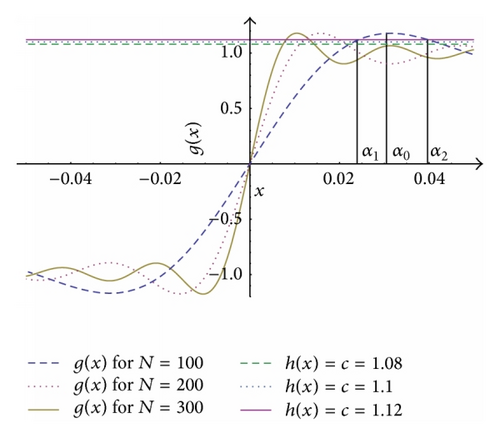
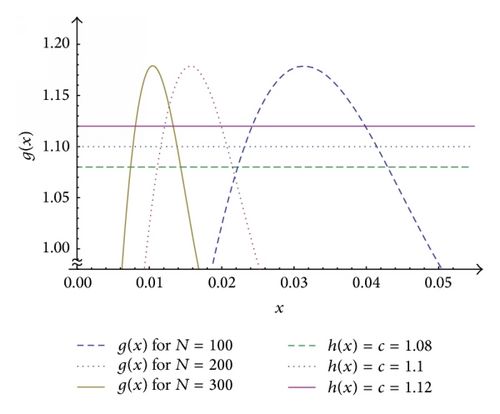
These results turn out to be extremely stable against variations of the trial initial root x₀. Indeed, in the computationally most difficult situation, namely, when N = 300, a change of x₀ from 0.008 to 0.020 leads to a variation of x_∗ from x₂ to just x₆ with the same asymptotic α₀ = 0.0104648 and α₁ = 0.00807732 (for c = 1.12).

5. Conclusions

This paper demonstrates that the quadratic degeneracy of the solution of the present inverse problem, explicit when using H(γ, x, m), is a nonlinear indicator of the existence of Gibbs’ phenomenon. It provides also a distribution-theoretic proof for the existence of this phenomenon. The reported analysis of numerical solvability of this problem illustrates the following:

(i)
When converge continuously in x and are nonzero at α₁ (or α₂), there exists a neighborhood (defined by I) of α such that, for all starting values x₀ in the neighborhood, {x_n} will converge to α₁ (or α₂).
(ii)
When converge continuously in x and are nonzero at α₁ and α₂ (but not at α₀) and if φ(x) has a second derivative, which might be zero, at α₁ and α₂ (and at α₀) then the convergence of {x_n} is quadratic or faster. If φ^′′(x) ≠ 0 at α₁ and α₂, then the convergence of {x_n} is merely quadratic.
(iii)
The convergence of the Newton-Raphson iterative process to α₀ can also be quadratic, but restrictions on the derivatives of φ(x) have to be observed up to the third order. Otherwise, the convergence of {x_n} to α₀ can slow down to become only linear [12] with a rate .
(iv)
The reported computations clearly illustrate that α₀ → 0 and |α₁ − α₂| → 0 when N → ∞; that is, the infinite Fourier series will sum to f(x) in the neighborhood of a discontinuity, except at the discontinuity itself.

Conflict of Interests

The author declares that there is no conflict of interests regarding the publication of this paper.

Acknowledgment

The numerical computations of Examples 9 and 10 have been performed, using Mathematica 8, by Mounir Abou Yassine, of the Department of CCE of AUL.

Appendix

To illustrate the Gibbs-Wilbraham effect we shall use here the same arguments employed by Wilbraham in 1848 in analyzing a similar square wave.

Example A.1. Let f(x) be a square wave periodic signal, which is defined over one period by

()

Its Fourier series representation is

()

This defines the truncated series

()

which may be differentiated as

()

Since

()

then

()

It is possible to cancel the previous artificially induced differentiation by integrating the last result as

()

This integral starts at zero when x = 0 in agreement with (A.2) and increases until 2Nξ = π. Then ξ = π/2N defines a turning point x₁. The integral starts to decrease, at which point the numerator sin⁡2Nξ goes negative. For large N the denominator sin⁡ξ remains positive.

The form (A.7), distinctively from (A.3), reveals that S_N(x) has turning points at the zeros of sin⁡2Nξ. These occur when 2Nξ = rπ; r = 1,2, 3,4, 5, …, that is, at ξ = r(π/2N). Clearly then x_r ~ ξ_r = r(π/2N) are turning points for S_N(x). In particular x₁ ~ ξ₁ = π/2N defines the overshoot peak location α₀ and is its magnitude. To evaluate S_N(x₁) = S_N(α₀) numerically, let us change the variable of integration; namely, 2Nξ = w, or ξ = w/2N, to rewrite the previous integral as . Clearly when N → ∞, sin⁡w/2N = w/2N, and

()

correct to two decimal points.

As for x₂, x₃, x₄, …, x_r, …, lim_N→∞⁡[S_N(x_r) − f(x)] decreases as we move away from the discontinuity, but it should be remarked however that the location of the overshoot α₀ = x₁ = π/2N moves towards the discontinuity according to

()

References

1 Butzer P. L. and Nessel R. J., Fourier Analysis and Approximation, Volume I: One-Dimensional Theory, 1971, Birkhäuser.
10.1007/978-3-0348-7448-9
Google Scholar
2 Edwards R. E., Fourier Series: A Modern Introduction, 1967, Holt, Rinehart & Winston.
Google Scholar
3 Thompson W. J., Fourier series and the Gibbs phenomenon, American Journal of Physics. (1992) 60, no. 5, 425–429, https://doi.org/10.1119/1.16895.
10.1119/1.16895
Web of Science® Google Scholar
4 Jerri A. J., The Gibbs Phenomenon in Fourier Analysis, Splines & Wavelet Approximations, 1990, Kluwer Academic Publishers, Boston, Mass, USA, https://doi.org/10.1007/978-1-4757-2847-7.
Google Scholar
5 Rim K. S. and Yun B. I., Gibbs phenomenon removal by adding Heaviside functions, Advances in Computational Mathematics. (2013) 38, no. 4, 683–699, https://doi.org/10.1007/s10444-011-9255-7, MR3044634, ZBL1269.42001, 2-s2.0-84876439578.
10.1007/s10444-011-9255-7
Web of Science® Google Scholar
6 Zemanian A. H., Distribution Theory and Transform Analysis, 1965, McGraw-Hill, MR0177293.
Google Scholar
7 Ayers G. R. and Dainty J. C., Iterative blind deconvolution method and its applications, Optics Letters. (1988) 13, no. 7, 547–549, https://doi.org/10.1364/ol.13.000547, 2-s2.0-0023936983.
10.1364/OL.13.000547
CAS PubMed Web of Science® Google Scholar
8 Haidar N. H. S., A nonlinear method for a severely ill-posed generalized moment problem, Journal of Inverse & Ill-Posed Problems. (1997) 5, no. 4, 323–335.
10.1515/jiip.1997.5.4.323
Google Scholar
9 Bradley G. L. and Smith K. J., Calculus, 1995, Prentice Hall.
Google Scholar
10 Öffner P., Sonar T., and Wirz M., Detecting strength and location of jump discontinuities in numerical data, Applied Mathematics. (2013) 4, no. 12, 1–14, https://doi.org/10.4236/am.2013.412A001.
10.4236/am.2013.412A001
Google Scholar
11 Atkinson K. E., An Introduction to Numerical Analysis, 1989, John Wiley & Sons, New York, NY, USA, MR1007135.
Google Scholar
12 Süli E. and Mayers D. F., An Introduction to Numerical Analysis, 2003, Cambridge University Press, Cambridge, UK, https://doi.org/10.1017/cbo9780511801181, MR2006500.
10.1017/CBO9780511801181
Google Scholar
13 Wang P., A third-order family of Newton-like iteration methods for solving nonlinear equations, Journal of Numerical Mathematics and Stochastics. (2011) 3, no. 1, 13–19, MR2771857.
Google Scholar

All articles

Numerical Solvability and Solution of an Inverse Problem Related to the Gibbs Phenomenon

Abstract

1. Introduction

2. Distribution-Theoretic Proof for the Gibbs-Wilbraham Effect

3. The Inverse Problem for Truncated Fourier Series

3.1. The Tangent Half-Angle Stereographic Projection

3.2. The Stereographic Fourier Series

4. Numerics of Solving the Inverse Problem

4.1. Computation of the Peak Location α₀

4.2. Convergence Analysis

4.3. Applications

5. Conclusions

Conflict of Interests

Acknowledgment

Appendix

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Numerical Solvability and Solution of an Inverse Problem Related to the Gibbs Phenomenon

Abstract

1. Introduction

2. Distribution-Theoretic Proof for the Gibbs-Wilbraham Effect

3. The Inverse Problem for Truncated Fourier Series

3.1. The Tangent Half-Angle Stereographic Projection

3.2. The Stereographic Fourier Series

4. Numerics of Solving the Inverse Problem

4.1. Computation of the Peak Location α0

4.2. Convergence Analysis

4.3. Applications

5. Conclusions

Conflict of Interests

Acknowledgment

Appendix

References

Figures

References

Related

Information

4.1. Computation of the Peak Location α₀