The family of consecutive-type reliability systems is under investigation. More specifically, an up-to-date presentation of almost all generalizations of the well-known consecutive k-out-of-n: F system that have been proposed in the literature is displayed, while several recent and fundamental results for each member of the aforementioned family are stated.

1. Introduction

A linear (circular) consecutive k-out-of-n: F system consists of n components which are linearly (circularly) arranged and the system fails if and only if at least k consecutive components fail. The most popular applications of these systems pertain to computer network, telecommunication, pipeline network modeling, engineering, or integrated circuitry design. The consecutive k-out-of-n: F system has been subject of substantial research interest for many years and a lot of generalizations have been suggested in order to accommodate more flexible operation principles. For a detailed presentation of the consecutive k-out-of-n: F systems and some generalizations, the interested reader is referred to the excellent monograph of Kuo and Zuo [1] or the work of Chang et al. [2].

Let T be the lifetime of a reliability system with n components and X₁, X₂, …, X_n its components’ lifetimes. If we assume that X₁, X₂, …, X_n are exchangeable (and therefore identically distributed but not necessarily independent), the signature of the system is defined as the probability vector (s₁(n), s₂(n), …, s_n(n)) with

()

where X_1:n ≤ X_2:n ≤ ⋯≤X_n:n are the order statistics of the sample X₁, X₂, …, X_n. It can be easily verified that, in the exchangeable case, the signature of a reliability system depends only on its structure and not on the specific underlying distribution of X_i. In other words, s_i(n) is the proportion of permutations, among the n! equally likely permutations of X₁, X₂, …, X_n, which result in a minimal cut set failing upon the occurrence of X_i:n.

The signature of the system, which was first introduced by Samaniego [3], is closely related to many well-known reliability characteristics, a fact turning it to a very useful tool for studying coherent systems and their ageing properties. For example, the reliability polynomial of a structure can be easily expressed in terms of its signature. More precisely, Samaniego [3] proved that for any coherent system with independent and identical components which have absolutely continuous cumulative density functions, system’s reliability can be expressed as

()

Navarro and Rychlik [4] proved that the above representation also holds true when the lifetimes X₁, X₂, …, X_n have an absolutely continuous exchangeable distribution (this property had been mentioned earlier by Kochar et al. [5]). Moreover, Eryilmaz and Bayramoglu [6] used the system signature in order to evaluate the extreme residual lifetimes of the remaining components after the complete failure of the system.

Both reliability function and signature of a structure can be evaluated based on either recursive formulas or explicit expressions. In some cases, where neither of the aforementioned methods can be established for a specific system, approximating and limiting results are available. In the present review article, the family of consecutive-type reliability systems is under investigation. More specifically, Section 2 offers an up-to-date presentation of almost all generalizations of the well-known consecutive k-out-of-n: F system that have been proposed and studied in the literature. For each structure, the corresponding fundamental work and selected results are displayed either briefly or in detail. In Section 3, applications of these reliability systems in several fields are described, while Section 4 presents a full-detailed diagram which connects the aforementioned structures by giving the information under which conditions a system can be treated as a special case of another one.

2. Family of Consecutive-Type Reliability Systems

In this section, we study in detail almost all generalizations of the well-known consecutive k-out-of-n: F systems that have been proposed in the literature till now. For each reliability structure that is included in the family of consecutive-type systems, the general operational structure is described, while several important and some recent relevant results are displayed.

2.1. m-Consecutive-k-out-of-n: F Systems

An m-consecutive-k-out-of-n: F system consists of n components and fails if and only if there exist at least m nonoverlapping runs of k consecutive failed components. This system was first introduced by Griffith [7] and since then it has attracted a considerable research attraction. In the sequel, we present the main results appearing in the literature, such as recurrence relations and closed formulas for the evaluation of the reliability function and signature vector of m-consecutive-k-out-of-n: F systems. It is worth mentioning that the aforementioned system generalizes the well-known consecutive-k-out-of-n: F system (for m = 1), while for k = 1 the m-consecutive-k-out-of-n: F system reduces to an ordinary m-out-of-n: F system.

2.1.1. Recursive Schemes for the Reliability of m-Consecutive-k-out-of-n: F Systems

The following theorems provide recurrence for the calculation of reliability of an m-consecutive-k-out-of-n: F system.

Theorem 1 (Papastavridis [8]). Let denote the reliability function of a linear m-consecutive-k-out-of-n: F system, where p_i is the reliability of its ith component. Then satisfies the following recurrence relation:

()

where n ≥ km + 1 and

In order to launch the above recurrence scheme, a set of initial of conditions would be necessary. Observing that for n ≥ k + 1 the following ensues

()

while

()

we have at hand the set of initial values needed to evaluate reliability of the system.

Note that for the i.i.d case (e.g., p₁ = p₂ = ⋯ = p_n = p), the recurrence of Theorem 1 reduces to the following form:

()

Theorem 2 (Alevizos et al. [9]). Let denote the reliability function of a circular m-consecutive-k-out-of-n: F system, where p_i (q_i = 1 − p_i) is the reliability (unreliability) of its ith component. Then satisfies the following recurrence:

()

where n ≥ km + 2 and

denotes the reliability of a linear d-consecutive-k-out-of-c: F subsystem with components i + 2, i + 3, …, n − sk + i − 1.

To launch the above recursive scheme, a set of initial of conditions would be necessary. Observing that the following ensue

(i)
, for n < km,
(ii)
, for n = km,
(iii)
, for n = km + 1,

we have at hand the set of initial values needed to evaluate reliability of the system.

Note that for the i.i.d case (e.g., p₁ = p₂ = ⋯ = p_n = p), the recurrence of Theorem 2 reduces to the following form:

()

It is worth mentioning that the computational complexity of recurrence included in Theorem 1 is equal to O(nm), while the corresponding one for equations of Theorem 2 equals O(nkm³).

2.1.2. Exact Formulas for the Reliability of m-Consecutive-k-out-of-n: F Systems

The following theorems offer closed expressions for the evaluation of reliability of an m-consecutive-k-out-of-n: F system.

Theorem 3 (Papastavridis [8]). Let denote the reliability function of a linear m-consecutive-k-out-of-n: F system, where p is the common reliability of its i.i.d. components. Then is given as follows:

()

where n ≥ km, s^∗(x) denotes the greatest integer lower bound of x and N(i, j) can be expressed as

()

Theorem 4 (Makri and Philippou [10]). Let denote the reliability function of a linear m-consecutive-k-out-of-n: F system composed by i.i.d. components, where p is their common reliability. Then is given as follows:

()

where

()

is the well-known multinomial coefficient, while the inner summation is over all nonnegative integers x₁, x₂, …, x_k such that

Theorem 5 (Makri and Philippou [10]). Let denote the reliability function of a circular m-consecutive-k-out-of-n: F system, where p(q) is the common reliability (unreliability) of its components. Then, can be expressed as follows:

(i)
()
where
()
is the well-known multinomial coefficient, while the inner summation is overall nonnegative integers x₁, x₂, …, x_k such that . Moreover, in the above expression [x] denotes the greatest integer in x, while δ_i,j is the Kronecker delta function.
(ii) Consider
()
where
()

2.1.3. Approximations for the Reliability of m-Consecutive-k-out-of-n: F Systems

The following theorems offer some limiting results for the evaluation of reliability of an m-consecutive-k-out-of-n: F system.

Theorem 6 (Papastavridis [8]). Let q(t) = (λt) ^a + O(t^a) be the common failure distribution of the components of an m-consecutive-k-out-of-n: F system, where λ, a are positive constants. Then the following ensues

()

where T_n is the time of first failure of the system.

Theorem 7 (Godbole [11]). Let q_j = 1 − p_j, j = 1,2, …, n be the failure probability of the jth component of an m-consecutive-k-out-of-n: F system. Then the reliability R_m,k,n(p_j) of the system satisfies the following inequality:

()

where q = max_j≥1q_j and

2.1.4. Signature Vector of m-Consecutive-k-out-of-n: F Systems

Let p denote the common reliability of the components of an m-consecutive-k-out-of-n: F system. The following theorem offers a generating function approach of the aforementioned system.

Theorem 8. Let (s₁(n, k, m), s₂(n, k, m), …, s_n(n, k, m)) and R_m,k,n(p) be the signature and the reliability function of an m-consecutive-k-out-of-n: F system, respectively. Then

(a)
the double generating function of is given by
()
(Eryilmaz et al. [12]),
(b)
the generating function of R_m,k,n(p) is given as follows:
()
(Koutras [13]).

The next theorem offers expressions for the evaluation of the signature vector of an m-consecutive-k-out-of-n: F system.

Theorem 9 (Eryilmaz et al. [12]). Let (s₁(n, k, m), s₂(n, k, m), …, s_n(n, k, m)) be the signature vector of an m-consecutive-k-out-of-n: F system. Then the following ensues

(a)
the quantities s_i(n, k, m) satisfy the recurrence relation:
()
for i = 1,2, …, n and n ≥ k + 1.
(b)
the quantities s_i(n, k, m) can be expressed as
()
for mk ≤ i ≤ n and s_i(n, k, m) = 0 if i < mk, where
()

2.1.5. Additional Results for m-Consecutive-k-out-of-n: F Systems

Beyond the results mentioned in the previous subsections, additional studies have appeared in the literature for the m-consecutive-k-out-of-n: F system. Eryilmaz [14] derived explicit expressions for the component importance measures for the aforementioned structure consisting of exchangeable components. More specifically, Eryilmaz [14] studied in detail the well-known Birnbaum and Barlow-Proschan importance measures for a m-consecutive-k-out-of-n: F system. Furthermore, Ghoraf [15] offered recursive formulas for calculating the reliability function of the circular case of the aforementioned structure couching on the corresponding recurrence equations for the linear one.

2.2. r-within-Consecutive-k-out-of-n: F Systems

An r-within-consecutive-k-out-of-n: F system consists of n components and fails if and only if there exist k consecutive components which include among them at least r failed components. This system was first introduced by Griffith [7], but its mathematical modelling has been done earlier by Greenberg [16] and Saperstein [17]. In the sequel, we present the main results appearing in the literature, such as recurrence relations and closed formulas for the evaluation of the reliability function and signature vector of r-within-consecutive-k-out-of-n: F systems. It is worth mentioning that the aforementioned system generalizes the well-known consecutive-k-out-of-n: F system (for r < k), while for k = n the r-within-consecutive-k-out-of-n: F system reduces to an ordinary r-out-of-n: F system.

2.2.1. Recursive Schemes for the Reliability of r-within-Consecutive-k-out-of-n: F Systems

The following theorems provide recurrence for the calculation of reliability of an r-within-consecutive-k-out-of-n: F system.

Theorem 10 (Sfakianakis et al. [18]). Let denote the reliability function of a linear r-within-consecutive-k-out-of-n: F system, where p is the common reliability of its components. Then, for n = r + λ, λ ≤ r, satisfies the following recurrence relation:

()

where

, if x > λ.

Theorem 11 (Eryilmaz [19]). Let denote the reliability function of a linear r-within-consecutive-k-out-of-n: F system, where p is the common reliability of its components. Then, for n ≤ 2k, satisfies the following recurrence relation:

()

where

is the reliability of s-within-consecutive-(n − m)-out-of-2(n − m): F system with components 1,2, …, n − m, m + 1, …, n, while

denotes the lifetime of k-out-of-m: F subsystem of components with the lifetimes T_i, T_i+1, …, T_i+m−1, 1 ≤ i ≤ n − m + 1.

Theorem 12 (Koutras [13]). Let denote the reliability function of a linear r-within-consecutive-k-out-of-n: F system, where p is the common reliability of its components. Then, satisfies the following recurrence relation:

()

2.2.2. Exact Formulas for the Reliability of r-within-Consecutive-k-out-of-n: F Systems

The following Theorem offers closed expressions for the evaluation of reliability of an r-within-consecutive-k-out-of-n: F system.

Theorem 13 (Sfakianakis et al. [18]). Let ( denote the reliability function of a linear (circular) 2-within-consecutive-k-out-of-n: F system, where p is the common reliability of its components. Then the following recurrences ensue:

(i)
()
where m = [(n + k − 1)/k],
(ii)
()
where m = [n/k].

2.2.3. Approximations for the Reliability of r-within-Consecutive-k-out-of-n: F Systems

The following theorems offer some limiting results for the evaluation of reliability of an r-within-consecutive-k-out-of-n: F system.

Theorem 14 (Eryilmaz et al. [20]). Let denote the reliability function of a linear r-within-consecutive-k-out-of-n: F system. Then, for 1 ≤ r ≤ k ≤ n, satisfies the following inequalities:

(i)
()
where is the rth smallest lifetime among T_j, T_j+1, …, T_j+k−1, r ≤ k, 1 ≤ j ≤ n − k + 1 and
()
(ii) Consider
()
where h = [n/k] and
()
Let us next denote by A_i the event where there are at least r failed components from i to i + k − 1, for i = 1,2, …, n − k + 1, while S₁, S₂, S₃ are defined as follows:
()

Theorem 15 (Sfakianakis et al. [18]). Let denote the reliability function of a linear r-within-consecutive-k-out-of-n: F system, where p is the common reliability of its components. Then satisfies the following inequalities:

(i)
()
where
()
(ii)
()
where
()

For the next Theorem, the following definitions are necessary:

(i)
Z_i denotes the event that the linear r-within-consecutive-k-out-of-i: F system consisting of the components 1,2, …, i is good (i = k, k + 1, …, n).
(ii)
X_i denotes the event that the ith component fails and there are at least r − 1 failures among components i − k + 1, i − k + 2, …, i − 1, (i = k, k + 1, …, n).
(iii)
B_i denotes the event that there are at most r − 1 failures among components i − k + 1, i − k + 2, …, i − 1, (i = k, k + 1, …, n).
(iv)
C_i denotes the event that, for f = min(i − k, k − r + 1), there is no failure among components (i − k) − f + 1, (i − k) − f + 2, …, i − k, for i = k + 1, k + 2, …, n.

Theorem 16 (Papastavridis and Koutras [21]). Let denote the reliability function of a linear r-within-consecutive-k-out-of-n: F system. Then satisfies the following inequalities:

()

where q_i is the unreliability of the ith component, while γ_i = P(C_i)/P(B_i).

2.2.4. Signature Vector of r-within-Consecutive-k-out-of-n: F Systems

Let p denote the common reliability of the components of an r-within-consecutive-k-out-of-n: F system. The following theorem offers a generating function approach of the aforementioned system.

Theorem 17. Let (s₁(n), s₂(n), …, s_n(n)) and R_2,k,n(p) be the signature and the reliability function of an 2-within-consecutive-k-out-of-n: F system, respectively. Then

(a)
the double generating function of is given by
()
(Triantafyllou and Koutras [22]),
(b)
the generating function of R_2,k,n(p) is given as follows:
()
(Koutras [13]).

The next theorem offers expressions for the evaluation of the signature vector of an 2-within-consecutive-k-out-of-n: F system.

Theorem 18 (Triantafyllou and Koutras [22]). Let (s₁(n), s₂(n), …, s_n(n)) be the signature vector of an 2-within-consecutive-k-out-of-n: F system. Then the following ensues:

(i)
The quantities q_i(n) = (n) _is_i(n), i = 1,2, …, n, where (n)_i = n(n − 1) ⋯ (n − i + 1), satisfy the recurrence relation:
()
for i = 0,1, …, n − 1 and n ≥ 2k + 2.
(ii)
The quantities s_i(n) can be expressed as
()

It is worth mentioning that well-performed simulations study of an r-within-consecutive-k-out-of-n: F system has been developed by Eryilmaz et al. [20]. Moreover, Kan et al. [23] studied the circular case of the aforementioned structure and offered a new approximation for its reliability.

2.3. (n, f, k) Systems

An (n, f, k) system involves two common failure criteria. More specifically, it consists of n components (ordered in a line or a circle) and fails if and only if there exist at least f failed components or at least k consecutive failed components. It is worth of mentioning that the configuration of an (n, f, k) system was first introduced by Tung [24] as an application to a complex infrared detecting system and since then it has attracted considerable research attention. In the sequel, we present the main results for (n, f, k) systems appearing in the literature, such as recurrence relations and closed formulas for the evaluation of the reliability function and signature vector. It is worth mentioning that the aforementioned system generalizes the well-known consecutive-k-out-of-n: F system (for f > k), while for f ≤ k the (n, f, k) system reduces to an ordinary f-out-of-n: F system.

2.3.1. Recursive Schemes for the Reliability of (n, f, k) Systems

The following theorems provide recurrence for the calculation of reliability of an (n, f, k) system.

Theorem 19 (Zuo et al. [25]). Let A(i, j, k) be the event that the (i, j, k) subsystem fails (the subsystem consists of components 1,2, …, i, i ≥ j ≥ 0, i ≥ k), while Q(i, j, k) denotes the corresponding failure probability P(A(i, j, k)). Then the unreliability function of the (i, j, k) system satisfies the following recurrence relation:

()

where p_a(q_a) is the reliability (unreliability) of the ath component.

In order to launch the aforementioned recursive scheme, the following set of initial conditions is necessary:

()

The complexity for calculating Q(n, f, k) using the above recurrence relation is equal to O(nf). The next theorem provides an alternative recursive scheme for the evaluation of the reliability function of the (n, f, k) system.

Theorem 20 (Triantafyllou and Koutras [26]). The reliability function R_n of an (n, f, 2) system with i.i.d. components satisfies the following recurrence relation:

()

where p denotes the common reliability of its components.

In order to launch the recursive scheme established above, an adequate number of initial conditions is necessary. These conditions are given as follows

()

where R_f,n:F is the reliability of a f-out-of: n: F system; that is,

2.3.2. Exact Formulas for the Reliability of (n, f, k) Systems

Let us first consider an (n, f, k) system, where f > k; we recall that for the case f ≤ k the (n, f, k) system coincides with the well-known f-out-of-n: F system and its reliability properties have been extensively studied in the past. Chang et al. [27] established a Markov chain representation of the (n, f, k) system, which leads to the computation of the reliability function of the aforementioned structure. More specifically, for the (n, f, k) system with f > k, let us define the state space for process {Y(t), t = 0,1, …} as

()

where (i, j) indicates a working state in which the system consisting of components 1,2, …, t has j failed components, its last i − 1 components have failed, and the (t − i)th component is working. State s_N indicates the system (1,2, …, t) fails. Then {Y(t)} is a Markov chain with transition matrix of the form

()

where

()

and N = (2f − k + 1)k/2 + 1.

As proved in Koutras [13], the reliability R_n of a structure can be expressed as

()

where Λ is the transition probability matrix associated to the structure and

()

Therefore, applying the above expression obtained for the transition matrix of an (n, f, k) system, one may easily calculate the reliability function of the aforementioned structure.

Let us next consider the following probabilities:

()

where X_i is the state of ith component (X_i ∈ {0,1}), for i = 1,2, …, n. The following theorem offers a closed expression for the evaluation of reliability of an (n, f, k) system.

Theorem 21 (Eryilmaz [28]). The reliability function R_n of an (n, f, k) system with exchangeable components can be expressed as follows:

()

where

()

In the sequel, we present results for an (n, f, k) system with Markov dependent components. Let X₁, X₂, …, X_n denote the states of the Markov dependent components with transition probabilities

()

with 1 ≤ i ≤ n and initial probabilities p₁ = P(X₁ = 1), p₀ = P(X₁ = 0). If we define g(n, r, l) as

()

the following theorem provides an expression for the evaluation of reliability of (n, f, k) systems.

Theorem 22 (Demir [29]). The reliability function R_n of an (n, f, k) system with Markov dependent components can be expressed as follows:

()

2.3.3. Signature Vector of (n, f, k) Systems

Let p denote the common reliability of the components of an (n, f, k) system. The following theorem offers a generating function approach of the aforementioned system.

Theorem 23 (Triantafyllou and Koutras [26]). Let (s₁(n), s₂(n), …, s_n(n)) be the signature of an (n, f, 2) system, respectively. Then the double generating function of is given by

()

where

()

Theorem 24 offers recursive relations for the evaluation of the signature vector of an (n, f, 2) system.

Theorem 24 (Triantafyllou [30]). The coordinates s_i(n) of the signature vector of an (n, f, 2) system satisfy the following recurrence relation:

()

Let T be the lifetime of a system whose components’ lifetimes are T₁, T₂, …, T_n and T_1:n < T_2:n < ⋯<T_n:n the order statistics associated with them. It is easy to observe that the lifetime of an (n, f, k) system can be represented as a function of the lifetimes of consecutive k-out-of-n: F and k-out-of-n: F systems. Generally speaking, the lifetimes of systems involving two common failure criteria can be expressed as either

()

where S denotes the lifetime associated with the system different from a-out-of-n structure but having the same components’ lifetimes T₁, T₂, …, T_n. The next theorem presents an alternative way of computing the signature of an (n, f, k) system.

Theorem 25 (Eryilmaz and Zuo [31]). Let (s₁, s₂, …, s_n) be the signature of the system with lifetime S. Then the signatures of the systems with lifetimes T_∗ and T^∗ are given, respectively, as

()

It is noteworthy that the dual system of an (n, f, k) structure has been studied by Cui et al. [32], while a generalization of these systems, named (n, f, k) systems, with weighted components has been introduced by Eryilmaz and Aksoy [33]. Gera [34] studied reliability systems with two working criteria and presented some results associated with the well-known qualification tests, while Kamalja [35] derived expressions for the Birnbaum importance measures for both structures.

2.4. Reliability Systems with Weighted Components

The idea that all components in a reliability structure are not created equal is seemingly an obvious concept. In other words, it is not quaint to assume that different components may have different failure probabilities. Generally speaking, a reliability system which consists of weighted components, for example, each component carries its own positive weight, fails if and only if the total weight of the failed components exceeds a specific benchmark. In the sequel, the literature on weighted reliability structures is briefly reviewed. Consider a system with n components and suppose that the ith component is associated with a weight w_i > 0, i = 1,2, …, n. Then the system is still working if and only if the sum of weights of the failed components is less than (or equal to) a certain threshold T > 0.

2.4.1. Weighted k-out-of-n Systems

A weighted k-out-of-n: G(F) system consists of n components, each with its own positive weight w_i > 0 (total system weight equal to w), such that the system works (fails) if and only if the total weight of the working (failed) components is at least k. It is noteworthy that the reliability of a weighted k-out-of-n: G system is the complement of the unreliability of a weighted (n − k + 1)-out-of-n: F system. It goes without saying that the k-out-of-n: G(F) system is a special case of the corresponding weighted k-out-of-n: G(F) system wherein the weight of each component equals 1. The next theorem offers an efficient algorithm for the evaluation of the reliability of the weighted k-out-of-n: G system.

Theorem 26 (Wu and Chen [36]). Let R(i, j) be the reliability of the weighted j-out-of-i: G system, while w_i > 0 is the weight of the ith component. Then if we denote by p_i(q_i) the reliability (unreliability) of the ith component, the reliability of the structure satisfies the following recurrence relation:

()

The following theorem provides a similar result concerning the dual structure.

Theorem 27 (Chen and Yang [37]). Let R(i, j) be the reliability of the weighted j-out-of-i: F system, while w_i > 0 is the weight of the ith component. Then if we denote by p_i(q_i) the reliability (unreliability) of the ith component, the reliability of the structure satisfies the following recurrence relation:

()

An extension of the aforementioned one-stage weighted k-out-of-n model has been proposed by Chen and Yang [37]. More specifically, Chen and Yang [37] considered a two-stage weighted k-out-of-n system, which consists of m subsystems. Each subsystem has a (one-stage) weighted k-out-of-n structure, which is called the second level structure. The interrelationship between the m subsystems follows a certain coherent structure, which is called the first-level structure. Generally speaking, a two-stage weighted k-out-of-n system can be decomposed into two hierarchical levels: the first (higher) level can be of any coherent structure and the second (lower) level has a weighted k-out-of-n structure.

An additional generalization of the well-known weighted k-out-of-n system has been introduced by Eryilmaz [38]. More specifically, Eryilmaz [38] assumed that the system has a performance level above c if there are at least k working components and the sum of the weights of all working components is above c. Among others, Eryilmaz [38] deduced recursive relations for the calculation of the system state probabilities, while a detailed simulation study has been taken into play in order to observe the time spent by the system in state c or above. Finally, Li and Zuo [39] studied the multistate weighted k-out-of-n systems, where each component may be in more than 2 states and therefore its contribution to the system’s weight can be differentiated analogously.

2.4.2. Consecutive Weighted k-out-of-n Systems

A weighted consecutive k-out-of-n: F system consists of n components, each with its own positive weight w_i > 0 (total system weight equal to w), such that the system fails if and only if the total weight of the failed components is at least k. It goes without saying that the consecutive k-out-of-n: F system is a special case of the corresponding weighted consecutive k-out-of-n: F system wherein the weight of each component equals 1. Efficient algorithms for the evaluation of the reliability of the linear weighted consecutive k-out-of-n: F system have appeared in the literature (for more details see Kuo and Zuo [1]), while Samaniego and Shaked [40] extended the idea of weighted components, by giving to the components weights that can take any positive value (not necessary integer-valued).

2.5. ((n₁, n₂, …, n_N), f, k) Systems

Cui and Xie [41] introduced a generalized k-out-of-n system, denoted by ((n₁, n₂, …, n_N), f, k). Such a system consists of N modules ordered in a line or a circle, while the ith module is composed of n_i ≥ 1 components in parallel. In other words, the ((n₁, n₂, …, n_N), f, k) system fails if and only if there are at least f failed components or at least k consecutive failed modules. It goes without saying that, for n₁ = n₂ = ⋯ = n_N = 1, an ((n₁, n₂, …, n_N), f, k) system reduces to a simple (N, f, k) while for coincides with the well-known consecutive k-out-of-N: F system and for N = 1 with the ordinary f-out-of-n: F structure. The following theorem offers recursive relations for the evaluation of the reliability function of a linear and circular ((n₁, n₂, …, n_N), f, k) system, respectively.

Theorem 28 (Cui and Xie [41]). (i) For a linear ((n₁, n₂, …, n_N), f, k) system, the reliability function R_L((n₁, n₂, …, n_N), f, k) satisfies the following recurrence:

()

where A(j, s) is the probability that, in module j, there are s failed components.

(ii) For a circular ((n₁, n₂, …, n_N), f, k) system, the reliability function R_C((n₁, n₂, …, n_N), f, k) satisfies the following recurrence:

()

It is worth mentioning that the ((n₁, n₂, …, n_N), f, k) system can be obtained by adding more components in parallel to the basic components of an (n, f, k) structure. Since the aforementioned system involves multiple failure criteria, Cui and Xie [41] studied the Birnbaum importance with respect to the kth failure criterion as an importance measure computed only under this failure criterion. Firstly, for a reliability system S with m ≥ 1 failure criteria, they assumed that, for any one of j (j ≤ m), the Birnbaum importance is different, while, for any one of m − j failure criteria, the Birnbaum importance is the same. Moreover, Cui and Xie [41] denoted by A₁ = {S works under failure criteria 1,2, …, j} and A₂ = {S works under failure criteria j + 1, …, m} the specific disjoint events and they proved that the Birnbaum importance of the reliability system S depends upon these j failure criteria. Finally, note that the well-known series and parallel reliability systems are included in the more general ((n₁, n₂, …, n_N), f, k) systems’ family as special cases (for f ≥ max{n_i} and k = 1 and

, resp.).

2.6. (n, f, k(i, j)) and 〈n, f, k(i, j)〉 Systems

Guo et al. [42] generalized the idea of the (n, f, k) system, studied by Chang et al. [27] and Zuo et al. [25]. More specifically, they introduced a reliability structure, named the (n, f, k(i, j)): F system, which consists of n components ordered in a line or circle and fails if and only if there exist at least f failed components or at least k consecutive failed components among components i, i + 1, …, j − 1, j. It is noteworthy that, for the circular case, component index should have modulo n property, that is, components i and n + i indicate the same one, while the following requirements should be satisfied:

(i)
j − i + 1 ≥ k, if j > i,
(ii)
n + j − i + 1 ≥ k, if j < i.

Otherwise, the consecutive k failure criterion can be removed. It goes without saying that when i = 1, j = n, or i − j = 1, the (n, f, k(i, j)): F system becomes the well-known (n, f, k) structure. Furthermore, Guo et al. [42] mentioned an additional justification of the aforementioned reliability systems. More precisely, they introduced the 〈n, f, k(i, j)〉: F system, which consists of n components ordered in a line or circle, and fails if and only if there exist at least f failed components and at least k consecutive failed components among components i, i + 1, …, j − 1, j. Finally, Guo et al. [42] considered the dual structures of the (n, f, k(i, j)): F and 〈n, f, k(i, j)〉: F systems, taking into account the argumentation applied by Cui et al. [32].

The main result of the aforementioned paper is the employment of a two-stage Markov chain in order to give the system reliability in the form of product of matrices. Generally speaking, the finite Markov chain imbedding technique is to embed a Markov chain {Y(t)} defined on the state space S = {1,2, …, N} and the discrete index space T = {1,2, …, n} into a given system, while the system fails if there exists t₀, 1 ≤ t₀ ≤ n, such that Y(t) = N, for all t₀ ≤ t ≤ n.

The unique justification is to divide the discrete index space and the nonabsorbing state space into two disjoined parts. For example, if we consider the (n, f, k(i, j)): F (〈n, f, k(i, j)〉: F) system with component reliabilities p_t(q_t = 1 − p_t), t = 1,2, …, n, by rearranging their components without changing the system reliability, we can transform it into the linear (n, f, k(n − j + i, n)): F (〈n, f, k(n − j + i, n)〉: F) system with component reliabilities u_t (υ_t = 1 − u_t), where p_t, q_t and u_t, υ_t satisfy the following relations:

()

The rearrangement is as follows by a transform:

()

where the first line (old-component order) denotes the components order before rearrangement, the second line (New-component order) denotes the components order after rearrangement, that is, we move to the end of the line that section to which the consecutive criterion applies so that the new system consists of components 1,2, …, i − 1, j + 1, j + 2, …, n, i, i + 1, …, j in an ordered line. Thus, the study of the aforementioned reliability structures is covered by the linear case (n, f, k(n − j + i, n)): F (〈n, f, k(i, j)〉: F) system with component reliabilities u_t.

It is worth noting that Guo et al. [42] presented a detailed study for the evaluation of the reliability function of the (n, f, k(i, j)): F (〈n, f, k(i, j)〉: F) systems, by employing a two-stage Markov chain procedure and illustrating numerical examples.

2.7. Consecutive k-out-of-n: F Systems with Cycle k

An r consecutive k-out-of-n: F system consists of n linearly arranged components and the system fails if and only if at least r nonoverlapping runs of k components fail. Boland and Papastavridis [43] studied the case where there are k distinct components with failure probabilities q_i, i = 1,2, …, k and where the failure probability of the jth component is q_i (j = mk + i (1 ≤ i ≤ k)). In other words, they focused on the special case of an r consecutive k-out-of-n: F system where there is a “cyclical” pattern in failure probabilities of the components. More precisely, Boland and Papastavridis [43] were interested in how the order of q₁, q₂, …, q_k affects the failure probability of this new structure, named r consecutive k-out-of-n: F system with cycle k.

Let us next denote by F(n, r) the failure probability of an r consecutive k-out-of-n: F system with cycle k, while p_i(q_i) is the reliability (unreliability) of the ith component. The following theorems offer recursive expressions for the unreliability of the aforementioned structure.

Theorem 29 (Boland and Papastavridis [43]). Consider an r consecutive k-out-of-n: F system with cycle k, where n = mk + i, 1 ≤ i ≤ k and m ≥ 0. Then for any integer r (except for r = m + 1 and i = k), the unreliability function of the system satisfies the following recurrence:

()

where

Theorem 30 (Boland and Papastavridis [43]). Consider an r consecutive k-out-of-n: F system with cycle k, where 1 ≤ i ≤ k and m ≥ 0. Then the unreliability function of the system satisfies the following recurrence:

()

It is clear from the above result that the unreliability F(n, r) is independent of the order q₁, q₂, …, q_k when n is a multiple of k. For n = mk + 1, it follows that

()

and therefore we deduce that the quantity F(n, r) = F(mk + 1, r) is maximized by maximizing p₁ or, generally speaking, the F(n, r) is maximized (minimized) when q₁ ≤ q₂ ≤ ⋯≤q_k (q₁ ≥ q₂ ≥ ⋯≥q_k). It is worth mentioning that Boland and Papastavridis [43] provided additionally interesting applications of the r consecutive k-out-of-n: F system with cycle k for the arrangement of sport competitions and inspections procedures in quality control.

2.8. m-Consecutive k-out-of-n: F Systems with Overlapping Runs

Agarwal and Mohan [44] introduced and studied the m-consecutive-k-out-of-n: F system with overlapping runs. This reliability structure consists of n linearly ordered components and fails if and only if there exist at least m overlapping sequences of k consecutive failed components (n ≥ m + k − 1). It is straightforward that for m = 1 the aforementioned system coincides with an ordinary consecutive-k-out-of-n: F structure. Graphical Evaluation and Review Technique (GERT) analysis is used for reliability evaluation of the system for both i.i.d. and (k − 1)-step Markov dependent components, in a unified manner. More specifically, Agarwal and Mohan [44] proved the following results:

(i)
For a m-consecutive-k-out-of-n: F system with overlapping runs composed by i.i.d components, the generating function of the waiting time for the occurrence of the system failure is given as
()
Hence the reliability function of the above structure can be expressed as
()
where ξ(u) is the coefficient of z^u in the power series expansion of the generating function W_0,m+k−1(0, z).
(ii)
For a m-consecutive-k-out-of-n: F system with overlapping runs composed by (k − 1)-step Markov dependent components, the generating function of the waiting time for the occurrence of the system failure is given as
()

Hence, the reliability function of the above structure can be expressed as

()

where ξ(u) is the coefficient of z^u in the power series expansion of the generating function

In addition, Eryilmaz [45] derived an explicit combinatorial expression for the number of its path sets including a specified number of working components. More specifically, Eryilmaz [45] proved the following result.

Theorem 31 (Eryilmaz [45]). The number of path sets r_i(n) of an m-consecutive-k-out-of-n: F system with overlapping runs including i working components can be expressed as follows:

()

where n − z_ϕ ≤ i < n, r_n(n) = 1 (z_ϕ = n − 1 − [(n − m − k + 1)/k]) and

()

Having at hand the above expression for the determination of r_i(n), one may easily compute important characteristics of the m-consecutive-k-out-of-n: F system with overlapping runs, such as its reliability function or its signature vector. Indeed, let us first denote by z_ϕ the maximum number of failed components such that the system with structure function ϕ can still work successfully and by p the common reliability of its components. Since the reliability and the signature of a coherent structure can be expressed as

()

respectively (for more details, see Boland [46] and Samaniego [3]), it is goes without saying that Theorem 31 leads immediately to the desired results.

2.9. Combined m-Consecutive k-out-of-n: F and Consecutive-k_c-out-of-n: F Systems

Mohan et al. [47] proposed and studied a new model, named the combined m-consecutive-k-out-of-n: F and consecutive-k_c-out-of-n: F systems. This reliability structure consists of n linearly ordered components and fails if and only if there exist at least k_c consecutive failed components or at least m nonoverlapping runs of k consecutive failed components, where k_c < mk. By assuming that the components are i.i.d., Mohan et al. [47] employed the well-known GERT analysis to evaluate the reliability function and presented interesting applications of the aforementioned structure in several areas, such as signal processing or bank automatic payment systems. More specifically, the failure probability of the aforementioned system is explained as a tree structure, while the direction of the calculating procedure is from the root node to a leaf node via intermediate ones. The main steps of the algorithm can be briefly described as follows:

(i)
At step 1, the failure probability at root node x₀ is determined as
()
where ξ(u) is the coefficient of z^u in the power series expansion of the generating function of the waiting time for the occurrence of the system failure at root node x₀.
(ii)
At step 2, the failure probability at node is deduced as follows:
()
where ξ(u) is the coefficient of z^u in the power series expansion of the generating function of the waiting time for the occurrence of the system failure at root node .
(iii)
At step 3, the total failure probability of the system is calculated as
()

It is noteworthy that the complexity of the proposed algorithm for the calculation of the reliability of a combined m-consecutive-k-out-of-n: F and consecutive-k_c-out-of-n: F systems has been determined to be equal to O([(n − k_c)/(k + 1)] ³). For an up-to-date overview of GERT analysis results of consecutive-k systems, the interested reader is referred to Sen et al. [48].

Moreover, Eryilmaz [49] derived an explicit expression for the number of its path sets including a specified number of working components. More specifically, Eryilmaz [49] proved the following result.

Theorem 32 (Eryilmaz [49]). The number of path sets r_i(n) of a combined m-consecutive-k-out-of-n: F and consecutive-k_c-out-of-n: F systems with i.i.d. components including i working ones can be expressed as follows:

()

where z_min ≤ i < n, r_n(n) = 1 (z_min indicates the minimum number of failed components at the moment of system failure) and the quantities C(s, k, k_c, l, x) can be calculated via the following recurrence:

()

with

()

Having at hand the above expression for r_i(n) and applying the well-known equalities for the evaluation of reliability function and signature of a coherent system in terms of r_i(n) (these equations have been already mentioned in previous section), one may easily compute these important characteristics of the combined m-consecutive-k-out-of-n: F and consecutive-k_c-out-of-n: F systems with i.i.d. components. Finally, note that Eryilmaz [49] studied also the aforementioned structure under the assumption of Markovian type dependence between its components and derived an expression for its reliability.

2.10. Constrained (k, d)-out-of-n Systems

Eryilmaz and Zuo [50] proposed and studied two new models, which generalize the well-known k-out-of-n: F and consecutive k-out-of-n: G systems. These extensions consider an additional constraint on the number of working components between successive failures. More precisely, in addition to the working conditions of k-out-of-n: F and consecutive k-out-of-n: G systems there must be at least d consecutive working components between any of two successive failures.

The first reliability structure introduced by Eryilmaz and Zuo [50] is called a constrained (k, d)-out-of-n: F system consisting of n linearly ordered components. This system fails if and only if there at least k failed components or there are less than d consecutive working components between any of two failed ones. It goes without saying that, for d = 0, the constrained (k, d)-out-of-n: F system reduces to the ordinary k-out-of-n:F system.

Let

denote the set of all binary sequences of length n where the runs of successes between two consecutive failures have length at least d. Then the reliability of constrained (k, d)-out-of-n: F system is given as follows:

()

where X = (X₁, X₂, …, X_n) denotes the states of components (X_i = 1 if the ith component is operating, and X_i = 0, otherwise), while

represents the total number of failed components. The following theorem offers expressions for the evaluation of the reliability function of the constrained (k, d)-out-of-n: F system with i.i.d. and Markov dependent components, respectively.

Theorem 33 (Eryilmaz and Zuo [50]). (i) For a constrained (k, d)-out-of-n: F system consisting of n independent and identical components with common reliability p, the reliability function is given as follows:

()

(ii) For a constrained (k, d)-out-of-n: F system consisting of n Markov dependent components with transition probabilities p_rs = P(X_i = s∣X_i−1 = r), r, s ∈ {0,1}, i = 2,3, …, n, and initial probabilities p₀ = P(X₁ = 0), p₁ = P(X₁ = 1), the reliability function is given as follows:

()

Moreover, an alternative reliability structure introduced by Eryilmaz and Zuo [50] is called a constrained consecutive (k, d)-out-of-n: G system consisting of n linearly ordered components. This system works if and only if there at least k consecutive working components and there are a least d consecutive working components between any of two failed ones. It goes without saying that, for d = 0, the constrained consecutive (k, d)-out-of-n: G system reduces to the ordinary consecutive k-out-of-n: G system.

Let

denote the longest run of successes. Then the reliability of a constrained consecutive (k, d)-out-of-n: G system is given as follows:

()

where X = (X₁, X₂, …, X_n) denotes the states of components. Theorem 34 offers expressions for the evaluation of the reliability function of the constrained consecutive (k, d)-out-of-n: G system with i.i.d. and Markov dependent components, respectively.

Theorem 34 (Eryilmaz and Zuo [50]). (i) For a constrained consecutive (k, d)-out-of-n: G system consisting of n independent and identical components with common reliability p, the reliability function is given as follows:

()

where

()

(ii) For a constrained consecutive (k, d)-out-of-n: G system consisting of n Markov dependent components with transition probabilities

()

and initial probabilities p₀ = P(X₁ = 0), p₁ = P(X₁ = 1), the reliability is given as

()

It is noteworthy that Eryilmaz and Zuo [50] proved explicit formulas for the calculation of the signature of both constrained (k, d)-out-of-n systems they considered.

2.11. Combined -Consecutive -out-of-n and -Consecutive--out-of-n Systems

The common m-consecutive k_c-out-of-n: F system consists of n linearly ordered components and fails if and only if there exist at least m nonoverlapping runs of k_c consecutive failed components. Gera [51] considered a more general reliability model, named the combined -consecutive -out-of-n and -consecutive--out-of-n systems. The new structure consists of n components and fails if and only if there exist at least nonoverlapping runs of consecutive failed components or at least nonoverlapping runs of consecutive failed ones. Gera [51] shed light on the cases where , and additionally is not an integer divisor of ; that is, is not integer-valued. It goes without saying that otherwise the aforementioned system reduces to an ordinary m-consecutive k_c-out-of-n structure.

Let Z denote the total number of components such that the system fails due to the specific requirements as mentioned, while X_z represents the state of the zth component (X_z = 1 (0) for success (failure)). In order to determine the reliability function of combined

-consecutive

-out-of-n and

-consecutive-

-out-of-n systems, it is necessary to evaluate the following probabilities:

()

Gera [51] managed to express the above quantities as follows:

()

where u[·], δ[·] are the unit step and delta function, respectively, and p(q) is the common reliability (unreliability) of the components, while

()

The following theorem gives the reliability of any subsystem including z elements of a combined

-consecutive

-out-of-n and

-consecutive-

-out-of-n systems.

Theorem 35 (Gera [51]). For combined -consecutive -out-of-n and -consecutive--out-of-n systems consisting of n independent and identical components with common reliability p, the reliability function of any subsystem including z elements is given as follows:

()

2.12. Linear m-Consecutive k-out-of-r-from-n: F Systems

Levitin and Dai [52] proposed a new reliability model that generalizes the linear r-within-consecutive-k-out-of-n: F system (or consecutive-k-out-of-r-from-n: F system) to the case of m consecutive overlapping runs of r elements. More specifically, the linear m-consecutive k-out-of-r-from-n: F system consists of n linearly ordered s-independent components and fails if and only if in each one of at least m consecutive overlapping groups of r consecutive elements at least k of them fail.

For the evaluation of the reliability function R of the aforementioned structure, Levitin and Dai [52] noticed that the following equality ensues

()

and developed an efficient algorithm for calculating the function R, by employing a procedure based on the universal z-transform (for more details about the universal moment generating function approach, the interested reader is referred to Ushakov [53]). It is noticeable that the linear m-consecutive k-out-of-r-from-n: F system meets interesting applications in different areas, such as heating systems’ modeling.

2.13. Linear m-Gap-Consecutive k-out-of-r-from-n: F Systems

Levitin [54] introduced a new reliability model that generalizes the linear r-within-consecutive-k-out-of-n: F system (or consecutive-k-out-of-r-from-n: F system). More specifically, the linear m-gap-consecutive k-out-of-r-from-n: F system consists of n linearly ordered, identical, and statistically independent components and fails if and only if the gap between any pair of groups of r consecutive elements containing at least k failed components is less than m components. For the evaluation of the reliability function of the aforementioned structure, Levitin [54] employed the universal moment generating function technique and deduced a recursive algorithm that leads to the exact value of system’s reliability.

2.14. Linear m-Consecutive-k, l-out-of-n: F Systems

Eryilmaz and Mahmoud [55] proposed a new reliability model that generalizes the linear m-consecutive-k-out-of-n: F system to the case of l-overlapping runs. More specifically, the linear m-consecutive k, l-out-of-n: F system consists of n linearly ordered components and fails if and only if there are at least ml-overlapping runs of k consecutive failed components (n ≥ m(k − l) + l, l < k). The number of l-overlapping runs of length k, each of which may have a part of length at most l overlapping with the previous run of length k. The inclusion of the new system parameter l provides flexibility for wider application of the model.

Moreover, Eryilmaz and Mahmoud [55] derived an explicit expression for the number of its path sets including a specified number of working components. More specifically, they proved the following result.

Theorem 36 (Eryilmaz and Mahmoud [55]). The number of path sets r_i(n) of a linear m-consecutive k, l-out-of-n: F system including i working components can be expressed as follows:

()

for n − z_ϕ ≤ i ≤ n, where z_ϕ denotes the maximum number of failed components such that the system can still work successfully, and the quantities C(β; a, r − a; m₁ − 1, m₂ − 1) can be calculated via the following formula (see, e.g., Makri et al. [56]):

()

Having at hand the above expression for r_i(n) and applying the well-known equalities for the evaluation of reliability and signature of a coherent system in terms of r_i(n) (see, e.g., Triantafyllou and Koutras [57]), one may easily compute these important characteristics of the linear m-consecutive k,l-out-of-n: F system.

2.15. Sparsely Connected Consecutive-k Systems

Zhao et al. [58] introduced generalized consecutive-k systems with sparse d. The consecutive failures with sparse d are defined as follows. When components are ordered in a line, two adjacent failed components have no failed components between them and the number of working components between the two failed components is equal to d; then the two failed components are called consecutive failures with sparse d. Zhao et al. [58] proposed the following reliability models:

(i)
The linear consecutive k-out-of-n: F system with sparse d, which consists of n linearly ordered components and fails if and only if there exist at least k consecutive failures with sparse d. For the aforementioned structure, Zhao et al. [58] employed the well-known Markov Chain Imbedding technique in order to achieve expressions for the reliability function of such systems. Moreover, Mohan et al. [59] proved that the generating function of the waiting time for the occurrence of the system failure is given as
()
Hence, the reliability function of the above structure can be expressed as
()
where ξ(u) is the coefficient of z^u in the power series expansion of the generating function .
(ii)
The m-consecutive k-out-of-n: F system with sparse d consists of n linearly ordered components and fails if and only if there exist at least m nonoverlapping runs of k consecutive failures with sparse d. For the aforementioned structure, Zhao et al. [58] employed the well-known Markov Chain Imbedding technique in order to achieve expressions for the reliability function of such systems. Moreover, Mohan et al. [59] proved that the generating function of the waiting time for the occurrence of the system failure is given as
()
(iii)
The linear (n, f, k): F system with sparse d consists of n linearly ordered components and fails if and only if there exist at least f total failures or at least k consecutive failures with sparse d. For the aforementioned structure, Zhao et al. [58] employed the well-known Markov Chain Imbedding technique in order to achieve expressions for the reliability function of such systems. Moreover, Mohan et al. [59] proposed an algorithm for the evaluation of the corresponding reliability function.

It is worth mentioning that, in case of d = 0, the consecutive-k systems with sparse d reduce to the ordinary consecutive k-out-of-n: F structures.

3. Applications

Applications of reliability models can range from electrical or engineering and mechanical field up to several contexts referring to humans’ activity. For example, an emergency backup power supply in a hospital or a power production at a specific voltage at the microscale may be viewed as direct implementations of reliability modeling. Moreover, double-loop computer networks, such as the daisy chain or the brained ring, can be studied through the lines of a reliability structure.

Let us consider a television screen characterized by a certain number of pixels and assume that the visual quality is not acceptable if and only if one of the following ensues:

(i)
there exist at least f failed pixels,
(ii)
there exist at least k consecutive failed pixels.

It is clear that the aforementioned device can be studied as an (n, f, k) system.

In addition, it is of some interest that vacuum systems in accelerators or belt conveyors in open-cast mining operate within the framework of the well-known consecutive k-out-of-n system. Among applications of k-out-of-n systems, the design of electronic circuits such as very large scale integrated (VLSI) and the automatic repairs of faults in an online system would be the most conspicuous. This type of structure consists of several parallel outputs channeled through a decision-making device that provides the required system function as long as at least a predetermined number k of n parallel outputs are in agreement.

It is worth mentioning that Kalyan and Kumar [60] studied in detail the redundancy optimization in consecutive k-out-of-n: F systems. More specifically, for a consecutive k-out-of-n structure that has a fluctuation of demand on the system performance, Kalyan and Kumar [60] considered extra resources in order to improve the system performance and developed alternative methods for the maximization of the structures’ reliability. It goes without saying that the reliability systems studied in the article of Kalyan and Kumar [60] can be classed under the so-called Protean systems.

Zhang et al. [61] presented an application of the well-known consecutive k-out-of-n: G system to a railroad operation. More specifically, they studied a railroad system consisting of 17 lines (numbered from 1 to 17), which was formulated as a reliability study of a linear consecutive k-out-of-n: G structure.

Zuo et al. [62] reported an application of k-out-of-n: F and consecutive-k-out-of-n: F systems in evaluation of the lifetime distribution of furnaces used in a petrochemical company. More precisely, different scenarios were investigated in modeling the reliability behaviors of the furnaces as a function of the reliabilities of the tubes used in the furnaces.

Lu and Liu [63] used the well-known k-out-of-n: G structure to quantify the reliability benefit of redundancy units in main circuit of prevailing static generators, called Static Synchronous Compensators (STATCOMs). The fundamental aim of applying a reliability study in the aforementioned operation is to maintain specific parameters of the electric power system by using the variation of the outputs of the so-called STATCOM and describe the effect of the redundancy technique to the total device reliability performance. More specifically, Lu and Liu [63] provided the probabilistic model of the 50 MVA STATCOM devices which were brought into operation at a certain substation in Shanghai, China.

Many safety-critical applications including nuclear power plants are equipped with k-out-of-n or specific-voting-logic redundant safety signal generation systems for ensuring both safety and economy. Kang and Kim [64] developed a quantification method for the evaluation of the unreliability of a reactor protection system (RPS), while several configurations of k-out-of-n models are investigated.

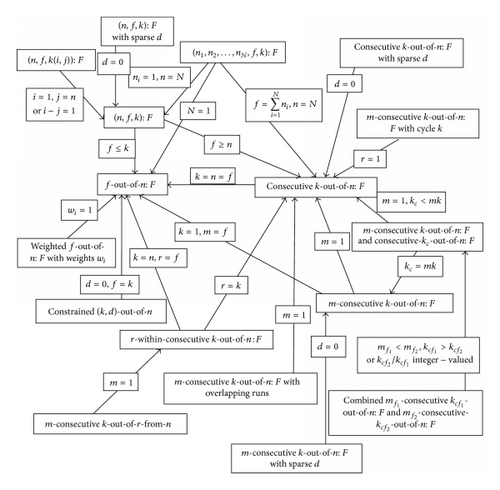
4. How Members of the Consecutive-Type Systems’ Family Are Connected

In the literature, there exist a lot of references that mark down the connection between two well-known reliability systems. It is really often for a newly introduced reliability structure to coincide with an older one under some specific restrictions concerning their design parameters. In this section, we attempt to harvest all information that refers to relations among all members of the generalized consecutive-type systems’ family.

Figure 1 displays for each system that is included in the consecutive-type systems’ family the way that is connected to one or more of its members. It goes without saying that both the k-out-of-n system and the consecutive k-out-of-n system play a crucial role in the aforementioned group of reliability structures. For example, based on Figure 1, one may easily observe that the constrained (k, d)-out-of-n system reduces to the well-known k-out-of-n structure if its design parameters are adjusted properly (e.g., d = 0, f = k).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Connection between members of the consecutive-type systems’ family.

Conflict of Interests

The author declares that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

The author is grateful to the Editor X. Li and the referees for their helpful comments and suggestions, which led to some improvements of the paper.

References

1 Kuo W. and Zuo M. J., Optimal Reliability Modeling: Principles and Applications, 2003, John Wiley & Sons, New York, NY, USA.
Google Scholar
2 Chang J. G., Cui L., and Hwang F. K., Reliabilities of Consecutive-k Systems, 2000, Kluwer Academic Publishers, Dordrecht, The Netherlands.
Google Scholar
3 Samaniego F. J., On closure of the IFR class under formation of coherent systems, IEEE Transactions on Reliability. (1985) R-34, no. 1, 69–72, https://doi.org/10.1109/tr.1985.5221935.
10.1109/TR.1985.5221935
Web of Science® Google Scholar
4 Navarro J. and Rychlik T., Reliability and expectation bounds for coherent systems with exchangeable components, Journal of Multivariate Analysis. (2007) 98, no. 1, 102–113, https://doi.org/10.1016/j.jmva.2005.09.003, ZBL1102.62111, 2-s2.0-33749992350.
10.1016/j.jmva.2005.09.003
Web of Science® Google Scholar
5 Kochar S., Mukerjee H., and Samaniego F. J., The signature of a coherent system and its application to comparisons among systems, Naval Research Logistics. (1999) 46, no. 5, 507–523, 2-s2.0-0010056619.
10.1002/(SICI)1520-6750(199908)46:5<507::AID-NAV4>3.0.CO;2-D
Web of Science® Google Scholar
6 Eryilmaz S. and Bayramoglu I., On extreme residual lives after the failure of the system, Mathematical Problems in Engineering. (2012) 2012, 11, 342940, https://doi.org/10.1155/2012/342940, 2-s2.0-84864919043.
10.1155/2012/342940
Web of Science® Google Scholar
7 Griffith W. S., A. P. Basu, On consecutive-k-out-of-n: failure systems and their generalizations, Reliability and Quality Control, 1986, Elsevier, Amsterdam, The Netherlands, 157–165.
Google Scholar
8 Papastavridis S., m-consecutive-k-out-of-n:F systems, IEEE Transactions on Reliability. (1990) 39, no. 3, 386–388, https://doi.org/10.1109/24.103024, 2-s2.0-0025469369.
10.1109/24.103024
Web of Science® Google Scholar
9 Alevizos P. D., Papastavridis S., and Sypsas P., H. Pham and M. H. Hamza, Reliability of cyclic m-consecutive-k-out-of-n:F system, Proceedings of the IASTED International Conference on Reliability, Quality Control and Risk Assessment, November 1992, Washington, DC, USA, 140–143.
Google Scholar
10 Makri F. S. and Philippou A. N., Exact reliability formulas for linear and circular m-consecutive-k-out-of-n:F systems, Microelectronics Reliability. (1996) 36, no. 5, 657–660, https://doi.org/10.1016/0026-2714(95)00153-0, 2-s2.0-0030148243.
10.1016/0026-2714(95)00153-0
Web of Science® Google Scholar
11 Godbole A. P., Approximate reliabilities of m-consecutive-k-out-of-n: failure systems, Statistica Sinica. (1993) 3, no. 2, 321–327, MR1243390.
Web of Science® Google Scholar
12 Eryilmaz S., Koutras M. V., and Triantafyllou I. S., Signature based analysis of m-consecutive-k-out-of-n: F systems with exchangeable components, Naval Research Logistics. (2011) 58, no. 4, 344–354, https://doi.org/10.1002/nav.20449, 2-s2.0-79954418701.
10.1002/nav.20449
Web of Science® Google Scholar
13 Koutras M. V., On a Markov chain approach for the study of reliability structures, Journal of Applied Probability. (1996) 33, no. 2, 357–367, https://doi.org/10.2307/3215059, MR1385345, ZBL0855.60069, 2-s2.0-0030523225.
10.2307/3215059
Web of Science® Google Scholar
14 Eryilmaz S., Component importance for linear consecutive-k-out-of-n and m-consecutive-k-out-of-n systems with exchangeable components, Naval Research Logistics. (2013) 60, no. 4, 313–320, https://doi.org/10.1002/nav.21535, MR3048000, 2-s2.0-84876688903.
10.1002/nav.21535
Web of Science® Google Scholar
15 Ghoraf N., On reliability of circular ‘r-consecutive-k-out-of-n: F systems’, International Journal of Reliability, Quality and Safety Engineering. (2013) 20, no. 4, 1350014, https://doi.org/10.1142/s0218539313500149.
10.1142/S0218539313500149
Google Scholar
16 Greenberg I., The first occurrence of n successes in N trials, Technometrics. (1970) 12, no. 3, 627–634, https://doi.org/10.2307/1267208.
10.1080/00401706.1970.10488702
Web of Science® Google Scholar
17 Saperstein B., On the occurrences of successes within N Bernoulli trials, Technometrics. (1973) 15, no. 4, 809–818.
10.2307/1267391
Web of Science® Google Scholar
18 Sfakianakis M., Kounias S., and Hillaris A., Reliability of a consecutive k-out-of-r-from-n:F system, IEEE Transactions on Reliability. (1992) 41, no. 3, 442–447, https://doi.org/10.1109/24.159817, ZBL0755.60071, 2-s2.0-0026926374.
10.1109/24.159817
Web of Science® Google Scholar
19 Eryilmaz S., Consecutive k-within-m-out-of-n:F system with nonidentical components, Mathematical Problems in Engineering. (2012) 2012, 8, 106359, https://doi.org/10.1155/2012/106359.
10.1155/2012/106359
Web of Science® Google Scholar
20 Eryilmaz S., Kan C., and Akici F., Consecutive k-within-m-out-of-n:F system with exchangeable components, Naval Research Logistics. (2009) 56, no. 6, 503–510, https://doi.org/10.1002/nav.20354, 2-s2.0-68949105668.
10.1002/nav.20354
Web of Science® Google Scholar
21 Papastavridis S. G. and Koutras M. V., Bounds for reliability of consecutive k-within-m-out-of-n:F systems, IEEE Transactions on Reliability. (1993) 42, no. 1, 156–160, https://doi.org/10.1109/24.210288, 2-s2.0-0027555825.
10.1109/24.210288
Web of Science® Google Scholar
22 Triantafyllou I. S. and Koutras M. V., Signature and IFR preservation of 2-within-consecutive k-out-of-n:F systems, IEEE Transactions on Reliability. (2011) 60, no. 1, 315–322, https://doi.org/10.1109/tr.2011.2105000, 2-s2.0-79952195670.
10.1109/TR.2011.2105000
Web of Science® Google Scholar
23 Kan C., Franko C., and Ozkut C. M., Reliability and some characteristics of circular consecutive-k-within-m-out-of-n:F system, Communications in Statistics: Simulation and Computation. (2014) 43, no. 5, 1078–1093, https://doi.org/10.1080/03610918.2012.725294, 2-s2.0-84887467954.
10.1080/03610918.2012.725294
Web of Science® Google Scholar
24 Tung S. S., Combinatorial analysis in determining reliability, Proceedings of the Annual Reliability And Maintainability Symposium, 1982, New York, NY, USA, 262–266.
Google Scholar
25 Zuo M. J., Lin D., and Wu Y., Reliability evaluation of combined k-out-of-n:F, consecutive-k-out-of-n:F and linear connected-(r, s)-out-of-(m, n):F system structures, IEEE Transactions on Reliability. (2000) 49, no. 1, 99–104, https://doi.org/10.1109/24.855542.
10.1109/24.855542
Web of Science® Google Scholar
26 Triantafyllou I. S. and Koutras M. V., Reliability properties of (n, f, k) systems, IEEE Transactions on Reliability. (2014) 63, no. 1, 357–366, https://doi.org/10.1109/tr.2014.2299495, 2-s2.0-84896314614.
10.1109/TR.2014.2299495
Web of Science® Google Scholar
27 Chang G. J., Cui L., and Hwang F. K., Reliabilities for (n, f, k) systems, Statistics & Probability Letters. (1999) 43, no. 3, 237–242, https://doi.org/10.1016/s0167-7152(98)00263-6, 2-s2.0-0005444973.
10.1016/S0167-7152(98)00263-6
Web of Science® Google Scholar
28 Eryilmaz S., Lifetime of combined k-out-of-n, and consecutive k_c-out-of-n systems, IEEE Transactions on Reliability. (2008) 57, no. 2, 331–335, https://doi.org/10.1109/tr.2008.920866, 2-s2.0-45549097727.
10.1109/TR.2008.920866
Web of Science® Google Scholar
29 Demir S., Reliability of combined k-out-of-n and consecutive-k_c-out-of-n:F systems of Markov dependent components, IEEE Transactions on Reliability. (2009) 58, no. 4, 691–693, https://doi.org/10.1109/tr.2009.2026816, 2-s2.0-77956340504.
10.1109/TR.2009.2026816
Web of Science® Google Scholar
30 Triantafyllou I. S., V. Zeimpekis, G. Kaimakamis, and N. J. Daras, Reliability study of military operations: methods and application, Military Logistics: Research Advances and Future Trends, 2015, 56, Springer, Berlin, Germany, 159–170, https://doi.org/10.1007/978-3-319-12075-1_9.
10.1007/978-3-319-12075-1_9
Google Scholar
31 Eryilmaz S. and Zuo M. J., Computing and applying the signature of a system with two common failure criteria, IEEE Transactions on Reliability. (2010) 59, no. 3, 576–580, https://doi.org/10.1109/TR.2010.2054170, 2-s2.0-77956342505.
10.1109/TR.2010.2054170
Web of Science® Google Scholar
32 Cui L., Kuo W., Li J., and Xie M., On the dual reliability systems of (n, f, k) and 〈n, f, k〉, Statistics & Probability Letters. (2006) 76, 1081–1088.
10.1016/j.spl.2005.12.004
Web of Science® Google Scholar
33 Eryilmaz S. and Aksoy T., Reliability of linear (n, f, k) systems with weighted components, Journal of Systems Science and Systems Engineering. (2010) 19, no. 3, 277–284, https://doi.org/10.1007/s11518-010-5131-0, 2-s2.0-77956874799.
10.1007/s11518-010-5131-0
Web of Science® Google Scholar
34 Gera A. E., Combined k-out-of-n:G, and consecutive k_c-out-of-n:G systems, IEEE Transactions on Reliability. (2004) 53, no. 4, 523–531, https://doi.org/10.1109/TR.2004.837524.
10.1109/TR.2004.837524
Web of Science® Google Scholar
35 Kamalja K. K., Birnbaum reliability importance for and system, Communications in Statistics: Theory & Methods. (2014) 43, 2406–2418.
10.1080/03610926.2012.749285
Web of Science® Google Scholar
36 Wu J.-S. and Chen R.-J., Algorithm for computing the reliability of weighted-k-out-of-n systems, IEEE Transactions on Reliability. (1994) 43, no. 2, 327–328, https://doi.org/10.1109/24.295016, 2-s2.0-0028449006.
10.1109/24.295016
Web of Science® Google Scholar
37 Chen Y. and Yang Q., Reliability of two-stage weighted-k-out-of-n systems with components in common, IEEE Transactions on Reliability. (2005) 54, no. 3, 431–440, https://doi.org/10.1109/tr.2005.853274, 2-s2.0-27844589484.
10.1109/TR.2005.853274
Web of Science® Google Scholar
38 Eryilmaz S., On reliability analysis of a k-out-of-n system with components having random weights, Reliability Engineering and System Safety. (2013) 109, 41–44, https://doi.org/10.1016/j.ress.2012.07.010, 2-s2.0-84866304131.
10.1016/j.ress.2012.07.010
Web of Science® Google Scholar
39 Li W. and Zuo M. J., Reliability evaluation of multi-state weighted k-out-of-n systems, Reliability Engineering and System Safety. (2008) 93, no. 1, 160–167, https://doi.org/10.1016/j.ress.2006.11.009, 2-s2.0-34548574666.
10.1016/j.ress.2006.11.009
Web of Science® Google Scholar
40 Samaniego F. J. and Shaked M., Systems with weighted components, Statistics & Probability Letters. (2008) 78, no. 6, 815–823, https://doi.org/10.1016/j.spl.2007.09.049, 2-s2.0-40749146836.
10.1016/j.spl.2007.09.049
Web of Science® Google Scholar
41 Cui L. and Xie M., On a generalized k-out-of-n system and its reliability, International Journal of Systems Science. (2005) 36, no. 5, 267–274, https://doi.org/10.1080/00207720500062470, 2-s2.0-27844446678.
10.1080/00207720500062470
Web of Science® Google Scholar
42 Guo Y., Cui L., Li J., and Gao S., Reliabilities for and systems, Communication in Statistics: Theory & Methods. (2006) 35, 1779–1789.
10.1080/03610920600728419
Web of Science® Google Scholar
43 Boland P. J. and Papastavridis S., Consecutive k-out-of-n:F systems with cycle k, Statistics & Probability Letters. (1999) 44, no. 2, 155–160, https://doi.org/10.1016/s0167-7152(99)00003-6, 2-s2.0-0042597515.
10.1016/S0167-7152(99)00003-6
Web of Science® Google Scholar
44 Agarwal M. and Mohan P., GERT analysis of m-consecutive-k-out-of-n:F system with overlapping runs and (k-1)-step Markov dependence, International Journal of Operational Research. (2008) 3, no. 1-2, 36–51, https://doi.org/10.1504/ijor.2008.016153, 2-s2.0-42049096745.
10.1504/IJOR.2008.016153
Google Scholar
45 Eryilmaz S., m-consecutive-k-out-of-n:F system with overlapping runs: signature-based reliability analysis, International Journal of Operational Research. (2012) 15, no. 1, 64–73, https://doi.org/10.1504/ijor.2012.048292, 2-s2.0-84864686251.
10.1504/IJOR.2012.048292
Google Scholar
46 Boland P. J., Signatures of indirect majority systems, Journal of Applied Probability. (2001) 38, no. 2, 597–603, https://doi.org/10.1239/jap/996986765, MR1834763, 2-s2.0-0035638851.
10.1239/jap/996986765
Web of Science® Google Scholar
47 Mohan P., Agarwal M., and Sen K., Combined m-consecutive-k-out-of-n: F and consecutive-k_c-out-of-n: F Systems, IEEE Transactions on Reliability. (2009) 58, 328–337.
10.1109/TR.2009.2020119
Web of Science® Google Scholar
48 Sen K., Agarwal M., and Mohan P., A. S. Gupta, T. Samanta, and A. Basu, GERT analysis of consecutive-k systems: an overview, Statistical Paradigms: Recent advances and Reconciliations, 2015, World Scientific, Singapore, 293–280.
Google Scholar
49 Eryilmaz S., Reliability of combined m-consecutive-k-out-of-n:F and consecutive k_c-out-of-n systems, IEEE Transactions on Reliability. (2012) 61, 215–219, https://doi.org/10.1109/TR.2011.2182401.
10.1109/TR.2011.2182401
Web of Science® Google Scholar
50 Eryilmaz S. and Zuo M. J., Constrained (k, d)-out-of-n systems, International Journal of Systems Science. (2010) 41, no. 6, 679–685.
10.1080/00207720903144537
Web of Science® Google Scholar
51 Gera A. E., Combined m₁-consecutive-k_c1-out-of-n and m₂-consecutive-k_c2-out-of-n systems, IEEE Transactions on Reliability. (2011) 60, no. 2, 493–497, https://doi.org/10.1109/TR.2011.2136550.
10.1109/TR.2011.2136550
Web of Science® Google Scholar
52 Levitin G. and Dai Y., Linear m-consecutive k-out-of-r-from-n:F systems, IEEE Transactions on Reliability. (2011) 60, no. 3, 640–646, https://doi.org/10.1109/TR.2011.2160670.
10.1109/TR.2011.2160670
Web of Science® Google Scholar
53 Ushakov I., Universal generating function, Soviet Journal of Computer and Systems Sciences. (1986) 24, 118–129.
Web of Science® Google Scholar
54 Levitin G., Linear m-gap-consecutive k-out-of-r-from-n:F systems, Reliability Engineering and System Safety. (2011) 96, no. 2, 292–298, https://doi.org/10.1016/j.ress.2010.09.009, 2-s2.0-78751575306.
10.1016/j.ress.2010.09.009
Web of Science® Google Scholar
55 Eryilmaz S. and Mahmoud B., Linear m-consecutive-k, l-out-of-n:F system, IEEE Transactions on Reliability. (2012) 61, no. 3, 787–791, https://doi.org/10.1109/TR.2012.2207573.
10.1109/TR.2012.2207573
Web of Science® Google Scholar
56 Makri F. S., Philippou A. N., and Psillakis Z. M., Polya, inverse Polya, and circular Polya distributions of order k for l-overlapping success runs, Communications in Statistics: Theory & Methods. (2007) 36, no. 4, 657–668, https://doi.org/10.1080/03610920601033942, 2-s2.0-33947203574.
10.1080/03610920601033942
Web of Science® Google Scholar
57 Triantafyllou I. S. and Koutras M. V., On the signature of coherent systems and applications, Probability in the Engineering and Informational Sciences. (2008) 22, no. 1, 19–35, https://doi.org/10.1017/s0269964808000028, 2-s2.0-37349047076.
10.1017/S0269964808000028
Web of Science® Google Scholar
58 Zhao X., Cui L., and Kuo W., Reliability for sparsely connected consecutive-k systems, IEEE Transactions on Reliability. (2007) 56, no. 3, 516–524, https://doi.org/10.1109/tr.2007.903202, 2-s2.0-34548615729.
10.1109/TR.2007.903202
Web of Science® Google Scholar
59 Mohan P., Agarwal M., and Sen K., R. Kang, H. Huang, M. J. Zuo, and Q. Mioo, Reliability analysis of sparsely connected consecutive-k systems: GERT approach, Proceedings of the 8th International Conference on Reliability, Maintainability and Safety (ICRMS ′09), July 2009, Chengdu, China, IEEE, 213–218, https://doi.org/10.1109/ICRMS.2009.5270207.
10.1109/ICRMS.2009.5270207
Google Scholar
60 Kalyan R. and Kumar S., A study of protean systems-redundancy optimization in consecutive-k-out-of-n:F systems, Microelectronics Reliability. (1990) 30, 635–638.
10.1016/0026-2714(90)90164-I
Web of Science® Google Scholar
61 Zhang W., Miller C., and Kuo W., Application and analysis for a consecutive-k-out-of-n:G structure, Reliability Engineering and System Safety. (1991) 33, no. 2, 189–197, https://doi.org/10.1016/0951-8320(91)90058-f, 2-s2.0-0025794476.
10.1016/0951-8320(91)90058-F
Web of Science® Google Scholar
62 Zuo M., Chiovelli S., and Huang J., Reliability evaluation of furnace systems, Reliability Engineering and System Safety. (1999) 65, no. 3, 283–287, https://doi.org/10.1016/S0951-8320(99)00008-3, 2-s2.0-0032624637.
10.1016/S0951-8320(99)00008-3
Web of Science® Google Scholar
63 Lu Z. and Liu W., Reliability evaluation of STATCOM based on the k-out-of-n: G model, Proceedings of the International Conference on Power System Technology (PowerCon ′06), October 2006, Chongqing, China, IEEE, 1–6, https://doi.org/10.1109/icpst.2006.321765, 2-s2.0-43549117960.
10.1109/icpst.2006.321765
Google Scholar
64 Kang H. G. and Kim H. E., Unavailability and spurious operation probability of k-out-of-n reactor protection systems in consideration of CCF, Annals of Nuclear Energy. (2012) 49, 102–108, https://doi.org/10.1016/j.anucene.2012.06.012, 2-s2.0-84864741850.
10.1016/j.anucene.2012.06.012
CAS Web of Science® Google Scholar

Citing Literature

All articles

Consecutive-Type Reliability Systems: An Overview and Some Applications

Abstract

1. Introduction

2. Family of Consecutive-Type Reliability Systems

2.1. m-Consecutive-k-out-of-n: F Systems

2.1.1. Recursive Schemes for the Reliability of m-Consecutive-k-out-of-n: F Systems

2.1.2. Exact Formulas for the Reliability of m-Consecutive-k-out-of-n: F Systems

2.1.3. Approximations for the Reliability of m-Consecutive-k-out-of-n: F Systems

2.1.4. Signature Vector of m-Consecutive-k-out-of-n: F Systems

2.1.5. Additional Results for m-Consecutive-k-out-of-n: F Systems

2.2. r-within-Consecutive-k-out-of-n: F Systems

2.2.1. Recursive Schemes for the Reliability of r-within-Consecutive-k-out-of-n: F Systems

2.2.2. Exact Formulas for the Reliability of r-within-Consecutive-k-out-of-n: F Systems

2.2.3. Approximations for the Reliability of r-within-Consecutive-k-out-of-n: F Systems

2.2.4. Signature Vector of r-within-Consecutive-k-out-of-n: F Systems

2.3. (n, f, k) Systems

2.3.1. Recursive Schemes for the Reliability of (n, f, k) Systems

2.3.2. Exact Formulas for the Reliability of (n, f, k) Systems

2.3.3. Signature Vector of (n, f, k) Systems

2.4. Reliability Systems with Weighted Components

2.4.1. Weighted k-out-of-n Systems

2.4.2. Consecutive Weighted k-out-of-n Systems

2.5. ((n1, n2, …, nN), f, k) Systems

2.6. (n, f, k(i, j)) and 〈n, f, k(i, j)〉 Systems

2.7. Consecutive k-out-of-n: F Systems with Cycle k

2.8. m-Consecutive k-out-of-n: F Systems with Overlapping Runs

2.9. Combined m-Consecutive k-out-of-n: F and Consecutive-kc-out-of-n: F Systems

2.10. Constrained (k, d)-out-of-n Systems

2.11. Combined -Consecutive -out-of-n and -Consecutive--out-of-n Systems

2.12. Linear m-Consecutive k-out-of-r-from-n: F Systems

2.13. Linear m-Gap-Consecutive k-out-of-r-from-n: F Systems

2.14. Linear m-Consecutive-k, l-out-of-n: F Systems

2.15. Sparsely Connected Consecutive-k Systems

3. Applications

4. How Members of the Consecutive-Type Systems’ Family Are Connected

Conflict of Interests

Acknowledgments

References

Citing Literature

Figures

References

Related

Information

2.5. ((n₁, n₂, …, n_N), f, k) Systems

2.9. Combined m-Consecutive k-out-of-n: F and Consecutive-k_c-out-of-n: F Systems